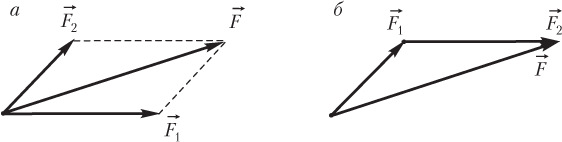Содержание
- Формула равнодействующей всех сил
- Второй закон Ньютона и формула модуля равнодействующей
- Примеры задач с решением
- О причинах изменений
- Сложение сил
- Задачи
- Что мы узнали?
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
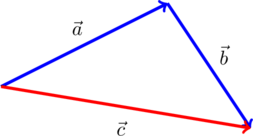
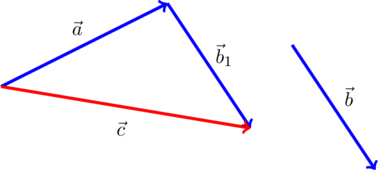
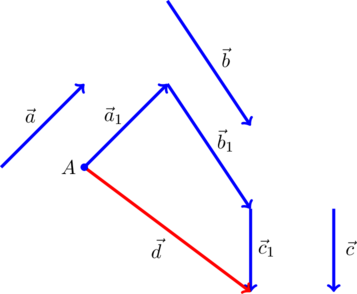
Складывают векторы, используя правило треугольника (рис.1)
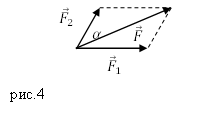
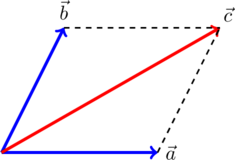
правило параллелограмма (рис.2).
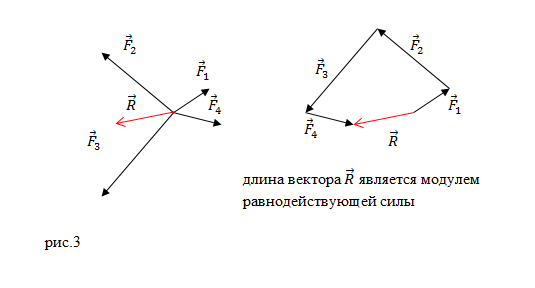
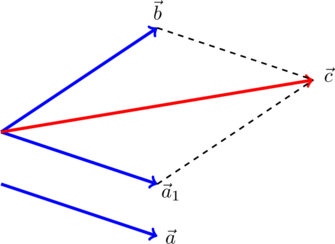
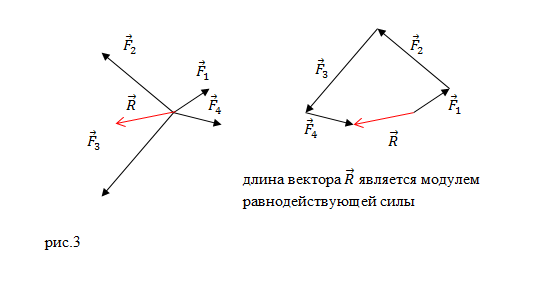
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
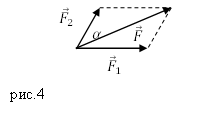
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Н
ight).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).
Сложение сил
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:
$mvec a = sumlimits_^n vec F_i$.
Рис. 1. Равнодействующая сил.
Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:
$F = sumlimits_^n vec F_i$
А силу $F_i$ представим в виде:
Тогда суммой двух сил будет новый вектор $F_ = (F_ + F_, F_ + F_, F_ + F_)$.
Рис. 2. Покомпонентное сложение векторов.
Абсолютное значение равнодействующей можно рассчитать так:
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Рис. 3. Правило треугольника и параллелограмма.
Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
Решение
Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.
$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:
Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.
Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.
Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Силу, заменяющую собой действие на тело нескольких сил, называют равнодействующей ; равнодействующая сила равна векторной сумме сил, приложенных к данному телу:
F → = F → 1 + F → 2 + . + F → N ,
где F → 1 , F → 2 , . F → N — силы, приложенные к данному телу.
Равнодействующую двух сил удобно находить графически по правилу параллелограмма (рис. 2.14, а ) или треугольника (рис. 2.14, б ).
Для сложения нескольких сил (вычисления равнодействующей) используют следующий алгоритм :
1) вводят систему координат и записывают проекции всех сил на координатные оси:
F 1 x , F 2 x , . F Nx ,
F 1 y , F 2 y , . F Ny ;
2) вычисляют проекции равнодействующей как алгебраическую сумму проекций сил:
F x = F 1 x + F 2 x + . + F Nx ,
F y = F 1 y + F 2 y + . + F Ny ;
3) модуль равнодействующей вычисляют по формуле
F = F x 2 + F y 2 .
Рассмотрим частные случаи равнодействующей.
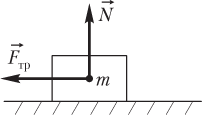
Силу взаимодействия тела с горизонтальной опорой , по которой может происходить движение тела, рассчитывают как равнодействующую силы трения и силы реакции опоры (рис. 2.15):
F → вз = F → тр + N → ,
ее модуль вычисляется по формуле
F вз = F тр 2 + N 2 ,
где F → тр — сила трения скольжения или покоя; N → — сила реакции опоры.
Частные случаи равнодействующей:
Силу взаимодействия тела с комбинированной опорой (например, креслом автомобиля, самолета и т.п.) рассчитывают как равнодействующую сил давления на вертикальную и горизонтальную части опоры (рис. 2.16):
F → вз = F → гор + F → верт ,
где F → гор — сила давления, действующая на тело со стороны горизонтальной части опоры (численно равная весу тела); F → верт — сила давления, действующая на тело со стороны вертикальной части опоры (численно равная силе инерции).
Частные случаи равнодействующей:
Равнодействующая силы тяжести и силы Архимеда называется подъемной силой (рис. 2.17):
F → под = F → А + m g → ,
ее модуль вычисляется по формуле
F под = F А − m g ,
где F → А — сила Архимеда (выталкивающая сила); m g → — сила тяжести.
Частные случаи равнодействующей:
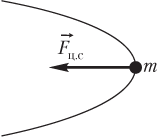
Если под влиянием нескольких сил тело равномерно движется по окружности, то равнодействующая всех приложенных к телу сил является центростремительной силой (рис. 2.18):
F → ц .с = F → 1 + F → 2 + . + F → N .
где F → 1 , F → 2 , . F → N — силы, приложенные к телу.
Модуль центростремительной силы, направленной по радиусу к центру окружности, может быть вычислен по одной из формул:
F ц .с = m v 2 R , F ц .с = m ω 2 R , F ц .с = m v ω ,
где m — масса тела; v — модуль линейной скорости тела; ω — величина угловой скорости; R — радиус окружности.
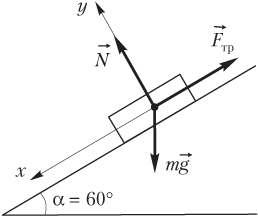
Пример 21. По дну водоема, наклоненному под углом 60° к горизонту, начинает скользить тело массой 10 кг, полностью находящееся в воде. Найти модуль равнодействующей всех сил, приложенных к телу, если между телом и дном водоема воды нет, а коэффициент трения составляет 0,15.
Решение. Так как между телом и дном водяная прослойка отсутствует, то сила Архимеда на тело не действует.
Искомой величиной является модуль векторной суммы всех сил, приложенных к телу:
F → = F → тр + m g → + N → ,
где N → — сила нормальной реакции опоры; m g → — сила тяжести; F → тр — сила трения. Указанные силы и система координат изображены на рисунке.
Вычисление модуля результирующей силы F проведем в соответствии с алгоритмом.
1. Определим проекции сил, приложенных к телу, на координатные оси:
проекция силы трения
F тр x = − F тр = − μ N ;
проекция силы тяжести
( m g ) x = m g sin 60 ° = 0,5 3 m g ;
проекция силы реакции опоры
проекция силы трения
проекция силы тяжести
( m g ) y = − m g cos 60 ° = − 0,5 m g ;
проекция силы реакции опоры
где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения.
2. Вычислим проекции равнодействующей на координатные оси, суммируя соответствующие проекции указанных сил:
F x = F тр x + ( m g ) x = − μ N + 0,5 3 m g ;
F y = ( m g ) y + N y = − 0,5 m g + N .
Движение по оси Oy отсутствует, т.е. F y = 0, или, в явном виде:
Отсюда следует, что
что позволяет получить формулу для расчета силы трения:
F тр = μ N = 0,5 μ m g .
3. Искомое значение равнодействующей:
F = F x 2 + F y 2 = | F x | = − 0,5 μ m g + 0,5 3 m g = 0,5 m g ( 3 − μ ) .
F = 0,5 ⋅ 10 ⋅ 10 ( 3 − 0,15 ) = 79 Н.
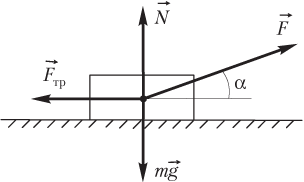
Пример 22. Тело массой 2,5 кг движется горизонтально под действием силы, равной 45 Н и направленной под углом 30° к горизонту. Определить величину силы взаимодействия тела с поверхностью, если коэффициент трения скольжения равен 0,5.
Решение. Силу взаимодействия тела и опоры найдем как равнодействующую силы трения F → тр и силы нормальной реакции опоры N → :
F → вз = F → тр + N → ,
модуль которой определяется формулой
F вз = F тр 2 + N 2 .
Силы, приложенные к телу, показаны на рисунке.
Модуль силы нормальной реакции опоры определяется формулой
N = m g − F sin 30 ° ,
а модуль силы трения скольжения —
где m — масса тела; g — модуль ускорения свободного падения; µ — коэффициент трения; F — модуль силы, вызывающей движение тела.
С учетом выражений для N и F тр формула для расчета искомой силы принимает вид:
F вз = ( μ N ) 2 + N 2 = N μ 2 + 1 = ( m g − F sin 30 ° ) μ 2 + 1 .
F вз = ( 2,5 ⋅ 10 − 45 ⋅ 0,5 ) ( 0,5 ) 2 + 1 ≈ 2,8 Н.
Пример 23. Во сколько раз изменится подъемная сила, если с аэростата сбросить балласт, равный половине его массы? Плотность воздуха считать равной 1,3 кг/м 3 , массу аэростата с балластом — 50 кг. Объем аэростата составляет 50 м 3 .
Решение. Подъемная сила, действующая на аэростат, является равнодействующей силы Архимеда F → А и силы тяжести m g → :
F → под = F → А + m g → ,
модуль которой определяется формулой
где F A = ρ возд gV — модуль силы Архимеда; ρ возд — плотность воздуха; g — модуль ускорения свободного падения; V — объем аэростата; m — масса аэростата (с балластом или без него).
Модуль подъемной силы может быть рассчитан по формулам:
- для аэростата с балластом
F под 1 = ρ возд g V − m 1 g ,
- для аэростата без балласта
F под 2 = ρ возд g V − m 2 g ,
где m 1 — масса аэростата с балластом; m 2 — масса аэростата без балласта.
Искомое отношение модулей подъемных сил составляет
F под 2 F под 1 = ρ возд V − m 2 ρ возд V − m 1 = 1,3 ⋅ 50 − 25 1,3 ⋅ 50 − 50 ≈ 2,7 .
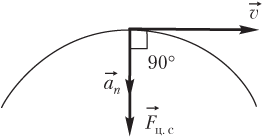
Пример 24. Модуль равнодействующей всех сил, действующих на тело, равен 2,5 Н. Определить в градусах угол между векторами скорости и ускорения, если известно, что модуль скорости остается постоянным.
Решение. Скорость тела не изменяется по величине. Следовательно, тело обладает только нормальной составляющей ускорения a → n ≠ 0 . Такой случай реализуется при равномерном движении тела по окружности.
Равнодействующая всех сил, приложенных к телу, является центростремительной силой и показана на рисунке.
Векторы силы, скорости и ускорения имеют следующие направления:
- центростремительная сила F → ц .с направлена к центру окружности;
- вектор нормального ускорения a → n направлен так же, как и сила;
- вектор скорости v → направлен по касательной к траектории движения тела.
Следовательно, искомый угол между векторами скорости и ускорения равен 90°.
Как найти модуль силы действующей на тело
Содержание
- Формула равнодействующей всех сил
- Второй закон Ньютона и формула модуля равнодействующей
- Примеры задач с решением
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Н
ight).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок).
Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)
Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:
Таким образом, равнодействующая всех сил равна
а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?
Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.
«Систему отсчета считать инерциальной.» Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.
ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.
Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.
т.е. в инерциальной системе отсчёта нет силы трения?
и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?
Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.
Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.
Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол — 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.
Подскажите пожалуйста, где в моих рассуждениях ошибка?
Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.
Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.
а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!
Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с
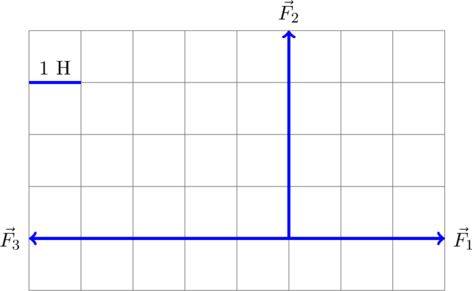
На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)
На рисунке обозначена равнодействующая векторов
и
Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора
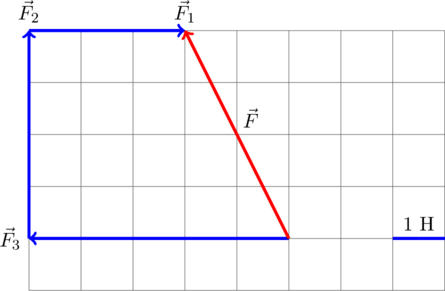
А как определили эту равнодействующую трёх сил, я понять не могу?!
Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).
Если сложить вектор и вектор
, получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор
. В результате и получается то, что показано красной стрелкой.
векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!
Когда Вы складываете параллельные вектора, у Вас просто получается «вырожденный треугольник». Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.
Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)
Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен
Под действием одной силы F1 тело движется с ускорением 4 м/с 2 . Под действием другой силы F2, направленной противоположно силе F1, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F1 и F2? (Ответ дайте в метрах в секундах в квадрате.)
Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него:
Силы
и
по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением
Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)
Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен
в условии написано,что нужно найти вес тела.
а в решении модуль силы тяжести.
Как вес может измеряться в Ньютонах.
В условии ошибка(
Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.
Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.
Понятие «вес тела» введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.
Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?
Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.
Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.
Здесь сразу вспоминается детская задачка: «Что весит больше: килограмм пуха или килограмм свинца?» Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.
С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?
В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос 🙂 И если силой Архимеда в воздухе во всех обычных случаях можно пренебречь, а значит, на величину веса она особо повлиять не может, то для тела в жидкости это уже критично.
Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства 🙂
Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.
Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне «Ваш e-mail» должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.
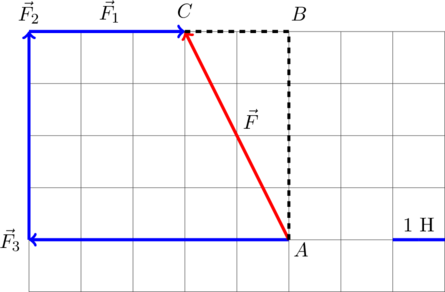
Задание 2. На рисунке показаны силы (в заданном масштабе), действующие на материальную точку. Сторона клетки соответствует 1 Н. Определите модуль равнодействующей приложенных к телу сил.
Сначала сложим силы F1 и F3. Так как они противоположно направлены, то получим результирующую силу, направленную как F3, но на одну клетку меньше (см. синяя линия на рисунке ниже).
Складывая полученную силу с силой F2, имеем результирующую силу, направление которой показано красной линией на рисунке. Модуль этой силы найдем по теореме Пифагора из прямоугольного треугольника с катетами 4 и 3:

Модуль равнодействующей силы
Четверг, 24 декабря, 2015
В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.
Как найти модуль равнодействующей силы
Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку.
Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.
1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы и
. Суммарный вектор есть вектор
:
Если векторы и
не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор
заменен на равный ему вектор
, и
:
2. Правило треугольника. На рисунке по правилу треугольника складываются векторы и
. В сумме получается вектор
:
Если вектор отложен не от конца вектора
, нужно заменить его равным и отложенным от конца вектора
, после чего воспользоваться правилом треугольника. Например, на рисунке вектор
заменен равным ему вектором
, и
:
3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки
в конец последнего отложенного вектора. На рисунке
:
Задача на нахождение модуля равнодействующей силы
Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.
Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:
Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник :
Требуется найти гипотенузу этого треугольника. «По клеточкам» находим длину катетов:
Н,
Н. Тогда по теореме Пифагора для этого треугольника получаем:
Н. То есть искомый модуль равнодействующей сил равен
Н.
Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!
Репетитор по физике на Юго-Западной
Сергей Валерьевич
Формула модуля равнодействующей силы в физике
Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(1right).]
Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
[overline{F}=sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(2right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
Пример 1
Задание. К материальной точке приложены силы, направленные под углом $alpha =60{}^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline{F}$ найдем, применяя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{40}^2+{20}^2+2cdot 40cdot 20{cos (60{}^circ ) }}approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Пример 2
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A{cos (omega t)(м) }$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
[overline{F}=moverline{a}left(2.1right).]
Следовательно, модуль силы можно найти как:
[F=ma left(2.2right).]
Ускорение точки будем искать, используя связь между ним и перемещением точки:
[a=frac{d^2s}{dt^2}left(2.3right).]
Первая производная от $s$ по времени равна:
[frac{ds}{dt}=frac{d}{dt}(A{cos (omega t))=-Aomega {rm sin}?(omega t) (м) }left(frac{м}{с}right)(2.4);;]
вторая производная:
[frac{d^2s}{dt^2}=-A{omega }^2{cos left(omega tright) } left(frac{м}{с^2}right)(2.5).]
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
[F=mA{omega }^2{cos left(omega tright) }left(Нright).]
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
[F_{max}=mA{omega }^2 left(Нright).]
Ответ. $F=mA{omega }^2{cos left(omega tright) }left(Нright); F_{max}=mA{omega }^2 left(Нright)$
Читать дальше: формула периода колебаний математического маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Как найти модуль силы
Сила является векторной величиной. Если вектор силы произвольно располагается в системе координат, его можно разделить на две или три составляющие. Зная их, найти модуль силы можно, руководствуясь теоремой Пифагора.

Инструкция
Вычислять модуль силы рационально не всегда. Если динамометр имеет конструкцию, допускающую расположение по диагонали, измерьте эту величину непосредственно.
Если же динамометр допускает присоединение к объекту лишь под прямыми углами или же он оборудован двумя датчиками, измеряющими все составляющие силы по координатам одновременно, запишите показания прибора по всем координатам. Если прибор устроен таким образом, что измеряет силу по разным координатам в разных единицах (такие измерители встречаются нечасто), переведите результаты всех измерений в одни и те же единицы. Некоторые многокоординатные динамометры индицируют не силы, а напряжения на выходах датчиков. Тогда нужно умножить их на калибровочные коэффициенты, указанные в таблице или предварительно определенные для каждого из датчиков экспериментально.
Обнаружив, что из двух или трех составляющих силы ненулевую величину имеет только одна, никаких вычислений не осуществляйте. Просто возьмите из результата соответствующего измерения модуль.
В случае же, если ненулевую величину имеют сразу две или три составляющие силы, возведите каждую из них в квадрат. Обратите внимание на тот факт, что после осуществления этой операции получатся положительные результаты, даже если исходные данные были отрицательными.
Результаты возведения составляющих силы в квадрат сложите между собой, а затем из полученной суммы извлеките квадратный корень. Это и будет модуль силы. Он будет выражен в тех же единицах, что и исходные данные, например, в ньютонах (Н) или килограммах силы (кгс).
Полученный модуль силы можно использовать в качестве исходного параметра при вычислении других связанных с ним физических величин. Например, чтобы вычислить давление, разделите его на площадь, к которой приложена сила. Если же разделить модуль силы на массу тела, получится ускорение.
Источники:
- модуль средней силы
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.