Электрон из состояния
покоя разгоняется в однородном электростатическом поле, модуль напряженности
которого 3,0 МВ/м. Определите модуль скорости электрона через 1,0 нс после
начала движения.
Решение.
В качестве физической
системы рассмотрим электрон. Если пренебречь взаимодействием электрона с
гравитационным, электрическим и магнитными полями Земли, а также предположить,
что он движется в вакууме, то разгон происходит только под действием
ускоряющего поля.
Поэтому движение электрона в инерциальной системе отсчета
можно описать вторым законом Ньютона и кинематическими законами
равноускоренного прямолинейного движения.
В качестве тела отсчета
возьмем лабораторию, ось OX направим в сторону
движения (т.е. против поля), выбрав начало координат в точке, из которой
электрон начал двигаться. Если спроецировать векторы, изображающие
соответствующие величины, на ось OX, с учетом того, что v0 = 0, получим:
ma
= eE, x = at2/2, v = at.
Откуда искомая скорость
v = eEt/m.
Подставив числовые
значения заряда и массы электрона, а также значения E и t, получим v = 5,3•108 м/с,
что больше скорости света в вакууме.
Так как ни в какой
системе отсчета тело не может двигаться со скоростью превышающей скорость света
в вакууме, то полученное значение скорости не может быть ответом задачи. Причиной
ошибки явилось неявно сделанное предположение о том, что движение электрона
может быть описано законами классической механики.
Изменение импульса тела
равно импульсу силы, действующей на него, т.е. Dp = FDt, не только в
классической, но и в релятивистской механике. Причем пот релятивистских
скоростях движения импульс тела p = gmv.
С учетом этого,
применительно к ситуации, описанной в задаче, теорему об изменении импульса
можно записать в виде: D(gmv)=eEDt.
Принимаем во внимание,
что Dv = v –
v0 = v, Dt = t – t0 = t (т.е. в момент времени t0 = 0 скорость v0 = 0).
Откуда находим модуль
искомой скорости электрона v.
Ответ: v = 2,6•108 м/с.
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Условие задачи:
Каким должен быть модуль скорости электрона, чтобы его движение было прямолинейным, когда он влетает во взаимно перпендикулярные электрическое поле с напряженностью 1 кВ/м и магнитное поле с индукцией 1 мТл?
Задача №8.2.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(E=1) кВ/м, (B=1) мТл, (upsilon-?)
Решение задачи:
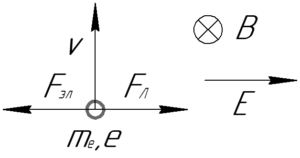
[{F_Л} = Bupsilon esin alpha ;;;;(1)]
Здесь (B) – индукция магнитного поля, (upsilon) – скорость электрона, (e) – модуль заряда электрона, (alpha) – угол между вектором скорости и вектором магнитной индукции. Угол (alpha) примем равным 90°, чтобы у нас не появилось неизвестной величины, хотя его величина может быть и другой, при этом электрон также будет двигаться равномерно.
Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.
Также на электрон со стороны электрического поля напряженностью (E) действует сила (F_{эл}), модуль которой можно определить по формуле:
[{F_{эл}} = Ee;;;;(2)]
Так как электрон имеет заряд отрицательного знака, то направление силы (F_{эл}) противоположно направлению вектора напряженности (E).
Электрон будет двигаться прямолинейно, если силы (F_Л) и (F_{эл}) будут равны, поэтому приравняем (1) и (2):
[Bupsilon esin alpha = Ee]
[Bupsilon sin alpha = E]
Откуда искомая скорость (upsilon) равна:
[upsilon = frac{E}{{Bsin alpha }}]
Посчитаем ответ:
[upsilon = frac{{1000}}{{{{10}^{ – 3}} cdot sin 90^circ }} = {10^6};м/с]
Ответ: 106 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.2.15 Электрон, имея скорость 2000 км/с, влетел в однородное магнитное поле с индукцией
8.2.17 Двухвалентный ион движется со скоростью 481 км/с в однородном магнитном поле
8.2.18 Циклотрон предназначен для ускорения протонов до энергии 5 МэВ. Определить
Закон движения электрона в магнитном поле
Содержание:
- Каково движение электрона в магнитном поле
-
Как найти скорость
- Траектория движения
- Период обращения электрона в магнитном поле
- Отклонение электронов в магнитном поле
- Примеры решения задач
Каково движение электрона в магнитном поле
Известно, что магниты представляют собой металлы, обладающие свойством к притяжению прочих магнитов и металлических предметов определенного состава. Во внутренней области таких объектов сгенерировано магнитное поле, действие которого можно наблюдать в реальных условиях. Эффект проявляется по-разному, то есть магнит отталкивает или притягивает предметы.
Роль источника, формирующего магнитное поле, играют заряженные частицы, которые пребывают в движении. Если перемещение зарядов обладает определенным направлением, то такой процесс называют электрическим током. Таким образом, легко сделать вывод об образовании магнитного поля, благодаря наличию электричества.
Электрический ток ориентирован по перемещению зарядов со знаком плюс и направлен противоположно относительно передвижения частиц, которые заряжены отрицательно. Если предположить, что имеется некая трубка в форме кольца с потоком воды, то какой-то ток примет противоположное ему направление. Электрический ток записывают с помощью буквы I.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если рассматривать металлические предметы, то в них образование тока связано с перемещением отрицательных зарядов. На наглядном изображении продемонстрировано передвижение частиц, заряженных отрицательно, то есть электронов, в левую сторону. В то время как электричество ориентировано в правую сторону.
Источник: habr.com
В начале исследований электричества ученые не обладали информацией о природе и свойствах носителей электрического тока. При рассмотрении аналогичного проводника слева, как на рисунке выше, можно заметить, что ток перемещается от наблюдателя, а магнитное поле окружает его по часовой стрелке.
Источник: habr.com
Эксперимент можно продолжить, используя компас. При размещении прибора около проводника, изображенного на схеме, произойдет разворот стрелки перпендикулярно относительно рассматриваемого проводника, параллельно по отношению к силовым линиям магнитного поля, то есть параллельно кольцевой стрелке, обозначенной черным цветом на изображении.
Представим, что имеется некий шарообразный предмет, заряженный положительно. Заряд со знаком плюс обусловлен недостаточным количеством электронов. Данному шарику можно задать направление путем подбрасывания вперед. В таком случае вокруг объекта сформируется аналогичное предыдущему примеру магнитное поле кольцевого типа, которое закручивается вокруг шарика по направлению часовой стрелки.
Источник: habr.com
В данном случае заряженные частицы перемещаются в определенном направлении. Таким образом, целесообразно сделать вывод о наличии электрического тока. В результате при возникновении электричества вокруг него формируется магнитное поле. Передвигающийся заряд, либо какое-то количество таких частиц, формирует около себя «тоннель» в виде магнитного поля. При этом стенки «тоннеля» более плотные около перемещающейся заряженной частицы.
Удаляясь от перемещающегося заряда, напряженность, то есть сила генерируемого магнитного поля, слабеет. В результате компасная стрелка меньше реагирует на него. Закон, согласно которому напряженность рассматриваемого поля распределяется около источника, аналогичен закономерности формирования электрического поля вокруг заряда. Таким образом, величина напряженности и квадрат расстояния до источника находятся в обратной пропорциональной зависимости.
Рассмотрим следующую ситуацию, когда шарик с положительным зарядом движется по траектории в форме круга. В таком случае кольцевые линии магнитных полей, сформированных вокруг предмета, складываются. В итоге получается магнитное поле, обладающее перпендикулярным направлением относительно плоскости, в рамках которой происходит движение заряженного шарика.
Источник: habr.com
Заметим, что «тоннель» магнитного поля, образованный около заряженного объекта, сворачивается, и получается кольцо, которое схоже по форме с бубликом. Аналогичную ситуацию можно наблюдать в процессе сворачивания в кольцо проводника с электричеством. Тогда проводник, деформированный так, что получается катушка с множеством витков, называют электромагнитом. Около подобного предмета формируются магнитные поля за счет перемещающихся в нем зарядов, то есть электронов.
При условии вращения шарика с зарядом вокруг собственной оси возникает магнитное поле по аналогии с тем, что образовано у нашей планеты, которое ориентировано вдоль оси вращательного движения. Тогда имеет место возникновение кругового электрического тока, который определяют как ток, провоцирующий образование магнитного поля во время перемещения по круговой траектории заряженной частицы относительно оси шарика.
Источник: habr.com
В этом случае процесс аналогичен перемещению шарика по кругу. Отличие состоит в том, что радиус орбиты движения уменьшен до величины радиуса шарообразного объекта. Вышеизложенные выводы имеют смысл и тогда, когда заряд шарика имеет знак минуса, а магнитное поле ориентировано противоположно.
Описанный выше эффект удалось выявить экспериментальным путем Роуланду и Эйхенвальду. Исследователи фиксировали магнитные поля около дисков, обладающих зарядом и совершающих вращательные движения. Вблизи этих объектов замечали отклонения компасной стрелки. Ознакомиться с наглядным представлением опыта можно на рисунке ниже:
Источник: habr.com
На изображении отмечены направления магнитных полей, которые зависят от положительного или отрицательного заряда дисков, расположенных в системе. По рисунку заметно, как эти направления меняются при смене знака заряда. Если диск, не обладающий зарядом, привести во вращательное движение, то магнитное поле отсутствует. Стационарные заряды также не образуют вокруг себя поля.
Как найти скорость
В плане изучения интересен процесс перемещения зарядов в пространственной области при наличии магнитного и электрического поля. Применительно к такой ситуации целесообразно воспользоваться соотношением для силы Лоренца, которая представляет собой суммарную величину сил, оказывающих воздействие на заряд, перемещающийся в электрическом и магнитном полях.
Представим, что заряд равен q и перемещается со скоростью (overrightarrow{v}) в условиях однородного магнитного поля, индукция которого составляет (overrightarrow{В}), а также в присутствии электрического поля с определенной напряженностью (overrightarrow{N}). Запишем силу воздействия электрического поля на заряд по модулю:
(Fэ = qE)
Этот компонент силы Лоренца принято называть электрической составляющей. Применительно к магнитному полю, на перемещающийся заряд воздействует магнитная составляющая силы Лоренца. Модуль определяют по закономерности Ампера. Представим, что проводник, по которому течет электричество, расположен в однородном магнитном поле. Вдоль этого объекта перемещаются заряды. Проанализирует ситуацию на отрезке данного проводника, который в длину составляет (triangle l), а площадь его поперечного сечения равна S.
Источник: иванов-ам.рф
Формула для вычисления силы тока, протекающего по проводнику:
(I = qnυS)
Зная, что:
(F_{А} = BItriangle l sin alpha)
Получим следующее выражение:
(FA = BqnvSΔtriangle l sin alpha)
Здесь (N = nStriangle l) обозначает количество зарядов, входящих в объем (Striangle l).
Исходя из записанной формулы, несложно выразить скорость движения заряда с учетом второго закона Ньютона:
(v = frac{qBR}{m})
Траектория движения
Изучить направление, в котором перемещаются заряженные частицы в магнитном поле, целесообразно на примере простейшего случая. При этом происходит движение заряда в однородном магнитном поле с индукцией, которая является перпендикуляром исходной скорости заряженной частицы. Схематично передвижение заряда изображено на рисунке:
Источник: иванов-ам.рф
В связи со стабильным значением модуля скорости заряда, не меняется модуль магнитной составляющей силы Лоренца по аналогии. Исходя из того, что рассматриваемая сила является перпендикуляром к скорости, можно заключить наличие центростремительного ускорения у перемещающейся частицы. Данная величина также не меняется по модулю, что позволяет сделать вывод о постоянстве радиуса кривизны R рассматриваемой траектории. Таким образом, подтверждается ранее выведенная формула скорости:
(v = frac{qBR}{m})
Период обращения электрона в магнитном поле
Запишем математическое соотношение, позволяющее выразить период обращения заряженной частицы в магнитном поле:
(T=frac{2 cdot{pi}cdot r}{upsilon};)
(r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B}.)
Отклонение электронов в магнитном поле
Из предыдущего анализа движения заряда известно, что процесс сопровождается воздействием на частицу, перемещающуюся в магнитном поле, силы Лоренца. Данная сила определяется величиной и знаком рассматриваемой частицы, а также зависит от быстроты ее перемещения и индукции магнитного поля. В итоге траектория, по которой движется заряд, изменяется. Опытным путем явление можно наблюдать с помощью системы магнитного поля и электронного луча осциллографа.
В ходе эксперимента необходимо выключить горизонтальную развертку луча и с помощью рукояток отрегулировать положение луча по вертикали и горизонтали. В результате последовательных манипуляций луч окажется направленным непосредственно в центральную область экрана. Следует расфокусировать образованное световое пятно, увеличивая яркость до максимально возможного значения. Если поместить рядом с прибором постоянный магнит, то можно наблюдать смещение пятна вбок, как изображено на рисунке:
Источник: duckproxy.com
Изменение положение пятна наблюдается в процессе приближения или удаления магнита от осциллографа. Таким образом, справедливо сделать вывод о том, что смещение пятна зависит от величины индукции магнитного поля. Если перевернуть магнит, то направление индукции изменится, а пятно на экране переместится в противоположную сторону.
Примеры решения задач
Задача 1
Созданы условия для движения электрона в однородном магнитном поле. Индукция данного поля составляет (B=4cdot {10}^{-3} {Тл}). Требуется вычислить, чему равен период обращения рассматриваемой отрицательно заряженной частицы.
Решение
В первую очередь следует записать данные из условия задачи. Так как речь в задании идет об электроне, то следует выписать справочные величины заряда и массы:
({q}_{e}=-1.6cdot {10}^{-19} {Кл})
({m}_{e}=9.1cdot {10}^{-31} {кг})
Вспомним формулу для расчета период обращения заряженной частицы в магнитном поле из ранее пройденного теоретического материала:
(T=frac{2 cdot{pi}cdot r}{upsilon}; r=frac{m cdot upsilon}{|q| cdot B} Rightarrow T=frac{2 cdot pi cdot m}{|q| cdot B})
Подставим численные значения и получим:
(T=frac{2 cdot 3.14 cdot 9.1cdot {10}^{-31},text{кг}}{|-1.6cdot {10}^{-19},text{Кл}| cdot 4cdot {10}^{-3},text{Тл}}=8.9cdot {10}^{-9},с)
Ответ: период обращения электрона в магнитном поле равен (8.9cdot {10}^{-9} с).
Задача 2
Имеется однородное магнитное поле, величина индукции которого составляет (10^{-3} Тл) . В это поле попадает отрицательно заряженная частица по направлению перпендикулярно относительно линий магнитной индукции и под углом (alpha=frac{pi}{4}) к границе рассматриваемого поля. Скорость электрона по модулю соответствует (10^{6} м/с). В направлении оси абсциссы и ординаты поле не имеет границ. Известно, что заряд частицы к ее массе относится как (frac{е}{m}=1,76cdot 10^{11} Кл/кг). Необходимо вычислить расстояние, на котором от точки взлета электрон покинет поле.
Решение
Изобразим схематично условие задания:
Источник: иванов-ам.рф
В данном случае целесообразно применить правило левой руки, чтобы определить направление силы Лоренца с учетом отрицательного заряда наблюдаемой частицы. Схематично это представлено на рисунке выше. В условиях воздействия магнитного поля электрон подвержен действию магнитной составляющей силы Лоренца. В результате отрицательно заряженная частица будет перемещаться по дуге окружности. Следует вычислить радиус этой окружности. Воспользуемся вторым законом Ньютона:
(moverrightarrow{a}=overrightarrow{F_{л}})
Поскольку центростремительное ускорение:
(а = frac{v^{2}}{R})
В результате получим, что:
(frac{mv^{2}}{R}=evB Rightarrow R=frac{mv}{eB})
При рассмотрении (triangle O^{,}OC) можно сделать вывод:
(OC = frac{l}{2} = R sin alpha)
Тогда:
(l = 2R sin alpha = 2frac{mv sin alpha}{eB})
При подстановке численных значений получим:
(l = frac{2cdot 10^{6} cdot sin frac{pi}{4}}{1,76 cdot 10^{11}cdot 10^{-3} } = 0,008м = 8 мм)
Ответ: 8 мм.
Electrons are one of the three basic constituents of atoms, the other two being protons and neutrons. Electrons are extremely small even by the standards of subatomic particles, with each having a mass of 9 × 10-31 kg.
Because electrons carry a net charge, the value of which is 1.6 × 10-19coulombs (C), they are accelerated in an electromagnetic field in a manner analogous to the way ordinary particles are accelerated by a gravitational field or other external force. If you know the value of this field’s potential difference, you can calculate the speed (or velocity) of an electron moving under its influence.
Step 1: Identify the Equation of Interest
You may recall that in everyday physics, the kinetic energy of an object in motion is equal to (0.5)mv2, where m equals mass and v equals velocity. The corresponding equation in electromagnetics is:
qV=0.5mv^2
where m = 9 × 10-31 kg and q, the charge of a single electron, is 1.6 × 10-19 C.
Step 2: Determine the Potential Difference Across the Field
You may have come to regard voltage as something pertaining to a motor or a battery. But in physics, voltage is a potential difference between different points in space within an electric field. Just as a ball rolls downhill or is carried downstream by a flowing river, an electron, being negatively charged, moves toward areas in the field that are positively charge, such as an anode.
Step 3: Solve for the Speed of the Electron
With the value of V in hand, you can rearrange the equation
qV=0.5mv^2
to
v=sqrt{frac{2qV}{m}}
For example, given V = 100 and the constants above, the speed of an electron in this field is:
v=sqrt{frac{2times 1.6times 10^{-19}times 100}{9times 10^{-31}}}=6times 10^6text{ m/s}
Как найти скорость электрона
Найти скорость ν электрона, прошедшего разность потенциалов U , равную 10 В
Дано:
Решение:
Закон сохранения энергии
С корость электрона
Ответ: 
Как рассчитать скорость электрона
Электроны являются одним из трех основных компонентов атомов, два других — протоны и нейтроны. Электроны чрезвычайно малы даже по меркам субатомных частиц, каждый из которых имеет массу 9 × 10 -31 кг.
Поскольку электроны несут суммарный заряд, величина которого составляет 1, 6 × 10 -19 кулонов (C), они ускоряются в электромагнитном поле аналогично тому, как обычные частицы ускоряются гравитационным полем или другой внешней силой. Если вы знаете значение разности потенциалов этого поля, вы можете рассчитать скорость (или скорость) электрона, движущегося под его влиянием.
Шаг 1: Определите уравнение интереса
Вы можете вспомнить, что в повседневной физике кинетическая энергия движущегося объекта равна (0, 5) mv 2 , где m равно массе, а v равно скорости. Соответствующее уравнение в электромагнитике имеет вид:
где m = 9 × 10 -31 кг и q, заряд одного электрона, составляет 1, 6 × 10 -19 С.
Шаг 2: Определить потенциальную разницу по полю
Возможно, вы стали рассматривать напряжение как нечто, относящееся к двигателю или батарее. Но в физике напряжение — это разность потенциалов между различными точками пространства в электрическом поле. Подобно тому, как шарик катится вниз или течет вниз по течению по течению реки, электрон с отрицательным зарядом движется к областям поля с положительным зарядом, таким как анод.
Шаг 3: Решите для скорости электрона
Имея значение V в руке, вы можете изменить уравнение
Например, учитывая V = 100 и приведенные выше константы, скорость электрона в этом поле равна:
Как рассчитать скорость воздуха
Скорость воздуха или скорость потока имеют единицы объема в единицу времени, например, галлонов в секунду или кубических метров в минуту. Это может быть измерено различными способами с использованием специализированного оборудования. Основное физическое уравнение скорости воздуха имеет вид Q = AV, где A = площадь, а V = линейная скорость.
Опишите четыре квантовых числа, используемых для характеристики электрона в атоме
Квантовые числа являются значениями, которые описывают энергию или энергетическое состояние электрона атома. Числа указывают спин электрона, энергию, магнитный момент и угловой момент. Согласно университету Пердью, квантовые числа происходят из модели Бора, уравнения Шредингера Hw = Ew, правил Хунда и .
Размер электрона по сравнению с атомом и хромосомой
Люди имеют естественную способность сравнивать и сопоставлять разные объекты. Принимая сенсорный вклад, люди могут классифицировать объекты и создавать ментальные модели мира. Но когда вы выходите за пределы нормального диапазона человеческого восприятия, эта классификация не так проста. Микроскопические объекты все маленькие. В .



