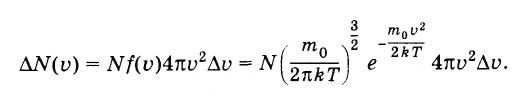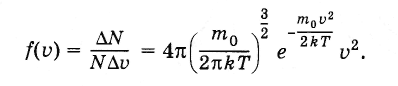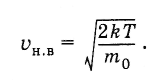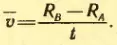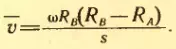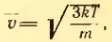Распределение модулей скоростей молекул
Найдем
среднее число молекул, скорости которых
по модулю лежат в интервале от v
до
v
+ Δv.
Распределение
Максвелла (4.6.4) определяет число молекул,
проекции скоростей которых лежат в
интервалах значений от vx
до
vx
+ Δvx,
от
vy
до
vy
+ Δvy,
от
vz
до
vz
+ Δvz.
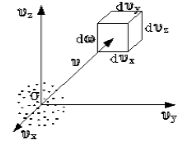
Векторы
этих скоростей оканчиваются внутри
объема ΔvxΔvyΔvz
(см. рис. 4.8). Таким образом задается
среднее число молекул, имеющих определенный
модуль и определенное направление
скоростей, задаваемые положением объема
ΔvxΔvyΔvz
в
пространстве скоростей.
Все
молекулы, модули скоростей которых
лежат в интервале от v
до
v
+
Δv,
располагаются в пространстве скоростей
внутри шарового слоя радиусом v
и
толщиной Δv
(рис. 4.10). Объем шарового слоя равен
произведению площади поверхности слоя
на его толщину: 4πv2Δv.
Число
молекул, находящихся внутри этого слоя
и, следовательно, обладающих заданными
значениями модуля скорости в интервале
от v
до
v
+ Δv,
может
быть найдено из формулы (4.6.2), если
заменить объем ΔvxΔvyΔvz
на
объем 4πv2Δv.
Рис. 4.10
Таким образом,
искомое среднее число молекул равно:
(4.6.7)
Так
как вероятность определенного значения
модуля скорости молекулы равна отношению
,
то для плотности вероятности получим:
(4.6.8)
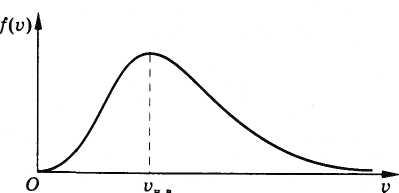
График,
выражающий зависимость этой функции
от скорости, показан на рисунке 4.11. Мы
видим, что функция f(v)
имеет
максимум уже не в нуле, как плотность
вероятности f(vx,
vy,
vz).
Причина
этого состоит в следующем. Плотность
точек, изображающих молекулы в пространстве
скоростей, по-прежнему будет наибольшей
вблизи v
=
0, но за счет роста объемов шаровых слоев
с увеличением модулей скоростей (~
v2)
происходит
увеличение функции f(v).
При
этом число точек внутри шарового слоя
растет быстрее, чем убывает функция
f(vx,
vy,
vz)
вследствие
уменьшения плотности точек.
Рис. 4.11
Можно
пояснить сказанное наглядным примером.
Допустим, обычную мишень с концентрическими
кругами обстреливает достаточно меткий
стрелок. Попадания пуль концентрируются
вокруг центра мишени. Плотность попаданий
— число попаданий на единицу площади
— будет максимальной вблизи центра
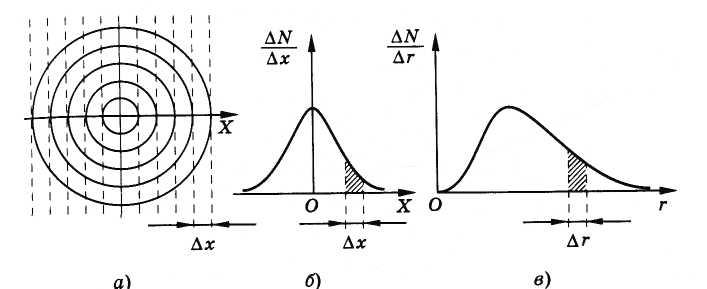
мишени. Разделим мишень на отдельные
узкие полоски шириной Ах (рис. 4.12, а).
Тогда отношение числа попаданий на
данную полоску к ее ширине будет
максимально вблизи центра мишени.
Зависимость отношения числа попаданий
в данную полоску к ее ширине имеет вид,
показанный на рисунке 4.12, б.
Здесь опять
получается гауссова кривая, как и для
распределения f(vx)
по проекциям
скоростей (см. рис. 4.9).
Рис. 4.12
Но
совсем другой результат получится, если
подсчитывать число попаданий в различные
кольца мишени. В этом случае отношение
числа попаданий в кольцо радиусом r
к
его ширине графически будет характеризоваться
кривой, изображенной на рисунке 4.12, в.
Хотя
плотность попаданий по мере удаления
от центра мишени убывает, но площади
колец растут пропорционально г, что и
приводит к смещению максимума кривой
от нуля.
Наиболее вероятная скорость молекул
Зная
формулу (4.6.8) для плотности вероятности
модулей скоростей молекул, можно найти
значение скорости, соответствующей
максимуму плотности этой вероятности*.
Скорость (ее называют наиболее
вероятной)
оказывается равной:
* Это делается по
правилам нахождения максимума известной
функции. Нужно вычислить производную
этой функции по скорости и приравнять
ее нулю.
(4.6.9)
Большинство молекул
имеют скорости, близкие к наиболее
вероятной (см. рис. 4.11).
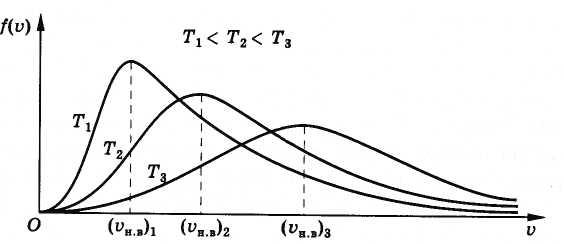
По
мере увеличения абсолютной температуры
Т
наиболее
вероятная скорость увеличивается и при
этом кривая зависимости f(u)
становится
все более сглаженной (рис. 4.13).
Рис. 4.13
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Средняя скорость теплового движения молекул. Уравнение (2.9) дает возможность найти среднюю скорость теплового движения молекул. Подставляя в это уравнение 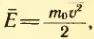

Отсюда средняя скорость молекулы (точнее, средняя квадратическая скорость) равна:

Вычисляя по формуле (2.12) скорость молекул, например азота, при t = 0°C, получим: 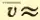
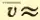
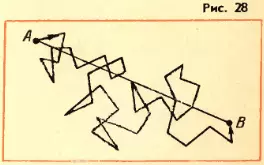
Когда впервые были получены эти числа (вторая половина XIX в.), многие физики были ошеломлены. Скорости молекул газа по расчетам оказались большими, чем скорости артиллерийских снарядов! Высказывали на этом основании даже сомнения в справедливости кинетической теории. Ведь известно, что запахи распространяются довольно медленно: нужно время порядка десятков секунд, чтобы запах духов, пролитых в одном углу комнаты, распространился до другого угла. Это нетрудно объяснить. Из-за столкновений молекул траектория каждой молекулы представляет собой запутанную ломаную линию (рис. 28). Большие скорости молекула имеет на прямолинейных отрезках ломаной. Перемещение же молекулы в каком либо направлении в среднем невелико даже за время нарядна нескольких минут. При перемещении молекулы из точки A в точку B пройденный ею путь оказывается гораздо больше расстояния |AB|.
Экспериментальное определение скоростей молекул. Опыты по определению скоростей молекул доказали справедливость формулы (2.12). Один из опытов был предложен Штерном в 1920 г.
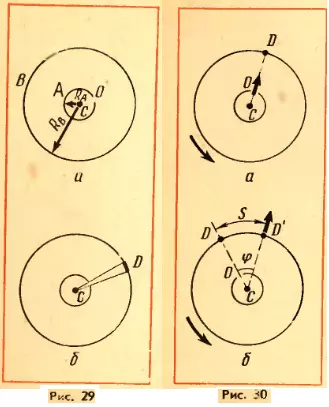
Прибор Штерна состоит из двух коаксиальных цилиндров А и В, жестко связанных друг с другом (рис. 29, а). Цилиндры могут вращаться с постоянной угловой скоростью. Вдоль оси малого цилиндра натянута тонкая платиновая проволочка C, покрытая слоем серебра. По проволочке пропускают электрический ток. В стенке этого цилиндра имеется узкая щель O. Воздух из цилиндров откачан. Цилиндр B находится при комнатной температуре.
Вначале прибор неподвижен. При прохождении тока по нити слой серебра испаряется и внутренний цилиндр заполняется газом из атомов серебра. Некоторые атомы пролетают через щель O и, достигнув внутренней поверхности цилиндра B, осаждаются на ней. В результате прямо против щели образуется узкая полоска серебра D (рис. 29, б).
Затем цилиндры приводит во вращение с угловой скоростью ω. Теперь за время t, необходимое атому для прохождения пути, равного разности радиусов цилиндров RB — RA, цилиндры повернутся на некоторый угол φ. В результате атомы, движущиеся с постоянной скоростью, попадут на внутреннюю поверхность большого цилиндра не прямо против щели O (рис. 30, а), а на некотором расстоянии s от конца радиуса, проходящего через середину щели (рис. 30, б). Ведь атомы движутся прямолинейно. Расстояние s равно:
s = φ RB = ωtRB (2.13)
В действительности не все атомы серебра имеют одну и ту же скорость. Поэтому расстояния s для различных атомов будут несколько различаться. Под s следует понимать расстояние между участками на полоскал D и D’ с наибольшей концентрацией атомов серебра. Этому расстоянию будет соответствовать средняя скорость атомов.
Средняя скорость атома равна:
Подставляя в эту формулу значение t из выражения (2.13), получим:
Зная ω, RA и RB и измеряя среднее смещение s полоски серебра, вызванное вращением прибора, находим среднюю скорость атомов серебра.
Модули скоростей, определенные из опыта, совпадают с теоретическим значением средней квадратической скорости. Это служит экспериментальным доказательством справедливости формулы (2.12), а следовательно и (2.9), согласно которой средняя кинетическая энергия молекулы прямо пропорциональна абсолютной температуре.
Средняя скорость броуновской частицы. Формула (2.12) позволяет понять почему интенсивность броуновского движения возрастает с повышением температуры жидкости и уменьшается при увеличении массы частицы. Ведь броуновская частица, участвует в тепловом движении молекул. Поэтому ее средняя кинетическая энергия также определяется формулой (2.9), а средняя квадратическая скорость — формулой
где m — масса броуновской частицы. Если масса частицы велике, то средняя скорость ее движения настолько мала, что движение частицы практически нельзя обнаружить.
1. Как изменится средняя квадратическая скорость движения молекул при увеличении температуры в 4 раза? 2. Какие молекулы в атмосфере движутся быстрее: молекулы азота или молекулы кислорода? 3. Почему толщина слоя полоски серебра на поверхности внешнего вращающегося цилиндра в опыте Штерна неодинакова по ширине полоски?
Значительная часть явлений молекулярной физики определяется скоростями молекул. Несмотря на это, нахождение скоростей молекул газа приобретает как теоретического, так и практического значения.
Виды скоростей молекул газа
Скорости газовых молекул в результате их хаотического движения отличаются как по величине, так и по направлению. Скорость данной молекулы газа в данный момент времени есть величина случайная. В молекулярно-кинетической теории газов пользуются понятиями средней (vv), средней квадратичной (vквv_{кв}) и наиболее вероятной (νHν_H) скоростей. Эти скорости задаются для равновесных состояний газа.
Средняя (или среднеарифметическая) скорость определяется уравнением
v=1n∑i=1nviv=frac{1}{n}sumlimits_{i=1}^{n}{{{v}_{i}}}
где viv_i – скорость ii-й молекулы;
nn –количество молекул.
Средняя квадратичная скорость определяется как:
vкв=v2=3kTm{{v}_{кв}}=sqrt{{{v}^{2}}}=sqrt{frac{3kT}{m}}
По этой формуле можно вычислить также скорость броуновских частиц. Конечно, при этом mm –масса броуновской частицы.
Выражению vквv_{кв} можно придать более удобный вид, умножив числитель и знаменатель под корнем на число Авогадро и учитывая, что kN=RkN = R и mN=МmN = М,
vкв=3RTM{{v}_{кв}}=sqrt{frac{3RT}{M}}
Среднюю квадратичную скорость называют еще тепловой. Значение vкв для газов достаточно велики. Так, для водорода при комнатной температуре vкв=1,9⋅103v_{кв} = 1,9 · 10^3 м/с, то есть около 2 км/с.
Тепловая скорость, как видно из уравнения, пропорциональна корню температуры и обратно пропорциональна корню массы. Это обстоятельство определяет, что тепловое движение– достаточно интенсивно для молекул, заметно для микроскопически малых частиц, которые осуществляют броуновское движение, и совершенно незаметно для тяжелых тел.
Экспериментальное определение скоростей газовых молекул
Большой интерес представляет непосредственное экспериментальное определение скоростей газовых молекул. Оно является прямым подтверждением многих результатов и положений молекулярно-кинетической теории. Впервые такое исследование провел А. Штерн в 1920 г. Источником атомов, скорость которых измерялась, в опыте Штерна был молекулярный пучок атомов серебра Ag. Схема установки приведены на рис. 1. На оси системы двух коаксиальных цилиндрических поверхностей натянуто платиновый провод, покрытый слоем серебра.
В других опытах использовали также висмут, кадмий, цезий.
Проволока разогревается электрическим током. Так, при температуре около 1300°С серебро с поверхности проволоки испаряется. Таким образом создавался линейный источник «Ag-лучей» и в камере цилиндров, воздух из которой предварительно откачивался при давлении 1,3 · 10-4 Па, образовывался одноатомный газ серебра. Часть атомов серебра через диафрагмы s1 и s2 проходила, образуя молекулярный пучок, к поверхности внешнего цилиндра, где оседала на прозрачной пластинке, создавая слой в виде узкой полосы.
Рис. 1
На первой стадии опыта Штерна установка находится в состоянии покоя. При достижении равновесного состояния (температура проволоки достигала определенного значения, которое определяли по её свечению) атомы серебра оседали у точки а1. На второй стадии опыта оба цилиндра приводились в достаточно быстрое вращение с частотой 41,7 с-1.
При этом атомы серебра, двигаясь в вакууме прямолинейно, оседали у точки b. Смещение полосы объясняется тем, что пока атомы серебра пролетают по инерции путь r, внешний цилиндр успевает вернуться на угол φ=ωtφ = ωt, то есть каждая точка внешнего цилиндра смещается на расстояние Δs=ωrtΔs = ωrt, где ωω –угловая скорость его вращения; tt –время, за который атомы серебра проходят путь r. Таким образом,
t=rv=Δsωrt=frac{r}{v}=frac{Delta s}{omega r}
где vv – скорость атомов серебра.
Отсюда
v=ωr2Δsv=frac{omega {{r}^{2}}}{Delta s}
Измеряя смещение полос атомов серебра ΔsΔs и угловую скорость вращения прибора, можно определить скорость атомов серебра. Она приблизительно описывалась выражением
(3,5kTm)12{{left( 3,5frac{kT}{m} right)}^{frac{1}{2}}}
что согласуется со средней скоростью молекул, которые определяются по формуле
v=8kTπmv=sqrt{frac{8kT}{pi m}}
Результаты опытов Штерна показали, что на самом деле картина структуры полосы сложнее.
Смещенная возле точки b полоса была не резко ограниченной, а размытой (рис. 2).
Рис. 2
Несмотря на то, что атомы серебра имеют разные скорости, более быстрым атомам должны соответствовать меньшие смещения, а тем более медленным – большие. Таким образом, результаты опыта Штерна вполне передают реальную картину теплового движения молекул.
Тест по теме «Скорость движения молекул»
Андрей Геннадьевич Блохин
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Закон распределения молекул по скоростям
Закон распределения молекул по скоростям описывает распределение частиц макроскопической системы при условии, что эта система находится в состоянии термодинамического равновесия, распределение является стационарным и внешние силы на систему не действуют. Данное распределение выполняется как для газов, так и жидкостей, если в них можно использовать законы классической механики.
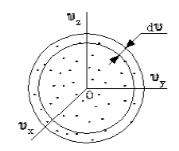
Определить, каким образом распределены молекулы по скоростям, — это значит ответить на вопрос: «сколько молекул имеет ту или иную скорость при заданной температуре в состоянии равновесия?» Для разъяснения вопроса введем понятие: «пространство скоростей» (рис.1). В таком пространстве на декартовых осях отложены не координаты, а проекции скоростей.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рис. 1
В таком случае поставленный вопрос изменится на вопрос о том, как распределены молекулы в пространстве скоростей. Понятно, что молекулы распределены неравномерно.
Если в пространстве скоростей выделить параллелепипед объема $dw=dv_xdv_ydv_z$, тогда количество молекул, которые попадут в него $dN_v.$ Предположим, что N- количество молекул газа, $f(v)$- некоторая функция скорости. Тогда
Распределение Максвелла
Как было отмечено, газ находится в состоянии равновесия, все направления движения частиц равноправны, следовательно, распределение молекул в пространстве скоростей можно считать сферически симметричным (рис.2).
Рис. 2
Найдем число молекул в шаровом слое $dv$:
Разделим (2) на число частиц (N) и найдем вероятность$ (dW_v)$ того, что модуль скорости молекулы находится в пределах от $v до v+dv$:
«Закон распределения молекул по скоростям» 👇
где $Fleft(vright)$- функция распределения вероятности значения $v. $Эту функцию теоретически получил Д. Максвелл.
Таким образом, распределение молекул по скоростям (вернее их модулям) запишем как:
[dN_v=N4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2dv left(5right),]
при этом $v=sqrt{{v_x}^2+{v_y}^2+{v_z}^2}$, $m_0$- масса молекулы, k — постоянная Больцмана.
Можно записать распределение Максвелла по проекциям скоростей:
[dN=Nfleft(v_xright)fleft(v_yright)fleft(v_zright)dv_xdv_ydv_{z }left(6right),]
при этом
[fleft(v_iright)={left(frac{m_0}{2pi kT}right)}^{frac{1}{2}}expleft(-frac{m_0{v_i}^2}{2kT}right) left(i=x,y,zright)left(7right),]
где $v_x,v_y,v_{z }$ — проекции скорости молекулы на оси координат.
Еще один из вариантов написания распределения Максвелла по модулям скоростей представлен в виде:
[dN=Nfrac{4}{sqrt{pi }{v_{ver}}^3}{exp left(-{left[frac{v}{v_{ver}}right]}^2v^2right) }dvleft(8right),]
где $v_{ver}$ — вероятнейшая скорость молекулы.
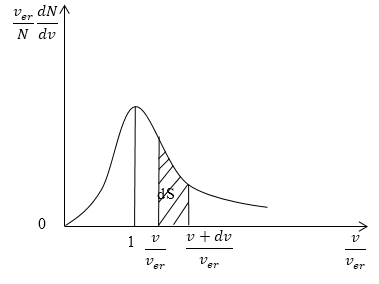
Рис. 3
На рисунке 3 изображена кривая закона распределения молекул по скоростям. Доля молекул газа, скорости которых лежат в интервале от $v до v+dv,$ пропорциональна заштрихованной площади dS под кривой.
Поскольку скорости всех молекул лежат в интервале от $0 до+infty $, то выполняется равенство:
[intnolimits^{infty }_0{fleft(vright)dv}=1 left(9right).]
Это так называемое условие нормировки функции распределения.
Таким образом, распределение Максвелла зависит от массы молекулы газа и его температуры. Давление и объем в распределение не входят.
Пример 1
Задание: Используя распределение Максвелла, найдите наиболее вероятную скорость молекул газа в равновесном состоянии газа при температуре T.
Решение:
За основу возьмем распределение молекул по модулям скоростей:
[dN_v=N4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}expleft(-frac{m_0v^2}{2kT}right)v^2dv left(1.1right).]
Наиболее вероятной скорости соответствует максимум функции, то продифференцируем выражение (1.1) по скорости и приравняем к нулю, получим:
[frac{dN_v}{dv}=N4pi {left(frac{m_0}{2pi kT}right)}^{frac{3}{2}}left[2v_{ver}expleft(-frac{m_0{v_{ver}}^2}{2kT}right)-{v_{ver}}^2frac{m_02v_{ver}}{2kT}expleft(-frac{m_0{v_{ver}}^2}{2kT}right)right]=0to ]
[2v_{ver}-{v_{ver}}^2frac{m_02v_{ver}}{2kT}=0to 1-{v_{ver}}^2frac{m_0}{2kT}=0to {v_{ver}}^2=frac{2kT}{m_0}]
[v_{ver}=sqrt{frac{2kT}{m_0}} (1.2)]
Ответ: Наиболее вероятная скорость молекул газа $v_{ver}=sqrt{frac{2kT}{m_0}}.$
Пример 2
Задание: Пусть $Т_1
Решение:
Из формулы для наиболее вероятной скорости молекул газа, полученной в предыдущем примере:
[v_{ver}=sqrt{frac{2kT}{m_0}} (2.1)]
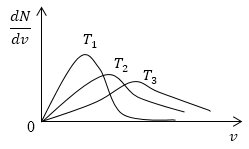
очевидно, что с увеличением температуры скорость растет, то есть максимум кривой смещается в сторону больших скоростей. Площадь под кривой распределения величина постоянная, следовательно, кривые изобразим следующим образом (рис.4).
Рис. 4
Пример 3
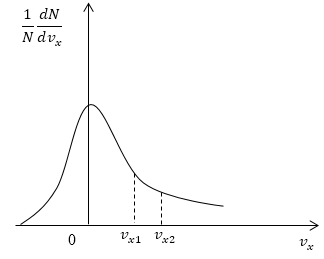
Задание: На рис. 5 представлен график функции распределения молекул по проекциям скорости $v_x$. Сравнить числа молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$и от $v_{x1}$ до $v_{x2}$.
Рис. 5
Решение:
Как уже отмечалось в теоретической части, доля молекул газа, скорости которых лежат в интервале от $0 до v_{x1},$ пропорциональна площади $S_1$ фигуры, которая ограничена кривой распределения, вертикальной осью (0$ frac{1}{N}frac{dN}{dv_x})$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей проходящей через точку $v_{x1}$. Во втором случае доля молекул газа, скорости которых лежат в интервале от $v_{x1} до v_{x2},$ пропорциональна площади $S_2$ фигуры, которая ограничена кривой распределения, вертикальной прямой параллельной оси (0$ frac{1}{N}frac{dN}{dv_x}), проходящей через точку v_{x1}$ и пунктирной вертикальной линией перпендикулярной оси проекций скоростей, проходящей через точку $v_{x2}$. Очевидно, что $S_1>S_2. $ Следовательно, молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_{x1}$ до $v_{x2}$.
Ответ: Молекул, имеющих проекции скорости в интервалах: от 0 до $v_{x1}$ больше, чем молекул, имеющих проекции скорости в интервалах: от $v_{x1}$ до $v_{x2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Идеальный газ в МКТ. Среднее значение квадрата скорости молекул
- Подробности
- Обновлено 13.08.2018 12:38
- Просмотров: 735
«Физика — 10 класс»
Вспомните, что такое физическая модель.
Можно ли определить скорость одной молекулы?
Идеальный газ.
У газа при обычных давлениях расстояние между молекулами во много раз превышает их размеры. В этом случае силы взаимодействия молекул пренебрежимо малы и кинетическая энергия молекул много больше потенциальной энергии взаимодействия. Молекулы газа можно рассматривать как материальные точки или очень маленькие твёрдые шарики. Вместо реального газа, между молекулами которого действуют силы взаимодействия, мы будем рассматривать его модель — идеальный газ.
Идеальный газ — это теоретическая модель газа, в которой не учитываются размеры молекул (они считаются материальными точками) и их взаимодействие между собой (за исключением случаев непосредственного столкновения).
Естественно, при столкновении молекул идеального газа на них действует сила отталкивания. Так как молекулы газа мы можем согласно модели считать материальными точками, то размерами молекул мы пренебрегаем, считая, что объём, который они занимают, гораздо меньше объёма сосуда.
В физической модели принимают во внимание лишь те свойства реальной системы, учёт которых совершенно необходим для объяснения исследуемых закономерностей поведения этой системы.
Ни одна модель не может передать все свойства системы. Сейчас нам предстоит решить задачу: вычислить с помощью молекулярно-кинетической теории давление идеального газа на стенки сосуда. Для этой задачи модель идеального газа оказывается вполне удовлетворительной. Она приводит к результатам, которые подтверждаются опытом.
Давление газа в молекулярно-кинетической теории.
Пусть газ находится в закрытом сосуде. Манометр показывает давление газа р0. Как возникает это давление?
Каждая молекула газа, ударяясь о стенку, в течение малого промежутка времени действует на неё с некоторой силой. В результате беспорядочных ударов о стенку давление быстро меняется со временем примерно так, как показано на рисунке 9.1. Однако действия, вызванные ударами отдельных молекул, настолько слабы, что манометром они не регистрируются. Манометр фиксирует среднюю по времени силу, действующую на каждую единицу площади поверхности его чувствительного элемента — мембраны. Несмотря на небольшие изменения давления, среднее значение давления р0 практически оказывается вполне определённой величиной, так как ударов о стенку очень много, а массы молекул очень малы.
Среднее давление имеет определённое значение как в газе, так и в жидкости. Но всегда происходят незначительные случайные отклонения от этого среднего значения. Чем меньше площадь поверхности тела, тем заметнее относительные изменения силы давления, действующей на данную площадь. Так, например, если участок поверхности тела имеет размер порядка нескольких диаметров молекулы, то действующая на неё сила давления меняется скачкообразно от нуля до некоторого значения при попадании молекулы на этот участок.
Среднее значение квадрата скорости молекул.
Для вычисления среднего давления надо знать значение средней скорости молекул (точнее, среднее значение квадрата скорости). Это не простой вопрос. Вы привыкли к тому, что скорость имеет каждая частица. Средняя же скорость молекул зависит от того, каковы скорости движения всех молекул.
Чем отличается определение средней скорости тела в механике от определения средней скорости молекул газа?
С самого начала нужно отказаться от попыток проследить за движением всех молекул, из которых состоит газ. Их слишком много, и движутся они очень сложно. Нам и не нужно знать, как движется каждая молекула. Мы должны выяснить, к какому результату приводит движение всех молекул газа.
Характер движения всей совокупности молекул газа известен из опыта. Молекулы участвуют в беспорядочном (тепловом) движении. Это означает, что скорость любой молекулы может оказаться как очень большой, так и очень малой. Направление движения молекул беспрестанно меняется при их столкновениях друг с другом.
Скорости отдельных молекул могут быть любыми, однако среднее значение модуля этих скоростей вполне определённое.
В дальнейшем нам понадобится среднее значение не самой скорости, а квадрата скорости — средняя квадратичная скорость. От этой величины зависит средняя кинетическая энергия молекул. А средняя кинетическая энергия молекул, как мы вскоре убедимся, имеет очень большое значение во всей молекулярно-кинетической теории. Обозначим модули скоростей отдельных молекул газа через υ1, υ2, υ3, … , υN. Среднее значение квадрата скорости определяется следующей формулой:
где N — число молекул в газе.
Но квадрат модуля любого вектора равен сумме квадратов его проекций на оси координат OX, OY, OZ.
Из курса механики известно, что при движении на плоскости υ2 = υ2x + υ2y. В случае, когда тело движется в пространстве, квадрат скорости равен:
υ2 = υ2x + υ2y + υ2z. (9.2)
Средние значения величин υ2x, υ2y и υ2z можно определить с помощью формул, подобных формуле (9.1). Между средним значением 
Действительно, для каждой молекулы справедливо равенство (9.2). Сложив такие равенства для отдельных молекул и разделив обе части полученного уравнения на число молекул N, мы придём к формуле (9.3).
>Внимание! Так как направления трёх осей OX, OY и OZ вследствие беспорядочного движения молекул равноправны, средние значения квадратов проекций скорости равны друг другу:
Учитывая соотношение (9.4), подставим в формулу (9.3) 


т. е. средний квадрат проекции скорости равен 

Скорости молекул беспорядочно меняются, но средний квадрат скорости вполне определённая величина.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика
Почему тепловые явления изучаются в молекулярной физике —
Основные положения молекулярно-кинетической теории. Размеры молекул —
Примеры решения задач по теме «Основные положения МКТ» —
Броуновское движение —
Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел —
Идеальный газ в МКТ. Среднее значение квадрата скорости молекул —
Основное уравнение молекулярно-кинетической теории газов —
Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» —
Температура и тепловое равновесие —
Определение температуры. Энергия теплового движения молекул —
Абсолютная температура. Температура — мера средней кинетической энергии молекул —
Измерение скоростей молекул газа —
Примеры решения задач по теме «Энергия теплового движения молекул» —
Уравнение состояния идеального газа —
Примеры решения задач по теме «Уравнение состояния идеального газа» —
Газовые законы —
Примеры решения задач по теме «Газовые законы» —
Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»