Тема: Определить среднюю ЭДС самоиндукции (Прочитано 7738 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Индуктивность L катушки равна 2 мГн. Ток частотой ν = 50 Гц, протекающий по катушке, изменяется по синусоидальному закону. Определить среднюю ЭДС самоиндукции, возникающую за интервал времени Δt, в течение которого ток в катушке изменяется от минимального до максимального значения. Амплитудное значение силы тока I0 = 10 А. Сделать рисунок.
« Последнее редактирование: 11 Мая 2015, 06:22 от alsak »
Записан
Решение.
Среднюю Э.Д.С. самоиндукции возникающая в контуре определим по формуле:
[ xi =-Lcdot frac{{{I}_{max }}-{{I}_{min }}}{Delta t} (1), {{I}_{max }}=10 A, {{I}_{min }}=0. ]
Ток в катушке изменяется от минимального до максимального значения за четверть периода.
[ Delta t=frac{T}{4}, T=frac{1}{nu }, Delta t=frac{1}{4cdot nu } (2). ]
Подставим (2) в (1) определим среднюю Э.Д.С. самоиндукции возникающая в контуре.
[ xi =left| Lcdot frac{{{I}_{max }}}{Delta t} right| ,xi =left| Lcdot {{I}_{max }}cdot 4cdot nu right| (3). ]
ξ = 4 В.
« Последнее редактирование: 11 Мая 2015, 06:23 от alsak »
Записан

3. МАГНЕТИЗМ
Основные формулы и определения
● Вокруг проводника с током существует магнитное поле, направление которого определяется правилом правого винта (или буравчика). Согласно этому правилу, нужно мысленно закручивать буравчик по направлению тока, тогда рукоятка буравчика будет вращаться, описывая окружность, по касательной к которой направлен вектор магнитной индукции. Модуль вектора магнитной индукции В, созданного прямым бесконечно длинным проводником с током, прямо пропорционален силе тока в проводнике I и обратно пропорционален расстоянию от проводника до точки наблюдения r. Для
|
вакуума: В = µ0 · I / (2π · r), |
где µ0 – магнитная постоянная. |
|
● На заряженную частицу, движущуюся в магнитном поле, действует сила |
|
|
В |
|
|
Лоренца, FЛ = q[v × B] , |
где q – заряд частицы; v – скорость частицы; B – |
вектор магнитной индукции. Квадратные скобки означают векторное произведение двух векторов.
Модуль силы Лоренца равен: FЛ = q × v × B × sin (v ^ B) . Направление силы Лоренца, если движется положительный заряд, определяется по правилу левой
руки. Согласно этому правилу, вектор магнитной индукции B должен входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца.
● Сила Ампера, т. е. сила, действующая на прямой проводник с током в магнитном поле, равна: FА = I [ℓ× B] , где I – сила тока; ℓ – длина проводника;
В – вектор магнитной индукции. Направление силы Ампера определяется по правилу левой руки, согласно которому вектор магнитной индукции должен входить в ладонь, четыре вытянутых пальца левой руки – показывать направление тока, тогда отогнутый большой палец покажет направление силы Ампера.
● При изменении магнитного потока в замкнутом контуре возникает индукционный ток, который, согласно закону Фарадея – Ленца, создает магнитное поле, препятствующее изменению магнитного потока.
Среднее значение ЭДС самоиндукции равно: εi = – L · ( I / t), где L – индуктивность; I – изменение силы тока, произошедшее за промежуток времени t.
Тест 3-1
На рис. 64 изображены сечения двух параллельных прямолинейных длинных проводников с противоположно направленными токами, причем I1 = 2I2.
Индукция B результирующего
|
магнитного поля равна нулю в некоторой |
Рис. 64 |
|
|
точке интервала… |
||

|
Варианты ответов: |
||||||
|
1) d; |
2) c; |
3) a; |
4) b. |
|||
|
Решение |
||||||
|
Направление вектора магнитной |
||||||
|
индукции |
находится |
по |
правилу |
|||
|
правого винта (или буравчика): если |
||||||
|
поступательное |
движение |
винта |
||||
|
происходит в направлении тока, то |
||||||
|
головка |
винта |
вращается |
по |
|||
|
окружности, по касательной к |
||||||
|
которой направлен вектор магнитной |
||||||
|
индукции. На рис. 65 показаны линии |
Рис. 65 |
|||||
|
магнитной |
индукции, |
которые |
||||
|
представляют |
собой |
окружности, |
охватывающие проводники с током. Как видно из этого рисунка, ток I1 течет на нас, буравчик выкручивается и его рукоятка вращается против часовой стрелки.
Поэтому вектор магнитной индукции B1 , созданный током I1, в интервале a
будет направлен вниз, а в интервалах b, c, d направлен вверх.
В проводнике с током I2 ток течет за чертеж, буравчик закручивается и вектор магнитной индукции B2 В в интервалах a, b, c направлен вверх, а в интервале d – вниз. Результат находится по принципу суперпозиции полей: В = B1 + B2 . Понятно, что индукция B результирующего магнитного поля может
быть равна нулю в тех точках интервала, где векторы B1 и B2 противоположно
направлены, т. е. в интервалах a и d.
Модуль вектора магнитной индукции, созданного прямым бесконечно длинным проводником с током, для вакуума равен: В = µ0 · I / (2π · r), где µ0 – магнитная постоянная. В интервале a индукция В1 > В2, так как токи I1 > I2, а соответствующие расстояния r1 < r2. Поэтому индукция магнитного поля может быть равна нулю только в некоторой точке интервала d.
Ответ: вариант 1.
Задание С3-1 для самостоятельного решения
В условиях теста 3-1 укажите интервал, в некоторой точке которого магнитная индукция равна нулю, если ток I1 так же, как и ток I2, направлен за чертеж.
Варианты ответов те же, что в тесте 3-1.
Тест 3-2
Магнитное поле создано двумя параллельными длинными проводниками с токами I1 и I2, расположенными перпендикулярно плоскости чертежа (рис. 66).
Если I1 = 2I2, то вектор B индукции результирующего поля в точке А направлен…

Варианты ответов:
1) вправо; 2) вниз; 3) вверх; 4) влево.
Решение
Модуль вектора магнитной индукции, Рис. 66 созданного прямым бесконечно длинным проводником с током, прямо пропорционален силе тока в проводнике и обратно пропорционален расстоянию от проводника
до точки наблюдения. Так как расстояние от обоих проводников до точки наблюдения А одинаково, а сила тока в первом проводнике в 2 раза больше, чем
во втором, то B1 = 2 B2 . Направление векторов B1 и B2 можно найти по правилу
правого винта. Для этого нужно мысленно, если ток течет к нам, выкручивать буравчик. Тогда рукоятка буравчика будет вращаться против часовой стрелки, описывая окружность, по касательной к которой направлен вектор магнитной
индукции. Следовательно, вектор B1 в точке А будет направлен вверх, вектор В
– вниз, результирующий вектор найдём по принципу суперпозиции. В скалярной форме: В = В1 – В2, т. е. В будет направлен вверх, в сторону большего вектора.
Ответ: вариант 3.
Задание С3-2 для самостоятельного решения
В условиях теста 3-2 определите в точке А направление результирующего
вектора магнитной индукции В , если направление тока I1 изменится на обратное, т. е. ток будет направлен от нас за чертёж.
Варианты ответов те же, что в тесте 3-2.
Тест 3-3
На рис. 67 показан длинный проводник с током, около которого находится небольшая проводящая рамка. При выключении в проводнике тока заданного направления в рамке…
Варианты ответов:
1) Индукционного тока не возникнет;
2) Возникнет индукционный ток в Рис. 67 направлении 1 – 2 – 3 – 4;
3) Возникнет индукционный ток в направлении 4 – 3 – 2 – 1.
Решение
Вокруг проводника с током существует магнитное поле, направление которого определяется правилом правого винта (или буравчика). Согласно этому правилу, нужно мысленно закручивать буравчик по направлению тока, тогда рукоятка буравчика будет вращаться, описывая окружность, по касательной к которой направлен вектор магнитной индукции. В нашем

примере вектор магнитной индукции, пронизывающий рамку, направлен за чертёж.
При выключении тока в проводнике в замкнутом контуре возникает индукционный ток, который, согласно закону Фарадея – Ленца, создает магнитное поле, препятствующее изменению магнитного потока. Поэтому магнитное поле индукционного тока тоже должно быть направлено за чертёж, чтобы препятствовать уменьшению тока. Направление индукционного тока также можно определить по правилу правого винта (буравчика), т.е. поступательное движение буравчика должно совпадать с направлением вектора магнитной индукции, созданной индукционным током. Тогда рукоятка буравчика будет двигаться в направлении индукционного тока в рамке. Поэтому в нашем примере индукционный ток возникнет в направлении 1 – 2 – 3 – 4.
Ответ: вариант 2.
Задание С3-3 для самостоятельного решения
Используя условие теста 3-3, определите направление индукционного тока в проводящей рамке, если не выключать, а включать ток в проводнике?
Варианты ответов те же, что в тесте 3-3.
Тест 3-4
На рис. 68 показан длинный проводник с током, около которого находится небольшая проводящая рамка.
При движении рамки к проводнику со скоростью v в рамке…
Рис. 68
Варианты ответов:
1)Возникнет индукционный ток в направлении 4 – 3 – 2 – 1;
2)Индукционного тока не возникнет;
3)Возникнет индукционный ток в направлении 1 – 2 – 3 – 4.
Решение
Вокруг проводника с током существует магнитное поле, направление которого определяется правилом правого винта (или буравчика). Согласно этому правилу, нужно мысленно завинчивать буравчик по направлению тока, тогда рукоятка буравчика будет вращаться, описывая окружность, по касательной к которой направлен вектор магнитной индукции. В нашем примере вектор магнитной индукции, пронизывающий рамку, направлен к нам перпендикулярно чертёжу. При движении рамки к проводнику магнитное поле усиливается, и в рамке, представляющей собой замкнутый проводящий контур, возникает индукционный ток, который, согласно закону Фарадея – Ленца, создает магнитное поле, препятствующее изменению магнитного потока. Поэтому магнитное поле индукционного тока должно быть направлено за чертёж, чтобы препятствовать его изменению. Направление индукционного
тока тоже можно определить по правилу правого винта (буравчика). Поступательное движение буравчика должно совпадать с направлением вектора магнитной индукции, созданной индукционным током, тогда рукоятка буравчика будет двигаться в направлении индукционного тока. Поэтому в нашем примере индукционный ток возникнет в направлении 1 – 2 – 3 – 4.
Ответ: вариант 3.
Задание С3-4 для самостоятельного решения
Используя условие теста 3-4, определите направление индукционного тока, если рамку удалять от проводника с током?
Варианты ответов те же, что в тесте 3-4.
Тест 3-5
Полная система уравнений Максвелла для электромагнитного поля имеет
вид:
|
∫ |
E d l = −∫ |
∂B dS |
||||
|
( L) |
(S ) ∂t |
; |
||||
|
∫ |
= ∫ |
∂D |
||||
|
H d l |
j + |
∂t |
dS ; |
|||
|
( L) |
(S ) |
|||||
|
∫ |
D d S = ∫ |
ρ d V ; |
||||
|
(S ) |
(V ) |
|||||
|
∫(S ) |
B d S = 0 |
|||||
|
. |
Следующая система уравнений:
|
∫ |
E d l = −∫ |
∂B dS |
||||
|
( L) |
(S ) ∂t |
; |
||||
|
∫ |
= ∫ |
|||||
|
(L) |
H d l |
∂D dS; |
||||
|
∫ |
(S ) |
∂t |
||||
|
(S ) |
D d S = 0; |
|||||
|
∫(S ) |
B d S = 0 |
|||||
|
. |
справедлива…
Варианты ответов:
1)В отсутствие заряженных тел;
2)В отсутствие заряженных тел и токов проводимости;
3)В отсутствие токов проводимости;
4)При наличии заряженных тел и токов проводимости.
Решение
В полной системе уравнений Максвелла величина j обозначает плотность
∂D
тока проводимости, ∂t – плотность тока электрического смещения, а
величина ρ – плотность электрических зарядов. В исследуемой системе уравнений нет величин j и ρ. Следовательно, система уравнений справедлива в
отсутствие заряженных тел и токов проводимости. Ответ: вариант 2.
Тест 3-6
Полная система уравнений приведена в тесте 3-5. Следующая система уравнений:
∫(L) E d l = 0;
∫(L) H d l = ∫(S ) j dS;∫(S ) D d S = ∫(V ) ρ d V ;
∫(S ) B d S = 0 .
справедлива для…
Варианты ответов:
1)Стационарного электромагнитного поля в отсутствие заряженных тел;
2)Стационарного электромагнитного поля в отсутствие токов проводимости;
3)Переменного электромагнитного поля при наличии заряженных тел и токов проводимости;
4)Стационарных электрических и магнитных полей.
Решение
Уравнения Максвелла являются обобщением основных законов электрических и магнитных явлений. В них приняты следующие обозначения:
– напряженность электрического поля; H – напряженность магнитного поля;
|
D – вектор электрического смещения; B – вектор магнитной индукции. |
|
|
Величина обозначает плотность тока проводимости, величина |
|
|
– |
плотность тока электрического смещения, а ρ – плотность электрических зарядов.
Первое уравнение Максвелла показывает, что переменное магнитное поле
∂B / ∂t порождает электрическое поле. Второе уравнение Максвелла показывает, что электрический ток j и переменное электрическое поле
порождают магнитное поле. Для стационарных полей = const и = const.
Так как в исследуемой системе уравнений отсутствуют производные
∂D / ∂t и ∂B / ∂t , то исследуемая система уравнений справедлива для
стационарных электрических и магнитных полей.
Ответ: вариант 4.
Задание С3-5 для самостоятельного решения Полная система уравнений приведена в тесте 3-5. Следующая система уравнений:
∫(L) E d l = 0;
∫(L) H d l = ∫(S ) j dS;∫(S ) D d S = 0;
∫(S ) B d S = 0 .
справедлива для…
Варианты ответов:
1)Стационарного магнитного поля;
2)Стационарного электрического поля;
3)Стационарных электрических и магнитных полей;
4)Стационарного электромагнитного поля в отсутствие заряженных тел.
Задание С3-6 для самостоятельного решения Полная система уравнений приведена в тесте 3-5. Следующая система уравнений:
∫(L) E d l = 0;∫( L) H d l = 0;
∫(S ) D d S = ∫(V ) ρ d V ;
∫(S ) B d S = 0 .
справедлива для …
Варианты ответов:
1)Стационарного магнитного поля;
2)Стационарного электрического поля;
3)Стационарных электрических и магнитных полей;
4)Стационарного электромагнитного поля в отсутствие токов проводимости.

Рис. 69
Тест 3-7
Пучок однократно ионизированных изотопов магния 24 Mg и 25 Mg, движущихся с одинаковой скоростью, влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции (рис. 69).
Радиусы окружностей, по которым движутся ионы, связаны соотношением…
|
Варианты ответов: |
||||||||||||||
|
1) R1 = |
25 |
R2; 2) R1 = |
24 |
R2; |
||||||||||
|
24 |
25 |
|||||||||||||
|
24 |
25 |
|||||||||||||
|
3) R1 = |
25 R2; |
4) R1 = 24 |
R2. |
Решение
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца. Направление силы Лоренца, если движется
положительный заряд, определяется по правилу левой руки. Согласно этому правилу, линии магнитной индукции должны входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца.
Если частица влетает в магнитное поле перпендикулярно линиям магнитной индукции с постоянной по величине скоростью, то она движется по окружности (рис. 69).
Следовательно, сила Лоренца является центростремительной силой. Согласно второму закону Ньютона, получим: mv2/R = qvB. Отсюда найдём радиус траектории: R = mv/(qB). Поскольку q, v, B – постоянные величины, то отношение радиусов окружностей равно отношению их масс: R1/R2 = m1/m2.
Массы частиц в атомных единицах массы (а.е.м.) указаны перед обозначениями химических элементов.
Следовательно, m1 = 24 а.е.м. и m2 = 25 а.е.м.
После численной подстановки получим R1 = (24/25) · R2. Ответ: вариант 3.
Задание С3-7 для самостоятельного решения
Ионы, имеющие одинаковые скорости, но разные удельные заряды, влетают в однородное магнитное поле. Их траектория приведена на рис. 70.
Величина наименьшего удельного заряда соответствует траектории…
Варианты ответов:
1) 1; 2) 2; 3) 3.
Примечание: удельным зарядом называется
отношение заряда частицы к её массе. Значение
Рис. 70

удельного заряда можно найти из равенства силы Лоренца и центростремительной силы.
Тест 3-8
На рис. 71 указаны траектории заряженных частиц, имеющих одинаковую скорость и влетающих в однородное магнитное поле, перпендикулярное плоскости чертежа.
При этом для частицы 1…
Варианты ответов:
1) q = 0; 2) q < 0; 3) q > 0.
Решение
На заряд, движущийся в магнитном поле, действует сила Лоренца, направление которой, если движется положительный заряд, определяется по правилу левой руки. Согласно этому правилу,
вектор магнитной индукции B должен входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца. Следовательно, под действием силы Лоренца положительно заряженные частицы при данном направлении
|
Рис. 71 |
вектора |
магнитной |
индукции B будут |
|
отклоняться вправо, |
отрицательно заряженные |
||
|
частицы – |
влево, а частицы, которые не имеют |
заряда, не будут отклоняться. Частица 1, как показывает рис. 71, отклоняется влево. Следовательно, для частицы 1 q < 0.
Ответ: вариант 2.
Задание С3-8 для самостоятельного решения
По рис. 71 определите, какая из отклоненных частиц имеет наибольшую массу m, если скорости и заряд отклоненных частиц одинаковы.
Примечание: если скорость перпендикулярна вектору магнитной
индукции В, то сила Лоренца FЛ = q v В равна центростремительной силе FЦ.С. = m · v2/R.
Варианты ответов:
Тест 3-9
В постоянном однородном магнитном поле, созданном электромагнитом с дискообразными полюсами, на некотором расстоянии от оси полюсов закреплена положительно заряженная частица (рис. 72).

|
Частица |
выстреливается перпендикулярно |
||
|
силовым линиям магнитного поля по касательной |
|||
|
к окружности, плоскость которой перпендикулярна |
|||
|
полю, а центр лежит на оси полюсов. Скорость |
|||
|
выстреливания такова, что частица движется |
|||
|
именно по этой окружности. В некоторый момент |
|||
|
ток в обмотках электромагнита начинает |
|||
|
увеличиваться. |
Правильное |
сочетание |
|
|
направлений скорости и ускорения частицы в этот |
Рис. 72 |
||
|
момент представлено на рисунке… |
|||
|
Варианты ответов: |
|||
|
1) |
2) |
Решение
На заряженную частицу, движущуюся в магнитном поле, действует сила
Лоренца, FЛ = q[v × B] , где q – заряд частицы; v – скорость частицы, B – вектор магнитной индукции. Квадратные скобки означают векторное
произведение двух векторов. Модуль силы Лоренца равен: FЛ = q v В sin( v ^ B ). Направление силы Лоренца, если движется положительный заряд, определяется по правилу левой руки. Согласно этому правилу, вектор
магнитной индукции B должен входить в ладонь, четыре вытянутых пальца левой руки должны показывать направление скорости, тогда отогнутый большой палец покажет направление силы Лоренца.
Если частица влетает в однородное постоянное магнитное поле перпендикулярно линиям магнитной индукции с постоянной по величине
скоростью, то sin ( v ^ B ) = sin 90º = 1 и сила Лоренца равна FЛ = q v В. Под действием силы Лоренца она движется по окружности, следовательно, сила
|
Лоренца |
является центростремительной силой FЦ.С. = m an , где |
m – |
масса |
|
частицы, |
an = v2 / R – нормальное ускорение, направленное |
к |
центру |
|
окружности перпендикулярно скорости. |

При увеличении тока в обмотках электромагнита увеличивается значение вектора магнитной индукции. Согласно закону электромагнитной индукции переменное магнитное поле создаёт вихревое электрическое поле. Направление силовых линий этого поля показано на рис. 73. Под действием электрической
силы 



|
Полное ускорение равно векторной сумме a |
|||
|
= an + aτ и находится по правилу параллелограмма (рис. |
|||
|
73). Таким образом, правильное сочетание направлений |
|||
|
скорости и ускорения частицы в момент, когда ток в |
|||
|
обмотках электромагнита начинает увеличиваться, |
|||
|
представлено на рисунке варианте 1. |
|||
|
Ответ: вариант 1. |
|||
|
Рис. 73 |
Задание С3-9 для самостоятельного решения
В рамках задания теста 3-9 указать правильное сочетание направлений скорости и ускорения частицы в тот момент, когда ток в обмотках электромагнита стал уменьшаться.
Варианты ответов те же, что в тесте 3-9.
Тест 3-10
На рис. 74 показана зависимость силы тока от времени в электрической цепи с индуктивностью 1 мГн. Модуль среднего значения ЭДС самоиндукции на интервале от 0 до 5 с (в мкВ) равен…
Варианты ответов:
1) 0; 2) 6; 3) 15; 4) 30.
Решение
В соответствии с законом Фарадея –
|
Ленца, |
среднее |
значение |
ЭДС |
|
самоиндукции равно: εi = – L · ( I / |
t), где |
||
|
L – индуктивность; |
I – изменение силы |
||
|
тока, произошедшее за промежуток |
|||
|
времени |
t. Вычислим модуль среднего |
||
|
значения |
ЭДС за |
промежуток времени |
|
t = 5 – 0 = 5 с. Из |
рис. |
74 |
найдём |
|
изменение силы тока на этом промежутке |
|||
|
времени: I = 30 – 0 = 30 |
мА. |
Рис. 74 |
Тогда среднее значение εi = 1 · 30/5 = 6 мкВ. Ответ: вариант 2.

Рис. 76
Задание С3-10 для самостоятельного решения
На рис. 74 показана зависимость силы тока от времени в электрической цепи с индуктивностью 1 мГн. Определить среднее значение ЭДС самоиндукции (в мкВ) на интервалах времени от 10 до 15 с и от 15 до 20 с.
|
Варианты ответов: |
|||
|
1) –2 и 0; |
2) 0 и 4; |
3) 0 и –2; 4) –2 |
и –4. |
|
Тест 3-11 |
|||
|
Рамка с |
током |
с магнитным |
дипольным |
моментом 
индукцией B .
Момент сил, действующий на рамку с током,
|
направлен… |
Рис. 75 |
|
|
Варианты ответов: |
||
1)От нас;
2)К нам;
3)Вдоль вектора магнитной индукции;
4)Против вектора магнитной индукции.
Решение
Момент сил, действующий на рамку с током в магнитном поле, равен векторному произведению магнитного дипольного момента рамки Pm на 
вектор магнитной индукции: M = [Pm × B]. Направление вектора момента сил определяется в соответствии с правилом векторного произведения двух
векторов: вектор M должен быть перпендикулярен плоскости, в которой лежат перемножаемые векторы (т. е. к нам или от нас). Направление векторного произведения определяется по правилу правого винта: если первый вектор поворачивать ко второму, то поступательное движение винта покажет
направление векторного произведения. В нашем случае вектор M направлен за чертёж, т. е. от нас.
Ответ: вариант 1.
Задание С3-11 для самостоятельного решения
Рамка с током с магнитным дипольным моментом 
индукцией B . Момент сил, действующий на рамку с током, направлен…
Варианты ответов те же, что в тесте 3-11.

Задание С3-12 для самостоятельного решения
Рамка с током с магнитным дипольным моментом 

|
Рис. 77 |
Варианты ответов те же, что в тесте 3-11. |
|
Тест 3-12 |
|
|
На рис. 78 |
изображен проводник |
массой m, подвешенный на проводящих нитях, через которые подведен ток.
Укажите правильную комбинацию направления вектора магнитной индукции и направления тока в проводнике, чтобы сила натяжения нитей стала равной нулю.
|
Варианты ответов: |
Рис. 78 |
|
1) Ток в направлении L – M; вектор |
|
|
магнитной индукции вниз; |
2)Ток в направлении M – L; вектор магнитной индукции B вверх;
3)Ток в направлении L – M; вектор магнитной индукции B от нас;
4)Ток в направлении M – L; вектор магнитной индукции B от нас.
Решение
Для того, чтобы сила натяжения нитей стала равной нулю, нужно чтобы сила Ампера, т. е. сила, действующая на проводник с током в магнитном поле, была направлена против силы тяжести. Поскольку сила тяжести направлена вниз, то сила Ампера должна быть направлена вверх. Направление силы Ампера определяется по правилу левой руки, согласно которому линии магнитной индукции должны входить в ладонь, четыре вытянутых пальца левой руки показывать направление тока, тогда отогнутый большой палец покажет направление силы Ампера. Правильная комбинация направления вектора магнитной индукции и направления тока в проводнике будет соответствовать
варианту 3: ток в направлении L – M; вектор магнитной индукции B от нас. Ответ: вариант 3.
Тест 3-13
На рис. 79 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре не возникает на интервале…
Варианты ответов:
Рис. 79
1)интервал С;
2)интервал D;
3) интервал А; 4) интервал Е; 5) интервал В.
Решение
Согласно закону Фарадея – Ленца, ЭДС в замкнутом контуре появляется при изменении магнитного потока: εi = – Ф/ t. Поскольку на интервале В магнитный поток не изменяется, то на этом интервале в контуре ЭДС не возникает.
Ответ: вариант 5.
Задание С3-13 для самостоятельного решения
На рис. 79 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре положительна и по величине максимальна на интервале…
Варианты ответов те же, что в тесте 3-13.
Задание С3-14 для самостоятельного решения
На рис. 79 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре положительна и по величине минимальна на интервале…
Варианты ответов те же, что в тесте 3-13.
Задание С3-15 для самостоятельного решения
На рис. 79 представлена зависимость магнитного потока, пронизывающего некоторый замкнутый контур, от времени. ЭДС индукции в контуре по модулю максимальна на интервале…
Варианты ответов те же, что в тесте 3-13.
Тест 3-14
При помещении диамагнетика в стационарное магнитное поле…
Варианты ответов:
1)У атомов индуцируются магнитные моменты; вектор намагниченности образца направлен против направления внешнего поля;
2)У атомов индуцируются магнитные моменты; вектор намагниченности образца направлен по направлению внешнего поля;
3)Происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен по направлению внешнего поля;
4)Происходит ориентирование имевшихся магнитных моментов атомов; вектор намагниченности образца направлен против направления внешнего поля.
Решение
Если поместить диамагнетик в стационарное магнитное поле, то у атомов, согласно правилу Ленца, индуцируются магнитные моменты, направленные против внешнего магнитного поля. Вектор намагниченности представляет собой векторную сумму магнитных моментов отдельных атомов, делённую на

Рис. 80
объём, поэтому у диамагнетиков он направлен против внешнего магнитного поля.
Ответ: вариант 1.
Задание С3-16 для самостоятельного решения
Выберите вариант ответа из теста 3-14 для парамагнетика, помещенного в стационарное магнитное поле.
Тест 3-15
На рис. 80 представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н. Укажите зависимость, соответствующую
диамагнетикам.
Варианты ответов:
|
1) график 1; |
2) график 2; |
|
3) график 3; |
4) график 4. |
Решение
Вектор намагниченности представляет собой векторную сумму магнитных моментов отдельных атомов, делённую на
объём. Как показывает опыт, зависимость величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н имеет вид: I = χ · Н, где χ – магнитная восприимчивость.
У диамагнетиков χ – величина отрицательная, малая по абсолютному значению и является константой. У парамагнетиков χ тоже невелика, но положительна и в сильных магнитных полях наблюдается отступление от пропорциональности между намагниченностью парамагнетика I и напряженностью Н. У ферромагнетиков χ – положительная величина, которая является функцией напряженности магнитного поля и может принимать очень большие значения. При больших значениях Н намагниченность ферромагнетика I достигает насыщения.
Таким образом, зависимость, соответствующая диамагнетикам, представлена на графике 4.
Ответ: вариант 4.
Задание С3-17 для самостоятельного решения
На рис. 80 представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н. Укажите зависимость, соответствующую парамагнетикам.
Варианты ответов те же, что в тесте 3-15.
Задание С3-18 для самостоятельного решения
На рис. 80 представлены графики, отражающие характер зависимости величины намагниченности I вещества (по модулю) от напряженности магнитного поля Н. Укажите зависимость, соответствующую ферромагнетикам.
Варианты ответов те же, что в тесте 3-15.
Соседние файлы в папке Физика_1
- #
- #
- #
Задания
Версия для печати и копирования в MS Word
Задания Д9 B15 № 1504
На рисунке приведен график зависимости силы тока от времени в электрической цепи, индуктивность которой 1 мГн.
Определите модуль среднего значения ЭДС самоиндукции в интервале времени от 10 до 15 с.
1) 2 мкВ
2) 3 мкВ
3) 5 мкВ
4) 0
Спрятать решение
Решение.
Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока в цепи и индуктивности:
Поскольку в интервале времени от 10 до 15 с ток в цепи не менялся, получаем, что модуль среднего значения ЭДС самоиндукции в этом интервале времени равен нулю.
Ответ: 4.
[an error occurred while processing this directive]
Глава вторая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.
Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,
| T | T | |||
| w = | ∫ | i2r dt = | ∫ | Im2sin2 ωt r dt.. |
| 0 | 0 |
При неизменном во времени токе энергия
W = I2rT
Приравняв правые части
| T | ||
| I2rT = | ∫ | Im2sin2 ωt r dt,. |
| 0 |
получим действующее значение тока
| I = | √ | 1 | = | Im | = 0,707Im . | |
| T | √2 |
Таким образом, действующее значение тока меньше амплитудного в √2 раз.
Аналогично определяют действующие значения ЭДС и напряжения:
Е = Em /√2, U = Um /√2.
Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока
Im = √2I = 1,41 • 10 = 14,1 A,
и мгновенное значение тока
i = Im sin (ωt + ψ) = 14,1 sin (ωt + ψ).
При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за
полпериода (среднее значение за период, как известно, равно нулю):
| T2 | ||||||||||
| Еср = | ∫ | Ет sin ωt dt = | ∫ | sin ωt dωt = | |cos ωt|π0 = | = 0,637Ет . | ||||
| 0 | 0 |
Аналогично можно найти средние значения тока и напряжения:
Iср = 2Iт /π; Uср = 2Uт /π.
Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока
| Кф = | Е | = | I | = | U | = | π | = 1,11. |
| Ес | Iср | Uср | 2√2 |
[an error occurred while processing this directive]
Сергей Сергеевич Соев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение электромагнитной индукции
Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.
Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.
ЭДС индукции
Существование явления электромагнитной индукции говорит о том, что при изменении магнитного потока в контуре появляется электродвижущая сила индукции (ЭДС, ${{mathcal E}}_i$). Величина ${{mathcal E}}_i$ не зависит от способа изменения магнитного потока $(Ф)$, и связана со скоростью его изменения ($frac{dФ}{dt}$). С изменением знака скорости изменения потока направление ЭДС индукции тоже изменяется:
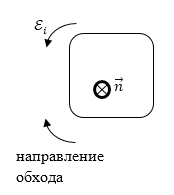
Знак потока $Ф$ и знак ${{mathcal E}}_i$ связывают с выбором направления нормали к плоскости контура. ${{mathcal E}}_i$ считают положительной если ее направление образует с направлением нормали к контуру правый винт. Для рис 1. и заданном направлении нормали «от нас», перпендикулярно плоскости рисунка ($overrightarrow{n}$) $frac{dФ}{dt} >0, {{mathcal E}}_i
Рисунок 1.
«Электромагнитная индукция» 👇
Основной единицей измерения индукционной ЭДС служит вольт $(В)$. Если скорость изменения магнитного потока равна $1frac{Вб}{с}$ в контуре индуцируется ЭДС, равная $1 В$.
В гауссовой системе формула (1) принимает вид:
где $с$ — скорость света в вакууме. Основной единицей измерения магнитного потока в СГСЭ является максвелл $(Мкс)$, тогда ${{mathcal E}}_i$ измеряется в СГСЭ — единицах потенциала. Для того, чтобы перевести ЭДС из системы гаусса в вольты необходимо умножить имеющееся значение на $300$. Следовательно, формулой связи системы СИ и СГСЭ можно записать выражение:
Среднее значение ЭДС индукции может быть определено как:
Поток сцепления
Если контур, в котором индуцируется ЭДС, состоит из $N$ витков (соленоид), витки соединены последовательно, ${{mathcal E}}_i$ равна сумме ЭДС, которые индуцируются каждым витком в отдельности. Следовательно, используя формулу (1), можно записать:
Величину $Psi$, равную:
называют потоком сцепления, или полным магнитным потоком. В том случае, если поток, который пронизывает каждый из витков, одинаковый, то можно записать, что:
В сложном контуре ${{mathcal E}}_i$ вычисляют как:
Уравнение (8) называют основным законом электромагнитной индукции (уравнением Фарадея — Максвелла).
Частные случаи применения закона электромагнитной индукции
- Если проводник длины $l $движется в однородном магнитном поле (с индукцией $В$) с постоянной скоростью $v$, то на его концах возникает разность потенциалов $U$:
где $alpha $ — угол между направлением скорости и вектором магнитной индукции.
- ЭДС индукции возникает в рамке, которая содержит $N$ витков, имеет площадь $S$ и вращается с постоянной угловой скоростью $omega$ в однородном магнитном поле с индукцией $В$ и она равна:
где $omega t$ — мгновенное значение угла между вектором магнитной индукции ($overrightarrow{B}$) и вектором нормали к плоскости рамки ($overrightarrow{n}$).
Пример 1
Задание: Найдите мгновенное значение ЭДС индукции рамки, которое соответствует углу поворота рамки $alpha ,$ площадь рамки, равна $S$, она содержит $N$ витков. Рамка вращается в постоянном магнитном поле с индукцией $B$. Частота вращения рамки равна $n$.
Решение:
За основу решения задачи примем уравнение Фарадея — Максвелла:
[{{mathcal E}}_i=-frac{d Psi}{dt} left(1.1right),]
где потокосцепление можно определить как:
[Psi=NФ left(1.2right),]
где $N$ — количество витков, которые пронизывает магнитный поток $Ф$. Соответственно (1.1) примет вид:
[{{mathcal E}}_i=-Nfrac{dФ}{dt} left(1.3right).]
Если рамку вращать, то магнитный поток изменяется в соответствии с законом:
[Ф=BScosomega tleft(1.4right),]
где $omega $ — угловая частота вращения. Подставим выражение (1.4) в (1.3), получим:
[{{mathcal E}}_i=NBSomega sinomega tleft(1.5right).]
Связь угловой частоты и часты вращения, определим как:
[omega =2pi n left(1.6right),] [omega t=alpha left(1.7right).]
Подставим выражения (1.6), (1.7) в формулу (1.5) получим:
[{{mathcal E}}_i=2pi nNBSsinalpha .]
Ответ: ${{mathcal E}}_i=2pi nNBSsinalpha .$
Пример 2
Задание: Определите среднее ЭДС индукции ($leftlangle {{mathcal E}}_irightrangle )$, если магнитный поток, который пронизывает контур, изменяется от $Ф_1=40Вб$ до $Ф_2=0Вб$ в течении промежутка времени равного $2 с$.
Решение:
За основу решения примем формулу, определяющую среднюю ЭДС индукции:
[leftlangle {{mathcal E}}_irightrangle =-frac{Delta Ф}{Delta t}left(2.1right).]
Проведем вычисления:
[leftlangle {{mathcal E}}_irightrangle =-frac{0-40}{2}=20 left(Вright).]
Ответ: $leftlangle {{mathcal E}}_irightrangle =20 В$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме