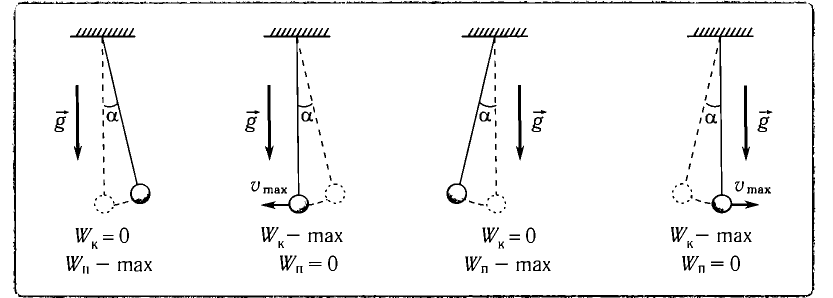
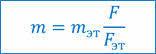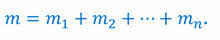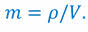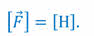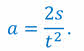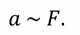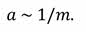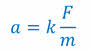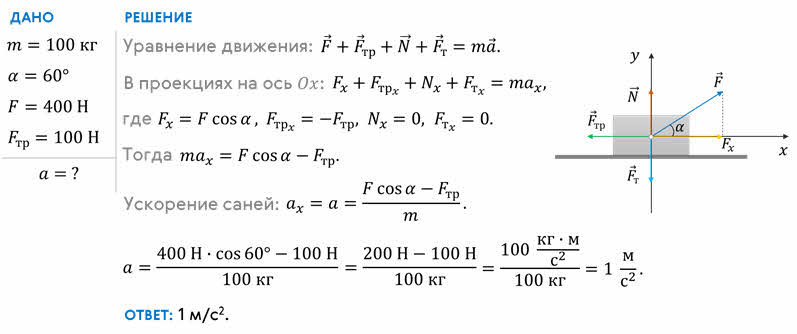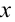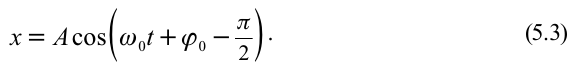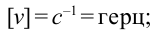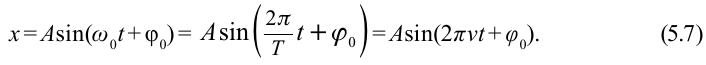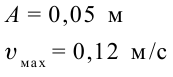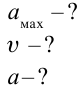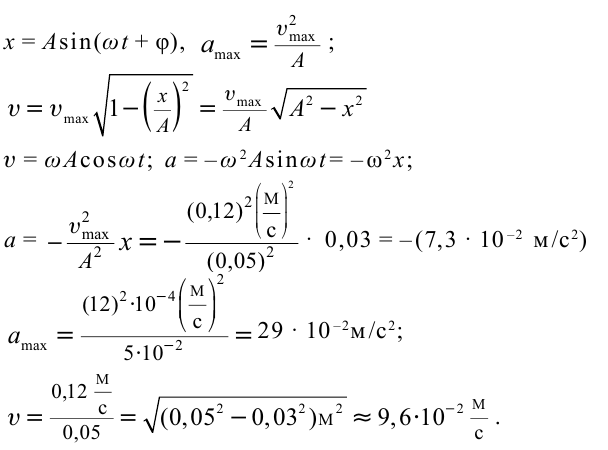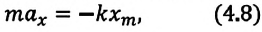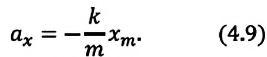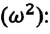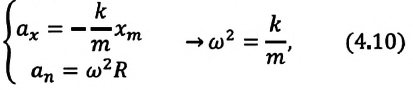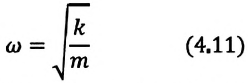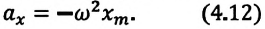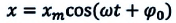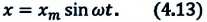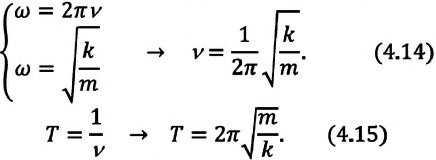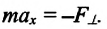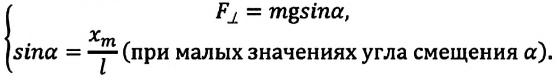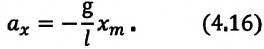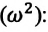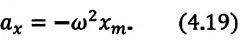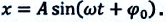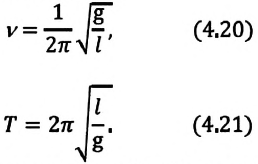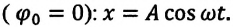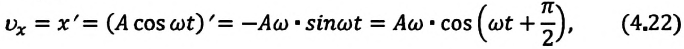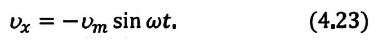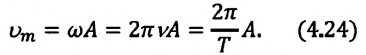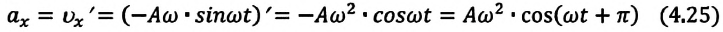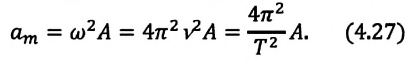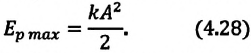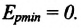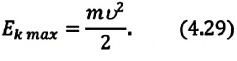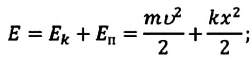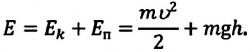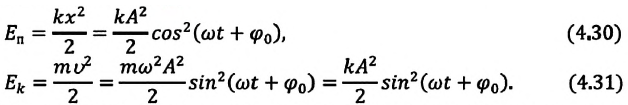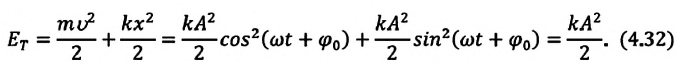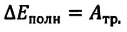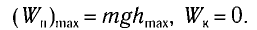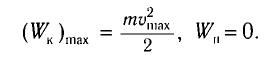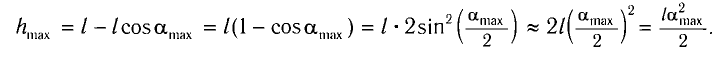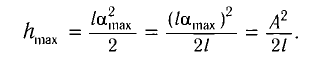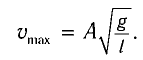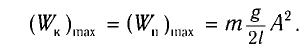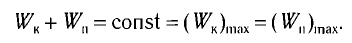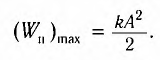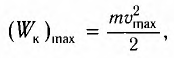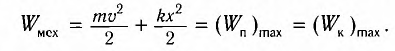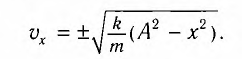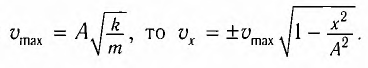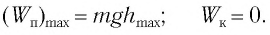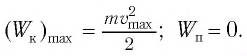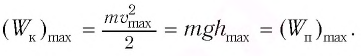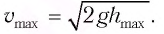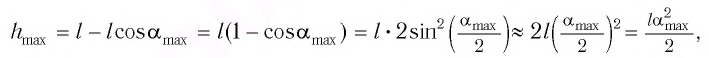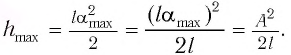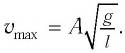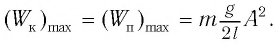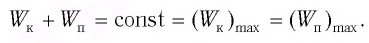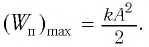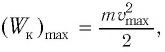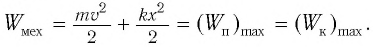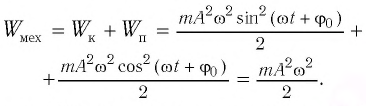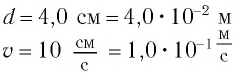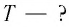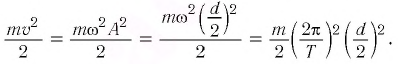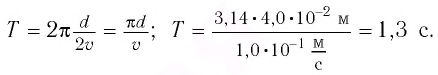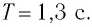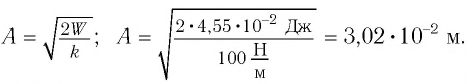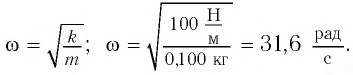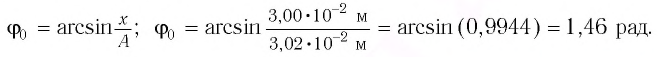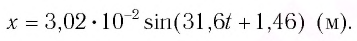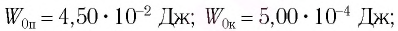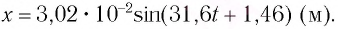Решение: на шарик в верхней точке траектории действует две силы: mg – сила тяжести, направленная вертикально вниз и T – сила натяжения нити, направленная вдоль нити. Ускорение тела при движении по дуге окружности можно разложить на два слагаемых:
[ vec{a}={{vec{a}}_{tau }}+{{vec{a}}_{n}}. ]
Тангенциальное ускорение aτ — направлено по касательной к траектории и характеризует изменение скорости по модулю. Центростремительное или нормальное ускорение an — возникает всегда при движении точки по дуге окружности конечного радиуса, характеризует изменение скорости по направлению и направлено перпендикулярно вектору мгновенной скорости (к центру окружности).
В нижней точке траектории у тела только центростремительное ускорение, т.е.
[ a=frac{{{upsilon }^{2}}}{l},text{ }(1) ]
Где l – длина нити. В верхней точке траектории скорость тела равна нулю (υ = 0), тогда центростремительное ускорение тела тоже равно нулю.
[ {{a}_{n}}=frac{{{upsilon }^{2}}}{l}=0. ]
Тогда ускорение шарика в верхней точке равно тангенциальному:
a1 = aτ.
Ось z направим по касательной к траектории. Запишем второй закон Ньютона в векторном виде и спроецируем его на выбранную координатную ось.
[ vec{T}+mvec{g}=mcdot {{vec{a}}_{1}},text{ }mgcdot sin alpha =mcdot {{a}_{tau }},text{ }{{a}_{1}}={{a}_{tau }}=gcdot sin alpha . ]
Остаётся определить угол отклонения α нити от вертикали в верхнем положении. Для этого запишем закон сохранения энергии (за нулевой уровень потенциальной энергии примем нижнее положение шарика), тогда в нижней точке – только кинетическая энергия, в верхней точке – только потенциальная. Как видно из рисунка, высота подъёма шарика равна
[ h=l-lcdot cos alpha =lcdot left( 1-cos alpha right). ]
Тогда
[ begin{align}
& {{E}_{0}}={{E}_{1}},text{ }frac{mcdot {{upsilon }^{2}}}{2}=mcdot gcdot h,text{ } \
& text{ }frac{{{upsilon }^{2}}}{2}=gcdot lcdot left( 1-cos alpha right),text{ }frac{{{upsilon }^{2}}}{2cdot gcdot l}=1-cos alpha \
end{align} ]
Таким образом, с учётом (1), получим (используя основное тригонометрическое тождество)
[ 1-cos alpha =frac{1}{2cdot g}cdot frac{{{upsilon }^{2}}}{l},cos alpha =1-frac{a}{2cdot g},sin alpha =sqrt{1-{{cos }^{2}}alpha }=sqrt{1-{{left( 1-frac{a}{2cdot g} right)}^{2}}}. ]
Искомое ускорение
[ {{a}_{1}}=gcdot sin alpha =gcdot sqrt{1-{{left( 1-frac{a}{2cdot g} right)}^{2}}}. ]
[ {{a}_{1}}=9,8cdot sqrt{1-{{left( 1-frac{4}{2cdot 9,8} right)}^{2}}}=5,9. ]
Ответ: a = 5,9 м/с2
« Последнее редактирование: 06 Мая 2016, 06:18 от alsak »
Записан
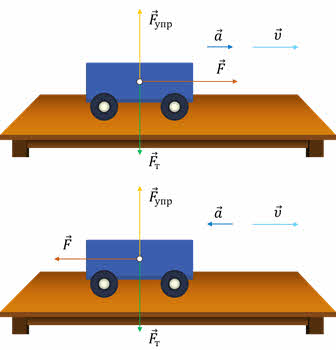
Цель работы: вычислить ускорение, с которым скатывается шарик по наклонному желобу. Для этого измеряют длину перемещения s шарика за известное время t. Так как при равноускоренном движении без начальной скорости
то, измерив s и t, можно найти ускорение шарика. Оно равно:
Никакие измерения не делаются абсолютно точно. Они всегда производятся с некоторой погрешностью, связанной с несовершенством средств измерения и другими причинами. Но и при наличии погрешностей имеется несколько способов проведения достоверных измерений. Наиболее простой из них — вычисление среднего арифметического из результатов нескольких независимых измерений одной и той же величины, если условия опыта не изменяются. Это и предлагается сделать в работе.
Средства измерения: 1) измерительная лента; 2) метроном.
Материалы: 1) желоб; 2) шарик; 3) штатив с муфтами и лапкой; 4) металлический цилиндр.
Порядок выполнения работы
1. Укрепите желоб с помощью штатива в наклонном положении под небольшим углом к горизонту (рис. 175). У нижнего конца желоба положите в него металлический цилиндр.
2. Пустив шарик (одновременно с ударом метронома) с верхнего конца желоба, подсчитайте число ударов метронома до столкновения шарика с цилиндром. Опыт удобно проводить при 120 ударах метронома в минуту.
3. Меняя угол наклона желоба к горизонту и производя небольшие передвижения металлического цилиндра, добивайтесь того, чтобы между моментом пуска шарика и моментом его столкновения с цилиндром было 4 удара метронома (3 промежутка между ударами).
4. Вычислите время движения шарика.
5. С помощью измерительной ленты определите длину перемещения s шарика. Не меняя наклона желоба (условия опыта должны оставаться неизменными), повторите опыт пять раз, добиваясь снова совпадения четвертого удара метронома с ударом шарика о металлический цилиндр (цилиндр для этого можно немного передвигать).
6. По формуле
найдите среднее значение модуля перемещения, а затем рассчитайте среднее значение модуля ускорения:
7. Результаты измерений и вычислений занесите в таблицу:
|
Номер опыта |
s, м |
sср, м |
Число ударов метро нома |
t, с |
aср, м/с2 |
При прямолинейном равноускоренном движении без начальной скорости
где S — путь, пройденный телом, t — время прохождения пути. Средства измерения: измерительная лента (линейка), метроном (секундомер).
Лабораторная установка и порядок выполнения работы подробно описаны в учебнике.
|
№ опыта |
t, с |
S, м |
 |
|
1 |
6 |
0,5 |
0,028 |
|
2 |
5,5 |
0,5 |
0,033 |
|
3 |
5 |
0,49 |
0,039 |
|
4 |
5,5 |
0,49 |
0,032 |
|
5 |
6,5 |
0,51 |
0,024 |
|
среднее значение |
5,7 |
0,5 |
0,031 |
Вычисления:
Вычисление погрешностей
Точность приборов: Измерительная лента:
Секундомер:
Вычислим абсолютные погрешности:
Вычислим относительную погрешность:
Абсолютная погрешность косвенного измерения:
Найденное в результате работы ускорение можно записать так:
но при данной абсолютной погрешности последняя цифра в значении аср значения не имеет, поэтому запишем так:
На прошлом уроке мы с вами говорили о первом законе Ньютона, где постулируется существование инерциальных систем отсчёта, в которых выполняется закон инерции. Давайте вспомним, что согласно закону инерции, скорость движения тела остаётся постоянной, если на него не действуют другие тела или их действия компенсируются.
Движение тела, которое происходит без действия на него других тел, называют движением по инерции. А свойство тел, проявляющееся в том, что скорость их движения остаётся неизменной до тех пор, пока на них не действуют другие тела, называется инертностью.
Опыты показывают, что чем больше время изменения скорости тела, тем оно более инертно. В седьмом классе вы узнали, что мерой инертности тела является масса, единица измерения которой в системе СИ является килограмм.
— А как сравнить массы двух тел?
Конечно это можно сделать взвешиванием на рычажных или пружинных весах.
Во всех случаях весы — это прибор для определения массы тела по действующей на него силе тяжести. Для всех весов определение массы производится путём сравнения двух сил: силы притяжения к Земле взвешиваемого тела и силы притяжения к Земле эталона (гирь):
— А можно ли сравнить массы тел, не используя силы притяжения?
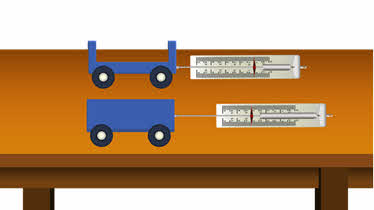
Ответим на этот вопрос, проведя такой опыт. Поставим на горизонтальную поверхность две тележки разной массы, способные катиться почти без трения. Будем разгонять тележки так, чтобы они ускорялись одинаково, не обгоняя и не отставая друг от друга.
Как видно из опыта, показания первого динамометра в три раза больше чем второго. Значит первую тележку в три раза труднее разогнать, чем вторую, то есть она в три раза более инертна. Такой опыт подтверждает, что масса тела является мерой его инертности.
Напомним ещё о двух практически важных свойствах массы:
· общая масса нескольких тел равна сумме их масс:
· масса однородного вещества, заключённого в объёме, пропорциональна этому объёму:
Теперь поговорим о взаимодействии тел. Как мы с вами знаем, в мире всё находится в непрерывном движении и изменении. Но, двигаясь, тела действуют друг на друга, то есть взаимодействуют. Взаимодействие, как и движение, является неотъемлемым свойством материи.
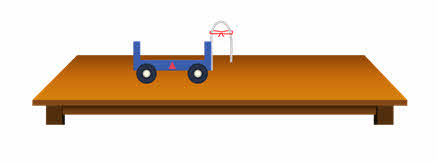
Чтобы получить первые представления о сущности этого понятия, рассмотрим такой пример. На экране вы видите тележку, с прикреплённой к ней стальной линейкой. Тележка находится в покое в инерциальной системе отсчёта, связанной со столом. Будет ли тележка двигаться, если линейка выпрямится?
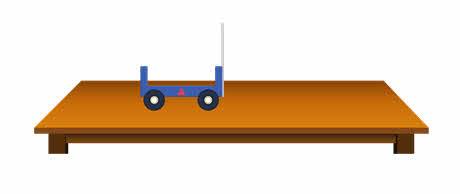
Ответ на вопрос может дать эксперимент. Пережжём нить. Пластина резко выпрямляется, но тележка остаётся на прежнем месте.
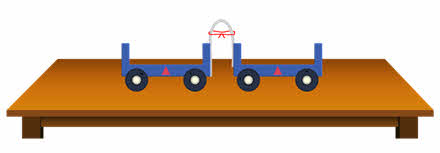
Поставим по другую сторону согнутой линейки ещё одну такую же тележку.
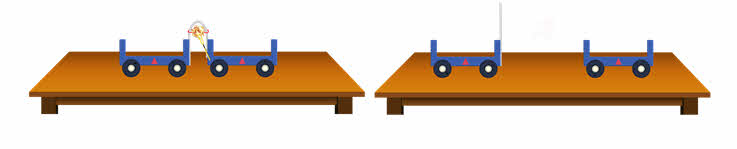
После пережигания нити обе тележки приходят в движение и разъезжаются в разные стороны.
Из результатов эксперимента можно сделать вывод: для изменения скорости тележки понадобилось второе тело — вторая тележка. В движение пришли обе тележки, обе они стали двигаться относительно стола и обе подействовали друг на друга. Значит, действие одного тела на другое не может быть односторонним.
Для количественного описания действия одного тела на другое в механике вводится понятие «сила». Сила — одно из основных понятий динамики, ведь не случайно слово «динамика» происходит от греческого «динамис» — сила.
Сила — это физическая векторная величина, являющаяся количественной мерой воздействия одного тела на другое.
Единицей силы в СИ является ньютон:
Так как сила — величина векторная, то мы должны ясно представлять себе: к какой точке тела приложена сила; по какой линии и как она направлена; и каков модуль этой силы.
Если на тело действуют сразу несколько сил, то оно движется с ускорением, если их равнодействующая не равна нулю.
Вспомним, что равнодействующей называется сила, оказывающая такое же действие, как несколько сил совместно.
Так как в результате действия силы возникает ускорение, то логично предположить, что должна существовать некая количественная взаимосвязь между этими величинами.
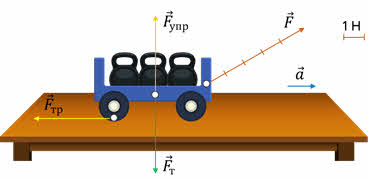
Проведём простой опыт. К тележке, движущейся по гладкой горизонтальной поверхности с некоторой скоростью, приложим силу. Поскольку сила тяжести и сила упругости компенсируют друг друга, а сила сопротивления пренебрежимо мала, то приложенная нами сила равна результирующей всех приложенных к тележке сил. Если силу направить по скорости, то она будет разгонять тележку, если против скорости — тормозить её.
— А куда направлено ускорение тележки?
Из кинематики мы знаем, что при разгоне оно направлено по скорости, а при торможении — противоположно ей. Но в обоих случаях направления векторов ускорения и силы совпадают.
Проведённый опыт, как и множество других опытов с движущимися телами, показывает, что ускорение тела направлено по результирующей всех сил, приложенных к нему, при любом движении тела по любой траектории.
Теперь рассмотрим такой опыт. Положим на наклонную плоскость шарик, удерживаемый динамометром. На шар будут действовать сила тяжести, сила упругости плоскости (её ещё называют силой реакции опоры и обозначают буквой N), и сила упругости пружины динамометра. В состоянии покоя равнодействующая этих сил равна нулю.
Отпустим шарик. Он начнёт скатываться с некоторым ускорением. В этом опыте можно пренебречь силой трения качения и сопротивлением воздуха. Следовательно, результирующая сил, действующих на тележку, равна геометрической сумме сил тяжести и реакции опоры. Тогда из формулы следует, что модуль результирующей всех сил, приложенных к шарику при её движении, равен показаниям динамометра при её покое.
Продолжим опыт. Выясним, как зависит ускорение тележки от действующих на неё сил и от её массы. Для этого измерим время движения шарика и пройденный им путь.
Модуль ускорения шарика определим по формуле кинематики
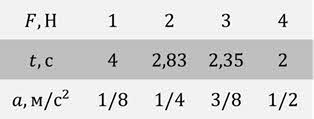
Теперь, увеличивая угол наклона, будем увеличивать значение равнодействующей силы в два, три и четыре раза, и определять ускорение шарика для каждого случая.
Опыт показывает, что при увеличении модуля силы в два, три и четыре раза модуль ускорения увеличится тоже в два, три и четыре раза.
Следовательно, модуль ускорения тела прямо пропорционален модулю результирующей всех приложенных к нему сил:
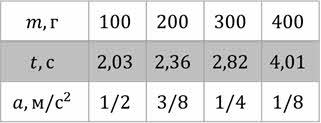
Будем теперь проводить измерения для тел разных масс при одном и том же значении модуля силы. Постоянство силы будем поддерживать, регулируя наклон плоскости и контролируя её значение динамометром. Массу будем изменять, используя шарики из различных материалов, массы которых заранее известны. Как и в прошлом опыте, для каждого случая будем определять ускорение.
Из результатов опыта видно, что под действием одной и той же силы, тело в два, три, четыре раза большей массы приобретает в два, три, четыре раза меньшее ускорение.
Значит, модули ускорений, приобретаемых телами под действием одинаковых сил, обратно пропорциональны массам этих тел:
Полученные нами закономерности можно выразить одной формулой:
где k — это постоянный коэффициент, который зависит от выбора единицы силы.
Мы знаем, что единицей силы в СИ является один ньютон — эта сила, под действием которой тело массой один килограмм движется с ускорением один метр на секунду в квадрате. Поэтому в СИ коэффициент k = 1.
Таким образом, ускорение, приобретаемое телом под действием приложенных к нему сил, прямо пропорционально результирующей силе и обратно пропорционально массе тела.
Это основной закон динамики — второй закон Ньютона.
Формула, выражающая математическую запись второго закона Ньютона, подчёркивает, что сила является причиной, а ускорение — следствием. Поэтому эту формулу ещё называют уравнением движения тела.
Второй закон Ньютона — один из самых фундаментальных законов природы. Его называют основным законом динамики, так как он позволяет найти положение тела в любой момент времени, то есть решить основную задачу механики.
Отметим также то, что второй закон Ньютона выполняется только в инерциальных системах отсчёта.
Закрепления материала.
Сани массой сто килограмм тянут по горизонтальному участку пути, прикладывая силу под углом 60о к горизонту. Модуль прикладываемой силы равен 400 Н, а модуль силы трения скольжения — 100 Н. Определите модуль ускорения движения саней.
Определите ускорение шарика при его движении по окружности
Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности.
Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, кусочек пробки с отверстием, лист бумаги, линейка.
1. Приведем груз во вращение по нарисованной окружности радиуса R= 20 см. Измеряем радиус с точностью 1 см. Измерим время t, за которое тело совершит N=30 оборотов.
2. Определяем высоту конического маятника h по вертикали от центра шарика до точки подвеса. h=60,0 +- 1 см.
3.Оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности и измеряем модуль составляющей F1 F1= 0,12 Н, масса шарика m=30 г +- 1 г.
4.Результаты измерений заносим в таблицу.
5.Вычислим аn по формулам, приведенным в таблице.
6.Результат вычисления заносим в таблицу.
Вывод: сравнивая полученные три значения модуля центростремительного ускорения, убеждаемся, что они примерно одинаковы. Это подтверждает правильность наших измерений.
Лаб. 3
$F_y·x=2 Н· 0.045 м = 0.09$
| Опыт | $N$ | $t$ | $T$ | $a$ | $ω$ | $v$ |
| $1$ | $10$ | $12.13$ | $-$ | $-$ | $-$ | $-$ |
| $2$ | $10$ | $12.2$ | $-$ | $-$ | $-$ | $-$ |
| $3$ | $10$ | $11.8$ | $-$ | $-$ | $-$ | $-$ |
| $4$ | $10$ | $11.41$ | $-$ | $-$ | $-$ | $-$ |
| $5$ | $10$ | $11.72$ | $-$ | $-$ | $-$ | $-$ |
| Ср. | $10$ | $11.85$ | $1.18$ | $4.25$ | $0.63$ | $0.09$ |
$Delta t_<случ_1>=|t_1-langle trangle|=|12.13-11.85|=0.28$
1. Как изменяется линейная скорость шарика при его движении по окружности, если модуль скорости $v = const$?
Линейная скорость характеризуется направлением и величиной (модулем). Модуль — величина постоянная, а направление при таком движении способно изменяться.
2. Как доказать соотношение $v = ωR$?
Так как $v = dfrac<1>$, связь циклической частоты с периодом и частой $2π = VT$, откуда $V = 2πR$. Связь линейной скорости и угловой $2πR = VT$, отсюда $V = dfrac<2πr>$. ($R$ — радиус описанной, $r$ — радиус вписанной).
3. Как зависит период обращения $T$ шарика от модуля его линейной скорости?
Чем выше показатель скорости, тем меньше показатель периода.
Выводы: научился определять период вращения, модули, центростремительного ускорения, угловую и линейную скорости при равномерном вращении тела и рассчитывать абсолютную и относительную погрешности прямых измерений промежутка времени движения тела.
Определите ускорение шарика при его движении по окружности, если за время $Δt = 1$ с он прошел $dfrac<1><6>$ длины окружности, имея постоянный модуль линейной скорости $v = 10$ м/с.
Физика. Информатика. Портфолио.
Нашёл ошибку!?
Кто здесь?
Сейчас на сайте 287 гостей и нет пользователей
Последние слова
- Timurasfdc
Информатика
Глобус
Статистика
- Пуск
- Физика 10
- Лабораторные работы
- № 01 Изучение движения тела по окружности
№ 01 Изучение движения тела по окружности
Лабораторная работа № 1
Тема: Изучение движения тела по окружности.
Цель работы: определение центростремительного ускорения шарика при его равномерном движении по окружности.
Оборудование:
- штатив с муфтой и лапкой;
- лента измерительная;
- циркуль;
- динамометр лабораторный;
- весы с разновесами;
- шарик на нити;
- кусочек пробки с отверстием;
- лист бумаги;
- линейка.
Теоретическая часть
Эксперименты проводятся с коническим маятником. Небольшой шарик движется по окружности радиусом R. При этом нить АВ, к которой прикреплен шарик, описывает поверхность прямого кругового конуса. На шарик действуют две силы: сила тяжести mg и натяжение нити F (смотри рис а). Они создают центростремительное ускорение аn, направленное по радиусу к центру окружности. Модуль ускорения можно определить кинематически. Он равен:
an = ω 2 R = 4π 2 R/T 2
Для определения ускорения надо измерить радиус окружности R и период обращения шарика по окружности Т. Центростремительное (нормальное) ускорение можно определить также, используя законы динамики. Согласно второму закону Ньютона ma = mg + F. Разложим силу F на составляющие F1 и F2, направленные по радиусу к центру окружности и по вертикали вверх. Тогда второй закон Ньютона можно записать следующим образом:
Направление координатных осей выберем так, как показано на рисунке б. В проекции на ось O1Y уравнение движения шарика примет вид: 0 = F2 — mg. Отсюда F2 = mg. Составляющая F2 уравновешивает силу тяжести mg, действующую на шарик. Запишем второй закон Ньютона в проекции на ось О1Х: man = F1. Отсюда аn = F1/m. Модуль составляющей F1 можно определить различными способами. Во-первых, это можно сделать пользуясь подобием треугольников ОАВ и FBF1:
F1/R = mg/h
Отсюда F1 = mgR/h и an = gR/h.
Во-вторых, модуль составляющей F1 можно непосредственно измерить динамометром. Для этого оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу R окружности (рис. в), и определяем показание динамометра. При этом сила упругости пружины уравновешивает составляющую F1. Сопоставим все три выражения для аn:
и убедимся, что числовые значения центростремительного ускорения, полученные тремя способами, близки между собой.
В данной работе с наибольшей тщательностью следует измерять время. Для этого полезно отсчитывать возможно большее число N оборотов маятника, уменьшая тем самым относительную погрешность.
Взвешивать шарик с точностью, которую могут дать лабораторные весы, нет необходимости. Вполне достаточно взвешивать с точностью до 1 г. Высоту конуса и радиус окружности достаточно измерить с точностью до 1 см. При такой точности измерений относительные погрешности величин будут одного порядка.
Порядок выполнения работы.
1. Определяем массу шарика на весах с точностью до 1 г.
2. Нить продеваем сквозь отверстие в пробке и зажимаем пробку в лапке штатива (смотри рис. в).
3. Вычерчиваем на листе бумаги окружность, радиус которой около 20 см. Измеряем радиус с точностью до 1 см.
4. Штатив с маятником располагаем так, чтобы продолжение нити проходило через центр окружности.
5. Взяв нить пальцами у точки подвеса, вращаем маятник так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.
6. Отсчитываем время, за которое маятник совершает заданное число оборотов (к примеру, N = 50).
7. Определяем высоту конического маятника. Для этого измеряем расстояние по вертикали от центра шарика до точки подвеса (считаем h
l).
8. Находим модуль центростремительного ускорения по формулам:
an = 4π 2 R/T 2 и an = gR/h
9. Оттягиваем горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измеряем модуль составляющей F1. Затем вычисляем ускорение по формуле аn = F1/m.
10. Результаты измерений заносим в таблицу.
| № опыта | R | N | Δt | T = Δt/N | h | m | an = 4π 2 R/T 2 | an = gR/h | an = F1/m |
| 1 |
Сравнивая полученные три значения модуля центростремительного ускорения, убеждаемся, что они примерно одинаковы.
http://superresheba.by/resh/450
http://www.fizika.degtjarka8.ru/index.php/fizika-10/laboratornye-raboty/111-01-izuchenie-dvizheniya-tela-po-okruzhnosti
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
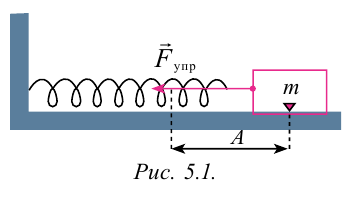
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 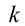
Если груз, который находится в равновесии, потянем вправо на расстояние 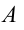
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
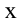
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 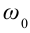
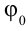
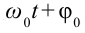
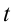
Из математики известно, что 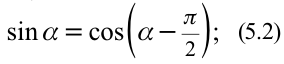
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 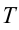

б) частота колебания 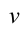
Единица
c) циклическая частота 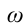
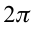
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
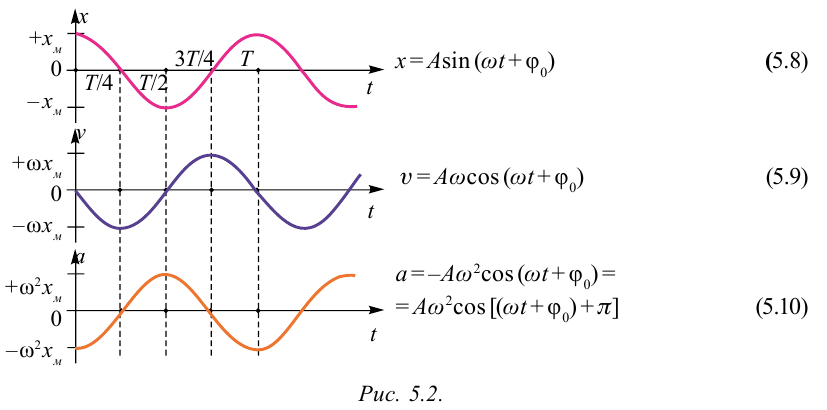
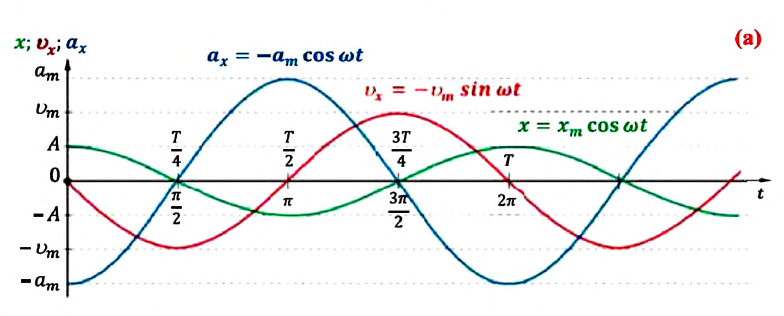
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
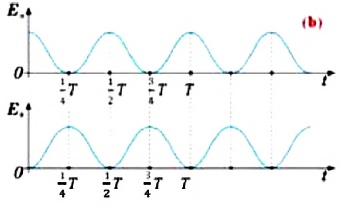
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
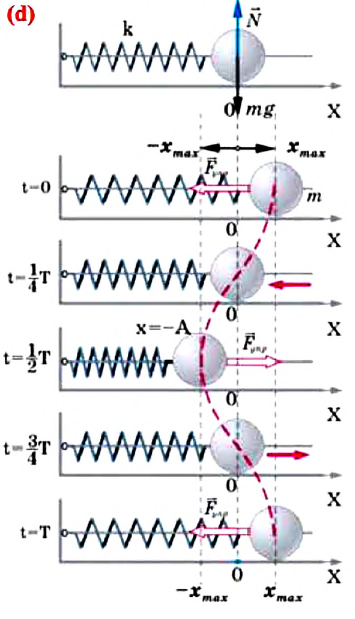
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 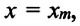
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 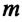
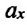
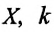
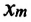
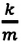
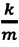
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 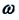
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 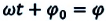
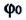
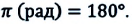
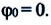

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 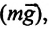
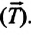
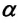
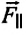
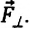
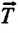
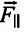
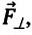
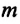
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 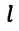
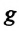
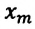
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 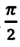
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 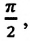
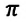
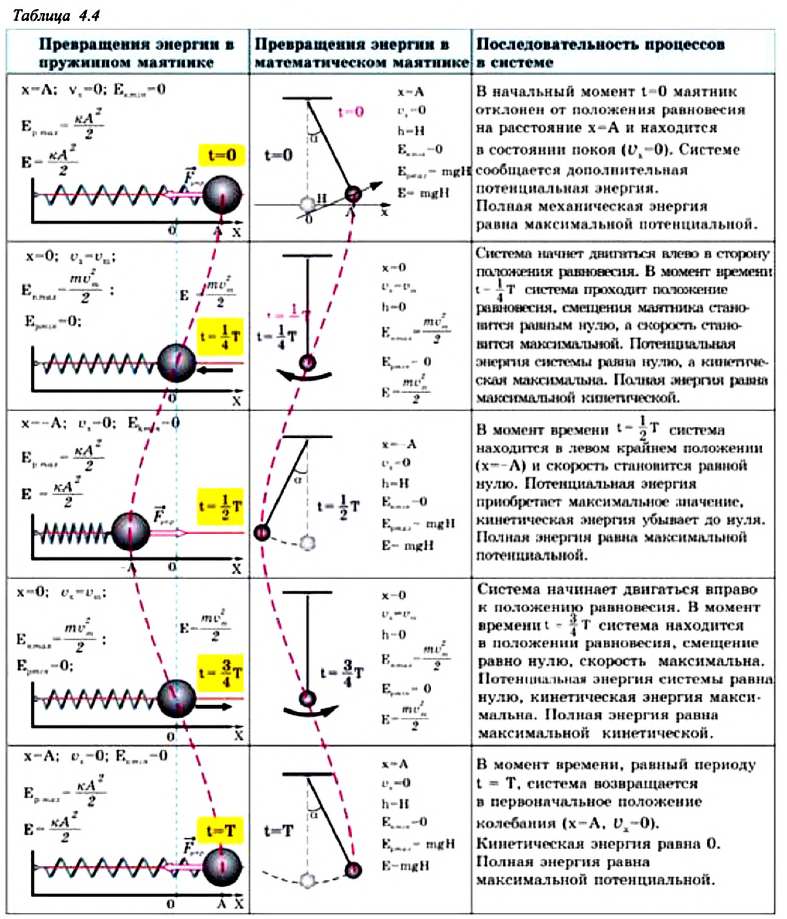
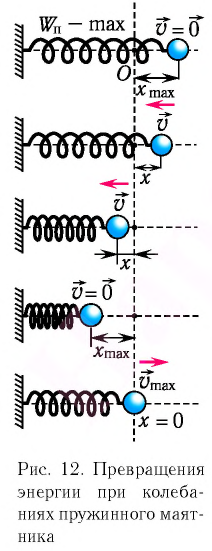
Превращения энергии при гармонических колебаниях
Теоретический материал
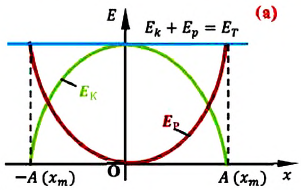
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 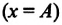
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 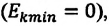
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 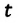
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
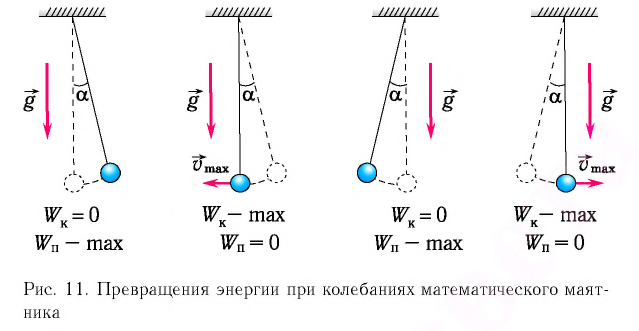
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
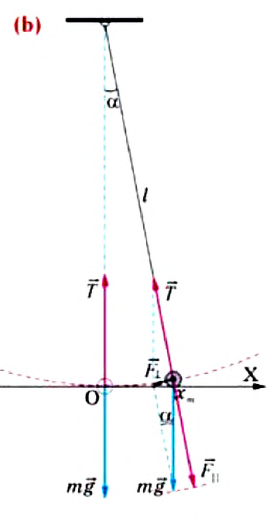
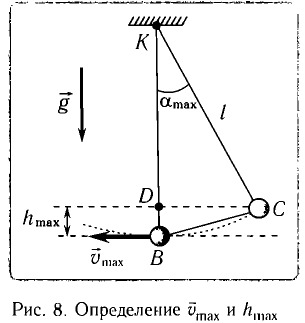
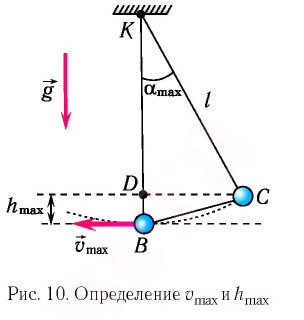
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
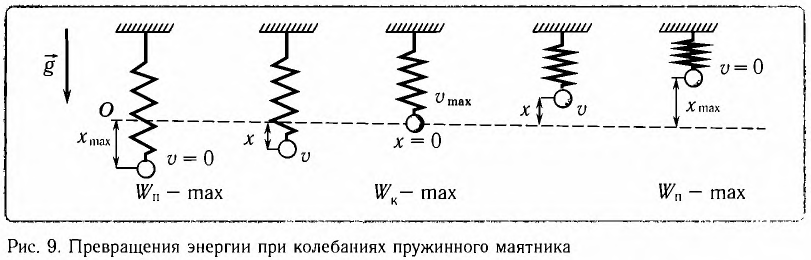
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
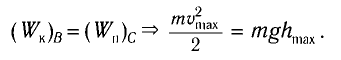
Отсюда найдем модуль максимальной скорости маятника:
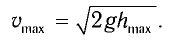
Высоту 
Если колебания малые, то 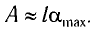
Отсюда
Подставив выражение для 
Подставляя выражения для 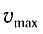

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 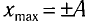
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 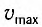
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 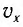
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 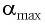
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 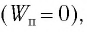
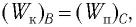
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 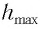
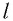
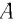
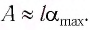
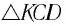
или
Подставив выражение (3) для 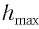
Подставляя выражения (3) для 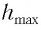
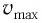
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 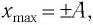
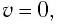
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 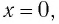
где 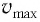
В положениях между крайними точками полная энергия
С учетом выражений для координаты 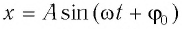
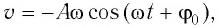
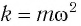
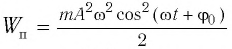
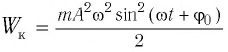
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 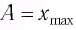
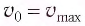
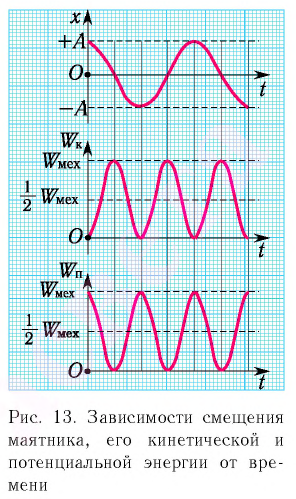
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 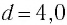
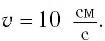
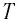
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 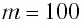
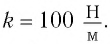
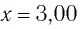
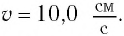
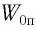
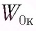
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
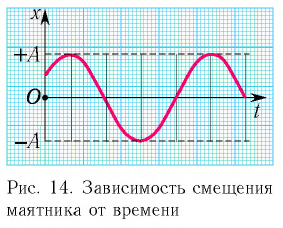
В начальный момент времени 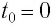
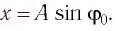
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике