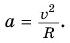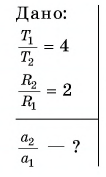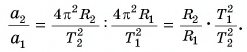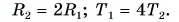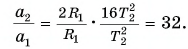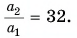Преподаватель который помогает студентам и школьникам в учёбе.
Ускорение точки при ее движении по окружности в физике — формулы и определения с примерами
Ускорение точки при ее движении по окружности:
При равномерном прямолинейном движении ускорение равно нулю. А почему ускорение возникает при движении по окружности? Как оно направлено? Чему равен его модуль?
Пусть тело (рассматриваемое как материальная точка) движется по окружности радиусом R со скоростью, модуль которой не изменяется
Найдем ускорение тела в точке А. Перенесем вектор 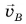
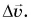
где 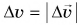
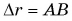
При малых 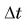
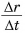
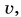
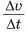
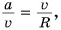
Формула (4) определяет модуль ускорения 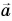
А каково направление ускорения 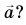
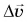
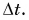
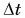
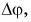
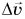
Значит, ускорение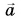
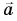
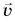
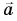
А как связано центростремительное ускорение с угловой скоростью? Подставляя в формулу (4) выражение 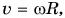
Отсюда, учитывая, что 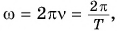
Выведите самостоятельно выражение для центростремительного ускорения через угловую и линейную скорости:
Для любознательных:
А как направлено ускорение 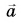
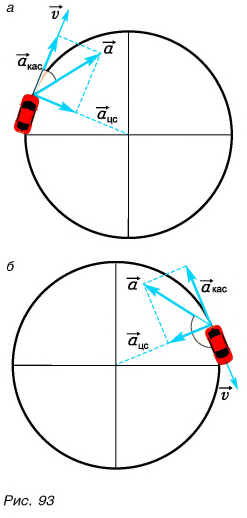
На рисунке 93, а (вид сверху) мчащийся по кольцевой трассе автомобиль набирает скорость. Ускорение автомобиля 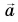
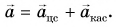
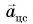
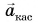
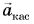
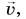
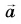
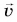
На рисунке 93, б автомобиль тормозит. Модуль скорости уменьшается, составляющая 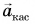
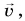
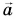
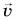
Главные выводы:
- Тело, движущееся по окружности со скоростью, модуль которой
обладает центростремительным ускорением.
- Центростремительное ускорение перпендикулярно скорости и направлено к центру окружности.
- Модуль центростремительного ускорения
- Заказать решение задач по физике
Пример решения задачи:
Период вращения 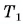
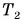
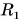
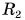
Решение
Согласно формуле (6) отношение модулей центростремительных ускорений точек на ободе второго и первого колеса:
По условию задачи:
Тогда
Ответ:
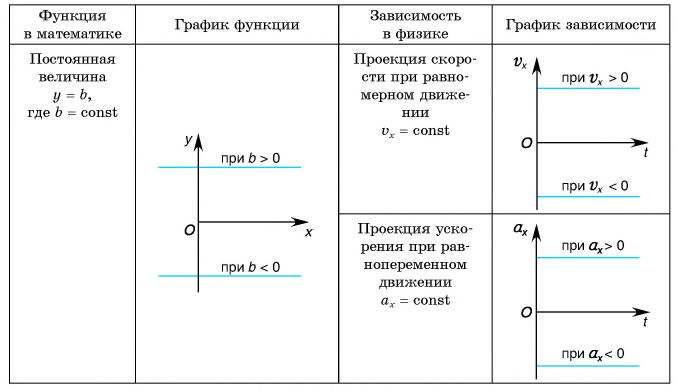
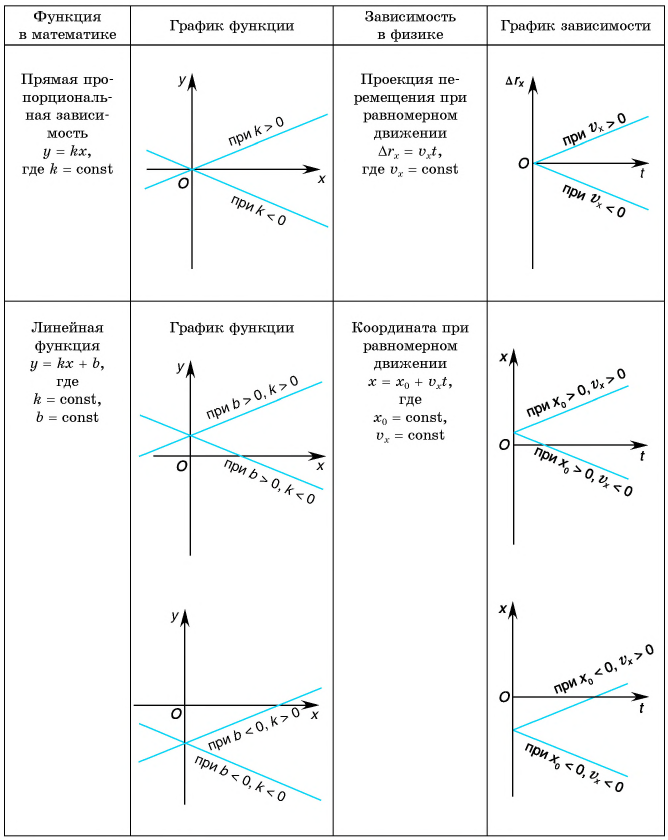
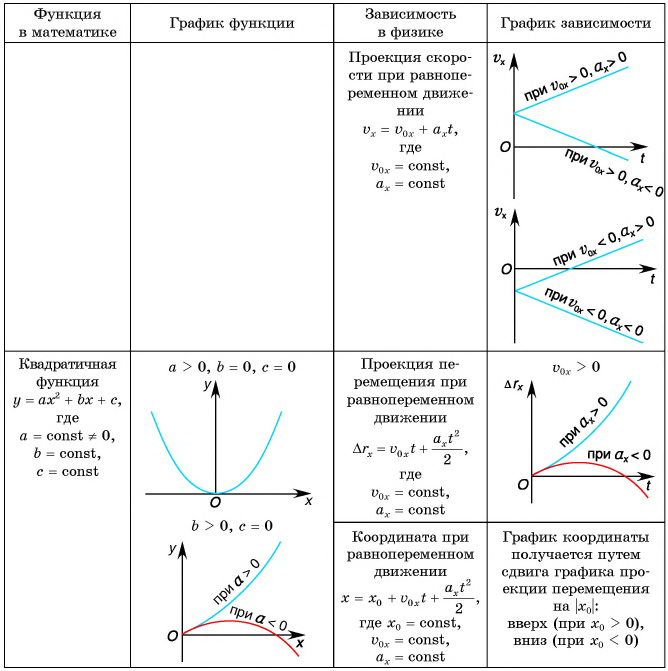
Основные кинематические величины и их графики:
- Инерциальные системы отсчета
- Энергия в физике
- Мощность в физике
- Взаимодействие тел
- Ускорение в физике
- Скорость при равнопеременном движении
- Перемещение, координата и путь при равнопеременном движении
- Криволинейное движение
Центростремительное ускорение
Вернемся теперь к нашей задаче — найти ускорение, с которым тело движется по окружности с постоянной по модулю скоростью.
Ускорение, как известно, определяется по формуле
$vec{a} = frac{ vec{v} — vec{v}_{0} }{t}$,
где $vec{v}_{0}$ — скорость тела в некоторый начальный момент времени, а $vec{v}$ — его скорость через промежуток времени $t$. В нашем случае модули скоростей $vec{v}$ и $vec{v}_{0}$ равны друг другу.
рис. 1
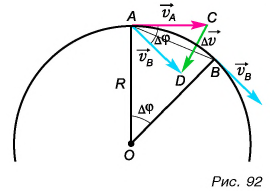
Предположим, что тело движется по окружности радиусом $r$ и что в некоторый момент времени оно находится в точке $A$ (рис. 1).
Чему равно ускорение в этой точке? Скорость $vec{v}_{0}$ в этой точке направлена по касательной к окружности в точке $A$. Через $t$ с тело оказывается в точке $B$, и скорость его $vec{v}$ теперь направлена по касательной к окружности в точке $B$. По модулю скорости $vec{v}$ и $vec{v}_{0}$ равны (длины стрелок $vec{v}$ и $vec{v}_{0}$ одинаковы).
Мы хотим найти ускорение в точке $A$ окружности (мгновенное ускорение). Поэтому точки $A$ и $B$ мы должны взять близкими друг к другу, настолько близкими, чтобы дуга $AB$ как бы стянулась в точку.
Выясним сначала, как направлено это ускорение.
рис. 2
Проведем из центра $O$ окружности радиусы к точкам $A$ и $B$. Радиус окружности перпендикулярен к касательной в точке касания, следовательно, радиусы $OA$ и $OB$ перпендикулярны векторам $vec{v}_{0}$ и $vec{v}$. Чтобы узнать направление вектора ускорения, нужно найти вектор, равный разности векторов $vec{v}$ и $vec{v}_{0}$. Его направление — это и есть направление вектора ускорения. Как производят вычитание векторов, мы уже знаем (см. «Действия над векторами: вычитание векторов»). Чтобы найти разность $vec{v} — vec{v}_{0}$, векторы $vec{v}$ и $vec{v}_{0}$, расположим так, чтобы они исходили из одной точки (рис. 2), и соединим их концы, направив стрелку от вычитаемого к уменьшаемому (от конца вектора $vec{v}_{0}$ к концу вектора $vec{v}$). Вектор $vec{CD}$ и есть разность векторов $vec{v} — vec{v}_{0}$. Следовательно, вдоль вектора $vec{CD}$ направлено ускорение. Что можно сказать об этом направлении?
Треугольник $ADC$ (см. рис. 2) равнобедренный. Угол при вершине $A$ равен углу $phi$ между радиусами $OA$ и $OB$ (рис. 1), так как они образованы взаимно перпендикулярными сторонами. Точки $A$ и $B$ расположены близко друг к другу, поэтому угол $phi$ очень мал (близок к нулю). Каждый из углов при основании треугольника $ADC$ близок к прямому, так как сумма углов треугольника равна двум прямым. Это означает, что вектор $vec{CD} = vec{v} — vec{v}_{0}$ перпендикулярен вектору скорости. Значит, и ускорение перпендикулярно скорости. Но скорость направлена по касательной к окружности в течке $A$, а касательная перпендикулярна радиусу. Значит, и ускорение направлено по радиусу к центру окружности. Его поэтому называют центростремительным ускорением.
При равномерном движении тела по окружности ускорение в любой ее течке перпендикулярно скорости движения и направлено к центру окружности.
рис. 3
Эта интересная особенность ускорения при движении по окружности с постоянней по модулю скоростью показана на рисунке 3.
Найдем теперь модуль центростремительного ускорения. Для этого нужно найти, чему равно абсолютное значение величины $frac{ vec{v} — vec{v}_{0} }{t}$. Из рисунка 2 видно, что модуль разности векторов $| vec{v} — vec{v}_{0} |$ равен длине отрезка $CD$. Так как угол $phi$ очень мал, то отрезок $CD$ мало отличается от дуги $CD$ окружности (показанной пунктиром) с центром в течке $A$. Радиус этой окружности $r$ численно равен $v$ ($r = v$). Но, как мы знаем (см. § 24), длина такой дуги равна $r phi = v phi$. Следовательно, $| vec{v} — vec{v}_{0} | = CD = v phi$. Абсолютное значение ускорения $| vec{a} |$ равно $frac{| vec{v} — vec{v}_{0} |}{t} = frac{v phi}{t}$. Но $frac{ phi }{t }$ — это угловая скорость $omega$. Поэтому
$| vec{a} | = |v omega |$.
Ускорение тела, движущемся по окружности, равно произведению его линейной скорости и угловой cкорости поворота радиуса, проведенного к телу.
Формулу для центростремительного ускорения удобнее представить в таком виде, чтобы в нее входила величина радиуса окружности, по которой движется тело. Так как угловая н линейная скорости связаны соотношением $v = omega r$ ($r$ — радиус окружности), то, подставив это выражение в формулу $| vec{a} | = | v omega |$, получим:
$| vec{a} | = | omega r omega | = omega^{2} r$.
Но $omega = frac{v}{r}$, поэтому формулу для центростремительного ускорения можно записать еще и так:
$| vec{a} | = v frac{v}{r} = frac{v^{2} }{r}$.
При равномерном движении по окружности тело движется с ускорением, которое направлено по радиусу к центру окружности и модуль которого определяется выражением $| vec{a} | = omega^{2}r$, или $| vec{a} |= frac{v^{2} }{r}$.
Следовательно, верно и обратное: если известно, что скорость тела равна $v$ и ускорение тела во всех точках перпендикулярно вектору его скорости и по абсолютному значению равно $| vec{a} |$, то можно утверждать, что такое тело движется по окружности, радиус которой $r$ определяется формулой
$r = frac{v^{2} }{| vec{a} |}$.
Значит, если нам известны начальная скорость тела и абсолютное значение его центростремительного ускорения, мы можем изобразить окружность, по которой тело будет двигаться, и найти его положение в любой момент времени (начальное положение тела должно быть, конечно, известно). Тем самым будет решена основная задача механики.
Напомним, что ускорение при равномерном движении по окружности нас интересует потому, что всякое движение по криволинейной траектории представляет собой движение по дугам окружностей различных радиусов.
рис. 4
Теперь мы можем сказать, что при равномерном движении в любой точке криволинейной траектории тело движется с ускорением, направленным к центру той окружности, частью которой является данная траектория вблизи этой точки. Численное же значение ускорения зависит от скорости тела в этой точке и от радиуса соответствующей окружности. На рисунке 4 показана некоторая сложная траектория и указаны векторы центростремительного ускорения в различных точках траектории.
Задача. Самолет, выходя из пике, движется по дуге, которая в нижней своей части является дугой окружности радиусом 500 м (рис. 5). Вычислите ускорение самолета в наинизшей точке, если его скорость равна 800 км/ч, и сравните полученное значение с ускорением свободного падения.
рис. 5
Решение. Ускорение самолета вычисляем по формуле
$| vec{a} | = frac{v^{2} }{r}$.
Подставив сюда значения
$v = frac{800 cdot 10^{3} м}{3600 с} = 222 frac{м}{с}$ и $r = 500 м$,
получаем:
$| vec{a} | = frac{ left ( 222 frac{м}{с^{2} } right )^{2} }{500 м} = 97,7 frac{м}{с^{2} }$.
Так как
$g = 9,8 frac{м}{с^{2} }$, то $| vec{a} | approx 10g$.
Физика, 10 класс
Урок 04.Равномерное движение точки по окружности
Перечень вопросов, рассматриваемых на уроке:
- Равномерное движение точки по окружности и его характеристики.
- Центростремительное ускорение.
Глоссарий по теме
Криволинейное движение – это движение по дугам окружностей разных радиусов.
Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.
Ключевые слова
Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56
Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.
Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.
При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.
Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.
Возьмем разные точки на линии и нарисуем векторы скорости 
Векторы 

Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости 

2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.
Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение
Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.
Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.
Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была
Модули скоростей равны:

но вектора скоростей 
Поэтому построим вектор 





Вспомним, что вектор
Что можно сказать об угле между векторами 
Рассмотрим равнобедренный треугольник со сторонами 

Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 900
Вектор 



Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами 
Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю. Тогда можно сказать, что длина хорды s равна длине дуги АВ при
Длина дуги АВ это путь, пройденный точкой от А до В,
тогда запишем:
Умножим на
В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:
Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными
- Криволинейное движение — это движение по дугам окружностей разных радиусов.
А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.
Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.
Основные выводы:
— движение криволинейное, так как траекторией является окружность;
— движение равномерное, так как модуль скорости не меняется;
— вектор скорости направлен по касательной к окружности;
-вектор ускорения направлен к центру окружности;
— модуль центростремительного ускорения равен:
Примеры и разбор решения заданий
1. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением
где R = 50 м; υ= 
Тогда ac = (10 м/с)2 / 50 м = 2 м/с2.
Ответ: 2 м/с2
2. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
Дано:
R1 =10см = 0,10 м
R2 = 30см = 0,30 м
Найти — 
Задано два объекта:
1) материальная точка, которая движется по окружности R1;
2) материальная точка, которая движется по окружности R2.
При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением
Для тела 1 уравнение (1) примет вид:
для тела 2:
Тогда
Центростремительное ускорение тела (2) меньше 
Основные ссылки
CSS adjustments for Marinelli theme

Вы здесь
Главная » Центростремительное ускорение. Равнопеременное…
Центростремительное ускорение. Равнопеременное движение по окружности.
| Центростремительное ускорение. | ||
|
Вычислим величину ускорения при равномерном движении точки по окружности и найдем его направление. Пусть за некоторый промежуток времени t тело переместилось из точки А в точку А1 с постоянной по модулю скоростью. Изобразим вектора скорости в этих точках и найдем вектор изменения скорости Рассмотрим треугольники АА1О и А1СВ. Эти треугольники равнобедренные и углы при их вершинах равны, т.к. АО┴СВ и А1О┴А1С (углы со взаимно перпендикулярными сторонами). Следовательно, эти треугольники подобны. Из подобия треугольников следует пропорция: Разделим правую и левую части равенства на промежуток времени, за которое совершено перемещение, и учтем, что |
Примеры: — Земля при вращении вокруг оси ацс=0,03 м/с2, — Земля при вращении вокруг Солнца ацс=0,006 м/с2, — Солнечная система при вращении вокруг центра Галактики ацс=3.10-10 м/с2. |
|
|
Теперь определим направление ускорения. Т.к. мы должны для определения ускорения брать предел при Δt→0, то из рисунка видно, что угол φ будет уменьшаться (→0), а b→900. Это значит, что прямая А1В (вектор Следовательно, вектор ускорения при равномерном движении по окружности направлен к центру окружности (центру вращения). Поэтому ускорение наз. центростремительным ускорением. |
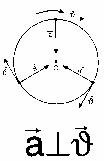 |
|
|
Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости. Используя связь между угловой и линейной скоростями, получим: |
||
|
Равнопеременное движение по окружности. Все уравнения для этого движения получим по аналогии с равнопеременным прямолинейным движением. |
||
|
Равнопеременное прямолинейноедвижение. |
Равнопеременное движение по окружности.
|
Равномерное движение по окружности.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна
. Скорость
называется линейной скоростью точки.
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
. (1)
Частота обращения — это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду. Измеряется частота в об/с (обороты в секунду).
Пусть, например, . Это означает, что за время
точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
 |
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при
точка имела координаты
. Пусть за время
точка повернулась на угол
и заняла положение
.
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
. (2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол
. Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
. (4)
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
.
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Равномерное движение по окружности.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023




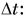


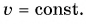



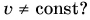
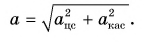
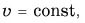 обладает центростремительным ускорением.
обладает центростремительным ускорением.