Длина направленного отрезка определяет числовое значение вектора и называется длиной, или модулем, вектора.
Из теоремы Пифагора следует, что в треугольнике (ABC) длина отрезка (AB), которая является модулем вектора
AB→
, равна
AC2+CB2
, и, следовательно, модуль (длина) вектора
AB→
рассчитывается по формуле
AB→=x2+y2
.
Пример:
вычисли длину вектора
AB→=5;3
.
Расстояние между двумя точками
Как известно, координаты вектора можно определить, если даны координаты начальной и конечной точек вектора
Ax1;y1
и
Bx2;y2
.
Если
x=x2−x1
,
y=y2−y1
и
AB→=x2+y2
, то вместо (x) и (y) можно поставить их выражения.
Новую формулу называют не только формулой длины вектора, но и формулой расстояния между двумя точками с заданными координатамиAB=x2−x12+y2−y12.
Так как выражения в скобках в квадрате, то справедливо, что
.
То есть, не важна последовательность координат в разности.
Обрати внимание!
Если даны координаты начальной и конечной точек вектора
Ax1;y1
и
Bx2;y2
, то
AB→x2−x1;y2−y1
.
Обязательно из координат конечной точки надо вычитать координаты начальной точки!
Но при определении длины вектора в формуле последовательность координат не имеет значения:
AB→=x2−x12+y2−y12=x1−x22+y1−y22
.
Содержание:
- Формула
- Примеры вычисления модуля вектора
Формула
Чтобы найти модуль вектора, заданного своими координатами, нужно найти его длину, то есть извлечь корень из суммы
квадратов его координат. Если вектор задан на плоскости и имеет координаты $bar{a}=left(a_{x} ; a_{y}right)$, то его модуль вычисляется по формуле
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
То есть модуль вектора равен корню квадратному из суммы квадратов координат.
Если вектор задан в пространстве координатами
, то его модуль вычисляется по формуле
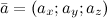
$$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$$
Примеры вычисления модуля вектора
Пример
Задание. Найти модуль вектора $bar{a}=(-1 ; 1)$
Решение. Для нахождения модуля вектора, заданного на плоскости воспользуемся формулой:
$$|bar{a}|=sqrt{a_{x}^{2}+a_{y}^{2}}$$
Подставляя в неё координаты заданного вектора, будем иметь:
$$|bar{a}|=sqrt{(-1)^{2}+1^{2}}=sqrt{1+1}=sqrt{2}$$
Ответ. $|bar{a}|=sqrt{2}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В пространстве заданны точки
$A(2 ;-4 ; 1)$ и $B(-2 ; 0 ; 3)$. Найти модуль вектора
$overline{A B}$
Решение. Найдем координаты вектора $overline{A B}$. Для этого из координат конца
(точки $B$ ) вычтем соответствующие координаты начала (точки
$A$ ):
$$overline{A B}=(-2-2 ; 0-(-4) ; 3-1)=(-4 ; 4 ; 2)$$
Далее для нахождения модуля вектора $overline{A B}$ воспользуемся формулой:
$|overline{a}|=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}$
Подставляя координаты вектора $overline{A B}$, получим:
$$|overrightarrow{A B}|=sqrt{(-4)^{2}+4^{2}+2^{2}}=sqrt{16+16+4}=sqrt{36}=6$$
Ответ. $|overrightarrow{A B}|=6$
Читать дальше: как найти координаты вектора.
Заказать задачи по любым предметам можно здесь от 10 минут
Модуль вектора
Формула
Чтобы найти модуль вектора по координатам нужно извлечь квадратный корень из суммы квадратов его координат, то есть найти длину вектора.
Если вектор задан на плоскости в виде $ overline{a} = (x;y) $, то вычисляется модуль по формуле: $$ |overline{a}|=sqrt{x^2+y^2} $$
В случае, когда вектор задан в пространстве тремя координатами $ overline{a}= (x;y;z) $, то модуль находится по формуле: $$ |overline{a}|=sqrt{x^2+y^2+z^2} $$
Для нахождения модуля вектора нам понадобится знать:
- Координаты вектора
- Формулы
Примеры решений
| Пример |
| Найти модуль вектора $ overline{a} = (3;4;0) $ |
| Решение |
|
Зная координаты мы первым делом определяем на плоскости или в пространстве задана задача. В нашем случае координат у вектора три, поэтому в пространстве (было бы две координаты, то на плоскости). Используем вторую формулу для пространственной задачи: $$ |overline{a}|=sqrt{x^2+y^2+z^2} $$ Подставляя в формулу в место $ x,y,z $ числа из задания получаем модуль: $$ |overline{a}|=sqrt{3^2+4^2+0^2} = sqrt{9+16+0} = sqrt{25}=5 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ |overline{a}|= sqrt{25}=5 $$ |
Определение длины вектора
Определение.
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Основное соотношение. Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
Формулы длины вектора
Формула длины вектора для плоских задач
В случае плоской задачи модуль вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой:
Формула длины вектора для пространственных задач
В случае пространственной задачи модуль вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой:
Формула длины n -мерного вектора
В случае n-мерного пространства модуль вектора a = {a1 ; a2; … ; an} можно найти воспользовавшись следующей формулой:
Примеры задач на вычисление длины вектора
Примеры вычисления длины вектора для плоских задачи
Пример 1. Найти длину вектора a = {2; 4}.
Решение: |a| = √22 + 42 = √4 + 16 = √20 = 2√5.
Пример 2. Найти длину вектора a = {3; -4}.
Решение: |a| = √32 + (-4)2 = √9 + 16 = √25 = 5.
Примеры вычисления длины вектора для пространственных задачи
Пример 3. Найти длину вектора a = {2; 4; 4}.
Решение: |a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Пример 4. Найти длину вектора a = {-1; 0; -3}.
Решение: |a| = √(-1)2 + 02 + (-3)2 = √1 + 0 + 9 = √10.
Примеры вычисления длины вектора для пространств с размерностью большей 3
Пример 5. Найти длину вектора a = {1; -3; 3; -1}.
Решение: |a| = √12 + (-3)2 + 32 + (-1)2 = √1 + 9 + 9 + 1 = √20 = 2√5
Пример 6. Найти длину вектора a = {2; 4; 4; 6 ; 2}.
Решение: |a| = √22 + 42 + 42 + 62 + 22 = √4 + 16 + 16 + 36 + 4 = √76 = 2√19.
Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.
Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!
Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Модуль вектора
Определение и формула модуля вектора
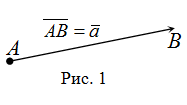
Если вектор задан, например, в двумерном пространстве, своими координатами 
, то его модуль равен корню квадратному из суммы квадратов координат:
![[left|bar{a}right|=sqrt{a_{1}^{2} +a_{2}^{2} } ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-ba06bcc316f44f279de456d17de01f76_l3.png "Rendered by QuickLaTeX.com")
Примеры нахождения модуля векторов
| Понравился сайт? Расскажи друзьям! | |