Уравнение биссектрисы в треугольнике — формула, свойства и решение задач
Прямая на плоскости
Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
- На плоскости, где достаточно двух координат для описания любых геометрических объектов.
- В трехмерном пространстве, где любая точка имеет три координаты.
Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:
- Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
- Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
- Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
- Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.
Делящая пополам угол линия
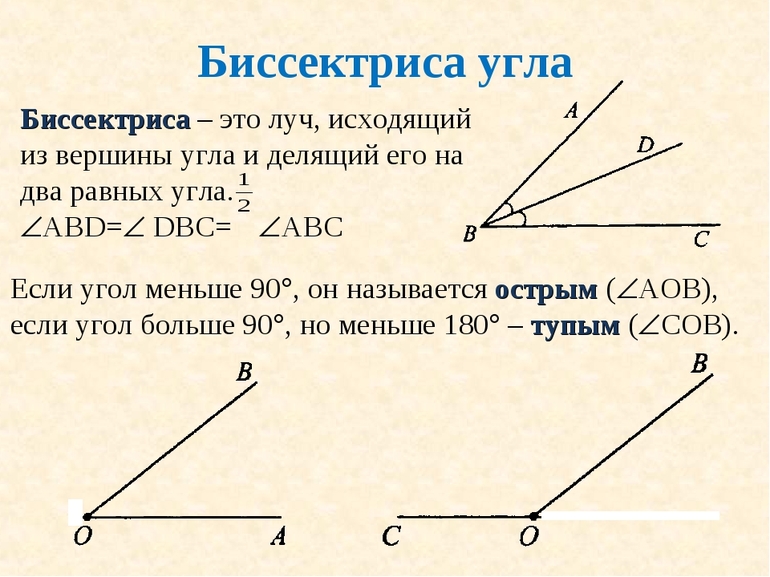
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.
Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.
Способы построения
В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:
- С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
- С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.
Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.
В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.
Основные свойства
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.
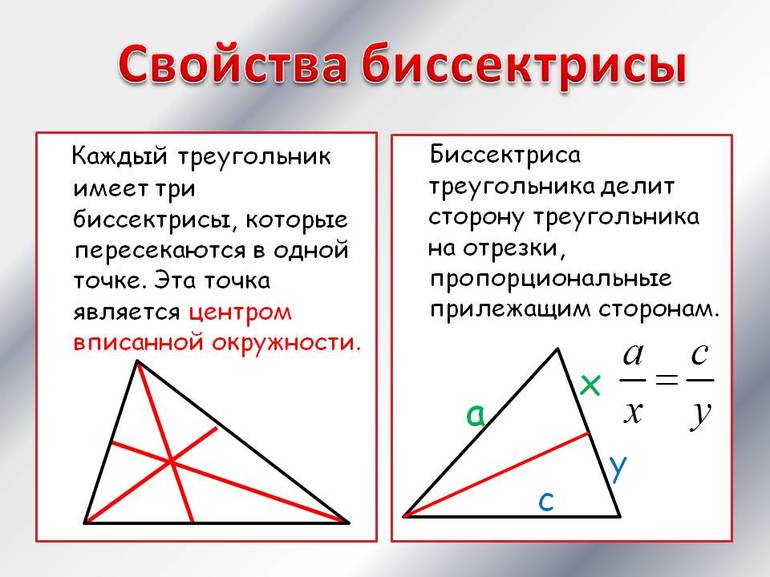
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.
Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.
В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:
Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.
Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:
Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.
Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.
Уравнение биссектрисы треугольника
Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.
В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):
- Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
- Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
- Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.
Пример решения задачи
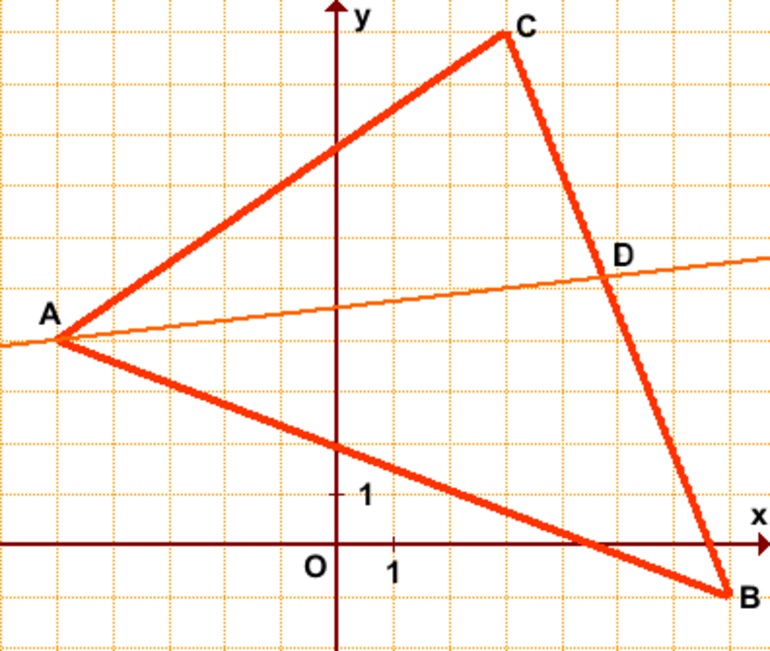
Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.
Сначала нужно написать уравнения прямых для сторон AB и CB, получается:
- AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
- CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.
Составить уравнения биссектрис можно так:
| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.
Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:
- y*(6−3*3 0,5 ) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
- y*(3*3 0,5 +6) -x*(4+3*3 0,5 )+12+6*3 0,5 = 0.
Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:
Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:
При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:
- D1A = 1,4; D1C = 3,635;
- D2A = 0,621; D2C = 1,614.
Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:
BD2 = 2,014 единицы.
Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.
Уравнение биссектрисы в треугольнике — формула, свойства и решение задач
Треугольник является одной из самых простых фигур, которая часто встречается школьникам в задачах по геометрии. В свою очередь, биссектриса представляет собой важный элемент, характеризующий тот или иной угол. Решение геометрических проблем с участием этих объектов требует наличия определенных знаний. Чтобы уметь составлять по координатам вершин уравнение биссектрисы треугольника, необходимо понимать выражения для прямых линий.
Прямая на плоскости
Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:
Делящая пополам угол линия
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.
Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.
Способы построения
В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:
Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.
В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.
Основные свойства
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.
Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.
В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:
Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.
Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:
Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.
Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.
Уравнение биссектрисы треугольника
Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.
В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):
Пример решения задачи
Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.
Сначала нужно написать уравнения прямых для сторон AB и CB, получается:
- AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
- CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.
Составить уравнения биссектрис можно так:
| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.
Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:
- y*(6−3*3 0,5 ) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
- y*(3*3 0,5 +6) -x*(4+3*3 0,5 )+12+6*3 0,5 = 0.
Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:
Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:
При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:
- D1A = 1,4; D1C = 3,635;
- D2A = 0,621; D2C = 1,614.
Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:
BD2 = 2,014 единицы.
Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.
Вектор, который является биссектрисой угла между векторами! помогите
Дано: вектор а с координатами (-4;3;0) и вектор b с координатами (12;-15;16) найти : координаты вектора с, являющийся биссектрисой угла между векторами а и b
Чтобы получить вектор, направленный по биссектрисе угла между векторами, нужно сложить векторы, сонаправленные с заданными векторами, но равной длины. Нарпример, найдём орты заданных векторов, поделив координаты векторов на их длины. Получим вектор (-4/5; 3/5, 0) и вектор (12/25; -15/25; 16/25). Искомый вектор имеет координаты, равные суммам соответствующих координат.
http://sprint-olympic.ru/uroki/geometrija/129894-yravnenie-bissektrisy-v-treygolnike-formyla-svoistva-i-reshenie-zadach.html
http://sprashivalka.com/tqa/q/20350200
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Вектор медианы, вектор высоты, вектор биссектрисы
|
|||
|
В треугольнике с вершинами А(3;4;5), В(4;6;8), С(0;1;-2) найти: Векторы медианы и высоты нашла, осталась биссектриса. Решаю по книге Выш. Мат. Терёхина Л.И. и Фикс И.И. (замечательная книга), но там не примера с биссектрисой.
|
||
| Вернуться к началу |
|
||
|
Higin |
Заголовок сообщения: Re: Вектор медианы, вектор высоты, вектор биссектрисы
|
|
Благодарю!
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Пересечения медианы, высоты и биссектрисы
в форуме Геометрия |
Avgust |
16 |
373 |
13 сен 2021, 15:33 |
|
Уравнение высоты и медианы треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Sonnoe Chudo |
5 |
888 |
12 окт 2014, 06:16 |
|
Составить уравнение медианы и высоты
в форуме Аналитическая геометрия и Векторная алгебра |
dmlch |
1 |
153 |
08 дек 2020, 12:57 |
|
Найти уравнения медианы и высоты
в форуме Аналитическая геометрия и Векторная алгебра |
Yntykbay |
1 |
589 |
09 ноя 2015, 22:38 |
|
Написать уравнение сторон треугольника, медианы, высоты и
в форуме Геометрия |
kity2503 |
1 |
752 |
01 май 2016, 21:14 |
|
Найти вектор высоты тетраэдра
в форуме Аналитическая геометрия и Векторная алгебра |
ulyana26081995 |
7 |
2245 |
31 дек 2016, 18:29 |
|
Биссектрисы в треугольнике
в форуме Геометрия |
Alex_Korneplod |
2 |
253 |
12 дек 2021, 15:32 |
|
Биссектрисы трапеции
в форуме Геометрия |
Nora |
2 |
304 |
21 дек 2016, 08:33 |
|
Биссектрисы углов
в форуме Геометрия |
sfanter |
1 |
626 |
26 июн 2014, 00:11 |
|
Биссектрисы трапеции
в форуме Геометрия |
sfanter |
1 |
354 |
05 апр 2015, 22:10 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: Yandex [bot] и гости: 13 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
Как составить уравнение биссектрисы треугольника по координатам его вершин?
1 способ
Используя уравнение биссектрисы угла:
Пример.
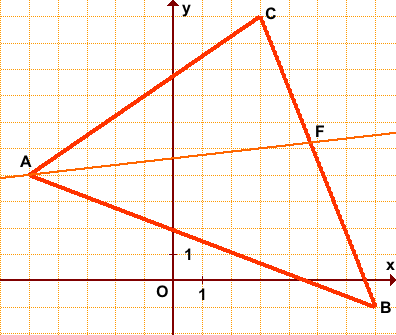
Даны вершины треугольника A(-5;4), B(7;-1) и C(3;10).
1) Составить уравнение биссектрисы треугольника ABC, выходящей из вершины A.
2) Найти длину этой биссектрисы.
Решение:
1) Угол A образован прямыми AB и AC. Составим уравнения этих прямых.
Уравнение прямой, проходящей через две точки, можно найти, например, по формуле
Уравнение прямой AB:
Уравнение прямой AC:
Подставляем уравнения прямых AB и AC в формулы уравнения биссектрис угла:
и
то есть
и
Из этих уравнений является уравнением биссектрисы внутреннего угла BAC треугольника, другое — биссектрисой внешнего угла при вершине A. Как отличить уравнение биссектрисы внутреннего угла?
Точки B и C лежат по одну сторону от биссектрисы внешнего угла, поэтому при подстановке координат B и C в уравнение мы получим числа одинакового знака. От биссектрисы внутреннего угла B и C лежат по разные стороны, поэтому подстановка их координат в уравнение биссектрисы внутреннего угла даёт нам числа разных знаков.
Подставляем в уравнение x-8y+37=0 координаты B и C.
B(7;-1): 7-8·(-1)+37>0
C(3;10): 3-8·10+37<0.
Таким образом, уравнение x-8y+37=0 является уравнением биссектрисы AF треугольника ABC.
2) Чтобы найти длину биссектрисы, найдём точку пересечения прямых AF и BF.
Уравнение прямой BC:
Координаты точки пересечения прямых AF и BC находим из системы уравнений
Решение системы —
Длину биссектрисы AF находим по формуле расстояния между точками A и F:
2 способ
Используя свойство биссектрисы треугольника:
По формулам деления отрезка в данном отношении
разделим отрезок BC в отношении 13 к 10, то есть
Составим уравнение биссектрисы AF треугольника ABC как уравнение прямой, проходящей через точки
Прямая на плоскости
Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
- На плоскости, где достаточно двух координат для описания любых геометрических объектов.
- В трехмерном пространстве, где любая точка имеет три координаты.
Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:
- Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
- Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
- Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
- Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.
Делящая пополам угол линия
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.
Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.
Способы построения
В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:
- С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
- С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.
Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.
В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.
Основные свойства
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.
Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.
В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:
DB/DC = AB/AC.
Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.
Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:
L (A) = 2/(b+c)*(b*c*p*(p-a))^0,5.
Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.
Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.
Уравнение биссектрисы треугольника
Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.
В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):
- Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
- Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
- Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.
Пример решения задачи
Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.
Сначала нужно написать уравнения прямых для сторон AB и CB, получается:
- AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
- CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.
Составить уравнения биссектрис можно так:
| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.
Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:
- y*(6−3*3 0,5) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
- y*(3*3 0,5+6) -x*(4+3*30,5)+12+6*3 0,5 = 0.
Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:
x = 2*y + 3.
Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:
- D1 = (-0,2515;-1,6258);
- D2 = (1,556;-0,722).
При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:
- D1A = 1,4; D1C = 3,635;
- D2A = 0,621; D2C = 1,614.
Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:
BD2 = 2,014 единицы.
Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.
7.3. Разложение вектора по базису. Координаты вектора Модуль вектора. Направляющие косинусы
Пусть
— единичные векторы осей координат, т.е.
и каждый из них одинаково направлен с
координатными осями.
Тройка векторов
называется
координатным
базисом.
Теорема.
Любой вектор пространства можно разложить
по базису
,
т.е. представить
в виде
,
где
— некоторые числа (буквы:
— «мю»,
— «ню»).
Это разложение
единственное.
Доказательство.
Приложим вектор
к началу координат, обозначим его конец
.
Проведем
через точку
плоскости,
перпендикулярные осям координат. Пусть
,
,
— точки
пересечения этих плоскостей с осями
координат.
Существует
единственная тройка чисел
,
,
таких, что
.
Формула
называется
разложением вектора по координатному
базису.
Числа
,
,
— называются
координатами
вектора
,
т.е. координаты
вектора есть его проекции на соответствующие
координатные оси. В символическом виде
записывают
.
Например, если,
то его
координаты
.
Зная координаты
вектора
,
длину его можно найти по формуле
Если известны
координаты точек
и
,
то координаты вектора равны:
.
Пусть углы вектора
с осями
,
,
соответственно равны
,
,
.
Числа
,
,
называются
направляющими косинусами вектора
.
;
;
;
— основное
свойство направляющих косинусов вектора.
7.4. Действия над векторами, заданными координатами
Пусть векторы
и
заданы своими координатами.
При сложении
(вычитании) векторов их одноименные
координаты складываются (вычитаются),
т.е.
При умножении
вектора на число
координаты его умножаются на это число,
т.е.
.
Если вектор
коллинеарен вектору
,
то можно записать
,
где
— некоторое число, т.е.
,
,
.
Отсюда,
,
,
или
— условие коллинеарности векторов.
7.5. Деление отрезка в данном отношении
,
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
Пусть даны координаты
точек
и
;
и отношение
.
Требуется найти координаты точки
.
Из равенства
векторов следует равенство соответствующих
координат:
.
Аналогично,
;
.
В частном случае:
— середина
отрезка, т.
.
Пример.
Дан треугольник
,
где
,
,
.
Найти
координаты точки
—
пересечения
биссектрисы угла
со стороной
.
,
,
,
.
.
Ответ:
.
§ 8. Скалярное
произведение векторов
8.1. Определение
скалярного произведения
Определение.
Скалярным произведением вектора
на вектор
называется число
(скаляр),
равное произведению длин этих векторов
на косинус угла между ними.
Обозначается:
или
.
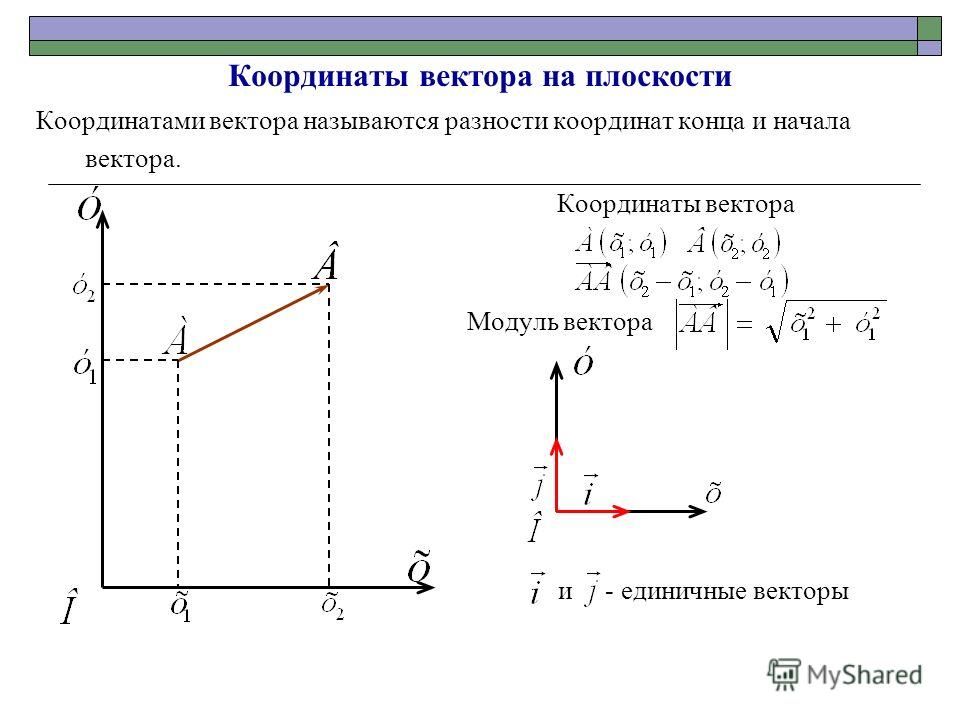
Найдем
проекцию вектора
на вектор
.
Из геометрии
известно
.
Умножим и разделим
левую часть на
:
,
аналогично находим
.
8.2. Свойства
скалярного произведения
1.
Доказательство.
.
2.
.
3.
.
4.
.
Определение:
Число, равное
,
называется скалярным
квадратом
вектора
.
5.
Скалярный квадрат вектора равен
квадрату его длины
.
Доказательство.
.
6.
Скалярное произведение базисных
векторов:
,
.
8.3. Вычисление
скалярного произведения векторов через
координаты
Теорема. Если
,
,
то
.
Доказательство.
Запишем векторы
и
в виде разложения по базису, т.е.
и
.
Тогда
По свойству
скалярного произведения базисных
векторов
:
Таким образом,
.
8.4. Приложения
скалярного произведения векторов
-
Установление
перпендикулярности ненулевых векторов:
.
|
Если |
— |
2. Вычисление
проекции вектора на вектор:
и
.
|
3. Определение |
,
т.е.
.
4. Работа постоянной
силы.
Если
точка перемещается прямолинейно из
положения
в положение
под действием силы
,
то работа по перемещению равна:
.
Пример 1.
К точке
приложены три силы
.
Вычислить
работу по перемещению точки
в точку
.
— равнодействующая
трех сил.
.
.
Пример 2.
Дано:
,
,
,
.
Найти угол между
векторами
и
.
Так как
или
.
,
,
Таким образом,
.
Пример 3.
Найти длину вектора
,
если
,
,.
«Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.»
Министерство образования, науки и молодежной политики Краснодарского края государственное бюджетное профессиональное образовательное учреждение Краснодарского края
«Лабинский социально-технический техникум»
Методическая разработка
урока математики
по теме:
«Вектор.
Подготовила:
преподаватель математики
Пятакова З.В.
Лабинск, 2015
Вектор. Модуль вектора. Равенство векторов. Координаты вектора. Сложение векторов.
Цели урока:
Образовательные:Изучить, что такое “вектор в пространстве», как определяются координаты, вектора, если известны координаты его начала и конца, научится решать задачи, связанные с векторами.
Развивающие: расширение кругозора учащихся, формирование умений применять приёмы сравнивания, обобщения, выделения главного, переноса знаний в новую ситуацию, развитие мышления, речи, умение комментировать, развитие учебно-познавательных компетенций учащихся
Воспитательные: воспитывать трудолюбие, чувство товарищества и взаимопомощи, привитие навыков самооценки, умения работать в коллективе, умения правильно оценивать работуодногруппников,прививать интерес к предмету.
План урока:
-
Организационный момент.
-
Актуализация знаний.
-
Изучение нового материала.
-
Закрепление знаний.
-
Итоги урока.
-
Самостоятельная подготовка.
Оборудование: Интерактивная доска
Тип урока: Комбинированный.
Ход урока:
1. Организационный момент.
Приветствие учащихся, проверка готовности класса к уроку, организация внимания учащихся, раскрытие общих целей урока и плана его проведения.
2. Актуализация знаний
3. Изучение нового материала
Рассказ преподавателя:
ВЕКТОР. КООРДИНАТЫ ВЕКТОРА В ПРОСТРАНСТВЕ
В пространстве, как и на плоскости, вектором называется величина, которая задается своей длиной и направлением. Вектор изображатеся направленным отрезком, длина которого равна длине вектора.
(Слайд 2)
Буквально так же, как и на плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.
Но это не простое повторение, а обобщение, распространение свойств двумерной геометрии на трехмерную. Если в планиметрии для задания вектора достаточно указать две его координаты, то в стереометрии — три координаты.
Определение. Координатами вектора , начало которого точка A(x1,y1,z1), а конец — точкаВ(х2, у2, z2), называются числа a1= х2- x1, a2=y2-y1, a3=z2-z1.
Записывают такой вектор, указывая его координаты: (a1 а2, а3) или (a1 а2, а3).
(Слайд 3)
Например, если точки А(4; 0; 3) и B(0; 6; 4) — начало и конец направленного отрезка , тогда
а1 = 0 — 4 = -4, а2 = 6 — 0 = 6, а3 = 4 — 3 = 1.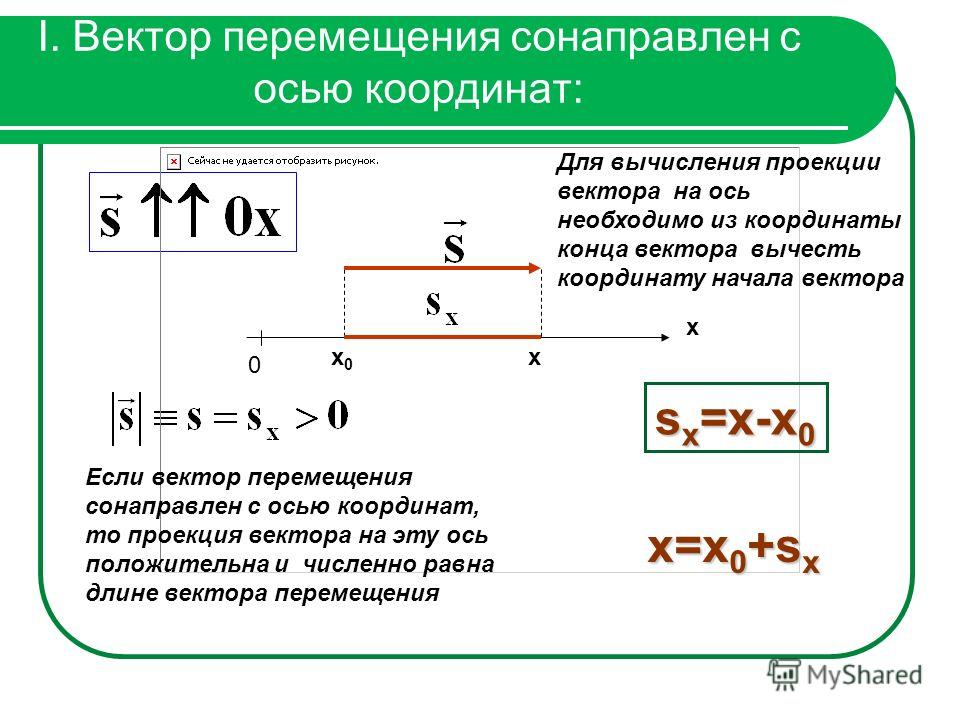
Значит, направленному отрезку соответствует вектор (-4; 6; 1) (рис. 67).
(Слайд 4)
Так же, как и на плоскости, равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание говорить о том, что любой вектор можно отложить от любой точки пространства.
(слайд 5)
Длину вектора (a1 а2, а3) можно выразить через его координаты. Отложим вектор от начала координат (рис. 68). Тогда четырехугольник OPAN — прямоугольник. Его стороны равны а1 и а2, поэтому ОАz2 = а12 + а22. В прямоугольном треугольнике ОА2 А второй катет Аz А = а3 и ОА2 = ОА2г + а32 = а12 + а22+ а32.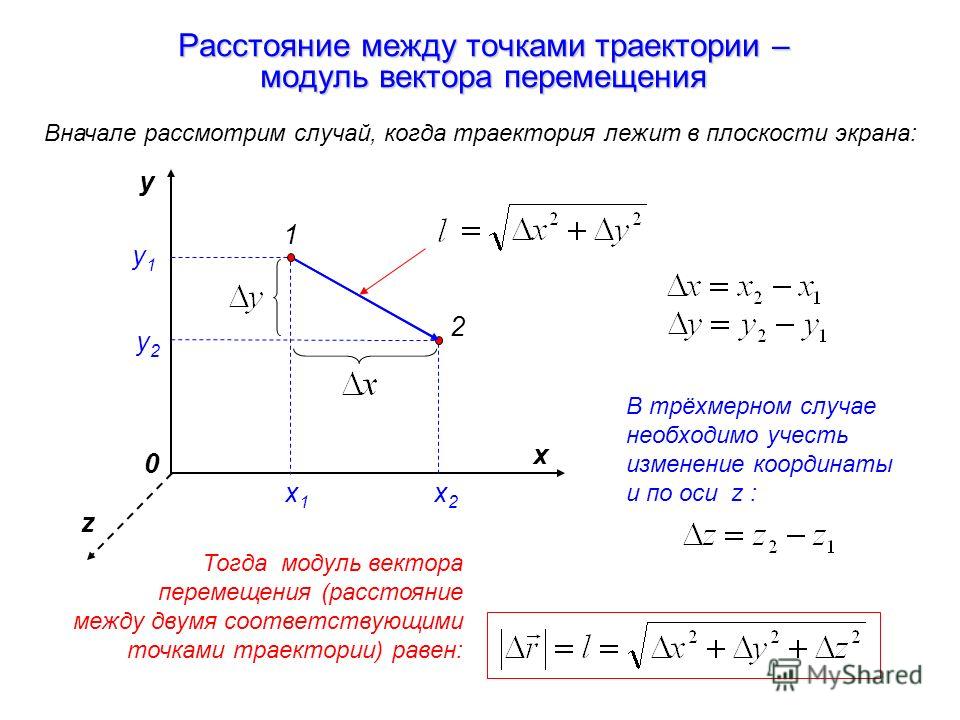
Длина любого ненулевого вектора — число положительное. Длина нулевого вектора равна нулю.
Вспомним, что два вектора, лежащих на одной прямой или параллельных прямых, называютколлинеарными. Коллинеарные векторы бывают сонаправлены (а b) или противоположно направлены (а b). Если векторы ON и ОМ коллинеарны, то точки О, N, М лежат на одной прямой. Нулевые векторы не имеют направлений и считаются коллинеарными к любому вектору.
ДЕЙСТВИЯ НАД ВЕКТОРАМИ В КООРДИНАТАХ
Действия над векторами в пространстве осуществляются аналогично тому, как они определялись для векторов на плоскости.
Определение. Суммой векторов a (a1 а2, а3) и b(b1 b2, b3) называется вектор а + b с координатами (а1 + b1; а2 + b2 ; а3 + b3)
Для любых векторов а , b и с справедливы равенства:
-
а+b=b+а — переместительный закон сложения;
-
а + (b + с) = (а+ b) + с — сочетательный закон сложения.
Чтобы доказать эти свойства, достаточно сравнить соответствующие
координаты левой и правой частей каждого векторного равенства.
Для любых трех точек А, В, С в пространстве имеет место векторное равенство + = .
Действительно, для любых трех точек A(a1 а2, а3), B(b1 b2, b3), C(c1, с2, с3) (b1 – а1; b2 — а2;b3 — а3) и (с1 — bг; с2 — b2, с3 — b3).
Отсюда + = (с1 – а1; с2 — а2; с3 — а3).
Геометрически сумму двух векторов пространства можно находить, пользуясь правилам треугольника(рис. 69).
Также применяется и правило параллелограмма. Оно часто используется в физике.
Если ABCD — параллелограмм (рис. 70), то + = .
Чтобы найти сумму нескольких векторов, используем правило многоугольника. Например, если в пространстве даны точки А, В, С, D, Е, F, то всегда
АВ + ВС +CD + DE + EF = AF.
(слайд 6)
Определение. Два вектора, сумма которых равна нулевому вектору, называютсяпротивоположными.
Из определения следует, что у противоположных векторов соответствующие координаты имеют противоположные знаки.
Определение. Разностью векторов а и b называется такой вектор с , который в сумме с вектором bдает вектор а .
Если а (а1; а2; а3) и b( b1; b2; b3), то — = (а1 –b1; а2 — b2; а3 – b3).
-
Закрепление знаний
Работа студентов по слайдам. Решение задач у доски по желанию.
(слайд7)
(слайд 
(слайд9)
(слайд10)
5.Итоги урока.
Комментирование ответов и решений задач. Выставление отметок.
-
Самостоятельная подготовка.
Составить краткий опорный конспект.
Графическое представление векторов с полярными единичными векторами без преобразования в декартовы координаты
Есть две вещи, которые делают это запутанным. Во-первых, хотя вы можете быть знакомы с математикой, где есть одна декартова система координат и одна полярная система координат, с хорошо известными формулами преобразования из одной системы координат в другую, люди используют не только эти плоские системы координат.
Во-вторых, люди иногда используют одни и те же буквы для обозначения очень разных вещей, в зависимости от таких вещей, как наличие или отсутствие «шапки» над буквой.
В полярных координатах можно записать вектор положения $vec r$
$vec r = (r, theta).$ Этими координатами нельзя манипулировать, как декартовыми координатами вектора.
Декартовы координаты $(x,y)$ соответствуют векторной сумме с коэффициентами $x$ и $y,$, а именно
$x hat imath + y hat jmath$, где $hatimath$ и $hatjmath$ — единичные векторы в направлениях $x$ и $y$,
но нет общего способа записать $vec r$ в виде векторной суммы с коэффициентами $r$ и $theta.$
Однако иногда люди интересуются описанием точки в полярных координатах, а также хотят ответить на определенные вопросы о том, что происходит в этой точке, например, о скорости или ускорении частицы, находящейся там в какой-то момент. во время.
Что они иногда делают, так это создают декартову систему координат.
«заказные» для этой точки плоскости:
вместо использования обычных единичных векторов $hatimath$ и $hatjmath$, параллельных осям $x$ и $y$,
они смотрят на вектор $vec r$ от начала своих полярных координат до конкретной интересующей точки,
и они образуют единичный вектор $hat r$ в том же направлении, что и $vec r.
$
Затем они делают другой единичный вектор $hat theta$ перпендикулярным $hat r,$
обычно указывая в направлении возрастания полярной координаты $theta$.
Итак, рассматриваемая точка на расстоянии и в направлении $vec r$ от начала координат
уже имеет полярные координаты $(r,theta),$ и мы знаем, как получить из них второй набор координат, а именно декартовы координаты
$x = r costheta,$ $y = r sintheta$;
но теперь кто-то ввел третью систему координат , отличную от любой из этих.
Новая система координат является другой декартовой системой координат, но в общем случае она не ориентирована так же, как система координат $(x,y)$
(если только $theta$ не равно нулю или другому целому кратному $2pi$),
и мы обычно не считаем, что оно имеет то же начало, что и координаты $(x,y)$ или координаты $(r,theta)$.
Если мы вообще подумаем о его происхождении как о точке на плоскости,
мы, скорее всего, будем думать о точке $(r,theta)$ как о начале этой новой системы.
Было бы очень странно захотеть записать вектор координат , такой как вектор позиции $vec r$ в этой новой системе координат; обычно это не то, для чего предназначена новая система.
Я был бы удивлен, увидев такое уравнение, как
$vec r = 10hat r + 30hat theta$ написано в книге, потому что $vec r$ обычно является вектором положения, а вещь в правой части уравнения — нет;
но я бы совсем не удивился, увидев вектор скорости, написанный
$vec v = 10шляпа r + 30шляпа тета.$
Таким образом, когда вы видите выражение вроде $10hat r + 30hat theta,$
вы не ищете способ записи вектора с использованием полярных координат.
Вы смотрите на набор декартовых координат в специальной декартовой системе координат.
Поскольку эти координаты действительно декартовы, вы можете использовать обычные правила декартовых координат, чтобы добавить их (просто добавляя координаты)
или найти величину вектора (используя теорему Пифагора).
И вам точно стоит
а не попытка скопировать полярные координаты
любой точки в эту систему координат; то есть вообще
$$ (r = a,theta = b) neq a hat r + btheta$$
(точка с полярными координатами $(r,theta) = (a,b)$ не находится путем построения векторной суммы $a hat r + btheta$).
Как найти величину и направление вектора0003
Учебное пособие по физике I для чайников с онлайн-практикой
Изучить книгу Купить на Amazon
В физике, когда вам даны векторные компоненты, такие как (3, 4), вы можете легко преобразовать их в величину/угол. вектора с помощью тригонометрии.
Например, взгляните на вектор на изображении.
Предположим, вам известны координаты конца вектора и вы хотите найти его величину v и угол тета. Благодаря вашим познаниям в тригонометрии вы знаете
Где тангенс тета — тангенс угла. Это значит, что
тета = тангенс –1 ( y / x )
Предположим, что координаты вектора равны (3, 4). Вы можете найти угол тета как тангенс –1 (4/3) = 53 градуса.
Вы можете использовать теорему Пифагора, чтобы найти гипотенузу — величину, v — треугольника, образованного x, y, и v:
Подставьте числа для этого примера, чтобы получить
Итак, если у вас есть вектор, заданный координатами (3, 4), его величина равна 5, а угол равен 53 градусам.
Пример вопроса
-
Преобразование вектора, заданного координатами (1.0, 5.0), в формат величина/угол.
Правильный ответ: звездная величина 5,1, угол 79 градусов.
-
Примените теорему Пифагора, чтобы найти величину. Подставьте числа, чтобы получить 5.1.
-
Применить уравнение тета=тангенс –1 ( y / x ), чтобы найти угол. Подставьте числа, чтобы получить тангенс –1 (5,0/1,0) = 79 градусов.
-
Практические вопросы
-
Преобразование вектора (5.0, 7.0) в форму величины/угла.
-
Преобразование вектора (13.0, 13.0) в форму величины/угла.
-
Преобразование вектора (–1,0, 1,0) в форму величины/угла.
-
Преобразование вектора (–5,0, –7,0) в форму величины/угла.
Ниже приведены ответы на практические вопросы:
-
Величина 8,6, угол 54 градуса
-
Применить уравнение
, чтобы найти звездную величину, которая равна 8,6.
-
Примените уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (7,0/5,0) = 54 градуса.
-
-
Величина 18,4, угол 45 градусов
-
Применить уравнение
, чтобы найти звездную величину, которая равна 18,4.
-
Примените уравнение theta = tan –1 ( y / x ), чтобы найти угол: tan –1 (13,0/13,0) = 45 градусов.
-
-
Величина 1,4, угол 135 градусов
-
Применить уравнение
, чтобы найти звездную величину, которая равна 1,4.
-
Примените уравнение тета = тангенс –1 ( y / x ), чтобы найти угол: tan –1 (1,0/–1,0) = –45 градусов.
Однако обратите внимание, что угол действительно должен быть между 90 и 180 градусами, потому что первая составляющая вектора отрицательна, а вторая положительна.
-