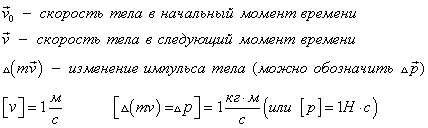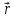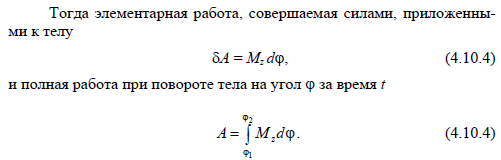Импульс
-
Второй закон Ньютона в импульсной форме
-
Пример вычисления силы
-
Импульс системы тел
-
Закон сохранения импульса
-
Закон сохранения проекции импульса
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.
Импульс тела — это векторная величина, равная произведению массы тела на его скорость:
.
Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:
.
Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.
к оглавлению ▴
Второй закон Ньютона в импульсной форме
Пусть — равнодействующая сил, приложенных к телу массы
. Начинаем с обычной записи второго закона Ньютона:
.
С учётом того, что ускорение тела равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:
.
Вносим константу под знак производной:
.
Как видим, в левой части получилась производная импульса:
. ( 1)
Соотношение ( 1) и есть новая форма записи второго закона Ньютона.
Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.
Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.
Производную в формуле ( 1) можно заменить на отношение конечных приращений:
. ( 2)
В этом случае есть средняя сила, действующая на тело в течение интервала времени
. Чем меньше величина
, тем ближе отношение
к производной
, и тем ближе средняя сила
к своему мгновенному значению в данный момент времени.
В задачах, как правило, интервал времени достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда
— средняя сила, действующая на мяч со стороны стенки во время удара.
Вектор в левой части соотношения ( 2) называется изменением импульса за время
. Изменение импульса — это разность конечного и начального векторов импульса. А именно, если
— импульс тела в некоторый начальный момент времени,
— импульс тела спустя промежуток времени
, то изменение импульса есть разность:
.
Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1):
 |
| Рис. 1. Изменение импульса |
Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен ) и отскакивает назад без потери скорости (импульс после удара равен
). Несмотря на то, что импульс по модулю не изменился (
), изменение импульса имеется:
.
Геометрически эта ситуация показана на рис. 2:
 |
| Рис. 2. Изменение импульса при отскоке назад |
Модуль изменения импульса, как видим, равен удвоенному модулю начального импульса мяча: .
Перепишем формулу ( 2) следующим образом:
, ( 3)
или, расписывая изменение импульса, как и выше:
.
Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:
.
(Обратите внимание, что оказывается ещё одной возможной единицей измерения импульса тела.)
Словесная формулировка равенства ( 3) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.
к оглавлению ▴
Пример вычисления силы
В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.
Задача. Шарик массы г, летящий горизонтально со скоростью
м/с, ударяется о гладкую вертикальную стену и отскакивает от неё без потери скорости. Угол падения шарика (то есть угол между направлением движения шарика и перпендикуляром к стене) равен
. Удар длится
с. Найти среднюю силу,
действующую на шарик во время удара.
Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом (рис. 3).
 |
| Рис. 3. К задаче (вид сверху) |
Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила — сила упругости, направленная перпендикулярно стене (рис. 4).
 |
| Рис. 4. К задаче |
Согласно ( 3) имеем: . Отсюда следует, что вектор изменения импульса сонаправлен с вектором
, то есть направлен перпендикулярно стене в сторону отскока шарика (рис. 5).
 |
| Рис. 5. К задаче |
Векторы и
равны по модулю
(так как скорость шарика не изменилась). Поэтому треугольник, составленный из векторов ,
и
, является равнобедренным. Значит, угол между векторами
и
равен
, то есть угол отражения действительно равен углу падения.
Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:
.
И тогда искомая средняя сила, действующая на шарик:
.
к оглавлению ▴
Импульс системы тел
Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами и
соответственно. Импульс
системы данных тел — это векторная сумма импульсов каждого тела:
.
Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1). Давайте выведем эту формулу.
Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть — результирующая внешняя сила, действующая на тело 1. Аналогично
— результирующая внешняя сила, действующая на тело 2 (рис. 6).
 |
| Рис. 6. Система двух тел |
Кроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой . Тогда тело 1 действует на тело 2 с силой
. По третьему закону Ньютона силы
и
равны по модулю и противоположны по направлению:
. Силы
и
— это внутренние силы, действующие в системе.
Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1):
, ( 4)
. ( 5)
Сложим равенства ( 4) и ( 5):
.
В левой части полученного равенства стоит сумма производных, равная производной суммы векторов и
. В правой части имеем
в силу третьего закона Ньютона:
.
Но — это импульс системы тел 1 и 2. Обозначим также
— это результирующая внешних сил, действующих на систему. Получаем:
. ( 6)
Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.
Формула ( 6) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.
Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:
.
Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4) и ( 5), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6) останется справедливым и в общем случае.
к оглавлению ▴
Закон сохранения импульса
Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.
Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: . В этом случае из ( 6) получаем:
.
Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:
.
Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.
Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.
Задача. Тело массы г движется со скоростью
м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы
г со скоростью
м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.
Решение. Ситуация изображена на рис. 7. Ось направим в сторону движения первого тела.
 |
| Рис. 7. К задаче |
Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:
,
.
Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:
. ( 7)
Импульс системы до удара — это сумма импульсов тел:
.
После неупругого удара получилось одно тело массы , которое движется с искомой скоростью
:
.
Из закона сохранения импульса ( 7) имеем:
.
Отсюда находим скорость тела, образовавшегося после удара:
.
Переходим к проекциям на ось :
.
По условию имеем: м/с,
м/с, так что
.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси . Искомая скорость:
м/с.
к оглавлению ▴
Закон сохранения проекции импульса
Часто в задачах встречается следующая ситуация. Система тел не является замкнутой (векторная сумма внешних сил, действующих на систему, не равна нулю), но существует такая ось , сумма проекций внешних сил на ось
равна нулю в любой момент времени. Тогда можно сказать, что вдоль данной оси наша система тел ведёт себя как замкнутая, и проекция импульса системы на ось
сохраняется.
Покажем это более строго. Спроектируем равенство ( 6) на ось :
.
Если проекция равнодействующей внешних сил обращается в нуль, , то
.
Следовательно, проекция есть константа:
.
Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция
импульса системы не меняется с течением времени.
Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.
Задача. Мальчик массы , стоящий на коньках на гладком льду, бросает камень массы
со скоростью
под углом
к горизонту. Найти скорость
, с которой мальчик откатывается назад после броска.
Решение. Ситуация схематически показана на рис. 8. Мальчик изображён прямогольником.
 |
| Рис. 8. К задаче |
Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.
Стало быть, система, которую образуют мальчик и камень, не замкнута. Почему? Дело в том, что векторная сумма внешних сил не равна нулю во время броска. Величина
больше, чем сумма
, и за счёт этого превышения как раз и появляется вертикальная компонента импульса системы.
Однако внешние силы действуют только по вертикали (трения нет). Стало быть, сохраняется проекция импульса на горизонтальную ось . До броска эта проекция была равна нулю. Направляя ось
в сторону броска (так что мальчик поехал в направлении отрицательной полуоси), получим:
,
откуда
.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Импульс» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
07.05.2023
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.1k
I. Механика
Тестирование онлайн
Импульс тела
Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.
Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.
Импульс это векторная величина, которая определяется по формуле
Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.
Направление вектора импульса всегда совпадает с направлением вектора скорости.
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.
Импульс силы
Это векторная величина, которая определяется по формуле
Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.
Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара — 30 м/с. Сила, с которой нога действовала на мяч — 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.
Изменение импульса тела
Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.
Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.
1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.
Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.
2) Изменение импульса 
3) Из второго закона Ньютона
Главное запомнить
1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела
Вывод второго закона Ньютона в общем виде
График F(t). Переменная сила
Импульс
тела
(или
количество
движения)
− это векторная физическая величина,
равная произведению массы тела на его
скорость.
Единица
измерения импульса в СИ – кг*м/с
Закон
сохранения импульса:
если сумма внешних сил, действующих на
точки системы, равна нулю, то сумма
импульсов всех точек системы остается
величиной постоянной.
15. Энергия. Кинетическая и потенциальная энергия. Теорема об изменении кинетической энергии. Закон сохранения энергии в механики.
Работа
− это
количественная характеристика процесса
обмена энергией между взаимодействующими
телами.
Кинетическая
энергия
− это энергия
тела, обусловленная его механическим
движением
Теорема
об изменении кинетической энергии:
Потенциальная
энергия
− часть общей механической энергии
системы, зависящей от взаимного
расположения материальных точек системы
и их положения во внешнем силовом поле.
К1
+ П1
= К2
+ П2
= const (1)
Величину
E
=
К + П называют полной
механической энергией
системы.
Из
соотношения (1) следует закон
сохранения полной механической энергии:
полная механическая энергия системы,
на материальные точки которой действуют
только консервативные силы, с течением
времени не изменяется:
E
= const.
16. Момент импульса материальной точки относительно некоторого центра. Чему равен модуль вектора момента импульса? Что называется плечом импульса? Момент импульса в си.
Момент
импульса
−
векторная величина, равная векторному
произведению радиус-вектора
точки,
проведенного из центра на ее импульс

Модуль
вектора момента импульса
относительно центра или оси − есть
скалярная величина, равная произведению
им-пульса p на плечо импульса d
относительно
этой оси.
Модуль
вектора момента импульса равен:
где
d
−
плечо импульса относительно точки О.
Плечо
импульса
− это расстояние, измеряемое по
перпендикуляру от оси вращения до
линии, вдоль которой направлен импульс.
В
системе СИ момент
импульса измеряется в единицах джоуль-секунда;
Дж·с.
17. Как определяется направление вектора момента импульса.
Направление
момента импульса совпадает с направлением
поступательного движения правого винта
при его вращении от радиус-вектора

и
он перпендикулярен как вектор

так и вектору
18.
Момент силы материальной точки
относительно некоторого центра.
Момент
силы
— векторная
величина, равная векторному произведению
радиус-вектора

приложения силы, на силу
19.
Формула для определения модуля вектора
момента силы. Плечо силы. Момент силы
в СИ.
Модуль
вектора момента силы равен:
где
d
=
r
sin
α − плечо силы относительно точки О.
Плечо
силы
−
это расстояние, измеряемое по
перпендикуляру от оси вращения до
линии, вдоль которой действует сила.
Момент
силы измеряется
в ньютон-метрах. 1
Н·м
20.
Как определяется направление вектора
момента силы.
Направление
момента силы
совпадает
с направлением поступательного движения
правого винта при его вращении от
радиус-вектора
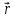

и он перпендикулярен как вектору
так и вектору
21.
Момент инерции тела относительно данной
оси. Физический смысл момента инерции.
Момент инерции в СИ
Моментом
инерции
твердого
тела относительно данной оси называется
физическая величина, являющаяся мерой
инертности тела во вращательном движении
вокруг этой оси и равная сумме произведений
масс всех частиц тела на квадраты их
расстояний от той же оси:
[I]
= 1 кг · м2
Физический
смысл момента инерции
можно
определить из выражения:
Момент
инерции тела является мерой инерции
тела при вращательном движении.
22.
Теорема Штейнера. Правило аддитивности
для момента инерции.
Теорема
Штейнера:
момент инерции тела Iz
относительно
произвольной оси равен сумме момента
инерции Ic
относительно
оси, параллельной данной и проходящей
через центр масс тела, и произведения
массы тела m
на квадрат расстояния a между осями:
Правило
аддитивности:
сумма моментов инерции частей системы
относительно оси равен моменту инерции
системы относительно данной оси:
23.
Формула для расчета работы силы при
вращении тела.
24.
Основное уравнение динамики вращательного
движения относительно точки. Закон
сохранения момента импульса.
Уравнение
динамики вращательного движения
относительно точки
(или
иначе закон
изменения момента импульса механической
системы)
Производная
по времени от момента импульса системы
относительно точки равна сумме моментов
внешних сил относительно этой точки.
Закон
сохранения момента импульса:
если момент внешних сил действующих
на механическую систему относительно
центра оси равен нулю, то момент импульса
системы остаётся величиной постоянной.
25.
Основное уравнение динамики вращательного
движения относительно неподвижной
оси. Закон сохранения проекции момента
импульса.
Основное
уравнение динамики вращательного
движения относительно неподвижной
оси:
Закон
сохранения проекции момента импульса:
Если
проекцию моментов внешних сил относительно
оси z равна нулю, то момент импульса
тела относительно этой оси остаётся
величиной постоянной.
26.
Кинетическая энергия тела вращающегося
вокруг неподвижной оси. Кинетическая
энергия тела при плоском движении.
27.
Свободные
гармонические колебания и их
характеристики( смещение, амплитуда,
частота и период колебаний, циклическая
частота фаз и начальная фаза колебаний).
Колебания
−
это движения или процессы, обладающие
той или иной степенью повторяемости
во времени.
Периодические
колебания
− значения физических величин,
изменяющихся в процессе колебания,
повторяются через равные промежутки
времени.
Гармонические
колебания
−
это периодическое изменение во времени
физической величины, происходящее по
закону косинуса или синуса. Уравнение
гармонических колебаний имеет вид:
28.
Дать определение частоты
обращения
тела. Дайте определение периода
обращения
тела.
Равномерное
движение по окружности характеризуют
периодом и частотой
обращения.
Период обращения — это время,
за которое совершается один оборот.
Если, например, за время t = 4 с тело,
двигаясь по окружности, совершило n = 2
оборота, то легко сообразить, что один
оборот длился 2 с. Это
и
есть период обращения.
29.Характеристики
колебательной системы. Коэффициент
затухания и логарифмический декремент
затухания. Время релаксации. Добротность
колебательной системы.
Во
всякой реальной колебательной системе
имеются силы сопротивления, действие
которых приводит к уменьшению энергии
системы. Если убыль энергии не восполняется
за счет работы внешних сил, то колебания
будут затухать.
30.
Уравнение состояния идеального
газа(Клапейрона – Менделеева).
Уравнением
состояния идеального газа или
уравнение
Менделеева − Клапейрона.
31.
Внутренняя энергия идеального газа.
Дать определение числа степеней свободы
молекулы газа. Работа газа при изменении
его объёма.
Число
степеней свободы
− это число
независимых координат (переменных),
которые полностью определяют положение
системы в пространстве.
Молекулу
одноатомного
газа
рассматривают как материальную точку,
которой приписывают три степени свободы
поступательного движения. Молекула
двухатомного
газа рассматривается как совокупность
двух материальных точек,
связанных
недеформированной связью. Эта система
кроме трех степеней свободы поступательного
движения имеет еще две степени свободы
вращательного движения. Трехатомная
молекула имеет шесть степеней свободы:
три поступательные и три вращательные.
Столько же степеней свободы будут иметь
и многоатомные молекулы (четырех, пяти
и т. д.).
Любое тело, обладающее скоростью, обладает импульсом.
Скорость тела будет меняться, когда на него подействует сила и появится ускорение. Об этом сообщает второй закон Ньютона. А если изменяется скорость тела, то будет изменяться его импульс.
Второй закон Ньютона в импульсной форме описывает изменение импульса тела под действием силы.
Формула второго закона Ньютона в импульсной форме
Импульсная форма записи второго закона выглядит так:
[ large boxed{ overrightarrow{Delta p} = overrightarrow{ F cdot Delta t} } ]
Словами это выражение можно сформулировать так:
[ large boxed { text {Изменение импульса тела = импульсу силы }} ]
(overrightarrow{Delta p} left( text{кг} cdot frac{text{м}}{c}right) ) – вектор изменения импульса тела;
( overrightarrow{ F cdot Delta t} left( H cdot text{м} right) ) – вектор импульса силы;
Слева и справа в формуле находятся два вектора. Так как между ними записан знак равенства, значит у векторов (overrightarrow{Delta p} ) и ( overrightarrow{ F cdot Delta t} ) совпадают обе характеристики — направление и длина.
С помощью математики фразу «длины векторов равны» можно записать так:
( left| overrightarrow{Delta p} right | = left| overrightarrow{ F cdot Delta t} right | )
Как посчитать длину вектора, и как ее обозначать, читайте тут.
Пояснения и вывод формулы с помощью геометрии
Чтобы получить импульсный вид записи для второго закона, рассмотрим такую задачу.
Представим, что мы склонились над бильярдным столом и смотрим на него сверху. А в это время по столу катится бильярдный шар с какой-то постоянной скоростью.
Примечание: с постоянной скоростью, значит — с одной и той же скоростью. О такой скорости физики часто говорят «с неизменной скоростью», а математики применяют для нее запись ( vec{v} = const ).
Пусть для определенности масса шара равна двум килограммам.
( m = 2 left( text{кг} right) )
Пусть до того, как мы подействовали на шар, он двигался по столу в направлении, указанном на рисунке 1а. Шар вначале движется по горизонтали (рис. 1а), вектор начальной скорости обозначен ( vec{v_{0}} ).
Подействуем теперь на шар, ударив его кием под углом к начальной скорости. Направление, вдоль которого мы ударили, показано на рисунке 1б с помощью вектора силы ( vec{F} ) .
После удара шар будет катиться уже не по горизонтали на рисунке. Физики скажут: направление движения шара изменилось. Направление, в котором шар движется после удара, обозначено вектором ( vec{v} ) на рисунке 2в. Вектор ( vec{v} ) — конечная скорость шара.
Рис. 1. Направление движения шара а) — до удара, в) – после удара, б) – в эту сторону шар подтолкнули силой
Нам известны начальная и конечная скорости тела, а также, его масса. Мы можем вычислить импульс тела до удара (рис 2а), и после удара (рис 2б).
( m cdot vec{v_{0}} = vec{p_{0}}) – импульс тела до удара (начальный);
( m cdot vec{v} = vec{p}) – импульс тела после удара (конечный).
Рис. 2. Вектор скорости тела умножаем на скаляр — массу тела, получаем вектор импульса тела
Обратите внимание, что у векторов начального импульса ( vec{p_{0}}) и начальной скорости ( vec{v_{0}}) направления совпадают. Вектор конечного импульса ( vec{p}), так же, сонаправлен с вектором ( vec{v}) конечной скорости тела.
Для удобства совместим начала векторов ( vec{p_{0}}) и ( vec{p}) (рис. 3). Зададимся вопросом, как из вектора начального импульса ( vec{p_{0}}) получить конечный ( vec{p}) вектор?
Рис. 3. Начала векторов импульса тела до (черный) и после (красный) удара совмещены
Очевидно, нужно к вектору ( vec{p_{0}}) прибавить еще один вектор. Обозначим этот вектор ( overrightarrow{Delta p} ), он представлен на рисунке 4.
Рис. 4. К начальному вектору импульса прибавили вектор изменения импульса и получили конечный вектор импульса тела
Подробнее о том, как складывать векторы, написано тут.
Сумму можно записать так:
( vec{p_{0}} + overrightarrow{Delta p} = vec{p} )
Это уравнение записано в векторном виде. Стрелки над символами подчеркивают тот факт, что векторы складывают с помощью геометрии, то есть, учитывают их направления.
Выразим теперь вектор, обозначенный ( overrightarrow{Delta p} ). Для этого, из обеих частей уравнения вычтем вектор ( vec{p_{0}} ).
( overrightarrow{Delta p} = vec{p} — vec{p_{0}} )
Видно, что вектор ( overrightarrow{Delta p} ) – это разница между конечным ( vec{p} ) и начальным ( vec{p_{0}} ) векторами импульса тела.
Физики для вектора ( overrightarrow{Delta p} ) используют такое название:
( overrightarrow{Delta p} left( text{кг} cdot frac{text{м}}{c} right) ) – вектор изменения импульса тела.
Рассмотрим теперь совместно векторы ( overrightarrow{Delta p} ) и ( vec{F} ) на одном рисунке (рис. 5).
Рис. 5. Вектор изменения импульса тела сонаправлен с вектором силы, действующей на тело, длины векторов отличаются
Направления векторов совпадают, а длина – различается.
Примечание: Математики вместо выражения «длина вектора» употребляют термин «модуль вектора».
Предположим, у нас есть точный хронометр и мы измерили кусочек времени, в течение которого сила действовала на бильярдный шар.
Умножим теперь вектор ( vec{F} ) на этот промежуток времени ( Delta t ) — скаляр. Результат умножения представлен на рисунке 6.
Рис. 6. Вектор силы, действующей на тело, умножаем на скаляр – промежуток времени, в течение которого сила действовала, получили вектор импульса силы
Из рисунка 6 видно, что у векторов (overrightarrow{Delta p} ) и ( overrightarrow{ F cdot Delta t} ) совпадают не только направления, но и длины.
Если у векторов совпадают обе характеристики, то их можно приравнять. Подробнее о том, какие у векторов есть характеристики, написано тут.
[ large boxed{ overrightarrow{Delta p} = overrightarrow{ F cdot Delta t} } ]
Это выражение называют вторым законом Ньютона, записанным в импульсной форме.
Примечания
1). Сумму векторов
( vec{p_{0}} + overrightarrow{Delta p} = vec{p} )
можно теперь переписать в таком виде:
( vec{p_{0}} + overrightarrow{ F cdot Delta t} = vec{p} )
2). Складывать можно векторы, у которых размерность совпадает.
О сложении векторов простым языком написано тут.
Обратим внимание на размерность.
(overrightarrow{Delta p} left( text{кг} cdot frac{text{м}}{c}right) )
( overrightarrow{ F cdot Delta t} left( H cdot c right) )
На первый взгляд, она отличается, но с помощью простых преобразований можно показать, что
[ large 1 text{кг} cdot frac{ 1text{м}}{1 c} = 1 H cdot 1 c ]
Вывод формулы с помощью алгебры
Второй закон Ньютона в импульсной форме можно получить из алгебраических соображений.
Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона:
(displaystyle vec{a} = frac{vec{F}}{m})
Применим выражение для ускорения
(displaystyle vec{a} = frac{overrightarrow{Delta v}}{Delta t })
В этих уравнениях слева находится величина (vec{a}). Так как левые части уравнений равны, можно приравнять правые их части
(displaystyle frac{vec{F}}{m} = frac{vec{Delta v}}{Delta t })
Полученное выражение является пропорцией. Применив одно из свойств пропорции, получим такое выражение:
( overrightarrow{F cdot Delta t} = overrightarrow {Delta vcdot m} )
В правой части находится вектор (overrightarrow {Delta v} = vec {v} — vec {v_{0}} ) – это разница между конечной и начальной скоростью.
Преобразуем правую часть
(overrightarrow{Delta v}cdot m = left( vec {v} — vec {v_{0}} right) cdot m)
Раскрыв скобки, получим
(overrightarrow{Delta v}cdot m = vec {v} cdot m — vec {v_{0}} cdot m )
Вспомним обозначения:
(vec {v} cdot m = vec {p})
(vec {v_{0}} cdot m = vec {p_{0}} )
Подставляя их, получим
(overrightarrow{Delta v}cdot m = vec {p} — vec {p_{0}})
(vec {p} — vec {p_{0}}=overrightarrow{Delta p})
Или, сокращенно
(overrightarrow{Delta v}cdot m = overrightarrow{Delta p})
То есть, вектор (overrightarrow {Delta vcdot m}) – это вектор (overrightarrow {Delta p}).
Тогда второй закон Ньютона в импульсной форме запишем так
( overrightarrow{F cdot Delta t} = overrightarrow{Delta p})