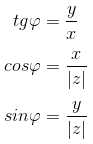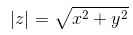Заказать задачи по любым предметам можно здесь от 10 минут
Модуль и аргумент комплексного числа
Пусть задано комплексное число $ z = a+bi $.
| Формула |
| Модуль комплексного числа равен корню квадратному из суммы квадратов мнимой и действительной части и находится по формуле: $$ |z| = sqrt{a^2 + b^2} $$ |
Если комплексное число состоит только из действительной части $ z = a $, то его модуль равен $ |z| = |a| $.
Стоит заметить, что модуль комплексных чисел всегда неотрицательный $ |z| ge 0 $ и равен нулю $ |z| = 0 $, только в случае $ z = 0 $.
| Формула |
Аргумент комплексного числа обозначается $ varphi = arg z $ и зависит от полуплоскости, в которой лежат числа $a,b$:
|
Введите комплексное число
Пример 1 Пример 2 Правила ввода
| Пример 1 |
| Найти модуль и аргумент комплексного числа $ z = 3 — 4i $. |
| Решение |
|
Комплексное число состоит из действительной и мнимой части: $$ a = Re z = 3 $$ $$ b = Im z = -4 $$ Применяя формулу вычисления модуля получаем: $$ |z| = sqrt{a^2 + b^2} = sqrt{3^2 + (-4)^2} = sqrt{9+16} = 5 $$ Теперь вычисляем аргумент. Так как $a = 3 > 0$, то получаем аргумент: $$varphi = arctg frac{b}{a} = arctg frac{-4}{3} = -arctg frac{4}{3}.$$ |
| Ответ |
| $$ |z| = 5, varphi = -arctg frac{4}{3} $$ |
| Пример 2 |
| Найти модуль и аргумент комплексного числа $ z = 3i $ |
| Решение |
|
В данном случае отсутствует действительная часть, а вернее она равна нулю: $$ a = Re z = 0 $$ Мнимая часть комплексного числа равна: $$ b = Im z = 3 $$ Вычисляем модуль по уже известной формуле: $$ |z| = sqrt{a^2 + b^2} = sqrt{0^2 + 3^2} = sqrt{9} = 3 $$ А вот аргумент здесь попадает под правило при $a = 0, b>0$ и значит равен $$varphi = frac{pi}{2}.$$ |
| Ответ |
| $$ |z| = 3, varphi = frac{pi}{2} $$ |
| Пример 3 |
| Найти модуль и аргумент комплексного числа $$ z = 1+sqrt{3}i $$ |
| Решение |
|
Выписываем действительную и мнимую часть: $$ a = 1 $$ $$ b = sqrt{3} $$ Так как $ a > 0 $, то аргумент равен $$ varphi = arctg frac{sqrt{3}}{1} = arctg sqrt{3} = frac{pi}{3} $$ Находим модуль извлекая квадратный корень из суммы квадратов действительной и мнимой части: $$|z| = sqrt{1^2 + (sqrt{3})^2} = sqrt{1+3}=2.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ varphi = frac{pi}{3}, |z| = 2 $$ |
| Пример 4 |
| Найти аргумент комплексного числа $$ z = -1 + sqrt{3}i $$ |
| Решение |
|
Действительная часть $$ a = Re z = -1 $$ Мнимая часть $$ b = Im z = sqrt{3} $$ Так как $ a < 0 $ и $ b > 0 $, то пользуемся второй формулой: $$ varphi = arg z = pi + arctg frac{sqrt{3}}{-1} = pi + arctg (-sqrt{3}) = $$ $$ = pi — arctg(sqrt{3}) = pi — frac{pi}{3} = frac{2pi}{3}. $$ |
| Ответ |
| $$ varphi = frac{2pi}{3} $$ |
Вычислить аргумент и модуль комплексного числа.
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки, соответствующей данному комплексному числу и обозначается Arg(z) = φ
Аргументом комплексного числа z называется угол φ в радианах радиус-вектора точки,
соответствующей данному комплексному числу и обозначается Arg(z) = φ
Из определения следуют следующие формулы:
Для числа z = 0 аргумент не определен.
Главным значением аргумента называется такое значение φ, что 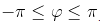
Обозначается: arg(z).
Свойства аргумента:
Модулем комплексного числа z = x + iy называется вещественное число |z| равное:
Для любых комплексных чисел z, z1, z2 имеют место следующие свойства модуля:
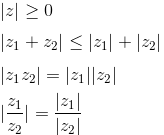
|
|
для пары комплексных чисел z1 и z2 модуль их разности |z1 − z2| равен расстоянию между соответствующими точками комплексной плоскости. |

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Модуль комплексного числа
Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами:
, и радиус-вектор
комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу.
Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.
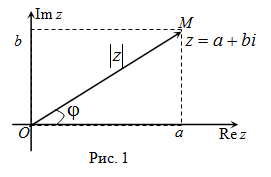
Таким образом, модуль вычисляется как квадратный корень из суммы квадратов действительной и мнимой частей комплексного числа.
Если является действительным числом, то его модуль
равен абсолютной величине этого действительного числа.
Например.
Свойства модуля
- Модуль комплексного числа не отрицателен:
, при этом
в том и только том случае, если
;
- Модуль суммы двух комплексных чисел меньше либо равен сумме модулей:
;
- Модуль произведения двух комплексных чисел равен произведению модулей:
, в том числе
;
- Модуль частного двух комплексных чисел равен частному модулей:
;
, т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Определение.
Модулем
комплексного числа
называется длина вектора, изображающего
это число, и обозначается
.
Модуль
числа z
= x
+ iy
определяется однозначно и может быть
найден по формуле
=
.
Нетрудно
видеть, что z
∙
=
и
.
Если
z
= 0 , то
.
Определение.
Аргументом
комплексного числа
z
≠ 0 называется любой угол ,
отсчитываемый от положительного луча
оси ОХ до радиус-вектора z.
Этот угол считается положительным, если
отсчет производится против часовой
стрелки, и отрицательным – в противоположном
случае. Для числа z
= 0 аргумент не определен.
В
отличие от модуля, аргумент комплексного
числа определяется неоднозначно.
Пример
6.1 Найти
аргумент комплексного числа 1 + i.
Решение.
Аргументами
числа 1 + i
являются углы
(рисунок 4),
(рисунок 5),
(рисунок 6) и, вообще, любой из углов.
,
k
Z.
Рисунок
4 Рисунок 5
Рисунок
6
Все
множество аргументов числа z
обозначается Arg
z,
(фр. Ar-gument
– аргумент). Такое значение
Arg
z,
которое принадлежит промежутку –
<
≤
либо 0 ≤
< 2
и называется главным
аргументом.
Он обозначается arg
z
и определяется однозначно
Arg
z = arg z + 2k,
k
Z,
–
< arg z ≤ .
Упражнения
7 Отметить на
плоскости точки, изображающие следующие
комплексные числа:
а)
2i
– 3; б)
;
в)
–6 + 2i;
г)
–2 – 2i; д)
(1 – i)4;
е)
.
8 Найти модуль и
аргумент комплексного числа:
а)
–
;
б)
;
в) 3 – 2;
г)
(i + 1)(i – 2); д)
.
§ 7 Тригонометрическая (полярная) форма
комплексного
числа
Модуль
и аргумент
комплексного числа z
= x
+ iy
≠ 0 – это, по существу, полярные координаты
(r;
)
точки М(х; у) – рису- нок 7.
Используя
связь между декартовыми и полярными
координатами точки М (рисунок 
,
можно
любое комплексное число z
≠ 0 представить в виде:
z
= x + iy = r ∙ cos
+ ir ∙ sin
= r(cos
+ i sin ).
Рисунок
7 Рисунок 8
Запись
z
= r(cos
+ i
sin
)
называется тригонометрической
или полярной
формой
комплексного числа.
Чтобы
записать число z
= x
+ iy
≠ 0 в тригонометрической форме, следует
найти его модуль по формуле
и один из аргументов, решив систему

Аргумент
комплексного числа можно определить
из соотношения
,
являющегося следствием последней
системы. Откуда
.
Однако
не все решения этого соотношения являются
решением системы. Напомним, что период
функции y
= tg
x равен .
При с
R
одно из решений уравнения tg
= c,
удовлетворяющее условию
,
обозначается arctg
c.
Таким образом, в промежутке (– ;
]
имеются два угла, тангенсы которых равны
.
Для определения четверти, в которой
лежит угол ,
нужно еще учесть знаки х, у – координат
точки z:
-
если
точка z
лежит в I
и IV
четверти, x
> 0, то
=
arg
z
=
(рисунок 9);
2)
если точка z
лежит во II
четверти, т.е. x
< 0, y
> 0, то
и
arg
z
=
(рисунок 10);
3)
Если точка z
лежит в III
четверти, т.е. x
< 0, y
< 0, то
и
(рисунок
11).
Рисунок 9
Рисунок 10
Рисунок 11
Для главного
аргумента справедливы формулы:
Пример
7.1 Записать
числа в тригонометрической форме:
1)
z = 4 + 4i.
Решение.
x
= 4, y
= 4 (I
четверть);
.
Так
как arg
z
=
,
то
z
= 4 + 4i =
2)
z =
–
i.
Решение.
x
=,
y
= –1 (IVчетверть);
Так
как x
> 0,
= arg
z
= arctg
=
Поэтому
– i
= 2
3)
z = – 2 –
i.
Решение.
x
= –2, y = –
(III четверть);
Так
как x
< 0 и y
< 0,
= arg
z
= –
–2
–
i
=
4)
z = –+
i.
Решение.
x
= –,
y
= 1 (II
четверть);
.
Так как x
< 0, y
> 0,
=
arg z =
–+
i =
5)
z = 5.
Решение.
Так
как число z
= 5 действительное и 5 > 0, то
= 0.
6)
z = –.
Решение.
,
=
(так как –<
0).
).
7)
z = 3i.
Решение.
Так
как число z
= 3i
– мнимое (х = 0, у = 3), причем y
= Im
z
=
=
3 > 0, то
,
= arg
z
=.

z = –i.
Решение.
x
= 0, y = –<
0;
,
= arg
z
= –
.
9)
z = cos
– isin
.
Решение.
Данная
запись числа не является тригонометрической.
Это чис-ло записано в алгебраической
форме, где
, у = –
.
Искомая
запись имеет вид z
= cos
+ isin
.
;

arg z = –.
–
Данное представление
могло быть получено, учитывая чет-ность
функции y = cos x и нечетность функции y =
sin x.
10)
z = –
Решение.
,
поэтому искомая запись имеет вид: z
= cos
+ i sin .
Так
как
,
то –
– sin
Соседние файлы в папке КЧ
- #
- #
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Длина радиус-вектора, который изображает заданное комплексное число $z=a+bi$, называется модулем данного комплексного числа.
Модуль заданного комплексного числа вычисляется по следующей формуле:
[r=|z|=|a+bi|=sqrt{a^{2} +b^{2} } .]
Пример 1
Вычислить модуль заданных комплексных чисел $z_{1} =13,, , z_{2} =4i,, , , z_{3} =4+3i$.
Решение:
Модуль комплексного числа $z=a+bi$ вычислим по формуле: $r=sqrt{a^{2} +b^{2} } $.
Для исходного комплексного числа $z_{1} =13$ получим $r_{1} =|z_{1} |=|13+0i|=sqrt{13^{2} +0^{2} } =sqrt{169} =13$
Для исходного комплексного числа $, z_{2} =4i$ получим $r_{2} =|z_{2} |=|0+4i|=sqrt{0^{2} +4^{2} } =sqrt{16} =4$
Для исходного комплексного числа $, z_{3} =4+3i$ получим $r_{3} =|z_{3} |=|4+3i|=sqrt{4^{2} +3^{2} } =sqrt{16+9} =sqrt{25} =5$
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Определение 2
Угол $varphi $, образованный положительным направлением вещественной оси и радиус-вектором $overrightarrow{OM} $, который соответствует заданному комплексному числу $z=a+bi$, называется аргументом данного числа и обозначается $arg z$.
Примечание 1
Модуль и аргумент заданного комплексного числа в явном виде используются при представлении комплексного числа в тригонометрической или показательной форме:
- $z=rcdot (cos varphi +isin varphi )$ — тригонометрическая форма;
- $z=rcdot e^{ivarphi } $ — показательная форма.
Пример 2
Записать комплексное число в тригонометрической и показательной формах, заданное следующими данными: 1) $r=3;varphi =pi $; 2) $r=13;varphi =frac{3pi }{4} $.
«Модуль и аргумент комплексного числа» 👇
Решение:
1) Подставим данные $r=3;varphi =pi $ в соответствующие формулы и получим:
$z=3cdot (cos pi +isin pi )$ — тригонометрическая форма
$z=3cdot e^{ipi } $ — показательная форма.
2) Подставим данные $r=13;varphi =frac{3pi }{4} $ в соответствующие формулы и получим:
$z=13cdot (cos frac{3pi }{4} +isin frac{3pi }{4} )$ — тригонометрическая форма
$z=13cdot e^{ifrac{3pi }{4} } $ — показательная форма.
Пример 3
Определить модуль и аргумент заданных комплексных чисел:
1) $z=sqrt{2} cdot (cos 2pi +isin 2pi )$; 2) $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$; 3) $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $; 4) $z=13cdot e^{ipi } $.
Решение:
Модуль и аргумент найдем, используя формулы записи заданного комплексного числа в тригонометрической и показательной формах соответственно
[z=rcdot (cos varphi +isin varphi );] [z=rcdot e^{ivarphi } .]
1) Для исходного комплексного числа $z=sqrt{2} cdot (cos 2pi +isin 2pi )$ получим $r=sqrt{2} ;varphi =2pi $.
2) Для исходного комплексного числа $z=frac{5}{3} cdot (cos frac{2pi }{3} +isin frac{2pi }{3} )$ получим $r=frac{5}{3} ;varphi =frac{2pi }{3} $.
3) Для исходного комплексного числа $z=sqrt{13} cdot e^{ifrac{3pi }{4} } $ получим $r=sqrt{13} ;varphi =frac{3pi }{4} $.
4) Для исходного комплексного числа $z=13cdot e^{ipi } $ получим $r=13;varphi =pi $.
Аргумент $varphi $ заданного комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:
[varphi =tgfrac{b}{a} ;cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } ;sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } .]
На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:
$varphi =arg z=left{begin{array}{c} {arctgfrac{b}{a} ,age 0} \ {arctgfrac{b}{a} +pi ,a
или решают систему уравнений
$left{begin{array}{c} {cos varphi =frac{a}{sqrt{a^{2} +b^{2} } } } \ {sin varphi =frac{b}{sqrt{a^{2} +b^{2} } } } end{array}right. $. (**)
Пример 4
Вычислить аргумент заданных комплексных чисел: 1) $z=3$; 2) $z=4i$; 3) $z=1+i$; 4) $z=-5$; 5) $z=-2i$.
Решение:
1) $z=3$
Так как $z=3$, то $a=3,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{3} =arctg0=0.]
2) $z=4i$
Так как $z=4i$, то $a=0,b=4$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{4}{0} =arctg(infty )=frac{pi }{2} .]
3) $z=1+i$.
Так как $z=1+i$, то $a=1,b=1$. Вычислим аргумент исходного комплексного числа, решая систему (**):
[left{begin{array}{c} {cos varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } \ {sin varphi =frac{1}{sqrt{1^{2} +1^{2} } } =frac{1}{sqrt{2} } =frac{sqrt{2} }{2} } end{array}right. .]
Из курса тригонометрии известно, что $cos varphi =sin varphi =frac{sqrt{2} }{2} $ для угла, соответствующего первой координатной четверти и равного $varphi =frac{pi }{4} $.
4) $z=-5$
Так как $z=-5$, то $a=-5,b=0$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{0}{-5} +pi =arctg0+pi =0+pi =pi .]
5) $z=-2i$
Так как $z=-2i$, то $a=0,b=-2$. Вычислим аргумент исходного комплексного числа, используя формулу (*):
[varphi =arg z=arctgfrac{-2}{0} =arctg(-infty )=frac{3pi }{2} .]
Примечание 3
Аргумент чисто мнимых чисел равен соответственно:
- $frac{pi }{2} $ с положительной мнимой частью;
- $frac{3pi }{2} $ с отрицательной мнимой частью.
Решение:
Число $z_{1} $ изображено точкой $(3;0)$, следовательно, длина радиус-вектора равна 3, т.е. $r=3$, а аргумент $varphi =0$ по примечанию 2.
Число $z_{2} $ изображено точкой $(-2;0)$, следовательно, длина соответствующего радиус-вектора равна 2, т.е. $r=2$, а аргумент $varphi =pi $ по примечанию 2.
Число $z_{3} $ изображено точкой $(0;1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{pi }{2} $ по примечанию 3.
Число $z_{4} $ изображено точкой $(0;-1)$, следовательно, длина соответствующего радиус-вектора равна 1, т.е. $r=1$, а аргумент $varphi =frac{3pi }{2} $ по примечанию 3.
Число $z_{5} $ изображено точкой $(2;2)$, следовательно, длина соответствующего радиус-вектора равна $sqrt{2^{2} +2^{2} } =sqrt{4+4} =sqrt{8} =2sqrt{2} $, т.е. $r=2sqrt{2} $, а аргумент $varphi =frac{pi }{4} $ по свойству прямоугольного треугольника.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме