Модуль числа — теория и решение задач
Модуль числа – это такая забавная концепция в математике, с пониманием которой у многих людей возникают трудности 🙂
А между тем она проста как апельсин. Но, чтобы ее понять, давай сначала разберемся, зачем и кому он нужен.
Вот смотри…
Ситуация первая
В жизни, часто встречаются ситуации, где отрицательные числа не имеют никакого практического смысла.
Например, мы не можем проехать на машине «минус 70 километров» (мы проедем 70 километров, не важно, в каком направлении), как и не можем купить «минус 5 кг апельсинов». Эти значения всегда должны быть положительными.
Именно для обозначения таких ситуаций математики придумали специальный термин – модуль или абсолютная величина.
Ситуация вторая
Ты покупаешь пакет чипсов «Lay’s». На пакете написано, что он весит 100 грамм. Но, если ты начнешь взвешивать пакеты, вряд ли они будут весить ровно 100 грамм. Какой-то из них будет весить 101 грамм, а какой-то 99.
И что, можно идти судиться с компанией «Lay’s», если они тебе недовесили?
Нет. Потому что «Lay’s» устанавливает допуск и говорит, что пакет будет весить 100 грамм, плюс-минус 1 грамм. Вот это «плюс-минус» – это и есть модуль.
Ситуация третья
В жизни вообще не бывает 100% точных величин. Всегда есть вот такие допуски. В зарплате, например: «Я согласен работать за 250 тыс рублей в месяц, плюс-минус 20 тыс!» 20 тысяч – это и есть модуль.
А вообще для простоты запомни, что модуль это расстояние от точки отсчета в любую сторону.
Ну вот, ты уже почти все знаешь. Давай теперь подробнее…
Модуль числа — коротко о главном
Определение модуля:
Модуль (абсолютная величина) числа ( displaystyle x) — это само число ( displaystyle x), если ( displaystyle xge 0), и число ( displaystyle -x), если ( displaystyle x<0):
( displaystyle left| x right|=left{ begin{array}{l}x, xge 0\-x, x<0end{array} right.)
Свойства модуля:
- Модуль числа есть число неотрицательное: ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0);
- Модули противоположных чисел равны: ( left| -x right|=left| x right|);
- Модуль произведения двух (и более) чисел равен произведению их модулей: ( left| xcdot yright|=left| x right|cdot left|yright|);
- Модуль частного двух чисел равен частному их модулей: ( displaystyle left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0});
- Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел:( left| x+y right|le left| x right|+left| y right|);
- Постоянный положительный множитель можно выносить за знак модуля: ( left| cx right|=ccdot left| x right|) при ( displaystyle c>0);
- Квадрат модуля числа равен квадрату этого числа: ( {{left| x right|}^{2}}={{x}^{2}}).
Кстати, в продолжение этой темы у нас есть отличная статья: «Уравнения с модулем«. Когда прочитаешь эту статью, обязательно ознакомься и со второй.
И просто чтобы ты знал, модуль часто попадается при решении квадратных уравнений или иррациональных.
Что же такое модуль числа?
Представь, что это ты.
Предположим, что ты стоишь на месте и можешь двигаться как вперёд, так и назад. Обозначим точку отправления ( 0).
Итак, ты делаешь ( 3) шага вперёд и оказываешься в точке с координатой ( 3).
Это означает, что ты удалился от места, где стоял на (3) шага (( 3) единичных отрезка).
То есть, расстояние от начала движения до точки, где ты в итоге оказался, равно ( 3).
Но ведь ты же можешь двигаться и назад!
Если от отправной точки с координатой ( 0) сделать ( 3) шага в обратную сторону, то окажешься в точке с координатой ( -3).
Какое расстояние было пройдено в первом и во втором случае?
Конечно же, расстояние, пройденное в первом и во втором случае, будет одинаковым и равным трем, ведь обе точки (( 3) и ( -3)), в которых ты оказался одинаково удалены от точки, из которой было начато движение (( 0)).
Таким образом, мы приблизились к понятию модуля.
Получается, что модуль показывает расстояние от любой точки на координатном отрезке до точки начала координат.
Так, модулем числа ( 5) будет ( 5). Модуль числа ( -5) также равен ( 5).
Потому что расстояние не может быть отрицательным! Модуль – это абсолютная величина.
Обозначается модуль просто:
( |mathbf{a}|,) (( a) — любое число).
Итак, найдём модуль числа ( 3) и ( -3):
( left| mathbf{3} right|=mathbf{3})
( left| -mathbf{3} right|=mathbf{3}.)
Основные свойства модуля
Первое свойство модуля
Модуль не может быть выражен отрицательным числом ( |mathbf{a}|text{ }ge text{ }mathbf{0})
То есть, если ( mathbf{a}) – число положительное, то его модуль будет равен этому же числу.
Если ( mathbf{a}text{ }>text{ }mathbf{0},) то ( displaystyle left| a right|=a).
Если ( a) – отрицательное число, то его модуль равен противоположному числу.
Если ( atext{ }<text{ }mathbf{0},) то ( |mathbf{a}|text{ }=text{ }-mathbf{a})
А если ( a=0)? Ну, конечно! Его модуль также равен ( 0):
Если ( a=0), то ( |mathbf{a}|=mathbf{a}), или ( displaystyle left| 0 right|=0).
Из этого следует, что модули противоположных чисел равны, то есть:
( left| -4 right|text{ }=text{ }left| 4 right|text{ }=text{ }4;)
( left| -7 right|text{ }=text{ }left| 7 right|text{ }=text{ }7.)
А теперь потренируйся:
- ( left| 9 right|text{ }=text{ }?;)
- ( left| -3 right|text{ }=text{ }?;)
- ( left| 16 right|text{ }=text{ }?;)
- ( left| 8 right|text{ }=text{ }?;)
- ( left| -17 right|text{ }=text{ }?.)
Ответы: 9; 3; 16; 8; 17.
Довольно легко, правда? А если перед тобой вот такое число: ( left| 2-sqrt{5} right|=?)
Как быть здесь? Как раскрыть модуль в этом случае? Действуем по тому же сценарию.
Сначала определяем знак выражения под знаком модуля, а потом раскрываем модуль:
- если значение выражения больше нуля, то просто выносим его из-под знака модуля,
- если же выражение меньше нуля, то выносим его из-под знака модуля, меняя при этом знак, как делали это ранее в примерах.
Ну что, попробуем? Оценим ( 2-sqrt{5}):
( 2<sqrt{5}) (Забыл, что такое корень? Бегом повторять!)
Если ( 2<sqrt{5}), то какой знак имеет ( 2-sqrt{5})? Ну конечно, ( 2-sqrt{5}<0)!
А, значит, знак модуля раскрываем, меняя знак у выражения:
( left| 2-sqrt{5} right|=-left( 2-sqrt{5} right)=-2+sqrt{5}=sqrt{5}-2)
Разобрался? Тогда попробуй сам:
- ( left| sqrt{3}-1 right|=?)
- ( left| 3-sqrt{7} right|=?)
- ( left| 2-sqrt{7} right|=?)
- ( left| sqrt{13}-4 right|=?)
Ответы:
( sqrt{3}-1; 3-sqrt{7}; sqrt{7}-2; 4-sqrt{13.})
Какими же ещё свойствами обладает модуль?
Во-первых, если нам нужно перемножить числа внутри знака модуля, мы спокойно можем перемножить модули этих чисел.
То есть: ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|)
Выражаясь математическим языком, модуль произведения чисел равен произведению модулей этих чисел.
Например:
( left| mathbf{5}cdot mathbf{7} right|text{ }=text{ }left| mathbf{5} right|cdot left| mathbf{7} right|text{ }=text{ }mathbf{5}cdot mathbf{7}text{ }=text{ }mathbf{35};)
( left| mathbf{3}cdot left( -mathbf{2} right) right|text{ }=text{ }left| mathbf{3} right|cdot left| -mathbf{2} right|text{ }=text{ }mathbf{3}cdot mathbf{2}text{ }=text{ }mathbf{6}.)
А что, если нам нужно разделить два числа (выражения) под знаком модуля? Да то же, что и с умножением! Разобьем на два отдельных числа (выражения) под знаком модуля:
( displaystyle |frac{a}{b}|=frac{|a|}{|b|}) при условии, что ( mathbf{b}ne mathbf{0}) (так как на ноль делить нельзя).
Еще одно свойство модуля…
Модуль суммы чисел всегда меньше или равен сумме модулей этих чисел.
( |a+bleft| text{ }le text{ } right|aleft| + right|b|)
Почему так? Всё очень просто! Как мы помним, модуль всегда положителен. Но под знаком модуля может находиться любое число: как положительное, так и отрицательное.
Допустим, что числа ( a) и ( b) оба положительные. Тогда левое выражение будет равно правому выражению. Рассмотрим на примере:
| ( left| mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{10} right|text{ }=text{ }mathbf{10}) | ( left| mathbf{3} right|+left| mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Выражения также равны, если оба числа отрицательны:
| ( displaystyle |-3+(-7)|~=~|-3-7|~)( displaystyle=|-10|=10) | ( |-mathbf{3}left| + right|-mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
Если же под знаком модуля одно число отрицательное, а другое положительно, левое выражение всегда окажется меньше правого:
| ( left| -mathbf{3}+mathbf{7} right|text{ }=text{ }left| mathbf{4} right|text{ }=text{ }mathbf{4}) | ( |-mathbf{3}left| + right|mathbf{7}|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
или
| ( left| mathbf{3}+left( -mathbf{7} right) right|text{ }=text{ }left| -mathbf{4} right|text{ }=text{ }mathbf{4}) | ( left| mathbf{3} right|+left| -mathbf{7} right|text{ }=text{ }mathbf{3}+mathbf{7}text{ }=text{ }mathbf{10}) |
( mathbf{4}<mathbf{10})
Рассмотрим еще парочку полезных свойств модуля
Что если перед нами такое выражение:
( left| 7x right|)
Что мы можем сделать с этим выражением?
Значение x нам неизвестно, но зато мы уже знаем, что ( |acdot bleft| text{ }=text{ } right|aleft| cdot right|b|), а значит ( left| 7x right|=left| 7 right|cdot left| x right|). Число ( 7) больше нуля, а значит можно просто записать:
( left| 7x right|=left| 7 right|cdot left| x right|=7left| x right|)
Вот мы и пришли к другому свойству, которое в общем виде можно представить так:
( left| cx right|=ccdot left| x right|,) при ( c>0)
А чему равно такое выражение:
( {{left| x right|}^{2}}=?)
Итак, нам необходимо определить знак под модулем. А надо ли здесь определять знак?
Конечно, нет, если помнишь, что любое число в квадрате всегда больше нуля! Если не помнишь, смотри тему степень и ее свойства.
И что же получается? А вот что:
( {{left| x right|}^{2}}={{x}^{2}})
Здорово, да? Довольно удобно. А теперь конкретный пример для закрепления:
( {{left| 5 right|}^{2}}={{5}^{2}}=25)
( {{left| -5 right|}^{2}}=?)
Ну, и почему сомнения? Действуем смело!
( {{left| -5 right|}^{2}}={{5}^{2}}=25)
Во всем разобрался? Тогда вперед тренироваться на примерах!
Тренировка на примерах
1. Найдите значение выражения ( |xleft| text{ }+text{ } right|y|), если ( x=text{ }-7,5text{ },y=text{ }12.)
2. У каких чисел модуль равен ( 5)?
3. Найдите значение выражений:
а) ( |3|text{ }+text{ }|-9|;)
б) ( |-5|text{ }-text{ }|6|;)
в) ( |15left| cdot right|-3|;)
г) ( displaystyle frac{|8|}{|-2|}).
Если не все пока ясно и есть затруднения в решениях, то давай разбираться:
Решение 1:
Итак, подставим значения ( x) и ( y) в выражение ( |mathbf{x}left| text{ }-text{ } right|mathbf{y}|.) Получим:
( |-7,5|text{ }+text{ }|12|text{ }=7,5text{ }+text{ }12text{ }=text{ }19,5.)
Решение 2:
Как мы помним, противоположные числа по модулю равны. Значит, значение модуля, равное ( 5) имеют два числа: ( 5) и ( -5).
Решение 3:
а) ( |3|text{ }+text{ }|-9|=text{ }3+9=text{ }12;)
б) ( |-5|-text{ }left| 6 right|text{ }=text{ }5-6=text{ }-1;)
в) ( |15left| cdot right|-3|text{ }=text{ }15cdot 3=text{ }45;)
г) ( frac{|8|}{|-2|}=frac{8}{2}=4.)
Все уловил? Тогда пора перейти к более сложному!
Решение более сложных примеров
Попробуем упростить выражение ( left| sqrt{3}-2 right|+left| sqrt{3}+5 right|)
Решение:
Итак, мы помним, что значение модуля не может быть меньше нуля. Если под знаком модуля число положительное, то мы просто можем отбросить знак: модуль числа будет равен этому числу.
Но если под знаком модуля отрицательное число, то значение модуля равно противоположному числу (то есть числу, взятому со знаком «–»).
Для того, чтобы найти модуль любого выражения, для начала нужно выяснить, положительное ли значение оно принимает, или отрицательное.
( displaystyle sqrt{3} approx 1,7). Получается, значение первого выражения под модулем ( displaystyle sqrt{3}-2approx 1,7-2approx -0,3text{ }).
( -0,3<0), следовательно, выражение под знаком модуля отрицательно. Второе выражение под знаком модуля всегда положительно, так как мы складываем два положительных числа.
Итак, значение первого выражения под знаком модуля отрицательно, второго – положительно:
Это значит, раскрывая знак модуля первого выражения, мы должны взять это выражение со знаком «–». Вот так:
Модуль числа и его свойства (строгие определения и доказательства)
Модуль (абсолютная величина) числа ( x) — это само число ( x), если ( xge 0), и число ( -x), если ( x<0):
( left| x right|=left{ begin{array}{l}x,text{ }xge 0\-x,text{ }x<0end{array} right.)
Например: ( left| 4 right|=4;text{ }left| 0 right|=0;text{ }left| -3 right|=-left( -3 right)=3.)
Пример:
Упростите выражение ( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|).
Решение:
( sqrt{5}-3<0Rightarrow left| sqrt{5}-3 right|=-left( sqrt{5}-3 right)=3-sqrt{5};)
( sqrt{5}+1>0Rightarrow left| sqrt{5}+1 right|=sqrt{5}+1;)
( left| sqrt{5}-3 right|+left| sqrt{5}+1 right|=3-sqrt{5}+sqrt{5}+1=4.)
Основные свойства модуля (итог)
Для всех ( x,yin mathbb{R}):
- ( left| x right|ge 0,text{ }left| x right|=0Leftrightarrow x=0;)
- ( left| -x right|=left| x right|;)
- ( left| xcdot y right|=left| x right|cdot left| y right|;)
- ( left| frac{x}{y} right|=frac{left| x right|}{left| y right|},text{ y}ne text{0};)
- ( left| x+y right|le left| x right|+left| y right|)
- ( left| cx right|=ccdot left| x right|, при text{ }c>0)
- ( {{left| x right|}^{2}}={{x}^{2}})
Докажите свойство модуля: ( left| x+y right|le left| x right|+left| y right|)
Доказательство:
Предположим, что существуют такие ( x;yin mathbb{R}), что ( left| x+y right|>left| x right|+left| y right|.) Возведем левую и правую части неравенства в квадрат (это можно сделать, т.к. обе части неравенства всегда неотрицательны):
( displaystyle begin{array}{l}left| x+y right|>left| x right|+left| y right|Leftrightarrow \{{left( x+y right)}^{2}}>{{left( left| x right|+left| y right| right)}^{2}}Leftrightarrow \{{x}^{2}}+2xy+{{y}^{2}}>{{x}^{2}}+2cdot left| x right|cdot left| y right|+{{y}^{2}}Leftrightarrow \xy>left| x right|cdot left| y right|Leftrightarrow \xy>left| xy right|,end{array})
а это противоречит определению модуля.
Следовательно, таких ( x;yin mathbb{R}) не существует, а значит, при всех ( x,text{ }yin mathbb{R}) выполняется неравенство ( left| x+y right|le left| x right|+left| y right|.)
А теперь самостоятельно…
Докажите свойство модуля: ( left| cx right|=ccdot left| x right|, при text{ }c>0)
Воспользуемся свойством №3: ( left| ccdot x right|=left| c right|cdot left| x right|), а поскольку ( c>0text{ }Rightarrow text{ }left| c right|=c), тогда
( left| cx right|=ccdot left| x right|), ч.т.д.
Упростите выражение ( left| frac{31}{8}-sqrt{15} right|+left| frac{15}{4}-sqrt{15} right|)
Чтобы упростить, нужно раскрыть модули. А чтобы раскрыть модули, нужно узнать, положительны или отрицательны выражения под модулем:
Подготовка к ЕГЭ на 90+ в мини-группах
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
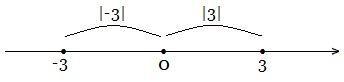
Расстояние от данной точки до начала отсчёта, до точки (О(0)), называют модулем числа.
Расстояние от точки (M)((-4)) до нуля (см. рисунок) и от точки (N)((4)) до нуля равно (4) единичным отрезкам.
Число (4) является модулем числа (-4) и числа (4).
−4=44=4
Противоположные числа имеют равные модули:
Модуль числа (0) равен (0):
Модуль числа не может быть отрицательным. Модуль положительного числа и нуля равен самому числу, а
модуль отрицательного числа — число ему противоположное.
−16=16271=27110004=1000482,1=82,1−0,7=0,7−3,005=3,005−34=3494=94−278=278
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Модуль числа
Поддержать сайт
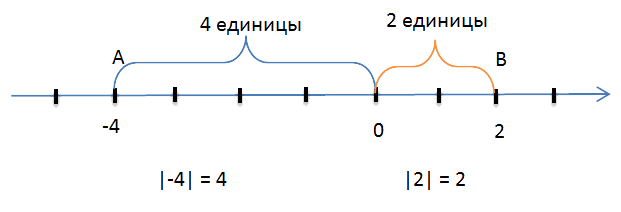
Обозначим на
координатной прямой две точки, которые соответствуют числам
«−4» и 2.
Точка «A», соответствующая числу «−4»,
находится на расстоянии
4 единичных отрезков от точки 0
(начала отсчёта), то есть длина отрезка «OA»
равна 4 единицам.
Число 4 (длина отрезка «OA») называют модулем
числа «−4».
Обозначают модуль числа так: |−4| = 4
Читают символы выше следующим образом: «модуль числа
минус четыре равен четырём».
Точка «B», соответствующая
числу «+2», находится на расстоянии двух единичных отрезков от начала отсчёта,
то есть длина отрезка «OB» равна двум единицам.
Число 2 называют модулем числа
«+2» и записывают:
|+2| = 2 или |2| = 2.
Если взять некоторое число «a» и изобразить его
точкой «A» на координатной прямой, то
расстояние от точки «A» до начала отсчёта
(другими словами длина отрезка «OA») и будет называться
модулем числа «a».
|a| = OA
Запомните!
Модулем рационального числа называют расстояние от
начала отсчёта до точки координатной прямой, соответствующей этому числу.
Так как расстояние (длина отрезка) может выражаться только положительным числом или нулём, можно сказать,
что модуль числа не может быть отрицательным.
Запишем свойства модуля с помощью буквенных выражений, рассмотрев все возможные случаи.
- Модуль положительного числа равен самому числу.
|a| = a, если a > 0 - Модуль отрицательного числа равен противоположному числу.
|−a| = a, если a < 0 - Модуль нуля равен нулю.
|0| = 0, если a = 0 - Противоположные числа имеют равные модули.
|−a| = |a| = a
Примеры модулей рациональных чисел:
- |−4,8| = 4,8
- |5| = 5
- |0| = 0
- |− | =
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
18 января 2016 в 17:47
Евгения Плотникова
Профиль
Благодарили: 0
Сообщений: 1
Евгения Плотникова
Профиль
Благодарили: 0
Сообщений: 1
Модуль координаты точки равен 1)2;2)4;3)3.Вопрос.Какую координату может иметь точка.
0
Спасибо
Ответить
19 сентября 2016 в 10:45
Ответ для Евгения Плотникова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Знак моддуля, означает, что под ним может скрываться как отрицательное, так и положительное значение. Следовательно:
1) 2;2
-2;2
-2;-2
2;-2
2) 4;0
-4;0
0;4
0;-4
3) 3;0
-3;0
0;3
0;-3
подробнее здесь.
0
Спасибо
Ответить
17 января 2016 в 18:05
Заира Надырова
Профиль
Благодарили: 0
Сообщений: 1
Заира Надырова
Профиль
Благодарили: 0
Сообщений: 1
а) Что можно сказать о числе х, если известно, что модуль х=х?
б)модуль х=?х
0
Спасибо
Ответить
21 января 2016 в 16:18
Ответ для Заира Надырова
Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
то что х=х больше х
0
Спасибо
Ответить
Модуль числа вводится новое понятие в математике. Разберем подробно, что такое модуль числа и как с ним работать?
Рассмотрим пример:
Мы вышли из дома в магазин. Прошли 300 м, математически это выражение можно записать как +300, смысл числа 300 от знака “+” не поменяется. Расстояние или модуль числа в математике это одно и тоже можно записать так: |300|=300. Знак модуля числа обозначается двумя вертикальными линиями.
А потом в обратном направлении прошли 200м. Математически обратный путь мы можем записать как -200. Но мы не говорим так “мы прошли минус двести метров”, хотя мы вернулись, потому что расстояние как величина остается положительной. Для этого в математике ввели понятие модуля. Записать расстояние или модуль числа -200 можно так: |-200|=200.
Свойства модуля.
Определение:
Модуль числа или абсолютная величина числа – это расстояние от отправной точки до точки назначения.
Или есть более классическое определение модуля числа.
Модуль числа a называют расстояние от начала координат до точки, изображающей это число на координатной прямой.
Модуль целого числа не равного нулю, всегда положительное число.
Записывается модуль так:
1. Модуль положительного числа равно самому числу.
|a|=a
2. Модуль отрицательного числа равно противоположному числу.
|-a|=a
3. Модуль нуля, равен нулю.
|0|=0
4. Модули противоположных чисел равны.
|a|=|-a|=a
Вопросы по теме:
Что такое модуль числа?
Ответ: модуль — это расстояние от отправной точки до точки назначения.
Если перед целым числом поставить знак “+” , что произойдет?
Ответ: число не поменяет свой смысл, например, 4=+4.
Если перед целым числом поставить знак “-” , что произойдет?
Ответ: число изменится на противоположное число, например, 4 и -4.
У каких чисел одинаковый модуль?
Ответ: у положительных чисел и нуля модуль будет тот же. Например, 15=|15|.
У каких чисел модуль – противоположное число?
Ответ: у отрицательных чисел, модуль будет равен противоположному числу. Например, |-6|=6.
Пример №1:
Найдите модуль чисел: а) 0 б) 5 в) -7?
Решение:
а) |0|=0
б) |5|=5
в)|-7|=7
Пример №2:
Существуют ли два различных числа, модули которых равны?
Решение:
|10|=10
|-10|=10
Модули противоположных чисел равны.
Пример №3:
Какие два противоположных числа, имеют модуль 9?
Решение:
|9|=9
|-9|=9
Ответ: 9 и -9.
Пример №4:
Выполните действия: а) |+5|+|-3| б) |-3|+|-8| в)|+4|-|+1|
Решение:
а) |+5|+|-3|=5+3=8
б) |-3|+|-8|=3+8=11
в)|+4|-|+1|=4-1=3
Пример №5:
Найдите: а) модуль числа 2 б) модуль числа 6 в) модуль числа 8 г) модуль числа 1 д) модуль числа 0.
Решение:
а) модуль числа 2 обозначается как |2| или |+2| это одно и тоже.
|2|=2
б) модуль числа 6 обозначается как |6| или |+6| это одно и тоже.
|6|=6
в) модуль числа 8 обозначается как |8| или |+8| это одно и тоже.
|8|=8
г) модуль числа 1 обозначается как |1| или |+1| это одно и тоже.
|1|=1
д) модуль числа 0 обозначается как |0|, |+0| или |-0| это одно и тоже.
|0|=0
На чтение 2 мин. Просмотров 36k.
Модулем числа а (записывают |a|) называют расстояние от начала отсчета до точки, соответствующей данному числу а.
Значение модуля любого числа неотрицательно. |3|=3; |-3|=3, т.к. расстояние от начала отсчета и до числа -3, и до числа 3 равно трем единичным отрезкам. Противоположные числа имеют равные модули. Модуль нуля равен нулю: |0|=0.
По определению модуля числа: |a|=a, если a≥0 и |a|=-a, если а < 0. Читают: модуль неотрицательного числа равен самому этому числу; модуль отрицательного числа равен противоположному числу.
Рассмотрим ниже несколько примеров.
Пример 1
Вычислить: а) |5|-2; б) |-12| : 6; в) |-24| + |13|; г) |65|-|-45|.
Решение. а) |5|-2=5-2=3;
б) |-12| : 6=12 : 6=2;
в) |-24|+|13|=24+13=37;
г) |65|-|-45|=65-45=20.
Пример 2
Решить уравнение: а) |m|+4=10; б) 6-|x|=2.
Решение.
а) |m|+4=10;
|m|=10-4; из суммы вычли известное слагаемое;
|m|=6. Так как |-6|=6 и |6|=6, то m=-6 или m=6.
Ответ: -6; 6.
б) 6-|x|=2.
|x|=6-2;
|x|=4, отсюда х=-4 или х=4.
Ответ: -4; 4.
Пример 3
Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5.

Ответ: множество А={-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Пример 4
Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5.
Решение. Из всех чисел, показанных на рисунке штриховкой, нам нужно выбрать натуральные, т.е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.
( 12 оценок, среднее 4.17 из 5 )