Содержание:
- § 1 Правило нахождения модуля суммы слагаемых с одинаковыми знаками
- § 2 Правило нахождения модуля суммы слагаемых с разными знаками
§ 1 Правило нахождения модуля суммы слагаемых с одинаковыми знаками
В этом уроке рассмотрим правило вычисления алгебраической суммы двух чисел.
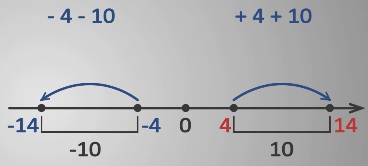
Найдем значения выражений: -4 – 10 и +4+10 с помощью координатной прямой.
Вспомним, что вычитание – это движение влево, а сложение – движение вправо по координатной прямой.
На координатной прямой отметим точки -4 и +4. От точки -4 отложим влево 10 единичных отрезков, получим координату -14. От точки +4 отложим вправо 10 единичных отрезков, получим координату +14.
По рисунку видно, что -4-10 = -14; +4+10 = +14.
Проанализируем выражения. В каждом выражении слагаемые имеют одинаковые знаки: в первом знак минус, во втором знак плюс, значения суммы имеют тот же знак, что и слагаемые.
Найдем сумму модулей l-4l + l-10l = l-14l.
l -4l = 4
l-10l = 10
4+10 = 14, а 14 – модуль числа -14.
Аналогично l4l + l10l = l14l
l4l = 4
l10l = 10
4+10=14, а 14 – модуль и +14 тоже.
Можно сделать вывод:
Если слагаемые имеют одинаковые знаки, то значение суммы имеет тот же знак, что и слагаемые, а модуль суммы равен сумме модулей слагаемых.
Например:
В сумме -14-23 оба слагаемых имеют знак минус, значит, значение суммы тоже будет иметь знак минус, складываем модули 14+23=37, в итоге значение суммы -37.
§ 2 Правило нахождения модуля суммы слагаемых с разными знаками
Найдем значения выражений, в которых слагаемые имеют разные знаки.
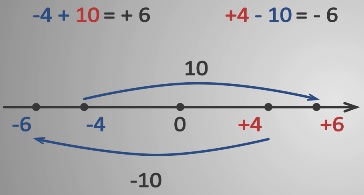
Например, -4+10 и +4-10.
Отметим на координатной прямой точки -4 и +4. От координаты -4 отложим вправо 10 единичных отрезков, получим число +6. От координаты +4 отложим влево 10 единичных отрезков, получим точку -6. Таким образом, -4+10= +6 и +4-10 = -6.
Сделаем анализ выражений.
Сравним модули слагаемых l-4l < l10l; l+4l < l-10l,обратим внимание, результат суммы имеет знак слагаемого с большим модулем. Из большего модуля вычтем меньший:
l+10l – l-4l = 6 и l-10l – l+4l = 6, значит
-4+10= 6, а +4-10= -6.
Вывод:
Если слагаемые имеют разные знаки, то значение суммы имеет тот же знак, что и слагаемое с большим модулем, а модуль суммы равен разности модулей слагаемых при условии, что из большего модуля вычитается меньший модуль.
Например, найдем значение выражения 9 – 25, слагаемые имеют разные знаки +9 и -25, найдем модули слагаемых l+9l = 9, l-25l = 25.
Больший модуль 25, значит, знаком результата суммы будет знак минус. Найдем разность модулей 25 – 9 = 16. Значит значение суммы равно минус 16.
Вспомним, противоположные числа – это числа, которые отличаются знаками, их модули одинаковые. Следовательно, сумма противоположных чисел равна 0, так как разность одинаковых модулей равна 0.
Вывод:
Сумма противоположных чисел равна 0. Также можно утверждать, что если сумма двух чисел равна 0, то данные числа будут противоположными.
Если одно из слагаемых равно 0, то значение суммы равно другому слагаемому.
Например, -8,3 + 0, слагаемые с разными знаками, модуль -8,3 больше чем модуль 0, значит знак суммы — минус, найдем разность модулей l-8.3l – l0l = 8, 3, следовательно сумма равна -8,3.
Итак, на этом уроке Вы познакомились с правилом вычисления алгебраической суммы двух чисел.
Список использованной литературы:
- Математика.6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича //автор-составитель Л.А. Топилина. Мнемозина 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович.- М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. /Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013.
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
Основные правила математики с примерами. 6 класс. Часть 1.
Содержание
Продолжение: Основные правила математики с примерами. 6 класс. Часть 2.
- Делимость натуральных чисел
- Простые и составные числа
- Признаки делимости натуральных чисел
- Разложение числа на простые множители
- Основное свойство дроби
- Сокращение дробей
- Наибольший общий делитель
- Наименьшее общее кратное
- Модуль числа
- Сложение и вычитание дробей
- Сложение и вычитание рациональных чисел
Делимость натуральных чисел
Если натуральное число делится нацело на натуральное число
, то число
называют кратным числа
, число
— делителем числа
.
12 -кратное числам 1, 2, 3, 4, 6, 12.
1, 2, 3, 4, 6, 12 — делители 12.
Для любого натурального числа каждое из чисел
a · 1, a · 2, a · 3,…
является кратным числа .
Число 6. Кратные 6 · 1, 6 · 2, 6 · 3, 6 · 4, … или по-другому запишем 6, 12, 18, 24, …
Наименьшим делителем любого натурального числа является число
, а наибольшим — само число
.
Число 6. Наименьший делитель: 1. Наибольший делитель: 6.
Среди чисел, кратных , наибольшего нет, а наименьшее есть — это само число
.
Число 6. Наименьшее кратное: 6. Наибольшее кратное: нет.
Если каждое из чисел и
делится нацело на число
,то и сумма
также делится нацело на число
.
12 : 3 = 4 -целое, 6 : 3 = 2 — целое 12 и 6 делятся нацело на 3.
+
= 12 + 6 =18 18 : 3 = 6-целое. 18 делится нацело на 3.
Если число делится нацело на число
, а число
не делится нацело на число
, то сумма
также не делится нацело на число
.
12 : 3 = 4 — целое, 7 : 3 = нецелое число. 7 не делится нацело на 3.
+
= 12 + 7 =19 19 : 3 = нецелое число. 19 не делится нацело на 3.
Простые и составные числа
Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число.
Натуральное число, имеющее более двух делителей, называют составным.
Числа 2, 3 , 5, 7 — простые. Каждое имеет 2 делителя: 1 и само число.
Числа 4, 6, 8 — составные. Делители 4: 1, 2, 4; 6: 1, 2, 3, 6; 8: 1, 2, 4, 8 — делителей больше 2-ух.
Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.
Число 6. Представим в виде произведения простых чисел: 6 = 2 · 3.
Число 8. Представим в виде произведения простых чисел: 8 = 2 · 2 · 2.
Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.
Числа 7 и 15. Наибольший общий делитель этих чисел одновременно — это 1. 7 и 15 — взаимно простые.
Признаки делимости натуральных чисел
Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.
100 делится на 10, так как оканчивается на 0.
Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.
17 не делится на 10, так как не оканчивается на 0.
Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.
Если 17 разделить на 10, то остаток 7.
Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.
Четные цифры: 0, 2, 4, 6, 8. Число 18 заканчивается на четную цифру 8, поэтому делится на 2.
Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.
Нечетные цифры: 1, 3, 5, 7, 9. Число 19 заканчивается на нечетную цифру 9, поэтому не делится на 2.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.
Числа 20 и 35 делятся на 5, так как оканчиваются на 0 или 5 соответственно.
Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.
Число 27 не оканчивается ни на 0, ни на 5, поэтому на 5 не делится.
Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.
Число 117. 1 + 1 +7 = 9; 9 : 9 = 1; 9 нацело делится на 9, поэтому 117 делится на 9.
Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.
Число 110. 1 + 1 + 0 = 2; 2 нацело не делится на 9, поэтому 110 не делится на 9.
Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.
Число 57. 5 + 7 = 12; 12 : 3 = 4. 12 нацело делится на 4, поэтому 57 делится на 3.
Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.
Число 56. 5 + 6 = 11; 11 нацело не делится на 3, поэтому 56 не делится на 3.
Разложение числа на простые множители
Разложить числа 12 и 16 на простые множители, представить числа в виде произведения простых множителей:
12631223 1684212222 12 = 2 · 2 · 3 = 22 · 316 = 2 · 2 · 2 · 2 = 24;;
Основное свойство дроби
Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:
ab = a · nb · n
равенство сохраняется.
Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:
a : nb : n = ab
равенство сохраняется.
Сокращение дробей
Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.
3 — общий делитель чисел 9 и 24.
Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.
несократимая дробь, так как числа 3 и 8 взаимно простые.
Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.
2436 = 24 : 1236 : 12=23
Есть общие делители чисел 24 и 36: 1, 2, 3, 4, 6, 12. Но число 12 — наибольший общий делитель .
Наибольший общий делитель
Найти наибольший общий делитель чисел 12 и 16.
Разложим на простые множители. Выбираем только те множители, которые есть и в первом, и во втором разложении
12631223 1684212222 НОД(12,16) = 2 · 2 = 4; Или другая запись: представим в виде произведения простых множителей12 = 2 · 2 · 3 ;16 = 2 · 2 · 2 · 2 ; НОД(12,16) = 2 · 2 = 4
Наименьшее общее кратное
Найти наименьшее общее кратное чисел 12 и 16. Разложим числа на простые множители. Выпишем разложение первого числа. Дополним числами из разложения второго числа без повторений
12631223 1684212222 НОК(12,16) = 2 · 2 · 3· 2 · 2 = 24 · 3 = 48;
Другая запись : представим в виде произведения простых множителей
12 = 2 · 2 · 3 ;16 = 2 · 2 · 2 · 2 ; НОК(12,16) =2 · 2 · 3 · 2 · 2 = 48.
Приведение дробей к наименьшему общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю, надо:
- найти наименьший общий знаменатель данных дробей;
- найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Привести дроби к наименьшему общему знаменателю.
524 и 136
1. Найти Наименьшее общее кратное чисел 24 и 36 — это число 72( 72 нацело делится и на 24, и на 36)
2. Посчитать дополнительные множители
72 : 24 = 3;72 : 36 = 2.3. 5324=5 · 324 · 3=1572;1236=1 ·2 36 · 2=272.
Целые числа. Рациональные числа
Все натуральные числа, противоположные им числа и число 0 называют целыми числами.
Натуральные числа называют целыми положительными числами. Числа -1, -2, -3, … называют целыми отрицательными числами.
Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.
Объединив целые числа с дробными, получим рациональные числа.
Модуль числа
Модулем числа называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
Модуль числа < обозначают так:
a
(читают: «модуль a»).
Модуль положительного числа равен этому числу; модуль отрицательного числа равен числу, противоположному данному;
a = a, a≥0—a, a<0
Модуль числа принимает только неотрицательные значения. Модули противоположных чисел равны:
a = —a
5 = 5, —5 = —(—5) = 5 или5 = —5 = 5
Сложение и вычитание дробей
Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
15 + 25 = 1 + 25 = 3567 — 27 = 6 — 27 = 47
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
15 + 25 = 1 + 25 = 3567 — 27 = 6 — 27 = 47
Сложение и вычитание рациональных чисел
Чтобы сложить два числа с разными знаками, надо:
- найти модули слагаемых;
- из большего модуля вычесть меньший модуль;
- перед полученным числом поставить знак слагаемого с большим модулем.
—17⏞—17=17+ ⏞>15⏞15=15= —(17 — 15) = —2;—12 + 15 =15 — 12 = 3 —здесь можно 2ое слагаемое вынести вперед и решить как простой пример на вычитание
Чтобы сложить два отрицательных числа, надо:
- найти модули слагаемых;
- сложить модули слагаемых;
- перед полученным числом поставить знак «-».
— 17⏞—17=17—12⏞—12=12 = —(17 + 12) = —29
Сумма двух противоположных чисел равна нулю:
—a+a=0 или a—a=0
—5 + 5 = 0;5 — 5 = 0.
a+0 = 0+a = a
7 + 0 = 0 + 7 = 7.
Чтобы найти разность двух чисел можно
к уменьшаемому прибавить число, противоположное вычитаемому.
15 — 3 = 15 + (—3) = 12.
Продолжение: Основные правила математики с примерами. 6 класс. Часть 2.
Данная информация составлена на базе УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир. Примеры составлены мной Косыхиной Н.В.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Рациональные числа
- Сложение рациональных чисел
Примеры:
Примеры:
Обратите внимание: любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.
На основе примеров 



Чтобы сложить два числа с разными знаками, надо:
1) найти модули слагаемых;
2) из большего модуля вычесть меньший модуль;
3) перед полученным числом поставить знак слагаемого с большим модулем.
На основе примера 


Чтобы сложить два отрицательных числа, надо:
1) найти модули слагаемых;
2) сложить модули слагаемых;
3) перед полученным числом поставить знак «
На основе примера 

Также справедливо следующее правило:
Примеры:
1) 5 + 0 = 0 + 5 = 5;
2) 


Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Модуль числа
Рациональные числа
Сравнение рациональных чисел
Вычитание рациональных чисел
Умножение рациональных чисел
Деление рациональных чисел
Свойства действий с рациональными числами
Раскрытие скобок
Решение уравнений
Рациональные числа
Правило встречается в следующих упражнениях:
6 класс
Номер 954,
Мерзляк, Полонский, Якир, Учебник
Номер 956,
Мерзляк, Полонский, Якир, Учебник
Номер 957,
Мерзляк, Полонский, Якир, Учебник
Номер 1014,
Мерзляк, Полонский, Якир, Учебник
Задание 1020,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1064,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1072,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1130,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1132,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1488,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 21,
Мерзляк, Полонский, Якир, Учебник
Номер 41,
Мерзляк, Полонский, Якир, Учебник
Номер 134,
Мерзляк, Полонский, Якир, Учебник
Номер 140,
Мерзляк, Полонский, Якир, Учебник
Номер 374,
Мерзляк, Полонский, Якир, Учебник
Номер 377,
Мерзляк, Полонский, Якир, Учебник
Номер 571,
Мерзляк, Полонский, Якир, Учебник
Номер 695,
Мерзляк, Полонский, Якир, Учебник
Номер 928,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 70,
Мерзляк, Полонский, Якир, Учебник
Номер 106,
Мерзляк, Полонский, Якир, Учебник
Номер 112,
Мерзляк, Полонский, Якир, Учебник
Номер 122,
Мерзляк, Полонский, Якир, Учебник
Номер 190,
Мерзляк, Полонский, Якир, Учебник
Номер 193,
Мерзляк, Полонский, Якир, Учебник
Номер 201,
Мерзляк, Полонский, Якир, Учебник
Номер 210,
Мерзляк, Полонский, Якир, Учебник
Номер 291,
Мерзляк, Полонский, Якир, Учебник
Найдём значения выражений (3+(-7)) и (-3+7),
определим знаки слагаемых и их сумм, модули слагаемых и их сумм, разность модулей слагаемых и сравним знак суммы со знаками слагаемых.
1. (3+(-7)=-4).
|
Знаки слагаемых |
Знак суммы |
Модули слагаемых |
Модуль суммы |
Разность модулей слагаемых |
Сравнение знака суммы со знаками слагаемых |
|
Разные |
(«-») |
3=3−7=7 |
−4=4 |
−7−3=47−3=4 |
Знак результата ((-4)) такой же, как и у числа, большего по модулю ((-7)) |
2. (-3+7=4).
|
Знаки слагаемых |
Знак суммы |
Модули слагаемых |
Модуль суммы |
Разность модулей слагаемых |
Сравнение знака суммы со знаками слагаемых |
|
Разные |
(«+») |
−3=37=7 |
4=4 |
7−−3=47−3=4 |
Знак результата (4) такой же, как и у слагаемого с большим модулем (7) |
Видим, что знаки слагаемых и их сумм в обоих случаях разные, а в результате получается разность модулей слагаемых: из большего по модулю числа вычли меньшее по модулю число. Результат имеет такой же знак, что и число с большим модулем.
Чтобы сложить числа с разными знаками, надо:
- из большего модуля вычесть меньший модуль;
- в результате поставить знак слагаемого с большим модулем.
Представим
себе такую историю…
–
Паша, помоги мне, пожалуйста, – попросил у друга Саша.
–
Давай помогу, – сказал Паша.
–
Вчера на улице было мороза.
Утром мне старший брат сказал, что сегодня намного теплее, так как температура
стала выше на ,
– начал Саша. – Но я не могу понять, какая сегодня погода.
–
Что же здесь непонятного? – удивился Паша. – Надо к прибавить
6.
Но как сложить отрицательное и положительное числа, я не знаю.
–
Вот и я не знаю, – сказал Саша.
–
Может, спросим у Мудряша? – предложил другу Паша.
–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и
выполним устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Разберёмся, как сложить отрицательное
число и положительное число. Для этого мы начертим
координатную прямую. Отметим на ней начало отсчёта и единичный отрезок. Вы
сказали, что вчера было мороза.
Отметим точку А ()
на координатной прямой. Сегодня температура повысилась на ,
а значит, на нашей координатной прямой мы переместимся на 6
единичных отрезков вправо и окажемся в точке В (2). Тогда мы с вами
можем записать, что .
–
А если бы, например, температура понизилась на ,
то нам надо было бы к прибавить
.
Как бы мы это сделали? – спросил у Мудряша Саша.
–
В этом случае мы бы переместились на 3
единичных отрезка влево и оказались в точке С (),
– ответил Мудряш. – То есть можно записать так: .
Запомните!
Если к числу а прибавить положительное число b,
то точка с координатой a
переместится по координатной прямой на b
единичных
отрезков вправо.
Если
к числу a прибавить отрицательное
число b, то точка с координатой a
переместится
по координатной прямой на минус b
единичных отрезков влево.
–
Давайте вычислим суммы: ;
;
, –
предложил мальчишкам Мудряш. – Снова воспользуемся координатной прямой. Итак,
сложим и
5.
Сначала отметим точку с координатой на
координатной прямой. Затем переместимся на 5
единичных отрезков вправо и окажемся в точке с координатой .
То есть .
Теперь
к прибавим
6,5.
Для этого из точки с координатой переместимся
на 6,5
единичных отрезков вправо и окажемся в точке с координатой 3,5.
То есть .
И
в последнем примере мы сложим 4 и .
Отметим точку с координатой 4 и, так как прибавляем
отрицательное число ,
переместимся на 7 единичных отрезков влево
и окажемся в точке с координатой .
Запишем это так: .
–
В каждом из рассмотренных примеров мы находили сумму чисел с разными знаками, –
заметили мальчишки.
–
И обратите внимание, что в каждом примере знак суммы такой же, что и у
слагаемого, модуль которого больше. Так, в первом примере .
И сумма имеет знак «».
Во втором примере .
Сумма – положительное число. И в третьем примере .
Сумма со знаком «»,
– объяснил Мудряш.
–
Понятно, как определять знак суммы, – сказали Саша и Паша. – Но можно ли найти
её значение без помощи координатной прямой?
–
Конечно, можно, – ответил Мудряш. – Давайте сформулируем правило сложения двух
чисел с разными знаками. Запомните! Чтобы сложить два числа с разными
знаками, надо: 1) найти модули слагаемых; 2) из большего модуля вычесть меньший модуль; 2) перед
полученным числом поставить знак слагаемого с большим
модулем.
Давайте
ещё раз решим наши примеры, но уже с помощью правила.
Первый
пример: .
;
.
Значение модуля отрицательного слагаемого у нас больше значения модуля
положительного слагаемого. А значит, сумма у нас будет со знаком «».
Найдём теперь: .
Следующий
пример: .
;
.
Модуль положительного слагаемого больше модуля отрицательного слагаемого.
–
А значит, сумма у нас будет со знаком «»,
– подсказали ребята. – Теперь из большего
модуля вычтем меньший и получим: .
–
Верно, – сказал Мудряш. – При этом знак «»
ставить совсем не обязательно. И последний пример: .
;
.
–
Здесь сумма будет со знаком «»,
так как ,
– продолжили мальчики. – Найдём разность: .
–
Молодцы! – похвалил Сашу и Пашу Мудряш и предложил. – Давайте мы с вами решим
ещё несколько примеров: ;
;
.
–
Нам надо будет снова вычислить сумму. Мы это уже умеем делать, – обрадовался
Саша.
–
Посмотри внимательнее, – сказал Паша. – В каждом примере оба слагаемых
отрицательные числа. А мы пока не умеем их складывать.
–
Ребята, чтобы решить эти примеры, мы с вами снова воспользуемся координатной
прямой. Начертим её. Отметим начало отсчёта и
выберем единичный отрезок. В первом примере нам надо к прибавить
.
Отметим точку с координатой .
Затем переместимся на 2 единичных отрезка влево и
окажемся в точке с координатой .
То есть .
Чтобы
вычислить сумму ,
отметим точку с координатой .
Переместимся 4,5 единичных отрезка влево и окажемся в
точке с координатой .
То есть .
И
вычислим последнюю сумму .
–
Для этого отметим точку с координатой ,
– продолжили ребята. – Потом переместимся влево на 2,5 единичных
отрезка и окажемся в точке с координатой .
Получим: .
А
может, как и для чисел с разными знаками, есть правило сложения отрицательных
чисел?
–
Такое правило есть, – сказал Мудряш. – Сформулируем его. Чтобы сложить два
отрицательных числа, надо: 1) найти модули слагаемых; 2) сложить модули
слагаемых; 3) перед полученным числом поставить знак «».
Решим
с помощью этого правила рассмотренные выше примеры. Итак, первый пример: .
;
.
Запишем сумму модулей и поставим перед ней знак
«»:
. Выполним
сложение в скобках и получим .
Второй
пример: .
;
.
Запишем сумму модулей и поставим перед ней знак
«»:
. Выполним
сложение в скобках и получим .
И
последний пример: .
;
.
Запишем сумму модулей и перед ней поставим
знак «»:
.
Сложим числа в скобках и получим .
–
Интересно, а чему равна сумма двух противоположных чисел? – задал вопрос
Мудряшу Паша.
–
Это хороший вопрос! – сказал Мудряш. – Снова воспользуемся координатной прямой,
чтобы найти, например, сумму и
5.
Отметим точку с координатой .
Теперь переместимся на 5 единичных отрезков
вправо и окажемся в точке с координатой 0.
То есть сумма и
5
равна 0.
Давайте
ещё вычислим сумму 3,5 и .
Отметим на координатной прямой точку с координатой 3,5.
Затем переместимся на 3,5 единичных отрезка влево
и окажемся в точке с 0. А значит, сумма 3,5
и равна
0.
–
То есть при сложении двух противоположных чисел всегда получаем 0?
– спросили мальчишки.
–
Всё верно, – сказал Мудряш. – Запомните! Сумма двух противоположных
чисел равна нулю. Для любого рационального числа a
верно равенство: .
Давайте
для закрепления новых знаний выполним несколько заданий.
Задание
первое: выполните сложение:
а)
;
б) ;
в) ;
г) .
Решение: заметим,
что в каждом из примеров нам надо сложить два числа с разными знаками. А
значит, мы с вами будет пользоваться правилом сложения двух чисел с разными
знаками. В первом примере нам надо вычислить сумму и
53.
;
. Значение
модуля положительного слагаемого у нас больше значения модуля отрицательного слагаемого.
Поэтому сумма у нас будет положительной. Из большего
модуля вычтем меньший модуль, то есть из ,
и получим 11.
Во
втором примере мы вычислим сумму и
.
;
.
Значение модуля отрицательного слагаемого у нас больше значения модуля положительного
слагаемого. А значит, сумма у нас будет со знаком «».
Запишем разность большего и меньшего модулей со знаком «»,
то есть .
Выполним вычитание в скобках и получим в результате .
В
следующем примере нам надо найти сумму и
.
Найдём модуль каждой дроби: ;
.
Чтобы сравнить значения модулей, приведём дробь
к
знаменателю 6: .
.
Сумма будет положительной, так как модуль положительной дроби больше, чем
модуль отрицательной дроби. Отнимаем от
:
.
Сокращаем дробь на
3
и получаем .
И
в последнем примере нам надо найти сумму противоположных чисел и
.
Мы с вами знаем, что сумма двух противоположных чисел равна 0.
А значит, .
Второе
задание: выполните сложение:
а)
;
б) ;
в) ;
г) .
Решение: в
этом задании мы будем складывать отрицательные числа. Для этого мы
воспользуемся правилом сложения двух отрицательных чисел.
В
первом примере надо найти сумму и
.
Сначала найдём модули слагаемых. ;
. Запишем
сумму модулей и перед ней поставим знак «»:
.
Выполним вычисления и получим .
Во
втором примере надо найти сумму и
.
;
.
Запишем сумму модулей и перед ней поставим
знак «»:
.
Выполним вычисления и получим .
В
следующем примере нам надо найти сумму двух отрицательных десятичных дробей и
.
;
. Запишем
сумму модулей и поставим перед ней знак «»:
Выполним
вычисления и получим .
И
последний пример .
;
.
Перед суммой модулей дробей поставим знак «»:
. И,
выполнив вычисления, получим .