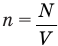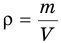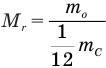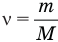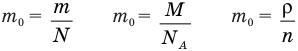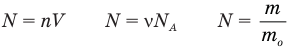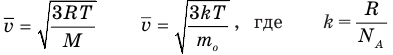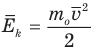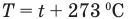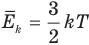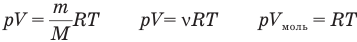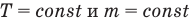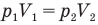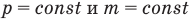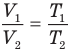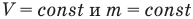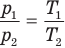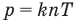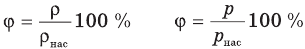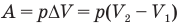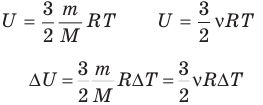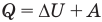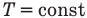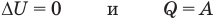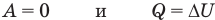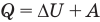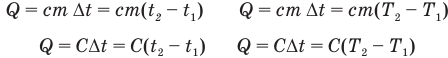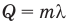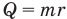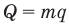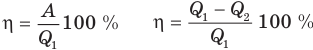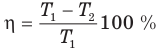В этой статье мы узнаем о том, как рассчитать молярную массу по давлению молекул газа и как ее можно рассчитать по давлению, объему, плотности и подробным фактам.
Молекула, содержащая один моль собственного вещества, называется молярной массой этого конкретного вещества. Упрощенно, это вес одного моля вещества. С помощью числа Авогардо мы можем вычислить молярную массу.
Обозначается формулой,
М=м/н, Где m молярная масса вещества в граммах, m это масса вещества в грамме,n это число молей вещества.
Как рассчитать молярную массу по давлению ?
Используя уравнение идеального газа, мы можем легко вычислить молярную массу по давлению.
Это следует из уравнения идеального газа
PV = NRT
P = давление газа, V = объем газа, R = универсальная газовая постоянная, T = температура, n = количество молей газовой молекулы.
Опять же, мы знаем
n = m/M = масса / молярная масса
поэтому, подставляя значение n в приведенное выше уравнение, мы получаем
PV=(м/м)RT
Итак, M = m(RT/PV)
М α 1/П [где α — постоянная пропорциональности]
Итак, мы можем сказать, что из приведенного выше уравнения Молярная масса обратно пропорциональна давлению молекул газа. Это означает, что чем выше молярная масса газа, тем ниже будет его давление и наоборот., как рассчитать молярную массу от давления является важным фактором.
Рассчитать молярную массу по температуре
Из уравнения идеального газа можно рассчитать молярную массу по температуре.
PV = NRT
P = давление газа, V = объем газа, R = универсальная газовая постоянная, T = температура, n = количество молей газовой молекулы.
Опять же, мы знаем
n = m/M = масса / молярная масса
поэтому, подставляя значение n в приведенное выше уравнение, мы получаем,
PV=(м/м)RT
Итак, M = m(RT/PV)
М α Т [где α — постоянная пропорциональности]
Таким образом, в приведенном выше соотношении отношение между молярной массой и температурой прямо пропорционально друг другу. Таким образом, чем выше температура, тем выше будет молярная масса. как рассчитать молярную массу по давлению, здесь важный фактор, но здесь мы строим зависимость между молярной массой и температурой.
Рассчитать молярную массу по объему
Молярную массу по объему можно рассчитать с помощью уравнения идеального газа.
PV = NRT
P = давление газа, V = объем газа, R = универсальная газовая постоянная, T = температура, n = количество молей газовой молекулы.
Опять же, мы знаем
n = m/M = масса / молярная масса
поэтому, подставляя значение n в приведенное выше уравнение, мы получаем,
PV=(м/м)RT
Итак, M = m(RT/PV)
М α 1/В [где α — постоянная пропорциональности]
Итак, мы можем сказать, что из приведенного выше уравнения Молярная масса обратно пропорциональна объему газообразных молекул. Это означает, что чем выше молярная масса газа, тем меньше будет его объем, и наоборот. как рассчитать молярную массу по давлению, здесь важный фактор, но здесь мы строим зависимость между молярной массой и объемом.
Рассчитать молярную массу по плотности
Плотность равна отношению массы вещества к его объему.
Используя уравнение идеального газа, мы можем легко вычислить молярную массу по плотности.
PV = NRT
P = давление газа, V = объем газа, R = универсальная газовая постоянная, T = температура, n = количество молей газовой молекулы.
Опять же, мы знаем
n = m/M = масса / молярная масса
поэтому, подставляя значение n в приведенное выше уравнение, мы получаем,
PV=(м/м)RT
M = (м/В)(RT/P)
М=ρ(РТ/П)
Итак, M α ρ [где α — постоянная пропорциональности]
Таким образом, плотность прямо пропорциональна молярной массе газообразной молекулы. как рассчитать молярную массу от давления является важным фактором. здесь, но мы строим зависимость между молярной массой и плотностью здесь.
Рассчитать молярную массу по осмотическому давлению
Использование формулы коллигативных свойств для расчета молярной массы по осмотическому давлению.
Из коллигативного свойства
Π=iCRT
Где Π — осмотическое давление данного вещества, I = коэффициент Вант-Гоффа (это константа), C = концентрация растворенного вещества в конкретном растворе, R = универсальная газовая постоянная, t = температура.
Для газообразных молекул концентрация растворенного вещества в конкретном растворе будет преобразована в молярную массу, и мы опускаем коэффициент I, поскольку он является постоянным членом..
Теперь уравнение становится П=МРТ.
So Π α М [где α — постоянная пропорциональности]
Таким образом, осмотическое давление также прямо пропорционально молярной массе газообразной молекулы. как рассчитать молярную массу от давления является важным фактором. здесь, но мы строим зависимость между молярной массой и осмотическим давлением здесь.
Рассчитать молярную массу по давлению паров
Из коллигативного свойства мы знаем, что относительное понижение давления пара является более подходящим, чем давление пара.
Таким образом, здесь мы не только рассчитываем молярную массу по давлению, но и рассчитываем молярную массу растворенного вещества по относительному снижению давления пара.
Из закона Рауля
(P0-П)/П0 = X2……(я)
Где Р0 — давление пара чистого растворителя, а P — давление пара над раствором. Икс2 — молярная доля растворенного вещества.
И снова Х2 = п2 / (n1+n2)
Для идеального решения n1>>>н2
Таким образом, уравнение сводится к
X2=n2/n1 ………(ii)
n2=W2/M2 и н1=W1/M1
тогда уравнение (ii) принимает вид
X2=(Вт2/M2)|(М1/W1)….(iii)
Сравнивая уравнения (i) и (iii), получаем,
(W2/M2)(М1/W1)=(П0-П)/П0
M2= (Вт2/W1)M1 (P0/p0-п)
Таким образом, молярная масса прямо пропорциональна снижению давления паров летучей молекулы. как рассчитать молярную массу от давления является важным фактором. здесь, но мы строим зависимость между молярной массой и давлением пара здесь.
Часто задаваемый вопрос
Как рассчитать молярную массу по закону идеального газа?
Используя закон идеального газа PV=nRT, мы можем легко вычислить молярную массу.
Используя этот закон, мы можем рассчитать, как рассчитать молярную массу по давлению, отношению между молярной массой и давлением, молярной массой и температурой, а также молярной массой и объемом.
В чем принципиальная разница между молем и молярной массой?
Моль определяется как количество веществ, приходящееся на число Авогадро. а молярная масса равна одному молю этого вещества.
Моль определяется как n=N/NA, где НA число Авогадро, а значение равно 6.023*1023.
Сколько атомов соответствует одному молю?
Один моль равен 6.023*1023 атомов поскольку он содержит число атомов Авогадро.
Что такое молярная масса?
Молярная масса = масса вещества (в граммах)/количество молей
Итак, единицей молярной массы является грамм/ Моль.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
-
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе? - Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Точность вычисления
Знаков после запятой: 2
Теперь немного формул.
Уравнение Клапейрона-Менделеева
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Теперь немного формул.
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Конвертер величин
Калькулятор закона состояния идеального газа (давление–объем–температура–количество)
Калькулятор закона состояния идеального газа определяет одну из четырех величин, входящих в уравнение состояния (давление, объем, температура или количество), если известны три другие величины.
Пример: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 800 молей метана при 30 °С.
Еще несколько примеров решения задач о состоянии идеального газа под приводится калькулятором.
Для расчета выберите неизвестную величину и введите три известные величины из четырех имеющихся в уравнении состояния газа (давление, объем, температура, количество). Четвертая величина будет рассчитана после нажатия на кнопку Рассчитать. Количество можно ввести в молях или указать молярную массу и массу газа. Для определения молярной массы любого газа можно использовать калькулятор молярной массы. Если нужно определить молярную массу смеси газов, например, сухого воздуха, нужно определить молярные массы каждого газа и умножить их на процентное содержание по массе каждого газа в воздухе.
Примеры решения задач по уравнению состояния идеального газа (уравнению Менделеева — Клапейрона)
Задача 1: Плотность воздуха при нормальных условиях (температура 0 °С и атмосферное абсолютное давление 100 кПа) составляет 1,28 кг/м³. Определить среднюю молярную массу воздуха.
Решение: Поскольку плотность воздуха задана, это означает, что в калькулятор можно ввести массу одного кубического метра воздуха, равную 1,28 кг. Введите в калькулятор данные:
- Выберите n (Количество в молях) в селекторе Выберите неизвестную величину.
- Введите абсолютное давление P = 100 кПа.
- Введите объем V = 1 м³.
- Введите температуру T = 0 °C.
- Нажмите кнопку Рассчитать.
- Калькулятор покажет количество молей в 1 м 3 воздуха.
- Введите массу воздуха m = 1,28 кг и нажмите кнопку Рассчитать.
- Калькулятор рассчитает молярную массу воздуха M = 0,029 кг/моль
Задача 2: Молярная масса газа кислорода (O₂) M = 32 г/моль. Определить абсолютную температуру 128 г. кислорода, находящегося в 10-литровом сосуде под давлением P = 3 МПа.
Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:
- Выберите T (Температура) в селекторе Выберите неизвестную величину.
- Введите молярную массу кислорода N = 32 г/моль.
- Введите массу кислорода m = 128 г.
- Калькулятор рассчитает количество кислорода в молях.
- Введите объем V = 4 л и давление P = 3 МПа.
- Нажмите кнопку Рассчитать.
- Считайте температуру в кельвинах.
Задача 3: В сосуде высокого давления находится газ под давлением P = 0.5 МПа при температуре T = 15 °С. Объем газа V = 5 л. Рассчитать объем этой массы газа при нормальных условиях (P = 100 кПа, T = 0 °С).
Решение: Нажмите кнопку Reset и введите в калькулятор данные задачи:
- Выберите T (Температура) в селекторе Выберите неизвестную величину.
- Введите давление P = 500 кПа.
- Введите температуру T = 15 °C.
- Введите объем V = 5 л.
- Нажмите кнопку Рассчитать.
- Калькулятор рассчитает количество в молях, которое будет использовано в следующем шаге.
- Выберите Объем в селекторе Выберите неизвестную величину.
- Введите температуру и давление P = 100 kPa, T = 0 °C (нормальные условия) и нажмите кнопку Рассчитать.
- Калькулятор рассчитает новый объем газа V = 23.69 л при нормальных условиях.
Задача 4: Рассчитать давление в паскалях в 70-литровом баке работающего на метане автомобиля, если в нем хранится 12,8 кг метана (молярная масса 16 г/моль) при 30 °С.
Определения и формулы
Идеальный газ
Идеальный газ — теоретическая модель, в которой газ представляется в виде множества свободно движущихся частиц бесконечно малого размера, которые взаимодействуют друг с другом абсолютно упруго, то есть при столкновении двух частиц их кинетическая энергия не изменяется и не превращается ни в какую другую форму энергию, например, в потенциальную энергию или в тепло. Считается, что суммарный размер частиц настолько мал, что занимаемый ими объем в сосуде пренебрежимо мал. Эта теоретическая модель полезна, так как она упрощает многие расчеты, а также в связи с тем, что идеальный газ подчиняется законам классической механики. Идеальный газ можно представить себе в виде множества абсолютно твердых сфер, которые только сталкиваются друг с другом и больше никак не взаимодействуют.
В обычных условиях, например, при стандартных условиях (при температуре 273,15 К и давлении в 1 стандартную атмосферу) большинство реальных газов ведут себя как идеальный газ. В общем случае, газ ведет себя как идеальный при низком давлении и высокой температуре, когда расстояния между молекулами газа относительно велики. В этих условиях потенциальная энергия вследствие действия межмолекулярных сил намного меньше кинетической энергии частиц. Размер молекул также незначителен по сравнению с расстоянием между ними. Идеальная модель не работает при низких температурах и высоких давлениях, а также для тяжелых газов. При понижении температуры и повышении давления реальный газ может стать жидкостью или даже перейти в твердое состояние, то есть может произойти фазовый переход. В то же время, модель идеального газа не допускает жидкого или твердого состояния.
Закон идеального газа
Идеальный газ, как и любой другой газ, можно охарактеризовать четырьмя переменными и одной константой, а именно:
- давление (P),
- объем (V),
- количество в молях (n),
- температура (T), and
- универсальная газовая постоянная (R)
Эти четыре переменные и одна константа объединены в приведенном ниже уравнении, которое называется уравнением состояния идеального газа:
Это уравнение также известно под названием закона идеального газа и уравнения Менделеева — Клапейрона или уравнения Клапейрона, так как уравнение было впервые выведено в 1834 г. французским инженером Эмилем Клапейроном (1799–1864). О вкладе Д. И. Менделеева — чуть ниже. В этом уравнении:
- P — абсолютноедавление, измеряемое в СИ в паскалях (Па),
- V — объем, измеряемый в СИ в кубических метрах (м³),
- n — количество вещества (газа) в молях (сокращение моль). Один моль любого вещества в граммах численно равен средней массы одной молекулы в соединении, выраженной в атомных единицах массы. Например, один моль кислорода с атомной массой 16 соответствует 16 граммам. Один моль идеального газа при стандартных условиях занимает 22,4 литра.
- T — абсолютнаятемпература.
- R — универсальная газовая постоянная, являющаяся физическим коэффициентом пропорциональности уравнения состояния идеального газа.
Приведенное выше уравнение показывает, что при нулевой абсолютной температуре получается нулевой объем. Однако это не означает, что объем реального газа действительно исчезает. При очень низких температурах все газы становятся жидкостями и уравнение идеального газа к ним неприменимо.
Универсальная газовая постоянная соответствует работе, выполненной при расширении одного моля идеального газа при нагревании на 1 К при постоянном давлении. Размерность постоянной — работа на количество вещества на температуру. Постоянная в точности равна 8,31446261815324 Дж⋅К⁻¹⋅моль⁻¹. Универсальная газовая постоянная также определяется как произведение числа Авогадро NA и постоянной Больцмана k:
Входящая в уравнение состояния идеального газа универсальная газовая постоянная была предложена и введена в уравнение Дмитрием Менделеевым в 1877 г. Поэтому уравнение состояния идеального газа в литературе на русском языке и ее переводах на другие языки, называется уравнением Менделеева — Клапейрона.
Количество газа в молях часто бывает удобно заменить массой газа. Количество газа в молях n, его масса m в граммах и молярная масса M в граммах на моль связаны формулой:
Заменяя в уравнении состояния идеального газа n на m/M, имеем:
Для определения молярной массы элемента, его относительная атомная масса умножается на коэффициент молярной массы в кг/моль
Например, молярная масса кислорода как элемента в единицах системы СИ
Если ввести в уравнение состояния идеального газа плотность ρ = m/V, мы получим:
Теперь введем понятие удельной газовой постоянной, которая представляет собой отношение универсальной газовой постоянной R к молярной массе M:
Например, удельная газовая постоянная сухого воздуха приблизительно равна 287 Дж·кг⁻¹·К⁻¹. Подставив удельную газовую постоянную в уравнение состояния идеального газа, получим:
Закон идеального газа объединяет четыре более простых эмпирических газовых закона, открытых в XVII–XIX вв. несколькими учеными, которые аккуратно измеряли свойства газа. Простые газовые законы можно также вывести из уравнения состояния идеального газа (PV=nRT). Поскольку в этом уравнении R является постоянной величиной, можно записать
Поскольку PV/NT — постоянная величина, можно записать это иначе:
Здесь индексы 1 и 2 показывают начальное и конечное состояние газа в системе. Мы будем использовать это уравнение ниже при описании четырех газовых законов.
Отметим, что исторически именно эмпирические законы поведения газа, описанные ниже, привели к открытию обобщенного закона состояния идеального газа. Эти законы были открыты несколькими учеными, которые проводили эксперименты, изменяя только две переменные состояния газа и оставляя две другие переменные постоянными.
Закон Бойля — Мариотта (T=const, n=const)
Изменим предыдущее уравнение с учетом, что количество газа в молях n и его температура Т остаются неизменными:
Это закон Бойля — Мариотта, описывающий зависимость объема V фиксированного количества газа в молях n от давления P при постоянной температуре T. Давление фиксированной массы газа при неизменной температуре обратно пропорционально его объему. Закон был сформулирован англо-ирландским химиком и физиком Робертом Бойлем в 1662 г. В России и континентальной Европе это закон называют законом Бойля — Мариотта с учетом вклада в открытие закона французского физика и священника Эдма Мариотта.
Закон Авогадро (T=const, P=const)
Если температура и давление остаются неизменными, можно записать
Это закон Авогадро, указывающий, что при неизменных температуре и давлении равные объемы любых газов содержат одинаковое количество молекул. Это уравнение показывает, что, если количество газа увеличивается, объем газа пропорционально растет. Иными словами, количество атомов или молекул газа не зависит от их размеров или от молярной массы газа. Закон назван в честь итальянского ученого Амедео Авогадро, который опубликовал гипотезу об отношениях объема газа и его количества в молях в 1811 году. Число Авогадро также носит его имя.
Закон Гей-Люссака (P=const, n=const)
При постоянном давлении объем фиксированного количества газа в молях пропорционален абсолютной температуре системы с газом.
В англоязычной литературе этот закон называется законом объемов и законом Шарля. Закон описывает как расширяется любой газ при увеличении его абсолютной температуры. Закон был сформулирован в неопубликованной работе французским ученым Жаком Шарлем в 80-х гг. XVIII в. Его соотечественник Жозеф Луи Гей-Люссак опубликовал этот закон в 1803 г. и указал, что приоритет открытия принадлежит Жаку Шарлю. Поэтому этот закон в литературе не на английском языке часто называют законом Гей-Люссака. В русскоязычной литературе закон носит имя Гей-Люссака. Итальянцы называют этот закон первым законом Гей-Люссака (ит. prima legge di Gay-Lussac).
Закон Шарля (или второй закон Гей-Люссака) (V=const, n=const)
Закон Шарля (называемый также вторым законом Гей-Люссака) гласит, что давление фиксированного количества газа в молях при его неизменном объеме прямо пропорционально абсолютной температуре газа:
Закон был сформулирован Гей-Люссаком в 1802 г. В литературе на других языках этот закон также называют законом Амонтона по имени французского ученого Гийома Амонтона, который на сто лет раньше обнаружил количественную зависимость объема газа от его температуры. Иногда закон называют вторым законом Гей-Люссака и законом Шарля, так как сам Гей-Люссак считал, что закон открыт Шарлем. Закон зависимости давления от температуры был также независимо открыт английским физиком Джоном Дальтоном в 1801 г. Итальянцы называют этот закон вторым законом Вольта–Гей-Люссака (ит. seconda legge di Volta – Gay-Lussac), потому что итальянец Алессандро Вольта независимо проводил исследования газов и получил аналогичные результаты.
Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.
Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.
Ограничения практической применимости:
- температуры ниже -100°C и выше температуры диссоциации / разложения
- давления выше 90 бар
- вакуум глубже чем 99%
Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры.
- в СИ R= 8,3144 Дж/(моль*К) — это основная (но не единственная) инженерная система измерений в РФ и большинстве стран Европы
- в СГС R= 8,3144*10 7 эрг/(моль*К) — это основная (но не единственная) научная система измерений в мире
- m-масса газа в (кг)
- M-молярная масса газа кг/моль (таким образом (m/M) — число молей газа)
- P-давление газа в (Па)
- Т-температура газа в ( °K)
- V-объем газа в м 3
Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) — что верно для большинства газов в указанных выше пределах применимости.
1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.
Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.
Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V1 и V2, при температурах, соответственно, T1 и T2 и, пусть T1 V2 для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:
- показатели объемного счетчика газа тем «весомее», чем выше давление
- выгодно поставлять газ низкого давления
- выгодно покупать газ высокого давления
Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.
http://www.translatorscafe.com/unit-converter/ru-RU/calculator/ideal-gas-law/?mode=pressure&pu=MPa&mm=16&mmu=g/mol&m=12.8&mu=kg&t=30&tu=C&v=70&vu=l
http://tehtab.ru/Guide/GuideTricks/KlaiperonMendeleevEquity/
Прменение уравнения Менделеева — Клапейрона в рассчетах объма и количества газообразных веществ
Задача 36.
Рассчитайте, какой объем (в литрах) занимают:
а) 1,2 кг водяного пара при 100 °С и 1,013· 10 5 Па;
б) 1,2 кг метана при 25 °С и 1,013· 10 5 Па.
Решение:
M[Н2О(пар)] = 18 кг/моль . 10 -3 ;
М(СН4) = 16 кг/моль . 10 -3 ;
T1 = 100 °С = (100 + 273) = 373 K;
T2 = (25 + 273 = 298 K);
P1 = P2 = 1,013· 10 5 Па.
Для решения задачи прменим уравнение Менделеева — Клапейрона:
PV = nRT = mRT/M, где
n – число молей газа;
P – давление газа (например, в атм или Па;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная [0,0821 л·атм/моль·K)] или [8,314 Дж/(моль . К)];
M — молярная масса вещества (в г/моль или кг/моль;
m — масса вещества (например, в г или кг).
Рассчитаем объемы газов:
а) объем 1,2 кг водяного пара:
PV = mRT/M, V(пар) = mRT1/MР = [1,2 . 8,314 Дж/(моль . К) . 373 К]/[(18 кг/моль . 10 -3 ) . 1,013· 10 5 Па] =
= 3721,3464/1823,4 = 2,04 м 3 = 2040 л.
б) объем 1,2 кг метана:
V(СН4) = mRT1/MР = [1,2 . 8,314 Дж/(моль . К) . 298 К]/[(16 кг/моль . 10 -3 ) * 1,013· 10 5 Па] =
= 2973,0864/1620,8 = 1,834 м 3 = 1834 л.
Ответ: V(пар) = 2040 л; V(СН4) = 1834 л.
Задача 37.
Некоторое количество газа гелия при 78 °С и давлении 15,6 атм занимает объем 26,5 л. Каков объем этого газа при нормальных условиях? Сколько это молей гелия?
Решение:
Для решения задачи прменим уравнение Менделеева — Клапейрона:
n – число молей газа;
P – давление газа (например, в атм или Па;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная [0,0821 л·атм/моль·K)] или [8,314 Дж/(моль . К)].
Уравнение Клапейрона-Менделеева одинаково справедливо как для начального состояния газа, так и для конечного:
Если почленно разделим верхнее уравнение на нижнее, то при неизменном числе молей n мы получаем:
Найдем число молей гелия:
n(Hе) = V/Vm = 321,5/22,4 = 14,35 моль.
Ответ: V2(He) = 321,5 л; n(Hе) = 14,35 моль.
Задача 38.
В стальном баллоне объемом 40 л находится водород под давлением 60 атм и температуре 25 °С. Сколько молей водорода в баллоне? Сколько граммов? Какой объем займет водород из баллона при н.у.?
Решение:
М(Н2) — 2 г/моль;
V1 = 40 л;
Р1 — 60 атм;
Т1 = Т0 = 25 °С = 298 К;
Р0 = 1 атм.
n(H2) = ?
m(H2) = ?
V0(Н2) = ?
Для решения задачи прменим уравнение Менделеева — Клапейрона:
n – число молей газа;
P – давление газа (например, в атм или Па;
V – объем газа (в литрах);
T – температура газа (в кельвинах);
R – газовая постоянная [0,0821 л·атм/моль·K)] или [8,314 Дж/(моль / К)].
1. Расчитаем сколько молей водорода в баллоне, получим:
PV = nRT, n = PV/RT;
n(H2) = P1V1/RT1 = (60 . 40)/(0,0821 . 298) = 2400/24,4658 = 98,1 моль.
2. Находим массу водорода в баллоне:
m(H2) = n(H2) . М(Н2) = 98,1 . 2 = 196,2 г.
3. Рассчитаем объем водорода из баллона (н.у.), получим:
PV = nRT, V = nRT/P;
V0(Н2) = n(H2)RT0/P0 = (98,1 . 0,0821 . 298)/1 = 2400 л.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:
Примеры задач на уравнение Менделеева-Клапейрона
В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)
В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.
Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
Теперь немного формул.
где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль
Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также
где n — число молей газа
И как нетрудно заметить, соотношение
есть величина постоянная для одного и того же количества моль газа.
И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.
Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.
Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры
Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры
Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.
Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.
Как найти моль из уравнения менделеева клапейрона
Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем Vm и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:
pV = RT , где R — универсальная газовая постоянная,
R = 8,31 Дж/(моль . К)
Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = NАkT,
где NА — число Авогадро, k — постоянная Больцмана.
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.
Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.
Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.
Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.
Итак, из закона pV = (М/m) . RT выводятся следующие законы:
p = const => V/T = const — закон Гей — Люссака .
V= const => p/T = const — закон Шарля
Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.
Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро NA = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.
В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна NA?
Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.
Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/NA. Отсюда:
NA = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23
PV 7,95 . 10 -4 . 3 . 10 -2
В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.
источники:
http://planetcalc.ru/4265/
http://www.sites.google.com/site/opatpofizike/uravnenie-mendeleeva-klapejrona
Формулы молекулярной физики
Формула концентрации молекул
Здесь n — концентрация 

Формула плотности
Здесь 


Формула относительной молекулярной массы
Здесь 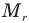

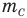
Формула количества вещества (количества молей)
Здесь v — количество вещества (количество молей) (моль), m — масса вещества (кг), М — молярная масса (кг/моль).
Формулы массы одной молекулы
Здесь 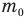
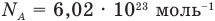



Формулы количества молекул
Здесь A — количество молекул (безразмерное), п — концентрация молекул 

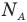
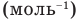

Формулы средней квадратичной скорости молекул
Здесь 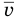
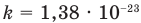

Основное уравнение кинетической теории идеального газа
Здесь р — давление газа (Па), 

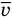

Формула средней кинетической энергии молекул
Здесь 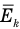
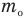
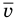
Связь шкал Цельсия и Кельвина
Здесь Т — абсолютная температура (К), t — температура по шкале Цельсия.
Связь средней кинетической энергии молекул идеального газа с абсолютной температурой
Здесь 
У равнение состояния идеального газа — уравнение Клапейрона — Менделеева
Здесь р — давление газа (Па), V — объем 
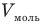
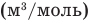
Объединенный газовый закон — уравнение Клапейрона
при
Здесь 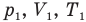

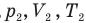

Закон Бойля — Мариотта (изотермический процесс)
при
Здесь Т — абсолютная температура газа (К), m — масса газа (кг), 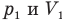

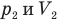

Закон Гей-Люссака (изобарный процесс)
при
Здесь р — давление газа (Па), m — масса газа (кг), 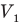
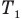

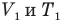

Закон Шарля
при
Здесь V — объем газа 
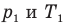
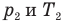
Связь давления идеального газа с концентрацией его молекул и температурой
Здесь р — давление газа (Па), к — постоянная Больцмана (Дж/К), п — концентрация молекул газа 
Формулы относительной влажности
Здесь 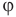
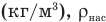
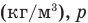
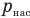
Работа при изобарном изменении объема газа
Здесь А — работа (Дж), р — давление газа (Па), 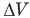
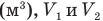

Внутренняя энергия идеального одноатомного газа
Здесь U — внутренняя энергия газа (Дж), m — масса газа (кг), М — молярная масса газа (кг/моль), R — молярная газовая постоянная (Дж/(моль • К), Т — абсолютная температура (К), v — количество вещества или число молей (моль), 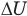
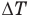
Первый закон термодинамики
Здесь Q — количество теплоты, переданное термодинамической системе (Дж), 
Применение первого закона термодинамики к термодинамическим процессам
к изотермическому: при
к изохорному: при V = const
к изобарному: при р = const
к адиабатному: при Q = 0
Здесь Т — абсолютная температура (К), 
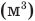
Формулы количества теплоты при нагревании или охлаждении тел
Здесь Q — количество теплоты, переданное телу при нагревании или отданное им при охлаждении (Дж), с — удельная теплоемкость вещества (Дж/(кг • К), т — масса тела (кг), 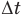
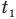
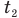
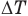
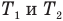
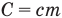
Формула количества теплоты при плавлении или кристаллизации
Здесь Q — количество теплоты (Дж), т — масса тела (кг), 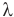
Формула количества теплоты при парообразовании или конденсации
Здесь Q — количество теплоты (Дж), m — масса тела (кг), r — удельная теплота парообразования (Дж/кг).
Формула количества теплоты при сгорании топлива
Здесь Q — количество выделившейся теплоты, m — масса топлива (кг), q — удельная теплота сгорания (Дж/кг).
Коэффициент полезного действия теплового двигателя
Здесь 
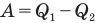
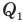
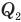
Коэффициент полезного действия идеального теплового двигателя
Здесь 
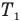
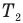
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Задачи по физике с решением
Возможно вам будут полезны эти страницы: