П
дана материальная точка, имеющая импульср. Пусть её положение
относительно точки О определяется
радиусом-векторомr.
Движение такой точки характеризуют
моментом импульсаL.
Моментом импульса материальной точки
относительно точки О называется
векторная величина, равная векторному
произведению радиуса-вектораr
и вектора импульсаp:
L=[r,p].
Модуль момента импульса L=rpsin,
где
— угол между векторамиr
и р. Направление вектора
момента импульса определяется по правилу
правого винта.
Размерность момента импульса [L]=кг.м2/с.
М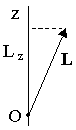
импульса тела относительно точки равен
векторной сумме моментов импульсов
частиц тела относительно той же точки
L=L1+L2+…+LN.
Проекция вектора момента импульса
относительно точки О на ось z,
проходящую через эту точку, называетсямоментом импульса относительно оси:
Lz=[r,p]z.
Момент импульса относительно оси
является скалярной величиной.
Момент импульса тела относительно оси
z равен проекции
момента импульса тела относительно
точки О на осьz,
проходящую через эту точку.
4.3. Связь момента силы и момента импульса
Момент импульса и момент силы связаны
между собой. Найдём выражение, связывающее
их.
Возьмём производную по времени от
выражения, определяющего момент импульса:
Член
равен нулю, так как угол между вектором
скоростиdr/dt и
вектором импульсар равен нулю.
Производная импульса по времени,
имеющаяся во втором члене полученного
выражения, равна силе (второй закон
Ньютона). Поэтому можем записать
полученное выражение в следующей форме:
.
Но [r,F]
есть по определению момент силыF относительно
той же точки О. Поэтому
т.е. скорость изменения момента импульса
частицы равна моменту силы,
действующему на эту частицу.
Проекция последнего уравнения на ось
zвыражает связь
момента импульса относительно осиzи момента силы
относительно той же оси.
.
4.4. Основной закон динамики вращательного движения
Пусть твёрдое тело вращается относительно
неподвижной оси z.
Выразим момент импульса твёрдого тела
относительно оси вращения. Для этого
представим твёрдое тело как совокупность
элементарных масс. Момент
импульса одной элементарной массы
относительно осиz
Момент импульса всего тела равен сумме
моментов импульсов всех элементарных
масс
Скорость vу разных
элементарных масс различна, а угловая
скорость одинакова.
Поскольку v=r,
Поскольку угловая скорость со одинакова
для всех элементарных масс, её можно
вынести за знак суммы
Введём обозначение
.
С учётом этого
Lz=Jz..
Ранее мы получили, что момент импульса
и момент силы связаны следующим
образом:
.
Заменив Lz
наJzωи с учётом того, чтоJz
с течением времени не изменяется,
получаем
Учитывая, что производная угловой
скорости по времени равна угловому
ускорению , получаем
.
Полученное выражение — основной закон
динамики вращательного движения,
связывающий между собой меру внешнего
воздействия — момент силы Mz
с результатом внешнего воздействия
— угловым ускорением.
Коэффициент Jz, стоящий
в этом уравнении, зависит от массы тела
и от того, как она распределена по
объёму тела (это видно из определения
величиныJz).
Чем меньше Jz, тем большее
угловое ускорение получит тело при
воздействии момента силыMz.
Это говорит о том, что коэффициентJz.
характеризует инертность вращающегося
тела. ПоэтомуJz называют
моментом инерции тела относительно осиz.
Знание величины момента инерции тела
необходимо для описания вращательного
движения. Поэтому обсудим более подробно,
что такое момент инерции и как его
вычислить.
Соседние файлы в папке часть 1
- #
- #
- #
- #
- #
- #
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси
- Подробности
- Обновлено 09.08.2018 23:15
- Просмотров: 850
«Физика — 10 класс»
Почему для увеличения угловой скорости вращения фигурист вытягивается вдоль оси вращения.
Должен ли вращаться вертолёт при вращении его винта?
Заданные вопросы наводят на мысль о том, что если на тело не действуют внешние силы или действие их скомпенсировано и одна часть тела начинает вращение в одну сторону, то другая часть должна вращаться в другую сторону, подобно тому как при выбросе горючего из ракеты сама ракета движется в противоположную сторону.
Момент импульса.
Если рассмотреть вращающийся диск, то становится очевидным, что суммарный импульс диска равен нулю, так как любой частице тела соответствует частица, движущаяся с равной по модулю скоростью, но в противоположном направлении (рис. 6.9).
Но диск движется, угловая скорость вращения всех частиц одинакова. Однако ясно, что чем дальше находится частица от оси вращения, тем больше её импульс. Следовательно, для вращательного движения надо ввести ещё одну характеристику, подобную импульсу, — момент импульса.
Моментом импульса частицы, движущейся по окружности, называют произведение импульса частицы на расстояние от неё до оси вращения (рис. 6.10):
L = mvr.
Линейная и угловая скорости связаны соотношением v = ωr, тогда
L = mr2ω.
Все точки твёрдого дела движутся относительно неподвижной оси вращения с одинаковой угловой скоростью. Твёрдое тело можно представить как совокупность материальных точек.
Момент импульса твёрдого тела равен произведению момента инерции на угловую скорость вращения:
Момент импульса — векторная величина, согласно формуле (6.3) момент импульса направлен так же, как и угловая скорость.
Основное уравнение динамики вращательного движения в импульсной форме.
Угловое ускорение тела равно изменению угловой скорости, делённому на промежуток времени, в течение которого это изменение произошло: 

Таким образом,
ΔL = MΔt. (6.4)
Изменение момента импульса равно произведению суммарного момента сил, действующих на тело или систему, на время действия этих сил.
Закон сохранения момента импульса:
Если суммарный момент сил, действующих на тело или систему тел, имеющих неподвижную ось вращения, равен нулю, то изменение момента импульса также равно нулю, т. е. момент импульса системы остаётся постоянным.
ΔL = 0, L = const.
Изменение импульса системы равно суммарному импульсу сил, действующих на систему.
Вращающийся фигурист разводит в стороны руки, тем самым увеличивает момент инерции, чтобы уменьшить угловую скорость вращения.
Закон сохранения момента импульса можно продемонстрировать с помощью следующего опыта, называемого «опыт со скамьёй Жуковского». На скамью, имеющую вертикальную ось вращения, проходящую через её центр, встаёт человек. Человек держит в руках гантели. Если скамью заставить вращаться, то человек может изменять скорость вращения, прижимая гантели к груди или опуская руки, а затем разводя их. Разводя руки, он увеличивает момент инерции, и угловая скорость вращения уменьшается (рис. 6.11, а), опуская руки, он уменьшает момент инерции, и угловая скорость вращения скамьи увеличивается (рис. 6.11, б).
Человек может также заставить вращаться скамью, если пойдёт вдоль её края. При этом скамья будет вращаться в противоположном направлении, так как суммарный момент импульса должен остаться равным нулю.
На законе сохранения момента импульса основан принцип действия приборов, называемых гироскопами. Основное свойство гироскопа — это сохранение направления оси вращения, если на эту ось не действуют внешние силы. В XIX в. гироскопы использовались мореплавателями для ориентации в море.
Кинетическая энергия вращающегося твёрдого тела.
Кинетическая энергия вращающегося твёрдого тела равна сумме кинетических энергий отдельных его частиц. Разделим тело на малые элементы, каждый из которых можно считать материальной точкой. Тогда кинетическая энергия тела равна сумме кинетических энергий материальных точек, из которых оно состоит:
Угловая скорость вращения всех точек тела одинакова, следовательно,
Величина в скобках, как мы уже знаем, это момент инерции твёрдого тела. Окончательно формула для кинетической энергии твёрдого тела, имеющего неподвижную ось вращения, имеет вид
В общем случае движения твёрдого тела, когда ось вращения свободна, его кинетическая энергия равна сумме энергий поступательного и вращательного движений. Так, кинетическая энергия колеса, масса которого сосредоточена в ободе, катящегося по дороге с постоянной скоростью, равна
В таблице сопоставлены формулы механики поступательного движения материальной точки с аналогичными формулами вращательного движения твёрдого тела.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Импульс материальной точки —
Закон сохранения импульса —
Реактивное движение. Успехи в освоении космоса —
Примеры решения задач по теме «Закон сохранения импульса» —
Механическая работа и мощность силы —
Энергия. Кинетическая энергия —
Примеры решения задач по теме «Кинетическая энергия и её изменение» —
Работа силы тяжести. Консервативные силы —
Работа силы упругости. Консервативные силы —
Потенциальная энергия —
Закон сохранения энергии в механике —
Работа силы тяготения. Потенциальная энергия в поле тяготения —
Примеры решения задач по теме «Закон сохранения механической энергии» —
Основное уравнение динамики вращательного движения —
Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси —
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Что в курсе механики (простой, не аналитической) всегда вызывало у меня удивление, так это вращательное движение, моменты сил, импульса… В этой заметке рассмотрим основные интересные вещи, связанные с вращением.
- Момент силы и момент импульса
- Момент инерции
- Сохранение момента импульса при изменяющемся моменте инерции
- Энергия поступательного и вращательного движения
- Вращательный дисбаланс
- Колесо на палке, волчок, прецессия
Литература
- Дуглас Джанколи — Физика в 2-х томах — Москва, Мир, 1989. Разделы 9,10 — Вращательное движение.
Момент силы и момент импульса
На рисунке 1 показано определение понятия «момент силы» (греческая буква тау) и «момент импульса» (буква L). Момент силы представляет собой векторное произведение силы, действующей на материальную точку, на радиус-вектор этой точки. Аналогично определяется момент импульса. Связь между моментом силы и моментом импульса мы найдем, если векторно умножим 2-й закон Ньютона для материальной точки на радиус-вектор этой точки.
Почему вообще вводят понятие «момент силы», «момент импульса»? Разве для того, чтобы рассчитать движение системы тел, не хватает обычных законов Ньютона? Да, не хватает. Рассматривая систему из нескольких тел (материальных точек) все силы делят на внутренние и внешние по отношению к системе. Внутренние силы действуют между телами системы, а внешние действуют на тела системы со стороны других тел, в систему не входящих. Так вот: если величины внешних сил обычно известны, то величины внутренних сил обычно неизвестны. Введение понятия момента силы позволяет исключить внутренние силы из рассмотрения, поскольку момент внутренних сил обращается в ноль благодаря тому, что силы между двумя материальными точками действуют вдоль линии их соединяющей и тому, что векторное произведение коллинеарных векторов равно нулю (см. рис. 2). Остается лишь момент внешних сил, поэтому скорость изменения момента импульса системы материальных точек оказывается равной моменту внешних сил.
И все же, откуда взялась эта идея векторного произведения? Нельзя же так с бухты барахты сказать: «а возьму ка я, да умножу векторно 2-й закон Ньютона для мат. точки на ее радиус-вектор»! Я думаю, тут не обошлось без Архимедова принципа рычага и понятий работы и энергии. Действительно, работа, совершаемая силой, поворачивающей тело рычаг на некоторый угол, в точности равна модулю векторного произведения силы на ее плечо, умноженному на этот угол. И в то же время ось вращения как раз перпендикулярна плоскости в которой лежит плечо рычага и сила. Напрашивается ввести понятие момента силы, причем интуитивно понятно и то, что это вектор, и то, каким должны быть его модуль и направление.
Является ли векторное произведение вектором?
Читая учебники, с удивлением узнаю, что векторное произведение несколько отличается от привычного понятия «вектор». На пальцах это объясняют так: возьмем два вектора и их найдем векторное произведение; теперь посмотрим на их отражение в зеркале и найдем векторное произведение векторов отраженных в зеркале — мы увидим, что векторное произведение отраженных векторов направлено противоположно произведению исходных векторов. Т. е. векторное произведение при отражении ведет себя не так, как ведут себя обычные вектора. Поэтому его называют псевдовектором. Однако в классической механике это совершенно неважно, а в остальном векторное произведение ведет себя как обычный вектор, т. е. подчиняется законам коммутативности и ассоциативности сложения, дистрибутивности умножения вектора на скаляр относительно сложения векторов и другим.
Момент относительно точки и относительно оси
Приведенное выше определение — это определение момента силы и импульса относительно точки. Существуют еще понятия момента силы и импульса относительно оси. Эти понятия используются, как правило, при решении задач о вращении тела вокруг некоторой… оси. Момент относительно точки — это вектор (точнее — псевдовектор), момент относительно оси — скаляр (точнее — псевдоскаляр). Момент относительно оси — это проекция на эту ось момента относительно любой точки на оси. Момент силы относительно оси равен произведению силы на расстояние от оси до точки приложения силы (это расстояние называется плечом силы). Аналогично — с моментом импульса. Как показано в следующем разделе, ось вращения можно указать для произвольного движения тела в произвольный момент времени. Другое дело, что эта ось может менять свое направление со временем.
Как будет двигаться твердое тело, на которое не действуют внешние силы?
Этот вопрос меня интересовал. Интуитивно представляется, что это тело будет двигаться поступательно с постоянной скоростью и при этом вращаться вокруг некоторой оси. То, что скорость поступательного движения (скорость центра масс тела) постоянна, легко следует из законов Ньютона. Но как быть с вращением вокруг оси? Наличие оси вращения подразумевает наличие в теле линии, точки которой неподвижны относительно центра масс. Как доказать, что такая линия существует? На помощь приходит теорема Эйлера: Произвольное перемещение твёрдого тела, имеющего неподвижную точку, можно осуществить посредством вращения вокруг некоторой оси, проходящей через эту точку. В доказательстве показывается, что любая матрица поворота имеет собственное число равное 1, а соответствующий собственный вектор задает направление оси вращения. Также Эйлер придумал геометрический способ нахождения оси вращения. Как эта теорема поможет доказать, что тело вращается вокруг оси? А вот как: если рассмотреть бесконечно малое перемещение, которое тело совершает за бесконечно малый промежуток времени, то это перемещение, в виду его бесконечной малости, можно выполнить единственным способом и этот способ согласно теореме Эйлера представляет собой чистое вращение. Ось этого вращения называется «мгновенной осью вращения». Вектор угловой скорости направлен вдоль оси. Поскольку ось проходит через центр масс, вектор момента импульса прямо пропорционален вектору угловой скорости (об этом — ниже). А поскольку момент внешних сил равен нулю, то момент импульса не изменяется, следовательно не изменяется и вектор угловой скорости, следовательно мгновенная ось вращения не меняет своего направления со временем, что и следовало доказать. Аналогично показывается, что если на твердое тело действуют внешние силы, но момент их относительно центра масс тела равен нулю, то тело будет двигаться поступательно и вращаться с постоянной угловой скоростью вокруг некоторой оси, проходящей через его центр масс. Ось вращения будет двигаться поступательно вместе с центром масс тела.
Момент инерции
Если записать аналог 2-го закона Ньютона для тела, вращающегося вокруг оси (рис. 3), то становится очевидной аналогия между силой и моментом силы, скоростью и угловой скоростью, а также массой и некоей величиной, называемой моментом инерции. Насколько я понимаю, момент инерции задается только относительно оси, задавать момент инерции относительно точки бессмысленно. Причем момент инерции имеет смысл задавать относительно не любой оси, а именно той, вокруг которой тело вращается в данный момент. Момент инерции материальной точки относительно оси равен произведению массы этой точки на квадрат расстояния ее до оси. Проекция момента импульса тела на его мгновенную ось вращения равна произведению момента инерции на угловую скорость вращения. Соответственно проекция момента внешних сил на ось вращения равна произведению момента инерции на производную от угловой скорости по времени.
Существует довольно очевидная теорема связи моментов инерции, вычисленных относительно двух параллельных осей (одна из которых проходит через центр масс тела), находящихся на некотором расстоянии друг от друга — эта теорема проиллюстрирована на рисунке 3.
Сохранение момента импульса при изменяющемся моменте инерции.
В учебниках в качестве примера действия закона сохранения момента импульса приводят вращающегося на льду фигуриста. На фигуриста не действует момент сил, поэтому его момент импульса не меняется. Однако фигурист может изменить угловую скорость своего вращения прижимая руки к корпусу или наоборот вытягивая их в стороны, т. е. изменяя свой момент инерции. И если с математической точки зрения тут все понятно, то с точки зрения интуиции… может быть и не очень. Раз угловая скорость повышается, то повышается тангенциальная скорость. Значит, казалось бы, на тело действует тангенциальное ускорение. Но откуда же ему взяться, если мы знаем, что никакой тангенциальной силы на тело не действует? Поэтому я решил рассмотреть эту задачу без привлечения понятия момента, используя только законы Ньютона. На рисунке 4 показана задачка вычисления зависимости скорости вращения груза на веревке, которую тянут по направлению к оси вращения. В задачке я выделяю два направления: нормальное (буква n) — к оси вращения и тангенциальное (буква тау) — по касательной к окружности, которая проходит через вращающийся груз и центр которой находится на оси вращения; эти два направления перпендикулярны друг другу. Так вот, оказывается, что хотя тангенциальная составляющая скорости груза и увеличивается по мере его приближения к оси вращения, это вовсе не означает, что существует ненулевая тангенциальная составляющая ускорения груза. Дело в том, что нормальная составляющая скорости — т. е. та скорость, с которой груз подтягивают к оси вращения, постоянно меняет свое направление, что означает наличие ускорения.
Произвольное движение как сумма поступательного и вращательного
Произвольное движение тела можно описать как поступательное движение его центра масс плюс вращение вокруг оси, проходящей через центр масс. Оговоримся, что поступательное движение центра масс вовсе не обязано быть равномерным так же как ось вращения, проходящая через центр масс не обязана сохранять свое направление неизменным. Кинетическая энергия движения равна сумме кинетической энергии центра масс и кинетической энергии вращения вокруг оси, проходящей через центр масс. Что понимается под обеими энергиями — показано на рисунке 5.
Аналог 2-ого закона Ньютона для вращательного движения справедлив в только инерциальной системе отсчета и в еще одной системе отсчета, которая в общем случае не является инерциальной (но является очень удобной с точки зрения представления движения в виде суммы поступательного и вращательного) — системе центра масс. Доказательство этого приведено в [Джанколи, раздел 10.5].
Вращательный дисбаланс
Неожиданным может показаться тот факт, что в общем случае момент импульса не сонаправлен с осью вращения. Яркий пример, иллюстрирующий это — дисбаланс колес автомобиля (рис. 6). Если ось вращения не совпадает с осью симметрии вращающегося тела (предполагаем, что тело однородно), то момент импульса сам будет вращаться вокруг оси вращения, а это значит, что будет существовать момент сил (тоже вращающийся). Откуда берется момент сил? Это силы реакции опор оси вращения. Эти силы будут приводить к разбалтыванию оси, особенно, если частота вращения колеса близка к резонансной частоте колебаний оси.
Колесо на палке, волчок, прецессия
Еще одна вещь, связанная с вращением, которая может показаться загадочной — волчок. Он, как известно, крутится и до определенного момента не падает. По мере того, как вращение волчка замедляется из-за трения, становится заметным, что его ось меняет направление — вращается (это называется прецессией). Момент силы тяжести всегда перпендикулярен моменту импульса волчка, поэтому момент импульса волчка будет поворачиваться вокруг вертикальной оси. Сам волчок никогда не стоит строго вертикально, его ось наклонена, и угол наклона зависит от момента импульса волчка. Аналогичен случай вращающегося колеса на палке (рис. 7). Несмотря на действие силы тяжести, ось колеса не повисает вертикально вниз, а начинает прецессировать. Можно рассчитать и угловую скорость прецессии. Эти примеры приведены в [Джанколи, раздел 10.9].

















