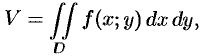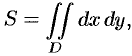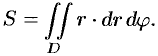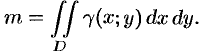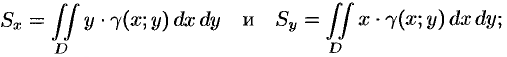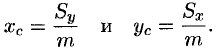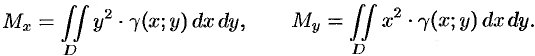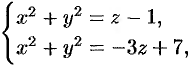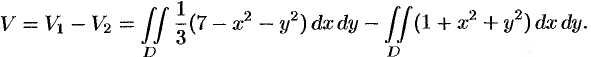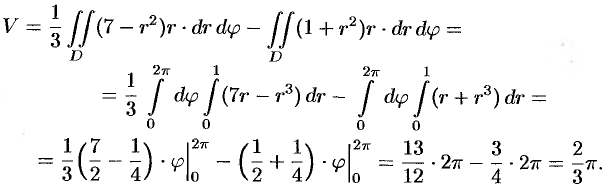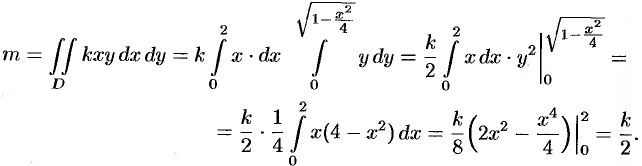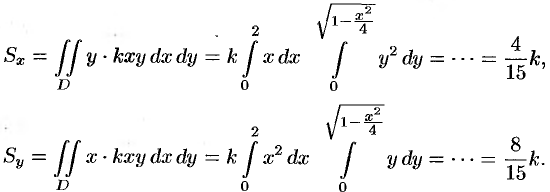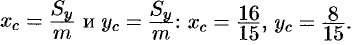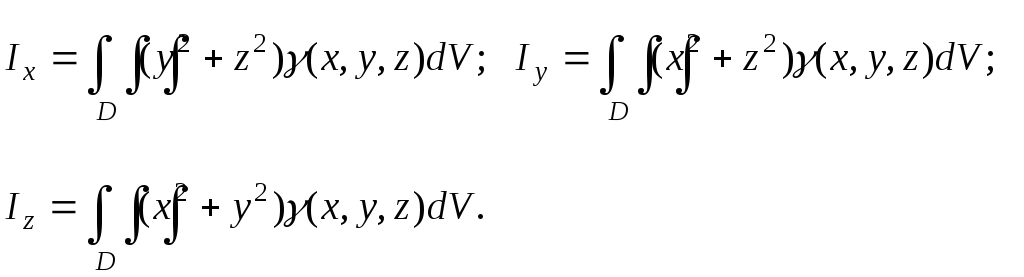Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где 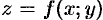
Площадь плоской фигуры
Если положить в формуле (53.4) 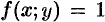
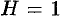




или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки 
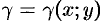
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры 

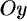
а координаты центра масс фигуры — по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы 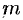
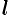
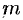
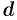
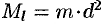

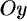
Момент инерции фигуры относительно начала координат — по формуле 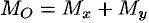
Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример №53.3.
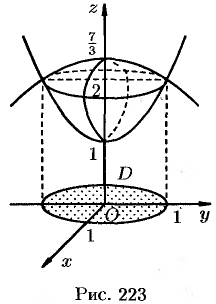
Найти объем тела, ограниченного поверхностями 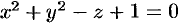
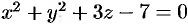
Решение:
Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
находим уравнение линии их пересечения: 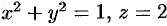
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 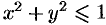
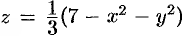
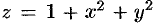
Переходя к полярным координатам, находим:
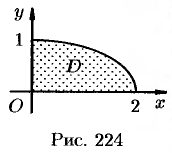
Пример №53.4.
Найти массу, статические моменты 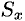
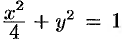
Решение:
По формуле (53.6) находим массу пластинки. По условию, 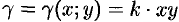
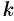
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Вычисление моментов инерции
Моменты инерции материальной кривой
Моментом инерции материальной точки относительно оси
называется число
, где
— масса точки, а
— ее расстояние от оси. Аналогично определяется момент инерции относительно точки.
Пусть — материальная линия, линейная плотность которой во всех точках равна единице. Тогда масса элементарного участка этой линии равна его длине
, а момент инерции
такого участка относительно оси абсцисс равен
. Интегрируя, получаем момент инерции относительно оси абсцисс всей линии:
. Так же доказывается, что
и
,
где — момент инерции относительно начала координат. Отсюда следует, в частности, что
.
Если линия задана параметрическими уравнениями
, то
Аналогичные формулы справедливы для и
Моменты инерции криволинейной трапеции
Перейдем к вычислению моментов инерции криволинейной трапеции. Будем считать, что ее поверхностная плотность равна единице. Сначала найдем момент инерции прямоугольника со сторонами и
относительно стороны
. Разобьем его на элементарные прямоугольники со сторонами
и
(см. рис. 61). Площадь (а потому и масса) каждого такого прямоугольника равна
. Значит, момент инерции элементарного прямоугольника относительно стороны
равен
, а момент инерции всего прямоугольника относительно этой стороны выражается формулой
Криволинейную трапецию разобьем на элементарные прямоугольники со сторонами и
. Момент инерции каждого из этих прямоугольников относительно оси абсцисс выражается формулой
. Интегрируя, получаем момент инерции всей криволинейной трапеции относительно оси абсцисс:
Аналогично доказывается, что момент инерции криволинейной трапеции относительно оси ординат выражается формулой
(момент инерции элементарного прямоугольника относительно оси ординат равен ).
Полярный момент инерции (т. е. момент относительно начала координат) в этом случае выражается формулой
Пример 9. Вычислить момент инерции равнобедренного треугольника относительно его основания.
Решение. Расположим оси координат так, как показано на рисунке 65.
Пусть основание треугольника , высота
. Прямая
проходит через точки
и
. Ее уравнение
, то есть
.
Ясно, что момент инерции треугольника
относительно оси
равен удвоенному моменту инерции треугольника
относительно той же оси. Значит,
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Механические приложения двойного интеграла
Будем считать, что $mathbf { textit { D } } $ — неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $mu (P)$. В механике $mu (P)$ определяется так. Точка $P$ окружается малой областью $mathbf { textit { S } } $, находится масса $mathbf { textit { m } } (mathbf { textit { S } } )$ и площадь этой области { площадь тоже будем обозначать буквой $mathbf { textit { S } } $ } и $mu (P)=mathop { lim } limits_ { diam(S)to 0 } frac { m(S) } { S } $.
Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $mathbf { textit { D } } $ на малые подобласти $mathbf { textit { D } } _ { 1 } $, $mathbf { textit { D } } _ { 2 } $,$mathbf { textit { D } } _ { 3 } , { ldots } , mathbf { textit { D } } _ { n } $, в каждой из подобластей $mathbf { textit { D } } _ { i } $ выберем произвольную точку $mathbf { textit { P } } _ { i } $, и, считая что в пределах $mathbf { textit { D } } _ { i } $ плотность постоянна и равна $mu (P_i )$, получим, что масса $mathbf { textit { D } } _ { i } $ приближённо есть $mu (P_i )cdot s(D_i )$, а масса всей пластины $sumlimits_ { i=1 } ^n { mu (P_i )cdot s(D_i ) } $.
Это интегральная сумма, при уменьшении $d=mathop { max } limits_ { i=1,2,ldots ,n } diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=mathop { lim } limits_ { begin{array} { l } dto 0 \ (nto infty ) \ end{array} } sumlimits_ { i=1 } ^n { mu (P_i )cdot Delta s(D_i ) } =iintlimits_D { mu (P)ds } $.
Аналогично находятся другие параметры пластины:
Координаты центра тяжести
$x_c =frac { 1 } { m(D) } iintlimits_D { xcdot mu (P)ds } $, $y_c =frac { 1 } { m(D) } iintlimits_D { ycdot mu (P)ds } $;
Моменты инерции пластины
- $I_x =iintlimits_D { y^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Ox } } $ } ,
- $I_y =iintlimits_D { x^2cdot mu (P)ds } $ { относительно оси $mathbf { textit { Oy } } $ } ,
- $I_O =iintlimits_D { (x^2+y^2)cdot mu (P)ds } =I_x +I_y $ { относительно начала координат } .
Пластина расположена в области (R) и ее плотность в точке ( { left( { x,y }right) } ) равна ( { rho left( { x,y }right) } ).
Масса пластины
(m = largeiintlimits_Rnormalsize { rho left( { x,y }right)dA } )
Статические моменты пластины
Момент пластины относительно оси (Ox) определяется формулой
( { M_x } = largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } )
Аналогично, момент пластины относительно оси (Oy) выражается в виде
( { M_y } = largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } )
Координаты центра масс пластины
- (bar x = largefrac { { { M_y } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { xrho left( { x,y }right)dA } = largefrac { { iintlimits_R { xrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize,;)
- (bar y = largefrac { { { M_x } } } { m } normalsize = largefrac { 1 } { m } normalsize largeiintlimits_Rnormalsize { yrho left( { x,y }right)dA } = largefrac { { iintlimits_R { yrho left( { x,y }right)dA } } } { { iintlimits_R { rho left( { x,y }right)dA } } } normalsize ).
Заряд пластины
(Q = largeiintlimits_Rnormalsize { sigma left( { x,y }right)dA } ),
где электрический заряд распределен по области (R) и его плотность в точке ( { left( { x,y }right) } ) равна ( { sigma left( { x,y }right) } ).
Среднее значение функции
(mu = largefrac { 1 } { S } iintlimits_Rnormalsize { fleft( { x,y }right)dA } ,;) где (S = largeiintlimits_Rnormalsize { dA } ).
Пример 1
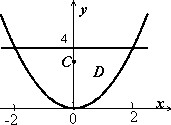
Найти параметры неоднородной плоской пластины, ограниченной кривыми
$D:left[{ begin{array} { l } y=x^2, \ y=4; \ end{array} }right.$ если плотность $mu (x,y)=y+1$.
Решение:
$m(D)=iintlimits_D { (y+1)dxdy } =2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =$ $ =2intlimits_0^2 { left( { 12-x^4/2-x^2 }right)dx } =2left. { left( { 12x-x^5/10-x^3/3 }right) }right|_0^2 =2left( { 24-frac { 16 } { 5 } -frac { 8 } { 3 } }right)=frac { 544 } { 15 } . $ $ x_c =frac { 1 } { m(D) } iintlimits_D { x(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { x(y+1)dy } =frac { 15 } { 544 } intlimits_ { -2 } ^2 { xleft. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } = $ $=frac { 15 } { 544 } intlimits_ { -2 } ^2 { left( { 12x-x^5/2-x^3 }right)dx } = quad =frac { 1 } { 544 } left. { left( { 6x^2-x^6/10-x^4/4 }right) }right|_ { -2 } ^2 =0$ { что и следовало ожидать, так как область и плотность симметричны относительно оси Оу). $ begin{array} { l } y_c =frac { 1 } { m(D) } iintlimits_D { y(y+1)dx } dy=frac { 15 } { 544 } intlimits_ { -2 } ^2 { dx } intlimits_ { x^2 } ^4 { y(y+1)dy } =frac { 15 } { 272 } intlimits_0^2 { left. { left( { y^3/3+y^2/2 }right) }right|_ { x^2 } ^4 dx } = \ =frac { 15 } { 272 } intlimits_0^2 { left( { 64/3+8-x^6/3-x^4/2 }right)dx } =frac { 15 } { 272 } left. { left( { 88x/3-x^7/21-x^5/10 }right) }right|_0^2 =frac { 15 } { 272 } left( { frac { 176 } { 3 } -frac { 128 } { 21 } -frac { 16 } { 5 } }right)=frac { 15 } { 272 } cdot frac { 1728 } { 35 } approx 2,72. \ end{array} $ $ I_x =iintlimits_D { y^2(y+1)dx } dy=2intlimits_0^2 { dx } intlimits_ { x^2 } ^4 { y^2(y+1)dy } =2intlimits_0^2 { left. { left( { y^4/4+y^3/3 }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { left( { frac { 256 } { 3 } -frac { x^8 } { 4 } -frac { x^6 } { 3 } }right)dx } = $ $ =2left. { left( { frac { 256 } { 3 } x-frac { x^9 } { 36 } -frac { x^7 } { 21 } }right) }right|_0^2 approx 300,7. $ $ I_y =iintlimits_D { x^2(y+1)dx } dy=2intlimits_0^2 { x^2dx } intlimits_ { x^2 } ^4 { (y+1)dy } =2intlimits_0^2 { x^2left. { left( { y^2/2+y }right) }right|_ { x^2 } ^4 dx } =2intlimits_0^2 { x^2left( { 12-frac { x^4 } { 2 } -x^2 }right)dx } = $ $ =2left. { left( { 4x^3-frac { x^7 } { 14 } -frac { x^5 } { 5 } }right) }right|_0^2 approx 32,9. quad I_O =iintlimits_D { left( { x^2+y^2 }right)(y+1)dx } dy=I_x +I_y approx 333,6. $
Пример 2
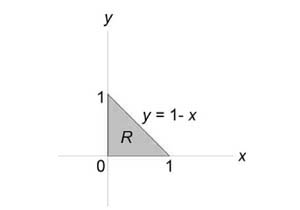
Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $rho left( { x,y }right) = xy.$
Решение:
Найдем момент инерции пластины относительно оси (Ox:) $ { { I_x } = iintlimits_R { { y^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 — x } { { y^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 — x } { { y^3 } dy } }right]xdx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^4 } } } { 4 } }right) }right|_0^ { 1 — x } }right]xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { { { left( { 1 — x }right) } ^4 } xdx } } = { frac { 1 } { 4 } intlimits_0^1 { left( { 1 — 4x + 6 { x^2 } — 4 { x^3 } + { x^4 } }right)xdx } } = \ = { frac { 1 } { 4 } intlimits_0^1 { left( { x — 4 { x^2 } + 6 { x^3 } — 4 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 4 } left. { left( { frac { { { x^2 } } } { 2 } — frac { { 4 { x^3 } } } { 3 } + frac { { 6 { x^4 } } } { 4 } — frac { { 4 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 4 } left( { frac { 1 } { 2 } — frac { 4 } { 3 } + frac { 3 } { 2 } — frac { 4 } { 5 } + frac { 1 } { 6 } }right) } = { frac { { 49 } } { { 120 } } . } $
Аналогично вычислим момент инерции относительно оси (Oy:) $ { { I_y } = iintlimits_R { { x^2 } rho left( { x,y }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 — x } { { x^2 } xydy } }right]dx } } = { intlimits_0^1 { left[ { intlimits_0^ { 1 — x } { ydy } }right] { x^3 } dx } } = { intlimits_0^1 { left[ { left. { left( { frac { { { y^2 } } } { 2 } }right) }right|_0^ { 1 — x } }right] { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { { { left( { 1 — x }right) } ^2 } { x^3 } dx } } = \ = { frac { 1 } { 2 } intlimits_0^1 { left( { 1 — 2x + { x^2 } }right) { x^3 } dx } } = { frac { 1 } { 2 } intlimits_0^1 { left( { { x^3 } — 2 { x^4 } + { x^5 } }right)dx } } = { frac { 1 } { 2 } left. { left( { frac { { { x^4 } } } { 4 } — frac { { 2 { x^5 } } } { 5 } + frac { { { x^6 } } } { 6 } }right) }right|_0^1 } = { frac { 1 } { 2 } left( { frac { 1 } { 4 } — frac { 2 } { 5 } + frac { 1 } { 6 } }right) } = { frac { 1 } { { 120 } } . } $
Пример 3
Электрический заряд распределен по площади диска ( { x^2 } + { y^2 } = 1) таким образом, что его поверхностная плотность равна $sigma left( { x,y }right) = 1 + { x^2 } + { y^2 } ;left( { text { Кл/м } ^2 }right)$ Вычислить полный заряд диска.
Решение:
В полярных координатах область, занятая диском, описывается множеством (left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].)
Полный заряд будет равен $ { Q = iintlimits_R { sigma left( { x,y }right)dxdy } } = { intlimits_0^ { 2pi } { left[ { intlimits_0^1 { left( { 1 + { r^2 } { { cos } ^2 } theta + { r^2 } { sin^2 } theta }right)rdr } }right]dtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { left( { 1 + { r^2 } }right)rdr } } = { 2pi intlimits_0^1 { left( { r + { r^3 } }right)dr } } = \ = { 2pi left. { left( { frac { { { r^2 } } } { 2 } + frac { { { r^4 } } } { 4 } }right) }right|_0^1 } = { 2pi left( { frac { 1 } { 2 } + frac { 1 } { 4 } }right) } = { frac { { 3pi } } { 2 } ;left( { text { Кл } }right). } $
I Вычисление объёмов тел
.
Пример
1. Вычислить
объём тела, ограниченного поверхностями
,
,
.
Решение.
Тело, представляет собой полушар с
конической выемкой. Проекция на плоскость
– круг радиуса
с центром в начале координат, следовательно,
координатаССК изменяется от 0 до
.
Проекция на плоскость– полукруг с вырезанным сектором
(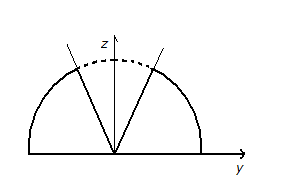
конусаэтой плоскостью – это
).
Координатаизменяется от
на образующих конуса до
на плоскости
.
И, наконец, координата.
Итак, объём тела
Здесь повторный
интеграл представляет собой произведение
трех интегралов, ибо внутренние интегралы
не зависят от внешних переменных.
II Вычисление масс тел
где
– плотность распределения массы.
Пример
2. Найти
массу шара
если плотность в каждой точке
пропорциональна расстоянию от
до некоторой фиксированной точки
поверхности шара.
Решение.
Поместим фиксированную точку в начало
координат, а центр шара на ось
.
Тогда уравнение сферы в сферических
координатах имеет вид (см. §6, замечание
3):,
.
Далее, плотность,.
Имеем для массы:
III Вычисление координат центра масс тела
Формулы для
координат центра масс тела выводятся
так же как аналогичные формулы для
плоской фигуры. Не будем выводить их, а
просто приведем:
П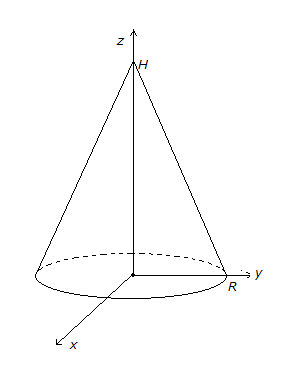
3. Найти
положение центра масс однородного
конуса с радиусом основания
и высотой
.
Решение.
Расположим конус обычным образом:
основание в плоскости
,
вершина на оси.
Выясним какие поверхности ограничивают
это тело. Одна из них – это плоскость,
а вторая – это нижняя часть конической
поверхности,
смещенная вверх наН.
Имеем:
Коэффициент
найдем из того усло-вия, что пересечение
этой поверхности с плоскостью– круг радиусаR:
.
Итак, задачу можно
сформулировать так: «Найти координаты
центра масс тела, ограниченного
поверхностями
и
,
если
».
Тело симметрично относительно оси
и в симметричных точках плотность
одинакова. Следовательно, центр масс
лежит на оси:
Итак, центр масс
однородного конуса расположен на его
оси на расстоянии четверти высоты от
основания.
IV Вычисление моментов инерции тела
Формулы для
всевозможных моментов инерции тела
аналогичны подобным формулам для плоской
фигуры.
Моменты инерции
относительно осей координат:
Моменты инерции
относительно координатных плоскостей:
Момент инерции
относительно начала координат:
Пример
4. Найти
момент инерции цилиндра
относительно фиксированной образующей,
если плотность в каждой его точке обратно
пропорциональна расстоянию от точки
до этой образующей.
Р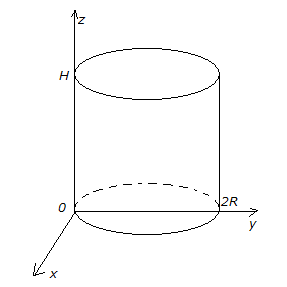
Пусть образующая, о которой говорится
в условии задачи, лежит на оси
,
а центр нижнего основания на оси.
Цилиндр ограничен поверхностями
Цилиндрическое
уравнение третьей поверхности:
.
Плотность
в силу условия
Итак, момент инерции:
V Вычисление силы притяжения точки телом
Пусть в точке А
находится
масса
,
а в точкеВ
– масса М.
Известно, что М
притягивает
(и наоборот) с силой
такой, что
,
где).
Пусть теперь эти
точки находятся в системе координат:
Проекции
силы
вычисляются по формулам
Но
поэтому, например,
где
Аналогичные формулы есть для
и
.
Итак, проекции силы:
Пусть теперь тело
имеет плотность
.
Как найти силу,
с которой телопритягивает массу
,
находящуюся в точке?
Можно поступить обычным, при построении
приложений интеграла, способом. Всю
областьразбиваем на части
,
выбираем точкии считаем, что вся масса
сосредоточена в
.
Получим системуматериальных точек:
с массой
.
(Подобным образом мы поступали при
вычислении координат центра масс и
моментов инерции плоской фигуры. Так
же можно поступить и при нахождении
этих характеристик пространственной
области.)
Точка
притягивает
с силой
,
где, например,
вычисляются
аналогично. Суммируя и переходя к
пределу, получим для проекций полной
силы
:
где
Пример 5.
Найти силу, с которой однородный конус
притягивает массу
,
находящегося в его вершине.
Решение.
Впишем данный конус в систему координат
так, как показано на рисунке. Такой конус
можно описать как тело, ограниченное
поверхностями
и
(смотри пример 3).
В силу симметрии
и однородности
сила притяжения направлена по оси
.
Имеем:
.
Переходим к
цилиндрическим координатам. Полярные
координаты проекции произвольной точки
тела на плоскость
изменяются в пределах
,
а координатаизменяется от конуса до плоскости, т.е.
отдо
.
Итак,
Соседние файлы в папке Лекции по мат.анализу
- #
- #
- #
- #
- #
- #