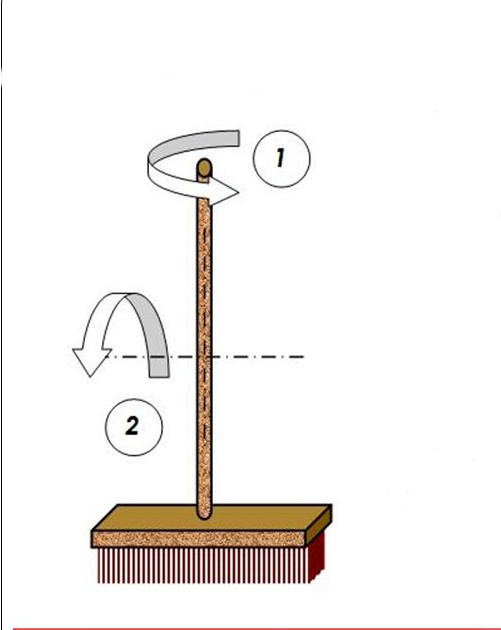
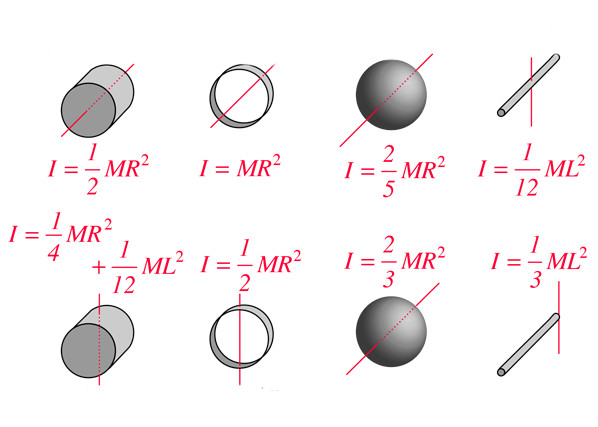Как найти момент инерции материальной точки - Исправление недочетов и поиск решений вместе с Examum.ru

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Инерция определяет, насколько хорошо тело может препятствовать изменению своей скорости. Инерция зависит от массы. По сути, чем больше масса, тем больше инертность тела. Как это связано? Очень просто. Поезд тормозит медленнее легковой машины, именно поэтому переходить пути надо еще внимательнее, чем дорогу. В поезде собственная масса в несколько тонн и еще сотни людей едут на работу. В машине их максимум пять. И чтобы остановить поезд, нужно приложить к нему силу, большую, чем потребуется для остановки машины. Все потому, что сила связана напрямую с ускорением, а не со скоростью. Согласно второму закону Ньютона:

F=maF=ma,

где
FF — сила;
mm — масса;
aa — ускорение.

Отсюда видно, что ускорение обратно пропорционально массе. Это объясняет, почему изменить скорость более массивного тела труденее чем более легкого.

Инерция материальной точки

В решении задач механики часто используют физическую модель под названием материальная точка (МТ).

Материальная точка

Это некое тело, имеющее массу, но не имеющее объема.

Соответственно, оно может подвергаться воздействию внешних сил. Именно эту абстракцию мы будем использовать для дальнейших объяснений.

Если представить, что МТ обладает массой утренней электрички, становится жутко. И тем не менее избавление от объема и лишних ассоциаций, возникающих с реальными объектами (как, например, изменится скорость электрички, если в ней «зайцы» убегают от контролеров?) дает возможность сосредоточиться на задачах, решаемых механикой.

Момент инерции материальной точки

Одно из важных понятий, связанных с инерцией, имеет название момента инерции (МИ).
Что называется моментом инерции материальной точки? Это понятие возникает только при рассмотрении криволинейного движения. Чаще всего под криволинейным движением понимается движение по окружности – им мы и займемся. Строго говоря, любую траекторию можно рассмотреть как совокупность движений по прямой и по окружности, именно поэтому эти типы движения изучаются особенно внимательно.

Почему момент инерции имеет смысл только при криволинейном движении? Потому что его ввели, когда оказалось, что при вращательном движении массы тела в качестве меры инертности недостаточно для расчетов. МИ – всего лишь сумма произведений элементарных масс тела на квадрат их расстояний до точки, относительно которой происходит вращение. Вот формула:

Момент инерции системы материальных точек

J=∑i=1Nmiri2J= displaystylesum_{i=1}^{N} m_ir_i^2

JJ — момент инерции;
mim_i — масса ii-ой частицы;
rir_i — расстояние ii-ой частицы к точке, относительно которой происходит вращение;
NN — количество частиц в системе.

По сути это формула для момента инерции системы NN частиц.
Для непрерывного тела сумма превращается в интеграл:

Момент инерции непрерывного тела

J=∫0mr2dmJ= displaystyleint_{0}^{m} r^2dm

mm — полная масса тела;
rr — расстояние от элемента массы dmdm к точке, относительно которой происходит вращение.

Проще говоря, если взять чайный пакетик, разбить его (мысленно!) на мелкие частички, посчитать массу каждой из них, умножить их на соответствующие квадраты расстояний до раскручивающих его за этикетку пальцев, а потом сложить все эти произведения — получится момент инерции относительно точки за которую мы держим этот пакетик.

А если сжать пакетик в материальную точку, оставив массу и лишив его объема, то и интегралы считать не надо — масса пакетика на квадрат расстояния будет моментом инерции МТ. При этом пальцы, держащие этикетку, будут центром инерции материальной точки.

Момент инерции часто рассматривают не только относительно точки, но и относительно некоторой оси. Говоря об оси или точке вращения, стоит заметить, что ось можно представить как частный случай точки. Тем не менее в задачах оси чаще всего достаточно. В чем вообще между ними разница? Ось (простейшее ее представление — стержень) дает телу всего одну плоскость вращения — перпендикулярную себе. А у точки этих плоскостей бесконечное количество. Потому, если нужно рассмотреть вращение в нескольких плоскостях, стоит взять точку, а если нет, то лучше ограничиться стержнем.

Сложности возникают, когда предмет нельзя взять и сжать в одну материальную точку. Например, он состоит из разных материалов или слишком велик в рамках решаемой задачи, чтобы ограничиться всего лишь точкой. Тогда на помощь приходит… система материальных точек. Тело разбивается на несколько частей, каждая из которой имеет свое фиксированное положение относительно других и имеет массу. И тогда момент инерции системы материальных точек вычисляется по формуле выше.

Зачем вообще нужна мера инерции в виде массы или момента инерции? А затем, что эти величины входят в основные уравнения динамики. Масса входит в уравнение Ньютона (его мы уже видели выше), а момент инерции встречается в уравнении движения для вращательного движения (аналог уравнения Ньютона):

M=JεM=J varepsilon,

где
MM — момент сил;
JJ — момент инерции;
εvarepsilon — угловое ускорение.

Нужно подчеркнуть, что в этой формуле момент сил MM и момент инерции JJ берется относительно одной и той же точки (или оси) иначе это уравнение попросту не будет иметь смысла.

Тест по теме «Инерция материальной точки»

Источник

Момент
инерции материальной точки относительно
оси — произведение массы материальной
точки на квадрат ее расстояния до оси.

Определение:
Моментом инерции материальной точки
относительно неподвижной оси называется
скалярная физическая величина, являющаяся
мерой инертности этой точки при
вращательном движении и, равная
произведению её массы на квадрат
расстояния до оси, т.е. , а также , где —
угловая скорость тела относительно
данной оси.

Моментом
инерции твердого тела относительно оси
называется скалярная величина, равная
сумме произведений массы каждой точки
тела на квадрат расстояния от этой точки
до оси.

Определение:
Моментом инерции системы материальных
точек относительно неподвижной оси
называется скалярная физическая
величина, являющаяся мерой инертности
этой системы при вращательном движении
и, равная алгебраической сумме произведений
масс всех материальных точек системы
на квадрат их расстояний до оси, т.е. .
момент инерции определен только
относительно оси.

21. Свойства момента инерции тела относительно оси. Теорема Штейнера.

Итак,
перечислим свойства момента инерции
относительно данной оси, которую мы
назовем осью z:

1. Момент инерции равен

2.
Если предмет состоит из нескольких
частей, причем момент инерции каждой
из них известен, то полный момент инерции
равен сумме моментов инерции этих
частей.

3.
Момент инерции относительно любой
данной оси равен моменту инерции
относительно параллельной оси, проходящей
через центр масс, плюс произведение
полной массы на квадрат расстояния
данной оси от центра масс

4. Момент инерции плоской фигуры
относительно оси, перпендикулярной к
ее плоскости, равен сумме моментов
инерции относительно любых двух других
взаимно перпендикулярных осей, лежащих
в плоскости фигуры и пересекающихся с
перпендикулярной осью.

В табл. 19.1 приведены моменты инерции
некоторых элементарных фигур, имеющих
однородную плотность масс, а в табл.
19.2 — моменты инерции некоторых фигур,
которые могут быть получены из табл.
19.1 с использованием перечисленных выше
свойств.

Теорема
Штейнера:
момент
инерции
тела

относительно
произвольной оси равен сумме момента
инерции этого тела

относительно параллельной ей оси,
проходящей через центр масс тела, и
произведения массы тела

на
квадрат расстояния

между осями:

где

—
известный
момент инерции относительно оси,
проходящей через центр масс тела,

—
искомый
момент инерции относительно параллельной
оси,

—
масса
тела,

—
расстояние
между указанными осями.

22. Главные и свободные оси инерции тела. Главные моменты инерции. Устойчивые оси вращения.

Оси,
относительно которых центробежный
момент инерции равен нулю, называются
главными
осями
(иногда
их называют главными
осями инерции).
Через любую точку, взятую в плоскости
сечения, можно провести в общем случае
две главных оси (в некоторых частных
случаях их может быть бесчисленное
множество). Для того чтобы убедиться в
справедливости этого утверждения,
рассмотрим, как изменяется центробежный
момент инерции при повороте осей на 90°
(рис.2.9).

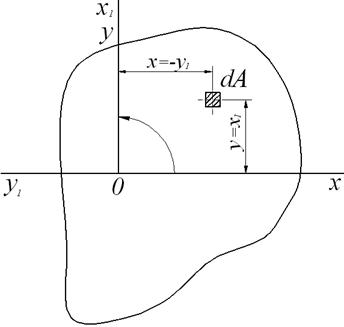
Рис.2.9.
К определению положения главных осей

Для
произвольной площадки ,
взятой
в первом квадранте системы осей
обе
координаты, а, следовательно, и их
произведение, положительны. В новой
системе координат,
повернутой
относительно первоначальной на 90°,
произведение координат рассматриваемой
площадки отрицательно. Абсолютная
величина этого произведения не изменяется,
т. е.
Очевидно, то же имеет место и для любой
другой элементарной площадки. Значит
и знак суммы
представляющей
собой центробежный момент инерции
сечения, при повороте осей на 90° меняется
на
противоположный, т. е.

величина
Ja,
равная сумме произведений масс всех n
материальных точек системы на квадраты
их расстояний до оси:

где:

mi
— масса i-й
точки,

ri
— расстояние от i-й
точки до оси.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Момент инерции материальной точки

Для динамического описания движения материальной точки по окружности используют следующие величины: момент силы (), момент импульса () и момент инерции (J). При этом основной закон динамики вращательного движения записывают в виде:

$[overline{M}=frac{doverline{L}}{dt} qquad (1)]$

Кроме этого, описывая движение по окружности вместо радиус-вектора () пользуются углом поворота (), вместо вектора скорости () используют вектор угловой скорости ().

Момент инерции

Роль массы при движении по окружности материальной точки выполняет момент инерции (J), который равен:

где r- расстояние от материальной точки до оси вращения. Для материальной точки, которая движется по окружности, момент инерции является постоянной величиной. При этом изменение момента импульса происходит только за счет изменения угловой скорости:

Используя момент инерции основное уравнение динамики (1) для движения материальной точки по окружности можно записать как:

$[overline{M}=Jfrac{doverline{omega}}{dt}=Joverline{varepsilon} qquad (4)]$

где – угловое ускорение материальной точки. Уравнение (4) отражает тот факт, что при движении материальной точки по окружности, момент силы исполняет роль силы (в поступательном движении), момент инерции – роль массы, угловое ускорение – роль линейного ускорения. Это легко увидеть, если записать второй закон Ньютона и сравнить его с уравнением (4):

Мерой инертности материальной точки при движении по окружности служит момент инерции.

Момент инерции является аддитивной величиной. Это означает то, что если в системе не одна, а несколько материальных точек, то момент инерции системы (J) равен сумме моментов инерции () отдельных точек:

$[J=sum^N_{i=1}{J_i}=sum^N_{i=1}{Delta m_ir^2_i} qquad (6)]$

где – масса ой материальной точки; расстояние от данной материальной точки до оси вращения. Момент инерции системы материальных точек зависит от распределения этих точек в пространстве. Чем ближе материальные точки находятся от оси вращения, тем меньше момент инерции данной системы. У твёрдых тел, которые можно представить как непрерывную совокупность материальных точек, момент инерции относительно оси является постоянной величиной.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Источник

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫_m(r² * dm) = ρ * ∫_V(r² * dV).

Где ρ — плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Теорема Штейнера и формула

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину I_O тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром I_O и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = I_O + M * h².

Здесь M — масса тела, h — расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r₀+ h.

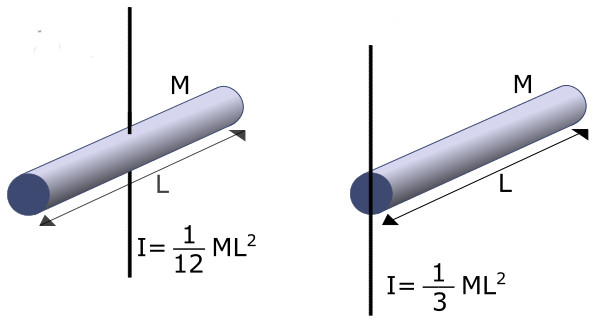
Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = I_O + M * (L / 2)² = 1 / 12 * M * L² + M * L²/ 4 = M * L²/ 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M — момент силы, α — угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d — плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = I_O + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

Источник