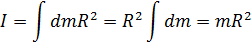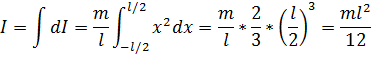Момент
инерции —
скалярная
физическая величина, характеризующая
распределение масс в теле, равная сумме
произведений элементарных масс на
квадрат их расстояний до базового
множества (точки, прямой или плоскости).
Единица
измерения СИ: кг·м².
Обозначение:
I
или J.

расчета моментов
инерции
тонкого диска
массы m
и радиуса R
выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси z
, перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо с
внутренним
радиусом
r
и наружным r+dr.
Площадь такого кольца ds=2r
$pi$ dr, а его
масса
,
гдеS= $pi$ R2
— площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется
интегралом
Вычисление
момента
инерции тонкого стержня:
Пусть
тонкий стержень имеет длину l
и массу m.
Разделим его на малые элементы длины
dx
(рис.27), масса которых
.
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции,
т.е.
Интегрируя
последнее соотношение в пределах от 0
до l/2
и удваивая полученное выражение (для
учета левой половины стержня), получим
Момент
инеpции обручаотносительно оси,
пpоходящей чеpез центp кольца пеpпендикуляpно
к его плоскости. В этом случае все
элементаpные массы обруча удалены от
оси на одинаковое pасстояние, поэтому
в сумме (3.18) r2 можно вынести за знак
суммы, т. е.
Теорема
Штейнера:
В
общем случае вращения тела произвольной
формы вокруг произвольной оси, вычисление
момента инерции может быть произведено
с помощью теоремы Штейнера: момент
инерции относительно произвольной оси
равен сумме момента инерции J0 относительно
оси, параллельной данной и проходящей
через центр инерции тела, и произведения
массы тела на квадрат расстояния между
осями: J=J0+ma^2.
Например,
момент инерции диска относительно оси
О’ в соответствии с теоремой Штейнера:
17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
Линия
— ось вращения.
— масса на квадрат радиуса окружности,
по которой движется материальная точка.
Все
тело мысленно разбиваем на маленькие
объемы. Масса этого кусочка
.
Твердое
тело представляется как совокупность
системы точечных масс.
— расстояние, на котором находится точка
от оси вращения.
— общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.
Момент
инерции шара.
Сплошной шар массы
m
и радиуса R
можно рассматривать как совокупность
бесконечно тонких сферических слоев с
массами dm
, радиусом r,
толщиной dr
(рис.35).
Рассмотрим
малый элемент сферического слоя $delta$
m с координатами
x, y, z.
Его моменты инерции относительно осей
проходящих через центр слоя — $delta$
Jx,
$delta$ Jy,
$delta$ Jz,
равны
Т.
е. можно записать
(п.26)
Так как для
элементов сферического слоя x2+y2+z2=r2
то
После
интегрирования по всему объему слоя
получим
(п.27)
Так как, в силу
симметрии для сферического слоя
dJx=dJy=dJz=dJ
, а

тоИнтегрируя по всему объему шара,
получаем
Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен
Разобьём
КОНУС
на цилиндрические слои
ось
толщиной dr.
Масса такого слоя
dm
= r2dr,
где
ρ – плотность
материала, из которого изготовлен конус.
Момент инерции этого слоя
dI = dm.r2.
Момент
инерции всего конуса
складывается
из моментов инерции всех слоёв:
I
=
=
ρπ
r
4
dr
=
ρR5.
Остаётся выразить
его через массу всего цилиндра:
m
=
=
=
R3,
отсюда ρ
=
,
I
=
=
mR2.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на тему «теорема Штейнера».
Сначала давайте соберем в «кучку» все формулы моментов инерции для часто встречающихся тел.
Момент инерции тонкого кольца (ось вращения перпендикулярна плоскости кольца и проходит через центр)
Момент инерции полого тонкостенного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции сплошного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции полого толстостенного цилиндра (ось вращения совпадает с осью цилиндра)
Момент инерции диска (ось вращения совпадает с осью диска)
Момент инерции диска (ось вращения совпадает с диаметром диска)
Момент инерции шара (ось вращения совпадает с центром)
Момент инерции полой тонкостенной сферы (ось вращения совпадает с центром)
Момент инерции тонкого стержня (ось вращения совпадает с центром)
Напоминаю теорему Штейнера: момент инерции тела относительно любой оси вращения равен моменту его инерции относительно параллельной оси, проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния между осями.
Теорема Штейнера
Теперь можно решить пару задач.
Задача 1.
Найти момент инерции обруча массой и радиусом
относительно оси, проходящей через его край перпендикулярно обручу.
Решение:
К задаче 1
По таблице определим момент инерции обруча (кольца), и прибавим произведение массы тела на квадрат расстояния между осями, а это – радиус кольца. Тогда
Ответ:
Задача 2. Найти момент инерции тонкого стержня массой и длиной
относительно оси, перпендикулярной стержню и проходящей через точку, отстоящую от конца стержня на одну треть его длины.
Решение.
К задаче 2
Расстояние между осями
Согласно таблице момент инерции стержня равен , тогда по теореме Штейнера
Ответ:
Задача 3.
Два шара радиусами см и массой
г каждый скреплены тонким стержнем массой
г и длиной
см. Найти момент инерции системы относительно оси, перпендикулярной стержню и проходящей через центр тяжести, а также относительно оси, перпендикулярной стержню и проходящей в
от его конца.
К задаче 3
Решение:
- Сначала найдем момент инерции системы относительно ее центра масс.
Здесь — момент инерции стержня,
— момент инерции одного из шаров.
Момент инерции стержня определим по таблице, так как очевидно, что его центр является центром масс системы и ось вращения будет проходить через центр масс стержня.
Определим момент инерции одного из шаров по теореме Штейнера:
Тогда ответом на пункт а) будет
б) Теперь пусть ось проходит на расстоянии четверти длины стержня от его конца. Тогда момент инерции стержня будет равен по теореме Штейнера
Момент инерции шара, ближнего к оси вращения:
Момент инерции шара, дальнего от оси вращения:
Тогда ответом на пункт б) будет
Ответ: а) кг
м
, б)
кг
м
.
Задача 4.
Имеется диск диаметром см и массой
г. В диске вырезали круглое отверстие диаметром 8 см, центр которого находится на расстоянии
от центра диска. Найти момент инерции
фигуры относительно оси, проходящей через центр диска и перпендикулярной его плоскости.
К задаче 4
Решение:
— момент инерции диска,
— вырезанная часть.
— масса вырезанной части. Массу вырезанной части найдем как
,
— поверхностная плотность диска.
Если — площадь диска, а
— площадь вырезанной части, то
Тогда момент инерции вырезанной части
И момент инерции фигуры
Ответ: кг
м
.
Вычисление момента инерции для тел симметричной формы
Нахождение момента инерции – вычислительная задача. Найдем моменты инерции для простейших геометрически правильных форм твердого тела, масса которого равномерно распределена по объему.
Момент инерции обруча относительно оси перпендикулярно его плоскости и проходящей через его центр.
Обруч будем считать бесконечно тонким, т. е. толщиной обода можно пренебречь по сравнению с радиусом R. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R2 можно вынести из-под знака интеграла:
где 
Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр.
Диск будем считать бесконечно тонким, т. е. его толщина много меньше радиуса R. Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие кольца радиусом г и шириной dr.
Площадь выделенного кольца равна произведению его длины окружности на ширину кольца: 2πrdr. Поскольку масса m диска распределена равномерно, то масса единицы площади диска равна m/(πR2).
Масса кольца:
dm = 2πrdr(m/πR2) = (2m/πR2)rdr.
Момент инерции кольца:
dI = drm2 = (2m/πR2)r3dr.
Просуммируем моменты инерций всех таких колец:

Момент инерции шара относительно его диаметра.
Объем диска dVz равен его площади, умноженной на толщину:
dVz = πr2dz. Массу выделенного диска dm находим, разделив массу шара т на его объем 4πR3/3 и умножив на объем диска:

Момент инерции диска в данном случае:

Момент инерции шара находится интегрирование по всем таким дискам:

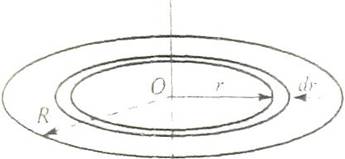
Момент инерции тонкого стержня относительно оси вращения, проходящей через его середину перпендикулярно стержню.
Пусть стержень имеет длину l. Направим ось х вдоль стержня. Начало координат пусть находится на середине стержня. Возьмем элемент стержня длиной dx, находящийся на расстоянии х от оси вращения. Его масса равна dm = (m/l)dx, а момент инерции стержня – dI = dmx2 = (m/l)x2dx
Отсюда находим момент инерции стержня:
Маятник Максвелла
Для определения момента инерции тел с вращательной симметрией используется маятник Максвелла. В нем исследуемое тело совершает сложное плоско-параллельное движение. Небольшой диск (маховичок), насаженный туго на ось, опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось маховичка. Нити во время движения разматываются до полной длины, раскрутившийся маховичок продолжает вращательное движение в том же направлении и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом вращение. Дойдя до верхней точки, диск опять опускается вниз и т. д. Маховичок будет совершать колебания вверх и вниз, поэтому устройство называют маятником.
Движение маятника Максвелла можно рассматривать как сложное, состоящее из поступательного движения вниз и вращательного вокруг своей оси симметрии. Поступательное движение описывается соответствующим уравнением динамики, которое мы запишем в проекциях на вертикальную ось, совпадающей по направлению с вектором g, где g – ускорение свободного падения:
mа = mg — 2Т.
Уравнение динамики для вращательной составляющей этого движения имеет следующий вид в проекциях на горизонтальную ось, совпадающей по направлению с вектором М:
Iε = M,
где m – масса маятника, 2T – суммарное натяжение нитей подвеса, I – момент инерции маятника относительно горизонтальной оси, ε – угловое ускорение, М – момент натяжения нитей, равный 2TR, где R – радиус оси подвеса маятника.
Взаимосвязь между поступательным и вращательным движениями:
а =εR,
а=2h/t2,
где h – путь, проходимый маятником от верхней точки до нижней, t – время движения маятника при прохождении пути h.
Из написанных выше уравнений получаем следующее:
I = mR2*(gt2/2h – 1) = md2/4*(gt2/2h – 1)
Эта формула выражает момент инерции маятника Максвелла, который состоит из оси, диска и кольца.
Таким образом, момент инерции маятника Максвелла можно записать в виде:
I = Iо + Iд + Iк,
где I – момент инерции маятника Максвелла, Iо – момент инерции оси подвеса, Iд – момент инерции диска, Iк – момент инерции накладного кольца.
Аналогично можно записать и массу маятника Максвелла:
m = mо + mд + mк,
где m – масса маятника Максвелла, mо – масса оси подвеса, mд – масса диска, mк – масса съемного кольца.
Выразим момент инерции кольца:
Iк = I — Iо — Iд.
Для исключения неизвестных величин проведем эксперимент с кольцами разной массы. Запишем для каждого кольца выражение
Iк1 = I1 — Iо — Iд,
Iк2 = I2 — Iо — Iд
Так как внешние и внутренние радиусы колец одинаковы, то:
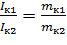
Решив систему уравнений, получим:


Для третьего кольца момент инерции будет равен:
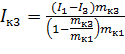
Таблица 1Формулы расчета момента инерции
где 

Экспериментальная часть
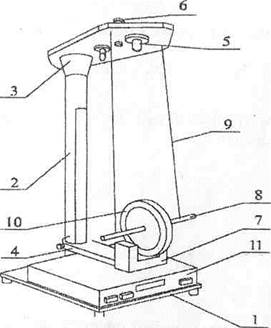
Для определения момента инерции тел вращения будем использовать специальную установку – маятник Максвелла.
1 – основание, 2 – стойка, 3 – неподвижный верхний кронштейн, 4 – подвижный кронштейн, 5 – электромагнит, 6 – вороток с фиксатором, 7 – фотодатчик, 8 – ось с закрепленным на ней диском, 9 – бифилярный подвес, 10 – сменное металлическое кольцо, 11 – миллисекундомер.
Упражнение 1. Определение момента инерции маятника Максвелла.
1. Включаем в сеть шнур питания миллисекундомера и нажимаем на кнопку «сеть», расположенную на лицевой панели секундомера. При этом загораются лампочки фотодатчика и цифровые индикаторы миллисекундомера.
2. Устанавливаем на диске маятника кольцо с массой mк1.
3. По шкале на стойке 2 определяем ход маятника h от верхней точки до нижней.
h = 23,2 см = 0,232 м
4. Вращая маятник, зафиксируем его в верхнем положении при помощи электромагнита, следя за тем, чтобы нить наматывалась на ось виток к витку. Нажимаем на кнопку «сброс» и убеждаемся, что индикатор секундомера обнулился.
5. Плавно нажимаем кнопку «пуск» на милисекундомере и измеряем время хода маятника t. Измерения повторяем 10 раз. Находим среднее значение хода маятника tср.
6. Проделываем пп. 2-5 с кольцами массой mк2 и mк3.
7. Измеряем штангенциркулем радиус оси Ro, радиус диска Rд, внешний Rвнеш и внутренний Rвн радиусы трех колец с разной массой. Измеряем длину оси λ, толщину диска bд и толщину накладных колец bк. Масса диска с осью равна 120г. Измерения выполнены с учетом поправки на 9,9 мм.
8. Результаты всех измерений оформляем в виде таблицы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. По формулам рассчитаем экспериментальные значение момента инерции маятника Максвелла с первым, вторым и третьим кольцом.
I = mR2*(gt2/2h – 1)
| N | I1, кг*м2 | I2, кг*м2 | I3, кг*м2 |
| 0,038 | 0,062 | 0,079 | |
| 0,04 | 0,062 | 0,096 | |
| 0,041 | 0,065 | 0,078 | |
| 0,039 | 0,066 | 0,078 | |
| 0,044 | 0,074 | 0,083 | |
| 0,039 | 0,063 | 0,077 | |
| 0,039 | 0,062 | 0,079 | |
| 0,039 | 0,065 | 0,074 | |
| 0,041 | 0,062 | 0,08 | |
| 0,043 | 0,065 | 0,076 | |
| ∑ | 0,403 | 0,427 | 0,8 |
| <I> | 0,04 | 0,043 | 0,08 |
10. Вычислим доверительный интервал в определении момента инерции маятника и относительную ошибку согласно теории погрешности для всех трех случаев.
| № | 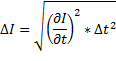
|
|
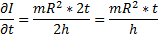
|
||

|
||

|

|
|

|

|
|

|

|
|

|

|
11. Запишем конечные результаты для моментов инерции маятника Максвелла с первым, вторым и третьим кольцом с учетом доверительного интервала и относительной погрешности.
| I = <I> ± ΔI | |
| mк1 | I1= (0,04 ± 0,00024) кг*м2 |
| mк2 | I2= (0,043 ± 0,00035) кг*м2 |
| mк3 | I3= (0,08 ± 0,0005) кг*м2 |
12. По формулам рассчитаем теоретические значения момента инерции маятника Максвелла с первым, вторым и третьим кольцом.
 , кг*м2 , кг*м2
|
0,0009 | ||
 , кг*м2 , кг*м2
|
0,00001 | ||
 , кг*м2 , кг*м2
|
0,00076 | 0,0012 | 0,0016 |
13. Вычислим относительную ошибку измерения:
Е = ∆ х / хист. * 100%
Упражнение 2. Определение момента инерции накладных колец.
1. Включаем в сеть шнур питания миллисекундомера и нажимаем на кнопку «сеть», расположенную на лицевой панели секундомера. При этом загораются лампочки фотодатчика и цифровые индикаторы миллисекундомера.
2. Устанавливаем на диске маятника кольцо с массой mк1.
3. По шкале на стойке 2 определяем ход маятника h от верхней точки до нижней.
h = 23,2 см = 0,232 м
4. Вращая маятник, зафиксируем его в верхнем положении при помощи электромагнита, следя за тем, чтобы нить наматывалась на ось виток к витку. Нажимаем на кнопку «сброс» и убеждаемся, что индикатор секундомера обнулился.
5. Плавно нажимаем кнопку «пуск» на милисекундомере и измеряем время хода маятника t. Измерения повторяем 10 раз. Находим среднее значение хода маятника tср.
6. Проделываем пп. 2-5 с кольцами массой mк2 и mк3.
7. Измеряем штангенциркулем радиус оси Ro, радиус диска Rд, внешний Rвнеш и внутренний Rвн радиусы трех колец с разной массой. Измерения выполнены с учетом поправки на 9,9 мм.
8. Результаты всех измерений оформляем в виде таблицы.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
9. По формулам рассчитаем экспериментальные значения момента инерции маятника Максвелла с первым, вторым и третьим кольцом.


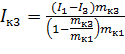
| I, кг*м2 | 0,00076 | 0,0012 | 0,0016 |
| Iк, кг*м2 | 0,00088 | 0,00132 | 0,00168 |
10. Вычислим доверительный интервал в определении момента инерции маятника и относительную ошибку согласно теории погрешности для всех трех случаев.
11. Запишем конечные результаты для моментов инерции маятника Максвелла с первым, вторым и третьим кольцом с учетом доверительного интервала и относительной погрешности.
12. По формуле рассчитаем теоретические значения момента инерции первого, второго и третьего кольца:
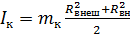
 , кг*м2 , кг*м2
|
0,000428 | 0,000642 | 0,00086 |
13. Вычислим относительную ошибку измерения:
Е = ∆ х / хист. * 100%
Вывод:
©2015- 2023 pdnr.ru Все права принадлежат авторам размещенных материалов.
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.