Расчет моментов
инерции онлайн
При выполнении расчетов часто приходится вычислять моменты инерции сложных сечений относительно различных осей, лежащих в плоскости фигуры. Для стандартных поперечных сечений стержней моменты инерции даны в таблицах ГОСТ 8509-93, ГОСТ 8510-86, ГОСТ 57837-2017, ГОСТ 8240-97. В остальных случаях, для выполнения онлайн расчета момента инерции круга, кольца, треугольника, прямоугольного контура, нестандартных сварных швеллера, уголка и двутавра можно воспользоваться данной страницей нашего сайта.
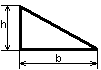
Момент инерции треугольника
Высота H, мм
Ширина B, мм
www.caetec.ru
©Copyright Кайтек 2020
- Момент инерции треугольника относительно центральной оси, параллельной одной из его сторон вычисляется по формуле:
Ix0 = B×H 3 / 36; - Момент инерции треугольника относительно оси, совпадающей с одной из его сторон:
Ix1 = B×H 3 / 12; - Момент инерции треугольника относительно оси, параллельной одной из его сторон и проходящей через противоположную вершину:
Ix2 = B×H 3 / 4.
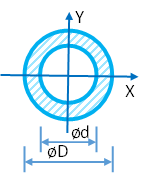
Момент инерции кольца
Диаметр D, мм
Диаметр d, мм
Полярный момент инерции Ip, м4
www.caetec.ru
©Copyright Кайтек 2020
- Момент инерции кольца относительно главной центральной оси:
Ix = π×D 4/64 — π×d 4/64; - Полярный момент инерции кольца:
Ip = π×D 4/32 — π×d 4/32.
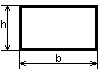
Момент инерции прямоугольника
Высота H, мм
Ширина B, мм
Высота H1, мм
Ширина B1, мм
www.caetec.ru
©Copyright Кайтек 2020
- Момент инерции прямоугольника относительно главных центральных осей:
- Ix = (B×H 3 — B1×H1 3)/12;
- Iy = (H×B 3 — H1×H1 3)/12.
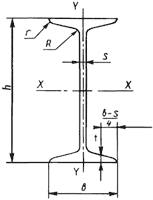
Момент инерции двутавра
Высота H, мм
Ширина B, мм
Толщина полки t, мм
Толщина стенки s, мм
www.caetec.ru
©Copyright Кайтек 2020
- Моменты инерции двутавра относительно главных центральных осей:
- Ix = (B×H 3 — (B — s)×(H — 2t) 3) / 12;
- Iy = (2t×B3 + (H — 2t)×s3) / 12.
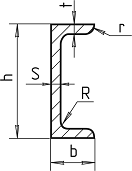
Момент инерции уголка
Высота H, мм
Ширина B, мм
Толщина d, мм
www.caetec.ru
©Copyright Кайтек 2020
- Моменты инерции уголка относительно центральных осей:
- Ix = (d×(H — y)3 + B×y3 — (B — d)×(y — d)3) / 3;
- Iy = (d×(B — x)3 + H×x3 — (H — d)×(x — d)3) / 3
- где x и y — расстояния от наружных сторон уголка до центральных осей Y и X соответственно.
Момент инерции швеллера
Высота H, мм
Ширина B, мм
Толщина полки t, мм
Толщина стенки s, мм
www.caetec.ru
©Copyright Кайтек 2020
- Моменты инерции швеллера относительно главных центральных осей:
- Ix = (B×H 3 — (B — s)×(H-2t)3) / 12;
- Iy = (H×x 3 — (H — 2t)×(x — s)3 + t×(B — x) 3)/3,
- где x — расстояния от наружной сторон швеллера до центральной оси Y.
Расчеты моментов инерции по умолчанию выполнены относительно центральных и главных центральных осей сечения. Моменты инерции относительно осей, параллельных главным центральным осям можно вычислить, прибавив к полученному результату произведение квадрата расстояния между соответствующими осями на площадь сечения.
©ООО»Кайтек», 2020. Любое использование либо копирование материалов или подборки материалов сайта, может осуществляться лишь с разрешения автора (правообладателя) и только при наличии ссылки на сайт www.caetec.ru
Расчёт геометрических характеристик сложного поперечного сечения
|
Операции Двутавр
Швеллер
Равнополочный уголок
Неравнопол. уголок
Неравнопол. уголок
Полоса (прямоугольник)
Круг
Полукруг
Четверть круга
Равнобедр. треугольник
Прямоуг. треугольник
Прямоуг. треугольник
Имена осей
Состав сечения В данном расчёте не задано ни одного профиля. Для задания профилей перейдите в панель «Операции» и выберите необходимый профиль. |
Внешний диаметр D =
Внутренний диаметр d =
Ответ: $A = 126$, $J_x = 6350$, $J_{rho} = 12700$, $W_x = 577$, $W_{rho} = 1155$
А теперь поподробнее:
Площадь сечения
$$A = frac{pi cdot D^2}{4}-frac{pi cdot d^2}{4} = frac{pi cdot (22^2-18^2)}{4} = 126$$
Отношение диаметров
$$alpha = frac{ d }{ D } = frac{ 18 }{ 22 } = 0.818$$
Осевые моменты инерции кольцевого (трубчатого) сечения
$$J_x = J_y = frac{pi cdot D^4}{64}(1-alpha^4) = frac{pi cdot 22^4}{64}(1-0.818^4) = 6350$$
Осевые моменты сопротивления
$$W_x = W_y = frac{pi cdot D^3}{32}(1-alpha^4) = frac{pi cdot 22^3}{32}(1-0.818^4) = 577$$
Полярный момент инерции
$$J_{rho} = frac{pi cdot d^4}{32}(1-alpha^4) = frac{pi cdot 22^4}{32}(1-0.818^4) = 12700$$
Полярный момент сопротивления
$$W_{rho} = frac{pi cdot d^3}{16}(1-alpha^4) = frac{pi cdot 22^3}{16}(1-0.818^4) = 1155$$
Размеры
h: мм
b: мм
Точка за которую перемещаем
Размеры
h: мм
b: мм
Угол
α:
Точка за которую перемещаем
Размеры
R: мм
Точка за которую перемещаем
Размеры
R: мм
Угол
α:
Точка за которую перемещаем
Двутавр
Угол
α:
Точка за которую перемещаем
Швеллер
Угол
α:
Точка за которую перемещаем
перейти к содержанию
Калькулятор свободного момента инерции и центроида
Рассчитать момент инерции, центроида, и модуль сечения для самых разных форм
Подробное руководство по нашему калькулятору момента инерции
SkyCiv Moment of Inertia и Centroid Calculator поможет вам определить момент инерции, центр тяжести, и другие важные геометрические свойства для различных форм, включая прямоугольники., круги, полые секции, треугольники, двутавровые балки, Т-образные балки, углы и каналы. У нас также есть несколько статей ниже о том, как рассчитать момент инерции., а также дополнительную информацию о центроидах и модуле сечения.
Вы можете решить до трех разделов, прежде чем вам потребуется зарегистрировать бесплатный аккаунт — что также дает вам доступ к большему количеству программного обеспечения и результатов. В нашем платном аккаунте будут показаны полные ручные расчеты того, как инструмент пришел к такому результату.. Обратитесь к калькулятору ниже для получения дополнительной информации по этой теме., а также ссылки на другие полезные инструменты и функции, которые SkyCiv может вам предложить.
Как использовать калькулятор момента инерции SkyCiv
Посмотрите демо-видео ниже, чтобы начать работу с нашим калькулятором..
Просто выберите форму поперечного сечения, которую вы хотите оценить, из раскрывающегося списка., введите размеры выбранного сечения и нажмите Рассчитать.
Этот бесплатный многоцелевой калькулятор взят из нашего полного программного обеспечения для анализа конструкций. Это позволяет вам:
- Рассчитать момент инерции (я) сечения луча (Второй момент области)
- Centroid Calculator используется для расчета Centroid (С) в осях X и Y балки
- Рассчитайте Первый момент площади (Статический момент инерции) (Q) сечения луча (Первый момент области)
- Калькулятор модуля сечения для расчета модуля сечения (С УЧАСТИЕМ) сечения луча
- Рассчитать постоянную кручения (J) сечения луча
Общие определения свойств раздела
Калькулятор момента инерции точно рассчитает ряд важных свойств сечения, используемых в проектировании конструкций.. Вот краткий список терминов и определений свойства раздела:
- Площадь раздела (А) — Площадь сечения — это довольно простой расчет, но непосредственно используется в расчетах осевого напряжения (чем больше площадь поперечного сечения, чем больше осевая сила)
- Момент инерции (Из, Iy)– также известный как второй момент площади, это расчет, используемый для определения прочности элемента и его сопротивления прогибу.. Чем выше это число, чем сильнее секция. Здесь две оси:
- Z-ось (Из)– Это относительно оси Z и обычно считается главной осью, поскольку обычно это самое сильное направление элемента.
- И-Ось (Iy)—Это касается оси Y и считается малой или слабой осью.. Это связано с тем, что секции не рассчитаны на то, чтобы воспринимать такую большую силу вокруг этой оси.
- Также стоит отметить, что если форма имеет одинаковые размеры в обоих направлениях (квадрат, круговой и т. д.) эти значения будут одинаковыми в обоих направлениях. См. Момент инерции круга, чтобы узнать больше..
- центроида (Чехия, Сай)– это центр масс сечения и обычно имеет компоненты Z и Y.. Для симметричных форм, это будет геометрический центр. Для несимметричных форм (например, угол, канал) они будут в разных местах. Узнайте, как рассчитать центр тяжести сечения балки. Приведенный выше калькулятор также действует как центроидный калькулятор., вычисление центроида X и Y любого типа формы.
- Статический момент инерции (Qz, Qy)– Также известен как «Первый момент площади»., это измеряет распределение площади сечения балки от оси. Как момент инерции, они расположены как в направлении Z, так и в направлении Y. Обычно они используются при расчетах напряжения сдвига., Таким образом, чем больше это значение, тем сильнее секция против сдвига.. Калькулятор предоставит это значение, но нажмите здесь, чтобы узнать больше о вычислении первого момента площади.
- Модуль упругого сечения (Sz, Си в Америке. Зз, Zy в Британии или Австралии)– Также известен как модуль статического сечения., и используются при расчете напряжения изгиба. Обычно они рассчитываются на верхнее и нижнее сечение волокон.. Например, Szt — модуль сечения относительно оси Z до верхнего волокна сечения..
- Постоянная кручения (J) — также известный как полярный момент инерции или J, это значение, которое описывает сопротивление материала деформации скручивания или кручения.
- Модуль пластического сечения (S) — измерение способности формы поперечного сечения сопротивляться пластическому изгибу, используется для оценки напряжения материала, когда он начинает текучесть (достичь своего пластического предела) под определенной нагрузкой и обычно используется для проектирования и анализа балок под нагрузкой.
Другие параметры — это более продвинутые результаты, рассчитанные с помощью полного конструктора разделов SkyCiv.:
- Продукт инерции (о оси Z и Y): Мера сопротивления формы вращению вокруг определенной оси., равно перекрестному произведению расстояния от оси до любой точки формы и соответствующей составляющей момента инерции точки.
- Модуль упругости пластического сечения (о оси Z и Y): Мера способности формы поперечного сечения сопротивляться пластическому изгибу., используется для оценки напряжения материала, когда он начинает текучесть (достичь своего пластического предела) под определенную нагрузку.
- Пластиковая нейтральная ось (о оси Z и Y): Ось в форме поперечного сечения, через которую должны пройти все силы, действующие на форму, чтобы вызвать пластическую деформацию..
- Площадь сдвига (о оси Z и Y): Площадь формы поперечного сечения, которая эффективна при сопротивлении поперечным силам.
- Расстояние от центра сдвига до центроида (как по оси Z, так и по оси Y): Калькулятор центроида SkyCiv помогает рассчитать расстояние между центром сдвига и центроидом формы поперечного сечения..
- Постоянная кручения (Использование FEA): Значение, описывающее сопротивление материала деформации скручивания или кручения., рассчитано с использованием анализа конечных элементов.
- Радиус кручения: Расстояние от оси, на котором должна быть сосредоточена площадь формы поперечного сечения, чтобы получить ту же постоянную кручения, что и фактическая форма..
- Константа деформации: Значение, описывающее сопротивление материала короблению или искривлению..
- Константа моносимметрии (о оси Z и Y): Мера того, насколько симметрична форма поперечного сечения относительно определенной оси., со значением нуля, указывающим на идеальную симметрию.
- Радиус вращения (о оси Z и Y): Расстояние от оси, на котором должна быть сосредоточена площадь формы поперечного сечения, чтобы получить тот же момент инерции, что и у фактической формы..
- Угол поворота главной оси: Угол между нейтральной осью и главной осью формы поперечного сечения.
О моменте инерции, Центроиды и другие свойства сечения
Мы также собрали дополнительную информацию для расчета момента инерции секций.. Это полное руководство должно помочь предоставить исчерпывающую базу знаний по всем вопросам, связанным с моментом инерции., центроиды, модуль сечения и другие важные свойства геометрического сечения. В следующих сегментах, включаем что такое момент инерции, как рассчитать центр тяжести, момент инерции и общие уравнения MOI с помощью SkyCiv Moment of Inertia and Centroid Calculator.
Что такое момент инерции?
Момент инерции (более технически известный как момент инерции площади, или второй момент площади) является важным геометрическим свойством, используемым в проектировании конструкций.. Это напрямую связано с количеством прочности материала, которое имеет ваша секция..
Вообще говоря, чем больше момент инерции, тем больше силы у вашей секции, и, следовательно, тем меньше он будет прогибаться под нагрузкой. Момент инерции прямоугольника, или любая форма в этом отношении, технически это измерение того, какой крутящий момент требуется для ускорения массы вокруг оси — отсюда и слово инерция в его названии.
Как найти момент инерции — прямоугольный
Вычислить момент инерции прямоугольника, вы можете использовать формулу:
я = (б * ч ^ 3) / 12
I — момент инерции прямоугольника
b — ширина прямоугольника
h — высота прямоугольника
Важно отметить, что единицы измерения для b и h должны быть одинаковыми. (например, дюймов, миллиметры, и т.п.). Также единица конечного результата зависит от единицы ввода, например, если ввод в метре, тогда единицей результата будет м ^ 4.
Пример расчета момента инерции
Допустим, у нас есть прямоугольник со следующими размерами:
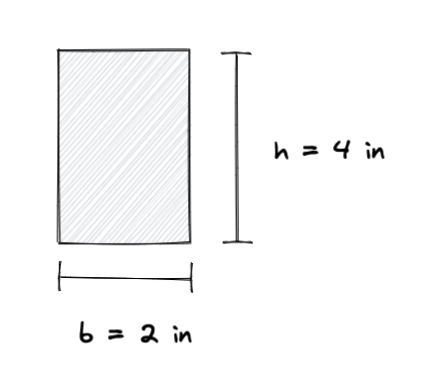
Используя формулу момента инерции, мы можем вычислить момент инерции прямоугольника следующим образом:
я = (б * ч ^ 3) / 12
я = (2 * 4^3) / 12
я = (2 * 64) / 12
знак равно 10.67 в^4
Значит, момент инерции прямоугольника равен 10.67 дюйм^4. Этот момент инерции относится к центральной оси, помните, что если вам нужно найти момент инерции относительно другой оси, вам нужно будет использовать другую формулу или выполнить преобразование. Вы также можете проверить, что единица всегда является произведением мощности входной единицы., в этом случае все единицы ввода — дюймы, так что результат в дюймах ^ 4.
Мы можем проверить этот результат с помощью приведенного выше калькулятора свободного момента инерции., который показывает тот же результат 10.6667 в^4:
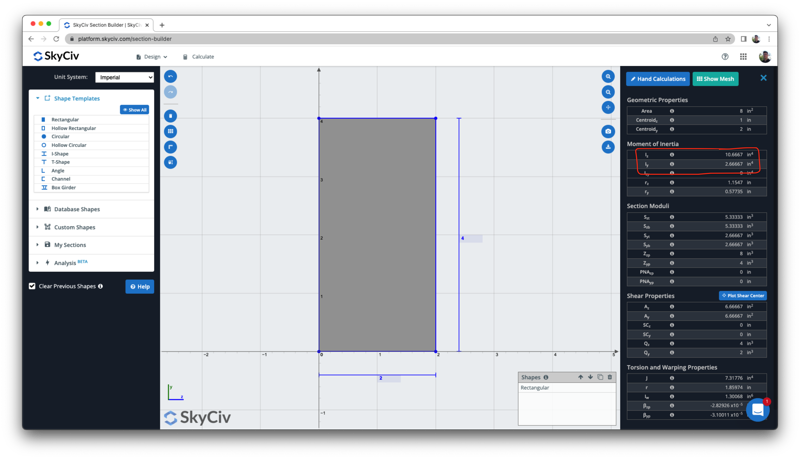
Как найти момент инерции — Я луч
Теперь давайте рассмотрим более сложный случай, когда поперечное сечение представляет собой двутавровую балку., с разными размерами фланца. Концепция такая же, однако подход в этом случае совсем другой. По сути, нам нужно смотреть на двутавровую балку как на комбинацию разных прямоугольников и суммировать разные части, чтобы получить сечения с полным моментом инерции.. Коротко, нам нужно выполнить эти три шага:
- Рассчитать нейтральную ось для всего сечения
- Рассчитать МВД каждой части
- Рассчитайте момент инерции, используя теорему о параллельных осях. — который по существу является суммой отдельных моментов инерции
Итак, давайте рассмотрим следующий раздел:
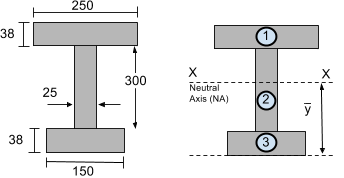
Нейтральная ось (Не Доступно) находится в центре тяжести. По сути, это средневзвешенное значение площади и расстояния от дна для каждого сегмента.. Нам просто нужно использовать уравнение центроида для расчета вертикальной (и) центроид многосегментной формы.

Мы возьмем базовую или опорную линию от нижней части сечения балки.. Теперь давайте найдем Ai и yi для каждого сегмента сечения двутавровой балки, показанного выше, чтобы можно было найти вертикаль или центр тяжести y..


Теперь у нас есть центроид. Мы можем продолжить вычисление момента инерции. Для расчета общего момента инерции сечения нам нужно использовать «Теорема о параллельной оси» как определено ниже:

Так как мы разделили его на три прямоугольные части, мы должны рассчитать момент инерции каждого из этих участков. Теперь мы можем использовать упрощенную прямоугольную формулу момента инерции:
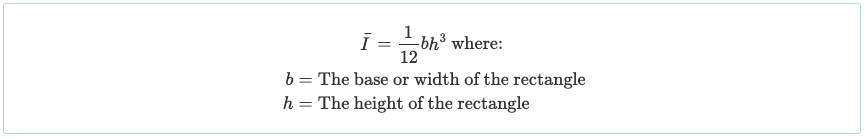
Теперь у нас есть вся информация, необходимая для использования «Теорема о параллельной оси» и найти общий момент инерции сечения двутавровой балки. В наш момент инерции пример:

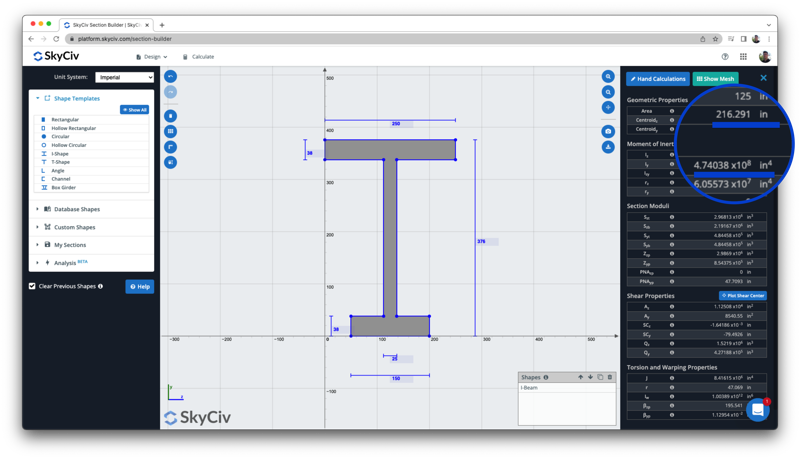
Снова, мы можем сравнить этот результат с результатом калькулятора свободного момента инерции, чтобы сравнить результаты как центроида, так и момента инерции., где оба центроида (216.29 в) и момент инерции (4.74 х 10^8 дюймов^4) совпадение:
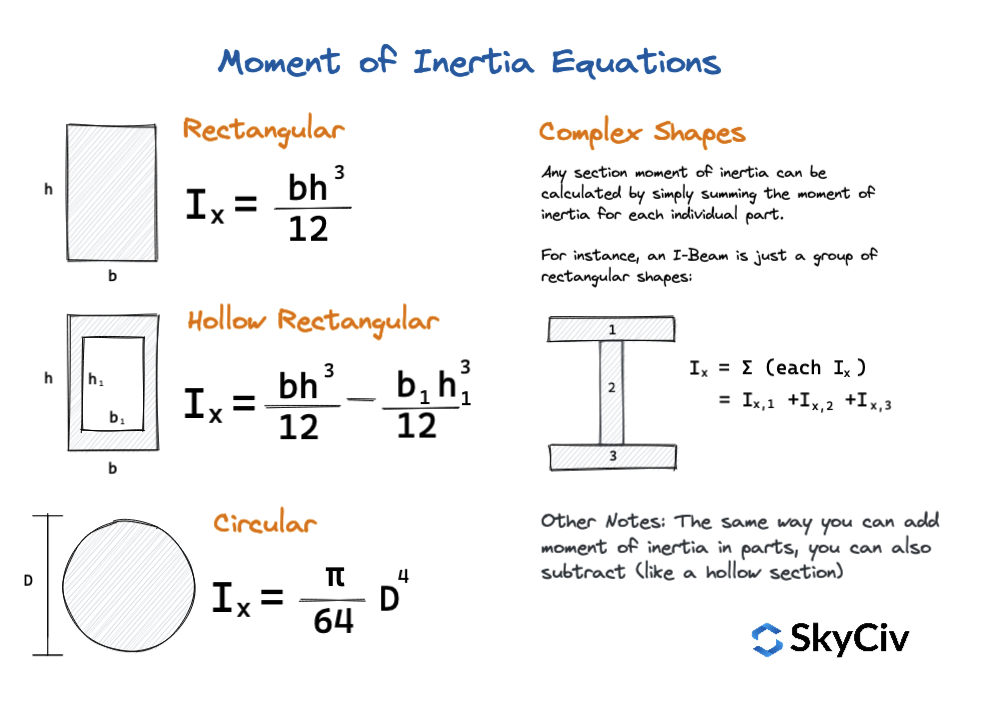
Уравнения момента инерции
Простые уравнения также можно использовать для расчета момента инерции обычных форм и сечений.. Это быстрые уравнения момента инерции, которые обеспечивают быстрые значения и являются отличным способом перекрестных ссылок или перепроверки ваших результатов.. Сосредоточьтесь только на простых формах, на диаграмме ниже показаны некоторые из этих уравнений:
Калькулятор центроида SkyCiv
Центроид, также известный как «геометрический центр», это центр масс объекта с равномерной плотностью. Упрощенная демонстрация центроида, будет местом, в которое вам нужно будет поместить карандаш, чтобы он балансировал на пальце.. Место, в котором карандаш сбалансирован и не падает с пальца, будет приблизительным положением центра тяжести карандаша.. Он учитывает массу и плотность материала, чтобы определить точку, в которой масса карандаша одинакова с обеих сторон вашего пальца., и, следовательно, представляет собой «центр масс» карандаша..
Калькулятор SkyCiv Centroid использует FEA для получения высокоточных результатов за считанные секунды., какой бы сложной ни была форма. В премиум версии, пользователи могут вводить координаты точек, которые определяют форму, и наш калькулятор даст вам координаты центроида. Это включает в себя возможность создавать собственные формы с помощью импорта DXF., несколько (построен) формы и пользовательские формы точек.
Помимо скорости и точности, наш калькулятор центроидов также невероятно прост в использовании. С простым пользовательским интерфейсом, вы можете ввести размеры вашего раздела и получить значения свойств вашего раздела (включая центр тяжести сечения балки) в течение нескольких секунд. Работаете ли вы над дизайн-проектом, экспериментировать с разными разделами или готовиться к экзамену, SkyCiv Centroid Calculator — идеальный инструмент, который поможет вам выполнить работу.
Калькулятор модуля сечения
Как отмечалось ранее, этот бесплатный инструмент также предоставляет вам расчет модуля упругости сечения, однако, если вы начинаете работать инженером, вы можете не понимать, что такое модуль сечения.. Проще говоря, модуль сечения — это свойство сечения поперечного сечения, которое измеряет сопротивление изгибу и рассчитывается как отношение момента инерции к расстоянию от нейтральной оси до наиболее удаленного волокна.. Модуль упругого сечения представлен в этом уравнении просто как:
куда,
- S — модуль сечения
- I — момент инерции сечения относительно нейтральной оси
- y — расстояние от нейтральной оси до самой дальней точки сечения
Существует два вида модуля сечения: Эластичный и пластичный. В Америке, S обычно используется для обозначения модуля упругого сечения, а Z используется для обозначения модуля пластического сечения.. В Великобритании и Австралии, они обычно обратные. Модуль упругого сечения обычно обозначается буквой Z., в то время как модуль пластического сечения обозначается буквой S.
В общем, Модуль упругости сечения используется для расчета сечения, поскольку он применим до предела текучести для большинства металлов.. Металлы обычно не рассчитаны на превышение предела текучести материала..
Дополнительная документация
Доступно больше бесплатных инструментов
SkyCiv также предлагает другие инструменты, такие как инструмент для измерения размера луча и бесплатное программное обеспечение для проектирования конструкций.. Ящик динамического сечения также покажет вам графическое представление вашего сечения луча.. Итак, если вы хотите рассчитать момент инерции круга, момент инерции прямоугольника или любых других форм, не стесняйтесь использовать приведенное ниже программное обеспечение или наш всеобъемлющий SkyCiv Section Builder.
SkyCiv предлагает широкий спектр программного обеспечения для анализа и проектирования облачных вычислений для инженеров. Как постоянно развивающаяся технологическая компания, мы стремимся к инновациям и стимулированию существующих рабочих процессов, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Инструмент для измерения размера луча
Калькулятор фермы
Frame Calculator
Луч калькулятор
Нужно больше функциональности?
Ручные расчеты
SkyCiv показывает, как рассчитать момент инерции, показывая пошаговые уравнения и моменты инерции.. Они также показывают расчеты центроида и площади..
Пользовательские и встроенные разделы
SkyCiv Section Builder использует FEA для расчета ключевых свойств раздела, позволяет моделировать все, что вам нужно. Просто обновите и получите доступ к мощному программному обеспечению.
Интегрировано с программным обеспечением для анализа
SkyCiv Section Builder полностью интегрирован со всем аналитическим программным обеспечением SkyCiv, включая SkyCiv Beam и SkyCiv Structural 3D. — так что вы можете проанализировать свой раздел под нагрузкой.
Инженер-профессионал?
Если вы инженер, вы можете получить больше пользы от использования нашего облачного программного обеспечения для 3D-анализа конструкций, помимо этого калькулятора. Это программное обеспечение включает в себя интегрированные модули дизайна, такие как AISC, ACI, ТАК КАК, Еврокод и CSA.
Программное обеспечение
SkyCiv Software
- SkyCiv Beam
- SkyCiv Структурная 3D
- SkyCiv Раздел Строитель
- SkyCiv Beam Shell FEA
- SkyCiv Connection Design
- SkyCiv RC Design
- SkyCiv Wind Load Design
- Конструкция опорной плиты SkyCiv
- SkyCiv Mobile
- SkyCiv API
промышленности
- Строительная инженерия
- Инженерное дело
- Морская инженерия
- Морская нефть & газ
- Фальсификация событий
- подмости
- Жилой
- Стальная конструкция
- Конкретный дизайн
- Древесина Дизайн
- Холоднокатаная сталь
- Дизайн сарая
Бесплатные инструменты
- Луч калькулятор
- Калькулятор фермы
- Frame Calculator
- Вал Калькулятор
- Калькулятор МВД
- Калькулятор ветровой нагрузки
- Фонд Калькулятор
- Калькулятор опорной плиты
- Калькулятор подпорной стены
- Калькулятор конструкции соединения
Около
Около
- Насчет нас
- Связаться с нами
- Наша команда
- Карьера
- ВОПРОСЫ-ОТВЕТЫ
- Документация
Подпишитесь на нашу рассылку
Получайте обновления о новых продуктах, технические руководства, и отраслевые идеи