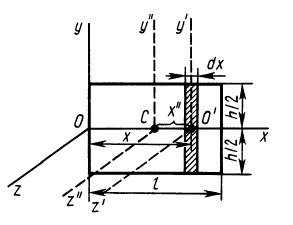
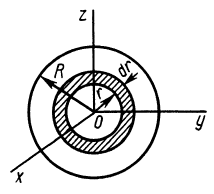
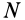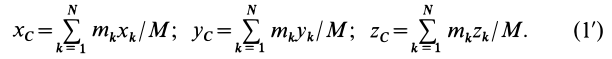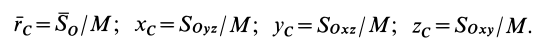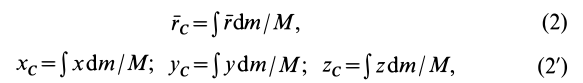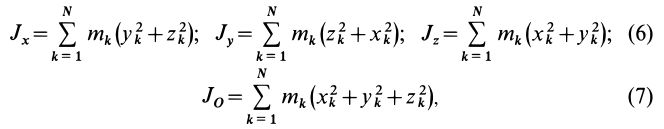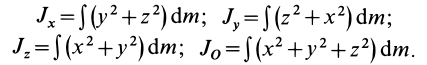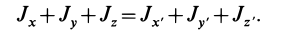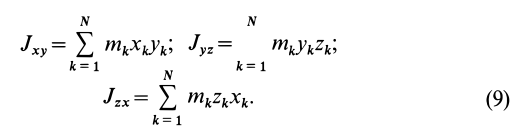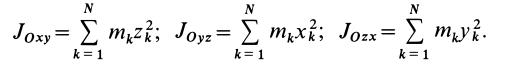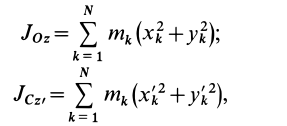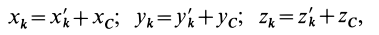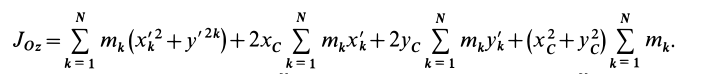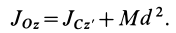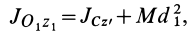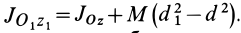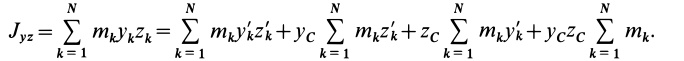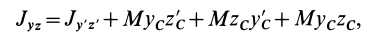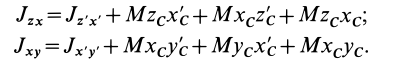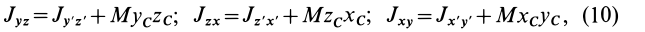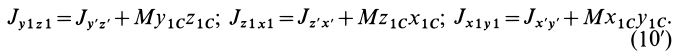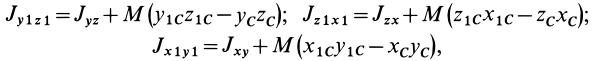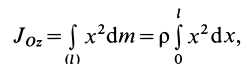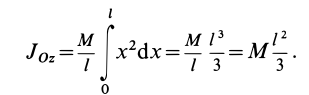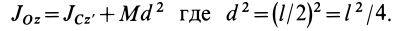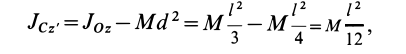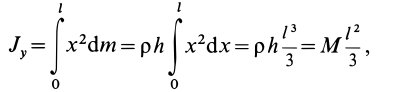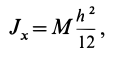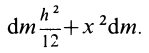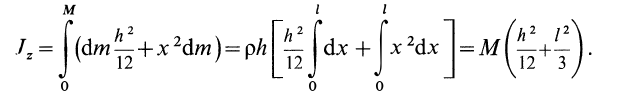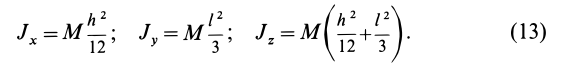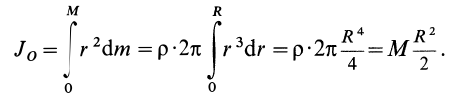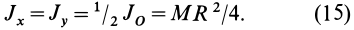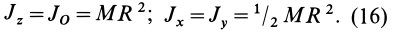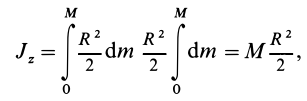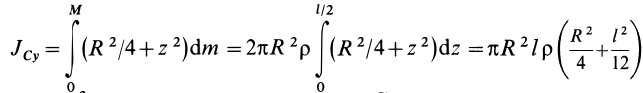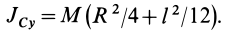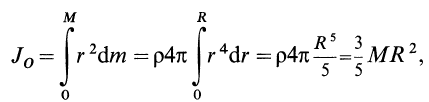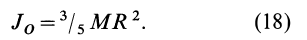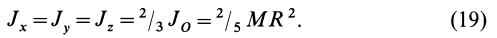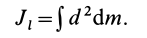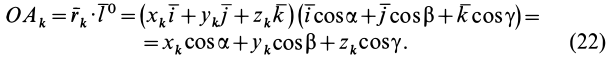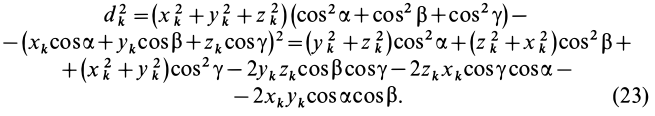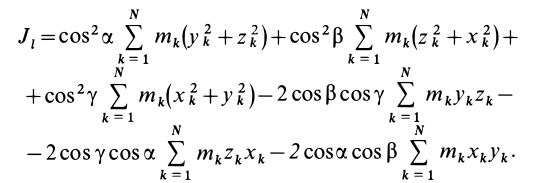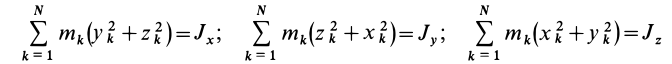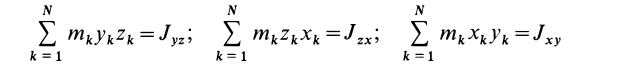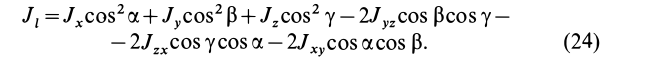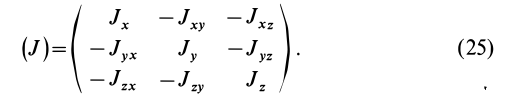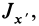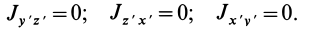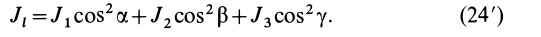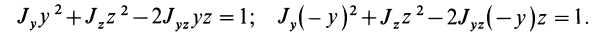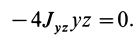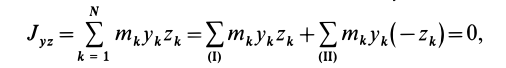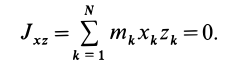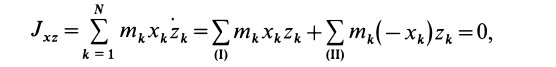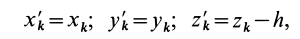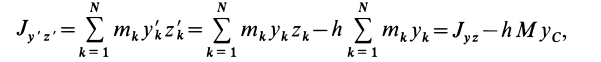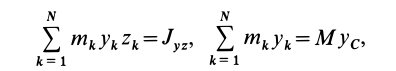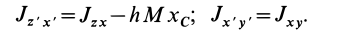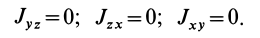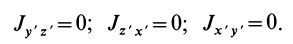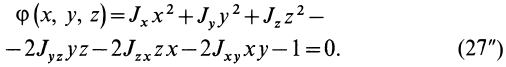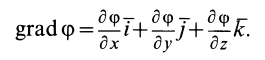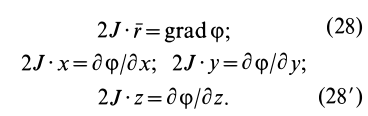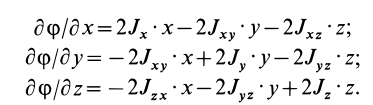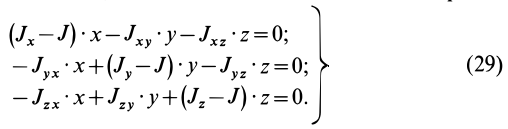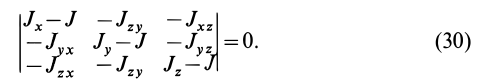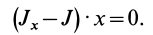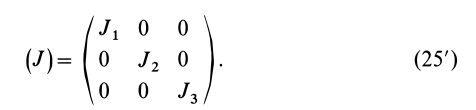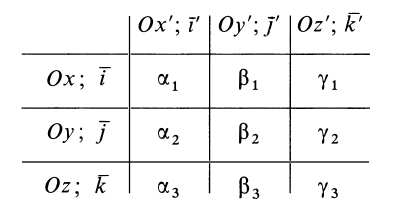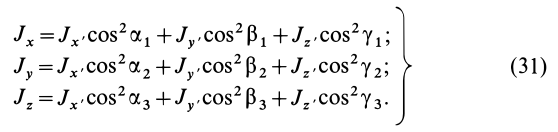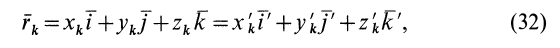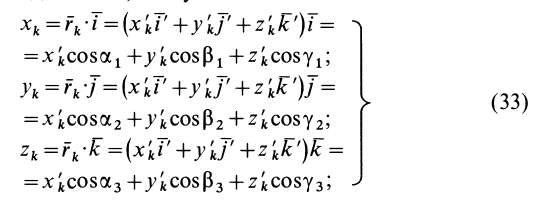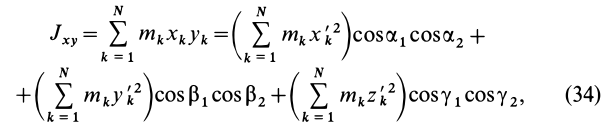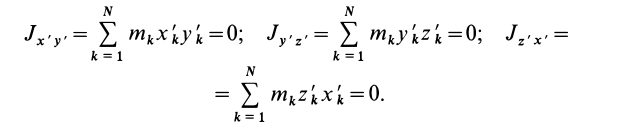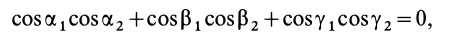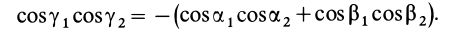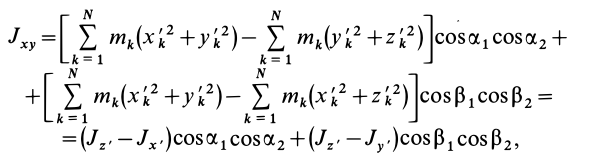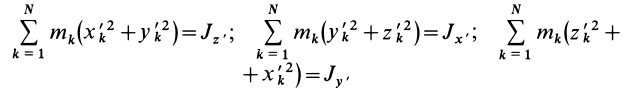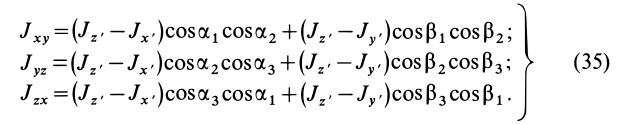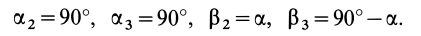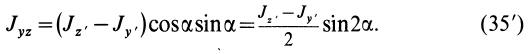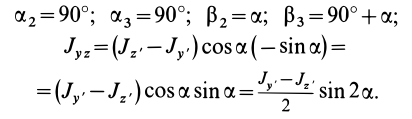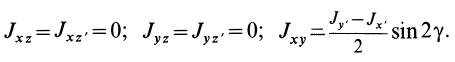Момент инерции
сложной фигуры равен сумме моментов
инерции ее составных частей:
.
(9.11)
Это непосредственно
следует из свойств определенного
интеграла
,
где
A=A1+A2+A3+
. . . .
Таким
образом, для вычисления момента инерции
сложной фигуры надо разбить ее
на ряд простых
фигур, вычислить моменты инерции
этих фигур и затем просуммировать эти
моменты
инерции.
Указанная теорема
справедлива также и для центробежного
момента инерции.
Моменты инерции
прокатных сечений (двутавров, швеллеров,
уголков и т. д.) приводятся в таблицах
сортамента.
17. Изменение моментов инерции при повороте осей
сумма моментов
инерции относительно любых взаимно
перпендикулярных осей не меняется
при их повороте.
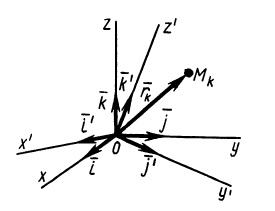
Формула
(9.18) может быть использована для вычисления
центробежного момента инерции относительно
осей х, у
по известным осевым моментам инерции
относительно осей х,
y
и x1,
y1.Для
вычисления момента инерции сложной
фигуры надо разбить ее
на ряд простых
фигур, вычислить моменты инерции
этих фигур и затем просуммировать эти
моменты инерции.
Сумма моментов
инерции относительно любых взаимно
перпендикулярных осей не меняется
при их повороте.
18 Главные оси инерции. Главные моменты инерции.
tg2α0
=2 Dxy
/ (Iy
–
Ix).
Эта
формула определяет положение двух осей,
относительно одной из которых осевой
момент инерции максимален, а относительно
другой — минимален,
Такие
оси называют главными. Моменты инерции
относительно главных осей называются
главными
моментами
инерции.
Ф
ормула
для определения главных моментов
инерции: для данного случая (Ix>Iy)
максимальный момент инерции Imax
имеет место относительно
главной оси, повернутой на
угол α0
по отношению к оси х, а минимальный
момент инерции — относительно другой,
перпендикулярной оси
Относительно
главных осей центробежный момент
инерции равен нулю.
Таким
образом, главными осями называют
оси, обладающие
следующими свойствами:
1. Центробежный
момент инерции относительно этих осей
равен нулю.
2. Моменты инерции
относительно главных осей имеют
экстремальные значении (относительно
одной—максимум, относительно другой
— минимум).
Главные оси,
проходящие через центр тяжести сечения,
называются главными центральными осями.
Во многих случаях
удается сразу определить положение
главных центральных осей. Если фигура
имеет ось симметрии, то она является
одной из главных центральных осей,
вторая проходит через центр тяжести
сечения перпендикулярно первой.
Сказанное следует из того обстоятельства,
что относительно оси симметрии и любой
оси ей перпендикулярной, центробежный
момент инерции равен нулю.
Если два главных
центральных момента инерции сечения
равны между собой, то у этого сечения
любая центральная ось является главной
и все главные центральные моменты
инерции одинаковы (круг, квадрат,
шестиугольник, равносторонний
треугольник).
19 Зависимость между центробежными моментами инерции относительно двух систем параллельных осей
Пусть
оси x0y0
—центральные
оси и момент инерции Dx0y0
известен. Найдем центробежный момент
инерции относительно осей х1
и у1.
Dx1y1=Dx0y0+Aab. Центробежный
момент инерции относительно системы
взаимно перпендикулярных осей,
параллельных центральным, равен
центробежному моменту инерции относительно
этих центральных осей плюс произведение
площади фигуры на координаты ее центра
тяжести относительно новых осей.
Если
оси x0
и y0
являются центральными главными
осями, то
относительно этих осей Dx0y0
=0
и формула (10.3а)
упрощается:
Dx1y1=Aab
.
Д
ля
сложной фигуры, состоящей из п
простых фигур,(
при
условии, что собственные центральные
оси каждой фигуры являются главными
осями).
Моменты
инерции относительно главных осей
называются
главными
моментами
инерции. Главные оси, проходящие через
центр тяжести сечения, называются
главными центральными осями. Центробежный
момент инерции относительно системы
взаимно перпендикулярных осей,
параллельных центральным, равен
центробежному моменту инерции относительно
этих центральных осей плюс произведение
площади фигуры на координаты ее центра
тяжести относительно новых осей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свойство любого объекта, который может вращаться.
Это скалярная величина, которая показывает, насколько трудно изменить скорость вращения объекта вокруг текущей оси вращения. Иными словами, во вращательном движении тело вращается вокруг фиксированной оси. Каждая частица в теле движется по кругу с линейной скоростью, то есть каждая частица движется с угловым ускорением.
Это свойство тела, благодаря чему оно сопротивляется угловому ускорению, которое представляет собой сумму произведений массы каждой частицы в теле на квадрат ее расстояния от оси вращения.
Обозначается момент инерции символом II (альтернативно обозначается JJ).
I=mr2I=mr^2,
где mm – масса тела, rr – расстояние от тела до оси вращения.
Момент инерции играет похожую роль в механике вращения с массой в обычной линейной механике. Действительно, момент инерции напрямую зависит от массы, а также от распределения этой массы относительно оси вращения.
Чем вращение массы тела происходит дальше от оси, тем труднее изменить скорость вращение этой системы.
Момент инерции в системе СИ измеряется в кг·м2 (килограмм умноженный на квадратный метр).
Связь момента инерции со вторым законом Ньютона
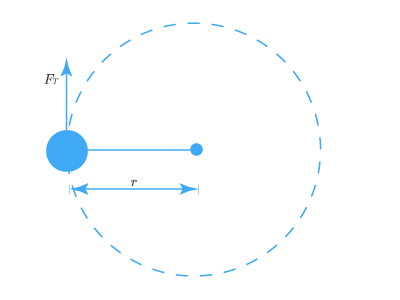
Момент инерции занимает место массы во «вращательной» версии второго закона Ньютона. Если рассмотреть массу mm, прикрепленную к одному концу стержня (для простоты объяснения массу стержня приравняем к 0). Другой конец стрежня прикреплен так, что вся система может вращаться вокруг центральной точки.
Далее система приводится во вращения, в результате действия тангенциальной силы FTFT на тело. Из второго закона Ньютона:
FT=maT или FT=m(rα)F_T = ma_T ~ или ~ F_T = m(rα)
В механике вращения крутящий момент τ=F⋅rτ = F·r занимает место силы. Умножив на rr последнее выражение, получим:
FTr=m(rα)rF_T r= m(rα) r, отсюда
τ=mr2ατ = mr^2α,
τ=Iατ = Iα
Это выражение можно использовать для определения поведения массы в ответ на действующий крутящий момент.
Момент инерции сложных фигур
Для более сложных фигур, чтобы найти момент инерции необходимо сделать несколько промежуточных вычислений. Для многих геометрических фигур существуют таблицы с уравнениями для моментов инерции. Более трудоемким будет вычисление момента инерции сложного тела, если представить его как сумму более простых тел.
Полученные моменты вращений каждого тела, объединяются в инерцию составного объекта.
Проблема, которая может возникнуть, состоит в том, что ось вращения для каждого тела будет отличаться и не будет совпадать с моментом инерции главного тела. Уравнение ниже позволяет связать момент инерции одного тела относительно момента инерции всего составного объекта:
I0=Ic+md2I_0 = I_c +md^2,
I0I_0 — момент инерции относительно точки OO (например, точка вокруг которой вращается составной главный объект), IcI_c — момент инерции относительно точки СС (например, точка вокруг которой вращается часть объекта), mm – масса части объекта, dd – расстояние между точками OO и CC.
Момент инерции важен почти во всех физических задачах, связанных с массой во вращательном движении. Он используется для расчета момента импульса и позволяет объяснить (посредством сохранения момента импульса), как изменяется вращательное движение при изменении распределения массы. А также при необходимости поиска энергии, которая хранится в виде вращательной кинетической энергии во вращающемся маховике.
Тест по теме «Момент инерции»
Содержание
- Что такое момент инерции?
- Пошаговая процедура определения момента инерции композитных или нестандартных форм
- Пример 1: дырокол для квадратных отверстий
- Решение
- Пример 2: C-образная форма
- Решение
- Пример 3 — Форма змеи
- Решение
- Пример 4: I-образная форма
- Решение
- Пример 5: Сложная фигура
- Решение
Что такое момент инерции?
Момент инерции, также называемый «угловой массой или вращательной инерцией», а «второй момент площади» — это инерция вращающегося тела по отношению к его вращению. Момент инерции, применяемый к областям, не имеет реального значения при рассмотрении сам по себе. Это просто математическое выражение, обычно обозначаемое символом я. Однако при использовании в таких приложениях, как изгибные напряжения в балках, это начинает иметь значение. Математическое определение момента инерции указывает, что площадь делится на маленькие части dA, и каждая площадь умножается на квадрат ее плеча момента вокруг оси отсчета.
I = ρ2 dA
Обозначение ρ (rho) соответствует координатам центра дифференциальной области dA.

Пошаговая процедура определения момента инерции композитных или нестандартных форм
1. Определите оси X и Y сложной фигуры. Если не указан, создайте свои оси, нарисовав оси X и Y на границах фигуры.
2. Определите и разделите сложную форму на основные формы, чтобы упростить вычисление момента инерции. При решении для момента инерции составной области разделите составную область на основные геометрические элементы (прямоугольник, круг, треугольник и т. Д.), Для которых известны моменты инерции. Вы можете показать разделение, нарисовав сплошные или пунктирные линии на неправильной форме. Обозначьте каждую основную форму, чтобы избежать путаницы и ошибок в расчетах. Пример показан ниже.
3. Найдите площадь и центр тяжести каждой базовой формы, создав табличную форму решения. Получите расстояния от осей центроида всей неправильной формы, прежде чем переходить к вычислению момента инерции. Всегда не забывайте вычитать области, соответствующие отверстиям. Обратитесь к статье ниже для расчета расстояний до центра тяжести.
- Расчет центроида сложных форм методом геометрической декомпозиции
4. После того, как вы получили положение центра тяжести по осям, переходите к вычислению момента инерции. Вычислите момент инерции каждой базовой формы и обратитесь к формуле для основных форм, приведенной ниже.
Ниже приведен момент инерции основных форм для его центральной оси. Чтобы успешно вычислить момент инерции сложной формы, вы должны запомнить основную формулу момента инерции основных геометрических элементов. Эти формулы применимы только в том случае, если центр тяжести основной формы совпадает с центром тяжести неправильной формы.
5. Если центр тяжести основной формы не совпадает, необходимо перенести момент инерции с этой оси на ось, где расположен центр тяжести составной формы, используя «Формулу переноса момента инерции».
Момент инерции относительно любой оси в плоскости области равен моменту инерции относительно параллельной центральной оси плюс коэффициент передачи, составленный из произведения площади основной формы на квадрат расстояние между осями. Формула передачи момента инерции приведена ниже.
6. Получите сумму моментов инерции всех основных форм, используя формулу передачи.

Пример 1: дырокол для квадратных отверстий
Решение
а. Найдите центр тяжести всей составной формы. Поскольку фигура симметрична в обоих направлениях, то ее центр тяжести находится в середине сложной фигуры.
Расположение центра тяжести сложной формы от осей x = 25 мм y = 25 мм
б. Найдите момент инерции сложной фигуры, вычтя момент инерции области 2 (A2) из области 1 (A1). Нет необходимости использовать формулу передачи момента инерции, поскольку центр тяжести всех основных форм совпадает с центром тяжести составной формы.
I = MOI A1 — MOI A2 I = bh ^ 3/12 — bh ^ 3/12 I = (50) (50) ^ 3/12 — (25) (25) ^ 3/12 I = 488281,25 мм ^ 4
Пример 2: C-образная форма
Решение
а. Найдите центр тяжести всей сложной формы, составив таблицу.
| Этикетка | Площадь (мм ^ 4) | х-стержень (мм) | Y-образный стержень (мм) | Топор | Ау |
|---|---|---|---|---|---|
|
A1 |
800 |
40 |
50 |
32000 |
40000 |
|
A2 |
800 |
40 |
10 |
32000 |
8000 |
|
A3 |
1200 |
10 |
30 |
12000 |
36000 |
|
ВСЕГО |
2800 |
76000 |
84000 |
Расположение центра тяжести составной формы от осей x = 76000/2800 x = 27,143 мм y = 84000/2800 y = 30 мм
б. Найдите момент инерции, используя формулу передачи. Слово «MOI» означает «момент инерции».
Ix = MOI A1 + MOI A2 + MOI A3 Ix = bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 Ix = (40) (20) ^ 3 / 12 + (800) (20) ^ 2 + (40) (20) ^ 3/12 + (800) (20) ^ 2 + (20) (60) ^ 3/12 Ix = 1053333,333 мм ^ 4
Iy = MOI A1 + MOI A2 + MOI A3 Iy = bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 + Ad ^ 2 Iy = (20) ( 40) ^ 3/12 + (800) (40 — 27,143) ^ 2 + (20) (40) ^ 3/12 + (800) (40 — 27,143) ^ 2 + (60) (20) ^ 3/12 + (1200) (27.143-10) ^ 2 Iy = 870476.1905 мм ^ 4
Пример 3 — Форма змеи
Решение
а. Найдите центр тяжести всей сложной формы, составив таблицу.
| Этикетка | Площадь | х-стержень (мм) | Y-образный стержень (мм) | Топор | Ау |
|---|---|---|---|---|---|
|
A1 |
300 |
15 |
5 |
4500 |
1500 |
|
A2 |
500 |
35 |
25 |
17500 |
12500 |
|
A3 |
300 |
55 |
45 |
16500 |
13500 |
|
ВСЕГО |
1100 |
38500 |
27500 |
Расположение центра тяжести сложной формы от осей x = 38500/1100 x = 35 мм y = 27500/1100 y = 25 мм
б. Найдите момент инерции, используя формулу передачи. Слово «MOI» означает «момент инерции».
Ix = MOI A1 + MOI A2 + MOI A3 Ix = bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 + bh ^ 3/12 + Ad ^ 2 Ix = (30) (10) ^ 3 / 12 + (300) (20) ^ 2 + (10) (50) ^ 3/12 + (30) (10) ^ 3/12 + (300) (20) ^ 2 Ix = 349166,6667 мм ^ 4
Iy = MOI A1 + MOI A2 + MOI A3 Iy = bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 + bh ^ 3/12 + Ad ^ 2 Iy = (10) (30) ^ 3 / 12 + (300) (20) ^ 2 + (50) (10) ^ 3/12 + (10) (30) ^ 3/12 + (300) (20) ^ 2 Iy = 289166,6667 мм ^ 4
Пример 4: I-образная форма
Решение
а. Найдите центр тяжести всей составной формы. Поскольку фигура симметрична в обоих направлениях, то ее центр тяжести находится в середине сложной фигуры.
Расположение центра тяжести составной формы от осей x = 20 мм y = 20 мм
б. Найдите момент инерции, используя формулу передачи. Слово «MOI» означает «момент инерции».
Ix = MOI A1 + MOI A2 + MOI A3 Ix = bh ^ 3/12 + Ad ^ 2 + bh ^ 3/12 + bh ^ 3/12 + Ad ^ 2 Ix = (40) (10) ^ 3 / 12 + (400) (15) ^ 2 + (10) (20) ^ 3/12 + (40) (10) ^ 3/12 + (400) (15) ^ 2 Ix = 193333,3333 мм ^ 4
Iy = MOI A1 + MOI A2 + MOI A3 Iy = bh ^ 3/12 + bh ^ 3/12 + bh ^ 3/12 Iy = (10) (40) ^ 3/12 + (20) (10 ) ^ 3/12 + (10) (40) ^ 3/12 Iy = 108333,3333 мм ^ 4
Пример 5: Сложная фигура
Решение
а. Найдите центр тяжести всей сложной формы, составив таблицу.
| Этикетка | Площадь | х-стержень (мм) | Y-образный стержень (мм) | Топор | Ау |
|---|---|---|---|---|---|
|
A1 |
157.0796327 |
10 |
34.24413182 |
1570.796327 |
191.3237645 |
|
A2 |
600 |
10 |
15 |
6000 |
9000 |
|
A3 |
300 |
26.67 |
10 |
8001 |
3000 |
|
ВСЕГО |
1057.079633 |
15571.79633 |
12191.32376 |
Положение центра тяжести составной формы от осей x = 15571.79633 / 1057.079633 x = 14.73095862 мм y = 12191.32376 / 1057.079633 y = 11.53302304 мм
б. Найдите момент инерции, используя формулу передачи. Слово «MOI» означает «момент инерции».
Ix = MOI A1 + MOI A2 + MOI A3 Ix = (pi) r ^ 4/4 + Ad ^ 2 + bh ^ 3/12 + Ad ^ 2 + bh ^ 3/36 + Ad ^ 2 Ix = ( пи) (10) ^ 4/4 + (157,0796327) (34,24413182 — 11,533) ^ 2 + (20) (30) ^ 3/12 + (600) (15 — 11,533) ^ 2 + (20) (30) ^ 3/36 + (300) (11,533 — 10) ^ 2 Ix = 156792,0308 мм ^ 4
Iy = MOI A1 + MOI A2 + MOI A3 Iy = (pi) r ^ 4/4 + Ad ^ 2 + bh ^ 3/12 + Ad ^ 2 + bh ^ 3/36 + Ad ^ 2 Iy = ( пи) (10) ^ 4/4 + (157.0796327) (14,73 — 10) ^ 2 + (30) (20) ^ 3/12 + (600) (14,73 — 10) ^ 2 + (30) (20) ^ 3/36 + (300) (26,67 — 14,73) ^ 2 Iy = 94227,79522 мм ^ 4
Содержание:
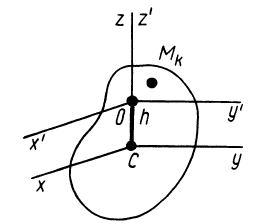
Геометрия масс:
Центр масс
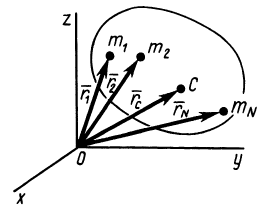
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек
где 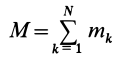
Рис. 21
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Векторная величина 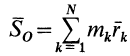
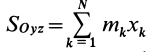
массы относительно координатной плоскости 
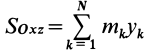
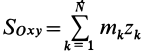
Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 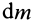
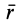
Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму
где 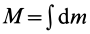
Для однородных сплошных тел 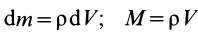
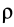
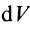
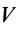
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 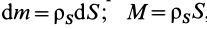
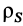
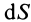
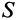
Для тонкой проволоки, которую можно принять за отрезок линии, 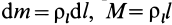
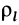
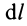
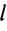
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Моменты инерции относительно точки и оси
Моментом инерции механической системы, состоящей из 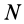
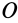
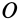
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем
где 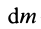
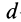
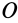
Моментом инерции 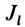
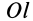
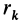
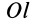
Рис. 22
В частном случае сплошного тела сумму следует заменить интегралом:
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 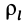
где 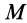
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.
Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины 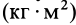
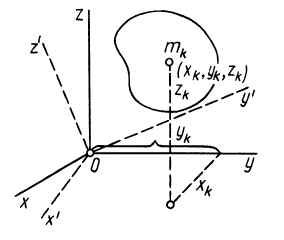
Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.
Моменты инерции относительно осей координат
Моменты инерции относительно декартовых осей координат 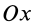
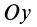
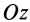
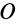
где 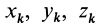
Из приведенных формул следует зависимость
Если через точку 
Из сравнения (8) и (8′) следует, что
Рис. 23
Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.
Для осей координат 
Центробежные моменты инерции часто называют произведениями инерции.
Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.
Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.
Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 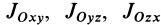
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
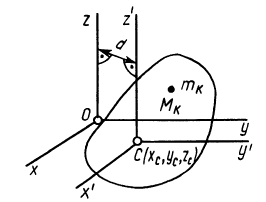
Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 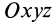
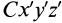
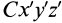
Рис. 24
По определению момента инерции относительно оси имеем
где 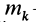
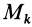
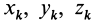
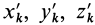
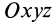
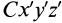
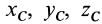
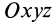
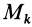
Подставим эти значения координат в выражение момента инерции 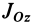
В этом соотношении 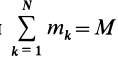
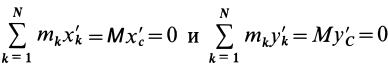
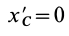
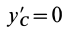
того, что по условию центр масс находится в начале координат этой системы координат.
Величина 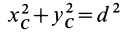
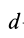
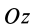
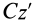
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.
Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.
Если взять ось 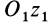
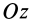
где 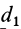
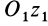
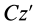
Исключая момент инерции 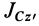
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем
Учитывая, что 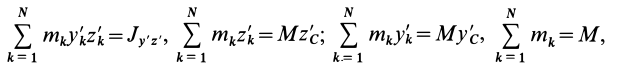
где 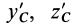
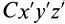
Так как начало системы координат 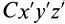
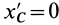
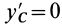
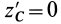
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).
Если производится параллельный перенос осей 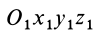
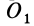
Исключая из (10) и (10′) центробежные моменты инерции Л’з» Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 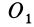
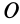
где 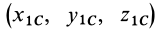
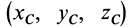
Моменты инерции простейших однородных тел
Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.
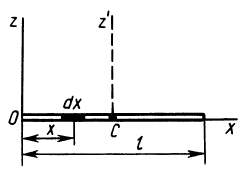
Однородный стержень
Имеем однородный стержень длиной 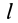
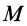
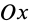
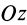
так как 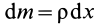
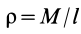
Вычисляя интеграл, получаем
Рис. 25
Таким образом,
Момент инерции стержня относительно оси 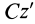
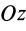
Следовательно,
т. е.
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры 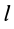
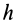
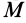
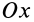
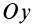
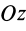
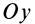
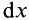
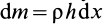
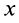
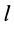
так как 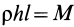
Аналогичные вычисления для оси 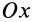
так как эта ось 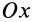
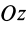
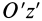
Рис. 26
Интегрируя это выражение в пределах от 0 до 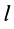
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:
Круглый диск
Имеем тонкий однородный диск радиусом 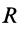
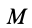
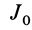
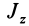
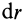
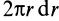
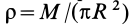
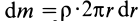
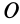
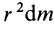
Таким образом,
Рис. 27
Для осей координат 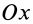
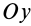
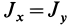
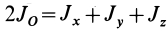
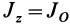
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем
Круглый цилиндр
Рис. 28
Для круглого однородного цилиндра, масса которого 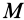
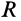
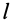
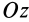
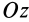
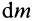
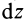
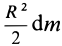
т.е.
Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 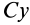
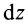
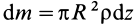
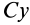
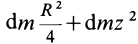
Чтобы получить момент инерции всего цилиндра относительно оси 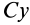
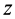
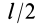
Но 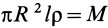
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.
Шар
Пусть масса шара 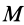
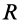
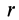
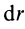
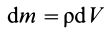
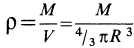
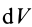
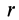
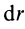
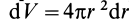
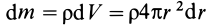
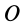
т.е.
Рис. 29
Для осей координат, проходящих через центр шара, в силу симметрии 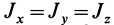
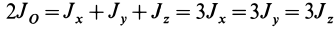
Моменты инерции относительно осей, проходящих через заданную точку
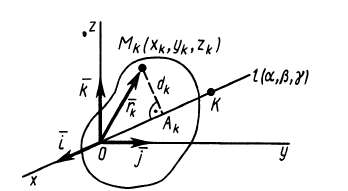
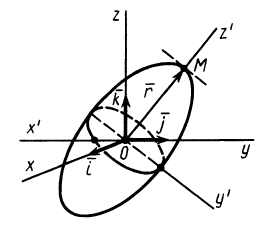
В заданной точке 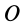
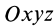
или для сплошных тел
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 
Из прямоугольного треугольника 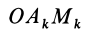
где 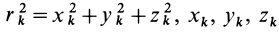
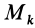
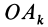
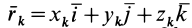
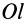
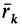
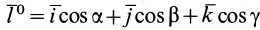
Умножая в (21) 
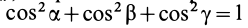
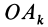
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем
Учитывая, что
— моменты инерции относительно осей координат, а
— центробежные моменты инерции относительно тех же осей, получим
Для определения момента инерции 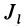
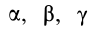

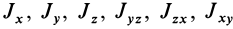
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке 
Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.
Рис. 30
Эллипсоид инерции
Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 

Геометрическое место концов отрезков 
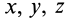
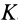
Подставляя эти значения косинусов углов в (24) и сокращая на 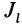
Это действительно уравнение эллипсоида, так как отрезок 

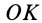
Для каждой точки 
В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям 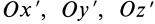
где 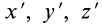
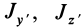
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.
Главные моменты инерции часто обозначают 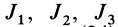
- Заказать решение задач по теоретической механике
Свойства главных осей инерции
Теорема 1. Если одна из декартовых осей координат, например 

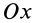
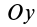

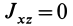
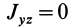
Главная ось инерции 
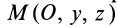
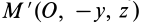
Вычитая из первого уравнения второе, имеем
Так как всегда можно выбрать точки, для которых 
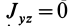
Рис. 31
Аналогичные рассуждения для двух симметричных относительно оси 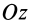
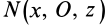
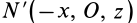
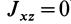
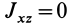
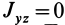

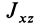
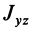


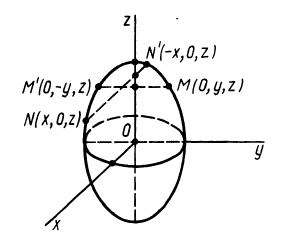
Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.
Рис. 32
Для доказательства теоремы выберем в плоскости симметрии 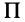

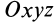

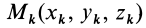
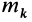
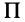
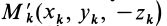
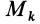
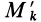
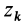
Для центробежного момента инерции 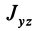
так как часть тела (I), соответствующая точкам с положительными координатами 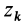
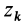
Так как центробежные моменты инерции 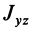
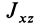



Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.
Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.
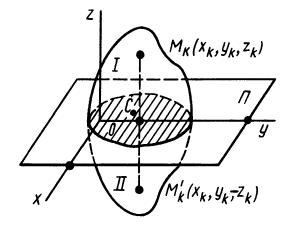
Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.
Теорема доказывается аналогично предыдущей. Для каждой точки тела 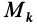
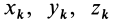
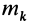
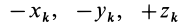

так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты 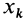
Аналогично доказывается, что 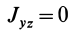
Таким образом, ось 
Теорема 4. Главные оси инерции для точки 
Выберем в точке 
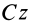
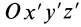
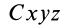
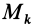
где 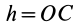
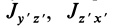
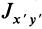
так как
где 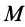
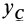
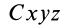
Если 
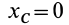
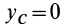
Используя полученные формулы при этих условиях, имеем:
Рис. 33
Следовательно, оси 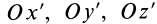
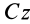
Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 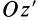
Определение главных моментов инерции и направления главных осей
Пусть известны компоненты тензора инерции в точке 
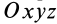
Если оси координат 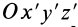
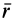
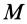
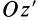
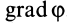
Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 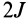
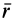
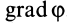
Рис. 34
В этих уравнениях 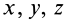
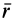
Для частных производных из (27′) получаем:
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 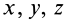
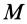
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 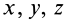
Это кубическое уравнение для определения 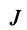
В общем случае имеется три различных действительных корня кубического уравнения 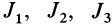
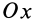
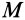
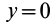
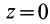
Так как 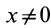
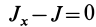
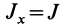
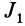
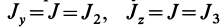
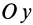
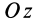
Подставляя в (29) 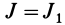
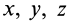
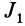
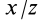
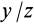
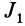
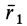
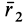
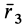
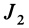
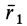
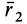
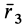
Таким образом, если известен тензор инерции для осей 
Выражение компонентов тензора инерции через главные моменты инерции
Определим компоненты тензора инерции в точке 

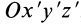
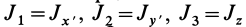

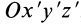
Осевые моменты инерции относительно осей 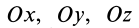
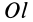
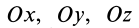
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки 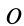

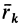
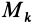
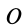
где 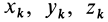
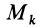
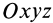
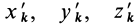
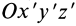
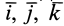
Рис. 35
Используя (33) для центробежного момента инерции 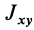
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.
Оси координат 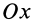
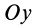
или
Используя это соотношение для исключения величины 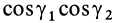
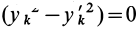
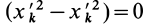
где
— главные моменты инерции. Аналогично получаются выражения для 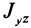
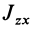
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 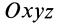
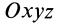
Если ось 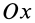
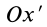
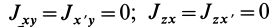
Из (35) имеем
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 
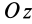
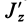
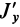
Рис. 36
Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 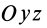
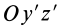
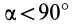
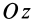
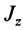
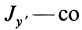
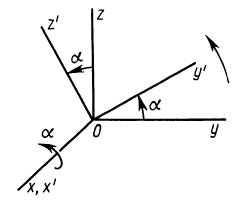
= 90°; р2 = а; Р3 = 90° + а;
Рис. 37
Аналогично при совпадении осей 
При совпадении осей 
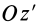
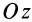
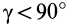
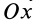
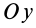
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
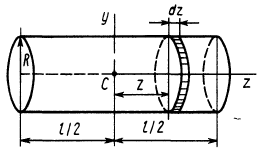
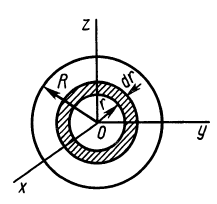
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.