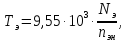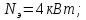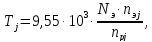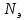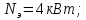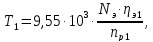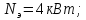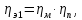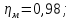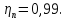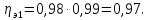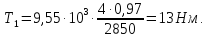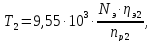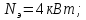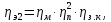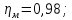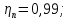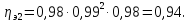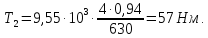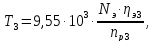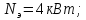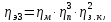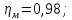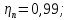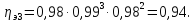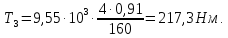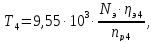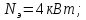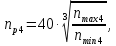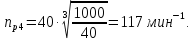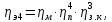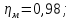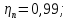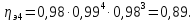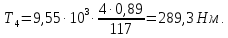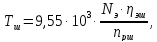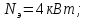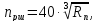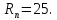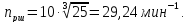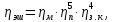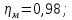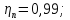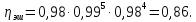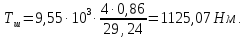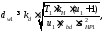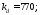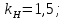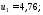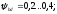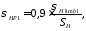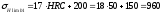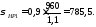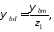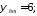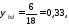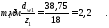Download Article
Download Article
You likely know that if you push or pull on an object (exert force), it will move a distance. The distance it moves depends on how heavy the object is and how much force you apply. However, if the object is fixed at some point (called the «rotational point» or «axis»), and you push or pull on the object at some distance from that point, the object will instead rotate around that axis. The magnitude of that rotation is torque (τ), expressed in newton-meters (N∙m). The most basic way to calculate torque is to multiply the Newtons of force exerted by the meters of distance from the axis. There’s also a rotational version of this formula for 3-dimensional objects that uses the moment of inertia and angular acceleration. Calculating torque is a physics concept requiring an understanding of algebra, geometry, and trigonometry.[1]
-
1
Find the length of the moment arm. The distance from the axis or rotational point to the point where force is applied is called the moment arm. This distance is typically expressed in meters (m).[2]
- Since torque is a rotational force, this distance is also a radius. For this reason, you’ll sometimes see it represented with an «r» in the basic torque equation.
-
2
Work out the force being applied perpendicular to the moment arm. The force applied perpendicular to the moment arm produces the greatest torque. The simplest torque equation assumes the force is being applied perpendicular to the moment arm.[3]
- In torque problems, you’ll typically be given the magnitude force. However, if you have to work it out yourself, you’ll need to know the mass of the object and the acceleration of the object in m/s2. According to Newton’s Second Law, force is equal to mass times acceleration (
).
Advertisement
- In torque problems, you’ll typically be given the magnitude force. However, if you have to work it out yourself, you’ll need to know the mass of the object and the acceleration of the object in m/s2. According to Newton’s Second Law, force is equal to mass times acceleration (
-
3
Multiply the force times the distance to find the torque. The basic formula for torque is
, where torque is represented by the Greek letter tau (τ) and equals the force (F) times the distance (or radius, r). If you know the magnitude of the force (in Newtons) and the distance (in meters), you can solve for the torque, expressed in newton-meters (N∙m).[4]
- For example, suppose you have a force perpendicular to your object exerting 20 Newtons of force on the object 10 meters from the axis. The magnitude of the torque is 200 N∙m:
- For example, suppose you have a force perpendicular to your object exerting 20 Newtons of force on the object 10 meters from the axis. The magnitude of the torque is 200 N∙m:
-
4
Show the direction of the force with positive or negative torque. You now know the magnitude of the torque, but you don’t know if it’s positive or negative. This depends on the direction of the rotation. If the object is rotating counterclockwise, the torque is positive. If the object is rotating clockwise, the torque is negative.[5]
- For example, if the object is moving clockwise and the magnitude of the torque is 200 N∙m, you would express this as -200 N∙m of torque. No sign is necessary if the magnitude of the torque is positive.
- The value given for the magnitude of the torque remains the same. If a negative sign appears before the value, it simply means that the object in question is rotating clockwise.
-
5
Total individual torques around a given axis to find the net torque (Στ). It’s possible to have more than one force acting on an object at a different distance from the axis. If one force is pushing or pulling in the opposite direction of the other force, the object will rotate in the direction of the stronger torque. If the net torque is zero, you have a balanced system. If you’re given the net torque but not some other variable, such as the force, use basic algebraic principles to solve for the missing variable.[6]
Advertisement
-
1
Start with the distance of the radial vector. The radial vector is the line that extends from the axis or point of rotation. It could also be any object, such as a door or the minute-hand of a clock. The distance to measure for the purposes of calculating torque is the distance from the axis to the point where the force is applied to rotate the vector.[7]
- For most physics problems, this distance is measured in meters.
- In the torque equation, this distance is represented by «r» for radius or radial vector.
-
2
Work out the amount of force being applied. In most torque problems, this value will also be given to you. The amount of force is measured in Newtons and will be applied in a particular direction. However, rather than being perpendicular to the radial vector, the force is applied at an angle, giving you a radial vector.[8]
- If you’re not provided with the amount of force, you would multiply mass times acceleration to find the force, which means you would need to be given those values. You might also be given the torque and told to solve for the force.
- In the torque equation, force is represented by «F.»
-
3
Measure the angle made by the force vector and the radial vector. The angle you measure is the one to the right of the force vector. If the measurement isn’t provided for you, use a compass to measure the angle. If the force is being applied to the end of the radial vector, extend the radial vector out in a straight line to get your angle.[9]
- In the torque equation, this angle is represented by the Greek letter theta, «θ.» You’ll typically see it referred to as «angle θ» or «angle theta.»
-
4
Use your calculator to find the sine of the angle θ. In the torque equation, you multiply the distance of the radial vector and the amount of force with the sine of the angle you just measured. Put the angle measurement into your calculator, then press the «sin» button to get the sine of the angle.[10]
- If you were determining the sine of the angle by hand, you would need the measurements for the opposite side and the hypotenuse side of a right triangle. Since most torque problems don’t involve making exact measurements, however, you shouldn’t have to worry about this.
-
5
Multiply the distance, force, and sine to find the torque. The full formula for torque when you have angled force is
. The result is expressed in newton-meters (N∙m).[11]
- For example, suppose you have a radial vector 10 meters long. You’re told that 20 Newtons of force is being applied to that radial vector at a 70° angle. You would find that the torque is 188 N∙m:
- For example, suppose you have a radial vector 10 meters long. You’re told that 20 Newtons of force is being applied to that radial vector at a 70° angle. You would find that the torque is 188 N∙m:
Advertisement
-
1
Find the moment of inertia. The amount of torque required to move an object with angular acceleration depends on the distribution of the object’s mass, or its moment of inertia, expressed in kg∙m2. When the moment of inertia isn’t provided, you can also look it up online for common objects.[12]
-
2
Determine the angular acceleration. If you’re trying to find torque, the angular acceleration will typically be given to you. This is the amount, in radians/s2, that the object’s velocity is changing as it rotates.[13]
- Remember that the angular acceleration can be zero if the object is moving at a constant speed and is neither speeding up nor slowing down.
-
3
Multiply the moment of inertia by the angular acceleration to find the torque. The full formula for torque using the moment of inertia and the angular acceleration is
, where «τ» stands for torque, «I» stands for the moment of inertia, and «α» stands for the angular acceleration. If you’re trying to find torque, simply multiply the moment of inertia and the angular acceleration to get your result. As with other equations, if you’re trying to find one of the other values, you can re-order the equation using common algebraic principles.[14]
Advertisement
Add New Question
-
Question
What is the formula to find the torque from the weight?
Tiagoroth
Community Answer
Torque is measured in Newton meters and is calculated by N·m = (kg*m²)/s². Manipulating the formula to find mass, we get kg = (N·m*s²)/m².
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The equation for torque is very similar to the equation for work (the physical force required for an object to move). However, with work, the force is parallel to the distance, whereas, with torque, the force is perpendicular to the distance vector.[15]
Thanks for submitting a tip for review!
Advertisement
-
Calculating torque requires knowledge of advanced algebraic concepts, geometry, and trigonometry. If you’re not strong in these areas, you might want to refresh your knowledge before you attempt torque calculations.
Advertisement
References
About This Article
Article SummaryX
To calculate torque, start multiplying the mass of the object exerting force by the acceleration due to gravity, which is 9.81. When the force is clockwise, its torque is negative, and when it’s moving counterclockwise, it’s positive. If more than one force is present, add up all the torques to get the net torque of the combined forces. For tips on how to calculate torque using angular acceleration, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 207,743 times.
Did this article help you?
В этой статье начнем говорить о кручении. Это одна из базисных тем в сопромате, как и растяжение-сжатие. Знания этой темы помогут тебе при изучении более сложных тем курса «сопротивление материалов».
Кручение – это такой вид деформации, при котором в сечениях стержня возникают крутящие моменты (T).
На кручение, как правило, работают детали, которые называются валами. Детали, которые широко используются в машиностроении.
Что такое крутящий момент?
Крутящий момент – это внутренний силовой фактор, возникающий в сечениях стержней испытывающих деформацию кручения.
На практике же стержни не работают исключительно на кручение, они могут и растягиваться, и изгибаться. Но это уже более продвинутые темы – сложное сопротивление. В этом же разделе будем рассматривать чистое кручение.
В чем измеряется крутящий момент и как обозначается?
Крутящие моменты обозначаются буквой – T (сокращённое с английского: Torque – крутящий момент), однако, часто в другой литературе ты можешь встретить обозначение — Мкр. Ты можешь использовать любое обозначение, какое больше нравиться, либо которое использует твой преподаватель.
В задачах тебе будут даны крутящие моменты, скорее всего, в Н·м либо кН·м.
Построение эпюры крутящих моментов
В этой статье расскажу, как строить эпюры при кручении: крутящих моментов, максимальных касательных напряжений и углов закручивания (углов поворотов).
На самом деле, многие рассматриваемые здесь принципы сильно похожи на те, что мы изучали ранее в уроке про построение эпюр при растяжении (сжатии). Здесь фактически будем делать всё то же самое, только оперировать другими обозначениями и названиями. После изучения того урока, с кручением у тебя точно не возникнет никаких трудностей.
В качестве примера, возьмём следующую расчётную схему:

Будем считать, что стержень изготовлен из стали (G = 8 · 1010 Па), а диаметры ступеней равны: d1=150 мм, d2=200 мм, d3=300 мм.
Под действием внешних моментов (M), их еще часто называют вращающими или скручивающими моментами, в поперечных сечениях стержня возникают внутренние моменты – крутящие (T).

Правило знаков для крутящих моментов
Чтобы построить эпюру крутящих моментов, необходимо задаться каким-то правилом знаков для крутящих моментов. В этой статье я буду использовать следующее правило:
- Если внешний момент (M), в плоскости сечения, поворачивает ПРОТИВ часовой стрелки, то крутящий момент (T) – положительный.

- Если внешний момент (M), в плоскости сечения, поворачивает ПО часовой стрелке, то крутящий момент (T) – отрицательный.

Можно учитывать знак крутящего момента ровно наоборот. Главное, придерживаться этого правила при расчёте всех участков и ориентироваться по полученным эпюрам: в какую сторону у тебя будут направлены внешние моменты, внутренние – крутящие моменты, куда будут поворачиваться сечения. Как видишь, знаки здесь нам нужны, чтобы задать определённые правила игры, а правило знаков – условное и не имеет физического смысла.
Расчёт крутящих моментов
Что же, давай, наконец, приступим к расчёту крутящих моментов. Пронумеруем расчётные участки:

Используя правило знаков, описанное выше, рассчитаем крутящие моменты на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры касательных напряжений при кручении
Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.
Расчёт максимальных касательных напряжений
Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.
Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи диаметры участков известны. Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Построение эпюры углов закручивания (поворотов)
Под действием внешних – скручивающих моментов, поперечные сечения стержня будут поворачиваться на определенный угол (φ). В этом разделе будем учиться определять эти углы закручивания (поворотов) поперечных сечений и строить эпюру.
Обозначим точки в характерных сечениях стержня:

Расчёт начинаем от жёсткой заделки и сразу можем записать, что в точке A, угол поворота равен нулю, т. к. здесь заделка ограничивает любые повороты сечения:
Чтобы рассчитать поворот сечения B, нужно учесть поворот предыдущего сечения:
А также, угол закручивания участка между расчётными сечениями:
Угол закручивания участка можно посчитать по формуле:

где l – длина участка; Ip – полярный момент инерции; G – модуль сдвига.
G – модуль сдвига (модуль упругости 2 рода) – определяется при испытании образцов на кручение, тем самым зависит от материала образца.
Модуль сдвига (G) известен, по условию задачи.
Формула для определения полярного момента инерции для круглого сечения следующая:

Зная диаметры, сразу вычислим полярные моменты инерции для каждого участка:

Определим угол закручивания сечения B, с учётом вышеуказанных формул:

Также можно перевести это значение в привычные градусы:

Для двух других сечений расчёт производится аналогичным образом.
Угол поворота сечения С

Угол поворота сечения D

По рассчитанным значениям, построим эпюру углов закручивания поперечных сечений:

Таким образом, свободный торец стержня, повернётся на 0.58 градуса, относительно неподвижного сечения A.
Расчеты на прочность при кручении
При кручении расчёты на прочность в целом похожи на расчёты при растяжении. Только здесь вместо нормальных напряжений расчёт ведётся по касательным напряжениям.
На кручение, как правило, работают детали, которые называются валами. Их назначение – передача крутящего момента от одного элемента к другому. При этом вал по всей длине имеет либо круглое сечение, либо кольцевое.
Условие прочности
За допустимое касательное напряжение [τ], часто в задачах по сопромату, принимают напряжение в два раза меньше, чем допустимое нормальное напряжение [σ]:

Максимальные касательные напряжения (τmax) в сечениях можно найти по формуле:

где T – крутящий момент в сечении;
Wp – полярный момент сопротивления сечения.
Полярные моменты сопротивления можно посчитать этим формулам.
8.1 Расчет крутящего момента
на валу электродвигателя
Для
определения крутящего момента на валу
электродвигателя привода главного
движения используется номинальная
мощность и номинальная частота вращения:
где
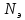
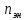
частота вращения электродвигателя,
мин-1:
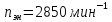
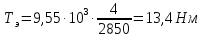
8.2 Расчет крутящего момента на валах
привода
Крутящий
момент на валах привода рассчитывается
по формуле:
где
– мощность электродвигателя, кВт:
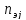
участка привода от электродвигателя
до соответствующего вала;
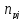
частота вращения соответствующего
вала, принимается по графику частот,
мин-1.
8.3 Расчет крутящего момента на первом
валу привода
Крутящий
момент на первом валу привода рассчитывается
по формуле:
где
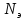
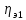
участка привода от электродвигателя
до 1-го вала;
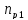
частота вращения на 1-ом валу, принимаем
по графику частот, мин-1:
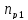
КПД
участка привода до первого вала
рассчитывается по формуле:
где
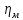
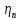
пары подшипников;
8.4 Расчет крутящего момента на втором
валу привода
Крутящий
момент на втором валу привода рассчитывается
по формуле:
где
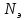
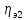
участка привода от электродвигателя
до 2-го вала;
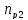
частота вращения на 1-ом валу, принимаем
по графику частот, мин-1:

КПД
участка привода до второго вала
рассчитывается по формуле:
где
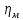
КПД зубчатой муфты;
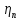
пары подшипников;
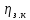
КПД зацепления зубчатых колес;
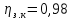
8.5 Расчет крутящего момента на третьем
валу привода
Крутящий
момент на третьем валу привода
рассчитывается по формуле:
где
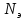
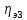
участка привода от электродвигателя
до 3-го вала;
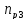
частота вращения на 1-ом валу, принимаем
по графику частот, мин-1:
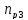
КПД
участка привода до третьего вала
рассчитывается по формуле:
где
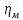
КПД зубчатой муфты;
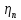
пары подшипников;
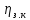
КПД зацепления зубчатых колес;
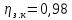
8.6 Расчет крутящего момента на четвертом
валу привода
Крутящий
момент на четвертом валу привода
рассчитывается по формуле:
где
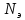
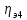
участка привода от электродвигателя
до 4-го вала;
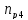
частота вращения на 4-ом валу, определяется
по формуле:
где
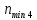
вала, мин-1:
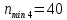
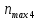
частота вращения четвертого вала, мин-1:
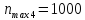
КПД
участка привода до четвертого вала
рассчитывается по формуле:
где
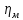
КПД зубчатой муфты;
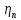
пары подшипников;
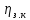
зацепления зубчатых колес;
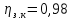
8.7 Расчет крутящего момента на шпинделе
Крутящий
момент на шпинделе рассчитывается по
формуле:
где
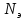
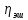
участка привода от электродвигателя
до шпинделя;
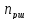
частота вращения шпинделя, определяется
по формуле:
где
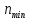
вала, мин-1:
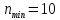
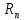
регулирования частот вращения шпинделя:
КПД
участка привода до шпинделя рассчитывается
по формуле:
где
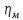
КПД зубчатой муфты;
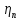
пары подшипников;
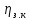
зацепления зубчатых колес;
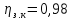
9 Проектный расчет передач
9.1 Расчет цилиндрической прямозубой
постоянной передачиz1–z2
9.1.1
Исходные данные
1.
Расчетный крутящий момент на первом
валу привода, H·м:
Т1
=
13 Н·м;
2.
Число зубьев шестерни: z1
=
18;
3.
Число зубьев колеса: z2
=
83;
4.
Передаточное число передачи: u1
=
4,76.
9.1.2
Выбор материала и термической обработки
зубчатых
колес
В
качестве материала для зубчатых колес
передачи выбираем сталь 40Х, которая
отвечает необходимым техническим и
эксплуатационным требованиям. В качестве
термической обработки выбираем объемную
закалку, позволяющую получить твердость
зубьев 40..50HRCэ.
9.1.3
Проектный расчет постоянной прямозубой
зубчатой передачи
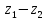
Диаметр
начальной окружности шестерни
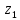
где
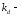
коэффициент: для прямозубых передач
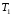
расчётный крутящий момент на первом
валу, Н·м: Т1=13
Н·м;
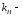
нагрузки для шестерни, равный 1,3..1,5:
принимаем
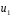
передаточное число:
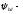
рабочей ширины венца передачи к начальному
диаметру шестерни:
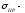
контактное напряжение, МПа.
Допускаемое
контактное напряжение для прямозубых
передач рассчитывается по формуле:
где

предел контактной выносливости
поверхностей зубьев, соответствующий
базовому числу циклов перемены напряжений,
МПа;
МПа;
SH
– коэффициент безопасности: SH
= 1,1.
Коэффициент
отношения рабочей ширины венца передачи
к начальному диаметру шестерни может
приниматься в пределах
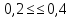
определяется
по формуле:
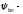
рабочей ширины венца передачи к модулю:
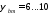
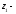
зубьев шестерни: z1
= 18.
что
находится в допустимых пределах
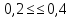
Таким
образом, диаметр начальной окружности
шестерни равен:
Модуль
постоянной прямозубой передачи
определяется из условия расчета на
контактную выносливость зубьев по
рассчитанному значению диаметра
начальной окружности шестерни по
формуле:
где
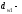
начальной окружности шестерни, мм:dw1
=
38,75 мм;
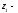
зубьев шестерни: z1
= 18.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Многие уверены, что главной характеристикой двигателя автомобиля является мощность, которая обычно измеряется в лошадиных силах (на самом деле — в ваттах, но применительно к машинам часто используют «лошадей»). Но ведь есть еще такая характеристика как крутящий момент.
- Что это такое
- На что влияет
- Что важнее — момент или мощность
- Дизель и бензин
Что такое крутящий момент?
Крутящий момент – это векторная величина, определяемая как произведение радиус-вектора точки приложения силы и вектора силы. В простейшем случае – это произведение прикладываемой силы на плечо рычага, к которому она прикладывается. Единица измерения у крутящего момента – соответствующая: ньютоны на метры (Н∙м).
Звучит сложно, но попытаемся объяснить на простом примере. Представьте себе механическую мясорубку, которую нужно крутить за ручку. Так вот, в ней прикладываемая сила – это та сила, с которой вы крутите ручку. А плечо – это сама ручка. И чем она длиннее, тем выше крутящий момент при тех же ваших усилиях.
Как это всё относится к двигателю автомобиля? Очень просто. В моторе сила давления сгорающей смеси бензина и воздуха передаётся через поршень на кривошипно-шатунный механизм. Сила «берётся» из сгорания топлива, а в качестве рычага выступают детали механизма.
На что влияет крутящий момент
Крутящий момент характеризует «итоговую» тягу двигателя. Он говорит «насколько двигатель сильный», какую силу тяги может создавать. При этом надо понимать, что на колёса крутящий момент доходит уже изменённым, ведь шины связаны с мотором не напрямую, а через трансмиссию, в которой момент изменяется в зависимости от передаточного соотношения.
Крутящий момент — величина не постоянная. Момент изменяется вместе с количеством поступающей в цилиндр смеси и оборотами двигателями. Поэтому для оценки возможностей двигателя обычно используют график крутящего момента, который иллюстрирует его зависимость от оборотов.

Особенность двигателей внутреннего сгорания в том, что с ростом оборотов крутящий момент рано или поздно начинает снижаться
(Фото: Shutterstock)
Чем большее усилие развивает двигатель — тем лучше автомобиль разгоняется. Поэтому максимальное ускорение получается на тех оборотах, при которых момент достигает пиковых значений.
Но особенность двигателей внутреннего сгорания в том, что с ростом оборотов крутящий момент рано или поздно начинает снижаться. Решить эту проблему помогает коробка передач: при разгоне мы включаем нужную передачу, поддерживая обороты на оптимальном уровне. И поэтому так важно, чтобы двигатель на как можно большем промежутке оборотов выдавал максимальную тягу.
Крутящий момент и мощность: что важнее
Но что важнее? Крутящий момент или мощность двигателя? Чтобы ответить на этот вопрос, сначала нужно понять, что такое вообще мощность.
С точки зрения физики мощность получается путём деления совершенной работы на время, за которое работа совершилась. То есть, эта характеристика показывает не «что было сделано», а «что было сделано за определённое время». Например, перенести из пункта А в пункт Б десять ящиков можно за пять минут, а можно за сорок. Выполненная работа будет одинакова. А вот мощность — нет.
Применительно к автомобильному двигателю мощность тоже является такой же «оценочной» характеристикой. При этом, можно сказать, что работой двигателя, по сути, является… крутящий момент. Ведь работа мотора — это крутить коленвал. Следовательно, крутящий момент и мощность — величины взаимосвязанные.
Вернемся к воображаемой мясорубке. Длинная ручка обеспечивает высокий крутящий момент, то есть вы можете прокручивать, например, не обычное мясо, а замороженное. Допустим, за один оборот сквозь мясорубку проходит 10 граммов такого мяса, а если у вас получится делать 100 оборотов в минуту — на выходе получится килограмм фарша. Это и есть ваша мощность.
В автомобилях мощность мотора равняется его крутящему моменту на данных оборотах в минуту, умноженному на число этих оборотов и разделённому на определённый коэффициент. Она показывает «суммарное количество» крутящего момента, то есть, работы, совершённой двигателем за определённое время. Чем больше момент, «сила кручения» — тем больше мощность.
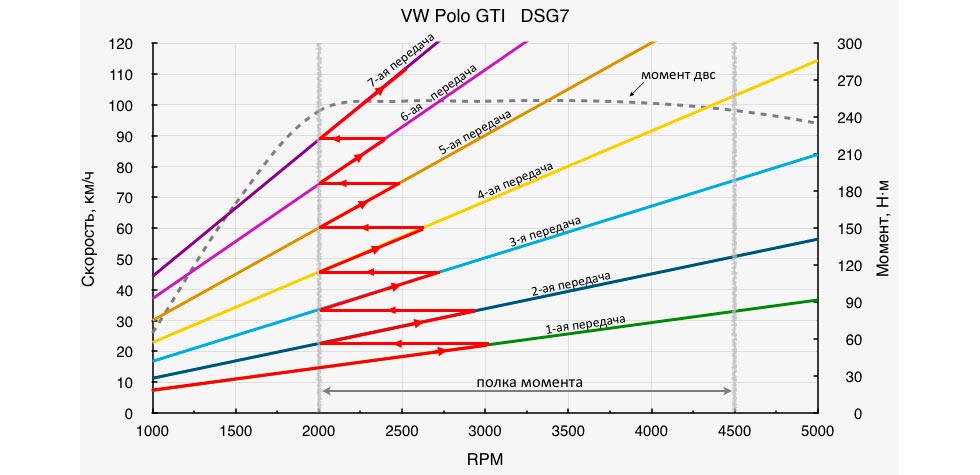
Часто на графике отображаются сразу две линии: одна обозначает момент, а другая — мощность.
(Фото: drive2.ru)
Отметим, что как для крутящего момента, так и для мощности существуют графики, демонстрирующие зависимость от числа оборотов. Более того, часто на графике отображаются сразу две линии: одна обозначает момент, а другая — мощность.
Вот и получается, что вопрос о том, что из этих показателей важнее — не совсем корректен. Во-первых, они взаимосвязаны. А, во-вторых, значение имеют не только сами эти показатели, но и обороты.
Крутящий момент в дизельных и бензиновых двигателях
Какой двигатель обладает большим крутящим моментом — бензиновый или дизельный? Как правило, у дизеля крутящий момент заметно выше, чем у аналогичного бензинового мотора. Причём на низких оборотах эта разница наиболее значительна. Дизель развивает хорошую тягу «сразу», чуть ли не с холостых оборотов. А бензиновый должен сперва раскрутиться.

Максимальное ускорение получается на тех оборотах, при которых момент достигает пиковых значений
(Фото: Shutterstock)
С другой стороны, у дизельных двигателей в силу особенности конструкции меньше рабочий диапазон оборотов: когда при разгоне бензиновый двигатель продолжает раскручиваться, дизельный уже требует перехода на высшую передачу.
Значит ли это, что дизель со своим большим крутящим моментом подходит только ля грузовиков и внедорожников? Когда-то многие были в этом уверены. Однако современные дизельные двигатели отлично ведут себя на быстрых спортивных автомобилях.
- Топ-5 автоподстав. Видеопримеры и разбор от экспертов
- Антидождь для автомобиля — что это за средство и как оно работает
- Автомагистраль: что это и чем она отличается от других дорог
Как найти крутящий момент
Чтобы найти крутящий момент силы, с помощью динамометра измерьте саму силу, и ее плечо. Их значения перемножьте и получите крутящий момент. Если известна мощность, развиваемая крутящимся механизмом, то момент силы можно найти, зная его частоту вращения. Также можно найти крутящий момент, измерив работу, выполненную двигателем.

Вам понадобится
- Для измерения понадобится секундомер, линейка или рулетка, динамометр, тахометр, амперметр.
Инструкция
Крутящий момент силы.Крутящий момент измеряется на вращающемся теле. Для этого определите точку его вращения и точку приложения силы, проведя между ними прямую линию. Измерьте острый угол между этой линией и направлением (вектором) силы. Крутящий момент будет равен произведению значения силы, которое измерите с помощью динамометра в ньютонах, на расстояние до точки вращения (плечо) и острого угла между плечом и вектором силы (M=F•l•sin(α)).
Максимальный момент достигается в том случае, когда сила перпендикулярна плечу, а если сила параллельна (совпадает с линией плеча), то момент силы будет равен нулю.
Крутящий момент в зависимости от мощности.Двигатель, выдающий крутящий момент, имеет определенную номинальную мощность, которую можно найти в технической документации или измерить. Для того чтобы найти его крутящий момент, с помощью тахометра измерьте частоту его вращения на валу в оборотах в минуту. Мощность двигателя измерьте в киловаттах. Чтобы получить значение крутящего момента двигателя значение мощности умножьте на 9550 и поделите на частоту вращения вала. Результатом будет крутящий момент в ньютонах на метр.
Крутящий момент электродвигателя.Самый простой электродвигатель – рамка из проводника с током в магнитном поле. Поместите рамку в магнитное поле с известной индукцией. Подключите ее к источнику электрического тока и с помощью амперметра измерьте силу тока в рамке. Линейкой измерьте плечо силы от оси вращения до вертикального проводника рамки, а также длину самих вертикальных проводников. Тогда максимальный крутящий момент будет равен произведению магнитной индукции на силу тока, длину вертикального проводника, и плечо действия силы. Результат умножьте на 2 (M=2•B•I•l•r). Такой крутящий момент будет развиваться в том случае, если плечо будет перпендикулярно направлению силы электромагнитного поля.
Источники:
- как найти момент на валу
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.