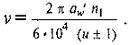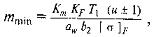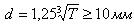Внимание. Это демо расчёт.
Демонстрационный расчет выполнен одной и той же программой, что и при полноценных расчетах, поэтому полноценный расчёт и демо расчёт имеют абсолютно одинаковое качество.
Полноценный расчёт можно начать на главной странице сайта.
Готово.
На этой странице выполнен расчет редуктора. Текст страницы, например, можно скопировать в редактор Ms Word.
При успешном расчете ссылки для скачивания сгенерированных чертежей можно найти после текста расчетов внизу страницы.
Содержание
Техническое задание
Введение
1. Кинематический расчет привода
1.1 Подбор электродвигателя
1.2 Уточнение передаточных чисел привода
1.3 Определение частот вращения и вращающих моментов на валах
2. Расчет цилиндрической передачи первой ступени
2.1 Выбор твердости, термической обработки и материала колес
2.2 Определение допускаемых контактных напряжений
2.3 Определение допускаемых напряжений изгиба
2.4 Проектный расчет
2.4.1 Межосевое расстояние
2.4.2 Предварительные основные размеры колеса
2.4.3 Модуль передачи
2.4.4 Суммарное число зубьев и угол наклона
2.4.5 Число зубьев шестерни и колеса
2.4.6 Фактическое передаточное число
2.4.7 Диаметры колес
2.4.8 Размеры заготовок
2.4.9 Проверка зубьев колес по контактным напряжениям
2.4.10 Силы в зацеплении
3. Расчет цилиндрической передачи второй ступени
3.1 Выбор твердости, термической обработки и материала колес
3.2 Определение допускаемых контактных напряжений
3.3 Определение напряжений изгиба
3.4 Проектный расчет
3.4.1 Межосевое расстояние
3.4.2 Предварительные основные размеры колеса
3.4.3 Модуль передачи
3.4.4 Суммарное число зубьев и угол наклона
3.4.5 Число зубьев шестерни и колеса
3.4.6 Фактическое передаточное число
3.4.7 Диаметры колес
3.4.8 Размеры заготовок
3.4.9 Проверка зубьев колес по контактным напряжениям
3.4.10 Силы в зацеплении
4. Эскизное проектирование
4.1 Проектные расчеты валов
4.2 Расстояние между деталями передач
4.3 Выбор типов подшипников
4.4 Схемы установки подшипников
4.5 Составление компоновочной схемы
5. Конструирование зубчатых колес первой ступени
5.1 Шестерня
5.2 Зубчатое колесо
6. Конструирование зубчатых колес второй ступени
6.1 Шестерня
6.2 Зубчатое колесо
7. Подбор шпоночных соединений
7.1 Подбор шпоноки для соединения зубчатого колеса и промежуточного вала
7.2 Подбор шпоноки для соединения зубчатого колеса и выходного вала
7.3 Подбор шпонок входного и выходного хвостовиков
8. Подбор подшипников качения на заданный ресурс
8.1 Подшипники быстроходного вала
8.2 Подшипники промежуточного вала
8.3 Подшипники тихоходного вала
9. Конструирование корпусных деталей
10. Конструирование крышек подшипников
11. Расчет ременной передачи
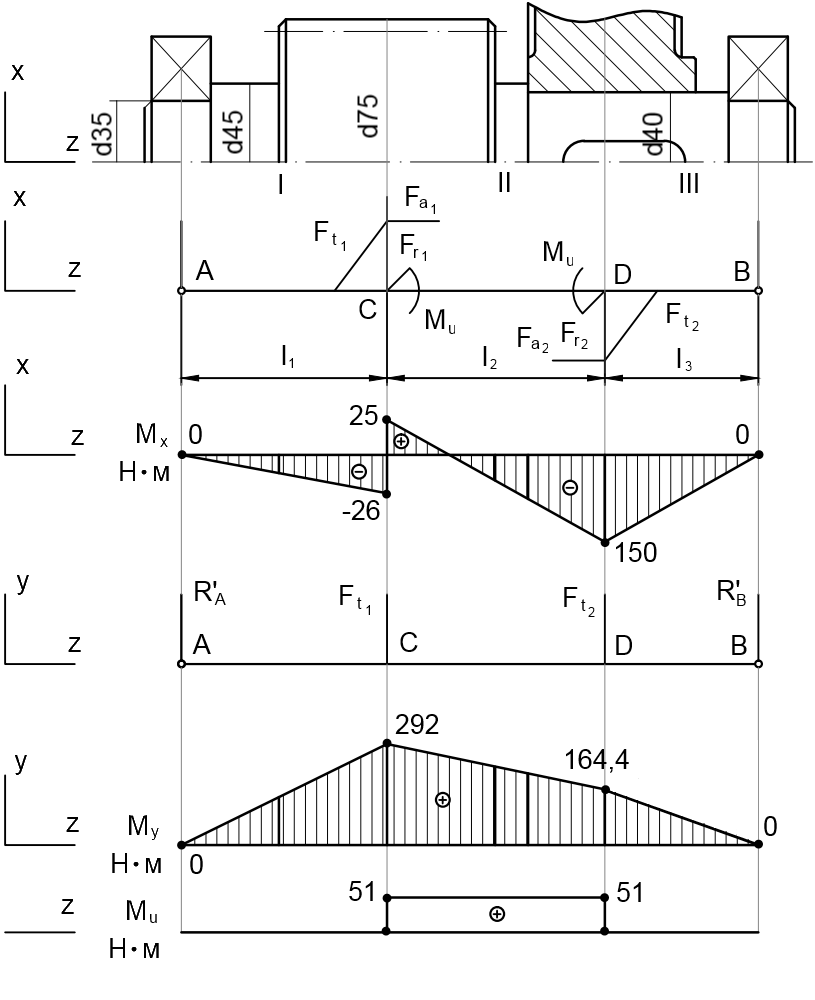
12. Расчет валов на прочность
12.1 Входной вал
12.2 Промежуточный вал
12.3 Выходной вал
13. Выбор манжетных уплотнений
13.1 Входной вал
13.2 Промежуточный вал
13.3 Выходной вал
14. Выбор смазочных материалов и системы смазывания
15. Расчет муфт
16. Порядок сборки привода, выполнение необходимых регулировочных работ
Список используемой литературы
1. Кинематический расчет
1.1 Подбор электродвигателя
Потребляемую мощность (кВт) привода (мощность на выходе) определяют по формуле:
Pв = Tв ∙ nв ∙ 2π = 1000 ∙ 60 ∙ 2 ∙ 3.1415 / (60 ∙ 1000) = 6.3 кВт.
Тогда требуемая мощность электродвигателя [1, стр. 5]
Pэ.тр = Pв/ηобщ,
где ηобщ = η1 η2 η3 …
Здесь η1, η2, η3 … — КПД отдельных звеньев кинематической цепи, ориентировочные значения которых с учетом потерь в подшипниках можно принимать по табл. 1.1 (1, стр. 6).
Общий КПД привода
ηобщ = ηз2ηремηмηоп;
где ηз — КПД зубчатой передачи; ηрем — КПД ременной передачи; ηм — КПД соединительной муфты; ηоп — КПД опор приводного вала.
По табл. 1.1: ηз = 0.97; ηрем = 0.95; ηм = 0.98; ηоп = 0.99;
Тогда
ηобщ = 0.972∙0.95∙0.98∙0.99 = 0.87;
Требуемая мощность электродвигателя
Pэ.тр = 6.3 / 0.87 = 7.24 кВт;
Требуемая частота вращения вала электродвигателя вычислим, подставляя в формулу для nэ.тр средние значения передаточных чисел из рекомендуемого диапазона для присутствующих передач.
|
Вид передачи |
Твердость зубьев |
Передаточное число |
|
|
Uрек |
Uпред |
||
|
Зубчатая цилиндрическая: тихоходная быстроходная быстроходная |
≤ 350 HB 40…56 HRCэ 56…63 HRCэ ≤ 350 HB 40…56 HRCэ 56…63 HRCэ ≤ 350 HB 40…56 HRCэ 56…63 HRCэ |
2,5…5,6 2,5…5,6 2…4 3,15…5,6 3,15…5 2,5…4 4…6,3 4…6,3 3,15…5 |
6,3 6,3 5,6 8 7,1 6,3 8 7,1 6,3 |
|
Коробка |
Любая |
1…2,5 |
3,15 |
|
Коническая |
≤ 350 HB ≥ 40 HRCэ |
1…4 1…4 |
6,3 5 |
|
Червячная |
— |
16…50 |
80 |
|
Цепная |
— |
1,5…3 |
4 |
|
Ременная |
— |
2…3 |
5 |
nэ.тр = nв ∙ Uцил2 ∙ Uр = 60 ∙ 42 ∙ 2 = 1920 мин-1;
где Uцил — передаточное число передачи одноступенчатого цилиндрического редуктора; Uр — пердаточное число ременной передачи.
По табл. 24.9 [1, стр. 417] выбираем электродвигатель АИР132S4: P = 7.5 кВт; n = 1440 мин-1.
Отношение максимального вращающего момента к номинальному Tmax/T = 2.2.
1.2 Уточнение передаточных чисел привода
После выбора n определяют общее передаточное число привода [1, стр. 8]
Uобщ = n/nв;
Uобщ = 1440 / 60 = 24;
Полученное расчетом общее передаточное число распределяют между редуктором и другими передачами, между отдельными ступенями редуктора.
Если в кинематической схеме кроме редуктора (коробки передач) имеется цепная или ременная передача, то предварительно назначенное передаточное число передачи не изменяют, принимая Uп = Uц или Uп = Uр или Uп = UцUр, а уточняют передаточное число редуктора [1, стр. 8]
Uп = Uр = 2 = 2;
Uред = Uобщ/Uп = 24 / 2 = 12;
Передаточные числа ступеней (Б — быстроходная, Т — тихоходная) [1, стр. 8]:
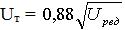
UТ = 3.05;
UБ = Uред/UТ = 3.93.
1.3 Определение частот вращения и вращающих моментов на валах
После определения передаточных чисел ступеней редуктора (коробки передач) вычисляют частоты вращения и вращающие моменты на валах передачи.
Если в заданной схеме отсутствует цепная передача на выходе, то частота вращения выходного вала редуктора
n3 = nв = 60 мин-1.
Частота вращения промежуточного вала редуктора
n2 = n2UТ = 60 ∙ 3.05 = 183 мин-1.
Частота вращения входного вала редуктора
n1 = n1UБ = 183 ∙ 3.93 = 719.19 мин-1.
Момент на выходном валу при отсутствии цепной передачи
T3 = Tв/(ηмηоп) = 1000 / (0.98 ∙ 0.99) = 1030.72 (Н∙м);
где ηоп — КПД опор приводного вала; ηм — КПД муфты.
Вращающий момент промежуточном валу редуктора
T2 = T3/ (UТηцил) = 1030.72 /(3.05 ∙ 0.97) = 348.39 (Н∙м).
где ηцил — КПД цилиндрической передачи; UТ — передаточное число тихоходной ступени.
Вращающий момент входном валу редуктора
T1 = T2/ (UБηцил) = 348.39 /(3.93 ∙ 0.97) = 91.39 (Н∙м).
где ηцил — КПД цилиндрической передачи; UБ — передаточное число быстроходной ступени.
Сводная таблица с данными необходимыми для расчета редуктора:
| Uред | n1, мин-1 | T1, Н∙м | n2, мин-1 | T2, Н∙м | n3, мин-1 | T3, Н∙м |
| 12 | 719.19 | 91.39 | 183 | 348.39 | 60 | 1030.72 |
Примечание: расчетные данные могут иметь погрешность до 3% из-за округлений в расчетах.
2. Расчет цилиндрической передачи первой ступени
2.1 Выбор твердости, термической обработки и материала колес
В зависимости от вида изделия, условий его эксплуатации и требований к габаритным размерам выбирают необходимую твердость колес и материалы
для их изготовления. Для силовых передач чаще всего применяют стали. Передачи со стальными зубчатыми колесами имеют минимальную массу и габариты, тем меньше,
чем выше твердость рабочих поверхностей зубьев, которая в свою очередь зависит от марки стали и варианта термической обработки (табл. 1). [1, стр.11]
Табл. 1 [1, табл. 2.1, стр. 11]
|
Марка стали |
Термообработка |
Предельные размеры заготовки, мм |
Твердость зубьев |
σт, МПа |
||
|
Dпр |
Sпр |
в сердцевине |
на поверхности |
|||
|
45 |
Улучшение |
125 |
80 |
235-262 HB |
235-262 HB |
540 |
|
Улучшение |
80 |
50 |
269-302 HB |
269-302 HB |
650 |
|
|
40Х |
Улучшение |
200 |
125 |
235-262 HB |
235-262 HB |
640 |
|
Улучшение |
125 |
80 |
269-302 HB |
269-302 HB |
750 |
|
|
Улучшение и закалка ТВЧ |
125 |
80 |
269-302 HB |
45-50 HRCэ |
750 |
|
|
40ХН, 35ХМ |
Улучшение |
315 |
200 |
235-262 HB |
235-262 HB |
630 |
|
Улучшение |
200 |
125 |
269-302 HB |
269-302 HB |
750 |
|
|
Улучшение и закалка ТВЧ |
200 |
125 |
269-302 HB |
48-53 HRCэ |
750 |
|
|
40ХНМА, 38Х2МЮА |
Улучшение и азотирование |
125 |
80 |
269-302 HB |
50-56 HRCэ |
780 |
|
20Х, 20ХН2М, 18ХГТ, 12ХН3А, 25ХГМ |
Улучшение, Цементация и закалка |
200 |
125 |
300-400 HB |
56-63 HRCэ |
800 |
На практике в основном применяют следующие варианты термической обработки (т.о.):
I — т.о. колеса — улучшение, твердость 235…262 HB; т.о. шестерни — улучшение, твердость 269…302 HB. Марки стали одинаковы для колеса и шестерни: 45, 40Х, 35 ХМ и др. Зубья колес из улучшаемых сталей хорошо прирабатываются и не подвержены
хрупкому разрушению, но имеют ограниченную нагрузочную способность. Применяют в слабо- и средненагруженных передачах.
II — т.о. колеса — улучшение, твердость 269…302 HB; т.о. шестерни — улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки стали (см. табл. 1) 45…50 HRCэ, 48…53 HRCэ. Твердость сердцевины зуба соотвествует термообработке улучшение. Марки сталей одинаковы для колеса и шестерни: 40Х, 40ХН, 35ХМ и др.
III — т.о. колеса и шестерни одинаковая — улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки сатили: 45…50 HRCэ, 48…53 HRCэ. Марки сталей одинаковы для колеса и шестерни: 40Х, 40ХН, 35ХМ и др.
IV — т.о. колеса — улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки стали (табл.1) 45…50 HRCэ, 48…53 HRCэ; т.о. шестерни — улучшение, цементация и закалка, твердость поверхности 56…63 HRCэ. Материал шестерни — стали марок 20Х, 20ХН2М, 18ХГТ, 12ХН3А и др.
V — т.о. колеса и шестерни одинаковая — улучшение, цементация и закалка, твердость поверхности 56…63 HRCэ. Цементация (поверхностное насыщение углеродом) с последующей закалкой наряду с большой твердостью поверхностных слоев обеспечивает и высокую прочность зубьев на изгиб. Марки сталей одинаковы для колеса и шестерни: 20Х, 20ХН2М, 18ХГТ, 12ХН3А, 25 ХГМ и др. [1, стр.11-12]
Шестерня.
Материал — Сталь 40Х. Назначаем термическую обработку шестерни — улучшение и закалка ТВЧ.
Предельные размеры заготовки: Dпр = 125 мм, Sпр = 80 мм.
Твердость зубьев: в сердцевине до 302 HB, на поверхности до 50 HRCэ.
Предельное напряжение σT = 750 МПа.
Колесо.
Материал — Сталь 40Х. Назначаем термическую обработку шестерни — улучшение.
Предельные размеры заготовки: Dпр = 200 мм, Sпр = 125 мм.
Твердость зубьев: в сердцевине до 262 HB, на поверхности до 262 HB.
Предельное напряжение σT = 640 МПа.
2.2 Определение допускаемых контактных напряжений
Допускаемые контактные напряжения [σ]H1 для шестерни и [σ]H2 для колеса определяют по общей зависимости (но с подстановкой соответствующих параметров для шестерни и колеса), учитывая влияние на контактную прочность долговечности (ресурса), шероховатости сопрягаемых поверхностей зубьев и окружной скорости:
[σ]H = [σ]HlimZNZRZV/SH.
Предел контактной выносливости [σ]Hlim вычисляют по эмпирическим формулам в зависимости от материала и способа термической обработки зубчатого колеса и средней твердости (HBср или HRCэ ср) на поверхности зубьев (табл. 2). [1, стр. 12]
Табл. 2 [1, табл. 2.2, стр. 13]
|
Способ термической или химико-термической обработки |
Средняя твердость на поверхности |
Сталь |
σHlim, МПа |
|
Улучшение Поверхностная закалка Цементация Азотирование |
< 350 HB 40…56 HRCэ > 56 HRCэ > 52 HRCэ |
Углеродистая и легированная Легированная |
2 HBср + 70 17 HRCэ ср + 200 23 HRCэ ср 1050 |
Для выбранной марки стали и ТО шестерни
[σ]Hlim 1 = 17∙HRCэ ср + 200 = 17∙48 + 200 = 1016 МПа.
Для выбранной марки стали и ТО колеса
[σ]Hlim 2 = 2∙HBср + 70 = 2∙246 + 70 = 562 МПа.
Минимальные значения коэффициента запаса прочности для зубчатых колес с однородной структурой материала (улучшенных, объемно закаленных) SH = 1,1; для зубчатых колес с поверхностным упрочнением SH = 1,2.
Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем SH 1 = 1.2.
Для выбранной ТО колеса (улучшение) принимаем SH 2 = 1.1.
Коэффициент долговечности ZN учитывает влияние ресурса
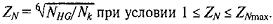
Число NHG циклов, соответсвующее перелому кривой усталости, определяют по средней твердости поверхностей зубьев [1, стр. 13]:
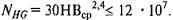
Твердость в единицах HRC переводят в единицы HB:
| HRCэ……… | 45 | 47 | 48 | 50 | 51 | 53 | 55 | 60 | 62 | 65 |
| HB…………. | 425 | 440 | 460 | 480 | 495 | 522 | 540 | 600 | 620 | 670 |
Переведенная средняя твердость поверхности зубьев для выбранного материала шестерни равна 451 HB.
NHG 1 = 30∙4512,4 = 70405590.
Для колеса
NHG 2 = 30∙2462,4 = 16464600.
Ресурс Nk передачи в числах циклов перемены напряжений при частоте вращения n, мин-1, и времени работы Lh, час:
Nk = 60nnзLh,
где nз — число вхождений в зацепление зуба рассчитываемого колеса за один его оборот (численно равно числу колес, находящихся в зацеплении с рассчитываемым). [1, стр. 13]
В общем случае суммарное время Lh (в ч) работы передачи вычисляют по формуле
Lh = L365Kгод24Kсут,
где L — число лет работы; Kгод — коэффициент годового использования передачи; Kсут — коэффициент суточного использования передачи.
Число зацеплений nз и для колеса и для шестерни в данном случае равно 1.
Lh = 8 ∙ 365 ∙ 0.55 ∙ 24 ∙ 0.87 = 33533.28, ч.
Для шестерни:
Nk ш = 60 ∙ 719.19 ∙ 1 ∙ 33533.28 = 1447007978.592.
Т.к. Nk ш > NHG, то принимаем Nk ш = NHG = 70405590. [1, стр. 13]
ZN ш = 1
Для колеса:
Nk кол = 60 ∙ 183 ∙ 1 ∙ 33533.28 = 368195414.4.
Т.к. Nk кол > NHG, то принимаем Nk кол = NHG = 16464600. [1, стр. 13]
ZN кол = 1
Коэффициент ZR, учитывающий влияние шероховатости сопряженных поверхностей зубьев, принимают для зубчатого колеса пары с более грубой поверхностью в зависимости от параметра Ra шероховатости (ZR = 1 — 0,9).
Большие значения соответствуют шлифованным и полированным поверхностям (Ra = 0,63 … 1,25 мкм).
Принимаем ZR как для шестерни так и для колеса равным 0,9.
Коэффициент ZV учитывает влияние окружной скорости V ( ZV = 1…1,15). Меньшие значения соответствуют твердым передачам, работающим при малых окружных скоростях (V до 5 м/с).
Принимаем ZV как для шестерни так и для колеса равным 1,05 — как удовлетворяющее в большинстве случаев.
Для шестерни:
[σ]H1 = [σ]HlimZN шZRZV/SH = 800.1 МПа.
Для колеса:
[σ]H2 = [σ]HlimZN колZRZV/SH = 482.81 МПа.
Допскаемое напряжение [σ]H для цилиндрических и конических передач с прямыми зубьями равно меньшему из допускаемых напряжений шестерни [σ]H1 и колеса [σ]H2. [1, стр. 14]
Принимаем минимальное допускаемое напряжение
[σ]H = 482.81 МПа.
2.3 Определение напряжений изгиба
Допускаемые напряжения изгиба зубьев шестерни [σ]F1 и колеса [σ]F2 определяют по общей зависимости (но с подстановкой соответсвующих параметров для шестерни и колеса), учитывая влияние на сопротивление усталости при изгибе долговечности (ресурса), шероховатости поверхности
выкружки (переходной поверхности между смежными зубьями) и реверса (двустороннего приложения) нагрузки:
[σ]F = [σ]FlimYNYRYA/SF.
Предел прочности [σ]Flim при отнулевом цикле напряжений вычисляют по эмпирическим формулам (табл. 3).
Табл. 3 [1, табл. 2.3., стр. 14]
|
Способ термической или химико-термической обработки |
Группа сталей |
Твердость зубьев |
σFlim, МПа |
|
|
на поверхности |
в сердцевине |
|||
|
Улучшение |
45, 40Х, 40ХН, 35ХМ |
< 350 HB |
< 350 HB |
1,75 HBср |
|
Закалка ТВЧ по контуру |
40Х, 40ХН, 35ХМ |
48 — 52 HRCэ |
27 — 35 HRCэ |
600 — 700 |
|
Закалка ТВЧ сквозная (m< 3мм) |
48 — 52 HRCэ |
48 — 52 HRCэ |
500 — 600 |
|
|
Цементация |
20Х, 20ХН2М, 18ХГТ, 25ХГМ, 12ХН3А |
57 – 62 HRCэ |
30 – 45 HRCэ |
750 – 800 |
|
Цементация с автоматическим |
850 — 950 |
|||
|
Азотирование |
38Х2МЮА, 40ХНМА |
< 67 HRCэ |
24 – 40 HRCэ |
12 HRCэ ср + 290 |
Принимаем для выбранной марки стали и ТО (Сталь 40Х, улучшение и закалка ТВЧ) шестерни
[σ]Flim 1 = 600 МПа.
Для колеса (Сталь 40Х, улучшение)
[σ]Flim 2 = 1,75 HBср = 1,75 ∙ 246 = 431 МПа.
Минимальное значение коэффициента запаса прочности: для цементованных и нитроцементованных зубчатых колес — SF = 1,55; для остальных — SF = 1,7.
Принимаем для шестерни (улучшение и закалка ТВЧ) SF 1 = 1.7.
Для колеса (улучшение) SF 2 = 1.7.
Коэффициент долговечности YN учитывает влияние ресурса:
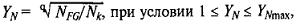
где YNmax = 4 и q = 6 — для улучшенных зубчатых колес; YNmax = 2,5 и q = 9 для закаленных и поверхностно упрочненных зубьев. Число циклов, соответсвующее перелому кривой усталости, NFG = 4 ∙ 106. [1, стр.15]
Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем YNmax 1 = 2.5 и q1 = 9.
Для выбранной ТО колеса (улучшение) принимаем YNmax 2 = 4 и q2 = 6.
Назначенный ресурс Nk вычисляют так же, как и при расчетах по контактным напряжениям.
В соотеветствии с кривой усталости напряжения σF не могут иметь значений меньших σFlim. Поэтому при Nk > Nsub>FG принимают Nk = NFG.
Для длительно работающих быстроходных передач Nk ≥ NFG и, следовательно YN = 1, что и учитывает первый знак неравенства в (2). Второй знак неравенства ограничивает допускаемые напряжения по условию предотвращения пластической деформации или хрупкого разрушения зуба.[1, стр.15]
Для шестерни:
Nk ш = 60 ∙ 719.19 ∙ 1 ∙ 33533.28 = 1447007978.592
Т.к. Nk ш > NFG, то принимаем Nk ш = NFG = 4000000.
YN ш = 1
Для колеса:
Nk кол = 60 ∙ 183 ∙ 1 ∙ 33533.28 = 368195414.4
Т.к. Nk кол > NFG, то принимаем Nk кол = NFG = 4000000.
YN кол = 1
Коэффициент YR, учитывающий влияние шероховатости переходной поверхности между зубьями, принимают: YR = 1 при шлифовании и зубофрезеровании с параметром шероъоватости RZ ≤ 40 мкм; YR = 1,05…1,2 при полировании (большие значения при улучшении и после закалки ТВЧ).
Принимаем YR = 1,1.
Коэффициент YA учитывает влияние двустороннего приложения нагрузки (реверса). При одностороннем приложении нагрузки YA = 1. При реверсивном нагружении и одинаковых нагрузке и числе циклов нагружения в прямом и обратном направлении (например, зубья сателлита в планетарной передаче): YA = 0,65 — для нормализованных и улучшенных сталей; YA = 0,75 — для закаленных и цементованных; YA = 0,9 — для азотированных.
Так как в проектируемой передаче планируется реверсивный ход, то с учетом ТО принимаем
для шестерни (улучшение и закалка ТВЧ) YA 1 = 0.75 ;
для колеса (улучшение) YA 2 = 0.65 .
Для шестерни:
[σ]F1 = [σ]Flim 1YN шYRYA 1/SF 1 = 291.18 МПа.
Для колеса:
[σ]F2 = [σ]Flim 2YN колYRYA 2/SF 2 = 181.27 МПа.
2.4 Проектный расчет
2.4.1 Межосевое расстояние
Предварительное значение межосевого растояния aw‘, мм:
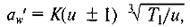
где знак «+» (в скобках) относят к внешнему зацеплению, знак «-» — к внутреннему; T1 — вращающий момент на шестерне (наибольший из длительно действующих), Н∙м; u — передаточное число.
Коэффициент K в зависимости от поверхностной твердости H1 и H2 зубьев шестерни и колеса соответсвенно имеет следующие значения [1, стр. 17]:
Поверхностная твердость и шестерни до 480 HB и колеса до 262 HB, поэтому коэффициент K принимаем равным 8.
U = 3.93;
aw‘ = 113 мм.
Окружную скорость ν, м/с, вычисляют по формуле:
ν = 1.73 м/с.
Степень точности зубчатой передачи назначают по табл. 4:
Табл. 4 [1, табл. 2.5, стр. 17]
|
Степень точности по ГОСТ 1643-81 |
Допустимая окружная скорость υ, |
|||
|
прямозубых |
непрямозубых |
|||
|
цилиндрических |
конических |
цилиндрических |
конических |
|
|
6 (передачи повышенной 7 (передачи нормальной 8 (передачи пониженной 9 (передачи низкой |
до 20 до 12 до 6 до 2 |
до 12 до 8 до 4 до 1,5 |
до 30 до 20 до 10 до 4 |
до 20 до 10 до 7 до 3 |
При окружно скорости 1.73 м/с (что меньше 4 м/с) выбираем степень точности 9.
Уточняем предварительно найденное значение межосевого расстояния:
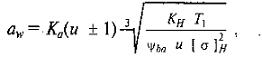
где Ka = 450 — для прямозубых колес; Ka = 410 — для косозубых и шевронных, МПа; [σ]H — в МПа.
ψba — коэффициент ширины принимают из ряда стандартных чисел: 0,1; 0,15; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63 в зависимости от положения колес относительно опор:
при симметричном расположении 0,315-0,5;
при несимметричном 0,25-0,4;
при консольном расположении одного или обоих колес 0,25-0,4;
Для шевронных передач ψba = 0,4 — 0,63; для коробок передач ψba = 0,1 — 0,2; для передач внутреннего зацепления ψba = 0,2 (u+1)/(u-1). Меньшие значения ψba — для передач с твердостью зубьев H ≥ 45HRC.
Принимаем ψba = 0,31.
Коэффициент нагрузки в расчетах на контактную прочность
KH = KHνKHβKHα.
Коэффициент KHν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса.
Значения KHν принимают по табл. 5 в зависимости от степени точности передачи по нормам плавности, окружной скоросто и твердости рабочих поверхностей.
Табл. 5 [1, табл. 2.6, стр. 18]
|
Степень точности по ГОСТ 1643-81 |
Твердость на поверхности зубьев колеса |
Значения KHυ при |
||||
|
1 |
3 |
5 |
8 |
10 |
||
|
6 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,10 1,04 |
1,16 1,06 |
1,20 1,08 |
|
≤ 350 HB |
1,03 1,01 |
1,09 1,03 |
1,16 1,06 |
1,25 1,09 |
1,32 1,13 |
|
|
7 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,12 1,05 |
1,19 1,08 |
1,25 1,10 |
|
≤ 350 HB |
1,04 1,02 |
1,12 1,06 |
1,20 1,08 |
1,32 1,13 |
1,40 1,16 |
|
|
8 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,15 1,06 |
1,24 1,09 |
1,30 1,12 |
|
≤ 350 HB |
1,05 1,02 |
1,15 1,06 |
1,24 1,10 |
1,38 1,15 |
1,48 1,19 |
|
|
9 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,17 1,07 |
1,28 1,11 |
1,35 1,14 |
|
≤ 350 HB |
1,06 1,02 |
1,12 1,06 |
1,28 1,11 |
1,45 1,18 |
1,56 1,22 |
Примечание. В числителе приведены значения для прямозубых, в знаменателе — для косозубых хубчатых колёс.
Для степени точности 9, максимальной окружной скорости 1.73 м/с, твердости HB≤350 принимаем KHν = 1.06.
Коэффициент KHβ учитывает неравномерность распределения нагрузки по длине контактных линий, обусловливаемую погрешностями изготовления (погрешностями направления зуба) и упругими деформациями валов, подшипников.
Зубья зубчатых колес могут прирабатываться: в результате повышенного местного изнашивания распределение нагрузки становится более равномерным. Поэтому рассматривают коэффициенты неравномерности распределения нагрузки в начальный период работы KHβ0 и после приработки KHβ.
Значение коэффициента KHβ0 принимают по таблице 6 в зависимости от коэффициента ψbd = b2/d1, схемы передачии твердости зубьев.
Так как ширина колеса и диаметр шестерни еще не определены, значение коэффициента ψbd вычисляют ориентировочно:
ψbd = 0,5ψba (u 
ψbd = 0,5 ∙ 0.31 ∙ (3.93 + 1) = 0.8.
Коэффициент KHβ определяют по формуле:
KHβ = 1 + (KHβ0 — 1)KHw,
где KHw — коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 7).
Коэффицент KHα определяют по формуле:
KHα = 1 + (K0Hα — 1)KHw,
где KHw — коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 7).
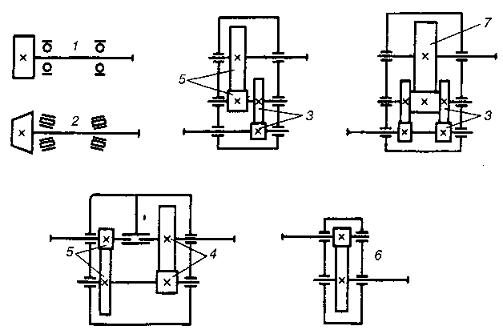
Рис. 1 [1, рис. 2.4, стр. 19]
Табл. 6 [1, табл. 2.7, стр. 19]
|
Ψbd |
Твердость на поверхности зубьев колеса |
Значения KHβo для |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
0,4 0,6 0,8 1,0 1,2 1,4 1,6 |
≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB |
1.17 1.43 1.27 — 1.45 — — — — — — — — — |
1,12 1,24 1,18 1,43 1,27 — — — — — — — — — |
1,05 1,11 1,08 1,20 1,12 1,28 1,15 1,38 1,18 1,48 1,23 — 1,28 — |
1,03 1,08 1,05 1,13 1,08 1,20 1,10 1,27 1,13 1,34 1,17 1,42 1,20 — |
1,02 1,05 1,04 1,08 1,05 1,13 1,07 1,18 1,08 1,25 1,12 1,31 1,15 — |
1,02 1,02 1,03 1,05 1,03 1,07 1,04 1,11 1,06 1,15 1,08 1,20 1,11 1,26 |
1,01 1,01 1,02 1,02 1,02 1,04 1,02 1,06 1,03 1,08 1,04 1,12 1,06 1,16 |
Табл. 7 [1, табл. 2.8, стр. 19]
|
Твердость на поверхности зубьев |
Значения KHw при |
|||||
|
1 |
3 |
5 |
8 |
10 |
15 |
|
|
200 HB 250 HB 300 HB 350 HB 43 HRCэ 47 HRCэ 51 HRCэ 60 HRCэ |
0,19 0,26 0,35 0,45 0,53 0,63 0,71 0,80 |
0,20 0,28 0,37 0,46 0,57 0,70 0,90 0,90 |
0,22 0,32 0,41 0,53 0,63 0,78 1,00 1,00 |
0,27 0,39 0,50 0,64 0,78 0,98 1,00 1,00 |
0,32 0,45 0,58 0,73 0,91 1,00 1,00 1,00 |
0,54 0,67 0,87 1,00 1,00 1,00 1,00 1,00 |
Начальное значение коэффициента K0Hα распределения нагрузки между зубьямив связи с погрешностями изготовления (погрешностями шага зацепления и направления зуба) определяют в зависимости от степени точности (nст = 5, 6, 7, 8, 9) по нормам плавности:
для прямозубых передач
K0Hα = 1 + 0,06(nст — 5), при условии 1 ≤ K0Hα ≤ 1,25;
для косозубых передач
K0Hα = 1 + A(nст — 5), при условии 1 ≤ K0Hα ≤ 1,6,
где A = 0,15 — для зубчатых колес с твердостью H1 и H2 > 350 HB и A = 0,25 при H1 и H2 ≤ 350 HB или H1 > 350 HB и H2 ≤ 350 HB.
K0Hα = 1 + 0.25(9 — 5) = 2
Принимаем коэффициент KHw по табл. 7 равным (ближайшее значение твердости по таблице 250 HB или 23 HRC к твердости колеса 262 HB) 0.28.
KHα = 1 + (2 — 1)0.28 = 1.28;
Принимаем коэффициент KHβ0 по табл. 6 (схема 3) равным 1.12.
KHβ = 1 + (1.12 — 1) 0.28 = 1.0336;
KH = 1.06 ∙ 1.0336 ∙ 1.28 = 1.4.
Уточнённое значение межосевого расстояния:
aw = 155 мм;
Вычисленное значение межосевого расстояния округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra 40 [1, табл. 24.1]. При крупносерийном производстве редукторов aw округляют до ближайшего стандартного значения: 50; 63; 71; 80; 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 260; 280; 300; 320; 340; 360; 380; 400 мм. [1, стр. 20]
Принимаем aw = 160 мм;
2.4.2 Предварительные основные размеры колеса
Делительный диаметр:
d2 = 2awu/(u 
d2 = 2 ∙ 160 ∙ 3.93 / (3.93 + 1) = 255.09 мм;
Ширина:
b2 = ψba ∙ aw;
b2 = 0.31 ∙ 160 = 50 мм.
Принимаем выбранное из стандартного ряда Ra 40 значение ширины:
b2 = 50 мм.
2.4.3 Модуль передачи
Максимально допустимый модуль mmax, мм, определяют из условия неподрезания зубьев у основания [1, стр. 20]
mmax ≈ 2aw/[17(u 
mmax ≈ 2 ∙ 160 / [17(3.93 + 1)] = 3.82 мм.
Минимальное значение модуля mmin, мм, определяют из условия прочности [1, стр. 20]:
где Km = 3,4 ∙ 103 для прямозубых и Km = 2,8 ∙ 103 для косозубых передач; вместо [σ]F подставляют меньшее из значений [σ]F2 и [σ]F1.
Табл. 8 [1, табл. 2.9, стр. 20]
|
Степень точности по ГОСТ 1643-81 |
Твердость на поверхности зубьев колеса |
Значения KFυ при |
||||
|
1 |
3 |
5 |
8 |
10 |
||
|
6 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,10 1,06 |
1,16 1,06 |
1,20 1,08 |
|
≤ 350 HB |
1,06 1,03 |
1,18 1,09 |
1,32 1,13 |
1,50 1,20 |
1,64 1,26 |
|
|
7 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,12 1,05 |
1,19 1,08 |
1,25 1,10 |
|
≤ 350 HB |
1,08 1,03 |
1,24 1,09 |
1,40 1,16 |
1,64 1,25 |
1,80 1,32 |
|
|
8 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,15 1,06 |
1,24 1,09 |
1,30 1,12 |
|
≤ 350 HB |
1,10 1,04 |
1,30 1,12 |
1,48 1,19 |
1,77 1,30 |
1,96 1,38 |
|
|
9 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,17 1,07 |
1,28 1,11 |
1,35 1,14 |
|
≤ 350 HB |
1,11 1,04 |
1,33 1,12 |
1,56 1,22 |
1,90 1,36 |
— 1,45 |
Примечание. В числителе приведены значения для прямозубых, в знаменателе — для косозубых зубчатых колес.
Коэффициент нагрузки при расчете по напряжениям изгиба
KF = KFνKFβKFα.
Коэффициент KFν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления шестерни и колеса. Значения KFν принимают по табл. 8 [1, табл. 2.9, стр. 20] в зависимости от степени точности по нормам плавности, окружной скорости и твердости рабочих поверхностей.
Для степени точности 9, максимальной окружной 1.73 м/с, твердости HB≤350 принимаем KFν=1.12.
KFβ — коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца, оценивают по формуле
KFα — коэффициент, учитывающий влияние погрешности изготовления шестерни и колеса на распределение нагрузки между зубьями, определяют так же как при расчетах на контактную прочность: KFα = KFα0.
В связи с менее благоприятным влиянием приработки на изгибную прочность, чем на контактную, и более тяжелыми последствиями из-за неточности при определении напряжений изгиба приработку зубьев при вычислении коэффициентов KFβ и KFα не учитывают. [1, стр. 21]
KF = KFν = 1.12.
mmin = 0.55 мм.
Из полученного диапазона (mmin…mmax) модулей принимают меньшее значение m, согласуя его со стандартным (ряд 1 следует предпочитать ряду 2) [1, стр. 21]:
| Ряд 1, мм ….. | 1,0; | 1,25; | 1,5; | 2,0; | 2,5; | 3,0; | 4,0; | 5,0; | 6,0; | 8,0; | 10,0; |
| Ряд 2, мм ….. | 1,12; | 1,37; | 1,75; | 2,25; | 2,75; | 3,5; | 4,5; | 5,5; | 7,0; | 9,0; |
Принимаем из стандартного ряда m = 1.75 мм.
Значения модулей m < 1 при твердости ≤ 350 HB и m<1,5 при твердости ≥ 40 HRCэ для силовых передач использовать нежелательно. [1, стр. 21]
2.4.4 Суммарное число зубьев и угол наклона
Минимальный угол наклона зубьев косозубых колес [1, стр. 21]
βmin = arcsin(4m/b2);
βmin = arcsin(4∙1.75/50) = 8.05o.
Суммарное число зубьев
zs = 2awcosβmin/m = 181.06.
Полученное значение zs округляют в меньшую сторону до целого числа и определяют действительное значение угла β наклона зуба:
β = arccos[zsm/(2aw)].
zs = 181;
β = arccos[181 ∙ 1.75/(2∙160)] = 8.17o.
Справочно: для косозубых колес β = 8…20o, для шевронных — β = 25…40o.
2.4.5 Число зубьев шестерни и колеса
Число зубьев шестерни [1, стр. 21]
z1 = zs / (u 
z1 = 181 / (3.93 + 1) = 36.71.
Значение z1 округляют в ближайшую сторону до целого числа. [1, стр. 21]
z1 = 37.
Число зубьев колеса внешнего зацепления z2 = zs — z1.
z2 = 181 — 37 = 144.
2.4.6 Фактическое передаточное число
uф = z2/z1 = 144/37 = 3.89.
Фактические значения передаточных чисел не должны отличаться от номинальных более чем на: 3% — для одноступенчатых, 4% — для двухступенчатых и 5% — для многоступенчатых редукторов.[1, стр. 22]
Отклонение от номинального передаточного числа
Δ = (u — uф)/u = 1.02 %.
2.4.7 Диаметры колес
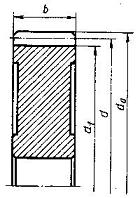
Рис. 2 [1, рис. 2.5, стр. 22]
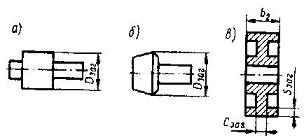
Рис. 3 [1, рис. 2.6, стр. 22]
Делительные диаметры d [1, стр. 22]:
шестерни…………………………………..d1 = z1m/cosβ;
колеса внешнего зацепления…………d2 = 2aw — d1;
колеса внутреннего зацепления……..d2 = 2aw + d1;
d1 = 37 ∙ 1.75 / cos8.17o = 65.41 мм;
d2 = 2 ∙ 160 — 65.41 = 254.59 мм.
Диаметры da и df окружностей вершин и впадин зубьев колес внешнего зацепления [1, стр. 22]:
da1 = d1 + 2(1 + x1 — y)m;
df1 = d1 — 2(1,25 — x1)m;
da2 = d2 + 2(1 + x2 — y)m;
df2 = d2 — 2(1,25 — x2)m;
где x1 и x2 — коэффициенты смещения у шестерни и колеса; y = -(aw — a)/m — коэффициент воспринимаемого смещения; a — делительное межосевое расстояние: a = 0,5m(z2 
a = 0.5 ∙ 1.75 ∙ (144+37) = 158.38 мм;
y = -(160 — 158.38)/1.75 = -0.93;
da1 = 65.41 + 2 ∙ [1-(-0.93)] ∙ 1.75 = 72.17 мм;
df1 = 65.41 — 2 ∙ 1,25 ∙ 1.75 = 61.04 мм;
da2 = 254.59 + 2 ∙ [1-(-0.93)] ∙ 1.75 = 261.35 мм;
df2 = 254.59 — 2 ∙ 1,25 ∙ 1.75 = 250.22 мм;
2.4.8 Размеры заготовок
Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, чтобы размеры Dзаг, Cзаг, Sзаг заготовок колес не превышали предельно допустимых значений Dпр, Sпр (табл. 1 [1, табл. 2.1, стр. 11]) [1, стр. 22]:
Dзаг ≤ Dпр; Cзаг ≤ Cпр; Sзаг ≤ Sпр.
Значения Dзаг, Cзаг, Sзаг (мм) вычисляются по формулам: для цилиндрической шестерни (рис. 3, а) Dзаг = da + 6 мм; для колеса с выточками (рис. 3, в) Cзаг = 0,5b2 и Sзаг =8m; для колеса без выточек (рис. 2) Sзаг = b2 + 4 мм.
Dзаг1 = 72.17 + 6 мм = 78.17 мм;
Dзаг2 = 261.35 + 6 мм = 267.35 мм;
Sзаг2 = 50 + 4 мм = 54 мм.
2.4.9 Проверка зубьев колес по контактным напряжениям
Расчетное значение контактного напряжения [1, стр. 23]
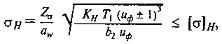
где Zσ = 9600 для прямозубых и Zσ = 8400 для косозубых передач, МПа1/2.
σH = 460.44 МПа;
Если расчетное напряжение σH меньше допустимого [σH] в пределах 15-20% или σH больше [σH] в пределах 5%, то ранее принятые параметры передачи принимают за окончательные. В противном случае необходим пересчет. [1, стр. 23]
σH меньше [σH] на 4.63%.
Ранее принятые параметры передачи принимаем за окончательные.
2.4.10 Силы в зацеплении
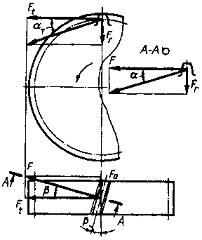
Рис. 4 [1, рис. 2.7, стр. 23]
Окружная
Ft = 2∙103∙T1/d1;
Ft = 2∙103∙91.39/65.41 = 2794.37 Н;
радиальная
Fr = Fttgα/cosβ
(для стандартного угла α=20o tgα=0,364);
Fr = 2794.37 ∙ 0.364/cos8.17o = 1027.59 Н;
осевая
Fa = Fttgβ;
Fa = 2794.37 ∙ tg8.17o = 401.32 Н.
3. Расчет цилиндрической передачи второй ступени
3.1 Выбор твердости, термической обработки и материала колес
В зависимости от вида изделия, условий его эксплуатации и требований к габаритным размерам выбирают необходимую твердость колес и материалы
для их изготовления. Для силовых передач чаще всего применяют стали. Передачи со стальными зубчатыми колесами имеют минимальную массу и габариты, тем меньше,
чем выше твердость рабочих поверхностей зубьев, которая в свою очередь зависит от марки стали и варианта термической обработки (табл. 9). [1, стр.11]
Табл. 9 [1, табл. 2.1, стр. 11]
|
Марка стали |
Термообработка |
Предельные размеры заготовки, мм |
Твердость зубьев |
σт, МПа |
||
|
Dпр |
Sпр |
в сердцевине |
на поверхности |
|||
|
45 |
Улучшение |
125 |
80 |
235-262 HB |
235-262 HB |
540 |
|
Улучшение |
80 |
50 |
269-302 HB |
269-302 HB |
650 |
|
|
40Х |
Улучшение |
200 |
125 |
235-262 HB |
235-262 HB |
640 |
|
Улучшение |
125 |
80 |
269-302 HB |
269-302 HB |
750 |
|
|
Улучшение и закалка ТВЧ |
125 |
80 |
269-302 HB |
45-50 HRCэ |
750 |
|
|
40ХН, 35ХМ |
Улучшение |
315 |
200 |
235-262 HB |
235-262 HB |
630 |
|
Улучшение |
200 |
125 |
269-302 HB |
269-302 HB |
750 |
|
|
Улучшение и закалка ТВЧ |
200 |
125 |
269-302 HB |
48-53 HRCэ |
750 |
|
|
40ХНМА, 38Х2МЮА |
Улучшение и азотирование |
125 |
80 |
269-302 HB |
50-56 HRCэ |
780 |
|
20Х, 20ХН2М, 18ХГТ, 12ХН3А, 25ХГМ |
Улучшение, Цементация и закалка |
200 |
125 |
300-400 HB |
56-63 HRCэ |
800 |
На практике в основном применяют следующие варианты термической обработки (т.о.):
I — т.о. колеса — улучшение, твердость 235…262 HB; т.о. шестерни — улучшение, твердость 269…302 HB. Марки стали одинаковы для колеса и шестерни: 45, 40Х, 35 ХМ и др. Зубья колес из улучшаемых сталей хорошо прирабатываются и не подвержены
хрупкому разрушению, но имеют ограниченную нагрузочную способность. Применяют в слабо- и средненагруженных передачах.
II — т.о. колеса — улучшение, твердость 269…302 HB; т.о. шестерни — улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки стали (см. табл. 9) 45…50 HRCэ, 48…53 HRCэ. Твердость сердцевины зуба соотвествует термообработке улучшение. Марки сталей одинаковы для колеса и шестерни: 40Х, 40ХН, 35ХМ и др.
III — т.о. колеса и шестерни одинаковая — улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки сатили: 45…50 HRCэ, 48…53 HRCэ. Марки сталей одинаковы для колеса и шестерни: 40Х, 40ХН, 35ХМ и др.
IV — т.о. колеса — улучшение и закалка ТВЧ, твердость поверхности в зависимости от марки стали (табл.9) 45…50 HRCэ, 48…53 HRCэ; т.о. шестерни — улучшение, цементация и закалка, твердость поверхности 56…63 HRCэ. Материал шестерни — стали марок 20Х, 20ХН2М, 18ХГТ, 12ХН3А и др.
V — т.о. колеса и шестерни одинаковая — улучшение, цементация и закалка, твердость поверхности 56…63 HRCэ. Цементация (поверхностное насыщение углеродом) с последующей закалкой наряду с большой твердостью поверхностных слоев обеспечивает и высокую прочность зубьев на изгиб. Марки сталей одинаковы для колеса и шестерни: 20Х, 20ХН2М, 18ХГТ, 12ХН3А, 25 ХГМ и др. [1, стр.11-12]
Шестерня.
Материал — Сталь 40Х. Назначаем термическую обработку шестерни — улучшение и закалка ТВЧ.
Предельные размеры заготовки: Dпр = 125 мм, Sпр = 80 мм.
Твердость зубьев: в сердцевине до 302 HB, на поверхности до 50 HRCэ.
Предельное напряжение σT = 750 МПа.
Колесо.
Материал — Сталь 40Х. Назначаем термическую обработку шестерни — улучшение.
Предельные размеры заготовки: Dпр = 200 мм, Sпр = 125 мм.
Твердость зубьев: в сердцевине до 262 HB, на поверхности до 262 HB.
Предельное напряжение σT = 640 МПа.
3.2 Определение допускаемых контактных напряжений
Допускаемые контактные напряжения [σ]H1 для шестерни и [σ]H2 для колеса определяют по общей зависимости (но с подстановкой соответствующих параметров для шестерни и колеса), учитывая влияние на контактную прочность долговечности (ресурса), шероховатости сопрягаемых поверхностей зубьев и окружной скорости:
[σ]H = [σ]HlimZNZRZV/SH.
Предел контактной выносливости [σ]Hlim вычисляют по эмпирическим формулам в зависимости от материала и способа термической обработки зубчатого колеса и средней твердости (HBср или HRCэ ср) на поверхности зубьев (табл. 10). [1, стр. 12]
Табл. 10 [1, табл. 2.2, стр. 13]
|
Способ термической или химико-термической обработки |
Средняя твердость на поверхности |
Сталь |
σHlim, МПа |
|
Улучшение Поверхностная закалка Цементация Азотирование |
< 350 HB 40…56 HRCэ > 56 HRCэ > 52 HRCэ |
Углеродистая и легированная Легированная |
2 HBср + 70 17 HRCэ ср + 200 23 HRCэ ср 1050 |
Для выбранной марки стали и ТО шестерни
[σ]Hlim 1 = 17∙HRCэ ср + 200 = 17∙48 + 200 = 1016 МПа.
Для выбранной марки стали и ТО колеса
[σ]Hlim 2 = 2∙HBср + 70 = 2∙246 + 70 = 562 МПа.
Минимальные значения коэффициента запаса прочности для зубчатых колес с однородной структурой материала (улучшенных, объемно закаленных) SH = 1,1; для зубчатых колес с поверхностным упрочнением SH = 1,2.
Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем SH 1 = 1.2.
Для выбранной ТО колеса (улучшение) принимаем SH 2 = 1.1.
Коэффициент долговечности ZN учитывает влияние ресурса
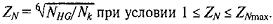
Число NHG циклов, соответсвующее перелому кривой усталости, определяют по средней твердости поверхностей зубьев [1, стр. 13]:
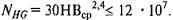
Твердость в единицах HRC переводят в единицы HB:
| HRCэ……… | 45 | 47 | 48 | 50 | 51 | 53 | 55 | 60 | 62 | 65 |
| HB…………. | 425 | 440 | 460 | 480 | 495 | 522 | 540 | 600 | 620 | 670 |
Переведенная средняя твердость поверхности зубьев для выбранного материала шестерни равна 451 HB.
NHG 1 = 30∙4512,4 = 70405590.
Для колеса
NHG 2 = 30∙2462,4 = 16464600.
Ресурс Nk передачи в числах циклов перемены напряжений при частоте вращения n, мин-1, и времени работы Lh, час:
Nk = 60nnзLh,
где nз — число вхождений в зацепление зуба рассчитываемого колеса за один его оборот (численно равно числу колес, находящихся в зацеплении с рассчитываемым). [1, стр. 13]
В общем случае суммарное время Lh (в ч) работы передачи вычисляют по формуле
Lh = L365Kгод24Kсут,
где L — число лет работы; Kгод — коэффициент годового использования передачи; Kсут — коэффициент суточного использования передачи.
Число зацеплений nз и для колеса и для шестерни в данном случае равно 1.
Lh = 8 ∙ 365 ∙ 0.55 ∙ 24 ∙ 0.87 = 33533.28, ч.
Для шестерни:
Nk ш = 60 ∙ 183 ∙ 1 ∙ 33533.28 = 368195414.4.
Т.к. Nk ш > NHG, то принимаем Nk ш = NHG = 70405590. [1, стр. 13]
ZN ш = 1
Для колеса:
Nk кол = 60 ∙ 183 ∙ 1 ∙ 33533.28 = 368195414.4.
Т.к. Nk кол > NHG, то принимаем Nk кол = NHG = 16464600. [1, стр. 13]
ZN кол = 1
Коэффициент ZR, учитывающий влияние шероховатости сопряженных поверхностей зубьев, принимают для зубчатого колеса пары с более грубой поверхностью в зависимости от параметра Ra шероховатости (ZR = 1 — 0,9).
Большие значения соответствуют шлифованным и полированным поверхностям (Ra = 0,63 … 1,25 мкм).
Принимаем ZR как для шестерни так и для колеса равным 0,9.
Коэффициент ZV учитывает влияние окружной скорости V ( ZV = 1…1,15). Меньшие значения соответствуют твердым передачам, работающим при малых окружных скоростях (V до 5 м/с).
Принимаем ZV как для шестерни так и для колеса равным 1,05 — как удовлетворяющее в большинстве случаев.
Для шестерни:
[σ]H1 = [σ]HlimZN шZRZV/SH = 800.1 МПа.
Для колеса:
[σ]H2 = [σ]HlimZN колZRZV/SH = 482.81 МПа.
Допскаемое напряжение [σ]H для цилиндрических и конических передач с прямыми зубьями равно меньшему из допускаемых напряжений шестерни [σ]H1 и колеса [σ]H2. [1, стр. 14]
Принимаем минимальное допускаемое напряжение
[σ]H = 482.81 МПа.
3.3 Определение напряжений изгиба
Допускаемые напряжения изгиба зубьев шестерни [σ]F1 и колеса [σ]F2 определяют по общей зависимости (но с подстановкой соответсвующих параметров для шестерни и колеса), учитывая влияние на сопротивление усталости при изгибе долговечности (ресурса), шероховатости поверхности
выкружки (переходной поверхности между смежными зубьями) и реверса (двустороннего приложения) нагрузки:
[σ]F = [σ]FlimYNYRYA/SF.
Предел прочности [σ]Flim при отнулевом цикле напряжений вычисляют по эмпирическим формулам (табл. 11).
Табл. 11 [1, табл. 2.3., стр. 14]
|
Способ термической или химико-термической обработки |
Группа сталей |
Твердость зубьев |
σFlim, МПа |
|
|
на поверхности |
в сердцевине |
|||
|
Улучшение |
45, 40Х, 40ХН, 35ХМ |
< 350 HB |
< 350 HB |
1,75 HBср |
|
Закалка ТВЧ по контуру |
40Х, 40ХН, 35ХМ |
48 — 52 HRCэ |
27 — 35 HRCэ |
600 — 700 |
|
Закалка ТВЧ сквозная (m< 3мм) |
48 — 52 HRCэ |
48 — 52 HRCэ |
500 — 600 |
|
|
Цементация |
20Х, 20ХН2М, 18ХГТ, 25ХГМ, 12ХН3А |
57 – 62 HRCэ |
30 – 45 HRCэ |
750 – 800 |
|
Цементация с автоматическим |
850 — 950 |
|||
|
Азотирование |
38Х2МЮА, 40ХНМА |
< 67 HRCэ |
24 – 40 HRCэ |
12 HRCэ ср + 290 |
Принимаем для выбранной марки стали и ТО (Сталь 40Х, улучшение и закалка ТВЧ) шестерни
[σ]Flim 1 = 600 МПа.
Для колеса (Сталь 40Х, улучшение)
[σ]Flim 2 = 1,75 HBср = 1,75 ∙ 246 = 431 МПа.
Минимальное значение коэффициента запаса прочности: для цементованных и нитроцементованных зубчатых колес — SF = 1,55; для остальных — SF = 1,7.
Принимаем для шестерни (улучшение и закалка ТВЧ) SF 1 = 1.7.
Для колеса (улучшение) SF 2 = 1.7.
Коэффициент долговечности YN учитывает влияние ресурса:
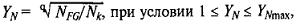
где YNmax = 4 и q = 6 — для улучшенных зубчатых колес; YNmax = 2,5 и q = 9 для закаленных и поверхностно упрочненных зубьев. Число циклов, соответсвующее перелому кривой усталости, NFG = 4 ∙ 106. [1, стр.15]
Для выбранной ТО шестерни (улучшение и закалка ТВЧ) принимаем YNmax 1 = 2.5 и q1 = 9.
Для выбранной ТО колеса (улучшение) принимаем YNmax 2 = 4 и q2 = 6.
Назначенный ресурс Nk вычисляют так же, как и при расчетах по контактным напряжениям.
В соотеветствии с кривой усталости напряжения σF не могут иметь значений меньших σFlim. Поэтому при Nk > Nsub>FG принимают Nk = NFG.
Для длительно работающих быстроходных передач Nk ≥ NFG и, следовательно YN = 1, что и учитывает первый знак неравенства в (2). Второй знак неравенства ограничивает допускаемые напряжения по условию предотвращения пластической деформации или хрупкого разрушения зуба.[1, стр.15]
Для шестерни:
Nk ш = 60 ∙ 183 ∙ 1 ∙ 33533.28 = 368195414.4
Т.к. Nk ш > NFG, то принимаем Nk ш = NFG = 4000000.
YN ш = 1
Для колеса:
Nk кол = 60 ∙ 183 ∙ 1 ∙ 33533.28 = 368195414.4
Т.к. Nk кол > NFG, то принимаем Nk кол = NFG = 4000000.
YN кол = 1
Коэффициент YR, учитывающий влияние шероховатости переходной поверхности между зубьями, принимают: YR = 1 при шлифовании и зубофрезеровании с параметром шероъоватости RZ ≤ 40 мкм; YR = 1,05…1,2 при полировании (большие значения при улучшении и после закалки ТВЧ).
Принимаем YR = 1,1.
Коэффициент YA учитывает влияние двустороннего приложения нагрузки (реверса). При одностороннем приложении нагрузки YA = 1. При реверсивном нагружении и одинаковых нагрузке и числе циклов нагружения в прямом и обратном направлении (например, зубья сателлита в планетарной передаче): YA = 0,65 — для нормализованных и улучшенных сталей; YA = 0,75 — для закаленных и цементованных; YA = 0,9 — для азотированных.
Так как в проектируемой передаче планируется реверсивный ход, то с учетом ТО принимаем
для шестерни (улучшение и закалка ТВЧ) YA 1 = 0.75 ;
для колеса (улучшение) YA 2 = 0.65 .
Для шестерни:
[σ]F1 = [σ]Flim 1YN шYRYA 1/SF 1 = 291.18 МПа.
Для колеса:
[σ]F2 = [σ]Flim 2YN колYRYA 2/SF 2 = 181.27 МПа.
3.4 Проектный расчет
3.4.1 Межосевое расстояние
Предварительное значение межосевого растояния aw‘, мм:
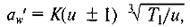
где знак «+» (в скобках) относят к внешнему зацеплению, знак «-» — к внутреннему; T1 — вращающий момент на шестерне (наибольший из длительно действующих), Н∙м; u — передаточное число.
Коэффициент K в зависимости от поверхностной твердости H1 и H2 зубьев шестерни и колеса соответсвенно имеет следующие значения [1, стр. 17]:
Поверхностная твердость и шестерни до 480 HB и колеса до 262 HB, поэтому коэффициент K принимаем равным 8.
U = 3.05;
aw‘ = 157 мм.
Окружную скорость ν, м/с, вычисляют по формуле:
ν = 0.74 м/с.
Степень точности зубчатой передачи назначают по табл. 12:
Табл. 12 [1, табл. 2.5, стр. 17]
|
Степень точности по ГОСТ 1643-81 |
Допустимая окружная скорость υ, |
|||
|
прямозубых |
непрямозубых |
|||
|
цилиндрических |
конических |
цилиндрических |
конических |
|
|
6 (передачи повышенной 7 (передачи нормальной 8 (передачи пониженной 9 (передачи низкой |
до 20 до 12 до 6 до 2 |
до 12 до 8 до 4 до 1,5 |
до 30 до 20 до 10 до 4 |
до 20 до 10 до 7 до 3 |
При окружно скорости 0.74 м/с (что меньше 4 м/с) выбираем степень точности 9.
Уточняем предварительно найденное значение межосевого расстояния:
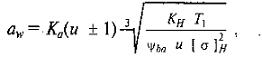
где Ka = 450 — для прямозубых колес; Ka = 410 — для косозубых и шевронных, МПа; [σ]H — в МПа.
ψba — коэффициент ширины принимают из ряда стандартных чисел: 0,1; 0,15; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63 в зависимости от положения колес относительно опор:
при симметричном расположении 0,315-0,5;
при несимметричном 0,25-0,4;
при консольном расположении одного или обоих колес 0,25-0,4;
Для шевронных передач ψba = 0,4 — 0,63; для коробок передач ψba = 0,1 — 0,2; для передач внутреннего зацепления ψba = 0,2 (u+1)/(u-1). Меньшие значения ψba — для передач с твердостью зубьев H ≥ 45HRC.
Принимаем ψba = 0,31.
Коэффициент нагрузки в расчетах на контактную прочность
KH = KHνKHβKHα.
Коэффициент KHν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления и погрешностями профилей зубьев шестерни и колеса.
Значения KHν принимают по табл. 13 в зависимости от степени точности передачи по нормам плавности, окружной скоросто и твердости рабочих поверхностей.
Табл. 13 [1, табл. 2.6, стр. 18]
|
Степень точности по ГОСТ 1643-81 |
Твердость на поверхности зубьев колеса |
Значения KHυ при |
||||
|
1 |
3 |
5 |
8 |
10 |
||
|
6 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,10 1,04 |
1,16 1,06 |
1,20 1,08 |
|
≤ 350 HB |
1,03 1,01 |
1,09 1,03 |
1,16 1,06 |
1,25 1,09 |
1,32 1,13 |
|
|
7 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,12 1,05 |
1,19 1,08 |
1,25 1,10 |
|
≤ 350 HB |
1,04 1,02 |
1,12 1,06 |
1,20 1,08 |
1,32 1,13 |
1,40 1,16 |
|
|
8 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,15 1,06 |
1,24 1,09 |
1,30 1,12 |
|
≤ 350 HB |
1,05 1,02 |
1,15 1,06 |
1,24 1,10 |
1,38 1,15 |
1,48 1,19 |
|
|
9 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,17 1,07 |
1,28 1,11 |
1,35 1,14 |
|
≤ 350 HB |
1,06 1,02 |
1,12 1,06 |
1,28 1,11 |
1,45 1,18 |
1,56 1,22 |
Примечание. В числителе приведены значения для прямозубых, в знаменателе — для косозубых хубчатых колёс.
Для степени точности 9, максимальной окружной скорости 0.74 м/с, твердости HB≤350 принимаем KHν = 1.02.
Коэффициент KHβ учитывает неравномерность распределения нагрузки по длине контактных линий, обусловливаемую погрешностями изготовления (погрешностями направления зуба) и упругими деформациями валов, подшипников.
Зубья зубчатых колес могут прирабатываться: в результате повышенного местного изнашивания распределение нагрузки становится более равномерным. Поэтому рассматривают коэффициенты неравномерности распределения нагрузки в начальный период работы KHβ0 и после приработки KHβ.
Значение коэффициента KHβ0 принимают по таблице 14 в зависимости от коэффициента ψbd = b2/d1, схемы передачии твердости зубьев.
Так как ширина колеса и диаметр шестерни еще не определены, значение коэффициента ψbd вычисляют ориентировочно:
ψbd = 0,5ψba (u 
ψbd = 0,5 ∙ 0.31 ∙ (3.05 + 1) = 0.6.
Коэффициент KHβ определяют по формуле:
KHβ = 1 + (KHβ0 — 1)KHw,
где KHw — коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 15).
Коэффицент KHα определяют по формуле:
KHα = 1 + (K0Hα — 1)KHw,
где KHw — коэффициент, учитывающий приработку зубьев, его значения находят в зависимости от окружной скорости для зубчатого колеса с меньшей твердостью (табл. 15).

Рис. 5 [1, рис. 2.4, стр. 19]
Табл. 14 [1, табл. 2.7, стр. 19]
|
Ψbd |
Твердость на поверхности зубьев колеса |
Значения KHβo для |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
|
0,4 0,6 0,8 1,0 1,2 1,4 1,6 |
≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB ≤ 350 HB > 350 HB |
1.17 1.43 1.27 — 1.45 — — — — — — — — — |
1,12 1,24 1,18 1,43 1,27 — — — — — — — — — |
1,05 1,11 1,08 1,20 1,12 1,28 1,15 1,38 1,18 1,48 1,23 — 1,28 — |
1,03 1,08 1,05 1,13 1,08 1,20 1,10 1,27 1,13 1,34 1,17 1,42 1,20 — |
1,02 1,05 1,04 1,08 1,05 1,13 1,07 1,18 1,08 1,25 1,12 1,31 1,15 — |
1,02 1,02 1,03 1,05 1,03 1,07 1,04 1,11 1,06 1,15 1,08 1,20 1,11 1,26 |
1,01 1,01 1,02 1,02 1,02 1,04 1,02 1,06 1,03 1,08 1,04 1,12 1,06 1,16 |
Табл. 15 [1, табл. 2.8, стр. 19]
|
Твердость на поверхности зубьев |
Значения KHw при |
|||||
|
1 |
3 |
5 |
8 |
10 |
15 |
|
|
200 HB 250 HB 300 HB 350 HB 43 HRCэ 47 HRCэ 51 HRCэ 60 HRCэ |
0,19 0,26 0,35 0,45 0,53 0,63 0,71 0,80 |
0,20 0,28 0,37 0,46 0,57 0,70 0,90 0,90 |
0,22 0,32 0,41 0,53 0,63 0,78 1,00 1,00 |
0,27 0,39 0,50 0,64 0,78 0,98 1,00 1,00 |
0,32 0,45 0,58 0,73 0,91 1,00 1,00 1,00 |
0,54 0,67 0,87 1,00 1,00 1,00 1,00 1,00 |
Начальное значение коэффициента K0Hα распределения нагрузки между зубьямив связи с погрешностями изготовления (погрешностями шага зацепления и направления зуба) определяют в зависимости от степени точности (nст = 5, 6, 7, 8, 9) по нормам плавности:
для прямозубых передач
K0Hα = 1 + 0,06(nст — 5), при условии 1 ≤ K0Hα ≤ 1,25;
для косозубых передач
K0Hα = 1 + A(nст — 5), при условии 1 ≤ K0Hα ≤ 1,6,
где A = 0,15 — для зубчатых колес с твердостью H1 и H2 > 350 HB и A = 0,25 при H1 и H2 ≤ 350 HB или H1 > 350 HB и H2 ≤ 350 HB.
K0Hα = 1 + 0.25(9 — 5) = 2
Принимаем коэффициент KHw по табл. 15 равным (ближайшее значение твердости по таблице 250 HB или 23 HRC к твердости колеса 262 HB) 0.26.
KHα = 1 + (2 — 1)0.26 = 1.26;
Принимаем коэффициент KHβ0 по табл. 14 (схема 5) равным 1.04.
KHβ = 1 + (1.04 — 1) 0.26 = 1.0104;
KH = 1.02 ∙ 1.0104 ∙ 1.26 = 1.3.
Уточнённое значение межосевого расстояния:
aw = 211.1 мм;
Вычисленное значение межосевого расстояния округляют до ближайшего числа, кратного пяти, или по ряду размеров Ra 40 [1, табл. 24.1]. При крупносерийном производстве редукторов aw округляют до ближайшего стандартного значения: 50; 63; 71; 80; 90; 100; 112; 125; 140; 160; 180; 200; 224; 250; 260; 280; 300; 320; 340; 360; 380; 400 мм. [1, стр. 20]
Принимаем aw = 220 мм;
3.4.2 Предварительные основные размеры колеса
Делительный диаметр:
d2 = 2awu/(u 
d2 = 2 ∙ 220 ∙ 3.05 / (3.05 + 1) = 331.36 мм;
Ширина:
b2 = ψba ∙ aw;
b2 = 0.31 ∙ 220 = 68 мм.
Принимаем выбранное из стандартного ряда Ra 40 значение ширины:
b2 = 71 мм.
3.4.3 Модуль передачи
Максимально допустимый модуль mmax, мм, определяют из условия неподрезания зубьев у основания [1, стр. 20]
mmax ≈ 2aw/[17(u 
mmax ≈ 2 ∙ 220 / [17(3.05 + 1)] = 6.39 мм.
Минимальное значение модуля mmin, мм, определяют из условия прочности [1, стр. 20]:
где Km = 3,4 ∙ 103 для прямозубых и Km = 2,8 ∙ 103 для косозубых передач; вместо [σ]F подставляют меньшее из значений [σ]F2 и [σ]F1.
Табл. 16 [1, табл. 2.9, стр. 20]
|
Степень точности по ГОСТ 1643-81 |
Твердость на поверхности зубьев колеса |
Значения KFυ при |
||||
|
1 |
3 |
5 |
8 |
10 |
||
|
6 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,10 1,06 |
1,16 1,06 |
1,20 1,08 |
|
≤ 350 HB |
1,06 1,03 |
1,18 1,09 |
1,32 1,13 |
1,50 1,20 |
1,64 1,26 |
|
|
7 |
> 350 HB |
1,02 1,01 |
1,06 1,03 |
1,12 1,05 |
1,19 1,08 |
1,25 1,10 |
|
≤ 350 HB |
1,08 1,03 |
1,24 1,09 |
1,40 1,16 |
1,64 1,25 |
1,80 1,32 |
|
|
8 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,15 1,06 |
1,24 1,09 |
1,30 1,12 |
|
≤ 350 HB |
1,10 1,04 |
1,30 1,12 |
1,48 1,19 |
1,77 1,30 |
1,96 1,38 |
|
|
9 |
> 350 HB |
1,03 1,01 |
1,09 1,03 |
1,17 1,07 |
1,28 1,11 |
1,35 1,14 |
|
≤ 350 HB |
1,11 1,04 |
1,33 1,12 |
1,56 1,22 |
1,90 1,36 |
— 1,45 |
Примечание. В числителе приведены значения для прямозубых, в знаменателе — для косозубых зубчатых колес.
Коэффициент нагрузки при расчете по напряжениям изгиба
KF = KFνKFβKFα.
Коэффициент KFν учитывает внутреннюю динамику нагружения, связанную прежде всего с ошибками шагов зацепления шестерни и колеса. Значения KFν принимают по табл. 16 [1, табл. 2.9, стр. 20] в зависимости от степени точности по нормам плавности, окружной скорости и твердости рабочих поверхностей.
Для степени точности 9, максимальной окружной 0.74 м/с, твердости HB≤350 принимаем KFν=1.04.
KFβ — коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца, оценивают по формуле
KFα — коэффициент, учитывающий влияние погрешности изготовления шестерни и колеса на распределение нагрузки между зубьями, определяют так же как при расчетах на контактную прочность: KFα = KFα0.
В связи с менее благоприятным влиянием приработки на изгибную прочность, чем на контактную, и более тяжелыми последствиями из-за неточности при определении напряжений изгиба приработку зубьев при вычислении коэффициентов KFβ и KFα не учитывают. [1, стр. 21]
KF = KFν = 1.04.
mmin = 0.81 мм.
Из полученного диапазона (mmin…mmax) модулей принимают меньшее значение m, согласуя его со стандартным (ряд 1 следует предпочитать ряду 2) [1, стр. 21]:
| Ряд 1, мм ….. | 1,0; | 1,25; | 1,5; | 2,0; | 2,5; | 3,0; | 4,0; | 5,0; | 6,0; | 8,0; | 10,0; |
| Ряд 2, мм ….. | 1,12; | 1,37; | 1,75; | 2,25; | 2,75; | 3,5; | 4,5; | 5,5; | 7,0; | 9,0; |
Принимаем из стандартного ряда m = 2.75 мм.
Значения модулей m < 1 при твердости ≤ 350 HB и m<1,5 при твердости ≥ 40 HRCэ для силовых передач использовать нежелательно. [1, стр. 21]
3.4.4 Суммарное число зубьев и угол наклона
Минимальный угол наклона зубьев косозубых колес [1, стр. 21]
βmin = arcsin(4m/b2);
βmin = arcsin(4∙2.75/71) = 8.91o.
Суммарное число зубьев
zs = 2awcosβmin/m = 158.07.
Полученное значение zs округляют в меньшую сторону до целого числа и определяют действительное значение угла β наклона зуба:
β = arccos[zsm/(2aw)].
zs = 158;
β = arccos[158 ∙ 2.75/(2∙220)] = 9.07o.
Справочно: для косозубых колес β = 8…20o, для шевронных — β = 25…40o.
3.4.5 Число зубьев шестерни и колеса
Число зубьев шестерни [1, стр. 21]
z1 = zs / (u 
z1 = 158 / (3.05 + 1) = 39.01.
Значение z1 округляют в ближайшую сторону до целого числа. [1, стр. 21]
z1 = 39.
Число зубьев колеса внешнего зацепления z2 = zs — z1.
z2 = 158 — 39 = 119.
3.4.6 Фактическое передаточное число
uф = z2/z1 = 119/39 = 3.05.
Фактические значения передаточных чисел не должны отличаться от номинальных более чем на: 3% — для одноступенчатых, 4% — для двухступенчатых и 5% — для многоступенчатых редукторов.[1, стр. 22]
Отклонение от номинального передаточного числа
Δ = (u — uф)/u = 0 %.
3.4.7 Диаметры колес

Рис. 6 [1, рис. 2.5, стр. 22]

Рис. 7 [1, рис. 2.6, стр. 22]
Делительные диаметры d [1, стр. 22]:
шестерни…………………………………..d1 = z1m/cosβ;
колеса внешнего зацепления…………d2 = 2aw — d1;
колеса внутреннего зацепления……..d2 = 2aw + d1;
d1 = 39 ∙ 2.75 / cos9.07o = 108.61 мм;
d2 = 2 ∙ 220 — 108.61 = 331.39 мм.
Диаметры da и df окружностей вершин и впадин зубьев колес внешнего зацепления [1, стр. 22]:
da1 = d1 + 2(1 + x1 — y)m;
df1 = d1 — 2(1,25 — x1)m;
da2 = d2 + 2(1 + x2 — y)m;
df2 = d2 — 2(1,25 — x2)m;
где x1 и x2 — коэффициенты смещения у шестерни и колеса; y = -(aw — a)/m — коэффициент воспринимаемого смещения; a — делительное межосевое расстояние: a = 0,5m(z2 
a = 0.5 ∙ 2.75 ∙ (119+39) = 217.25 мм;
y = -(220 — 217.25)/2.75 = -1;
da1 = 108.61 + 2 ∙ [1-(-1)] ∙ 2.75 = 119.61 мм;
df1 = 108.61 — 2 ∙ 1,25 ∙ 2.75 = 101.74 мм;
da2 = 331.39 + 2 ∙ [1-(-1)] ∙ 2.75 = 342.39 мм;
df2 = 331.39 — 2 ∙ 1,25 ∙ 2.75 = 324.52 мм;
3.4.8 Размеры заготовок
Чтобы получить при термической обработке принятые для расчета механические характеристики материала колес, требуется, чтобы размеры Dзаг, Cзаг, Sзаг заготовок колес не превышали предельно допустимых значений Dпр, Sпр (табл. 1 [1, табл. 2.1, стр. 11]) [1, стр. 22]:
Dзаг ≤ Dпр; Cзаг ≤ Cпр; Sзаг ≤ Sпр.
Значения Dзаг, Cзаг, Sзаг (мм) вычисляются по формулам: для цилиндрической шестерни (рис. 7, а) Dзаг = da + 6 мм; для колеса с выточками (рис. 7, в) Cзаг = 0,5b2 и Sзаг =8m; для колеса без выточек (рис. 6) Sзаг = b2 + 4 мм.
Dзаг1 = 119.61 + 6 мм = 125.61 мм;
Dзаг2 = 342.39 + 6 мм = 348.39 мм;
Sзаг2 = 71 + 4 мм = 75 мм.
3.4.9 Проверка зубьев колес по контактным напряжениям
Расчетное значение контактного напряжения [1, стр. 23]
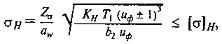
где Zσ = 9600 для прямозубых и Zσ = 8400 для косозубых передач, МПа1/2.
σH = 450.05 МПа;
Если расчетное напряжение σH меньше допустимого [σH] в пределах 15-20% или σH больше [σH] в пределах 5%, то ранее принятые параметры передачи принимают за окончательные. В противном случае необходим пересчет. [1, стр. 23]
σH меньше [σH] на 6.79%.
Ранее принятые параметры передачи принимаем за окончательные.
3.4.10 Силы в зацеплении

Рис. 8 [1, рис. 2.7, стр. 23]
Окружная
Ft = 2∙103∙T1/d1;
Ft = 2∙103∙348.39/108.61 = 6415.43 Н;
радиальная
Fr = Fttgα/cosβ
(для стандартного угла α=20o tgα=0,364);
Fr = 6415.43 ∙ 0.364/cos9.07o = 2364.78 Н;
осевая
Fa = Fttgβ;
Fa = 6415.43 ∙ tg9.07o = 1023.99 Н.
4. Эскизное проектирование
После определения межосевых расстояний, размеров колес и червяков приступают к разработке конструкции редуктора или коробки передач. Первым этапом конструирования является разработка эскизного проекта. При эскизном проектировании определяют положение деталей передач, расстояния между ними, ориентировочные диаметры ступенчатых валов, выбирают типы подшипников и схемы их установки. [1, стр. 42]
4.1 Проектные расчеты валов
Предварительные значения диаметров (мм) различных участков стальных валов редуктора определяют по формулам [1, стр. 42]:
для быстроходного (входного) вала
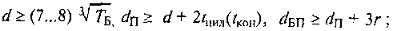
dвх = 18 мм;
для промежуточного
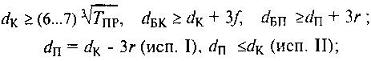
dК пр = 35.2 мм;
для тихоходного (выходного)
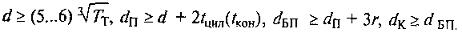
dвых = 40.4 мм;
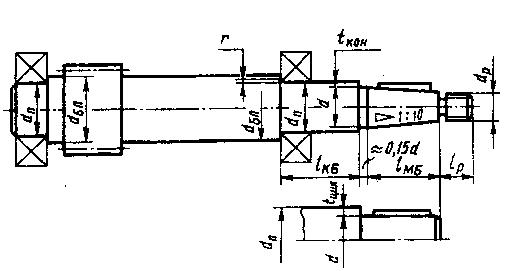
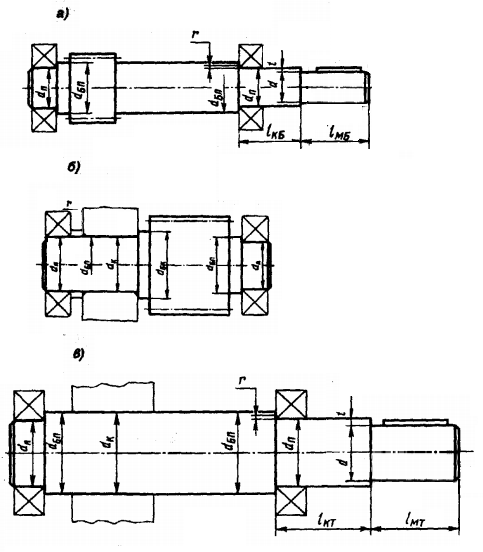
Рис. 9 [1, рис. 3.1(а), стр. 43]
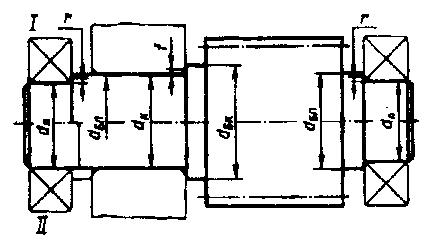
Рис. 10 [1, рис. 3.1(б), стр. 43]
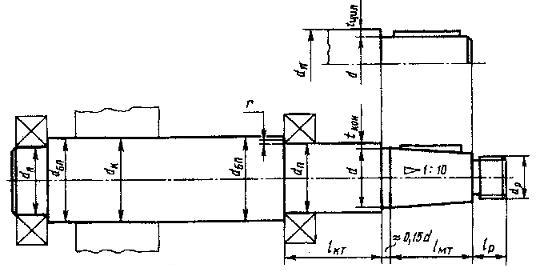
Рис. 11 [1, рис. 3.1(в), стр. 43]
В приведенных формулах TБ, TТ — номинальные моменты, Н∙м. Большие значенияБольшие значения d и dk принимают для валов на роликоподшипниках, для валов шевронных передач и промежуточных валов соосных передач при твердости колеса выше 55 HRCэ.
Вычисленные значения диаметров откругляют в ближайшую сторону до стандартных (см. табл. 24.1[1]).
Диаметры валов быстроходного, промежуточного и тихоходного валов согласуют с диаметрами валов по табл. 24.27 [1] и с диаметрами отверстий устанавливаемых на них деталей (шкива, звездочки, полумуфты).
Принимаем диаметры и длины концов согласно таблице 24.28 [1]
dвх = 18 мм;
dвых = 40 мм.
Высоту tцил(tкон) заплечника, координату r фаски подшипника и размер f (мм) фаски колеса принимают в зависимости от диаметра d [1, стр. 42].
Диаметры под подшипники:
dП вх = 18 + 2∙3 = 24 мм;
dП пр = 35.2 — 3∙2.5 = 27.7 мм;
dП вых = 40 + 2∙3.5 = 47 мм.
Принимаем посадочные места под подшипники согласно ГОСТ 8338-75 на подшипники шариковые радиальные однорядные (табл. 24.10 [1]):
dП вх = 25 мм;
dП пр = 30 мм;
dП вых = 50 мм.
Диаметры безконтактных поверхностей:
dБП вх = 25 + 3∙1.5 = 29.5 мм;
dБП пр = 30 + 3∙2.5 = 37.5 мм;
dБП вых = 50 + 3∙2.5 = 57.5 мм.
Принимаем диаметр тихоходного вала для установки зубчатого колеса:
dК вых = 59.5 мм.
4.2 Расстояния между деталями передач
Чтобы поверхности вращающихся колес не задевали за внутренние поверхности стенок корпуса, между ними оставляют зазор «а» (мм) [1, стр.45]:
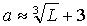
где L — расстояние между внешними поверхностями деталей передач, мм.
a = 11.4 мм.
Вычисленное значение a округляют в большую сторону до целого числа. В дальнейшем по a будем понимать также расстояние между внутренней поверхностью стенки корпуса и торцом ступицы колеса. [1, стр. 45]
Принимаем
a = 12 мм.
Расстояние b0 между дном корпуса и поверхностью колес или червяка для всех типов редукторов и коробок передач принимают [1, стр. 45]:
b0 ≥ 3a.
Принимаем
b0 = 36 мм.
4.3 Выбор типов подшипников
Для опор валов цилиндрических прямозубых и косозубых колес редукторов и коробок передач применяют чаще всего шариковые радиальные подшипники. Первоначально назначают подшипники легкой серии. Если при последующем расчете грузоподъемность подшипника окажется недостаточной, то принимают подшипники средней серии. При чрезмерно больших размерах шариковых подшипников в качестве опор валов цилиндрических колес применяют подшипики конические роликовые. [1, стр.47]
Предварительно назначаем шариковые радиальные подшипники легкой серии.
Обычно используют подшипники класса точности 0. Подшипники более высокой точности применяют для опор валов, требующих повышенной точности вращения или работающих при особо высоких чатотах вращения. [1, стр. 47]
4.4 Схемы установки подшипников
Схема установки подшипников «враспор» конструктивно наиболее проста. Ее широко применяют при относительно коротких валах. При установке в опорах радиальных шариковых подшипников отношение l/d ≈ 8…10. [1, стр. 49]
Валы в двухступенчатых цилиндрических редукторах считаются относительно короткими, поэтому назначаем схему установки подшипников «враспор».
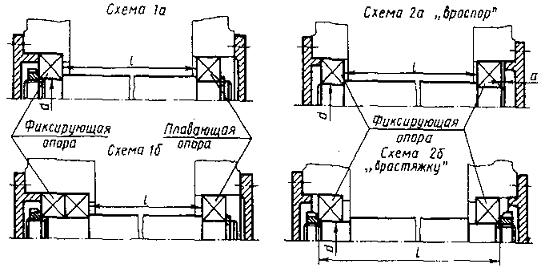
Рис. 12 [1, рис. 3.9, стр. 48]
4.5 Составление компоновочной схемы
Компоновочные схемы изделия составляют для того, чтобы оценить соразмерность узлов и деталей привода. Ранее выполненный эскизный проект редуктора (коробки передач) и выбранный электродвигатель, если их рассматривать отдельно, не дают ясного представления о том, что же в конечном итоге получилось. Нужно их упрощенно изобразить вместе с приводным валом, на одном листе, соединенными друг с другом непосредственно, с применением муфт или ременной (цепной) передачи. Компоновочные схемы выполняются в масштабе уменьшения. Они служат прообразом чертежа общего вида привода. [1, стр. 52]
5. Конструирование зубчатых колес первой ступени
По результатам разработки эскизного проекта были вычерчены контуры зубчатых колес и червяков. Следующим шагом является конструктивная обработка их формы. [1, стр. 62]
5.1 Шестерня
Форма зубчатого колеса может быть плоской (рис.8, а, б) или с выступающей ступицей (рис.8, в). Значительно реже (в одноступенчатых редукторах) колеса делают со ступицей, выступающей в обе стороны.[1, стр. 62]
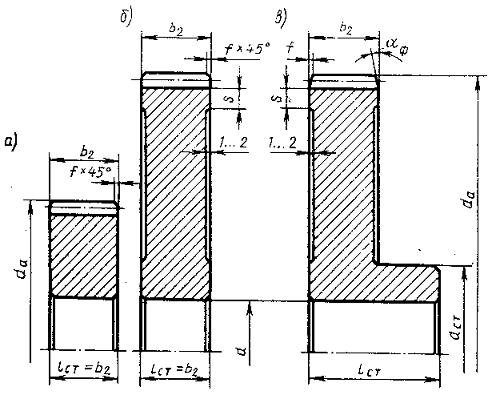
Рис. 13 [1, рис. 5.1, стр. 62]
На рис. 13 показаны простейшие формы колес, изготовляемых в единичном и мелкосерийном производстве. Чтобы уменьшить объем точной обработки резанием, на дисках колес выполняют выточки (рис. 13, б, в). При диаметре da < 80 мм эти выточки, как правило, не делают (рис. 13, а). [1, стр. 62]
da1 = 72.17 мм;
Так как da1 < 80 , то выточки не производим.
Длину lст посадочного отверстия колеса желательно принимать равной или больше b2 зубчатого венца (lст>b2). Принятую длину ступицы согласуют с расчетной (см. расчет соединения шлицевого, с натягом или шпоночного, выбранного для передачи вращающего момента с колеса на вал) и с диаметром посадочного отверстия d [1, стр. 63]:
lст = (0,8…1,5)d, обычно lст = (1,0…1,2)d.
Так как зубчатое колесо выполнено совместно с валом, то рассчитывать ступицу нет необходимости.
На торцах зубчатого венца (зубьях и углах обода) выполняют фаски f = (0,5…0,6)m, которые округляют до стандартного значения (см. ниже). [1, стр. 63]
На прямозубых зубчатых колесах при твердости рабочих поверхностей менее 350 HB — под углом αф = 45o (рис. 13, а, б), а при более высокой твердости αф = 15…20o(рис. 13, в). [1, стр. 63]
Фаска венца
f = 0,5 ∙ m = 0,5 ∙ 1.75 = 0.88 мм;
округленная до стандартного значения
f = 1 мм.
Стандартные значения фасок:
| d, мм ….. | 20…30 | 30…40 | 40…50 | 50…80 | 80…120 | 120…150 | 150…250 | 250…500 |
| f, мм ….. | 1,0 | 1,2 | 1,6 | 2,0 | 2,5 | 3,0 | 4,0 | 5,0 |
5.2 Зубчатое колесо
da2 = 261.35 мм;
Так как da2 > 80 , то выточки выполним выточки на торце колеса глубиной 2 мм.
Принимаем
lст = 1,2d = 1.2 ∙ 35.2 = 42.24 мм.
Принимаем lст = b2 = 50 мм.
Ширину S торцов зубчатого венца принимают [1, стр. 63]:
S = 2,2m + 0,05b2,
где m — модуль зацепления, мм.
S = 2.2 ∙ 1.75 + 0.05 ∙ 50 = 6.4 мм.
Фаска венца
f = 0,5 ∙ m = 0,5 ∙ 1.75 = 0.88 мм;
округленная до стандартного значения
f = 1 мм.
6. Конструирование зубчатых колес второй ступени
По результатам разработки эскизного проекта были вычерчены контуры зубчатых колес и червяков. Следующим шагом является конструктивная обработка их формы. [1, стр. 62]
6.1 Шестерня
da1 = 119.61 мм;
Так как da1 > 80 , то выточки выполним выточки на торце колеса глубиной 2 мм.
Так как зубчатое колесо выполнено совместно с валом, то рассчитывать ступицу нет необходимости.
Ширину S торцов зубчатого венца принимают [1, стр. 63]:
S = 2,2m + 0,05b2,
где m — модуль зацепления, мм.
S = 2.2 ∙ 2.75 + 0.05 ∙ 71 = 9.6 мм.
Фаска венца
f = 0,5 ∙ m = 0,5 ∙ 2.75 = 1.38 мм;
округленная до стандартного значения
f = 1.6 мм.
6.2 Зубчатое колесо
da2 = 342.39 мм;
Так как da2 > 80 , то выточки выполним выточки на торце колеса глубиной 2 мм.
Принимаем
lст = 1,2d = 1.2 ∙ 59.5 = 71.4 мм.
При lст>b2 выступающую часть ступицы располагают по направлению действия осевой силы Fa в зацеплении. [1, стр. 63]
Диаметр dст назначают в зависимости от материала ступицы: для стали dст = (1,5…1,55)d; чугуна dст = (1,55…1,6)d; легких сплавов dст = (1,6…1,7)d: меньшие значения для шлицевого колеса с валом, большие — для шпоночного и соединения с натягом. [1, стр. 63]
Назначаем
dст = 1.55d = 1.55 ∙ 59.5 = 92.23 мм;
Округлим полученные значения до целых
lст = 71 мм;
dст = 92 мм.
Ширину S торцов зубчатого венца принимают [1, стр. 63]:
S = 2,2m + 0,05b2,
где m — модуль зацепления, мм.
S = 2.2 ∙ 2.75 + 0.05 ∙ 71 = 9.6 мм.
Фаска венца
f = 0,5 ∙ m = 0,5 ∙ 2.75 = 1.38 мм;
округленная до стандартного значения
f = 1.6 мм.
7. Подбор шпоночных соединений
7.1 Подбор шпоноки для соединения зубчатого колеса и промежуточного вала
При установке колес на валах необходимо обеспечить надежное базирование колеса по валу, передачу вращающего момента от колеса к валу или от вала к колесу. [1, стр. 77]
Для передачи вращающего момента чаще всего применяют призамтические и сегментные шпонки. [1, стр. 77]
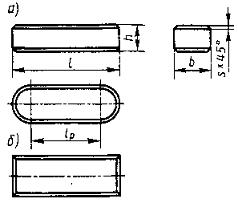
Рис. 14 [1, рис. 6.1, стр. 77]
Призматические шпонки имеют прямоугольное сечение; концы скругленные (рис. 9, а) или плоские (рис. 9, б). Стандарт для каждого диаметра вала определнные размеры поперечного сечения шпонки. Поэтому при проектных расчетах размеры b и h берут из табл. 9 [1, табл. 24.29] и определяют расчетную длину lр шпонки. Длину l = lр + b шпонки со скругленными или l = lр с плоскими торцами выбирают из стандартного ряда (табл. 9). Длину ступицы назначают на 8…10 мм больше длины шпонки.
Назначаем в качестве соединения призматическую шпонку со скругленными концами.
Табл. 9 [1, табл. 24.29, стр. 432] Шпонки призматические (из ГОСТ 23360-78)
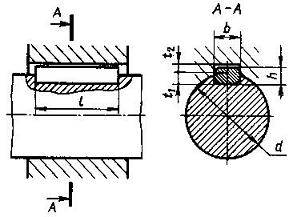
|
Диаметр |
Сечение |
Фаска |
Глубина |
Длина |
||
|
b |
h |
вала |
ступицы |
|||
|
Св. 12 >> 17 >> 22 >> 22 >> 30 |
5 6 8 |
5 6 7 |
0,25 – 0,4 |
3 3,5 4 |
2,3 2,8 3,3 |
10 – 56 14 – 70 18 – 90 |
|
>> 30 >> 38 >> 38 >> 44 >> 44 >> 50 >> 50 >> 58 >> 58 >> 65 |
10 12 14 16 18 |
8 8 9 10 11 |
0,4 – 0,6 |
5 5 5,5 6 7 |
3,3 3,3 3,8 4,3 4,4 |
22 – 110 28 – 140 36 – 160 45 – 180 50 – 200 |
|
>> 65 >> 75 >> 75 >> 85 >> 85 >> 95 |
20 22 25 |
12 14 14 |
0,6 – 0,8 |
7,5 9 9 |
4,9 5,4 5,4 |
56 – 220 63 – 250 70 – 280 |
Примечания. 1. Длину l (мм) призматической шпонки выбирают из ряда: 10, 12, 14, 16, 18, 20, 22, 25, 28, 32, 36, 40, 45, 50, 56, 63, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200, 250, 280.
При диаметре вала 35.2 мм и длине ступицы 50 выбираем шпонку со следующими параметрами:
b = 10 мм;
h = 8 мм;
s = 0.4 мм;
t1 = 5 мм;
t2 = 3.3 мм.
Длину шпонки назначим примерно на 8…10 мм меньше длины ступицы, согласно стандартному ряду длин для шпонок:
l = 45 мм.
При передаче момента шпоночным соединением посадки можно принимать по следующим рекомендациям (посадки с большим натягом — для колес реверсивных передач) [1, стр. 77]:
для колес цилиндрических прямозубых………………….. H7/p6 (H7/r6);
для колес цилиндрических косозубых и червячных…… H7/r6 (H7/s6);
для колес конических………………………………………….. H7/s6 (H7/t6);
для коробок передач……………………………………………. H7/k6 (H7/m6).
Назначаем посадку шпоночного соединения H7/r6.
Посадки шпонок регламентированы ГОСТ 23360-78 для призматических шпонок. Рекомендуют принимать поле допуска для ширины шпоночного паза вала для призматической шпонки P9, а ширины шпоночного паза отверстия P9.
7.2 Подбор шпоноки для соединения зубчатого колеса и выходного вала
Назначаем в качестве соединения призматическую шпонку со скругленными концами.
При диаметре вала 59.5 мм и длине ступицы 71 выбираем шпонку со следующими параметрами:
b = 18 мм;
h = 11 мм;
s = 0.4 мм;
t1 = 7 мм;
t2 = 4.4 мм.
Длину шпонки назначим примерно на 8…10 мм меньше длины ступицы, согласно стандартному ряду длин для шпонок:
l = 63 мм.
При передаче момента шпоночным соединением посадки можно принимать по следующим рекомендациям (посадки с большим натягом — для колес реверсивных передач) [1, стр. 77]:
для колес цилиндрических прямозубых………………….. H7/p6 (H7/r6);
для колес цилиндрических косозубых и червячных…… H7/r6 (H7/s6);
для колес конических………………………………………….. H7/s6 (H7/t6);
для коробок передач……………………………………………. H7/k6 (H7/m6).
Назначаем посадку шпоночного соединения H7/r6.
Посадки шпонок регламентированы ГОСТ 23360-78 для призматических шпонок. Рекомендуют принимать поле допуска для ширины шпоночного паза вала для призматической шпонки P9, а ширины шпоночного паза отверстия P9.
7.3 Подбор шпонок входного и выходного хвостовиков
Входной вал.
При диаметре хвостовика 18 мм и длине хвостовика 28 выбираем шпонку со следующими параметрами:
b = 6 мм;
h = 6 мм;
s = 0.25 мм;
t1 = 3.5 мм;
t2 = 2.8 мм.
Длину шпонки назначим примерно на 8…10 мм меньше длины хвостовика, согласно стандартному ряду длин для шпонок:
l = 16 мм.
Выходной вал.
При диаметре хвостовика 40 мм и длине хвостовика 110 выбираем шпонку со следующими параметрами:
b = 12 мм;
h = 8 мм;
s = 0.4 мм;
t1 = 5 мм;
t2 = 3.3 мм.
Длину шпонки назначим примерно на 8…10 мм меньше длины хвостовика, согласно стандартному ряду длин для шпонок:
l = 90 мм.
8. Подбор подшипников качения на заданный ресурс
Расчет подшипников проводится по рекомендациям Дунаева П.Ф., Леликова О.П. [1, стр. 105-112].
8.1 Подшипники быстроходного вала
Исходные данные для расчета:
частота вращения вала n = 719.19 мин-1;
требуемый ресурс при вероятности безотказной работы 90%: L’10ah = 33533.28 ч.;
диаметр посадочных поверхностей вала d = 25 мм;
максимальные длительно действующие силы: Fr1max = Fr/2 = 513.8 Н, Fr2max = Fr/2 = 513.8 Н, FAmax = 401.32 Н;
режим нагружения — III — средний нормальный;
ожидаемая температура работы tраб = 50oC.
Для типового режима нагружения III коэффициент эквивалентности KE = 0.56. Вычисляем эквивалентные нагрузки:
Fr1 = KEFr1max = 0.56 ∙ 513.8 = 287.73 Н;
Fr2 = KEFr2max = 0.56 ∙ 513.8 = 287.73 Н;
FA = KEFAmax = 0.56 ∙ 401.32 = 224.74 Н.
Предварительно назначаем шариковые радиальные подшипники легкой серии 205. Схема установки подшипников — враспор.
Для выбранной схемы установки подшипников следует:
Fa1 = FA = 224.74 Н;
Fa2 = 0.
Дальнейший расчет производим для более нагруженной опоры 1.
1. Для принятых подшипников из табл. 24.10 [1] находим:
Cr = 14000 Н;
C0r = 6950 Н.
2. Отношение iFa/C0r = 1∙224.74/6950 = 0.032.
Из табл. 7.1 [1, стр.104] выписываем, применяя линейную интерполяцию значений (т.к. значение iFa/C0r является промежуточным) X = 0.56, Y = 1.95, e = 0.23.
3. Отношение Fa/(VFr) = 224.74/(1∙287.73) = 0.781, что больше e = 0.23 (V=1 при вращении внутреннего кольца). Окончательно принимаем X = 0.56, Y = 1.95.
4. Эквивалентная динамическая радиальная нагрузка
Pr = (VXFr + YFa)KбKт.
Принимаем Kб [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o).
Pr = (1 ∙ 0.56 ∙ 287.73 + 1.95 ∙ 224.74) ∙ 1.4 ∙ 1 =
= 839.12 Н.
5. Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
L10ah = a1a23∙(Cr/Pr)k ∙ (106/60n) =
= 1 ∙ 0.7 ∙ (14000/839.12)3∙(106/60∙719.19) = 75338 ч.
6. Так как расчетный ресурс больше требуемого: L10ah > L’10ah (75338 > 33533.28), то предварительно назначенный подшипник 205 пригоден. При требуемом ресурсе 90%.
8.2 Подшипники промежуточного вала
Исходные данные для расчета:
частота вращения вала n = 183 мин-1;
требуемый ресурс при вероятности безотказной работы 90%: L’10ah = 33533.28 ч.;
диаметр посадочных поверхностей вала d = 30 мм;
максимальные длительно действующие силы: Fr1max = Fr/2 = 513.8 Н, Fr2max = Fr/2 = 513.8 Н, FAmax = 401.32 Н;
режим нагружения — III — средний нормальный;
ожидаемая температура работы tраб = 50oC.
Для типового режима нагружения III коэффициент эквивалентности KE = 0.56. Вычисляем эквивалентные нагрузки:
Fr1 = KEFr1max = 0.56 ∙ 513.8 = 287.73 Н;
Fr2 = KEFr2max = 0.56 ∙ 513.8 = 287.73 Н;
FA = KEFAmax = 0.56 ∙ 401.32 = 224.74 Н.
Предварительно назначаем шариковые радиальные подшипники легкой серии 206. Схема установки подшипников — враспор.
Для выбранной схемы установки подшипников следует:
Fa1 = FA = 224.74 Н;
Fa2 = 0.
Дальнейший расчет производим для более нагруженной опоры 1.
1. Для принятых подшипников из табл. 24.10 [1] находим:
Cr = 19500 Н;
C0r = 10000 Н.
2. Отношение iFa/C0r = 1∙224.74/10000 = 0.022.
Из табл. 7.1 [1, стр.104] выписываем, применяя линейную интерполяцию значений (т.к. значение iFa/C0r является промежуточным) X = 0.56, Y = 2.12, e = 0.21.
3. Отношение Fa/(VFr) = 224.74/(1∙287.73) = 0.781, что больше e = 0.21 (V=1 при вращении внутреннего кольца). Окончательно принимаем X = 0.56, Y = 2.12.
4. Эквивалентная динамическая радиальная нагрузка
Pr = (VXFr + YFa)KбKт.
Принимаем Kб [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o).
Pr = (1 ∙ 0.56 ∙ 287.73 + 2.12 ∙ 224.74) ∙ 1.4 ∙ 1 =
= 892.61 Н.
5. Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
L10ah = a1a23∙(Cr/Pr)k ∙ (106/60n) =
= 1 ∙ 0.7 ∙ (19500/892.61)3∙(106/60∙183) = 664683 ч.
6. Так как расчетный ресурс больше требуемого: L10ah > L’10ah (664683 > 33533.28), то предварительно назначенный подшипник 206 пригоден. При требуемом ресурсе 90%.
8.3 Подшипники выходного вала
Исходные данные для расчета:
частота вращения вала n = 60 мин-1;
требуемый ресурс при вероятности безотказной работы 90%: L’10ah = 33533.28 ч.;
диаметр посадочных поверхностей вала d = 50 мм;
максимальные длительно действующие силы: Fr1max = Fr/2 = 1182.39 Н, Fr2max = Fr/2 = 1182.39 Н, FAmax = 1023.99 Н;
режим нагружения — III — средний нормальный;
ожидаемая температура работы tраб = 50oC.
Для типового режима нагружения III коэффициент эквивалентности KE = 0.56. Вычисляем эквивалентные нагрузки:
Fr1 = KEFr1max = 0.56 ∙ 1182.39 = 662.14 Н;
Fr2 = KEFr2max = 0.56 ∙ 1182.39 = 662.14 Н;
FA = KEFAmax = 0.56 ∙ 1023.99 = 573.43 Н.
Предварительно назначаем шариковые радиальные подшипники легкой серии 210. Схема установки подшипников — враспор.
Для выбранной схемы установки подшипников следует:
Fa1 = FA = 573.43 Н;
Fa2 = 0.
Дальнейший расчет производим для более нагруженной опоры 1.
1. Для принятых подшипников из табл. 24.10 [1] находим:
Cr = 19500 Н;
C0r = 10000 Н.
2. Отношение iFa/C0r = 1∙573.43/10000 = 0.057.
Из табл. 7.1 [1, стр.104] выписываем, применяя линейную интерполяцию значений (т.к. значение iFa/C0r является промежуточным) X = 0.56, Y = 1.7, e = 0.26.
3. Отношение Fa/(VFr) = 573.43/(1∙662.14) = 0.866, что больше e = 0.26 (V=1 при вращении внутреннего кольца). Окончательно принимаем X = 0.56, Y = 1.7.
4. Эквивалентная динамическая радиальная нагрузка
Pr = (VXFr + YFa)KбKт.
Принимаем Kб [1, табл. 7.4 стр 107]; Kт = 1 (tраб < 100o).
Pr = (1 ∙ 0.56 ∙ 662.14 + 1.7 ∙ 573.43) ∙ 1.4 ∙ 1 =
= 1883.88 Н.
5. Расчетный скорректированный ресурс подшипника при a1 = 1 (вероятность безотказной работы 90%, табл. 7.5 [1]), a23 = 0.7 (обычные условия применения, см. стр. 108 [1]), k = 3 (шариковый подшипник):
L10ah = a1a23∙(Cr/Pr)k ∙ (106/60n) =
= 1 ∙ 0.7 ∙ (19500/1883.88)3∙(106/60∙183) = 70703 ч.
6. Так как расчетный ресурс больше требуемого: L10ah > L’10ah (70703 > 33533.28), то предварительно назначенный подшипник 206 пригоден. При требуемом ресурсе 90%.
9. Конструирование корпусных деталей
При конструировании литой корпусной детали стенки следует по возможности выполнять одинаковой толщины. Толщину стенок литых деталей стремятся уменьшить до величины, определяемой условиями хорошего заполнения формы жидким металлом. Поэтому чем больше размеры корпуса, тем толще должны быть его стенки.
Основной материал корпусов — серый чугун не ниже марки СЧ15.[1, стр. 257]
Назначаем материалом корпуса чугун марки СЧ15.
Для редукторов толщину δ стенки, отвечающую требованиям технологии литья, необходимой прочности и жесткости корпуса, вычисляют по формуле [1, стр. 257]
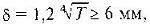
где T — вращающий момент на выходном (тихоходном валу), Н∙м.
δ = 6 мм.
Плоскости стенок, встречающиеся под прямым углом или тупым углом, сопрягают дугами радиусом r и R. Если стенки встречаются под острым углом, рекомендуют их соединять короткой вертикальной стенкой. В обоих случаях принимают: r ≈ 0,5δ; R ≈ 1,5δ, где δ — толщина стенки. [1, стр. 257]
Назначаем
r = 3 мм;
R = 9 мм;
Формовочные уклоны задают углом β или катетом a в зависимости от высоты h. [1, стр. 258]
Толщину наружных ребер жесткости у их основания принимают равной 0,9…1,0 толщины основной стенки δ. Толщина внутренних ребер из-за более медленного охлаждения металла должна быть 0,8δ. Высоту ребер принимают hp ≥ 5δ. Поперечное сечение ребер жесткости выполняют с уклоном. [1, стр. 258]
Часто к корпусной детали прикрепляют крышки, фланцы, кронштейны. Для их установки и крепления на корпусной детали предусматривают опорные платики. Эти платики при неточном литье могут быть смещены. Учитывая это, размеры сторон опорных платиков должны быть на величину С больше размеров опорных поверхностей прикрепляемых деталей. Для литых деталей средних размеров С = 2…4 мм. [1, стр. 258]
При конструировании корпусных деталей следует отделять обрабатываемые поверхности от «черных» (необрабатываемых). Обрабатываемые поверхности выполняют в виде платиков, высоту h которых можно принимать h = (0,4…0,5)δ. [1, стр. 258]
Во избежании поломки сверла поверхность детали, с которой соприкасается сверло в начале сверления, должна быть перпендикулярна оси сверла. [1, стр. 258]
Корпуса современных редукторов очерчивают плоскими поверхнотями, все выступающие элементы (бобышки, подшипниковые гнезда, ребра жеткости) устраняют с наружных поверхностей и вводят внутрь корпуса, лапы под болты крепления к основанию не выступают за габариты корпуса, проушины для транспортировки редуктора отлиты заодно с корпусом. При такой конструкции корпус характеризуют большая жесткость и лучшие виброакустические свойства, повышенная прочность в местах расположения болтов крепления, уменьшение коробления при старении, возможность размещения большего объема масла, упрощение наружной очистки, удовлетворение современным требованиям технической эстетики. Однако масса корпуса из-за этого несколько возрастает, а литейная оснастка усложнена. [1, стр. 262]
Назначаем крепление крышки редуктора к корпусу болтами.
Диаметр d(мм) болтов крепления крышки принимают в зависимости от вращающего момента Т (Н∙м) на выходном валу редуктора:
Назначаем болты для крепления крышки редуктора и корпуса М10-6g х **.58.016 ГОСТ 7796-70.
Гайки для болтов крепления крышки редуктора и корпуса М10-6H.5 ГОСТ 15521-70.
Шайбы под гайки крепления крышки редуктора и корпуса 10 65Г ГОСТ 6402-70 (высота 2.5 мм).
Диаметр винта крепления редуктора к плите (раме): dф ≈ 1,25d, где d — диаметр винта (болта) крепления крышки и корпуса редуктора. [1, стр. 267]
dф ≈ 1,25 ∙ 10 ≈ 13 мм.
Согласованное значение с ГОСТ.
dф = 12 мм.
Высота шайбы под этот винт 3 мм.
10. Конструирование крышек подшипников
Крышки подшипников изготавливают из чугуна марок СЧ15, СЧ20. [1, стр. 148]
Назначаем материал крышек — чугун марки СЧ20.
Различают крышки привертные и закладные. Выбираем привертный тип крышек. Схема крышки изображена на рис. 15. Схема крышки с монжетным уплотнением — рис. 16.
Рис. 15 [1, рис. 8.2, а, стр. 149]
Рис. 16 [1, рис. 8.3, а, стр. 149]
Определяющими при конструировании крышек является диаметр D отверстия в корпусе под подшипник. Ниже приведены рекомендации по выбору толщины δ стенки, диаметра d и числа z винтов крепления крышки к корпусу в зависимости от D:
| D, мм…….. | 50…62 | 63…95 | 100…145 | 150…200 |
| δ, мм…….. | 5 | 6 | 7 | 8 |
| d, мм…….. | 6 | 8 | 10 | 12 |
| z………….. | 4 | 4 | 6 | 6 |
Размеры других конструктивных элементов крышки:
δ1 = 1,2δ;
δ2 = (0,9…1)δ;
Dф = D + (4…4,4)d;
c ≈ d.
Крышки подшипников входного вала.
D = 52 мм.
Назначаем
δ = 5 мм;
d = 6 мм;
z = 4 мм;
δ1 = 6 мм;
δ2 = 5 мм;
Dф = 78 мм;
c = 6 мм.
Крышки подшипников промежуточного вала.
D = 62 мм.
Назначаем
δ = 5 мм;
d = 6 мм;
z = 4 мм;
δ1 = 6 мм;
δ2 = 5 мм;
Dф = 88 мм;
c = 6 мм.
Крышки подшипников выходного вала.
D = 90 мм.
Назначаем
δ = 6 мм;
d = 8 мм;
z = 4 мм;
δ1 = 7 мм;
δ2 = 6 мм;
Dф = 125 мм;
c = 8 мм.
11. Расчет ременной передачи
Расчет диаметра меньшего шкива d1, мм, если он не назначается по конструктивным соображениям исходя из габаритов установки, производят по формуле М.А. Саверина:
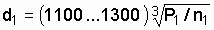
где Р1 – мощность на ведущем шкиве, кВт; n1 – частота вращения ведущего шкива, об/мин.
Имея n1 = 719.19 об/мин и требуемую мощность для привода Р1 = 7.24 кВт, и используя коэффициент 1200, получаем:
d1 = 259 мм.
Расчетный диаметр ведущего шкива не должен быть меньше минимально допустимого и принимаемого по рекомендациям табл. в зависимости от предварительно назначенного материала и типа ремня.
|
Число прокладок |
Резинотканевые |
||||||||
|
Б-800, |
БКНЛ-65, |
||||||||
|
|
|
||||||||
|
с |
без |
с |
без |
||||||
|
3 |
180/140 |
140/112 |
140/112 |
125/90 |
|||||
|
4 |
224/180 |
200/140 |
180/140 |
160/112 |
|||||
|
5 |
315/224 |
250/180 |
224/180 |
200/140 |
|||||
|
6 |
355/315 |
315/224 |
280/200 |
224/180 |
|||||
|
синтетические |
|||||||||
| Толщина d , мм |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
| dmin, мм |
28 |
36 |
45 |
56 |
63 |
71 |
80 |
90 |
100 |
В данной работе мы не определяем конструкцию шкивов, а определяем только значения диаметров, чтобы в дальнейшем определить тяговое усилие ремня, которое необходимо для расчета вала на прочность.
Округлим полученное значение диаметра до значения из стандартного ряда Ra:
d1 = 260 мм.
Определим диаметр ведомого шкива по формуле:
d2 = d1∙0,99∙Uр,
где Uр — заданное передаточное отношение ременной передачи (Uр = 2), а коэффициент 0,99 есть коэффициент упругого скольжения, принимаемый для резинотканевых ремней.
d2 = 514.8 мм.
Округлим полученное значение диаметра до ближайшего значения из стандартного ряда Ra:
d2 = 530 мм.
Действительное передаточное число ременной передачи:
Uр = d2/(0,99∙d1);
Uр = 2.06.
Определим тяговое усилие ремня на вал.
Fр = T1/d2;
где T1 — момент на входном валу редуктора.
Fр = 1000∙91.39/530 = 172.4 Н.
12. Расчет валов на прочность
Расчет на статическую прочность. Проверку статической прочтности выполняют в целях предупреждения пластических деформаций в период действия кратковременных перегрузок (например, при пуске, разгоне, реверсировании, торможении, срабатывании предохранительного устройства). [1, стр. 165]
Величина нагрузки зависит от конструкции передачи (привода). Так при наличии предохранительной муфты величину перегрузки определяет момент, при котором эта муфта срабатывает. При отсутствии предохранительной предохранительной муфты возможную перегрузку условно принимают равной перегрузке при пуске приводного электродвигателя. [1, стр. 165]
В расчете используют коэффициент перегрузки Kп = Tmax/T, где Tmax — максимальный кратковременный действующий вращающий момент (момент перегрузки); T — номинальный (расчетный) вращающий момент. [1, стр. 165]
Коэффициент перегрузки выбирается по справочной таблице 24.9 [1]. Для выбранного двигателя:
Kп = 2.2 .
В расчете определяют нормальные σ и касательные τ напряжения в рассматриваемом сечении вала при действии максимальных нагрузок:
σ = 103Mmax/W + Fmax/A; τ = 103Mкmax/Wк,
где 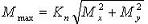
Частные коэффициенты запаса прочности по нормальным и касательным напряжениям (пределы текучести σт и τт материала см. табл. 10.2[1]) [1, стр. 166]:
Sтσ = σт/σ; Sтτ = τт/τ.
Общий коэффициент запаса прочности по пределу текучести при совместном действии нормальных и касательных напряжений [1, стр. 166]
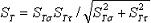
Статическую прочность считают обеспеченной, если Sт ≥ [Sт], где [Sт] = 1,3…2 — минимально допустимое значение общего коэффициента запаса по текучести (назначают в зависимости от ответсвенности конструкции и последствий разружения вала, точности определения нагрузок и напряжений, уровня технологии изготовления и контроля). [1, стр. 166]
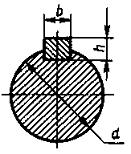
Рис. 17 [рис. 10.13, в]
Моменты сопротивления W при изгибе, Wк при кручении и площадь A вычисляют по нетто-сечению для вала с одним шпоночным пазом [1, стр. 166]:
W = πd3/32 — bh(2d-h)2/(16d);
Wк = πd3/16 — bh(2d-h)2/(16d);
A = πd2/4 — bh/2.
При расчетах принимают, что насаженные на вал детали передают силы и моменты валу на середине своей ширины. [1, стр. 164]
12.1 Входной вал
Расчет на статическую прочность. Расчет на прочность производится с помощью программных средств сайта http://sopromat.org
Длины участков для всех схем вала:
L1 = 37 мм; L2 = 37 мм; L3 = 36.5 мм; L4 = 14 мм.
Действующие номинальные нагрузки:
Ft = 2794.37 Н (тяговая нагрузка в зацеплении);
Fr = 1027.59 Н (радиальная нагрузка в зацеплении);
Fa = 401.32 Н (осевая нагрузка в зацеплении);
Fр = 172.4 Н (тяговая сила ремня);
T = 91.39 Н∙м.
В расчетной схеме предполагается, что продольная ось ремня параллельна действию тяговой нагрузки в зацеплении передачи.
Расчетная схема вала для построения эпюры Mx (на схеме Py(b)=Fr):
Эпюра Mx:
Расчетная схема вала для построения эпюры My (на схеме Py(b)=Ft, Py(d)=Fр):
Эпюра My:
Расчетная схема вала для построения эпюры N:
Эпюра N (осевые факторы):
Расчетная схема вала для построения эпюры Mкр:
Эпюра Mкр:
Очевидно, что опасным является место зубчатого зацепления, в котором действуют все виды внутренних факторов. Рассмотрим его:
Mx = 19010 Н∙мм;
My = 48550 Н∙мм;
F = 401 Н;
Mк = 91 Н∙м;
Mmax = 114706 Н∙мм;
Fmax = 2.2 ∙ 401 = 882.2 Н;
Mкmax = 2.2 ∙ 91 = 200.2 Н∙м.
Расчетный диаметр в сечении вала-шестерни: d = 29.5 мм.
W = 2520.38 мм3;
Wк = 5040.76 мм3;
A = 683.49 мм2.
σ = 46.8 МПа;
τ = 39.72 МПа.
Частные коэффициенты запаса:
STσ = 16.03;
STτ = 11.33;
Общий коэффициент запаса:
ST =9.25.
Полученный коэффициент запаса не дает сомнения в прочности вала. Принимаем ранее расчитанные параметры окончательными.
12.2 Промежуточный вал
Расчет на статическую прочность. Расчет на прочность производится с помощью программных средств сайта http://sopromat.org
Длины участков для всех схем вала:
L1 = 47.5 мм; L2 = 72.5 мм; L3 = 37 мм.
Действующие номинальные нагрузки:
Ft = 2794.37 Н (тяговая нагрузка в зацеплении);
Fr1 = 2364.78 Н (радиальная нагрузка в зацеплении шестерни на этом вале);
Fr2 = 1027.59 Н (радиальная нагрузка в зацеплении колеса на этом вале);
Fa1 = 1023.99 Н (осевая нагрузка в зацеплении шестерни на этом вале);
Fa2 = 401.32 Н (осевая нагрузка в зацеплении колеса на этом вале);
T = 348.39 Н∙м.
Расчетная схема вала для построения эпюры Mx (на схеме Py(b)=Fr2, Py(c)=Fr1):
Эпюра Mx:
Расчетная схема вала для построения эпюры My (на схеме Py(b)=Ft2, Py(c)=Ft1):
Эпюра My:
Расчетная схема вала для построения эпюры N:
Эпюра N (осевые факторы):
Расчетная схема вала для построения эпюры Mкр:
Эпюра Mкр:
Очевидно, что опасным является место зубчатого зацепления, в котором действуют все виды внутренних факторов. Рассмотрим его:
Mx = 78380 Н∙мм;
My = 150149 Н∙мм;
F = 623 Н;
Mк = 348 Н∙м;
Mmax = 372626.7 Н∙мм;
Fmax = 2.2 ∙ 623 = 1370.6 Н;
Mкmax = 2.2 ∙ 348 = 765.6 Н∙м.
Диаметр в сечении: d = 35.2 мм.
Размеры шпоночного соединения (см. рис. 17): b = 10 мм; h = 8 мм.
W = 3728.72 мм3;
Wк = 8010.54 мм3;
A = 933.14 мм2.
σ = 101.4 МПа;
τ = 95.57 МПа.
Частные коэффициенты запаса:
STσ = 7.4;
STτ = 4.71;
Общий коэффициент запаса:
ST =3.97.
Полученный коэффициент запаса не дает сомнения в прочности вала. Принимаем ранее расчитанные параметры окончательными.
12.3 Выходной вал
Расчет на статическую прочность. Расчет на прочность производится с помощью программных средств сайта http://sopromat.org
Длины участков для всех схем вала:
L1 = 47.5 мм; L2 = 47.5 мм; L3 = 85 мм; L4 = 55 мм.
Действующие номинальные нагрузки:
Ft = 6415.43 Н (тяговая нагрузка в зацеплении);
Fr = 2364.78 Н (радиальная нагрузка в зацеплении);
Fa = 1023.99 Н (осевая нагрузка в зацеплении);
T = 1030.72 Н∙м.
Расчетная схема вала для построения эпюры Mx (на схеме Py(b)=Fr):
Эпюра Mx:
Расчетная схема вала для построения эпюры My (на схеме Py(b)=Ft):
Эпюра My:
Расчетная схема вала для построения эпюры N:
Эпюра N (осевые факторы):
Расчетная схема вала для построения эпюры Mкр:
Эпюра Mкр:
Очевидно, что опасным является место зубчатого зацепления, в котором действуют все виды внутренних факторов. Рассмотрим его:
Mx = 56164 Н∙мм;
My = 152366 Н∙мм;
F = 1024 Н;
Mк = 1031 Н∙м;
Mmax = 357253.1 Н∙мм;
Fmax = 2.2 ∙ 1024 = 2252.8 Н;
Mкmax = 2.2 ∙ 1031 = 2268.2 Н∙м.
Диаметр в сечении: d = 59.5 мм.
Размеры шпоночного соединения (см. рис. 17): b = 18 мм; h = 11 мм.
W = 18254.1 мм3;
Wк = 38934.11 мм3;
A = 2681.51 мм2.
σ = 20.41 МПа;
τ = 58.26 МПа.
Частные коэффициенты запаса:
STσ = 36.75;
STτ = 7.72;
Общий коэффициент запаса:
ST =7.56.
Полученный коэффициент запаса не дает сомнения в прочности вала. Принимаем ранее расчитанные параметры окончательными.
13. Выбор манжетных уплотнений
Назначим манжеты по ГОСТ 8752-79. Выбор манжеты осуществляется таким образом, чтобы согласовывались диаметр отверстия манжеты и диаметр вала d, наружный диаметр D1, ширина манжеты h1 с соотеветсвующими размерами.
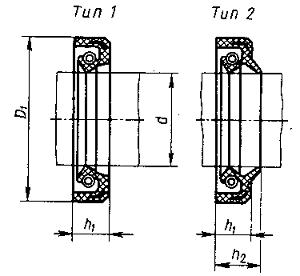
Рис. 18 [1, стр. 430]
В данном проектном расчете при подборе манжет будем учитывать только равенство диаметра вала и отверстия манжеты.
Назначаем тип манжет 1. Наружный диаметр D1 соответствует ряду 1 ГОСТа.
13.1 Входной вал
Размеры манжеты из ГОСТ 8752-79:
d = 25 мм;
D1 = 42 мм;
h1 = 8 мм.
13.2 Промежуточный вал
Размеры манжеты из ГОСТ 8752-79:
d = 30 мм;
D1 = 52 мм;
h1 = 10 мм.
13.3 Выходной вал
Размеры манжеты из ГОСТ 8752-79:
d = 50 мм;
D1 = 70 мм;
h1 = 10 мм.
14. Выбор смазочных материалов и системы смазывания
Для уменьшения потерь мощности на трение, снижение интенсивности изнашивания трущихся поверхностей, их охлаждения и очистки от продуктов износа, а также для предохранения от заедания, задиров, коррозии должно быть обеспечено надежное смазывание трущихся поверхностей. [1, стр. 172]
Для смазывания передач широко применяют картерную систему. В корпус редуктора или коробки передач заливают масло так, чтобы венцы колес были в него погружены. Колоса при вращении увдекают масло, разбрызгивая его внутри корпуса. Масло попадает на внутренние стенки корпуса, откуда стекает в нижнюю его часть. Внутри корпуса образуется взвесь частиц масла в воздухе, которая покрывает поверхность расположенных внутри корпуса деталей. [1, стр. 172]
Картерное смазывание применют при окружной скорости зубчатых колес и червяков от 0,3 до 12,5 м/c. При более высоких скоростях масло сбрасывает с зубьев центробежная сила и зацепление работает при недостаточном смазывании. Кроме того, заметно возрастают потери мощности на перемешивание масла, повышается его температура. [1, стр. 172]
Окружная скорость зацепления второй (см. пункт «Расчет межосевого расстояния»):
ν = 0.74 м/с.
Картерная система смазывания подходит для проектируемой передачи.
Выбор смазочного материала основан на опыте эксплуатации машин.
Преимущественное применение имеют масла. Принцип назначения сорта масла следующий: чем выше окружная скорость колеса, тем меньше должна быть вязкость масла и чем выше контактные давления в зацеплении, тем большей вязкостью должно обладать масло. Поэтому требуемую вязкость масла определяют в зависимость от контактного напряжения о окружной скорости колес (табл. 18).
Таблица 18 [1, табл. 11.1]
|
Контактные напряжения σH, МПа |
Рекомендуемая кинематическая вязкость, мм2/c при окружно скорости м/c |
|
|
до 2 |
2…5 |
св. 5 |
|
Для зубчатых передач при 40о C |
||||
|
До 600 600…1000 1000…1200 |
34 60 70 |
28 50 60 |
22 40 50 |
|
|
Для червячных передач при 100о C |
||||
|
До 200 200…250 250…300 |
25 32 40 |
20 25 30 |
15 18 23 |
|
Для предельного контактного напряжения 482.81 МПа и окружной скорости 0.74 м/с выбираем рекомендованное значение кинематической вязкости масла 34 мм2/c.
По табл. 19 выбирают марку масла для смазывания зубчатых и червячных передач. [1, стр. 172]
Таблица 19 [1, табл. 11.2]
|
Марка масла |
Кинематическая вязкость, мм2/c |
|
Для зубчатых передач при 40о C |
|
|
И-Л-А-22 И-Г-А-32 И-Г-А-46 И-Г-А-68 |
19…25 29…35 41…51 61…75 |
|
Для червячных передач при 100о C |
|
|
И-Г-С-220 И-Т-С-320 Авиац. МС-20 Цилиндровое 52 |
14 20 20,5 52 |
Для рекомендуемой вязкости 34 мм2/c выбираем масло индустриальное И-Г-А-32.
Уровень полгружения должен быть таким, чтобы в масло были погружены венецы зубчатых колес обоих ступеней, т.к. скорость в зацеплении меньше 1 м/с.
Список используемой литературы
1. Дунаев П.Ф., Леликов О.П., Конструирование узлов и деталей машин: Учеб. пособие для техн. спец. вузов. — 6-е изд., исп. — М.: Высш. шк., 2000. — 447 с., ил.
2. Анурьев В. И. Справочник конструктора – машиностроителя. В 3-х томах. Т.1. — 6е изд., перераб и доп. — М.: Машиностроение, 1982. — 736с.:ил.
Редуктор
§3. ОПРЕДЕЛЕНИЕ ВРАЩАЮЩИХ МОМЕНТОВ НА ВАЛАХ
Случай 1 (см. рис. 1.1).
Момент на приводном валу (Н · м)

где Ft — окружная сила, Н, на барабане или
тяговых звездочках; D6 и D3B —
диаметр барабана, м, делительный диаметр тяговых звездочек, м. Момент на
тихоходном валу редуктора (Н · м)
где ип
и ηπ —
передаточное число и КПД цепной или ременной передачи, расположенной после
редуктора; ηοπ — КПД опор
приводного вала. При отсутствии такой передачи в схеме привода
где ηΜ — КПД
муфты, соединяющей вал редуктора и приводной вал. Момент на промежуточном валу
редуктора (Н · м)
где η3Τ — КПД зубчатой передачи тихоходной ступени. Момент на
быстроходном валу редуктора (Н · м)
гДе
Лз.б — КПД зубчатой
передачи быстроходной ступени. Для одноступенчатой передачи
Случай 2
(см. рис. 1.2). Момент Гвых приведен в задании. Момент на тихоходной
ступени Тт=Тъых.
Моменты на промежуточном и быстроходном валах определяют по
формулам (1.17), (1.18), (1.19).
Случай 3 (см.
рис. 1.2). Мощность электродвигателя Рэ
(кВт) приведена в задании. Частота вращения вала электродвигателя пэ (об/мин) определена в § 1. Момент на валу
электродвигателя (Н · м)
Момент на быстроходном валу передачи (Н · м)
где ип и
ηπ—передаточное
число и КПД ременной (цепной) передачи, расположенной между электродвигателем и
редуктором (коробкой передач).
Если
в схеме привода отсутствует такая передача, момент на быстроходном валу
где ηΜ — КПД
муфты, соединяющей валы электродвигателя и редуктора (коробки передач).
Момент на промежуточном валу передачи (Н · м)
где иБ и
η3Β
— передаточное число и КПД быстроходной ступени.
Момент на тихоходном валу передачи (Н · м)
где η3Τ —
КПД тихоходной ступени передачи.
ГЛАВА 2 РАСЧЕТЫ ПЕРЕДАЧ
Расчеты
при курсовом проектировании должны выполняться с использованием вычислительной
техники. Эффективно выполнение расчетов на программируемых микрокалькуляторах
«Электроника» МК-52; МК-72; МК-61 и других типов. Для этих калькуляторов можно
составить программы расчета и хранить их в памяти калькулятора.
Из предыдущих
разделов имеем
Силы
в цилиндрическом зацеплении быстроходной
ступени: Ft2
= 557,4 Н, Fr2
= 206,3 Н. Fa2 =
103,1 Н.
Силы
в червячном зацеплении тихоходной
ступени: Ft1
= 665,6 Н, Fr1=2713,4
Н. Fa1=
7454,4 Н.
Реакции:
RDy
= 3726,6 Н,
RBy
=1219,5 Н,
.
Расстояния:
l1
= 80 мм,
l2
= 80 мм, l3
= 40 мм.
Определим величину изгибающих моментов в характерных сечениях а, b, с, d.
В горизонтальной
плоскости.
В
первом пролёте:
MDy
= 0;
MСy
= —RDx·l1
RDx=472,15
l1=80мм
MCy
=
-472,15·80·10-3
= -37,8 Н·м;
MBy
= —RDx·(l1+l2)+Ft1·l2
RDx=472,15
l1=l2=80мм
Ft1=665,6
H
MBy=
-472,15·160·10-3
+ 665,6·80·10-3
= -22,3 Н·м;
MАy
= 0;
Проверка:
:Во
втором пролёте
MBy
= —Ft2·l3
Ft2
= 557,4 H
l3
= 40мм
MBy=
-557,4·40·10 –3
= -22,3 Н·м;
В вертикальной
плоскости.
:В
первом пролёте
MDx
= 0;
MCx1
= RDy·l1
RDy=3726,6
H l1
= 80мм
MCx1=
3726,6·80·10-3
= 298,1 Н·м;
MCx2
= RDy·l1
– Fа1·½d1
MCx2=
3726,6·80·10-3–½·7454,4·100·10-3=-74,6
Н·м;
MBx
= RDy·(l1+l2)
– Fа1·½d1–Fr1·l2
MBx=
3726,6·160·10-3–½·7454,4·100·10-3––2713,4·80·10-3=
6,5 Н·м;
MAx=RDy·(l1+l2+l3)–Fа1·½d1–Fr1·(l2+l3)–RBy·l3
MAx=3726,6·200·10-3–½·7454,4·100·10-3–2713,4·120·10-3–1219,5·40·10-3=–1,8
Н·м;
Проверка:
:Во
втором пролёте
MAx
= –Fа2·½d2
MAx
=–103,1·½·34,6·10-3
=–1,8 Н·м;
Крутящий момент в сечениях вала.
Ft1=665,6
H
d1=100
мм
MK
=
665,6·100·10-3
/2 = 33,3 H·м
Строим эпюру
крутящих моментов.
Определение
опасного сечения
Как видно из эпюр
изгибающих моментов опасным сечением
вала является сечение С. Определяем
суммарный изгибающий момент в сечении
С.
Осевой
момент сопротивления сечения С.
Полярный
момент сопротивления сечения С.
Амплитуда
симметричного цикла по изгибу.
Амплитуда
касательных напряжений:
Среднее
напряжение цикла при изгибе
m
= 0, m
= a
= 0,12 МПа.
Принимаем
коэффициенты
-
концентрации
напряжений: K
= 1,9; K
= 1,6; -
масштабных
факторов: Е
= 0,723;
Е
= 0,653; -
коэффициенты,
учитывающие влияние среднего напряжения
цикла на усталостную прочность:
= 0,1, =
0,5.
О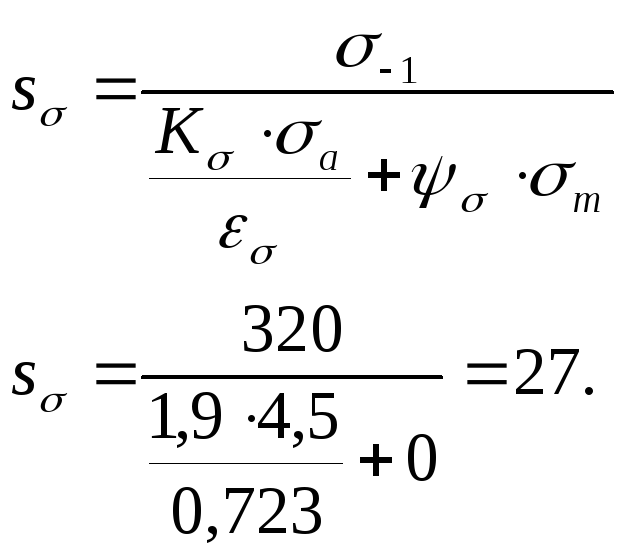
коэффициенты запаса прочности вала в
сечении С по напряжениям изгиба
Определяем
коэффициенты запаса прочности вала в
сечении С по напряжениям кручения
Расчетный
коэффициент запаса прочности :
s
[s]
= 1,5.
Сопротивление
усталости обеспечивается.
Но вал несёт
чрезмерный запас прочности, следовательно
необходимо изменение его диаметра.
Берём
df
= 40 мм
По
приведенным ранее формулам:
WOC
= 6280 мм3
осевой момент
Wp
=
12560 мм3
полярный момент
σа
= 47,85 МПа амплитуда симметричного цикла
по изгибу
τа
= 1,32 МПа
амплитуда касательных напряжений и
среднее напряжение цикла
При
уже принятых коэффициентах получим
Sσ
=
2,54 по напряжениям изгиба
Sτ
=
51,4 по напряжениям кручения
S
= 2,54 коэффициент запаса прочности
Р
7.1 Схема работы вала:
Проверочный расчет валов на прочность.
Быстроходный
вал.
Рис
7.3 Конструкция, расчетная схема и эпюры
изгибающих и крутящих моментов
быстроходного вала
Проверочный расчет
проводится для проверки прочности в
опасном сечении в зависимости от
направления и величины действующих на
него нагрузок. Напряжение изгиба
изменяется по симметричному циклу, а
касательные напряжения кручения по
пульсирующему.
Выбор
материала вала
Для
изготовления быстроходного вала выбрали
материал сталь 40Х, твердость не менее
200НВ; —1
= 320 МПа
и —1
= 200МПа
– пределы выносливости при симметричном
цикле изгиба и кручения.
Строим
расчетную схему вала.
Из предыдущих
разделов имеем
Силы
в зацеплении: Ft1
= 1494,6 Н, Fr2
= 1598,1 Н. Fa1=
4390,5 Н.
Консольная
сила от муфты: Fм
787,5 Н.
Реакции:
RGy
= -420,5 Н,
REy
= 2018,6 Н,
.
Расстояния:
lм=
60 мм,
lb
= 180 мм.
Определим
величину изгибающих моментов в характерных
сечениях E, F, G, H.
В горизонтальной
плоскости.
MHy
= 0;
MGy
= FМ·lм
= 787,5·60·10-3
= 47,25 Н·м;
MFy
= —FМ·(lм+½lб)-RGx·½lб
=
-787,5·150·10-3
— 484,8·90·10-3
=-161,757 Н·м;
MEy
= 0;
Проверка:
MFy
= -REx·½lб
= -1797,3·90·10-3=
-161,757 Н·м;
В вертикальной
плоскости.
MHx
= 0;
MGx
= 0;
Слева
MFx
= -REy·½lб
=-2018,6·90·10-3=-181,6
Н·м;
Справа
MFx
= RGy·½lб
= -420,5·90·10-3=-37,8
Н·м;
MEx
= 0;
Крутящий
момент в сечениях вала равен.
где
Ft
– окружная сила в зацеплении
d2
– диаметр червяка
Строим эпюру
крутящих моментов.
Определение
опасного сечения
Как
видно из эпюр изгибающих моментов
опасным сечением вала является сечение
F.
Определяем суммарный изгибающий момент
в сечении F.
где
Mu
– суммарный изгибающий момент в наиболее
нагруженных сечениях вала
Mx
и My
– изгибающие моменты в вертикальной
и горизонтальной плоскостях
Осевой
момент сопротивления сечения .
где
d
– диаметр вала
Полярный
момент сопротивления сечения .
где
d
– диаметр вала
Амплитуда
симметричного цикла по изгибу.
среднее
напряжение циклов m
= 0.
Амплитуда
касательных напряжений:
среднее
напряжение циклов m
= a
= 6,9 МПа.
где
Mk
– крутящий момент в сечениях вала
Wp
– полярный момент сопротивления
Принимаем
коэффициенты
коэффициенты
концентрации напряжений: K
= 1,9; K
= 1,6;
коэффициенты
масштабных факторов: Е
= 0,78; Е
= 0,68;
коэффициенты,
учитывающие влияние среднего напряжения
цикла на усталостную прочность:
= 0,1, =
0,5.
Определяем
коэффициенты запаса прочности вала в
сечении F
по
напряжениям изгиба
где
-1
– предел выносливости при симметричном
цикле изгиба
a
– амплитуда симметричного цикла по
изгибу
m
– среднее напряжение циклов
Определяем
коэффициенты запаса прочности вала в
сечении F
по
напряжениям кручения
где
—1
– пределы выносливости при симметричном
цикле кручения
a
– амплитуда касательных напряжений
Расчетный
коэффициент запаса прочности :
где
S
– коэффициент запаса прочности вала
по напряжениям изгиба
S
– коэффициент
запаса прочности вала по напряжениям
кручения
s
[s]
= 1,5.
Сопротивление
усталости обеспечивается.
8.2 Расчет валов
на усталостную прочность цилиндрического
зубчатого редуктора.
8.2.1 Проектный
расчет валов цилиндрического
двухступенчатого редуктора.
Рис
9.1
Эскизы валов
Проверочный
расчет проводится для проверки прочности
в опасном сечении в зависимости от
направления и величины действующих на
него нагрузок. Напряжение изгиба
изменяется по симметричному циклу, а
касательные напряжения кручения по
пульсирующему
Расчет
быстроходного вала
Выберем
материал сталь 45.
Предельное
напряжение: .
Предел
выносливости при симметричном цикле
изгиба:
Предел
выносливости при симметричном цикле
кручения: .
Силы
в зацеплении равны:
.
Крутящий
момент равен:
.
Составленная
на основании графического исполнения
вала расчетная схема представлена на
рис 7.
Реакции
равны:
.
Расстояния:
.
Построение
эпюр изгибающих моментов относительно
Ox
в сечениях, проходящих через точки A,
B,
C:
Сечение
I.
Сечение
II.
Эпюра
изгибающих моментов
Oy
в сечениях, проходящих через точки A,
B,
C:
Сечение
I.
Сечение
II.
Рис
9.2 Конструкция, расчетная схема и эпюры
изгибающих и крутящих моментов
быстроходного вала.
Как
следует из эпюры, наиболее опасное
сечение проходит через точку C.
Суммарный
изгибающий момент равен:
Момент
сопротивления кручению:
Максимальное
нормальное напряжение:
Максимальное
касательное напряжение:
Значения
и
не превосходят значений предельных
напряжений для данной марки стали.
Коэффициент
запаса прочности по нормальным
напряжениям:
где
— амплитуда цикла нормальных напряжений,
в данном случае равная ;
— коэффициент концентрации напряжений
(значение находится по таблице);
— масштабный коэффициент, учитывающий
появление раковин и пороков в заготовке;
— коэффициент, учитывающий состояние
поверхности;
— коэффициент асимметрии цикла, в данном
случае равен 0;
— среднее напряжение цикла нормальных
напряжений, так же равно 0.
Коэффициент
запаса прочности по касательным
напряжениям:
где
— амплитуда цикла касательных напряжений,
которая находится по формуле
Общий
коэффициент запаса по выносливости
равен:
где
.
Сопротивление
усталости обеспечивается.
11.2
Промежуточный вал
Материал:
сталь 45.
Предельное
напряжение: .
Предел
выносливости при симметричном цикле
изгиба:
Предел
выносливости при симметричном цикле
кручения: .
Силы
в зацеплении:
.
Крутящий
момент равен:
.
Реакции:
.
Расстояния:
.
Эпюра
изгибающих моментов
Ox
в сечениях, проходящих через точки A,
B,
C,
D:
I.
II.
III.
Эпюра
изгибающих моментов
Oy
в сечениях, проходящих через точки A,
B,
C,
D:
I.
II.
III.
Как
видно из эпюры, наиболее опасные сечения
приходятся на точки C
и D.
Суммарные
изгибающие моменты:
Моменты
сопротивления кручению:
Максимальные
нормальные напряжения:
Максимальные
касательные напряжения:
Рис
9.3 Конструкция, расчетная схема и эпюры
изгибающих и крутящих моментов тихоходного
вала
Значения
и
не превосходят значений предельных
напряжений для данной марки стали.
Для
нахождения коэффициентов запаса
прочности беру значения максимальных
напряжений в сечении D.
Коэффициент
запаса прочности по нормальным
напряжениям:
Коэффициент
запаса прочности по касательным
напряжениям:
Общий
коэффициент выносливости
где
.
Сопротивление
усталости обеспечивается.
11.3
Выходной (тихоходный) вал
Материал:
сталь 45.
Предельное
напряжение: .
Предел
выносливости при симметричном цикле
изгиба:
Предел
выносливости при симметричном цикле
кручения: .
Силы
в зацеплении:
Крутящий
момент равен:
.
Реакции:
.
Расстояния:
;
.
Эпюра
изгибающих моментов
Ox
в сечениях, проходящих через точки A,
B,
C,
D:
I.
II.
Эпюра
изгибающих моментов
Oy
в сечениях, проходящих через точки A,
B,
C,
D:
I.
II.
Как
видно из эпюры, наиболее опасное сечение
проходит через точку C.
На этом участке вала имеется шпоночная
канавка.
Суммарный
изгибающий момент равен:
Момент
сопротивления кручению равен:
Максимальное
нормальное напряжение равно:
Максимальное
касательное напряжение равно:
Рис
9.4 Конструкция, расчетная схема и эпюры
изгибающих и крутящих моментов тихоходного
вала.
Значения
и
не превосходят значений предельных
напряжений для данной марки стали.
Коэффициент
запаса прочности по нормальным
напряжениям:
Коэффициент
запаса прочности по касательным
напряжениям:
Общий
коэффициент запаса по выносливости
где
.
Сопротивление
усталости обеспечивается.