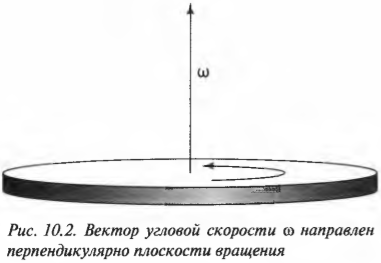
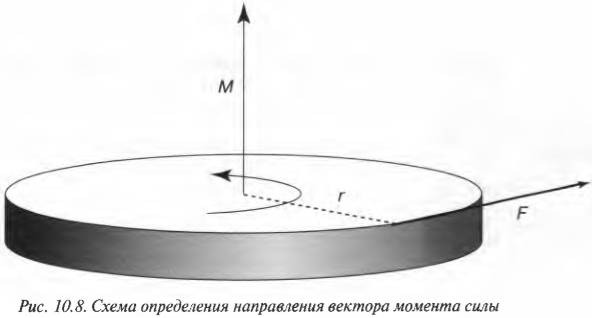
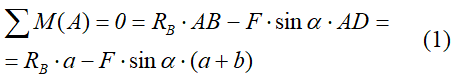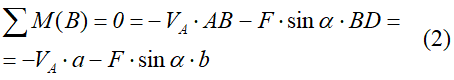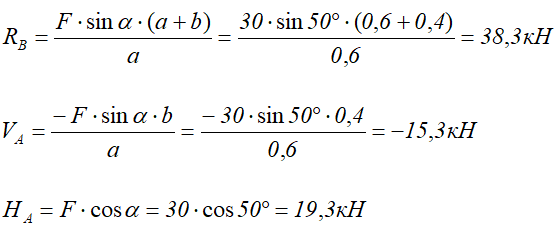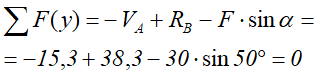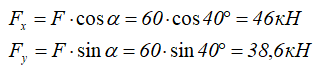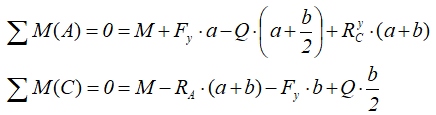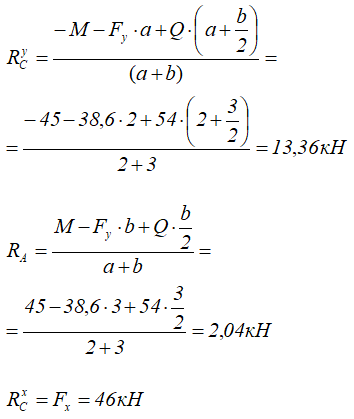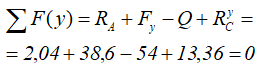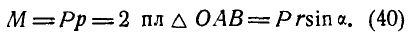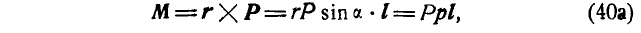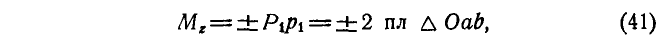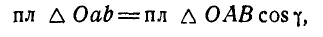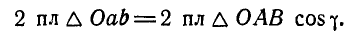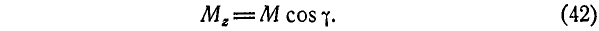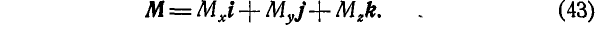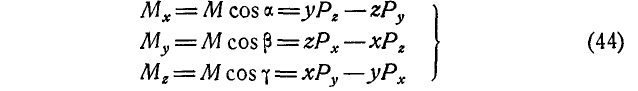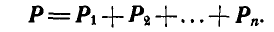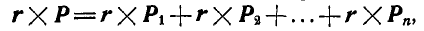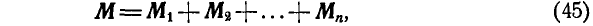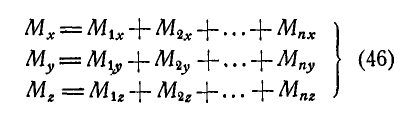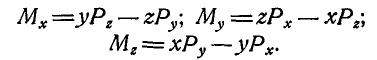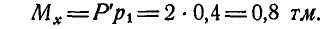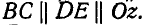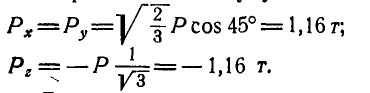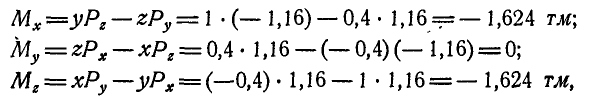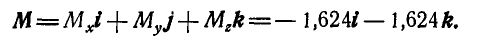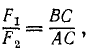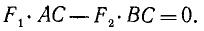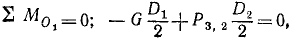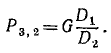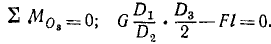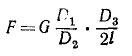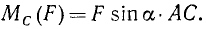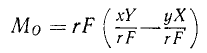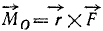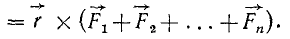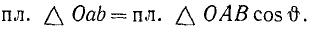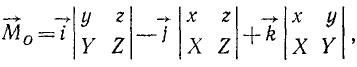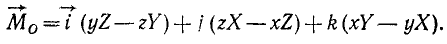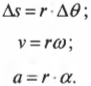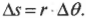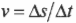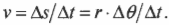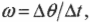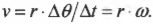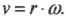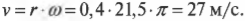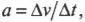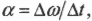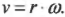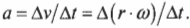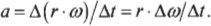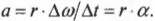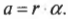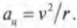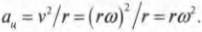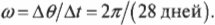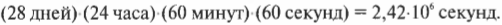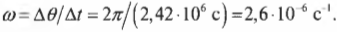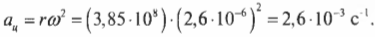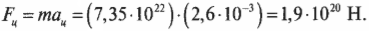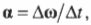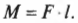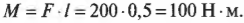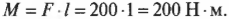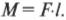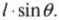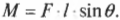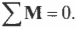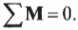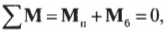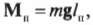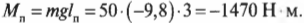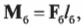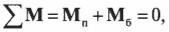Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
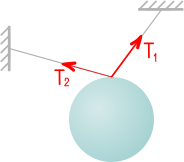
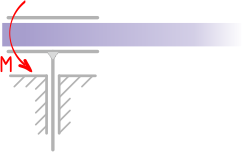
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

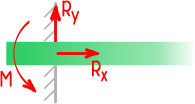
Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
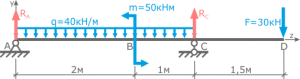
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
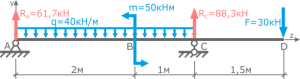
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:


Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:
Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:
Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:

Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Определением реакций опор называют расчет величины и направления реактивных (т.е. ответных) сил и моментов, возникающих в опорах конструкций под действием системы заданных внешних нагрузок.
В рассмотренных ниже примерах, для наглядности, заданные внешние нагрузки показаны синим или зеленым цветом, а реакции опор — красным или оранжевым.
При решении задач, определяемые реакции опор могут обозначаться по разному:
- буквой R (от англ. Reaction). В этом случае, для уточнения точки приложения и направления силы могут добавляться соответствующие индексы (например, RAy — это реакция в точке A направленная вдоль оси Y);
- буквами V (Vertical) и H (Horizontal) обозначаются соответственно вертикальная и горизонтальная составляющие полной реакции (например, HB — это реакция в точке B направленная вдоль оси балки);
- Также возможно обозначение реакций по осям координат — YA, XB и т.д.
Сохранить или поделиться с друзьями
Рассмотрим решение всех типов задач по расчету величины и направления опорных реакций в заделках, шарнирных опорах и стержнях:
Примеры нахождения реакций опор
Примеры нахождения реакций опор для различных способов закрепления и нагружения бруса, балок, рам и других элементов конструкций.
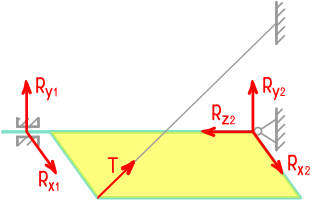
Реакции опоры и стержня системы
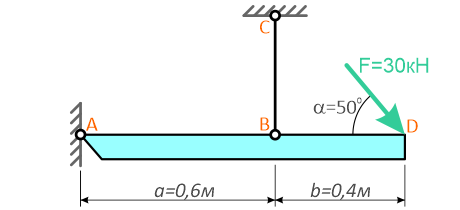
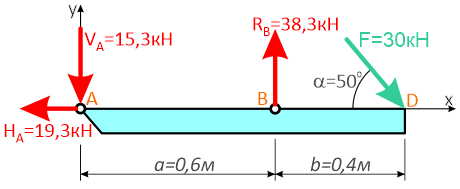
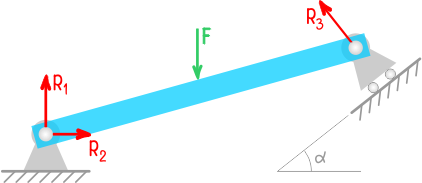
Невесомая балка удерживается в горизонтальном положении шарнирно-неподвижной опорой в т. A и вертикальным стержнем BC.
В точке D к балке приложена сосредоточенная сила F=30кН под углом 50°.
Требуется найти реакции, возникающие в опоре A и стержне BC.
Решение
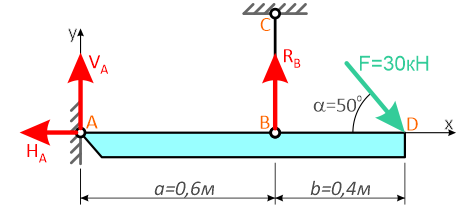
Для решения задачи, покажем систему координат x-y и зададим произвольное направление реакций.
В точке A реакция в опоре раскладывается на две составляющие — вертикальную VA и горизонтальную HA.
Реакция в стержне (RB) всегда направлена вдоль самого стержня.
Для определения трех реакций требуется три уравнения равновесия.
Это будут два уравнения суммы моментов относительно точек в опорах и сумма проекций всех сил на ось x равные нулю.
Составим их:
Из полученных уравнений выражаем и находим искомые реакции опор
Вертикальная реакция в опоре A получилась отрицательной, это значит что она направлена в противоположную сторону.
Направляем ее вниз, изменив знак на «плюс».
Выполним проверку найденных реакций, проецируя все силы на ось y.
Равенство нулю суммы проекций всех сил и реакций показывает то, что реакции опор найдены верно.
Таким образом, заданная балка удерживается в равновесии под действием одной активной и трех реактивных сил.
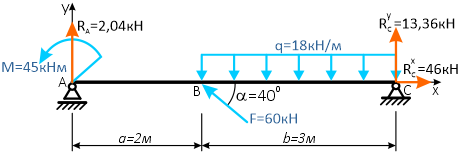
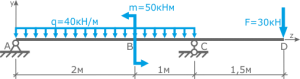
Расчет реакций опор балки
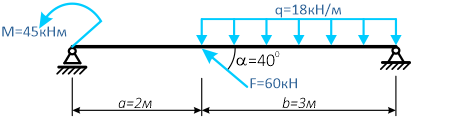
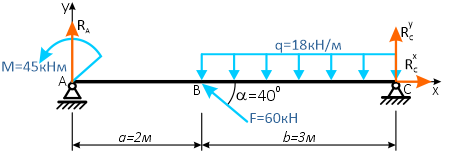
Простая балка на двух шарнирных опорах нагружена системой усилий, включающей силу F=60кН, приложенную под углом 40°, момент M=45кНм и равномерно распределенную нагрузку q=18кН/м.
Требуется определить реакции в опорах A и C.
Решение
Вычерчиваем заданную схему в масштабе, показываем численные значения нагрузок, систему координат x-y и задаем произвольное направление реакций.
Здесь, в шарнирно-подвижной опоре будет только одна составляющая реакции.
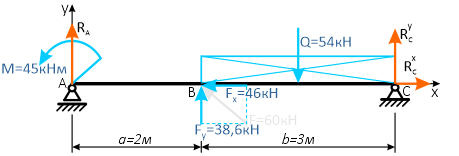
Для упрощения решения, распределенную нагрузку можно заменить её равнодействующей, которая при равномерном распределении q будет приложена по её центру
а силу F можно разложить на составляющие, спроецировав её на оси x и y.
В следющих примерах эти действия выполнять не будем, проводя вычисления напрямую со значениями q и F.
Аналогично тому, как это делалось при решении предыдущей задачи, записываем уравнения равновесия балки: нулевые суммы моментов всех нагрузок и искомых реакций относительно опор
и проекций сил на ось балки
Откуда находим все три опорные реакции
Все результаты положительны, следовательно, направление реакций было выбрано верно.
Проверяем найденные значения.
Величина реакций рассчитана правильно.
Подробное решение данного типа задач
Остальные задачи по определению опорных реакций с детальным разбором выполняемых действий:
При растяжении-сжатии стержней
Определение реакций в опорах стержней и стержневых систем при действии продольных сил.
- Расчет опорной реакции при растяжении-сжатии
- Расчет опорной реакции ступенчатого бруса
- Опорная реакция в заделке стержня с продольно распределенной нагрузкой
При кручении
Примеры расчета опорных моментов и реакций в подшипниках вала при кручении.
- Определение неизвестного крутящего момента вала
- Определение реакций подшипников пространственно нагруженного вала
- Расчет уравновешивающего момента вала
При изгибе балок и рам
Определение реакций в шарнирных опорах и заделках консольных балок и рам при действии систем внешних сил, моментов и распределенных нагрузок.
- Определение реакций в опорах двухопорной балки
- Расчет опорных реакций консольной балки
- Определение опорных реакций в жесткой заделке при изгибе
- Определение реакций опор балки, когда сила приложена под углом
- Проверка опорных реакций балки
- Расчет реакций в опорах рамы
- Определение опорных реакций балки (Видео)
Наш короткий видеоурок по расчету реакций опор балки:
Другие видео
Другие примеры определения реакций опор
Расчет реакций в опорах нестандартных систем.
- Определение реакции шарнира и опоры
- Реакции в шарнирах
- Реакции опор и шарнира
- Расчет веса противовеса и реакций в шарнирах
- Величина груза обеспечивающая равновесие и реакции в подшипниках
- Определение усилий в стержнях
- Натяжение троса и реакция опоры
- Реакции опор в точках системы
- Опорные реакции невесомой конструкции
- Опорные реакции в скользящей заделке
- Давление в шарнире и реакции в бискользящей заделке
- Реакции в скользящей заделке
- Расчет усилия в стержне
Типы опор и их реакции
В механике различают тела свободные: возможность перемещения, которых в любом направлении ничем не ограничена, и несвободные, когда перемещение данного тела ограничивают другие тела.
Сами тела ограничивающие свободу перемещения данного тела называют опорами (связями), а силы, с которыми опоры удерживают данное тело в равновесии, называют реакциями опор.
Направление реакций зависит от вида опор и схемы нагружения.
При решении задач очень важно правильно заменить опоры их реакциями, иначе записанные уравнения равновесия окажутся неверными.
И здесь важно помнить о том, что реакции могут появляться только по тем направлениям, в которых перемещение невозможно.
Рассмотрим определение реакций в основных типах опор:
Другие видео
Реакция гладкой поверхности
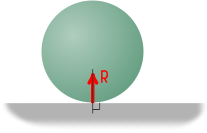
Пусть некоторое тело опирается на гладкую поверхность.
Здесь перемещение тела возможно только вдоль поверхности.
Движение перпендикулярно ей исключено.
Потому что перемещению в сторону поверхности препятствует сама поверхность, а при движении от нее нарушится сама связь.
Таким образом, гладкая поверхность препятствует перемещению тела только в направлении нормали, поэтому реакция гладкой поверхности всегда направлена по нормали к этой поверхности.
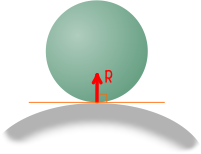
При взаимодействии криволинейных поверхностей аналогично, реакция направлена нормально к касательной в точке контакта тел.
То же самое будет при контакте в двух точках.
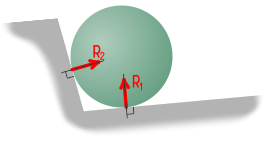
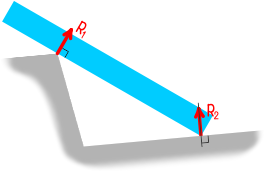
Реакция ребра
В случае, когда прямая балка опирается на ребро, реакции будут направлены перпендикулярно опираемой или опирающейся плоскости в точке их касания.
При повороте балки реакция всегда будет оставаться нормальной к соответствующей поверхности.
Гибкая связь
Для тела, подвешенного на нерастяжимой нити или тросе, связь не позволяет телу удаляться от точки подвеса в направлении самой нити.
Поэтому реакция гибкий связи будет направлена всегда только вдоль самой нити.
Реакции в стержнях
Как и в предыдущем пункте, в стержнях, которые с помощью шарниров соединяют какие-либо элементы с опорами, реакции направлены вдоль самих стержней.
Но в отличие от нитей, здесь может быть одно из двух направлений: растягивающее стержень или сжимающее его.
Реакции в шарнирных опорах
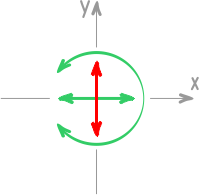
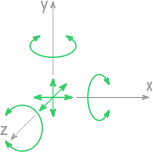
На плоскости возможны только три направления перемещения:
Линейные — вдоль осей x и y, и вращение относительно оси Z.
Поэтому в двумерных системах каждая опора может давать не более трех реакций.
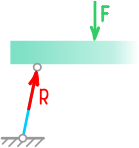
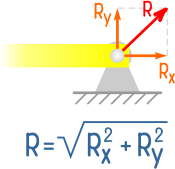
Если свободное тело закрепить шарнирно-неподвижной опорой, которая допускает вращение, но исключает любые линейные перемещения, то в такой опоре могут возникать две реакции.
Они являются осевыми проекциями полной реакции опоры, которая может быть найдена как корень из суммы квадратов её составляющих.
Направление вектора полной реакции зависит от схемы нагружения элемента.
Встречаются разные способы изображения шарнирно-неподвижных опор в расчетных схемах.
В шарнирно-подвижных опорах, помимо вращения возможно линейное перемещение вдоль поверхности, поэтому здесь будет только одна, нормальная к поверхности, составляющая реакции, которая по направлению и величине будет совпадать с полной.
У таких опор так же существуют дополнительные варианты схематичного изображения.
Пример направления реакций опор для балки на двух шарнирных опорах.
Реакции в заделках
Вид связи, при котором брус жестко закреплен в опоре называется глухой заделкой.
В этом случае исключены любые перемещения элемента.
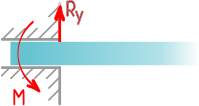
Поэтому в плоских заделках может возникать до трех реакций: горизонтальная и вертикальная составляющие полной реакции, а также момент.
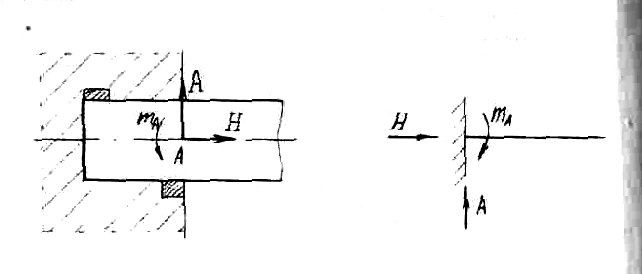
Скользящая заделка допускает линейное перемещение вдоль одной из осей.
Следовательно, по этой оси реакции не будет.
В бискользящей заделке исключается только угловое перемещение элемента.
Здесь из реакций будет один момент.
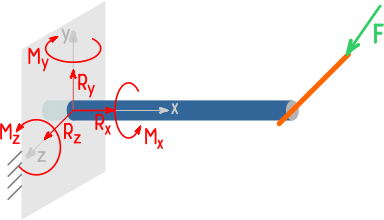
Реакции опор в трехмерных системах
В пространстве возможно уже шесть направлений движения:
Поступательные вдоль каждой из осей и вращение относительно них.
Поэтому в трехмерных системах опоры могут давать до шести реакций.
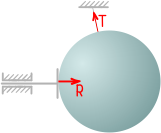
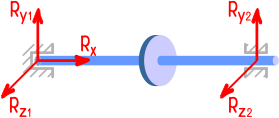
Шкив на валу, закрепленном подшипниками, может вращаться относительно продольной оси вала.
Любые другие перемещения невозможны.
В силу конструктивных особенностей подшипников моментов в них не возникает.
Здесь имеют место только реактивные силы.
В радиальном подшипнике (который справа) все реакции поперечны оси вала.
В радиально-упорном (который слева) добавляется еще и продольная.
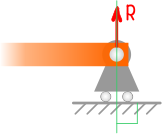
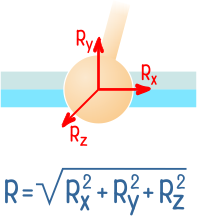
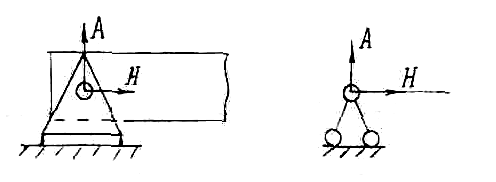
В трехмерном шарнире исключены любые линейные перемещения и возможны только повороты относительно трех осей, что дает до трех составляющих полной реакции R.
В жесткой заделке при общем случае нагружения может возникать до шести реакций: трёх сил и трех моментов.
Пример замены опор их реакциями для трехмерной системы:
Порядок расчета опорных реакций
В рассмотренных выше примерах при определении реакций в опорах выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок;
Расчетная схема балки - Выбирается система координат и обозначаются характерные сечения бруса;
Система координат для балки - Определяется количество и возможное направление связей;
Направление опорных реакций балки - Записываются уравнения статики (по количеству неизвестных реакций);
- Из уравнений равновесия находим величину и направление (по знаку) опорных реакций.
Опорные реакции балки
После расчетов выполняется проверка найденных значений.
Более подробно порядок расчета опорных реакций рассматривается в разделе «Статика» теоретической механики.
Другие примеры решения задач >
Лекция №3
Тема: «Внутренние
усилия в поперечных сечениях стержня»
Вопросы:
1. Опоры и
опорные реакции, и их определение
2. Поперечная
сила и изгибающий момент
3. Взаимосвязь
между изгибающим моментом, поперечной
силой и интенсивностью распределенной
нагрузки
1. Опоры
и опорные реакции, и их определение
При
расчете конструкций в основном встречаются
элементы, испытывающие изгиб.
Стержни,
работающие преимущественно
на изгиб, называют балками. Для того
чтобы балка
могла
испытывать
нагрузку и передавать ее на основание,
она должна
быть соединена с ним опорными связями.
На практике применяют
несколько типов опорных связей, или,
как говорят, несколько
типов опор.
Различают три
основных типа опор:
а)
шарнирно-подвижная опора:
б)
шарнирно-неподвижная опора:
в)
жесткая заделка.
Рис. 1
На
рис. 1 показана шарнирно-подвижная
опора, такая опора позволяет
балке свободно поворачиваться и
перемещаться в горизонтальном
направлении. Поэтому реакция в опоре
будет одна
вертикальная сила. Условное обозначение
такой опоры показано справа.
Рис. 2
На
рис. 2 показана шарнирно-неподвижная
опора. Такая опора
позволяет балке свободно поворачиваться,
но перемещаться она
не может. Поэтому могут возникать две
реакции — вертикальная и горизонтальная
силы. Их можно сложить и получить одну
результатирующую
силу, но нужно знать угол, под которым
oна
будет
направлена. Более удобно будет пользоваться
вертикальной и горизонтальной
составляющими реакции.
На
рис. 3 показана жесткая заделка. Она
не позволяет балке ни поворачиваться,
ни перемещаться. Поэтому могут возникать
три опорные
реакции: момент, вертикальная и
горизонтальная силы. Если балка не имеет
на конце опоры, то эта часть ее называется
консолью.
Рис. 3
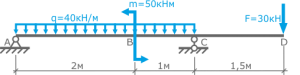
Определим
реакции опор для балки (см. рис. 4).
Рис.4
В опоре
А горизонтальная реакция равна нулю,
так как распределенная
нагрузка q
и сосредоточенная сила F
имеют
вертикальное
направление. Реакции опор
направим
вверх.
Составим два уравнения статического
равновесия сил. Сумма моментов относительно
каждой из опор равна нулю. Уравнения
моментов нужно составлять относительно
опор, так как в этом случае получаются
уравнения с одним неизвестным. Если
составить уравнения
относительно точек В и С, то получим
уравнения с двумя неизвестными,
а их решать сложнее. Моменты против
часовой стрелки будем считать
положительными, по часовой
отрицательными.
где
момент от равномерно распределенной
нагрузки.
Произведение
q
на расстояние, на котором она приложена,
из условия
равновесия системы равно сосредоточенной
силе, приложенной
посредине отрезка. Поэтому момент
равен:
– момент силы F
Внешний
момент m
на плечо не умножается, так
как
это
пара сил, т.е. две равные по величине,
противоположно направленные силы,
имеющие постоянное плечо.
или
.
Проверка:
Сумма всех сил на вертикальную ось Y
должна быть равна
нулю:
.
Момент
m
в условие статического равновесия
не записывают,
так как момент
это две равные по величине, противоположно
направленные силы и в проекции на любую
ось они дадут
ноль.
30-20-2-40+50=0:
80-80=0.
Реакции
определены правильно.
2. Поперечная
сила и изгибающий момент
Пусть
на балку действуют силы
,
реакции опор
.
Определим внутренние усилия в сечении,
расположенном на расстоянии от нулевого
конца (см. рис.5).
Рис. 5
Поскольку
все внешние силы действуют вертикально,
то горизонтальной составляющей у реакции
опоры А
не будет. Балка не будет сжиматься или
растягиваться, т.е. продольная сила в
поперечных сечениях равна нулю. Можно
было взять пример, когда
силы
были бы не вертикальными по направлению.
Тогда бы в опоре А
была бы и вторая реакция
горизонтальная сила, а в сечениях балки
продольная сила N.
В этом случае балка испытывала бы изгиб
с растяжением (сжатием), т.e.
был бы случай сложного сопротивления.
Его мы будем изучать позднее. Вначале
рассматривают более простые задачи и
идут к более сложным, а не наоборот.
Поскольку
внешние силы
лежат в одной плоскости,
проходящей через ось бруса, то возможно
возникновение
тpex
внутренних усилий: изгибающею момента
М,
поперечной силы Q
и
продольной силы N,
которая, как мы отмечали, равна нулю.
Значения М
и Q
определим
из уравнения статического равновесия
левой
части балки:
.
Вывод:
поперечная сила в сечении численно
равна алгебраической
сумме всех внешних сил, а изгибающий
момент
сумме
всех моментов, вычисленных относительно
сечения и приложенных
к рассматриваемой части балки.
Для
поперечных сил и изгибающих моментов
приняты обязательные
правила знаков (см. рис. 6).
Если
сила пытается повернуть рассматриваемую
часть балки по часовой
стрелке, то она вызывает положительную
поперечную силу, и, наоборот, если
действует против часовой стрелки
то поперечная
сила
отрицательная. На рис. 5
сила
вызывает положительное
Q,
а
отрицательное. Следует отметить, что
направление силы положительное для
левой части будет отрицательным для
правой части.
Это вызвано тем, что внутренние силы,
действующие на правую
и левую часть балки обязательно должны
быть равны и противоположно
направлены.
Если
внешняя сила или внешний момент изгибают
балку выпуклостью
вниз, то возникающий изгибающий момент
положительный
и, наоборот, выпуклостью вверх
отрицательный.
Рис. 6
3. Взаимосвязь
между изгибающим моментом,
поперечной силой
и интенсивностью распределенной нагрузки
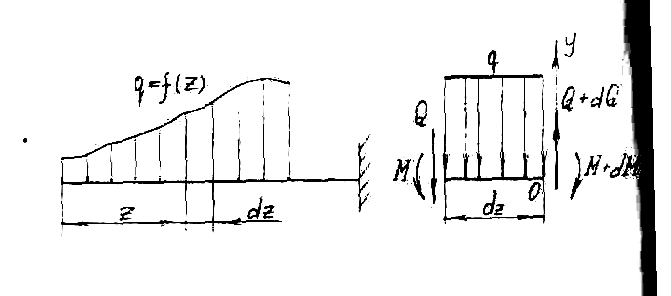
Пусть
на консольную балку (см. рис. 7)
действует
распределенная
нагрузка, изменяющаяся по длине балки.
На расстоянии z
от левого конца возьмем бесконечно
малый отрезок dz.
Рис. 7
Тогда
распределенную нагрузку на нем можно
рассматривать как постоянную.
В левой части рассматриваемого отрезка
будут внутренние усилия Q
и
М,
в правой
с учетом приращения внутренних
усилий Q+dQ
и
M+dM.
Составим
уравнения статического равновесия для
отрезка балки:
(1)
Третьим
членом можно пренебречь, как бесконечно
малой величиной
более высокого порядка, т.е.:
После преобразований
получим:
(2)
т.е. первая
производная от изгибающего момента по
абсциссе (длине балки) есть поперечная
сила.
Если
в формулу (1) подставить значение Q
из
формулы (2),
то
получим:
, (3)
т.е. вторая
производная от изгибающего момента
есть интенсивность распределенной
нагрузки.
Содержание:
- Момент силы
- Момент силы относительно точки (центра)
- Момент силы относительно оси
- Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
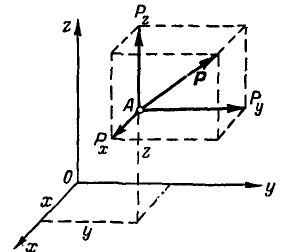
- Моменты силы относительно координатных осей
- Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Момент силы (момент силы относительно точки; также: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — эо векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Момент силы
Система сходящихся сил, которая будет рассмотрена в главе 2, является особой среди
систем сил. Только в этой системе линии действия сил имеют одну точку пересечения. Поэтому для ее изучения достаточно основных понятий статики, рассмотренных в разделе 1. Для изучения других систем сил необходимо ознакомиться с понятиями момента силы и пары сил.
Понятие о моменте силы — одно из основных понятий механики, которое широко используется и в теоретических исследованиях и при практических расчетах. К понятию момента силы человечество пришло, рассматривая равновесие и движение тел, имеющих точку или ось вращения (в частности блоков и рычагов, которые использовались в практике еще до нашей эры).
Например, на неподвижный блок (рис. 3.1) действует сила 


Момент силы относительно точки (центра)
Заданная сила 


где 
Определим величину (модуль) и направление вектора 

Обозначим 

где 

Вектор 
Заметим, что 
Модуль момента силы относительно точки равен удвоенной площади треугольника, вершинами которого является точка и начало и конец вектора
Если линия действия силы проходит через точку (центр), то h = 0, и из формулы (3.2) видно, что момент силы относительно этой точки будет равняться нулю.
Момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, поскольку неизменным остается плечо силы относительно точки (рис. 3.4).
Если на тело действует плоская система сил, то векторы моментов всех сил системы относительно некоторого центра, что лежит в плоскости действия сил, будут перпендикулярны этой плоскости, а следовательно, параллельные и их можно считать скалярными величинами, которые отличаются только величиной и знаками.
В этом случае целесообразно ввести понятие алгебраического момента силы относительно точки (центра), равный взятом со знаком «+» или «-» произведения модуля силы на плечо относительно этой точки (центра)
Будем считать момент положительным, если сила пытается вращать тело вокруг точки (центра) против хода часовой стрелки (рис. 3.5, а), и отрицательным — если по ходу часовой стрелки (рис. 3.5, б). Единицы момента силы:
Момент силы относительно оси
Изучая пространственные системы сил, будем использовать понятие момента силы относительно оси.
Моментом силы относительно оси называется величина, равная алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Пусть к телу в некоторой точке А приложена сила 



Точку пересечения плоскости П с осью 

Согласно определению
Таким образом, чтобы определить момент силы относительно оси, необходимо:
— спроектировать эту силу на плоскость, перпендикулярную оси;
— найти точку пересечения оси с этой перпендикулярной плоскостью;
— определить алгебраический момент полученной проекции относительно точки пересечения оси с плоскостью.
Из формулы (3.5) следует, что момент силы относительно оси равен нулю, если:
1) сила параллельна оси, тогда
2) линия действия силы пересекает ось, тогда
Эти два условия эквивалентны одному условию: момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости. поскольку момент силы относительно оси 
Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
Теорема 3.1. Проекция векторного момента силы относительно точки на ось, проходящей через эту точку, равен моменту силы относительно этой оси.
Доказательство. Сила 



Известно, что
где
Из курса элементарной геометрии известно, что
где 
Поскольку вектор 


Учитывая равенства (3.6), (3.7), получим
Знак 

Поскольку
что и требовалось доказать.
Моменты силы относительно координатных осей
Пусть на тело действует сила 
Определим момент силы 

Согласно (3.1),

Вектор силы 

где 

Тогда векторное произведение 
Раскрывая этот определитель, получим
Представим векторный момент 
Сравнивая правые части равенств (3.9) и (3.10), получим:
Поскольку точка О принадлежит осями 
Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Теорема 3.2. Момент равнодействующей пространственной системы сходящихся сил
относительно некоторого центра (точки) равна векторной сумме моментов составляющих сил относительно того же центра (точки).
Доказательство. На тело действует пространственная система сходящихся сил 
данную систему сил эквивалентной системой, все силы которой приложенные в точке В
(Рис. 3.10, б). Равнодействующую системы, прилагаемую в той же точке В, обозначим 



Известно, что 
Итак, получили равенство
Теорема доказана.
Уравнение (3.13) является математическим записи теоремы Вариньона для пространственной системы сходящихся сил.
В случае плоской системы сходящихся сил теорема Вариньона запишется так:
Итак, момент равнодействующей плоской системы сходящихся сил относительно некоторого центра (точки), лежащий в плоскости действия сил, равна алгебраической сумме моментов составляющих сил относительно этого самого центра (точки).
Рассмотрим пример на применение теоремы Вариньона.
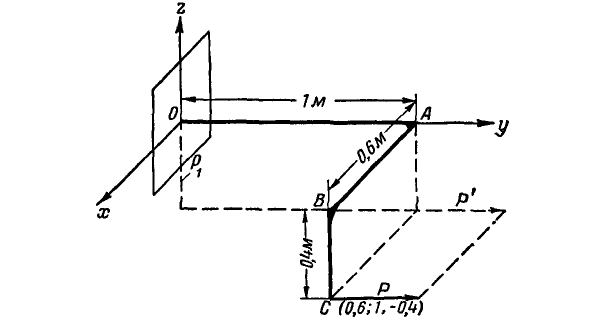
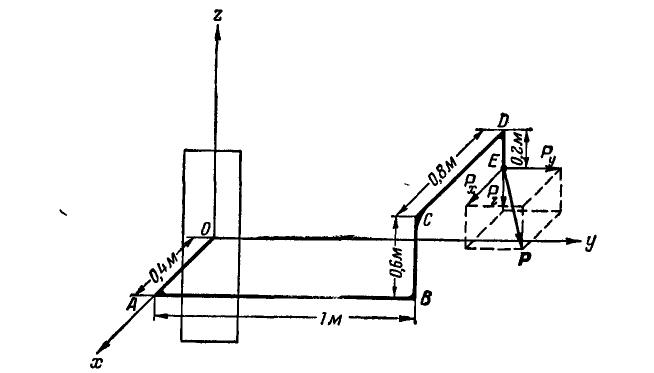
Задача. На согнутый под прямым углом стержень АВС действуют силы 

Решение.
Для определения момента силы 
Разложим силу 




Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Момент силы относительно точки и относительно оси в теоретической механике
Содержание:
Момент силы относительно точки и относительно оси:
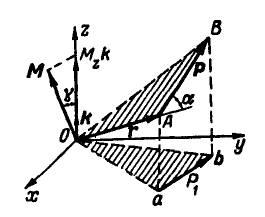
Пусть дана сила Р, направленная как угодно в пространстве, и произвольная точка О (рис. 100).
Опустим из точки О перпендикуляр на силу Р (на чертеже перпендикуляр не показан) и обозначим плечо силы Р относительно точки О через р. Тогда моментом силы Р относительно точки О (или линейным моментом силы) Называется вектор М, численно равный произведению Р на плечо р и отложенный от точки О перпендикулярно плоскости, проходящей через Р и О в такую сторону, чтобы, смотря с конца стрелки вектора М, сила Р вращала плоскость ОАВ вокруг точки О против часовой стрелки.
Если из центра моментов О провести радиус-вектор
Из сказанного следует, что, линейный момент силы может быть представлен, как векторное произведение радиуса-вектора 
где 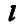
Наряду с линейным моментом силы введем в рассмотрение еще одно важное понятие момента силы относительно оси.
Пусть требуется найти момент силы Р относительно какой-либо оси, например z (рис. 100). Для этого силу Р спроектируем на любую плоскость, перпендикулярную к оси z, например на координатную плоскость хОу; обозначим эту проекцию через 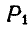
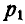
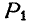
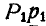
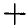

где знак 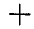
Следует заметить, что момент силы относительно оси обращается в нуль, когда сила параллельна оси или пересекает ось, т. е. когда вообще сила и ось расположены в одной плоскости.
С понятием момента силы относительно оси часто придется встречаться в дальнейшем. Если представить себе цилиндр (рис. 101), который может вращаться вокруг неподвижной оси z, то сила Р, действующая на цилиндр, не будет его вращать в двух случаях: когда она пересекает ось z (положение 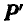
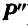
Найдем зависимость между моментом силы Р относительно оси, например z (рис. 100), и моментом силы Р относительно точки О, взятой на этой оси.
Обозначим линейный момент силы через М, а момент силы относительно оси z представим в виде вектора 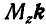
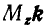
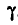
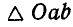
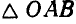
где 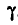
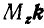
Умножив обе части последнего равенства на 2, получим:
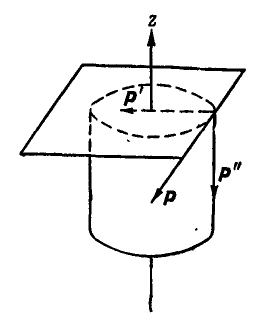
Тогда на основании равенств (40) и (41) будем иметь:
Из равенства (42) следует, что проекции линейного момента силы 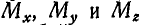
Линейный момент М может быть выражен по формуле (4) через компоненты:
Величины 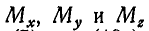
где 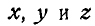
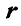
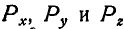
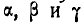
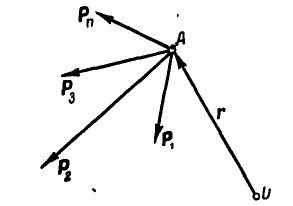
Если на точку А (рис. 102) действуют силы 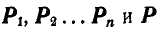
Умножая векторно обе части равенства на радиус-вектор 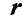
или
т. е. момент равнодействующей сил, линии действия которых пересекаются в точке, относительно любой точки равен геометрической сумме моментов сил составляющих относительно той же точки.
Проектируя векторное равенство (45) на координатные оси, согласно (42) получаем:
т. е. момент равнодействующей сил, линии действия которых пересекаются в одной точке, относительно какой-либо оси равен алгебраической сумме моментов сил составляющих относительной той же оси.
На основании последних равенств формулы (44) могут быть получены непосредственно из чертежа. Для этого представим силу Р (рис. 103), приложенную в точке А, определяемой координатами х, у и z в виде трех составляющих 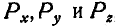
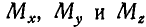
Задача:
Найти моменты 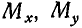
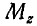
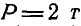
Решение. Момент силы Р относительно оси у равен нулю, так как сила Р параллельна оси Оу, т. е. 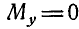
Для нахождения момента силы Р относительно оси Ох проектируем силу Р на плоскость yOz, перпендикулярную к оси Ох (проекция Р). Опустив далее из точки О пересечения оси Ох с плоскостью yOz перпендикуляр 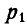
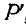
Аналогично находим, что 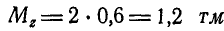
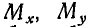
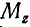
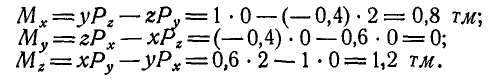
Задача:
Найти линейный момент М силы 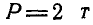
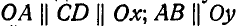
Решение. Проекции силы Р на координатные оси будут:
Так как точка приложения силы 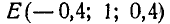
откуда по формуле (43) находим:
Момент силы относительно точки
Для равновесия рычага необходимо и достаточно, чтобы сумма моментов действующих на него сил относительно точки опоры равнялась нулю
Условие равновесия рычага. Твердое тело, имеющее возможность поворачиваться вокруг неподвижной оси под воздействием сил, линии действия которых расположены в плоскостях, перпендикулярных оси вращения, называют рычагом. Пусть рычаг (рис. 27) представляет собой невесомый жесткий стержень. На него действуют только две силы 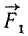
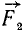
Если точка опоры С, т. е. точка пересечения оси вращения с плоскостью чертежа, лежит между линиями действия сил (рис. 27, а), то рычаг называют рычагом первого рода. Рычагом второго рода называют рычаг, в котором точка опоры находится по одну сторону от линий действия сил (рис. 27, б).
Для равновесия рычага необходимо и достаточно, чтобы равнодействующая активных сил 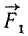
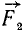
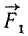
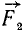
Будем называть расстояние от точки опоры до линии действия силы плечом силы, а произведение модуля силы на плечо—моментом силы относительно точки опоры С. Момент .мы считаем положительным, если сила стремится повернуть рычаг против вращения стрелок часов, и отрицательным, если сила стремится повернуть плечо в ту же сторону, в какую поворачиваются стрелки часов. Момент силы 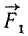
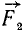
Таким образом, условие равновесия рычага выразим так: для равновесия рычага необходимо и достатнчно, чтобы сумма моментов сил относительно точки опоры равнялась нулю:
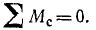
Задача:
Груз G (рис. 28, а) поднимают тросом, перекинутым через блок и намотанным на барабан l лебедки. Барабан лебедки жестко скреплен с зубчатым колесом ll, которое находится в зацеплении с зубчатым колесом lll, жестко скрепленным с рукояткой O3A. Определить силу F, прикладываемую к точке А рукоятки лебедки для равномерного поднятия груза G, в положении, изображенном на чертеже. Даны диаметры: D1, D2, D3. Длина рукоятки O3A=l.
Решение. Лебедку можно рассматривать как состоящую из двух рычагов. Один рычаг (назовем его первым) представляет собой твердое тело, состоящее из барабана l и шестерни ll и имеющее неподвижную ось O1. Другой рычаг—твердое тело, состоящее из шестерни lll и рукоятки O3A и имеющее неподвижную ось O3. Для решения задачи из условия равновесия первого рычага определим давление P3,2 между зубцами шестерен, а зная его, найдем F из условия равновесия второго рычага.
На первый рычаг действуют следующие силы (рис. 28, б): 1) сила натяжения троса, равная весу груза, направленная вверх и стремящаяся повернуть рычаг по ходу часовой стрелки; 2) давление P3,2 зубцов колеса lll на зубцы колеса ll, направленное вверх и поворачивающее первый рычаг против хода часов, и 3) реакция в оси O1.
Момент силы T относительно точки опоры O1 равен — 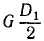
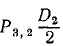
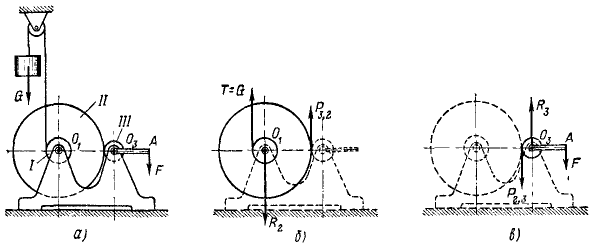
Рис. 28
Ко второму рычагу (рис. 28, в) приложены: I) сила давления зубцов колеса II, равная (по принципу равенства действия и противодействия) P3,2, но направленная вниз и стремящаяся повернуть второй рычаг против хода часов; 2) давление F руки человека, направленное вниз и поворачивающее рычаг по ходу часов, и 3) реакция в оси O3, момент которой относительно O3 равен нулю.
Момент силы P3,2 относительно точки опоры O3 равен 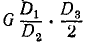
Мы выясни ли, что момент силы относительно точки опоры рычага зависит не только от величины силы, но и от ее положения по отношению к точке опоры рычага. Чем дальше от точки опоры лежит линия действия силы, тем больше момент. Если сила не перпендикулярна рычагу (рис. 29), то способность ее поворачивать рычаг вокруг точки опоры мы и в этом случае будем измерять моментом силы, а под плечом будем понимать кратчайшее расстояние от точки опоры до линии действия силы. Пусть сила F приложена к рычагу в точке А и составляет с ним некоторый угол а. Разложим силу на две составляющие, из которых одна (F sin a) перпендикулярна к рычагу, а другая (F cos a) направлена вдоль рычага. Эта вторая составляющая не может повернуть рычаг, а поворачивать его будет только первая составляющая (F sin a) или, как говорят, только эта составляющая создает вращающий момент.
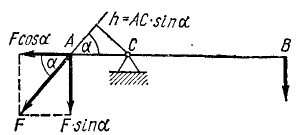
Рис. 29
Следовательно, момент силы F относительно опоры C
Но, как видно из чертежа, АC sin a= h. Называя плечом силы относительно точки длину перпендикуляра, опущенного из точки на линию действия силы, мы находим, что и в этом случае момент равен произведению модуля силы на плечо:
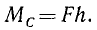
Момент силы относительно точки выражается произведением модуля силы на плечо, взятым со знаком плюс или минус
Момент силы относительно точки. Понятие момента применимо не только к силам, действующим на рычаг, но и к силам, приложенным ко всякому твердому телу. Момент силы может быть определен не только относительно опоры, но и относительно всякой точки. Точку, относительно которой определен момент силы, называют центром момента.
Таким образом, опуская из точки О перпендикуляр на линию действия силы 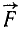
Так (рис. 30), моменты сил 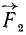
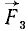
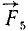
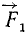
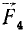
Одна и та же сила может иметь положительный момент относительно одной точки и отрицательный —относительно другой. Так, момент силы 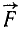
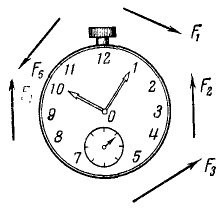
Рис. 30
Рис. 31
Момент силы относительно начала координат связан с проекциями X и Y силы на оси и с координатами х и у точки ее приложения соотношением M0=xY-yX.
Аналитическое выражение момента силы.
Пусть дана сила 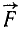
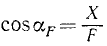
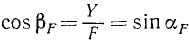
Проведем вектор 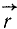
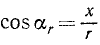
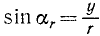
Плечо силы h относительно точки О определим из △OAN:
h = r sin δ.
И для определения величины момента силы получаем следующую формулу:
M0= r Fsin δ. (15)
Угол δ как внутренний угол ΔOAK равен внешнему aF без другого внутреннего, с ним не смежного—ar, поэтому
Подставляя сюда, а затем в (15) найденные выше значения тригонометрических величин, получим
M0= хY — yX 1 . (16)
Определяя момент силы по формуле (16), нет надобности определять его знак, сообразуясь с ходом часовой стрелки, т. к. знак получается непосредственно из формулы в зависимости от знаков χ, y, X, Y. В нашем курсе формуле (16) уделена значительная роль.
Момент силы относительно точки выражается векторным произведением радиуса-вектора точки приложения силы на вектор силы:
Момент силы относительно точки как вектор
Напомним, что векторным произведением 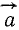
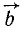
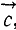
Следовательно, как видно из (15), величина момента силы равна модулю векторного произведения радиуса-вектора 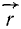
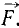
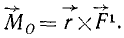
Вектор 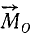
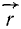
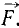
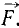
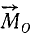
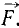
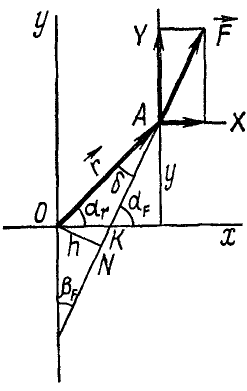
Рис. 32
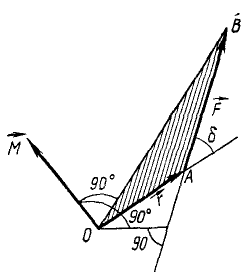
Рис. 33
Сравнивая это равенство с (14), найдем, что момент 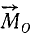
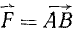
M0 = 2 пл. ΔOAB 1
Вектор момента направлен от точки О перпендикулярно к плоскости OAB в такую сторону, с которой вектор силы AB представляется поворачивающим треугольник OAB вокруг точки О против хода часов. По модулю он равен (в некотором выбранном масштабе) удвоенной площади треугольника OAB.
Если вектор силы AB переместить вдоль линии действия силы в пределах абсолютно твердого тела, к которому сила AB приложена, оставив точку О неизменной, то вектор момента не изменится, так как не изменятся плоскость и площадь треугольника OAB. Сила является вектором скользящим, и действие силы, а следовательно, и ее момент не изменяются при перенесении силы вдоль линии действия. Напротив, если мы переменим точку О, то положение и площадь треугольника OAB, вообще говоря, изменятся, а следовательно, изменится и момент силы. Поэтому момент силы относительно какой-либо точки О является вектором прикрепленным, он приложен к точке О и переносить его в какое-либо другое место тела нельзя.
Выражение момента силы относительно точки в виде вектора вполне соответствует физической сущности этого понятия, и если силы расположены в различных плоскостях, то моменты сил относительно точки складывают по правилу параллелограмма. Только при рассмотрении системы сил, расположенных в одной плоскости, можно игнорировать направление вектора момента, а учитывать его величину и знак, т. е. определять момент по формулам (14), (15) или (16). В такой системе, когда все силы и центр моментов расположены в одной плоскости, векторы моментов различных сил относительно какой-либо точки О направлены от точки О перпендикулярно к этой плоскости в ту или другую сторону, и в этом случае их складывают алгебраически.
Момент равнодействующей равен сумме моментов составляющих
Теорема Вариньона
Пусть даны пространственный пучок сил 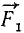
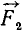
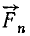
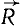
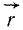
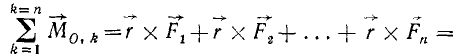
Заменяя согласно (1) геометрическую сумму всех сил сходящейся системы их равнодействующей, получим
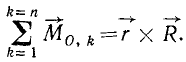
Словами это равенство можно прочитать так: момент равнодействующей системы сходящихся сил относительно какой-либо точки равен сумме моментов всех сил относительно той же точки. Момент
силы относительно точки есть вектор, поэтому сумма является геометрической. В частном случае, если все силы и центр моментов лежат в одной плоскости, то все векторы моментов направлены по одной прямой, перпендикулярной к этой плоскости, и геометрическое сложение моментов сил заменяется алгебраическим.
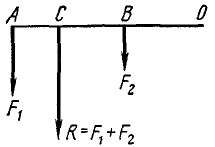
Рис. 35
Таким образом, момент равнодействующей плоской системы сходящихся сил равен алгебраической сумме моментов составляющих. Теорема Вариньона о моменте равнодействующей справедлива не только для пучка сил, ио для всякой системы сил, имеющей равнодействующую. Так, например, момент равнодействующей R двух параллельных сил F1 и F2 относительно произвольной точки О (рис. 35) равен:
что и требовалось доказать. Методом от n к n+1 нетрудно показать справедливость теоремы Вариньона для любого числа сил.
Момент силы относительно оси
Чтобы определить момент силы относительно оси, нужно спроецировать силу на плоскость, перпендикулярную к оси, и затем определить момент проекции силы относительно точки пересечения оси и плоскости
Момент силы относительно оси. Ознакомление с понятием момента силы относительно оси, имеющим большое значение, начнем с конкретного примера. Дверь (рис. 36) может поворачиваться вокруг оси. Механическое воздействие силы 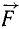
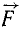
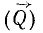
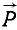
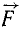
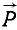
Установим теперь общее правило определения момента силы относительно оси.
Чтобы определить момент силы относительно оси, нужно эту силу спроецировать на перпендикулярную к оси плоскость и определить момент проекции силы относительно точки пересечения оси и плоскости. Момент силы относительно оси — скалярная величина, потому что у него нет собственного направления, а «направлен» он по оси в ту или иную сторону, т. е. определяется величиной и знаком и, конечно, направлением оси.
Где именно проведена перпендикулярная к оси плоскость, не имеет значения, так как проекции силы на параллельные плоскости и плечи проекций силы во всех случаях одни и те же.
Если сила параллельна оси или пересекает ось, то момент силы относительно оси равен нулю. Эти два случая можно объединить в один: момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
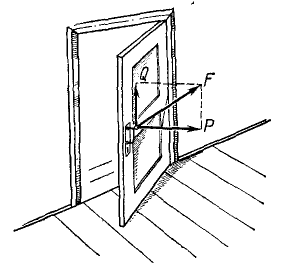
Рис. 36
Момент силы относительно оси равен проекции на эту ось момента силы относительно какой-либо точки, взятой на оси
Покажем, что момент силы относительно оси равен проекции на данную ось вектора момента силы относительно какой-либо точки той же оси.
Возьмем на оси zz’ произвольную точку О (рис. 37) и определим момент силы 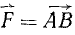
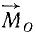
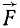
Проведем через точку О плоскость, перпендикулярную к оси. Чтобы определить момент Mz силы относительно оси, спроецируем силу на эту плоскость и определим момент проекции 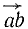
Но Δ Oab является проекцией Δ OAB на плоскость, перпендикулярную к оси. Площадь проекции равна площади проецируемой фигуры, умноженной на косинус двугранного угла между плоскостями, измеряемого линейным углом между перпендикулярами к этим плоскостям, т. е.
Спроецировав на ось момент силы относительно точки О и принимая во внимание это равенство, найдем, что численно
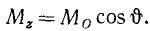
При решении задач особенно часто приходится определять моменты сил относительно координатных осей. Согласно только что доказанному момент силы относительно какой-либо из осей координат равен проекции на эту ось момента сил относительно любой точки этой оси, в частности относительно точки О начала координат:
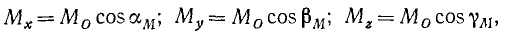
где cosaM, cosβM и CosγM-направляющие косинусы вектора момента силы относительно начала координат.
Если момент относительно оси умножим на единичный вектор этой оси, то получим не проекцию, а составляющую момента относительно точки, не скалярную, а векторную величину:
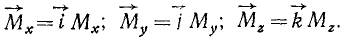
Из равенств (20) и (21) непосредственно получаем
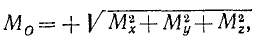
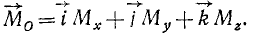
Аналитические выражения моментов силы относительно осей координат. Выразим моменты силы относительно осей координат через координаты точки приложения силы и проекции силы на координатные оси.
На чертеже (рис. 38) изображены оси координат и составляющие силы, приложенной к точке А (xyz) (сама сила на чертеже не показана). Чтобы определить моменты силы относительно оси Ох, нужно сначала спроецировать силу 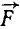
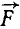
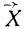
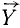
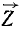
Теперь нам остается определить алгебраическую сумму моментов этих проекций относительно точки О, которая по теореме Вариньона равна моменту проекции равнодействующей на плоскость yОz, или, что то же, моменту силы 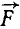
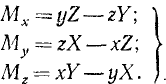
Для вывода формул (23) мы выбрали точку приложения силы в первом октанте (х, у и z положительны) и направили силу от начала координат (X, Y и Z положительны). Если координаты или проекции силы отрицательны, то в формулы (23) надо, конечно, подставить отрицательные значения.
Достаточно запомнить одну из формул (23), а следующую можно получить из предыдущей, применив круговую подстановку, т. е. заменив всюду икс на игрек, игрек на зет и зет на икс. Случаи, когда формулы можно получить одну из другой такой подстановкой, мы будем отмечать символом:
Выражение (23) можно получить непосредственно из свойств векторного произведения, если представить векторное произведение определителем третьего порядка:
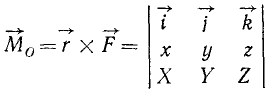
Раскладывая этот определитель по элементам первой строки, найдем:
Сравнив это равенство с (22′), получим формулы (23).
Обратим внимание на то, что правая часть третьей из формул (23) тождественна выражению (16) момента силы, лежащей в плоскости хОу, относительно начала координат. Объяснение заключается в том, что при выводе формулы (23) для определения Мz силу сначала спроецировали на плоскость хОу и затем определили момент проекции относительно начала координат. Формула же (16) выражает момент относительно начала координат силы, лежащей в плоскости хОу. Моменты этой силы относительно осей, расположенных с ней в одной плоскости, равны нулю (Mx= 0, My= 0), а момент относительно оси Oz численно равен величине момента относительно начала координат (Mz = M0).
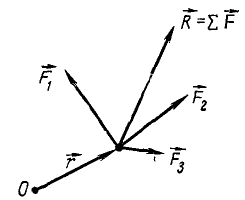
Рис. 34
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Теория пар, не лежащих в одной плоскости
- Произвольная пространственная система сил
- Центр параллельных сил и центр тяжести
- Поступательное движение твердого тела
- Равновесие системы, состоящей из нескольких тел
- Графостатика в теоретической механике
- Расчет ферм
- Пространственная система сходящихся сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Момент силы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.
То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.
Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.
Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.
Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
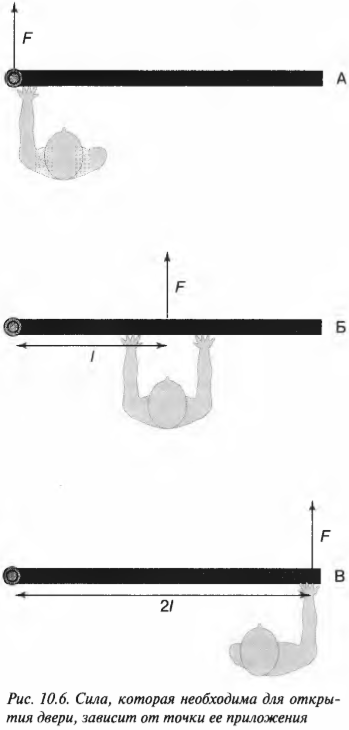
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.
То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!
Момент силы относительно точки B:
Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).
Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn = M’1 + M’2 +. + M’n
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.
Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.
Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?
Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?
Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?
Решение:
Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.
Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
Ответ: модуль силы тяжести, действующей на груз равен 750 Н
Глава 10. Вращаем объекты: момент силы
- Переходим от поступательного движения к вращательному движению
- Вычисляем тангенциальную скорость и тангенциальное ускорение
- Выясняем связь между угловым ускорением и угловой скоростью
- Разбираемся с моментом силы
- Поддерживаем вращательное движение
Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!
Переходим от прямолинейного движения к вращательному
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
- ( v=Delta
/Delta ) , где ( v ) — это скорость, ( Delta) — перемещение, a ( Delta ) — время перемещения; - ( a=Delta/Delta ) , где ( a ) — это ускорение, ( Delta ) — изменение скорости, a ( Delta ) — время изменения скорости;
- ( Delta
=v_0(t_1-t_0)+<>^1!/!_2a(t_1-t_0)^2 ) , где ( v_0 ) — это начальная скорость, ( t_0 ) — это начальный момент времени, a ( t_1 ) — это конечный момент времени; - ( v^2_1-v^2_0=2aDelta
) , где ( v_1 ) — это конечная скорость.
По аналогии можно легко вывести основные формулы вращательного движения:
- ( omega=Delta<theta>/Delta ) , где ( omega ) — угловая скорость, ( Delta <theta>) — угол поворота, ( Delta ) — время поворота на угол ( Delta <theta>) ;
- ( alpha=Delta<omega>/Delta ) , где ( alpha ) — угловое ускорение, ( Delta <omega>) — изменение угловой скорости, ( Delta ) — время изменения угловой скорости;
- ( theta=omega_0(t_1-t_0)+<>^1!/!_2a(t_1-t_0)^2 ) , где ( omega_0 ) — это начальная скорость;
- ( omega^2_1-w^2_0=2as ) , где ( omega_1 ) — это конечная скорость.
Разбираемся с параметрами вращательного движения
В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.
Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:
Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ) , равной 21,5 ( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.
Вычисляем линейную скорость вращательного движения
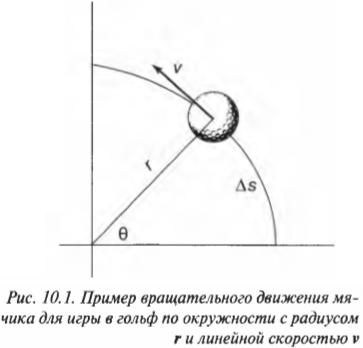
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf ) и линейной скоростью ( mathbf ) . Скорость ( mathbf ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf ) .
Угловая скорость связана с линейной скоростью соотношением ( v=romega ) , которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.
Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ) . Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ) , а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ) , охватывающая угол ( Deltatheta ) , равна:
Из формулы прямолинейного движения
путем подстановки выражения для ( Delta s ) получим:
где ( omega ) — угловая скорость, ( Delta <theta>) — угол поворота, ( Delta ) — время поворота на угол ( Delta <theta>) , то:
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ) , равной 21,5 ( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:
Подставляя в нее значения, получим:
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.
Вычисляем тангенциальное ускорение
Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением
где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?
Как мы уже знаем, линейная и угловая скорости связаны равенством
Подставим это выражение в предыдущую формулу линейного ускорения:
Поскольку радиус остается постоянным, то его можно вынести за скобки:
Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ) , то:
Итак, получаем следующую формулу связи между линейным и угловым ускорением:
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.
Вычисляем центростремительное ускорение
Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):
Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ) , получим:
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.
Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:
После подстановки этого значения в предыдущую формулу получим:
Средний радиус орбиты Луны равен 3,85·10 8 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
Зная это ускорение и массу Луны, которая равна 7,35·10 22 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ) , оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ) .
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где ( mathbf <alpha>) — вектор углового ускорения, а ( Deltamathbf <omega>) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
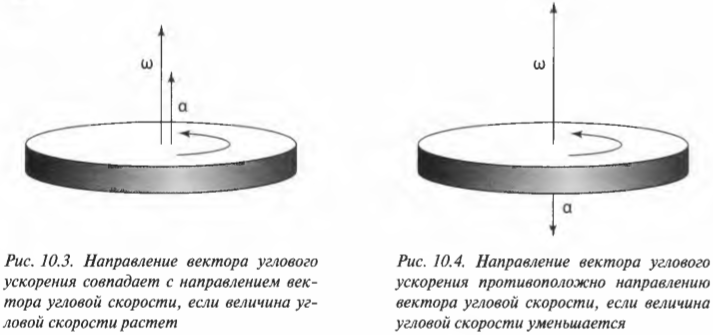
А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.
Поднимаем грузы: момент силы
В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.
Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).
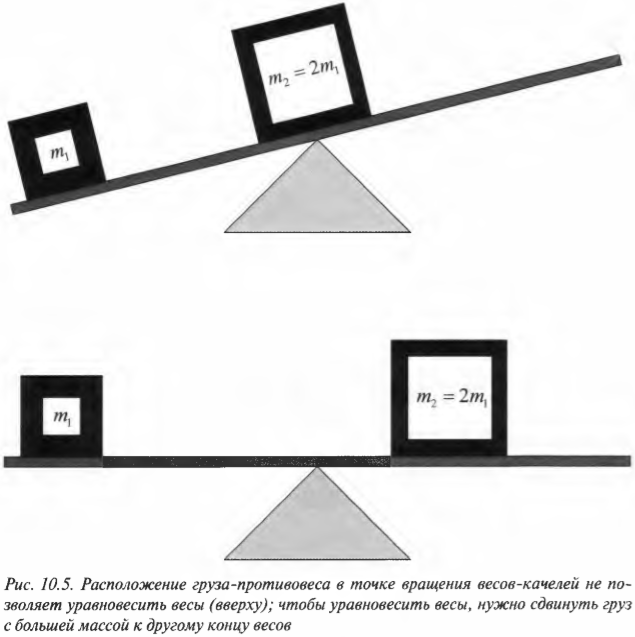
В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ) .
Знакомимся с формулой момента силы
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.
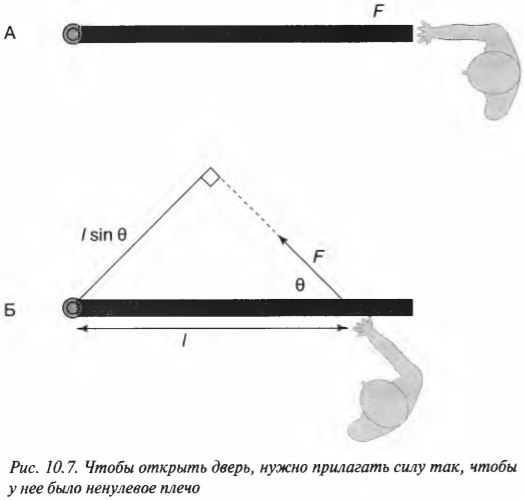
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).
На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ) :
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?
Разбираемся с направлением приложенной силы и плечом силы
Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
Размышляем над тем, как создается момент силы
Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.
Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ) . Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:
Однако в данном случае угол ( theta ) не является прямым.
В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.
Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:
Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).
Итак, получаем для момента силы для схемы Б на рис. 10.7:
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.
Определяем направление момента силы
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
На рис. 10.8 показан пример силы ( mathbf ) с плечом ( mathbf ) и соответствующего вектора момента сил ( mathbf ) .
Уравновешиваем моменты сил
В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).
Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:
Иначе говоря, результирующая действующая сила равна нулю.
Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.
Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Простой пример: вешаем рекламный плакат
Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.
Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.
Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:
где ( mathbf ) — это момент силы со стороны плаката, а ( mathbf ) — это момент силы со стороны болта.
Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:
где ( m ) = 50 кг — это масса плаката, ( mathbf ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.
Подставляя значения, получим:
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.
Момент силы со стороны болта определяется формулой:
где ( mathbf ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.
Подставляя полученные выражения для моментов сил в формулу:
Отсюда с помощью простых алгебраических преобразований получим искомую силу:
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.
Подставляя значения, получим искомый ответ:
Более сложный пример: учитываем силу трения при расчете равновесия
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.
Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:
- ( mathbf ) — нормальная сила со стороны стены;
- ( mathbf ) — вес рабочего;
- ( mathbf ) — вес лестницы;
- ( mathbf> ) — сила трения между поверхностью тротуара и концами лестницы;
- ( mathbf ) — нормальная сила со стороны тротуара.
Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:
Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf> ) , должна быть равна нулю, то есть:
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf ) , веса лестницы ( mathbf ) и нормальной силы со стороны тротуара ( mathbf ) , должна быть равна нулю, то есть:
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf ) , весом лестницы ( mathbf ) и нормальной силой со стороны стены ( mathbf ) :
Поскольку ( L_р=l_р ) , ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ) , ( alpha=360^<circ>-theta ) , ( beta=360^<circ>-theta ) и ( gamma=theta ) , то получим:
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf ) и ( mathbf ) :
Зададимся вопросом: соблюдается ли условие
Из системы двух уравнений получим:
Итак, остается выяснить, соблюдается ли условие:
После подстановки значений получим:
Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.
http://skysmart.ru/articles/physics/moment-sily