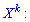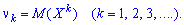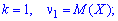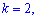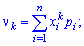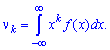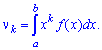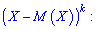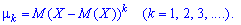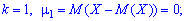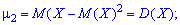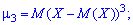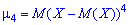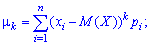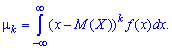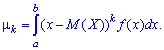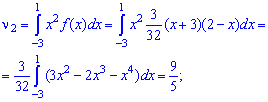Как найти момент первого порядка

Начальные и центральные моменты случайной величины

• Краткая теория
• Примеры решения задач

Краткая теория

---

Начальные моменты

Начальным моментом порядка

 случайной величины

 называют математическое ожидание величины

:

В
частности:

Пользуясь
этими моментами, формулу для вычисления дисперсии

 можно записать так:

Центральные моменты

Кроме
моментов случайной величины

 целесообразно рассматривать моменты отклонения

.

Центральным моментом порядка

 случайной величины

 называют математическое ожидание величины

:

В
частности,

Взаимосвязь центральных и начальных моментов

Легко
выводятся соотношения, связывающие начальные и центральные моменты:

Моменты
более высоких порядков применяются редко.

Формулы для вычисления моментов дискретных и непрерывных случайных величин

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Нетрудно
заметить, что при

 первый
начальный момент случайной величины

 есть ее
математическое ожидание, то есть

, при

 второй
центральный момент – дисперсия, то есть

.

Асимметрия и эксцесс случайной величины

Третий центральный момент

 служит для
характеристики асимметрии (скошенности) распределения. Он имеет размерность
куба случайной величины. Чтобы получить безразмерную величину, ее делят на

, где

 – среднее
квадратическое отклонение случайной величины

. Полученная величина

 называется
коэффициентом асимметрии случайной величины:

Если распределение симметрично относительно
математического ожидания, то коэффициент асимметрии

.

Четвертый центральный момент

 служит для
характеристики крутости (островершинности или плосковершинности) распределения.

Эксцессом (или коэффициентом
эксцесса) случайной величины называется число

Число 3 вычитается из отношения

 потому, что для
наиболее часто встречающегося нормального распределения отношение

. Кривые, более островершинные, чем нормальная,
обладают положительным эксцессом, более плосковершинные – отрицательным
эксцессом.

Смежные темы решебника:

• Асимметрия и эксцесс распределения
• Дискретная случайная величина
• Непрерывная случайная величина

Примеры решения задач

---

Пример 1

Дискретная
случайная величина X задана законом распределения:

	1	3	4	5
	0,2	0,3	0,1	0,4

Найти начальные моменты первого, второго и третьего
порядков.

Решение

Найдем
начальный момент 1-го порядка:

Начальный
момент 2-го порядка:

Начальный
момент 3-го порядка:

Ответ:

.

---

Пример 2

Дискретная
случайная величина X задана законом распределения:

	0	3	5	6
	0,3	0,2	0,3	0,2

Найти центральные моменты первого, второго,
третьего и четвертого порядков.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Центральный
момент первого порядка равен нулю:

Для
вычисления центральных моментов удобно воспользоваться формулами, выражающими
центральные моменты через начальные, поэтому предварительно найдем начальные
моменты:

Начальный
момент 2-го порядка:

Начальный
момент 3-го порядка:

Начальный
момент 4-го порядка:

Найдем центральные моменты:

Ответ:
.

---

Пример 3

Непрерывная случайная
величина X задана плотностью распределения:

Найти
математическое ожидание, дисперсию, асимметрию и эксцесс.

Решение

Математическое
ожидание (начальный момент первого порядка):

Начальный
момент второго порядка:

Дисперсия
(центральный момент второго порядка):

Среднее
квадратическое отклонение:

Начальный
момент третьего порядка:

Начальный
момент четвертого порядка:

Вычисляем
центральные моменты третьего и четвертого порядков:

Коэффициент
асимметрии:

Эксцесс:

Ответ:

.

• Краткая теория
• Примеры решения задач

Начальным
моментом k-го
порядка
случайной величины X
называется математическое ожидание
величины
X^k:

.
(5.10)

В частности,

Центральным
моментом k-го
порядка
случайной величины X
называется математическое ожидание
величины
[X–M(X)]^k:

.
(5.11)

В частности,

Воспользовавшись
определениями и свойствами математического
ожидания и дисперсии, можно получить,
что

,

,

.

Моменты более
высоких порядков применяются редко.

Предположим,
что распределение случайной величины
симметрично относительно математического
ожидания. Тогда все центральные нечетного
порядка равны нулю. Это можно объяснить
тем, что для каждого положительного
значения отклонения X–M[X]
найдется (в силу симметричности
распределения) равное ему по абсолютной
величине отрицательное значение, причем
их вероятности будут одинаковыми. Если
центральный момент равен нечетного
порядка не равен нулю, то это говорит
об асимметричности распределения и чем
больше момент, тем больше асимметрия.
Поэтому в качестве характеристики
асимметрии распределения разумнее
всего взять какой-нибудь нечетный
центральный момент. Так как центральный
момент 1-го порядка всегда равен нулю,
то целесообразно для этой цели использовать
центральный момент 3-го порядка. Однако
принять этот момент для оценки
асимметричности неудобно потому, что
его величина зависит от единиц, в которых
измеряется случайная величина. Чтобы
устранить этот недостаток, ³
делят на ³
и таким образом получают характеристику.

Коэффициентом
асимметрии
A
называется
величина

.
(5.12)

Рис.
5.1

Если коэффициент асимметрии
отрицателен, то это говорит о большом
влиянии на величину₃
отрицательных отклонений. В этом случае
кривые распределения более пологи слева
от M[X].
Если коэффициент A
положителен, то кривая более пологи
справа.

Как
известно, дисперсия (2-й центральный
момент) служит для характеристики
рассеивания значений случайной величины
вокруг математического ожидания. Чем
больше дисперсия, тем более полога
соответствующая кривая распределения.
Однако нормированный момент 2-го порядка
₂/₂
не может служить характеристикой
«плосковершинности» или
«островершинности» распределения
потому, что для любого распределения
D[x]/₂=1.
В этом случае используют центральный
момент 4-го порядка.

Эксцессом
E
называется
величина

.
(5.13)

Ч

Рис.
5.2

исло 3 здесь выбрано потому, что для
наиболее распространенного нормального
закона распределения₄/₄=3.
Поэтому эксцесс служит для сравнения
имеющихся распределе­ний с нормальным,
у которого экс­цесс равен нулю. Это
означает, что если у распределения
эксцесс положителен, то соответствующая
кривая распределения более «островершина»
по сравнению с кривой нормального
распределения; если у распределения
эксцесс отрица­телен, то соответствующая
кривая более «плосковершина».

Пример
5.6. ДСВ
X
задана следующим законом распределения:

X	1	3	5	7	9
P	0,1	0,4	0,2	0,2	0,1

Найти коэффициент
асимметрии и эксцесс.

Рис.
5.4

Решение.
Предварительно найдем начальные моменты
до 4-го порядка

Теперь вычислим
центральные моменты:

Таким образом,

Пример
5.7. НСВ
X
задана следующей плотностью распределения:

Найти коэффициент
асимметрии и эксцесс.

Рис.
5.5

Решение.
Предварительно найдем начальные моменты
до 4-го порядка

Теперь вычислим
центральные моменты:

.

Таким
образом,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Примеры с решением

Моменты случайной величины

Определение и основные свойства

Мы уже видели в предыдущей главе, какое большое значение имеют такие числовые характеристики распределения, как математическое ожидание и дисперсия. Обобщением этих понятий являются начальные и центральные моменты.

Определение. Начальным моментом порядка случайной величины называют математическое ожидание степени

Из определения ясно, что начальный момент первого порядка совпадает с математическим ожиданием.

Для дискретных случайных величин с законом распределения формула для начального момента порядка выглядит следующим образом:

для абсолютно непрерывных случайных величин с плотностью

если ряд (6.3) и интеграл (6.4) сходятся абсолютно.

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Определение. Центральным моментом порядка случайной величины называют математическое ожидание степени отклонения где математическое ожидание Мы уже видели, что первый центральный момент равен нулю, а второй центральный момент совпадает с дисперсией случайной величины

Для дискретных случайных величин формула для центрального момента порядка выглядит следующим образом:

для непрерывных случайных величин

Возможно вам будут полезны данные страницы:

Разлагая бином и пользуясь свойствами математического ожидания, нетрудно получить формулы, выражающие центральные моменты через начальные. Например,

откуда

так что

Полученная формула полностью идентична с уже известной формулой для дисперсии. Аналогично получаются следующие формулы, вывод которых предоставляется читателю:

Отметим следующие свойства третьего и четвертого центральных моментов. Свойство. Если величины независимы, то

Доказательство. Используя формулу куба суммы и свойство математического ожидания, имеем

По теореме умножения математического ожидания для независимых величин получим

Поскольку центральные моменты первого порядка равны нулю, то формула (6.12) отсюда следует непосредственно.

Доказанная формула непосредственно обобщается на произвольное число независимых слагаемых:

Для моментов четвертого порядка аналогичное свойство выглядит более сложным образом.

Свойство. Для независимых случайных величин выполняется формула

Доказательство полностью аналогично предыдущему и оставляется читателю. Для произвольного числа независимых слагаемых формула (6.14) приобретает следующий вид:

Рассмотрим ряд примеров нахождения моментов высших порядков для типичных законов распределения.

Примеры с решением

Пример 1:

Найти все центральные моменты до четвертого порядка включительно для случайной величины распределенной по биномиальному закону с параметрами

Решение:

Что касается нахождения центральных моментов первого и второго порядка, то ответ нам известен:

Чтобы найти воспользуемся формулой (6.13) и представлением случайной величины виде суммы индикаторов появления события испытании:

Для каждого слагаемого третий центральный момент находится непосредственно

Поэтому

Для нахождения центрального момента четвертого порядка воспользуемся формулой (6.15). Вначале найдем моменты для каждого слагаемого:

Отсюда

откуда окончательно получаем

Для нахождения всех начальных моментов непрерывной случайной величины проще использовать производящую функцию моментов.

Определение. Производящей функцией моментов случайной величины называют математическое ожидание случайной величины где действительный параметр:

Производящая функция моментов позволяет находить все начальные моменты случайной величины X. Справедлива следующая теорема.

Теорема 6.1. Если случайная величина имеет начальный момент порядка то производящая функция раз дифференцируема по и для всех выполняется соотношение

Если оставить в стороне вопрос о дифференцируемости данной функции, то соотношение (6.20) получается формально дифференцированием соотношения (6.19) раз по

Подставляя в последнее соотношение получим

откуда непосредственно вытекает равенство (6.19).

Сравнивая разложение производящей функции моментов в ряд Маклорена с равенствами (6.19), получим ее разложение в ряд с использованием начальных моментов:

Пример 2:

Найти производящую функцию моментов для случайной величины распределенной по нормальному закону

Решение:

Имеем по определению

Для вычисления этого интеграла рассмотрим отдельно показатель экспоненты, стоящей под знаком интеграла. Имеем

Выделим в числителе последней дроби полный квадрат по После небольшого числа тождественных преобразований получим:

Таким образом, выражение для характеристической функции приобретет вид:

Поскольку первый множитель равен 1 как интеграл от плотности нормальной случайной величины то окончательное выражение для характеристической функции нормального закона имеет вид:

Особенно простой вид имеет характеристическая функция стандартного нормального закона

Теперь нам будет нетрудно найти все начальные моменты стандартной нормальной случайной величины. Вместо того чтобы дифференцировать функцию (6.22), можно разложить ее в ряд и сравнить с рядом (6.20):

откуда имеем выражения для начальных моментов:

Пусть непрерывная случайная величина Х задана функцией распределения F(X). Допустим, что все возможные значения случайной величины принадлежат отрезку [A,B].

Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называется определенный интеграл

Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

При этом, конечно, предполагается, что несобственный интеграл сходится.

Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

Определение. Средним квадратичным отклонением Называется квадратный корень из дисперсии.

Определение. Модой М0 дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется Двухмодальным или Многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно называется Антимодальным.

Определение. Медианой MD случайной величины Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Определение. Начальным моментом Порядка K Случайной величины Х называется математическое ожидание величины ХK.

Для дискретной случайной величины: .

Для непрерывной случайной величины: .

Начальный момент первого порядка равен математическому ожиданию.

Определение. Центральным моментом Порядка K случайной величины Х называется математическое ожидание величины

Для дискретной случайной величины: .

Для непрерывной случайной величины: .

Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.

Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется Коэффициентом асимметрии.

Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая Эксцессом.

Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: .

Абсолютный центральНый момент: .

Абсолютный центральный момент первого порядка называется Средним арифметическим отклонением.

Пример. Для рассмоТРенного выше примера определить математическое ожидание и дисперсию случайной величины Х.

Пример. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину Х число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.

Т. к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или непоявления события в другом опыте).

Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна

Таким образом, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз.

Для составления закона распределения надо найти вероятности каждого из этих событий.

1) Белый шар не появился вовсе:

2) Белый шар появился один раз:

3) Белый шар появиться два раза: .

4) Белый шар появиться три раза:

5) Белый шар появиться четыре раза:

6) Белый шар появился пять раз:

Получаем следующий закон распределения случайной величины Х.

Х	0	1	2	3	4	5
Х2	0	1	4	9	16	25
Р(х)	0,0102	0,0768	0,2304	0,3456	0,2592	0,0778

При решении практических задач зачастую точно найти закон распределения случайной величины довольно сложно. Однако, все происходящие процессы, связанные со случайными величинами, можно разделить на несколько типов, каждому из которых можно поставить в соответствие какой – либо закон распределения.

Выше были рассмотрены некоторые типы распределений дискретной случайной величины такие как биноминальное распределение и распределение Пуассона.

Рассмотрим теперь некоторые типы законов распределения для непрерывной случайной величины.

< Предыдущая		Следующая >

Обобщенными числовыми характеристиками для случайных величин в теории вероятностей а также математической статистике являются начальные и центральные моменты. Задачи на отыскание моментов являются неотъемлемой частью теории вероятностей и математической статистики. Начальным моментом k-го порядка случайной величины Х называют математическое ожидание от величины в k-ой степени

Когда
Когда 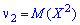и т. д.

Для дискретной случайной величины 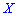начальные моменты определяют зависимостью

для непрерывной интегрированием

Если непрерывная величина задана интервалом 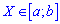, то моменты вычисляют по формуле

Центральным моментом k-го порядка называют математическое ожидание от величины

Когда

для 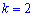имеем

при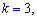

при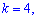

и так далее.

Для дискретной случайной величины центральные моменты вычисляют по формуле

для непрерывной по следующей

Если случайная величина определена интервалом 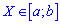, то центральные моменты определяют интегрированием

Рассмотрим пример отыскания приведенных величин.

————————————

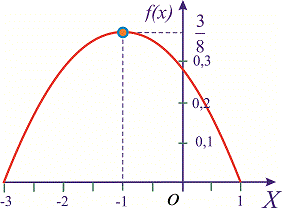
Пример 1. Задана функция плотности вероятностей

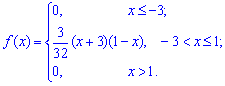
Вычислить начальные и центральные моменты второго и третьего порядка .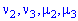
Решение. Для вычисления начальных моментов выполним интегрирование по вышеприведенным формулам

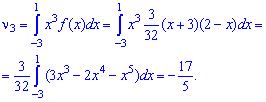
Промежуточные операции при интегрировании пропущены, они занимают много места, а Вам главное иметь инструкцию для вычислений, так как примеры у Вас будут другие.
Для вычисления центральных моментов инерции необходимо знать математическое ожидание случайной величины, поэтому определяем его первее

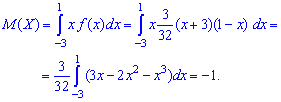
Найдено математическое ожидание подставляем в формулу центральных моментов. В случае получим

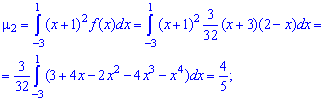
и при будем иметь

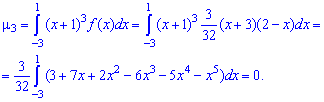
На этом решения примера завершено, функция плотности вероятностей приведена на графике

————————————

Примеры нахождения начальных и центральных моментов будут рассмотрены в следующей статье. Задачи совсем не сложные, а вычисления величин сводится к возведения в степень, интегрирование, умножение и суммирование.