Определить момент результирующей пары, эквивалентной системе трех пар, лежащих в одной плоскости. Первая пара образована силами P1 = P’1 = 2 кн, имеет плечо h1= 1,25 м и вращает по часовой стрелке; вторая пара образована силами P2 = P’2 = 3 кн, имеет плечо h2 = 2 м и вращает против часовой стрелки; третья пара образована силами P3 = P’3 = 4,5 кн, имеет плечо h3 = 1,2 м и вращает по часовой стрелке (см.рис.).
Решение. Вычисляем моменты составляющих пар:
М1 = P1·h1 = 2 ·1,25 = 2,5 кн·м;
М2 = —P2·h2 = —3 ·2 = —6 кн·м;
М3 = P3·h3 = 4,5 ·1,2 = 5,4кн·м.
Для определения момента результирующей пары складываем алгебраически моменты заданных пар
М = М1 + М2+ М3 = 2,5 — 6 + 5,4 = 1,9 кн·м.

36
Теорема
Система пар сил, действующая на тело, эквивалентна одной паре сил, момент которой равен алгебраической сумме моментов составляющих пар.
Пусть на твердое тело действуют три пары сил (Р1, Р1′), (Р2, Р2′), (Р3, Р3′) (рис. 5. 9), расположенные в одной плоскости. Моменты этих пар:
М1 = Р1 . d1 , М2 = Р2 . d2, М3 = — Р3 . d3
Выберем произвольный отрезок АВ длиной d в той же плоскости и заменим заданные пары эквивалентными (Q1, Q1′), (Q2, Q2′), (Q3, Q3′) с общим плечом d.
Найдем модули сил эквивалентных пар из соотношений
М1 = Р1 . d1 = Q1 . d, М2 = Р2 . d2 = Q2 . d, М3 = — Р3 . d3 = — Q3 . d .
Сложим силы, приложенные к концам отрезка АВ и найдем модуль их равнодействующей:
R = Q1 + Q2 — Q3
R′ = — R = (-Q′1 — Q′2 + Q′3)
Равнодействующие R и R′ составляют результирующую пару эквивалентную системе заданных пар.
Момент этой пары:
М = R . d = (Q1 + Q2 — Q3) d = Q1 . d + Q2 . d — Q3 . d = М1 + М2 + М3
Если на тело действует «n» пар, то момент результирующей пары равен алгебраической сумме моментов составляющих пар:
n
М = ∑ Мi
i=1
Уравновешивающей называется пара, момент которой равен по абсолютной величине моменту результирующей пары, но противоположен по направлению.
Пример 5.1
Определить момент результирующей пары для трех заданных пар (рис. 5.
10, а), если Р1 = 10 кН, Р2 = 15 кН, Р3 = 20 кН, d1 = 4 м, d2 = 2 м, d3 = 6 м.
Решени.
Определяем момент каждой пары сил:
М1 = 10 Н . 4 м = 40 Нм М2 = — 15 Н . 2 м = — 30 Нм М3 = — 20 Н . 6 м = — 120 Нм
Определяем момент результирующей пары:

37
3
М = ∑ Мi = М1 + М2 + М3 = 40 – 30 – 120 = — 110 Нм
1
Пример 5. 2
На раму (рис. 5. 10, б) действуют три пары сил (Р1, Р1′), (Р2, Р2′), (Р3, Р3′), приложенных в точках А1, А2, А3 соответственно. Определить момент
результирующей пары, если Р1 = 10 Н, Р2 = 15 Н, Р3 = 20 Н, а плечи пар сил d1 =
0,4 м, d2 = 0,2 м, d3 = 0,6 м.
Решение
Определяем моменты пар сил:
М1 = Р1 . d1 = 10 . 0,4 = 4 Нм М2 = — Р2 . d2 = — 15 . 0,2 = — 3 Нм М3 = — Р3 . d3 = — 20 . 0,6 = — 12 Нм
Определяем момент результирующей пары:
3
М = ∑ Мi = М1 + М2 + М3 = 4 – 3 – 120 = — 11 Нм
1
Пример 5. 3
На балку (рис. 5. 10, в) действуют три пары сил (Р1, Р1′), (Р2, Р2′), (Р3, Р3′), приложенных в точках А1, А2, А3. Определить момент результирующей пары,
если Р1 = 2 кН, Р2 = 3 кН, Р3 = 6 кН, а плечи пар сил d1 = 0,2 м, d2 = 0,4 м, d3 = 0,3 м.
Решение
Определяем моменты пар сил:
М1 = — Р1 . d1 = — 2 . 0,2 = — 0,4 кНм М2 = — Р2 . d2 = — 3 . 0,4 = — 1,2 кНм М3 = Р3 . d3 = 6 . 0,3 = 1,8 кНм
Определяем момент результирующей пары:
3
М = ∑ Мi = М1 + М2 + М3 = — 0,4 – 1,2 + 1,8 = 0,2 кНм
1
Пример 5. 4
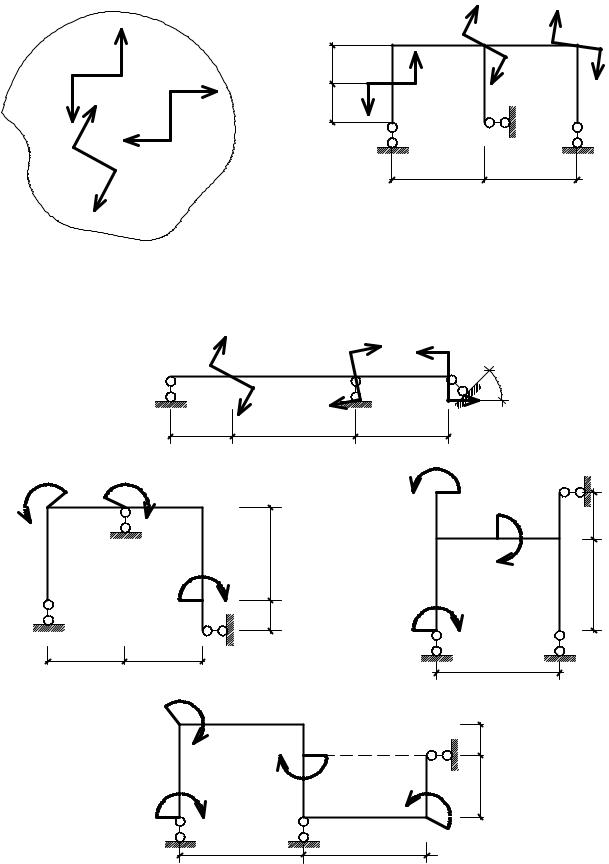
Определить моменты результирующих пар, действующих на рамы (рис. 5. 10, г, д, е) самостоятельно.
|
Результаты решения: |
|||
|
Рис. 5. |
10, г |
— |
М = — 50 кНм |
|
Рис. 5. |
10, д |
— |
М = — 80 кНм |
|
Рис. 5. 10, е |
— |
М = 20 кНм |
|
38 |
|||||||||||
|
б. |
_ |
_ |
|||||||||
|
P2 |
P3 |
||||||||||
|
a. |
_ |
||||||||||
|
d |
d3 |
_ |
|||||||||
|
_ |
2 |
||||||||||
|
d1 |
P1‘ |
_ |
2м |
_ |
|||||||
|
_ |
_ |
d1 |
P1‘ |
P3‘ |
|||||||
|
P3 |
P’ |
||||||||||
|
_ |
2м |
2 |
|||||||||
|
P1 |
_ |
d3 |
P1 |
||||||||
|
P2 |
P3‘ |
||||||||||
|
d2 |
|||||||||||
|
_ |
6м |
||||||||||
|
P2‘ |
|
в. |
_ |
_ |
||||||||
|
_ |
P3 |
|||||||||
|
P1 |
d1 |
d2 |
P2‘ |
d3 |
4 |
|||||
|
A3 |
_ |
5 |
||||||||
|
A1 |
_ |
A2 |
||||||||
|
_ |
P3‘Е |
|||||||||
|
2м |
P1‘ |
P2 |
3м |
|||||||
|
4м |
||||||||||
|
М1 = 10кНм |
М2 = 20кНм |
д. |
||||||||
|
г. |
1 |
= 10кНм |
A1 |
М2 = 40кНм |
||||||
|
A1 |
A2 |
М |
||||||||
|
6м |
A2 |
|||||||||
|
М3 = 40кНм |
||||||||||
|
A3 |
2м |
М3 |
= 50кНм |
|||||||
|
A3 |
||||||||||
|
4м |
4м |
8м |
||||||||
|
е. |
М2 |
= 20кНм |
||||||||
|
М3 |
= 30кНм |
2м |
||||||||
|
4м |
||||||||||
|
М1 = 10кНм |
М4 = 80кНм |
|||||||||
|
4м |
6м |
Рис. 5.10

39
5. 5. Сложение пар сил в пространстве
Теорема. Система пар сил, действующая на твердое тело, эквивалентна одной паре сил, момент которой равен геометрической сумме моментов составляющих пар.
Доказательство
Докажем теорему для двух пар сил, плоскости действия которых I и II, а моменты М1 и М2 (рис. 5. 11, а). Преобразуем пары сил так, чтобы плечами их был отрезок АВ, лежащий на линии пересечения плоскостей. Получим две пары сил (Р1, Р1′) и (Q2, Q2′), имеющих одинаковые плечи и измененные соответствующим образом модули сил, которые найдем из соотношений
М1 = Р1 . АВ
М2 = Q1 . АВ
Сложив силы, приложенные в точках А и В, найдем их равнодействующие
R = Р1 + Q1
R′ = Р1 ′ + Q1′
Параллелограммы сил равны и лежат в параллельных плоскостях. Следовательно, равнодействующие R и R′ равны по модулю, параллельны и направлены в противоположные стороны, т.е. составляют результирующую пару (R, R′).
Найдем момент этой пары:
М = r х R = АВ х R = АВ х (Р1 + Q1) = АВ х Р1 + АВ х Q1 = М1 + М2
Следовательно, момент пары М равен геометрической сумме моментов М1 и М2 и изображается диагональю параллелограмма, построенного на векторах М1 и М2.
Если на твердое тело действует «n» пар сил с моментами М1 , М2 … Мn , то результирующая пара будет иметь момент, равный геометрической сумме моментов этих пар
n
М = ∑ Мi
i=1
5. 6. Условия равновесия системы пар сил
Для равновесия пар сил на плоскости необходимо и достаточно, чтобы алгебраическая сумма моментов всех пар была равна нулю
n
∑ Мi = 0
i=1
Для равновесия пар сил в пространстве необходимо и достаточно, чтобы геометрическая сумма моментов всех пар была равна нулю
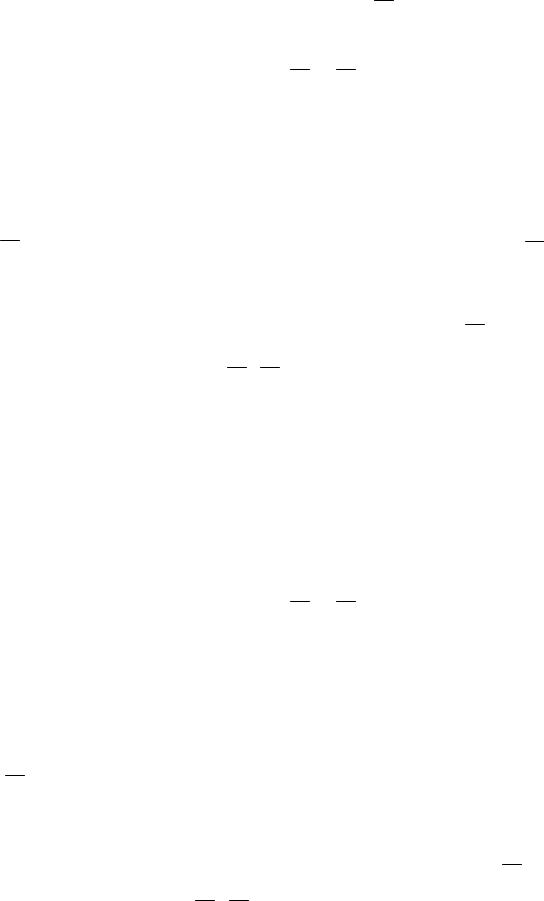
40
n
∑ Мi = 0
i=1
Пример 5. 5
Определить опорные реакции RА и RВ балки (рис. 5. 11, б), находящейся под действием двух пар сил, используя условия равновесия пар сил на плоскости.
Решение
1) Определим момент результирующей пары сил
М = М1 + М2 = — 40 + 30 = — 30 кНм Поскольку пара сил может быть уравновешена только парой, то реакции
RА и RВ должны составить пару сил. Линия действия реакции RВ определена (перпендикулярна опорной поверхности), линия действия реакции RА параллельна линии действия реакции RВ.
Примем направления реакций в соответствии с рис. 5. 11, б.
2)Определим момент уравновешивающей пары сил (RА , RВ)
М(RА , RВ) = МR = RА . АВ = RВ . АВ
3)Определим опорные реакции из условия равновесия пар сил
2
∑ Мi = 0 М + МR = 0
i=1
-30 + RА . 6 = 0
RА = 5 кН ; RВ = RА = 5 кН
Знак плюс указывает на правильное направление момента уравновешивающей пары сил (RА, RВ).
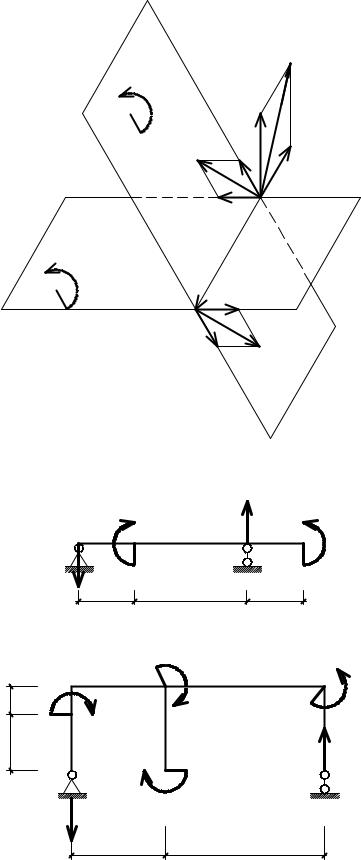
Пример 5. 6
Определить опорные реакции RА и RВ рамы (рис. 5. 11, в), находящейся под действием четырех пар сил, используя условия равновесия пар сил на плоскости.
Решение
1) Определим момент результирующей пары сил
М = М1 + М2 + М3 + М4 = — 10 – 40 + 80 — 20 = 10 кНм Поскольку пара сил может быть уравновешена только парой, то реакции
RА и RВ должны составить пару сил. Линия действия реакции RВ определена (перпендикулярна опорной поверхности), линия действия реакции RА параллельна линии действия реакции RВ.
Примем направления реакций в соответствии с рис. 5. 11, в.
2)Определим момент уравновешивающей пары сил (RА , RВ)
М(RА , RВ) = МR = RА . АВ = RВ . АВ = RА . 9
3)Определим опорные реакции из условия равновесия пар сил
41
|
М2 |
_ |
||
|
M |
|||
|
II |
_ |
||
|
M1 |
|||
|
_ |
|||
|
_ |
_ |
||
|
Q1‘ |
|||
|
R’ |
M2 |
||
|
_ |
|||
|
P1‘ |
A |
М1
_
P1
B _ _
Q1 R
|
М2 = 40кНм |
_ М1 = 10кНм |
|
|
RB |
||
|
A |
B |
|
|
2м |
4м |
2м |
М3 = 80кНм
_
RB
B
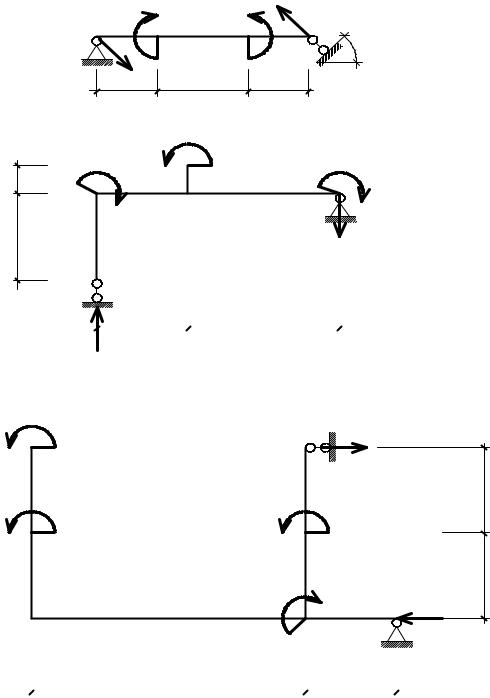
Рис. 5.11
42
|
a. |
М2 = 60кНм _ |
|
|
М1 = 40кНм |
||
|
A |
RB |
|
|
B |
||
|
_ |
||
|
RA |
||
|
2м |
3м |
2м |
б.
|
М2 = 10кНм |
М1 = 45кНм |
||
|
М3 |
= 3кНм |
||
3м 1м
|
3м |
5м |
|||
в.
_
М2 = 40кНм
М3 = 10кНм
М4 = 18кНм
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Теория пар сил
- Силы, направленные в одну сторону
- Силы направлены в противоположные стороны и различные по модулю
- Пара сил и ее момент
- Эквивалентность пары сил
- Добавление пар сил
- Условия равновесия пар сил
- Момент силы относительно точки на оси. Момент пары сил
- Момент силы относительно точки
- Теорема о моменте равнодействующей системы сходящихся сил
- Момент сил относительно оси
- Момент пары сил и его свойства
Парой сил называется система двух равных по модулю, противоположных по направлению параллельных сил.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Теория пар сил
Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы.
Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны. Пара сил не составляет системы сил, эквивалентной нулю. Пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.
Пара сил, действующая на твердое тело, характеризуется, прежде всего, плоскостью действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.
Силы, направленные в одну сторону
Пусть в абсолютно твердого тела в точках А и В приложены две параллельные силы




Поскольку 








Итак,
Силы 

действия имеют точку пересечения А. Перенесем силы 

Сила — скользящий вектор, поэтому 




Получим:
Поскольку силы 








Найдем точку приложения равнодействующей 



Поскольку

Итак, равнодействующая двух параллельных сил, направленных в одну сторону, параллельна этих сил, направленная в ту же сторону, что и составляющие силы; модуль
равнодействующей равна сумме модулей составляющих сил, а линия ее действия разделяет расстояние между точками приложения этих сил внутри на части, обратно
пропорциональны величинам этих сил.
Из изложенного следует, что произвольную силу можно разложить на две параллельные силы. Если 
Силы направлены в противоположные стороны и различные по модулю
Пусть параллельные силы 



Найдем равнодействующую сил 








Согласно (4.3), 
Поскольку 




Равнодействующая двух параллельных, разных по модулю, противоположно направленных сил параллельная им и направлена в сторону большей силы; модуль равнодействующей равна разности модулей составляющих сил. Линия действия равнодействующей 
Пара сил и ее момент
Система двух равных по модулю, параллельных, противоположно направленных сил, линии действия которых не совпадают, называется парой сил.
Пусть к некоторому абсолютно твердого тела приложена пара сил 
Согласно определению пары сил:
Элементами пары есть силы, составляющие пару, плечо пары, плоскость действия пары.
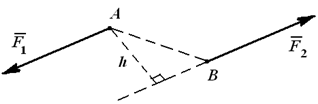
Плечо пары — это кратчайшее расстояние между линиями действия сил пары, то есть длина перпендикуляра h, опущенного из любой точки линии действия одной из сил пары на линию действия второй силы (рис. 4.3, а). Поскольку сила -скользящий вектор, то силы в паре всегда можно разместить так, чтобы расстояние АВ между точками их приложения было плечом пары (Рис. 4.3, б).
Плоскость действия пары — это плоскость, в которой размещены силы пара. Она единственная, поскольку через две параллельные линии можно провести только одну
плоскость.
Как будет показано в § 5.3, пара сил не имеет равнодействующей.
Пара сил не является системой уравновешенных сил, ибо в первой аксиомой статики две равные по модулю и противоположны по направлению силы будут уравновешенной системой сил только тогда, когда имеют общую линию действия. Силы, составляющих пару, не имеют общей линии действия.
Пара сил, действующая на тело, пытается вращать его. По мере вращательного действия силы в статике, как известно, является момент. Следовательно, и действие пары сил на тело должна характеризоваться моментом. Докажем это с помощью следующей теоремы.
Теорема 4.1. Векторная сумма моментов сил пары относительно произвольного центра
(Точки) в пространстве является величиной постоянной для данной пары.
Доказательство. Пусть задано пару сил
действие пары на тело характеризуется вращательным эффектом, найдем сумму моментов сил пары относительно центра О, произвольно расположенного в пространстве.
Получим:
где 


Здесь 


Известно, что вектор 


Аналогично, учитывая, что 
где вектор 


Следовательно, сумма моментов сил пары относительно произвольного центра в пространстве не зависит от выбора этого центра и равен моменту одной из сил пары относительно точки приложения другой силы. Теорема доказана.
Эта сумма моментов характеризует вращательное действие пары сил на тело. Назовем ее вектор-моментом пары сил. Обозначим вектор-момент пары сил 


С доказательства теоремы следует, что момент пары сил является вектором. Определим его величину и направление.
Величина момента пары по формулам (4.10) — (4.14) равна произведения величины одной из сил пары на плечо пары:
Вектор-момент пары сил направляется перпендикулярно к плоскости действия пары так, чтобы с его конца было видно попытки пары сил вращать тело против часовой стрелки (рис. 4.4).
Если на тело действует система пары сил, расположенных в одной плоскости, то вектор-моменты всех пар сил системы перпендикулярны этой плоскости. Итак, вектор-моменты такой системы пар является системой параллельных векторов, для составления которых достаточно знать их величины и знаки. Поэтому целесообразно ввести понятие алгебраического момента пары сил.
Алгебраическим моментом пары сил называется взятый со знаком «+» или «-» произведение одной из сил пары на плечо пары:
Алгебраический момент пары сил считаем положительным, если пара сил пытается вращать тело против часовой стрелки (рис. 4.5, а) и отрицательным, если пара сил пытается вращать тело по часовой стрелке (рис. 4.5, б). Алгебраические моменты пар сил на рисунках показывают дуговыми стрелками.
Эквивалентность пары сил
Рассмотрим теоремы, из которых вытекают основные свойства пары сил, которые предоставят нам возможность выполнять определенные действия над ними.
Теорема 4.2. Действие пары сил на тело не изменится при произвольном переносе этой пары в плоскости ее действия.
Доказательство. Пусть к некоторому телу приложена пара сил 


Силы выбираем так, чтобы
Согласно второй аксиомой статики
Перенесем силы 





Учитывая формулы (4.7) и (4.17), получим
Поскольку фигура 

и 











Это означает согласно формуле (4.18), заданной паре сил 

Покажем, что величина и направление векторов-моментов пар сил 


Из рис. 4.8 видно, что знак момента 



Теорема 4.3. Действие пары сил на твердое тело не изменится, если перенести эту пару в плоскость, параллельную плоскости ее действия.
Доказательство. Пусть на некоторое твердое тело действует пара сил 

Выберем в теле плоскость 



Приложим к телу в точках С и D две системы уравновешенных сил 

Проведем отрезки АС и ВD, точкой пересечения которых есть точка А.
Поскольку 

Добавим попарно силы 





Равнодействующая силы 

стороны. Итак, система сил 
и можно записать
Сравнивая соотношения (4.21) и (4.22), получим 


Вектор-моменты





Теорема доказана.
Теорема 4.4. Действие пары на тело не изменится, если изменить силы и плечо пары, оставляя неизменным ее вектор-момент.
Доказательство. Пусть к телу приложена пара сил 
Приложим к телу в точках А и В две силы 

За аксиомой параллелограмма сил найдем равнодействующие систем сил 

Учитывая, что 

Итак, 


силы

Плечо новой пары 


видно, что поскольку 







Из доказанных теорем следует:
1) пары эквивалентны, если равны их векторы-моменты;
2) вектор-момент пары сил является вектором свободным. Это означает, что его можно приложить в произвольной точке твердого тела.
Сформулированы три теоремы можно объединить в одну теорему: пары сил являются эквивалентными, если равны их векторы-моменты.
Из всего сказанного можно сделать вывод, что вектор-момент пары сил является полной характеристикой статическому воздействию пары на твердое тело. Поэтому действия над парами сил можно заменить эквивалентными операциями над их векторами-моментами.
Добавление пар сил
1. Геометрическое определение момента результирующей пары сил
Установим правило сложения пар сил, лежащих в плоскостях, которые пересекаются. Это правило вытекает из следующей теоремы.
Теорема 4.5. Две пары сил, которые лежат в плоскостях, пересекающихся эквивалентны одной паре, вектор-момент которой равен геометрической сумме векторов-моментов данных пар.
Доказательство. Пусть пары сил

Пользуясь теоремой 4.4, приведем обе пары к плечу АВ, размещенного на линии пересечения плоскостей П1 и П2 , то есть
При этом должны выполняться равенства

Добавим согласно аксиоме параллелограмма силы, приложенные в точках А и В. Получим 







Теорема доказана.
Аналогично можно добавить n пар сил в пространстве. В результате получим одну пару сил, вектор-момент которой равен векторной сумме векторивмоментив составляющих пар сил, а именно:
2. Аналитическое определение момента результирующей пары сил
Спроектируем равенство (4.25) на оси прямоугольной декартовой системы координат и используем теорему о проекции суммарного вектора на ось. Получим проекции момента результирующей пары сил на оси координат:
где 


и-й пары на оси выбранной системы координат.
Тогда величина вектора момента пары
а направление его найдем по формулам:
Известно (§ 4.2), что вектор-моменты пар, размещенных в одной плоскости, есть коллинеарными и поэтому добавляются алгебраически. Итак, момент результирующей
пары плоской системы пар равна сумме алгебраических моментов составляющих пар
Условия равновесия пар сил
1. Геометрическое условие равновесия пространственной системы пар сил
Пусть на тело действует n пар сил, произвольно расположенных в пространстве, вектори-моменты которых равны
В § 4.4 было доказано, что такая система пар сил эквивалентна одной паре сил, вектор-момент которой определяется формулой (4.25). очевидно, что тело под действием системы пар сил остается в равновесии, если вектор-момент результирующей пары будет равняться нулю
Это условие равновесия, учитывая формулу (4.25), запишем в виде
Формула (4.29) является геометрической условием равновесия пространственной системы пар, которую можно сформулировать так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда вектор-момент результирующей пары или геометрическая сумма векторов-моментов составляющих пар будет равняться нулю.
2. Аналитические условия равновесия пространственной системы пар сил
Из условия (4.29), учитывая формулу (4.26), получаем, что в случае равновесия пространственной системы пар сил то есть
Формулы (4.30) являются аналитическими условиями равновесия пространственной системы пар сил, которые формулируются так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда алгебраические суммы проекций
векторов-моментов составляющих пар на три взаимно перпендикулярные оси координат будут равны нулю.
3. Условие равновесия плоской системы пар сил
Условие равновесия плоской системы пар сил получаем из равенства (4.28).
Плоская система пар сил будет находиться в равновесии тогда и только тогда, когда сумма алгебраических моментов составляющих пар сил будет равняться нулю:
Условие равновесия плоской системы пар можно получить также из условий равновесия (4.30).
Действительно, пусть система пар сил размещена в координатной плоскости 



Поскольку 

Момент силы относительно точки на оси. Момент пары сил
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны, приложенных к телу в двух разных точках.
Момент силы относительно точки
Моментом силы 





Модуль этого векторного произведения:

Опустим перпендикуляр из точки 





Итак, момент силы относительно центра 
плечо, и направленный перпендикулярно к плоскости, проходящей через точку 


Очевидно, момент силы относительно точки имеет все свойства векторного произведения. Из формулы (2.1) можно найти проекции вектора 

Раскрывая этот определитель по элементам первой строки и раскладывая вектор 



Сравнивая левую и правую части равенства (2.5), имеем

Модуль, и направление момента силы относительно точки можно определить еще и так:
Заметим, что формулы (2.6) легко получить, пользуясь правилом циклической
перестановки индексов.
По определению момента силы относительно точки имеем:
1) если переместить силу вдоль линии ее действия, то момент силы относительно точки не изменится;
2) момент силы относительно точки всегда равен нулю, когда линия действия силы проходит через эту точку (в этом случае плече 
3) момент силы относительно точки численно равен удвоенной площади треугольника 

Теорема о моменте равнодействующей системы сходящихся сил
Теорема Вариньона. Момент равнодействующей сходящейся системы сил относительно произвольного центра равен векторной (геометрической) сумме моментов составляющих сил относительно того самого центра:

Доказательство. Пусть в точке А пересекаются линии действия системы сходящихся сил




получим:

что и требовалось доказать.
Если силы и точка О размещены в одной плоскости, то их моменты перпендикулярны этой плоскости и лежат на одной прямой. Поэтому момент равнодействующей такой системы сил равен алгебраической сумме моментов составляющих сил относительно этой
точки.
Момент сил относительно оси
Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси (рис. 2.5).
Из этого определения следует, что моменты сил относительно координатных осей вычисляются по формулам (2.6). Эти формулы, в частности, показывают, что момент силы
относительно оси не зависит от выбора точки на оси.
При решении конкретных задач моменты сил относительно осей удобно вычислять более наглядным способом (рис. 2.6) по следующему правилу.
1. Проводим произвольную плоскость 

пересечения этой плоскости с осью.
2. Проектируем силу 
3. Вычисляем момент проекции 

При этом момент силы относительно оси считается положительным, если наблюдатель видит со стороны положительного направления оси 


Как видно из рис. 2.6, численное значение момента силы относительно оси 

Из определения момента силы относительно оси следует, что он равен нулю, если линия действия силы и ось лежат в одной плоскости.
Пример 1. Сила 
с осью 





Вычислить момент этой силы относительно оси
Решение.
По формулам (2.6), есть


Известно, что 
или
Если 

Если 

Момент пары сил и его свойства
Парой сил называется система двух равных по величине сил 


Определим, чему равна сумма моментов сил, составляющих пар относительно произвольной точки.
Пусть О — произвольная точка пространства (Рис. 2.7, б), a 


Полученная векторная сумма не зависит от положение точки 
Векторное произведение


плечо пары.
Как видим, момент пары направленный перпендикулярно к плоскости действия пары в ту
сторону, откуда «вращение» пары происходит против часовой стрелки.
Итак, момент пары сил — вектор свободный и математически определен в виде

Ниже показано, что момент пары полностью определяет статическое действие пары сил на твердое тело, то есть полной характеристикой механического воздействия пары сил на это тело. Из определения момента пары сил и аксиомы I о двух силах следует, что пара сил является уравновешенной системой (система сил, эквивалентная нулю) тогда и только тогда, когда момент пары равна нулю. Другие свойства пары сил определяются следующими теоремами.
Теорема 1. Не меняя действия пары сил на твердое тело, его можно переносить и произвольно вращать в плоскости действия, изменяя величину силы, входящей в нее, и длину плеча так, чтобы момент пары оставался неизменным.
Доказательство. Пусть задано пару сил



на линиях, перпендикулярные к нему, приложим соответственно две системы сил







Перенесем теперь силы 



















Покажем, что при указанном перемещении пары сил можно изменять величину
силы, входящей в нее, и длину плеча, о чем говорится в теореме. Для этого рассмотрим исходную пару сил 
Приложим к точкам а и b систему сил 

равнодействующие сходящихся систему сил










Теорема 2. Две пары сил, которые лежат в одной или параллельных плоскостях и имеют одинаковые по величине, но противоположные по направлению моменты, составляют систему пар сил, эквивалентную нулю.
Доказательство. Пусть в плоскости заданы две пары сил 







С другой стороны, сумма моментов всех сил, которые составляют эти пары, определяется выражением:

которое является суммой моментов составляющих пар, равных нулю. Следовательно, эта система двух пар сил эквивалентна нулю.
Поскольку момент пары сил — вектор свободный, то доказанные теоремы справедливы также для случая пар сил, лежащих в параллельных плоскостях.
Из доказанных теорем следует вывод об эквивалентности двух пар сил, имеющих геометрически одинаковые моменты.
Кроме того, эти теоремы позволяют установить правило составления пар сил, которые лежат не только в параллельных плоскостях, но и в тех, которые пересекаются.
Так, если задан систему n пар 



Отметим, что пару сил нельзя заменить одной силой, которая была бы эквивалентна по действию на твердое тело двум равным по величиной, параллельным и противоположно направленным силам. Действительно, если предположить, что пара сил эквивалентна некоторой силе 



Итак, пара сил, действующих на твердое тело, образует новый самостоятельный элемент статики, который вместе с силой составляет важное понятия механики. Основные свойства этого элемента и основные преобразования, которым он подлежит, вполне устанавливаются доказанными теоремами о парах.
Эти свойства и превращения будут выглядеть так:
1) пару сил можно переносить в плоскости ее действия, в том числе и вращать на любой угол;
2) пару сил можно переносить в любую плоскость, параллельную плоскости действия этой пары;
3) можно изменять силы, образующие пару и плечо, не меняя момента пары;
4) несколько пар сил, произвольно расположенных в пространстве, можно заменить одной парой, момент которой равен геометрической сумме моментов составляющих пар.
Из изложенного в главах 1 и 2 приходим к такому важному выводу: механическое влияние в статике характеризуется тремя типами векторов: силой — скользящим вектором, моментом силы относительно точки — приложенным вектором и парой сил — свободным вектором.
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Парой сил называется система двух равных по величине, противоположных по направлению и не лежащих на одной прямой сил (рисунок 1.19).
Рисунок 1.19
Пара сил не имеет равнодействующей, т.е. не может быть заменена одной силой.
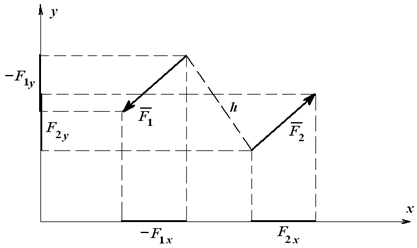
Сумма проекций сил пары на любую ось равна нулю, т.к. их проекции всегда равны и противоположны по знаку (рисунок 1.20).
Рисунок 1.20
Момент пары сил
Пара сил оказывает вращающее действие, которое может быть оценено моментом пары сил:
M(F1, F2) = F1h = F2h, (1.11)
где h – плечо пары.
Короткий видеоурок про момент силы с примерами:
Другие видео
Момент пары считается положительным, если силы пары стремятся повернуть плоскость, в которой они расположены, против хода часовой стрелки (рисунки 1.19, 1.20 – моменты этих пар сил положительны).
Момент пары сил может быть определен как векторная величина:
M(F1, F2) = AB×F2 = BA×F1, (1.12)
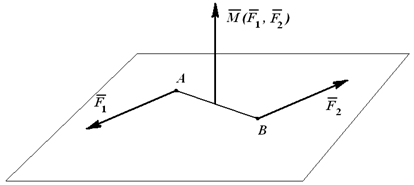
т.е. вектор M(F1, F2) всегда перпендикулярен плоскости, в которой расположена пара сил, и его направление определяется правилом векторного произведения (рисунок 1.21).
В разделе «Статика» дисциплины «Теоретическая механика» доказывается теорема о том, что сумма моментов сил пары относительно произвольной точки пространства равна моменту этой пары. Следовательно, вектор-момент пары сил может быть приложен (или перенесен) к любой точке твердого тела, на которое действует пара сил.
Рисунок 1.21
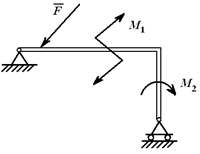
Поскольку действие пары сил оценивается величиной и направлением вращающего момента, то на плоскости пару сил изображают в любом месте твердого тела, задавая величину и направление вращающего действия (см. на рисунке 1.22 изображение пар сил M1 и M2).
Рисунок 1.22
См. также момент силы
Примеры решения задач >
Распределенные нагрузки >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
§1. Момент силы относительно центра (или точки)
Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее моментом.
Рассмотрим силу , приложенную в точке А твердого тела (рис. 1). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы
, называется плечом силы относительно центра О. Так как точку приложения силы можно произвольно перемещать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть:
1) от модуля силы F и длины плеча h;
2) от положения плоскости поворота ОАВ, проходящей через центр О и силу F;
3) от направления поворота к этой плоскости.
Рис.1. Сила, приложенная к телу
Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.
Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.
Момент силы относительно центра О будем обозначать M.
Следовательно, М= ±Fh. Единицы измерения в системе СИ : Н·м,
Правило знаков для момента силы: момент пары сил будем считать положительным, если пара стремиться повернуть тело по направлению хода часовой стрелки, и отрицательным, если пара сил стремится вращать тело против хода часовой стрелки.
Отметим следующие свойства момента силы:
1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.
2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).
3) Момент силы численно выражается удвоенной площадью треугольника ОАВ (рис. 1)
M= ± 2пл.ΔOAB
§2.Теорема Вариньона о моменте равнодействующей
Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.
Рис.2. Сходящаяся система сил
Рассмотрим систему сил , сходящихся в точке А (рис. 2). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.
Для доказательства теоремы найдем соответствующие выражения моментов М(), М(), … .
По формуле М() = +2пл.ΔОАВ1. Но, как видно из рисунка, где F1x — проекция силы на ось Ох; следовательно М() = ОА · F1x
Аналогично вычисляются моменты всех других сил.
Обозначим равнодействующую сил , через , где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:
или .
§3. Пара сил. Момент пары
Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис. 3). Очевидно, и
Рис. 3. Пара сил
Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:
.
Расстояние a между линиями действия сил называется плечом пары.
Если пара вращает тело против часовой стрелки, момент её считается отрицательным (как на рис. 3), если по часовой стрелке – положительным.
Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.
Вектор момента пары направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть оттуда, увидим вращение тела против часовой стрелки (рис. 4).
Нетрудно доказать, что вектор момента пары – есть вектор этого векторного произведения (рис. 4). И заметим, что он равен вектору момента силы относительно точки А, точки приложения второй силы:
.
Рис.4. Вектор момента пары сил
Видео-урок «Пара сил и ее свойства»
1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.
2) Найдём сумму моментов сил оставляющих пару, относительно какой-либо точки О (рис.5).
Рис.5. Пара сил
Покажем радиусы-векторы точек А1 и А2 и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О
.
Но
. Поэтому .
Но .
Значит .
Момент пары сил относительно любой точки равен моменту этой пары.
Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары
.
3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.
4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F1=F2=5 H и плече а = 4 см момент пары m = 20 H∙см. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Н∙см и действие пары на тело не изменится.
Все эти свойства можно объединить и, как следствие, сделать вывод, что пары с одинаковым вектором момента и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны.
Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m (рис. 6). Или, если это пространственная конструкция, показывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары
– свободный вектор. Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.
Рис.6. Эквивалентные пары сил
И ещё одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары
на эту ось: , где – угол между вектором и осью z.
Видео-уроки «Эквивалентность пар»
Пусть даны две пары с моментами m1 и m2, расположенные в пересекающихся плоскостях (рис. 7).
Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а образующих вторую пару:
.
Эти пары показаны на рис. 7, где . И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересечения плоскостей.
Рис.7. Пары сил с моментами m1 и m2
Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие . Так как , то эти силы и будут образовывать пару, момент которой
, где – радиус-вектор точки В, совпадающий с АВ.
Так как
, то момент полученной пары .
Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.
При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом .
Конечно, эта результирующая пара будет располагаться в плоскости перпендикулярной вектору .
Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар =0.
Это является необходимым и достаточным условием равновесия систем пар.
Если пары расположены в одной плоскости, векторы моментов их будут параллельны. И момент результирующей пары можно определить как алгебраическую сумму моментов пар.
Рис.8. Моменты пар сил, расположенные в одной плоскости
Например, пары, показанные на рис.8, расположены в одной плоскости и моменты их:
m1=2 Hсм , m2=5 Hсм, m3=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю:
Вопросы для самопроверки:
— Что называется моментом силы относительно центра на плоскости?
— Какая система сил называется парой?
— Можно ли заменить действие пары сил на тело одной силой?
— Что такое момент пары?
— Какая плоскость называется плоскостью действия пары?
— Какие пары называются эквивалентными?
— Что называется плечом пары?
— Запишите векторную и скалярную зависимости между элементами пары.
— Почему пара сил не имеет равнодействующей?
— Имеет ли пара сил равнодействующую?
— Каким образом можно уравновесить действие на тело пары сил?
— Что такое момент пары сил?
— Изменятся ли моменты пар сил, если положения сил, показанные на рис. а, изменить на положения, показанные на рис. б?
— Какие пары называются эквивалентными?
— Эквивалентны ли пары сил, изображенные на рисунке?
— Каким образом производится сложение пар сил?
— Сформулируйте условие равновесия пар сил.
— Чем характеризуется действие пары сил на твердое тело?
— Как направлен вектор момента пары сил?
— Как определяются моменты пар сил, лежащих в одной плоскости?
— Какие преобразования пары сил не изменяют ее действия на твердое тело?
— Сформулируйте теоремы об эквивалентности пар.
— Что называется результирующей парой?
— Запишите формулу для определения результирующей системы пар.
— Назовите условия равновесия плоской системы пар.
— Приведите векторную запись условия равновесия произвольной системы пар.
— Будет ли изменяться момент силы относительно точки, если, не меняя направления, переносить силу вдоль линии ее действия?
— На тело действуют две силы F1 = 40 Н и F2 = 50 Н, как показано на рисунке (а = 0,5 м, b = 0,8 м, ). Какая из сил создает больший момент относительно точки О?
— Что такое главный вектор и главный момент плоской системы сил?
— Как аналитически найти главный вектор и главный момент данной плоской системы сил?
— В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?
— Сформулируйте теорему Вариньона.
— Приведите векторную запись теоремы Вариньона.
— Чему равен главный вектор системы сил?
— Чему равен главный момент системы сил при приведении ее к точке?
— Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?