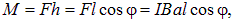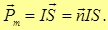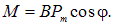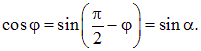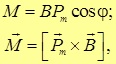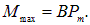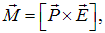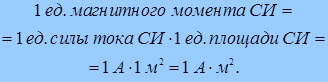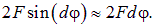Как найти момент сил действующих на виток

Момент сил, действующих на виток с током в магнитном поле

Механический
(вращательный) момент, действующий на
контур с током, помещенный в однородное
магнитное поле

или(3.58)

α— угол между векторами(направлен по нормали к контуру) и(рис.3.15)

Рис .3.15

Принцип суперпозиции магнитных полей

Каждый ток создает свое магнитное поле
независимо от других токов и вектора
(или)
этих полей складываются геометрически
(принцип суперпозиции).

Индукция результирующего магнитного
поля от сложения магнитных полей:

;.

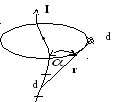
Закон Био-Савара-Лапласа и его применение к расчету магнитных полей

Этот закон позволяет определить величину
вектора магнитной индукции
(или
напряженности)
в любой точке поля на расстоянииrот проводника с токомI.
Так как форма проводника может быть
разной, то выделяется на проводнике
элементdℓ его длины столь
малый, что можно пренебречь его кривизной,
и тогда в векторном виде:

или

(3.59)

т.е. индукция
dВ магнитного поля,
созданная бесконечно малым элементомdℓпроводника с
токомIв точке поля на
расстоянииrот элемента
до этой точки, прямопропорциональна
силе токаIдлине элементаdℓи обратно
пропорциональнаr²от элемента до точки – это и естьзакон
Био-Савара-Лапласа (рис.3.16).

Рис.3.16

Угол α в формуле (3.59) это угол между
направлением тока и вектором-радиусом.

Пример: определим магнитную индукцию
в центре кругового тока IрадиусомR(рис.3.17)

Рис.3.17

(3.60)

с учетом того,
что в формуле (3.59) r=R,
α = 90⁰.

Аналогичным
образом, интегрируя уравнение (3.59) с
учетом формы проводника, получаем:

а) для бесконечно
длинного прямого тока:

или(3.61)

где r-
кратчайшее расстояние от оси провода
до точки, в которой определяется магнитная
индукция;

б)
для отрезка проводника с током I:

,
(3.62)

где α₁и α₂-углы между радиусами-векторами,
проведенными в данную точку поля
соответственно из начала и конца
проводника, и направлением тока;

в) закон
полного тока проводимости:

или (3.63)

где ℓ-длина
произвольного замкнутого контура в
магнитном поле;

n-число
витков, охватываемых контуром.

Пользуясь законом полного тока, рассчитаем
напряженность Н и индукцию
магнитного поля тороида и соленоида.
Пусть соленоид имеетNвитков с токомIи длинуL. Проведем замкнутый
контур ℓ через середину соленоида так,
чтобы он охватывал все витки. Тогда
алгебраическая сумма всех охватываемых
контуром токов будет:

С другой стороны
.
Приравняв, получим:

или,
(3.64)

Напряженность
магнитного поля вне бесконечного
длинного соленоида считаем равной нулю.
Поле внутри длинного соленоида однородно.
Для магнитной индукции поля соленоида
имеем:

(3.65)

Формулы (3.64) и (3.65) справедливы и для
тороида (кольцевого соленоида радиуса
R, где ℓ=2πR).
Рис. 3.18

Рис.3.18

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

0 Пользователей и 1 Гость просматривают эту тему.

---

---

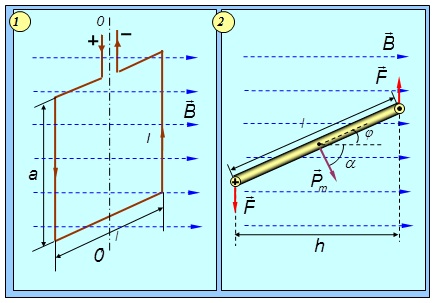
5.7. Контур с током в магнитном поле

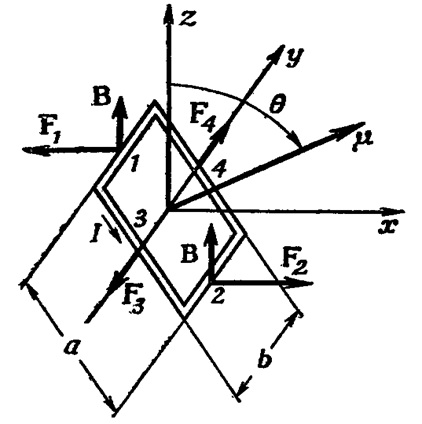
Пусть контур с током помещен в магнитное поле, причем он может вращаться вокруг вертикальной оси OO’ (рис. 5.30-1). Силы Ампера, действующие на стороны контура длиной l, перпендикулярны к ним и к магнитному полю и поэтому направлены вертикально: они лишь деформируют контур, стремясь растянуть его. Стороны, имеющие длину a, перпендикулярны B, так что на каждую из них действует сила F = BIa. Эти силы стремятся повернуть контур таким образом, чтобы его плоскость стала ортогональной B.

Рис. 5.30. Силы, действующие на контур с током в магнитном поле:
1 — вид сбоку; 2 — вид сверху (масштаб увеличен)

Видео 5.7. Контур с током в однородном магнитном поле.

Момент пары сил (рис. 5.30-2) равен

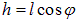
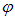
где — плечо пары сил, а — угол между вектором B и стороной l.

Величина, численно равная произведению силы тока I, протекающего в контуре, на площадь контура S = al называется магнитным моментом P_m плоского контура стоком

Таким образом, мы можем записать момент пары сил в виде

Магнитный момент контура с током — векторная величина. Направление Р_m совпадает с положительным направлением нормали к плоскости контура, которое определяется правилом винта: если рукоятка вращается по направлению тока в контуре, то поступательное движение винта показывает направление вектора P_m . Введем в формулу (15.36) угол a между векторами P_m и B. Справедливо соотношение

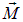
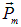
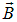
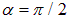
то есть момент сил , действующий на виток с током в однородном магнитном поле, равен векторному произведению магнитного момента витка на вектор индукции магнитного поля (рис. 5.31). При величина момента сил максимальна

Рис. 5.31. Силы, действующие на прямоугольный контур с током в магнитном поле.
Магнитное поле вертикально, а магнитный момент перпендикулярен плоскости контура

Опять-таки прозрачна аналогия с электростатикой: говоря об электрическом диполе, мы получили выражение для момента сил, действующих на него со стороны электрического поля в виде

где 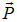— электрический дипольный момент.

В системе СИ единицей измерения магнитного момента контура является ампер на квадратный метр (А · м 2 )

Видео 5.10. «Сознательные катушки»: отталкивание и притяжение параллельных токов и поворот магнитного момента по магнитному полю.

Пример. По тонкому проводу в виде кольца радиусом 30 см течет ток 100 A. Перпендикулярно плоскости кольца возбуждено однородное магнитное поле с магнитной индукцией 20 мТл (рис. 5.32). Найти силу, растягивающую кольцо.

Рис. 5.32. Силы, растягивающие кольцо с током в магнитном поле

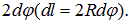
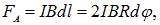
Решение. Пусть магнитное поле направлено от нас за плоскость рис. 5.32 (показано крестиками), а ток идет по часовой стрелке. Выделим элемент длины dl, видный из центра под углом На этот элемент действует сила Ампера направленная по радиусу кольца. Кроме того, из-за растяжения кольца на концы элемента действуют силы натяжения F, которые и требуется найти в задаче. Проекция этих сила на радиальное направление равна

Приравнивая эту проекцию силе Ампера, находим

Магнетизм. · Механический момент, действующий на контур с током (рис

· Механический момент, действующий на контур с током (рис. 32), помещенный в однородное магнитное поле

Рис. 32. Рамка с током

, где — вектор магнитного момента рамки с током; — вектор магнитной индукции (количественная характеристика магнитного поля). Единица измерения магнитной индукции тесла (Тл).

· Закон Био-Савара-Лапласа: каждый элемент проводника с током создает в некоторой точке А индукцию поля (рис. 33)

Рис. 33. Магнитное поле, созданное проводником с током

, где – магнитная индукция поля, создаваемого элементом проводника с током, Тл; μ – магнитная проницаемость; μ0 – магнитная постоянная (μ0 = 4π·10 -7 Гн/м); – вектор, равный по модулю длине dl проводника и совпадающий по направлению с током; I – сила тока; – радиус вектор, проведенный от середины элемента проводника к точке, магнитная индукция в которой определяется.

· Модуль вектора выражается формулой

,

где α – угол между векторами и .

· Магнитная индукция связана с напряженностью магнитного поля соотношением .

· Магнитная индукция в центре кругового проводника с током (рис. 34)

,

где r – радиус витка.

· Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током (рис. 35)

,

где R – расстояние от оси проводника.

· Магнитная индукция поля, создаваемая соленоидом в средней его части (рис. 36)

,

где n – число витков, приходящихся на единицу длины соленоида; I – сила тока в одном витке.

Рис. 34. Магнитное поле, созданное круговым проводником с током

Рис. 35. Магнитное поле, созданное длинным прямым проводником с током

Рис. 36. Магнитное поле, созданное соленоидом

· Принцип суперпозиции магнитных полей: магнитная индукция результирующего поля равна векторной сумме магнитных индукций складываемых полей .

В частном случае наложения двух полей

,

а модуль магнитной индукции

,

где α – угол между векторами и .

· Магнитная индукция поля, создаваемого движущимся точечным зарядом в вакууме

, или ,

где — скорость движущегося заряда; — радиус-вектор, направленный от заряда к точке, в которой определяется магнитная индукция; α – угол между векторами и .

,

где — вектор, по модулю равный dl и совпадающий по направлению с током; — вектор магнитной индукции.

Модуль силы Ампера вычисляется по формуле

,

где α – угол между векторами и .

В случае однородного магнитного поля и прямолинейного отрезка проводника , или .

Рис. 37. Правило левой руки

Направление вектора может быть найдено, согласно последней формуле, по общим правилам векторного произведения. Этим правилам соответствует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток (рис. 37).

· Магнитный момент контура с током

,

где — вектор, равный по модулю площади, охватываемой контуром, и совпадающий по направлению с нормалью к его плоскости.

· Сила Лоренца – сила действующая на одну заряженную частицу, движущуюся в магнитном поле.

, или ,

где α – угол, образованный вектором скорости движущейся частицы и вектором магнитной индукции (рис. 37).

· Магнитный поток Ф через плоский контур площадью S (рис. 38)

а) в случае однородного поля

Рис. 38. Магнитный поток через плоский контур

, или где α – угол между вектором нормали к плоскости контура и вектором магнитной индукции , Вn – проекция вектора на нормаль .

б) в случае неоднородного поля

,

где интегрирование ведется по всей поверхности S.

· Работа сил магнитного поля, совершаемая при перемещении контура с током в магнитном поле

,

где I – сила тока в контуре, которая поддерживается неизменной; Ф₂ и Ф₁ – магнитные потоки, пронизывающие контур, в конечном и начальном его положениях.

· Закон Фарадея-Максвелла (основной закон электромагнитной индукции)

,

где ε_i – электродвижущая сила индукции; N – число витков контура; ψ — потокосцепление.

· Электродвижущая сила самоиндукции, возникающая в замкнутом контуре при изменении силы тока в нем

,

где L – индуктивность контура.

· Энергия магнитного поля

,

где I – сила тока в контуре.

· Формула Томсона. Период собственных колебаний в контуре без активного сопротивления

,

где L – индуктивность контура, Гн; С – его электроемкость, Ф.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. Мягкая спиральная пружина подвешена так, что ее нижний конец погружен в металлическую чашечку с ртутью, а верхний присоединен к источнику постоянного тока. Что произойдет с пружиной при замыкании ключа К?

Решение: При замыкании ключа К по пружине потечет ток. Каждый виток пружины будет создавать магнитное поле и притягивать к себе соседние витки (разноименные полюса магнитов притягиваются). Пружина сожмется, нижний конец пружины поднимется из ртути, цепь разомкнется, и ток перестанет идти. Если нет тока, нет и магнитного поля между витками и пружина расправится.

После опускания нижнего конца пружины в ртуть весь процесс начнется сначала. Таким образом, пружина совершает периодические колебания.

Эту задачу можно решить и по-другому. Отдельные участки соседних витков, лежащие друг против друга, можно рассматривать как параллельные участки проводников, по которым текут токи в одном направлении (рис. 39б), такие проводники притягиваются друг к другу. Поэтому витки пружины будут притягиваться друг к другу и пружина сожмется, а нижний конец ее поднимется из ртути, разрывая цепь, по которой протекает ток. Исчезает магнитное поле проводников, и пружина вновь распрямляется. Конец пружины опускается в чашку с ртутью, вновь замыкая цепь, и т.д.

Пример 2. По длинному прямому тонкому проводу течет ток силой I = 20 А. Определить магнитную индукцию поля, создаваемого проводником в точке, удаленной от него на расстояние r = 4 см.

Решение: В задаче рассматривается явление создания магнитного поля проводником с током. Проведем силовую линию магнитного поля через точку А (рис. 40), в которой определяется магнитная индукция . Магнитное поле, создаваемое проводником бесконечной длины, обладает осевой симметрией. Поэтому в плоскости, проходящей через точку А и перпендикулярной проводу, проведем окружность радиуса OA = r (рис. 40).

Рис. 40. Правило буравчика

Направление силовой линии и направление тока связаны правилом правого винта (буравчика): если поступательное движение винта направить по току, то вращательное движение головки винта укажет направление силовой линии (рис. 40). Определение направления силовой линии следует из закона Био-Савара-Лапласа, записанного в векторной форме:

.

Вектор совпадает с касательной в точке А и направлен так же, как силовая линия. Запишем выражение для магнитной индукции поля бесконечно длинного проводника с током на расстоянии r от него из уравнения . Считая, что проводник находится в вакууме (μ = 1), вычисляем, подставляя все величины в единицах системы СИ:

Тл.

Пример 3.Два параллельных бесконечно длинных провода D и C, по которым текут в одном направлении электрические токи силой I₁ = I₂ = 60 А, расположены на расстоянии d = 10 см друг от друга. Определить магнитную индукцию поля, создаваемого проводником с током в точке A, отстоящей от оси одного проводника на расстояние r₁ = 5 см, от другого – r₂ = 12 см.

Решение: В задаче рассматривается явление создания магнитного поля системой проводников. Проведем через точку A (рис. 41) часть силовой линии магнитного поля, создаваемого током I1, а затем часть силовой линии магнитного поля, которое создается током I2 (пунктирные дуги).

Рис. 41. Магнитное поле, созданное двумя бесконечно длинными проводниками

Построим и как касательные к этим дугам в точке А. Так как магнитные индукции определяются по формулам:

и , (1)

Для нахождения в точке A магнитной индукции B, создаваемой системой проводников с токами, воспользуемся принципом суперпозиции магнитных полей. Для этого сложим и геометрически, по правилу параллелограмма: . Модуль вектора найдем по теореме косинусов:

, (2)

где α – угол между векторами и . Подставляя B₁ и B₂ (1) в формулу (2), и вынося за знак корня, получаем

. (3)

Найдем cos α из треугольника DAC. Заметим, что α = ∟DAC, как углы со взаимно перпендикулярными сторонами ( , ; AD и AC – радиусы; и – касательные в точке A). По теореме косинусов запишем , где d = DC – расстояние между проводами.

Отсюда ; .

Теперь можно все данные подставить в формулу (3) и найти индукцию поля:

Тл или 308 мкТл.

Пример 4.Электрон, пройдя ускоряющую разность потенциалов U = 400 В, попал в однородное магнитное поле напряженностью H = 1 кА/м. Определить радиус R кривизны траектории и частоту ν обращения электрона в магнитном поле. Вектор скорости перпендикулярен линиям поля .

Решение: В задаче рассматривается явление силового действия магнитного поля на движущийся заряд (рис. 42). На движущийся в магнитном поле заряд действует сила Лоренца (действием силы тяжести можно пренебречь). Сила Лоренца перпендикулярна вектору скорости и, следовательно, сообщает электрону нормальное ускорение.

Рис. 42. Движение электрона в однородном магнитном поле

По второму закону Ньютона , где a_n – нормальное ускорение

или , (1)

где |q| – модуль заряда электрона; υ – скорость электрона; В – магнитная индукция; m – масса электрона; R – радиус кривизны траектории; α – угол между векторами и (в данном случае α = 90 0 , sin α = 1).

Из формулы (1) найдем

. (2)

Входящий в это равенство импульс p = mυ может быть выражен через кинетическую энергию Е_к электрона:

, откуда . (3)

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U, определяется работой электрического поля по ускорению электрона и по закону сохранения энергии Е_к = А = |q|·U. Подставляя это выражение в формулу (3), получим .

Магнитная индукция B может быть выражена через напряженность H магнитного поля в вакууме: .

Подставив выражения для В и в формулу (2), получим

м или 5,37 см.

Учитывая, что частота обратно пропорциональна периоду , а период можно определить как , получим формулу, связывающую частоту со скоростью и радиусом: . Подставив в последнюю формулу выражение (2), получим

или .

с -1 .

Пример 5.Длинный соленоид с сердечником из немагнитного материала содержит N = 1200 витков провода, плотно прилегающих друг к другу. При силе тока I = 4 А магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию W магнитного поля соленоида, объемную плотность энергии магнитного поля w, если длина соленоида l = 1 м.

Решение: В задаче рассматривается явление создания магнитного поля соленоидом с током (рис. 43). Индуктивность L связана с потокосцеплением Ψ и силой тока I соотношением . (1)

Потокосцепление, в свою очередь, может быть определено через поток Ф и число витков N (при условии, что витки плотно прилегают друг к другу):

. (2)

Из формул (1) и (2) находим индуктивность соленоида

. (3)

Энергия магнитного поля соленоида: .

Выразив L согласно уравнению (3), получим энергию магнитного поля:

. (4)

Подставим значения физических величин в единицах СИ в формулы (3) и (4) и вычислим значения L и W:

Гн или 1,8 мГн.

Дж или 14,4 мДж.

Рис. 43. Соленоид

Энергию магнитного поля можно найти и другим способом. Запишем энергию магнитного поля как: , (5) где V, l – объем и длина соленоида, S – площадь витка. Напряженность магнитного поля длинного соленоида (d 0 = BS = μμ0HS = μ0nIS , где μ = 1 для немагнитного материала. Из этой формулы выразим площадь S: . (7) Подставим формулы (6) и (7) в формулу (5): . Учитывая, что , получим формулу для вычисления энергии поля соленоида: . Объёмная плотность энергии магнитного поля равна . Подставляя данные, получим, Дж/м 3 . Пример 6. Электрон, ускоренный разностью потенциалов U = 6 кВ, влетает в однородное магнитное поле под углом α = 30 o к направлению поля и движется по винтовой траектории. Индукция магнитного поля B = 13 мТл. Найти радиус R, шаг h винтовой траектории, период T обращения электрона, его кинетическую энергию. Решение: В задаче рассматривается явление действия магнитного поля на движущийся в нем заряд. Разложим скорость электрона, влетающего в магнитное поле, по двум направлениям: вдоль линий поля – и перпендикулярно ему – . На основании закона сохранения энергии работа электрического поля А = |q|U переходит в кинетическую энергию электрона , . (1) Из этой формулы определим скорость , м/с. Рис. 44. Движение электрона в однородном магнитном поле Из рис. 44 видно, что υ׀׀ = υ∙cosα, . Формула для радиуса R: . Тогда . Проведя вычисления, получим м. Шаг спирали найдем из соотношений: и , откуда . Проведя вычисления, получим м. Тогда период обращения электрона найдем как: с. Магнитный момент контура с током. Сила, действующая на контур с током. Работа при перемещении контура с током Магнитным моментом плоского замкнутого контура с током / называется вектор Рис. 15.9. Виток с током где S — площадь поверхности, ограниченной контуром, которую называют обычно поверхностью контура (или поверхностью, натянутой на контур); п — единичный вектор нормали к плоскости контура (рис. 15.9). Векторы Я и рт направлены перпендикулярно плоскости контура по правилу правого винта (см. рис. 15.1). Рис. 15.10. Прямоугольная рамка с током в магнитном поле На ребра а рамки с током во внешнем однородном магнитном поле, показанной на рис. 15.10, действуют силы F< и F2, которые стремятся только растянуть (или сжать) виток. На ребра b действуют силы, стремящиеся повернуть рамку так, чтобы ее плоскость была перпендикулярна к линиям магнитной индукции В. Следовательно, со стороны внешнего магнитного поля на контур с током действует вращающий момент пары сил, который, как можно показать, определяется векторным произведением где рт —ректор магнитного момента контура с током; В — вектор магнитной индукции. По определению векторного произведения скалярная величина момента где ср — угол между векторами рт и В. Можно доказать, что формула (15.22) справедлива для контура с током, находящегося в однородном магнитном поле независимо от формы этого контура. При повороте контура с током в магнитном поле на угол dф момент сил совершает работу, которую определяют как 6Л — М d(p — —pmBs’ (pd(p — = —dEp. Работа идет на изменение потенциальной энергии контура с током в магнитном поле. Тогда потенциальная энергия I Сила, действующая на контур с током. Силы Ампера, действующие на замкнутый проводник с током со стороны магнитного поля (внешнего и собственного поля тока в проводнике), вызывают деформацию проводника. Если контур находится в неоднородном магнитном поле В, не перпендикулярном к плоскости контура, то формула (15.22) справедлива, если размеры контура достаточно малы и поле можно считать в пределах контура приблизительно однородным. Тогда будут действовать и пара сил, стремящаяся повернуть контур с током, и результирующая сила, вызывающая поступательное перемещение контура, которая вычисляется, согласно уравнению (4.19), как где В — магнитная индукция внешнего магнитного поля. Под действием силы Трсз незакрепленный замкнутый контур с током в неоднородном магнитном поле будет перемещаться подобно магнитному диполю. Силы Ампера, действующие на отдельные участки витка, как и в случае однородного поля, перпендикулярны к току и к магнитному полю. Однако, поскольку линии магнитной индукции теперь не параллельны, эти силы составляют некоторый угол с плоскостью витка. Поэтому он будет втягиваться в область более сильного магнитного поля, если угол ср между векторами рт и В острый (ср л/2, рис. 15.11, б), то контур с током будет выталкиваться в область более слабого поля. Отметим, что положение контура, при котором рт ТI В, является неустойчивым. Положение устойчивого равновесия контура соответствует случаю, когда рт ТТ В. Если внешнее поле однородно <В= const и тогда рт = const), то на контур действует только вращающий момент (15.22). Работа при перемещении контура с током. Поскольку на проводник с током в магнитном поле действуют силы Ампера, то при движении проводника за счет источника тока совершается работа. Рис. 15.11. Виток с током в неоднородном магнитном поле: а — виток втягивается в область более сильного поля; 6 — виток выталкивается в область более слабого поля Рис. 15.12. К вычислению работы при поступательном движении проводника с током Рассмотрим прямолинейный участок проводника длиной / с постоянным током /, который движется поступательно параллельно самому себе. Пусть магнитное поле В направлено перпендикулярно к плоскости, в которой движется проводник (рис. 15.12). Работа 6Л силы Ампера F — 11, В] при перемещении проводника на расстояние dr определяется формулой где dS — площадь, описанная проводником при движении. Из определения магнитного потока (15.10) уравнение (15.25) можно представить в виде | где 6Л — работа при перемещении проводника с током, совершаемая силами магнитного поля; d — увеличение магнитного потока через поверхность^. Можно показать, что формула (15.25а) справедлива и в случае произвольного перемещения проводника любой формы во внешнем постоянном неоднородном магнитном поле. Поэтому если рассматривать контур с током произвольной формы, который движется в магнитном поле, то, разбивая проводник на элементарные участки, можно применять уравнение (15.25а). Тогда работа по перемещению контура с током где Ф, и Ф, — магнитный поток через площадь контура соответственно в начальном и конечном положениях. Таким образом, работа по перемещению в постоянном магнитном поле замкнутого контура с током равна произведению силы тока в контуре на изменение его потокосцепления. Формула (15.26) выполняется, если ток в контуре постоянен. источники: http://mydocx.ru/4-104589.html http://studref.com/504893/matematika_himiya_fizik/magnitnyy_moment_kontura_tokom_sila_deystvuyuschaya_kontur_tokom_rabota_peremeschenii_kontura_tokom

В предыдущем параграфе мы рассмотрели действие поля на искусственно выделенный прямолинейный участок проводника с током. Но ток, протекающий по проводнику, представляет собой замкнутую цепь, и действие магнитного поля на ток весьма сложным образом зависит от формы проводников и от их расположения в поле. Мы ограничимся рассмотрением сравнительно простых, но важных случаев, когда проводник представляет собой один виток или совокупность последовательно соединенных витков (соленоид). Для изучения действия магнитного поля на такой виток или соленоид удобно придать приборам форму, изображенную на рис. 239, где провода

 и

, подводящие ток от батареи, сделаны длинными и тонкими, так что они одновременно служат подвесами, дающими возможность витку легко поворачиваться и перемещаться. Помещая такой виток или соленоид в магнитное поле, например в магнитное поле Земли или между полюсами магнита или электромагнита, мы можем изучать действие поля на виток (соленоид). При этом можно пренебречь действием поля на подводящие провода, если они расположены очень тесно друг к другу или, еще лучше, обвивают друг друга. Действительно, по этим проводам текут токи одинаковой силы и противоположного направления и они находятся в одном и том же поле. Следовательно (§ 133), на подводящие провода действуют равные и противоположно направленные силы, так что подвес остается в покое.

Рис. 239. Виток с током (а) и соленоид (б) для проведения исследований в магнитном поле

Мы неоднократно обращали внимание на то, что виток, по которому течет ток, эквивалентен короткому магниту, направление которого перпендикулярно к плоскости витка, причем северный полюс этого магнита расположен на той стороне плоскости витка, с которой ток кажется циркулирующим против часовой стрелки (правило буравчика, § 124; см. также § 119), а южный на противоположной стороне. Соленоид же эквивалентен магниту, лежащему вдоль оси соленоида. Ось этого магнита совпадает с осью соленоида, а расположение северного и южного полюсов определяется правилом буравчика, так же как и в случае витка. Естественно поэтому, что на такой виток или соленоид поле действует, как на магнитную стрелку, а именно: однородное поле создает вращающий момент, стремящийся повернуть виток или соленоид так, чтобы ось его расположилась вдоль поля и направление от южного полюса витка (соленоида) к северному совпало с направлением поля (рис. 240). В неоднородном поле к этому вращающему моменту присоединяется сила, увлекающая повернувшийся виток (соленоид) в том направлении, в каком увеличивается магнитная индукция поля.

Рис. 240. Положение, которое принимают в магнитном поле виток с током (а) и соленоид (б)

Пользуясь сведениями, полученными нами в § 133 относительно действия магнитного поля на прямолинейный проводник с током, мы можем яснее представить себе происхождение вращающего момента и влекущей силы, которые действуют на виток с током в магнитном поле. Пусть виток имеет прямоугольную форму (рис. 241) и расположен в однородном поле так, что две его стороны параллельны направлению поля, а две перпендикулярны к нему. На первые две поле не действует (рис. 234, в), а на две вторые действует с равными и противоположно направленными силами

 и

, потому что обе эти стороны имеют одинаковую длину

 и по ним течет ток

 одинаковой силы, но противоположного направления (рис. 241). Таким образом, силы, с которыми однородное поле действует на виток с током, составляют пару сил, которая и обусловливает вращающий момент, поворачивающий виток так, что плоскость его устанавливается перпендикулярно к направлению поля.

Рис. 241. Рамка с током в однородном поле устанавливается так, чтобы плоскость ее была перпендикулярна к линиям поля: а) вид сбоку; б) вид сверху

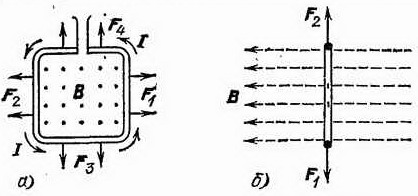
Рис. 242. Рамка с током, стоящая перпендикулярно к линиям однородного поля. Действующие на нее силы стремятся деформировать рамку (сжать или растянуть ее), не вызывая ее поступательного движения как целого: а) вид сбоку (магнитное поле направлено к наблюдателю); б) вид сверху

Если поле однородно, то этим поворотом и ограничивается воздействие поля, ибо в этом положении действие поля сводится к четырем направленным в разные стороны силам

 и

, которые не могут перемещать виток, а только стремятся его деформировать и уравновешиваются упругими силами, возникающими при деформации жесткого витка (рис. 242). Но если поле неоднородно и, следовательно, магнитная индукция поля в разных местах его имеет различное направление (и модуль), то результат будет несколько сложнее (рис. 243). Силы, действующие на разные стороны повернувшегося витка, теперь не равны и направлены не в прямо противоположные стороны, а составляют некоторый угол между собой (рис. 243, а), ибо эти силы перпендикулярны к направлению магнитной индукции поля. Их равнодействующая

 направлена в сторону возрастания магнитной индукции (рис. 243, б).

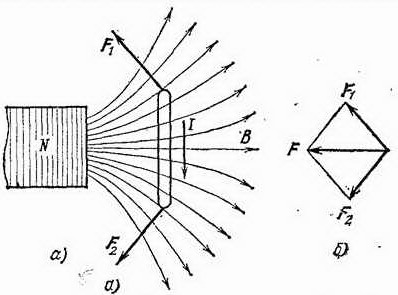
Рис. 243. а) Рамка, находящаяся в неоднородном поле (вид сверху). Действующие на нее силы вызывают движение рамки в область наибольшей магнитной индукции поля. б) Сложение сил
 и

, действующих на боковые стороны рамки. Равнодействующая сила

 стремится втянуть рамку в область наибольшей магнитной индукции поля

Наше рассмотрение касалось прямоугольного витка. Оно сохраняет свою силу и для витка любой формы, только в этом случае расчет более сложен, и мы его не приводим.

В случае соленоида сказанное применимо к каждому витку. Вращающие моменты, действующие на каждый виток жесткого соленоида, складываясь, дают результирующий вращающий момент, поворачивающий весь соленоид. При неоднородном поле силы, влекущие каждый виток в сторону возрастания магнитной индукции поля, окажут такое же действие и на весь соленоид в целом. Это рассмотрение объясняет нам, каким образом действие поля на каждый элементарный амперов ток приводит к повороту всей магнитной стрелки и к ее увлечению вдоль поля, если оно неоднородно.

134.1.
В горизонтальной плоскости лежит виток. Однородное магнитное поле направлено вертикально сверху вниз (рис. 244). Как будут направлены силы, действующие на виток: а) если по нему пропустить ток в направлении, указанном стрелкой; б) если ток идет в обратном направлении? Какую форму стремится принять виток, если он сделан из очень гибкой проволоки, в обоих случаях?

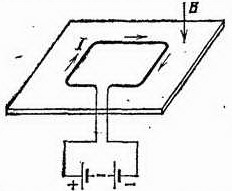
Рис. 244. К упражнению 134.1

134.2.
Если через проволочную спираль пропускать ток, то витки ее притягиваются друг к другу и спираль стягивается по оси. Объясните это явление.

134.3.
Объясните опыт с «танцующей пружиной», изображенной на рис. 245. Ток подводится к пружине через верхний неподвижный конец 1 и через чашечку с ртутью 2, в которую погружен нижний конец пружины. При включении тока пружина начинает периодически сжиматься и растягиваться, причем конец ее то выходит из ртути, то снова входит в нее. Какой из известных нам приборов напоминает это устройство? Для какой цели его можно было бы использовать?

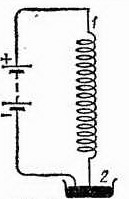
Рис. 245. К упражнению 134.3

134.4.
Кусок железа, помещенный перед катушкой, втягивается в нее при включении тока независимо от направления тока. На этом основано устройство амперметров и вольтметров так называемой электромагнитной системы, применяемых для измерения переменного тока и напряжения (на рис. 246 для ясности кусок железа снабжен стрелкой и показана шкала). Объясните этот опыт. Пришло бы железо в движение, если бы мы поместили его внутрь катушки, т. е. в область, где магнитное поле однородно?

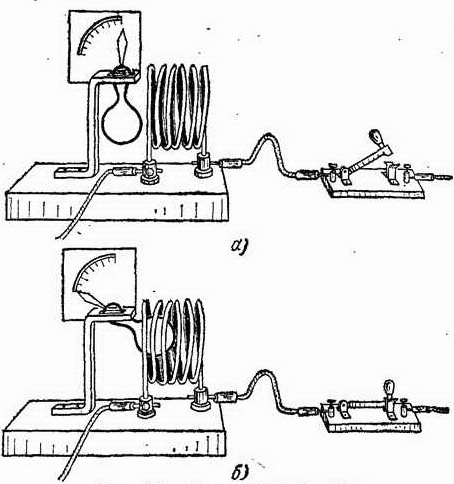
Рис. 246. К упражнению 134.4

134.5.
На рис. 247 изображена модель «электропушки», представляющая собой горизонтально укрепленный соленоид 1, намотанный на медную или стеклянную трубку. У одного конца его находится железный «снаряд» (гвоздь) 2. Если на короткое время включить достаточно большой ток, то снаряд втянется внутрь соленоида, пролетит сквозь него и вылетит с довольно значительной скоростью. В какой момент нужно выключить ток, чтобы снаряд вылетел из соленоида с наибольшей скоростью? Каково будет движение снаряда, если ток останется включенным все время?

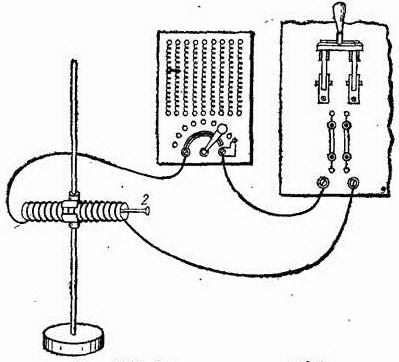
Рис. 247. К упражнению 134.5