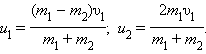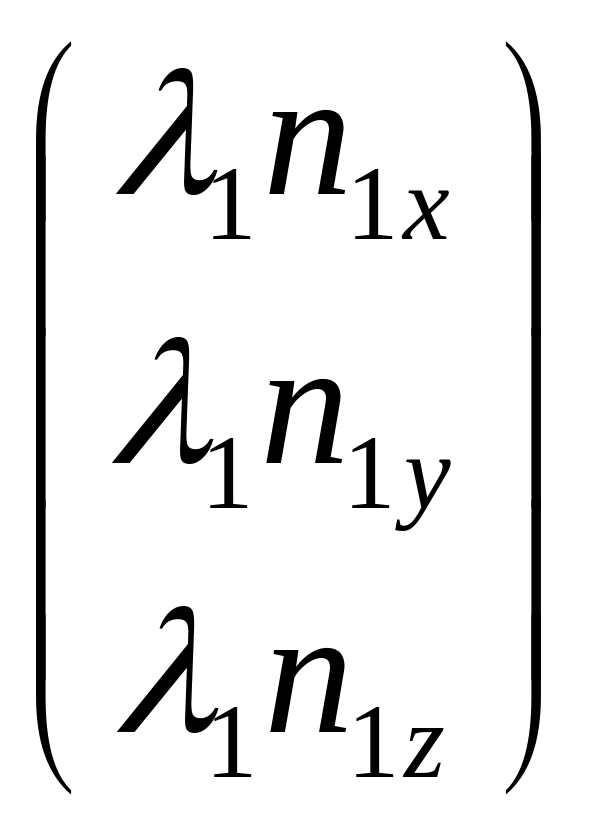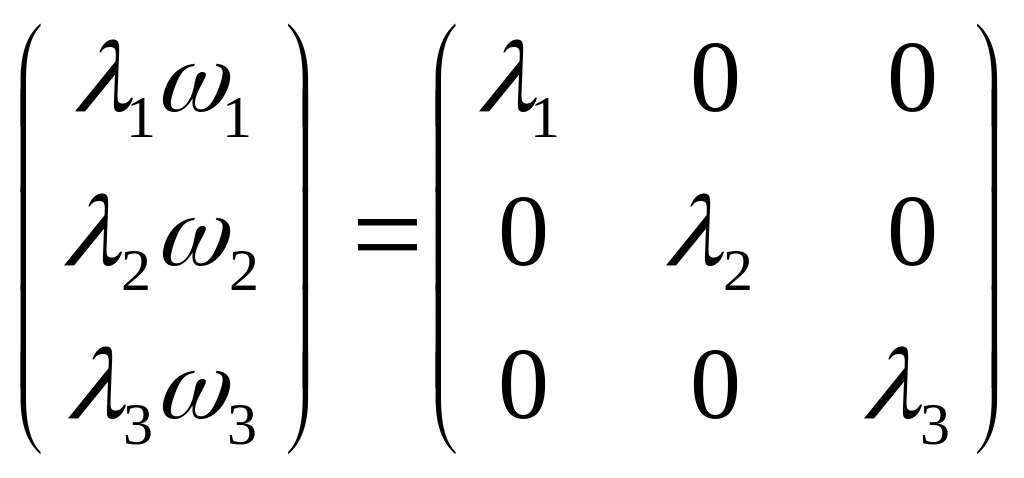Как найти момент силы цилиндра - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Самое лучшее определение вращательного момента – это тенденция силы вращать предмет вокруг оси, точки опоры или точки вращения. Вращательный момент можно рассчитать с помощью силы и плеча момента (перпендикулярное расстояние от оси до линии действия силы), или используя момент инерции и угловое ускорение.

1
Определите силы, действующие на тело и соответствующие им моменты. Если сила не перпендикулярна рассматриваемому плечу момента (т.е. она действует под углом), то вам может понадобиться найти ее составляющие с использованием тригонометрических функций, таких как синус или косинус.
- Рассматриваемая составляющая силы будет зависеть от эквивалента перпендикулярной силы.
- Представьте себе горизонтальный стержень, к которому нужно приложить силу 10 Н под углом 30° над горизонтальной плоскостью, чтобы вращать его вокруг центра.
- Поскольку вам нужно использовать силу, не перпендикулярную плечу момента, то для вращения стержня вам необходима вертикальная составляющая силы.
- Следовательно, нужно рассматривать y-составляющую, или использовать F = 10sin30° Н.
2
Воспользуйтесь уравнением момента, τ = Fr, и просто замените переменные заданными или полученными данными.
- Простой пример: Представьте себе ребенка массой 30 кг, сидящего на одном конце качели-доски. Длина одной стороны качели составляет 1,5 м.
- Поскольку ось вращения качели находится в центре, вам не нужно умножать длину.
- Вам необходимо определить силу, прилагаемую ребенком, с помощью массы и ускорения.
- Поскольку дана масса, вам нужно умножить ее на ускорение свободного падения, g, равное 9,81 м/с². Следовательно:
- Теперь у вас есть все необходимые данные для использования уравнения момента:
3
Воспользуйтесь знаками (плюс или минус), чтобы показать направление момента. Если сила вращает тело по часовой стрелке, то момент отрицательный. Если же сила вращает тело против часовой стрелки, то момент положительный.
- В случае нескольких приложенных сил, просто сложите все моменты в теле.
- Поскольку каждая сила стремится вызвать различные направления вращения, важно использовать знак поворота для того, чтобы следить за направлением действия каждой силы.
- Например, к ободу колеса, имеющего диаметр 0,050 м, были приложены две силы, F₁= 10,0 Н, направленная по часовой стрелке, и F₂ = 9,0 Н, направленная против часовой стрелки.
- Поскольку данное тело – круг, фиксированная ось является его центром. Вам нужно разделить диаметр и получить радиус. Размер радиуса будет служить плечом момента. Следовательно, радиус равен 0,025 м.
- Для ясности мы можем решить отдельные уравнения для каждого из моментов, возникающих от соответствующей силы.
- Для силы 1 действие направлено по часовой стрелке, следовательно, создаваемый ею момент отрицательный:
- Для силы 2 действие направлено против часовой стрелки, следовательно, создаваемый ею момент положительный:
- Теперь мы можем сложить все моменты, чтобы получить результирующий вращательный момент:
Реклама

1
Чтобы начать решать задачу, разберитесь в том, как действует момент инерции тела. Момент инерции тела – это сопротивление тела вращательному движению. Момент инерции зависит как от массы, так и от характера ее распределения.
- Чтобы четко понимать это, представьте себе два цилиндра одинакового диаметра, но разной массы.
- Представьте себе, что вам нужно повернуть оба цилиндра вокруг их центральной оси.
- Очевидно, что цилиндр с большей массой будет сложнее повернуть, чем другой цилиндр, поскольку он “тяжелее”.
- А теперь представьте себе два цилиндра различных диаметров, но одинаковой массы. Чтобы выглядеть цилиндрическими и иметь разную массу, но в то же время иметь разные диаметры, форма, или распределение массы обоих цилиндров должна отличаться.
- Цилиндр с большим диаметром будет выглядеть как плоская закругленная пластина, тогда как меньший цилиндр будет выглядеть как цельная трубка из ткани.
- Цилиндр с большим диаметром будет сложнее вращать, поскольку вам нужно приложить большую силу, чтобы преодолеть более длинное плечо момента.
2
Выберите уравнение, которое вы будете использовать для расчета момента инерции. Есть несколько уравнений, которые можно использовать для этого.
- Первое уравнение – самое простое: суммирование масс и плечей моментов всех частиц.
- Это уравнение используется для материальных точек, или частиц. Идеальная частица – это тело, имеющее массу, но не занимающее пространства.
- Другими словами, единственной значимой характеристикой этого тела является масса; вам не нужно знать его размер, форму или строение.
- Идея материальной частицы широко используется в физике с целью упрощения расчетов и использования идеальных и теоретических схем.
- Теперь представьте себе объект вроде полого цилиндра или сплошной равномерной сферы. Эти предметы имеют четкую и определенную форму, размер и строение.
- Следовательно, вы не можете рассматривать их как материальную точку.
- К счастью, можно использовать формулы, применимые к некоторым распространенным объектам:
3
Найдите момент инерции. Чтобы начать рассчитывать вращательный момент, нужно найти момент инерции. Воспользуйтесь следующим примером как руководством:
- Два небольших “груза” массой 5,0 кг и 7,0 кг установлены на расстоянии 4,0 м друг от друга на легком стержне (массой которого можно пренебречь). Ось вращения находится в середине стержня. Стержень раскручивается из состояния покоя до угловой скорости 30,0 рад/с за 3,00 с. Рассчитайте производимый вращательный момент.
- Поскольку ось вращения находится в середине стержня, то плечо момента обоих грузов равно половине его длины, т.е. 2,0 м.
- Поскольку форма, размер и строение “грузов” не оговаривается, мы можем предположить, что грузы являются материальными частицами.
- Момент инерции можно вычислить следующим образом:
4
Найдите угловое ускорение, α. Для расчета углового ускорения можно воспользоваться формулой α= at/r.
- Первая формула, α= at/r, может использоваться в том случае, если дано тангенциальное ускорение и радиус.
- Тангенциальное ускорение – это ускорение, направленное по касательной к направлению движения.
- Представьте себе объект, двигающийся по криволинейному пути. Тангенциальное ускорение – это попросту его линейное ускорение на любой из точек всего пути.
- В случае второй формулы, легче всего проиллюстрировать ее, связав с понятиями из кинематики: смещением, линейной скоростью и линейным ускорением.
- Смещение – это расстояние, пройденное объектом (единица СИ – метры, м); линейная скорость – это показатель изменения смещения за единицу времени (единица СИ – м/с); линейное ускорение – это показатель изменения линейной скорости за единицу времени (единица СИ – м/с²).
- Теперь давайте рассмотрим аналоги этих величин при вращательном движении: угловое смещение, θ – угол поворота определенной точки или отрезка (единица СИ – рад); угловая скорость, ω – изменение углового смещения за единицу времени (единица СИ – рад/с); и угловое ускорение, α – изменение угловой скорости за единицу времени (единица СИ – рад/с²).
- Возвращаясь к нашему примеру – нам были даны данные для углового момента и время. Поскольку вращение начиналось из состояния покоя, то начальная угловая скорость равна 0. Мы можем воспользоваться уравнением, чтобы найти:
5
Воспользуйтесь уравнением, τ = Iα, чтобы найти вращательный момент. Просто замените переменные ответами, полученными на предыдущих шагах.
- Вы можете заметить, что единица «рад» не подходит к нашим единицам измерения, поскольку считается безразмерной величиной.
- Это значит, что вы можете пренебречь ею и продолжить ваши расчеты.
- Для анализа единиц измерения мы можем выразить угловое ускорение в с^-2.
Реклама

Советы

В первом методе, если тело является кругом и ось его вращения находится в центре, то рассчитывать составляющие силы не нужно (при условии, что сила не приложена под наклоном), поскольку сила лежит на касательной к окружности, т.е. перпендикулярно плечу момента.
Если вам сложно представить, как происходит вращение, то возьмите ручку и попробуйте воссоздать задачу. Для более точного воспроизведения не забудьте скопировать положение оси вращения и направление приложенной силы.

Об этой статье

Эту страницу просматривали 23 928 раз.

Была ли эта статья полезной?

Источник

Определение требуемого крутящего момента в системе с вращающимся цилиндром

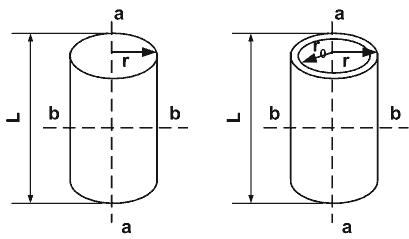
Система состоит из вертикально закрепленного на валу двигателя цилиндра массой m и моментом инерции J. Момент трения в подшипниках М тр . Определить величину вращающего момента М, который нужно приложить к цилиндрй, чтобы его угловое ускорение было равно ε.

Используемые обозначения:

r — радиус цилиндра (наружный)
r₀ — радиус цилиндра (внутренний)
L — длина
m — масса цилиндра
J — момент инерции цилиндра
J_дв — момент инерции двигателя
ω — угловая скорость

Для определения крутящего момента в системе с вращающимся цилиндром, необходимо знать момент инерции цилиндра:

Сплошной цилиндр, относительно оси a: J = 1/2 m * r².
Полый цилиндр, относительно оси a: J = 1/2 * m * (r²+r₀²)

Кинетическая энергия системы:

E=1/2(J+J_дв)ω²

Производная от кинетической энергии по времени:

dE/dt = (J+J_дв) ω ε

Мощности внешних сил в системе:

мощность момента трения: P_тр=M_трω
мощность крутящего момента: P_M=Mω
сумма мощностей всех сил: ∑P_i=Mω — M_трω

Производная кинетической энергии по времени определяется мощностями внешних сил:

dE/dt=∑P_i или
(J+J_дв) ω ε = Mω — M_трω

Величина вращающего момента M:

M=(J+J_дв) ε + M_тр

Источник

Момент сил трения качения

Определим для подвижного цилиндра
момент, тормозящий вращательное движение
тела. Рассматривая данный момент
относительно оси вращающегося колеса
(например, колеса автомобиля), находим,
что он равен произведению тормозного
усилия на оси на радиус колеса.
Относительно точки контакта движущегося
тела с землей момент будет равен
произведению внешней силы, уравновешивающей
силу трения, на радиус колеса (рис.
2):

С другой стороны, момент трения равен
моменту прижимающей силы
на
плечо, длина которого равна коэффициенту
трения качения f:

где

—
момент силы трения в [Н] · [м];
R — радиус тела качения;
P — внешняя сила;
F_t — сила трения качения;
f — коэффициент трения качения в
[м].

Коэффициент трения качения

Из выписанного выше уравнения следует,
что коэффициент трения качения может
быть определен как отношение момента
трения качения M_t к прижимной
силе N:

Графическая интерпретация коэффициента
трения качения f дана на рис. 3
и 4.

Коэффициент трения качения имеет
следующие физические интерпретации:

Если тело находится в покое и внешняя
сила отсутствует, то реакция опоры
лежит на той же линии, что и прижимающая
сила. Когда тело катится, то из условия
равновесия следует, что нормальная
составляющая реакции опоры параллельна
и противонаправлена прижимающей силе,
но не лежит с ней на одной линии.
Коэффициент трения качения равен
расстоянию между прямыми, вдоль которых
действуют прижимающая сила и нормальная
составляющая реакции опоры (рис. 4).

Движение катящегося тела без
проскальзывания можно рассматривать
как поворот вокруг мгновенной оси
вращения (на рис. 4 — точка
приложения вектора
),
которая для абсолютно твёрдых тел
совпадает с основанием перпендикуляра,
опущенного из центра круга на опору.
Для случая реальных (деформирующихся
под нагрузкой) материалов мгновенный
центр вращения смещён в направлении
качения тела, а величина смещения равна
значению коэффициента трения качения.

Билет 16.

Система материальных точек. Внутренние
и внешние силы. Закон сохранения импульса
изолированной системы.

В любой системе частиц имеется одна
замечательная точка, называемая центром
масс, которая обладает рядом интересных
и важных свойств. Ее положение относительно
начала данной системы координат
характеризуется радиус-вектором
,
определяемым как

(2.10)

где
–
масса и радиус-вектор
-й
частицы,
–
масса всей системы,
–
полное число частиц в системе. Если
взять производную по времени от обеих
частей уравнения и умножить обе части
на
,
то получится:

Или

где
–
скорость движения центра масс системы.
Таким образом, импульс системы материальных
точек равен произведению массы системы
на скорость ее центра масс:

(2.11)

Отсюда следует, что центр масс системы
материальных точек движется как
материальная точка, масса которой равна
суммарной массе всей системы, а действующая
сила – геометрической сумме всех внешних
сил, действующих на все точки системы. Этот
результат называется теоремой о движении
центра масс системы материальных точек.
Уравнение (2.11) по форме совпадает с
основным уравнением динамики материальной
точки и является его обобщением на
систему материальных точек: ускорение
системы как целого прямо пропорционально
результирующей всех внешних сил и
обратно пропорционально суммарной
массе системы.

Если система замкнута, то
и
уравнение (2.11) переходит в
,
следовательно,
.
Таким образом, центр масс замкнутой
системы движется прямолинейно и
равномерно или покоится.

Внутренние силы – это силы взаимодействия
между частицами системы тел.

Внешние силы – это силы, обусловленные
действием других тел, не входящих в
систему.

По способу приложения они могут быть
сосредоточенными и распределенными.
Сосредоточенные внешние силы действуют
на тело через очень маленькие площадки
и с достаточной степенью точности могут
считаться приложенными в точке. По
характеру действия внешние силы делятся
на постоянные и переменные.

Импульс системы может изменяться под
действием только внешних сил. Импульс
замкнутой системы частиц остается
постоянным. Закон сохранения импульса
изолированной системы:

Изолированная система – система,
состоящая из некоторого количества
тел, изолированных от всех остальных
тел и образующих механическую систему,
т.е. на эти тела не действуют внешние
силы, и сами эти тела взаимодействуют
друг с другом.

При этом импульсы отдельных частиц или
частей замкнутой системы могут меняться
со временем. Однако эти изменения всегда
происходят так, что приращение импульса
одной части системы равно убыли импульса
оставшейся части системы.

Внутренние силы – силы, с которыми
взаимодействуют тела, составляющие
механическую систему.

— сила, действующая со стороны тела

на

— антисимметричная матрица

Импульс изолированной системы сохраняется.
Импульсы системы тела – постоянны, если
внешние силы отсутствуют.

Билет 17.

Работа силы. Связь работы и энергии.
Мощность. Закон сохранения механической
энергии. Превращение энергии из одного
вида в другой. Примеры. Кинетическая
энергия поступательного движения.
Потенциальная энергия упругого
деформированного тела.

Работа силы.

Мощность
— величина, характеризующая скорость
совершения работы, называется. Мощность
численно равна отношению
к
промежутку времени
за
который она совершается.

или
в общем случае

Подставляя
значение
получим

Частный случай мощности при вращательном
движении:

M — момент силы,
—
угловая скорость, n — частота вращения
(число оборотов в минуту, об/мин).

Если тела, составляющие замкнутую
механическую систему, взаимодействуют
между собой только посредством сил
тяготения и упругости, то работа этих
сил равна изменению потенциальной
энергии тел, взятому с
противоположным знаком:

A = –(E_р2 – E_р1).

По теореме о кинетической энергии эта
работа равна изменению кинетической
энергии тел:

Следовательно

или

E_k1 + E_p1 = E_k2 + E_p2.

Сумма кинетической и потенциальной
энергии тел, составляющих замкнутую
систему и взаимодействующих между собой
посредством сил тяготения и сил упругости,
остается неизменной.

Это утверждение выражает закон
сохранения энергии в механических
процессах. Он является следствием
законов Ньютона. Сумму E = E_k + E_p называют полной
механической энергией. Закон сохранения
механической энергии выполняется только
тогда, когда тела в замкнутой системе
взаимодействуют между собой консервативными
силами, то есть силами, для которых можно
ввести понятие потенциальной энергии.

Рассмотрим
случай, когда материальная точка движется
из точки 1 в точку 2 под действием
приложенных к ней сил (рис.4.4.)

Причем
силы, действующие на материальную точку,
могут иметь разную природу, т.е. могут
быть консервативными и неконсервативными.
Уравнение движения в этом случае
запишется в виде

(4.6)

где

Перепишем
(4.6) в виде

(4.7)

Умножим
скалярно уравнение (4.7) на
и
проинтегрируем от точки1 до точки 2,
получим:

(4.8)

Учитываем
то, что
,
и интеграл в правой части выражения
(4.8) представляет собой работу всех сил,
на участке 1-2, можно записать:

(4.9)

Величина

(4.10)

называется
кинетической энергией материальной
точки. Таким образом, кинетическая
энергия материальной точки – это
энергия, которой обладает эта точка
вследствие своего движения.

Из
полученного выражения (4.9) следует, что
работа всех сил, действующих на
материальную точку на участке траектории
1-2 равна изменению ее кинетической
энергии на этом участке.

Физическая величина, равная половине
произведения коэффициента жесткости
на квадрат абсолютной деформации,
называется потенциальной энергией
упруго деформированного тела:

Билет 18.

Потенциальная энергия в однородном
поле силы тяжести.

Потенциальная
энергия — это энергия, обусловленная
взаимным расположением тел и характером
их взаимодействия. При соответствующих
условиях возможно изменение потенциальной
энергии, за счет чего совершается
работа. Для поднятия тела массой m на
высоту
необходимо
совершить работу против сил тяготения
Р:

знак
минус перед интегралом, т.к. сила Р
направлена в сторону противоположную
изменению h.

Проинтегрируем
это выражение:

Эта
энергия пойдет на увеличение энергии
замкнутой системы тело — Земля т.е.
численно равна

Считая
поверхности Земли
,
получим

Эта
энергия
системы
тело — Земля и является потенциальной
энергией тела, поднятого на высоту h:

Билет 19.

Абсолютно
упругий и абсолютно неупругий удары
(столкновения) Превращение энергии в
процессе столкновения. Законы сохранения
импульса и энергии. Связь между скоростями
соударяющихся тел до и после удара.
Убыль механической энергии в неупругом
ударе.

Ударом (или столкновением)
принято называть кратковременное
взаимодействие тел, в результате которого
их скорости испытывают значительные
изменения

Абсолютно неупругим ударом называют
такое ударное взаимодействие, при
котором тела соединяются (слипаются)
друг с другом и движутся дальше как одно
тело.

При абсолютно неупругом ударе механическая
энергия не сохраняется. Она частично
или полностью переходит во внутреннюю
энергию тел (нагревание).

Примером абсолютно неупругого удара
может служить попадание пули (или
снаряда) в баллистический маятник.
Маятник представляет собой ящик с песком
массой M, подвешенный на веревках.
Пуля массой m, летящая горизонтально
со скоростью
попадает
в ящик и застревает в нем. По отклонению
маятника можно определить скорость
пули.

Обозначим скорость ящика с застрявшей
в нем пулей через
.Тогда
по закону сохранения импульса

При застревании пули в песке произошла
потеря механической энергии:

Отношение M / (M + m) – доля
кинетической энергии пули, перешедшая
во внутреннюю энергию системы:

Эта формула применима не только к
баллистическому маятнику, но и к любому
неупругому соударению двух тел с разными
массами.

При m << M
почти
вся кинетическая энергия пули переходит
во внутреннюю энергию. При m = M
–
во внутреннюю энергию переходит половина
первоначальной кинетической энергии.
Наконец, при неупругом соударении
движущегося тела большой массы с
неподвижным телом малой массы (m >> М)
отношение

Дальнейшее движение маятника можно
рассчитать с помощью закона сохранения
механической энергии:

где h – максимальная высота подъема
маятника. Из этих соотношений следует:

Абсолютно упругим ударом называется
столкновение, при котором сохраняется
механическая энергия системы тел.

Во многих случаях столкновения атомов,
молекул и элементарных частиц подчиняются
законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с
законом сохранения импульса выполняется
закон сохранения механической энергии.

Простым примером абсолютно упругого
столкновения может быть центральный
удар двух бильярдных шаров, один из
которых до столкновения находился в
состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют
соударение, при котором скорости шаров
до и после удара направлены по линии
центров.

В общем случае массы m₁ и m₂ соударяющихся
шаров могут быть неодинаковыми. По
закону сохранения механической энергии

Здесь υ₁ – скорость первого
шара до столкновения, скорость второго
шара υ₂ = 0, u₁ и u₂ –
скорости шаров после столкновения.
Закон сохранения импульса для проекций
скоростей на координатную ось, направленную
по скорости движения первого шара до
удара, записывается в виде:

m₁υ₁ = m₁u₁ + m₂u₂.

Мы получили систему из двух уравнений.
Эту систему можно решить и найти
неизвестные скорости u₁ и u₂ шаров
после столкновения:

В частном случае, когда оба шара имеют
одинаковые массы (m₁ = m₂),
первый шар после соударения останавливается
(u₁ = 0), а второй движется со
скоростью u₂ = υ₁,
т. е. шары обмениваются скоростями
(и, следовательно, импульсами).

Если бы до соударения второй шар также
имел ненулевую скорость (υ₂ ≠ 0),
то эту задачу можно было бы легко свести
к предыдущей с помощью перехода в новую
систему отсчета, которая движется
равномерно и прямолинейно со
скоростьюυ₂ относительно
«неподвижной» системы. В этой системе
второй шар до соударения покоится, а
первый по закону сложения скоростей
имеет скорость υ₁‘ = υ₁ – υ₂.
Определив по приведенным выше формулам
скорости u₁ и u₂ шаров
после соударения в новой системе, нужно
сделать обратный переход к «неподвижной»
системе.

Таким образом, пользуясь законами
сохранения механической энергии и
импульса, можно определить скорости
шаров после столкновения, если известны
их скорости до столкновения.

Центральный (лобовой) удар очень редко
реализуется на практике, особенно если
речь идет о столкновениях атомов или
молекул. При нецентральном упругом
соударении скорости частиц (шаров) до
и после столкновения не направлены по
одной прямой.

Частным случаем нецентрального упругого
удара может служить соударение двух
бильярдных шаров одинаковой массы, один
из которых до соударения был неподвижен,
а скорость второго была направлена не
по линии центров шаров (рис. 1.21.3).

После нецентрального соударения
шары разлетаются под некоторым углом
друг к другу. Для определения
скоростей
и
после
удара нужно знать положение линии
центров в момент удара или прицельное
расстояние d (рис. 1.21.3), т. е.
расстояние между двумя линиями,
проведенными через центры шаров
параллельно вектору скорости
налетающего
шара. Если массы шаров одинаковы, то
векторы скоростей
и
шаров
после упругого соударения всегда
направлены перпендикулярно друг к
другу. Это легко показать, применяя
законы сохранения импульса и энергии.
При m₁ = m₂ = m эти
законы принимают вид:

Первое из этих равенств означает, что
векторы скоростей
,
и
образуют
треугольник (диаграмма импульсов), а
второе – что для этого треугольника
справедлива теорема Пифагора, т. е.
он прямоугольный. Угол между
катетами
и
равен 90°.

Билет 20.

Понятие абсолютно твердого тела.
Поступательное, вращательное и
плоско-параллельное движение твердого
тела. Связь между угловой и линейной
скоростями твердого тела.

Твердое тело (абсолютно твердое тело)
– это тело, которое ни при каких условиях
не может деформироваться; в абсолютно
твердом теле при всех условиях расстояние
между точками остается постоянным.

Поступательное движение твердого тела
– движение, при котором линия, соединяющая
любые две точки тела, сохраняет неизменное
направление в пространстве. При
поступательном движении любая линия
переносится параллельно самой себе,
т.е. смещение всех точек тела одинаково.
Поэтому при поступательном движении
все точки твердого тела обладают
одинаковыми линейными скоростями и
одинаковыми линейными ускорениями.

Вращательное движение – движение, при
котором траекторией всех точек являются
концентрические окружности с центрами
на одной прямой, называемой осью вращения.
Концентрические окружности – окружности,
у которых один центр.При вращательно
движении все точки данного тела обладают
одинаковыми угловыми скоростями и
одинаковыми угловыми ускорениями.

Линейные скорости вращающегося тела
одинаковы: чем дальше от оси вращения
отстоит точка, тем большей линейной
скоростью она обладает.

Плоскопараллельное движение – движение,
при котором любая точка твердого тела
во время движения остается в одной из
параллельных плоскостей.

Связь между линейной и угловой скоростями:

Билет 21.

Центр инерции твердого тела. Связь
координат и масс твердого тела в системе
координат, связанной с центром масс
(лемма о центре масс). Координаты центра
инерции. Закон движение центра инерции
твердого тела.

Если укрепить тело в центре тяжести, то
оно будет находиться в равновесии при
любом положении тела, т.е. сумма моментов
сил тяжести всех частиц тела относительно
любой горизонтальной оси, проходящей
через центр тяжести, будет равна нулю.

— лемма о центре масс

Если повернуть тело относительное оси

на

по
часовой стрелке, то ось

займет положение

,
и плечом силы тяжести относительно

будет являться

,
т.е

— саму произведения центра масс тела на
его радиус-вектор.

,
(

— скорость движения системы отсчета
относительно другой.)

а)

(масса
всей системы на скорость центра масс)

б)

ex – external – внешний

in – internal – внутренний

Центр инерции твердого тела движется
так, как если бы к нему были приложены
все внешние силы и масса, всего тела
была бы сосредоточена в центре масс.

Билет 22.

Момент силы. Закон динамики вращения
тела вокруг неподвижной оси (уравнение
вращательного движения). Момент инерции.

— уравнение вращательного движения

— момент инерции

Момент инерции зависит не только от
величины массы тела, но и от распределения
масс относительно оси.

Уравнение вращательного движения
является аналогом II-го
закона Ньютона. Что бы вызвать
поступательное движение точки, нужно
приложить силу; чтобы получить вращательное
движение тела, необходимо приложить
момент силы. Так же как сила вызывает
линейное ускорение, так и момент силы
вызывает появление углового ускорения.
Коэффициентами в этих уравнениях
является масса и момент инерции. Значит,
масса является мерой инерции для
поступательного движения, а момент
инерции является мерой инерции для
вращательного движения.

Билет 23.

Момент импульса. Уравнение моментов
(относительно оси). Закон сохранения
момента импульса.

— момент импульса точки относительно
оси

— момент импульса тела относительно оси

— уравнение моментов (относительно оси)

Если

Закон сохранения момента импульса:

Момент импульса твердого тела остается
постоянным, если суммарный момент
внешних сил равен нулю.

Билет 24.

Момент импульса и момент силы
относительно точки. Уравнение моментов
(относительно точки).

Связь моментов относительно точки и
моментов относительно оси:

Момент силы, относительно оси есть
проекция момента силы относительно
точки на эту ось; при этом полюс должен
лежать на оси вращения. Такая же связь
существует между моментом относительно
точки и моментом относительно оси.

Получим уравнение моментов относительно
точки в случае плоского движения.

на

слева

{левая часть}=

— уравнение моментов относительно точки.

Билет 25.

Кинетическая энергия вращающегося
тела. Работа по повороту вращающегося
тела.

Кинетическая энергия тела, движущегося
произвольным образом, равна сумме
кинетических энергий всех n материальных
точек па которые это тело можно разбить:
.
Если тело вращается вокруг неподвижной
оси с угловой скоростью
, то
линейная скорость i-ой точки равна
,
где
,
— расстояние от этой точки до оси вращения.
Следовательно.

,
где
—
момент инерции тела относительно оси
вращения. В общем случае движение
твердого тела можно представить в виде
суммы двух движений — поступательного
со скоростью, равной скорости
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду

,
где
—
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.

Работа по повороту твердого тела.

Рассмотрим действие внешней силы
,
приложенной к точке массой
.
За время
элементарная
масса
проходит
путь
Работа
силы
на
этом пути определяется проекцией силы
на направление перемещения, которая
очевидно, равна тангенциальной
составляющей
силы.

Но
равна
модулю момента
силы
относительно
оси вращения. Работа
,
и будет положительна, если
имеет
такое же направление, как и
отрицательное,
если направление векторов
и
противоположны.
С учетом, что

Работа всех сил, приложенных к телу

Полная работа

— дуга

Билет 26.

Аналогия между поступательным движением
материальной точки и вращательным
движением твердого тела.

Поступательное относительно точки	Вращательное движение твердого тела
S,	-угол
2., ,
3.	-от-но точки, -от-но оси
4.
5.m
6.	-точки от-но точки, F-тела от-но оси. — точки от-но оси
7.
8.
9.
10.

Билет 27.

Момент инерции. Вычисление моментов
инерции тел ( на примере моментов инерции
цилиндра, кольца, тонкого кольца, стержня
и шара)

Чтобы найти момент инерции тела, надо
просуммировать момент инерции всех
материальных точек, составляющих данное
тело

В
общем случае, если тело сплошное, оно
представляет собой совокупность
множества точек с бесконечно малыми
массами
,
и моменты инерции тела определяется
интегралом

где
—
расстояние от элемента
до
оси вращения.

Распределение массы в пределах тела
можно охарактеризовать с помощью

плотности

где
m — масса однородного тела, V — его объем.
Для тела с неравномерно распределенной
массой это выражение дает среднюю
плотность.

.
Плотность в данной точке в этом случае
определяется следующим образом

и тогда

Пределы интегрирования зависят от формы
и размеров тела Интегрирование уравнения
(5.5) наиболее просто осуществить для тех
случаев, когда ось вращения проходит
через центр тяжести тела. Рассмотрим
результаты интегрирования для простейших
(геометрически правильных) форм твердого
тела, масса которого равномерно
распределена по объему.

Момент инерции полого цилиндра с тонкими
стенками, радиуса R.

Для полого цилиндра с тонкими стенками

Сплошной однородный диск. Ось вращения
является осью диска радиуса
.
и массы m с плотностью
Высота
диска h. Внутри диска на расстоянии
вырежем пустотелый цилиндр с толщиной
стенки
и
массой
.
Для него

Весь диск можно разбить на бесконечное
множество цилиндров, а затем просуммировать:

Момент инерции шара относительно оси,
проходящей через центр тяжести.

Момент инерции стержня длиной L и
массой m относительно оси, проходящей:

а) через центр стержня —

б) через начало стержня —

Билет 28.

Момент инерции. Теорема Гюйгенса-Штейнера.

Теорема Гюйгенса-Штейнера. Момент
инерции тела относительно произвольной
оси равен сумме момента инерции тела
относительно оси, проходящей через
центр масс и параллельной данной оси,
плюс произведение массы тела на квадрат
расстояния между осями:

—
известный момент инерции относительно
известной оси,

—
искомый момент инерции,

—
масса тела,

—
расстояние между осями (известной и
относительно которой необходимо найти
момент инерции)

Чтобы найти момент инерции тела, надо
просуммировать момент инерции всех
материальных точек, составляющих данное
тело

В
общем случае, если тело сплошное, оно
представляет собой совокупность
множества точек с бесконечно малыми
массами
,
и моменты инерции тела определяется
интегралом

где
—
расстояние от элемента
до
оси вращения.

Распределение массы в пределах тела
можно охарактеризовать с помощью

плотности

.
Плотность в данной точке в этом случае
определяется следующим образом

и тогда

Пределы интегрирования зависят от формы
и размеров тела Интегрирование уравнения
наиболее просто осуществить для тех
случаев, когда ось вращения проходит
через центр тяжести тела.

Билет 29.

Момент импульса относительно точки.
Связь между импульсом относительно
точки и угловой скорость вращения
твердого тела. Тензор инерции.

Моментом импульса материальной точки
относительно неподвижной точки О
называется физическая величина,
определяемая векторным произведением:

∆
=
=

Тензор инерции

Тензором называют упорядоченную
совокупность чисел, называемых
компонентами тензора и зависящих от
выбора системы координат.

Размерность тензора называется
рангом.(количество индексов у
компонентов)оэтому вектор является
тензором первого ранга, а матрица
второго.

симметричная

Покажем, что элементами главной диагонали
являются моменты инерции относительно
координатных осей.

расстояние
от А до осин

момент
инерции относительно О_z

Билет 30.

Теорема о главных осях. Диагонализация
тензора инерции. Главные моменты инерции
твердого тела.

Для любого тела и любой точки О существует
3 взаимно перпендикулярных направления,
при вращении вокруг которых вектор
момента импульса сонаправлен с вектором
угловой скорости.

Такие направления называются главными
осями и для них

, λ-скаляр

Система линейных однородных уравнений

=0






=
=

Расписывая систему уравнений

и домнажая уравнение этой системы на
компоненты вектора

, после сложения получим:



Диагонализации тензора инерции.

Базис системы координат:

—
единичные вектора вдоль главных
направлений



-главные
моменты инерции

Если

,
то имеется бесконечное количество
главных осей, лежащих в плоскости
нормальной к

.

Билет 31.

Связь момента инерции твердого тела
относительно произвольной оси, проходящей
через центр масс, с тензором инерции
относительно системы координат, связанных
с центром масс.

—
момент импульса относительно центра
масс

-проекция

на ось
(момент
импульса относительно оси)



Билет 32.

Гироскопы. Гироскоп под действием сил
(приближенная теория). Прецессия
гироскопа. Гироскопические силы.
Нутации.

Гироскопом называют любое быстро
вращающееся симметричное тело, ось
которого может менять свое направление
в пространстве.

При
закреплении в кардановом подвесе
гироскоп можно рассматривать как
симмитричное твердое тело, закрепленное
в центре масс. Ось гироскопа может занять
любое положение в пространстве.

Свойства гироскопа (2 основных):

Устойчивость положения оси гироскопа
относительно малых воздействий;
Безынертность воздействия
моментов внешних сил (момент силы
создает не ускорение, а скорость
вращения оси гироскопа).

,

,
если N мал, то

Свободным называется гироскоп, к которому
приложен внешний момент сил. Свободный
гироскоп не изменят направления своей
оси, если ось вращения совпадает с
геометрической осью гироскопа (т.е. не
прецессирует).

Прецессией называется вращение оси
гироскопа в горизонтальной плоскости
под действием момента внешней силы.

Нутацией называется вращающая ось
гироскопа в вертикальной плоскости
(«нырки» при вращении).

Гироскопические
силы — силы, зависящие от
скоростей и обладающие тем свойством,
что сумма их работ (или мощностей) при
любом перемещении системы, на которую
действуют эти силы, равна нулю. Если

—
гироскопические силы, то для них

или

где
—
радиусы-векторы точек приложения
сил,
—
скорости этих точек. Хотя гироскопические
силы, как зависящие от скоростей, не
являются потенциальными, но на систему,
на которую кроме потенциальных сил
действуют ещё и гироскопические, тоже
распространяется закон сохранения
механической энергии.

Примерами гироскопических сил
являются сила
Кориолиса

материальной
точки с массой m,
движущейся со скоростью
по
отношению к подвижной (неинерциальной)
системе отсчёта (
—
угловая скорость этой системы отсчёта),
и сила Лоренца
,
действующая на заряженную частицу
с зарядом е,
движущуюся со скоростью v в
магнитном поле (B –
магнитная индукция, с — скорость
света). Каждая из этих сил
направлена перпендикулярно скорости,
поэтому их работа или мощность при любом
перемещении точки (частицы) равна нулю.

,

,

Билет 33.

Законы Кеплера. Закон всемирного
тяготения. Опыт Кавендиша.

Первый закон Кеплера (закон эллипсов)

Каждая планета Солнечной
системы обращается
по эллипсу,
в одном из фокусов которого находится Солнце.

Форма эллипса и степень его сходства с
окружностью характеризуется отношением
,
где c — расстояние от центра эллипса
до его фокуса (половина межфокусного
расстояния), a — большая
полуось.
Величина e называется эксцентриситетом эллипса.
При c = 0 и e = 0 эллипс
превращается в окружность.

Второй закон Кеплера (закон площадей)

Каждая планета движется в плоскости,
проходящей через центр Солнца, причём
за равные промежутки времени радиус-вектор,
соединяющий Солнце и планету, описывает
равные площади. Применительное к нашей
Солнечной системе, с этим законом связаны
два понятия: перигелий —
ближайшая к Солнцу точка орбиты,
и афелий —
наиболее удалённая точка орбиты. Таким
образом, из второго закона Кеплера
следует, что планета движется вокруг
Солнца неравномерно, имея в перигелии
большую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя
через перигелий, движется быстрее,
поэтому видимое перемещение Солнца
по эклиптике к
востоку также происходит быстрее, чем
в среднем за год. В начале июля Земля,
проходя афелий, движется медленнее,
поэтому и перемещение Солнца по эклиптике
замедляется. Закон площадей указывает,
что сила, управляющая орбитальным
движением планет, направлена к Солнцу.

Доказательство второго закона Кеплера. По
определению угловой
момент
точечной
частицы с массой m и
скоростью
записывается
в виде:

.где
—
радиус-вектор частицы а
—
импульс частицы. Площадь, заметаемая
радиус-вектором
за
время dt из геометрических соображений
равна
,
где θ представляет собой угол
между направлениями
и
.
По определению

В результате мы имеем
.Продифференцируем
обе части уравнения по времени
поскольку
векторное произведение параллельных
векторов равно нулю. Заметим, что F всегда
параллелен r, поскольку сила радиальная,
и p всегда параллелен v по
определению. Таким образом можно
утверждать, что
,
а следовательно и пропорциональная ей
скорость заметания площади
—
константа.

Квадраты периодов обращения планет
вокруг Солнца относятся как кубы больших
полуосей орбит
планет. Справедливо не только для
планет, но и для их спутников.

,
где T₁ и T₂ — периоды
обращения двух планет вокруг Солнца,
а a₁ и a₂ — длины
больших полуосей их орбит.

Ньютон установил,
что гравитационное
притяжение планеты
определенной массы зависит только от
расстояния до неё, а не от других свойств,
таких, как состав или температура. Он
показал также, что третий закон Кеплера
не совсем точен — в действительности
в него входит и масса планеты:
,
где M — масса Солнца, а m₁ и m₂ —
массы планет.

Поскольку движение и масса оказались
связаны, эту комбинацию гармонического
закона Кеплера и закона тяготения
Ньютона используют для определения
массы планет и спутников, если известны
их орбиты и орбитальные периоды.

Космическая
скорость (первая v₁, вторая v₂, третья v₃ и четвёртая v₄) —
это минимальная скорость, при которой
какое-либо тело в свободном движении с
поверхности небесного тела сможет:

v₁ —
стать спутником небесного
тела (то есть способность
вращаться по орбите вокруг НТ и не
падать на поверхность НТ).
v₂ —
преодолеть гравитационное
притяжение небесного
тела.
v₃ —
покинуть звёздную
систему, преодолев
притяжение звезды.
v₄ —
покинуть галактику.

Закон всемирного тяготения. Сила
гравитационного притяжения между двумя
материальными точками массы m₁ и m₂,
разделёнными расстоянием R,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния
между ними — то есть

Здесь G — гравитационная
постоянная, равная
м³/(кг
с²).

Опыт Кавендиша. Установка представляет
собой деревянное коромысло с прикреплёнными
к его концам небольшими свинцовыми
шарами диаметром 5 см и массой 775 г.
Оно подвешено на нити из посеребрённой
меди длиной 1 м. К шарам подносят шары
большего размера диаметром 20 см и
массой 49,5 кг, сделанные также из
свинца. В результате действия гравитационных
сил коромысло закручивается на некий
угол. Жёсткость нити была такой, что
коромысло делало одно колебание за 15
минут. Угол поворота коромысла определялся
с помощью луча света, пущенного на
зеркальце на коромысле, и отражённого
в микроскоп. Зная упругие свойства нити,
а также угол поворота коромысла, можно
вычислить гравитационную
постоянную. Для предотвращения
конвекционных потоков установка была
заключена в ветрозащитную камеру. Угол
отклонения измерялся при помощи
телескопа. Заподозрив в качестве причины
закручивания нити магнитное взаимодейстивие
железного стержня и свинцовых шаров,
Кавендиш заменил стержень медным,
получив те же результаты.
Г.
Кавендиш получил значение G=6,754×10⁻¹¹

Билет 10 . Кинетическая энергия вращающегося
тела. Работа по повороту твердого тела.

,
где
—
момент инерции тела относительно оси
вращения. В общем случае движение
твердого тела можно представить в виде
суммы двух движений — поступательного
со скоростью, равной скорости
центра
инерции тела, и вращения с угловой
скоростью
вокруг
мгновенной оси, проходящей через центр
инерции. При этом выражение для
кинетической энергии тела преобразуется
к виду

,
где
—
момент инерции тела относительно
мгновенной оси вращения, проходящей
через центр инерции.

Работа по повороту твердого тела.

Работа всех сил, приложенных к телу

Полная работа

Билет 34.

Гармонические колебания. Колебания
математического маятника и груза на
пружине. Уравнения колебаний и их
решения. Изменение смещения, скорости,
ускорения и энергии в процессе колебаний.

Функция

называется периодической, если для
любого

выполняется
соответствие

,
где t – период функции.

В периодическом явлении (процессе)
изменение какой-либо величины повторяется
в том же виде через определенное время,
называемым периодом колебаний.

Гармонические колебания представляют
собой периодический процесс, в котором
изменения наблюдаемой величины происходит
по закону синуса или косинуса.

,
где

— амплитуда (максимальное смещение);

— круговая (циклическая) частота

;

— начальная фаза;

— смещение из положения равновесия.

Математическим маятником называется
небольшое тело, подвешенное на нити,
при условии, что нить является невесомой
и нерастяжимой, а тело можно считать
материальной точкой.

—
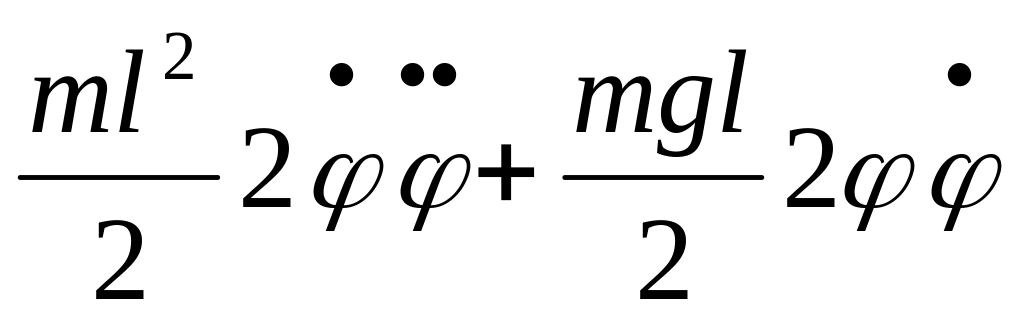
уравнение колебаний,

—
уравнение гармонического осциллятора

При уменьшении угла положение

приближается к положению оси

и поэтому, ввиду малости угла, проекции
возвращающей силы на эти направления
становятся одинаковы.

длина
дуги =

Билет 35.

Физический маятник. Уравнение колебаний
и его решение. Приведенная длина
физического маятника.

Физический маятник – достаточно тяжелое
тело, которое может совершать колебания
вокруг горизонта оси, проходящей выше
центра тяжести.

— возвращающий момент

Приведенной длинной физического маятника
называют длину математического маятника,
который совершает колебания с той же
частотой, что и физический.

— приведенная длина

Ц
ентр
качения физического маятника – точка,
расположенная на расстоянии приведенной
длины от точки подвеса до линии,
соединяющей точку подвеса и центр
тяжести.

— центр тяжести

Билет 36.

Физический маятник. Обратимость точки
подвеса и центра качаний.

Физическим маятником называется
достаточно тяжелое тело, которое может
совершать колебания вокруг горизонтальной
оси, проходящей выше центра тяжести.

Центром качаний физического маятника
называется точка, расположенная на
расстоянии приведенной длины от точки
подвеса по линии, соединяющей точку
подвеса и центр тяжести.

Теорема об обратимости точки подвеса
и центра качания.

Если ось вращения поместить в центр
качаний, то маятник будет совершать
колебания с той же частотой (т.е. новый
центр качаний будет совпадать со старой
точкой подвеса)

Докажем, что

(1)

(2)

(2)=>(1)

Билет 37.

Затухающие собственные колебания.
Уравнение колебаний и его решение.
Зависимость амплитуды колебаний от
времени. Условный период затухающих
колебаний. Коэффициент затухания и
логарифмический декремент затухания.

Собственными колебаниями называются
колебания системы, выведенной из
положения равновесия и предоставленной
самой себе.

Затухающими называются колебания, у
которых амплитуда уменьшается с течением
времени.

Пружинный маятник:

, h-коэф. силы трения

Решение:

-коэффициент
затухания

-время
релаксации, это время за которое амплитуда
колебаний уменьшается в е раз.

Декремент

логарифмический
декремент затухания

Билет 38.

Вынужденные колебания. Резонанс.
Амплитудно-частотная и фазо-частотная
характеристики. Резонансная частота

Вынужденными называются колебания,
которые происходят под действием внешней
периодической силы.

,
где

—
возвращающая сила,

—
сила трения,

—
периодическая сила

,
β=

—
коэффициент затухания

Следовательно, коэффициент
затухания β есть физическая
величина, обратная времени, в
течение которого амплитуда уменьшается
в е раз.

Время релаксации τ – время, в
течение которого амплитуда А уменьшается
в e раз.

Предположим, что возникающее под
действием силы установившиеся вынужденные
колебания системы также являются
гармоническими:
(7.22)
причем их циклическая частота равна
циклической частоте ω вынуждающей силы.

Явление резкого
возрастания амплитуды вынужденных
колебаний при приближении вынуждающей
частоты ω к частоте собственных колебаний
системы
называется
резонансом.

Для того, чтобы
полученное уравнение было справедливо
для всех времен, необходимо, чтобы
коэффициенты при

были тождественно равны 0.

—
резонансная частота. p обозначает
то значение циклической частоты ω
вынуждающей силы, при котором

С увеличением коэффициента затухания
ω явление резонанса проявляется все
слабее, и, наконец при
исчезает
совсем.

Резонансом называется резкое увеличение
амплитуды вынужденных колебаний при
приближении частоты вынуждающей силы
и частоте собственных колебаний системы.

—
вынуждающая сила.

Явление резонанса используется для
усиления колебаний, например,
электромагнитных. Однако при конструировании
различных машин и сооружений необходимо
учитывать даже самую небольшую
периодическую силу с тем, чтобы
предотвратить нежелательные последствия
резонанса.

X(t)=В cos
(Ѡt+ϕ)
ϕ-разность фаз между
колебаниями силы F и
смещением F(t)

При низких частотах колебания смещений
x(t) происходят
в фазе с колебаниями вынужденные силы,
при резонансе отстают на пи пополам.
При высоких частотах протекают в
противофазе с колебаниями вынужденные
силы.

Билет 39.

Колебания связанных систем. Собственная,
парциальная и нормальные частоты.
Синфазные и антифазные колебания.
Биения. Теоретический анализ биений.

Если между колебательными системами
имеется связь, через которую они
воздействуют друг на друга — связанная
система.

Системы с одной степенью свободы, на
которые можно расчленить связанную
систему, называются парциальными.
Частота парциальных колебаний будет
больше собственной частоты, т.к.
возвращающая к положению равновесия
сила состоит из двух слагаемых:
составляющая силы тяжести и упругой
силы деформированной пружины.

Биениями называются колебания с
амплитудой, меняющейся по периодическому
закону.

Амплитуда гармонических колебаний
постоянна, поэтому биения не являются
гармоническими колебаниями. Биения в
системе возникают при сложении 2-х
гармонических колебаний одинакового
направления, которые мало отличаются
друг от друга по частоте. Биения
возникают от того, что один из двух
сигналов постоянно отстаёт от другого
по фазе и
в те моменты, когда колебания происходят
синфазно, суммарный сигнал оказывается
усилен, а в те моменты, когда два сигнала
оказываются в противофазе, они взаимно
гасят друг друга. Эти моменты периодически
сменяют друг друга по мере того как
нарастает отставание. Биения звука можно
слышать при настройке струнного
музыкального инструмента по камертону.
Если частота струны незначительно
отличается от частоты камертона, то
слышно, что звук пульсирует — это и
есть биения. Струну нужно подтягивать
или ослаблять так, чтобы частота биений
уменьшалась. При совпадении высоты
звука с эталонным биения полностью
исчезают. Биения звука также можно
услышать при игре на музыкальных
инструментах, например пианино или
гитаре, когда различной высоты звуки
создают интервалы и многозвучия.
(аккорды).

Гармонические колебания, возникающие
в связанной системе, называются
нормальными колебаниями, а соответствующие
частоты называются нормальными частотами.
Система с двумя степенями свободы
обладает двумя начальными колебаниями:
синфазными и антифазными. Биения в
связанной системе возникают как результат
сложениями нормальных частот.

Частота синфазных колебаний Ѡ_С
равна частоте собственных колебаний
Ѡ₀ ,т.к. при синфазных колебаниях
связь не деформируется. Частота антифазных
колебаний Ѡ_А больше частоты
синфазных колебаний, т.к. пружина,
связывающая маятник, деформируется

Частота биений Ѡ_Б=Ѡ_А-Ѡ_С

Синфазность —
совпадение по фазе двух или нескольких
периодических колебаний.
Опираясь на более общее понятие
когерентности, С. можно определить как
частный случай когерентности, при
котором разность фаз
колебаний постоянна и
равна нулю [на рис. 1 см.синфазные гармонические
колебания, описываемые функциями
вида
где
A₁_,2 — амплитуды,
—
круговая (циклическая) частота, Т —
период колебаний,
—
начальная фаза; эти колебания синфазные,
если , где п = 0, 1, 2, …; на рис.
2- синфазные
колебания
взаимно перпендикулярных векторов
напряжённостей электрических и магнитных
полей].

Рис. 1.

Примеры синфазных колебаний: 1) колебания
всех точек стоячей
волны; они происходят с
различными отклонениями от нулевого
положения, но в одинаковой фазе (в то
время как в бегущей
волне, наоборот, колебания
всех точек происходят е одинаковыми
отклонениями, но в различных фазах);

Антифазные – это колебания маятников,
происходящие в противофазе с большей
из нормальных частот ω2.

Нормальные колебания
— собственные
(свободные) гармонические колебания
линейных систем с постоянными параметрами,
в которых отсутствуют как потери энергии,
так и приток ее извне. Каждое нормальное
колебание характеризуется определенным
значением частоты, с которой колеблются
все элементы системы, и формой —
распределением амплитуд и фаз. Число
степени свободы —
это совокупность независимых координат
перемещения и/или вращения, полностью
определяющая движение и/или положение
тела или системы тел нормальных
колебаний равно числу колебательных
степеней свободы системы.

Билет 40.

Преобразования Галилея. Принцип
относительности Галилея. Инварианты
преобразований Галилея. Специальный
принцип относительности. Постулаты
специальной теории относительности.
Преобразования Лоренца (без вывода).
Инварианты преобразований Лоренца.

Преобразования Галилея —
преобразования координат и времени при
переходе от одной инерциальной
системы отсчета (ИСО) к
другой.

Принцип относительности Галилея:

Во всех инерциальных системах отсчета
законы Ньютона имеют одинаковую форму;
инерциальные или галилеевы системы
равноправны с точки зрения ньютоновской
динамики.

—

преобразования Галилея

Инвариантами при некоторых
преобразованиях называются величины,
не меняющиеся при этих преобразованиях.

Инварианты преобразований Галилея.

Расстояние между двумя
точками;
Относительная скорость
(относительно друг друга) ;
Так как силы зависят от
относительного расположения тел или
от их относительных скоростей, то силы
являются инвариантами;
Поскольку, потенциальная
энергия зависит только от расстояния
между телами, то она инвариант;
Второй закон Ньютона
является инвариантом, сила и ускорение
являются инвариантами, поэтому масса
– инвариант.

Импульс и кинетическая
энергия не являются инвариантами.

Специальный принцип относительности:

Все инерциальные системы равноправны
(не только относительно ньютовской
динамики, а относительно все законов
природы, в частности законов
электромагнетизма)

Постулат о постоянстве
скорости света:

Скорость света в пустоте
не зависит от движения источника.

Преобразования Лоренца:

Билет 44.

Продольные и поперечные волны. Волновое
уравнение. Интерференция волн. Эффект
Доплера.

Продольными называются волны, в которых
частицы среды совершают колебания вдоль
направления распространения волны
(пример: звуковая волна)

Поперечными называются волны, в которых
частицы среды движутся поперек направления
распространения волны (например: волна
вдоль натянутой струны).

Волновой поверхностью (волновым фронтом)
называется поверхность равной фазой.

В зависимости от типа волнового фронта
различают сферические и плоские волны.

Пример сферической волны: звуковая
волна в однородной изотропной среде,
распространяющейся во всех направлениях
одинаково; волновым фронтом является
сфера с центром в источнике колебаний.

Пример плоской волны: волны,
распространяющиеся вдоль оси трубы от
колеблющегося поршня, волны сгущений
и раздражений; волновым фронтом является
плоскость, перпендикулярная оси трубы.

Волновое уравнение

1) Адиабатический процесс (Q=0)

Уравнение адиабаты

— коэффициент Пуассона, показатель
адиабаты

2)

,

,

3)

—
скорость света в среде

— равновесная плотность,

— изменение

Источник

Содержание книги

Предыдующая страница

§4. Основные законы динамики

4.6 Вращательное движение твердого тела. Момент силы.

Конечно, положение одной, даже «особой», точки далеко не полностью описывает движение всей рассматриваемой системы тел, но все-таки, лучше знать положение хотя бы одной точки, чем не знать ничего. Тем не менее, рассмотрим применение законов Ньютона к описанию вращения твердого тела вокруг фиксированной оси ^[1].

Начнем с простейшего случая: пусть материальная точка массы m прикреплена с помощью невесомого жесткого стержня длиной r к неподвижной оси OO’ (рис. 46). Материальная точка может двигаться вокруг оси, оставаясь от нее на постоянном расстоянии, следовательно, ее траектория будет являться окружностью с центром на оси вращения.

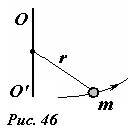
Безусловно, движение точки подчиняется уравнению второго закона Ньютона (~m vec a = vec F_0). Однако, непосредственное применение этого уравнения не оправдано: во-первых, точка обладает одной степенью свободы, поэтому в качестве единственной координаты удобно использовать угол поворота, а не две декартовые координаты; во-вторых, на рассматриваемую систему действуют силы реакции в оси вращения, а непосредственно на материальную точку – сила натяжения стержня. Нахождение этих сил представляет собой отдельную проблему, решение которой излишне для описания вращения. Поэтому имеет смысл получить на основании законов Ньютона специальное уравнение, непосредственно описывающее вращательное движение.

Пусть в некоторый момент времени на материальную точку действует некоторая сила (~vec F), лежащая в плоскости перпендикулярной оси вращения (рис. 47). При кинематическом описании криволинейного движения вектор полного ускорения (~vec a) удобно разложить на две составляющих: нормальную (~vec a_n), направленную к оси вращения, и тангенциальную (~vec a_{tau}) , направленную параллельно вектору скорости. Значение нормального ускорения для определения закона движения нам не нужно. Конечно, это ускорение также обусловлено действующими силами, одна из которых неизвестная сила натяжения стержня.

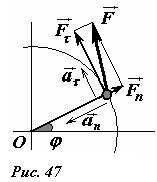
Запишем уравнение второго закона в проекции на тангенциальное направление:

(~m a_{tau} = F_{tau}) , (1)

заметим, что сила реакции стержня не входит в это уравнение, так как она направлена вдоль стержня и перпендикулярна выбранной проекции. Изменение угла поворота φ непосредственно определяется угловой скоростью (~omega = frac{Delta varphi}{Delta t}) , изменение которой в свою очередь описывается угловым ускорением (~varepsilon = frac{Delta omega}{Delta t}) . Угловое ускорение связано с тангенциальной составляющей ускорения соотношением a_τ = rε. Если подставить это выражение в уравнение (9), то получим уравнение, пригодное для определения углового ускорения. Удобно ввести новую физическую величину, определяющую взаимодействие тел при их повороте. Для этого умножим обе части уравнения (1) на r

(~m r^2 varepsilon = F_{tau} r) . (2)

и рассмотрим выражение в его правой части F_τr, имеющего смысл произведения тангенциальной составляющей силы, на расстояние от оси вращения до точки приложения силы. Это же произведение можно представить несколько иной форме (см. рис. 48)

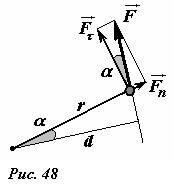
M = F_τr = Fr cos α = Fd, здесь d — расстояние от оси вращения до линии действия силы, которое также называют плечом силы. Эта физическая величина, произведение модуля силы на расстояние от линии действия силы до оси вращения (плечо силы) M = Fd называется моментом силы. Действие силы может приводить к вращению, как по часовой стрелке, так и против часовой стрелки. В соответствии с выбранным положительным направлением вращения следует определять и знак момента силы. Заметьте, что момент силы определяется той составляющей силы, которая перпендикулярна радиус-вектору точки приложения. Составляющая вектора силы, направленная вдоль отрезка, соединяющего точку приложения и ось вращения, не приводит к раскручиванию тела. Эта составляющая при закрепленной оси компенсируется силой реакции в оси, поэтому она не влияет на вращение тела.

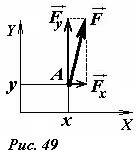
Запишем еще одно полезное выражения для момента силы. Пусть сила (~vec F) приложена к точке А, декартовые координаты которой равны x,y (рис. 49). Разложим силу (~vec F) на две составляющие (~vec F_x, vec F_y) , параллельные соответствующим осям координат. Момент силы (~vec F) относительно оси, проходящей через начало координат, очевидно равен сумме моментов составляющих (~vec F_x, vec F_y) , то есть M = xF_y — yF_x.

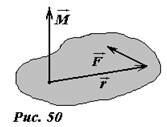
Аналогично, тому, как нами было введено понятие вектора угловой скорости, можно определить также и понятие вектора момента силы. Модуль этого вектора соответствует данному выше определению, направлен же он перпендикулярно плоскости, содержащей вектор силы и отрезок, соединяющий точку приложения силы с осью вращения. Вектор момента силы также может быть определен как векторное произведение радиус-вектора точки приложения силы на вектор силы

(~vec M = vec r times vec F) .

Заметим, что при смещении точки приложения силы вдоль линии ее действия момент силы не изменяется.

Обозначим произведение массы материальной точки на квадрат расстояния до оси вращения mr² = I (эта величина называется моментом инерции материальной точки относительно оси). С использованием этих обозначений уравнение (2) приобретает вид, формально совпадающий с уравнением второго закона Ньютона для поступательного движения

(~I varepsilon = M) . (3)

Это уравнение называется основным уравнением динамики вращательного движения. Итак, момент силы во вращательном движении играет такую же роль, как и сила в поступательном движении, именно он определяет изменение угловой скорости. Оказывается, (и это подтверждает наш повседневный опыт) влияние силы на скорость вращения определяет не только величина силы, но и точка его приложения. Момент инерции определяет инерционные свойства тела по отношению к вращению (говоря простым языком – показывает, легко ли раскрутить тело) — чем дальше от оси вращения находится материальная точка, тем труднее привести ее во вращение.

Уравнение (3) допускает обобщение на случай вращения произвольного тела. При вращении тела вокруг фиксированной оси угловые ускорения всех точек тела одинаковы. Поэтому, аналогично тому, как мы проделали при выводе уравнения Ньютона для поступательного движения тела, можно записать уравнения (3) для всех точек вращающегося тела и затем их просуммировать. В результате мы получим уравнение, внешне совпадающее с (3), в котором I — момент инерции всего тела, равный сумме моментов составляющих его материальных точек, M — сумма моментов внешних сил, действующих на тело.

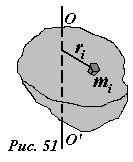
Покажем, каким образом вычисляется момент инерции тела. Важно подчеркнуть, момент инерции тела зависит не только от массы, формы и размеров тела, но и от положения и ориентации оси вращения. Формально процедура расчета сводится к разбиению тела на малые части, которые можно считать материальными точками (рис. 51), и суммированию моментов инерций этих материальных точек, которые равны произведению массы на квадрат расстояния до оси вращения

(~I = m_1 r^2_1 + m_2 r^2_2 + m_3 r^2_3 + ldots) .

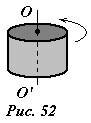
Для тел простой формы такие суммы давно подсчитаны, поэтому часто достаточно вспомнить (или найти в справочнике) соответствующую формулу для нужного момента инерции. В качестве примера: момент инерции кругового однородного цилиндра массы m и радиуса R для оси вращения совпадающей с осью цилиндра равен (~I = frac{1}{2} m R^2) .

Примечания

↑ В данном случае мы ограничиваемся рассмотрением вращения вокруг фиксированной оси, потому, что описание произвольного вращательного движения тела представляет собой сложную математическую проблему, далеко выходящую за рамки курса математики средней школы. Знания же других физических законов, кроме рассматриваемых нами, это описание не требует.

Следующая страница

Источник