Как найти момент силы пример

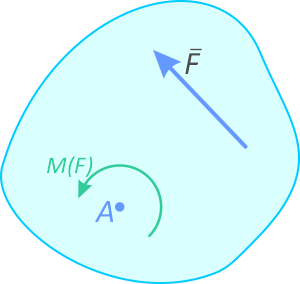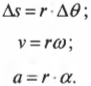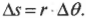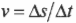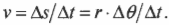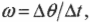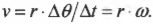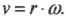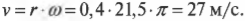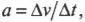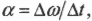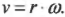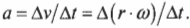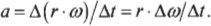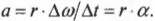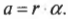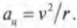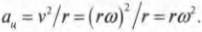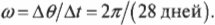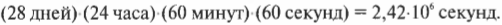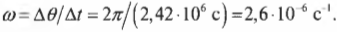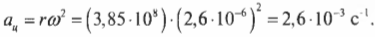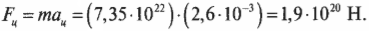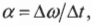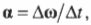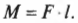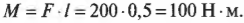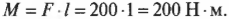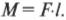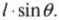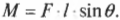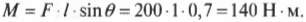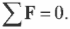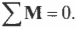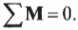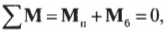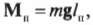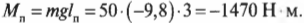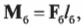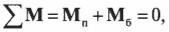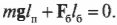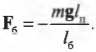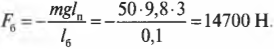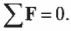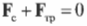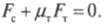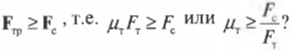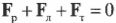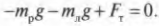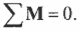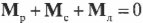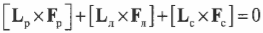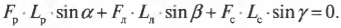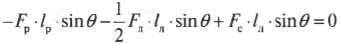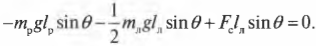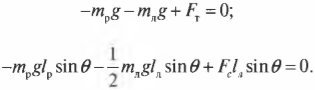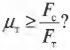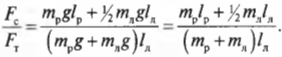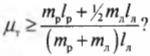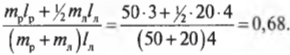
Моментом силы называют вращательное усилие создаваемое вектором силы относительно твердого тела, оси или точки.

Обозначение: M, m или M(F).

Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]

Аналогом момента силы является момент пары сил.

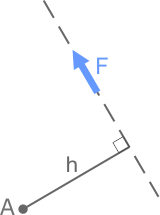
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.

Определение

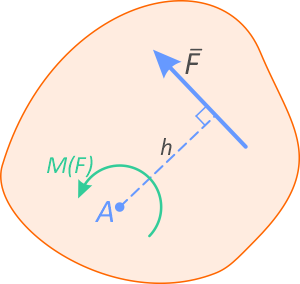
Момент определяется как произведение силы F на плечо h:

M(F)=F×h

Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.

Наш короткий видеоурок про момент силы с примерами:

Другие видео

Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки вращения создает момент M=7×0,35=2,45 кНм.

Пример момента силы

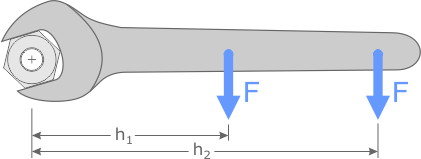
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.

Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.

Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h2>h1).

Плечом при этом служит расстояние от центра гайки до точки приложения силы.

Плечо момента силы

Рассмотрим порядок определения плеча h момента:

Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.

Покажем линию действия силы F (штриховая линия)

Проведем из точки A перпендикуляр h к линии действия силы

Длина отрезка h есть плечо момента силы F относительно точки A.

Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).

Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.

Примеры расчета момента силы

Сила расположена перпендикулярно оси стержня

Если сила F приложена перпендикулярно к оси бруса и известно расстояние между точками A и B.

То момент силы F относительно точки A:

М_A=F×AB

Сила расположена под углом к оси стержня

В случае, если сила F приложена под углом α к оси балки

Момент силы относительно точки B:

M_B=F×cosα×AB

Известно расстояние от точки до линии действия силы

Если известно расстояние от точки где определяется момент до линии действия силы (плечо h)

Момент силы относительно точки B:

M_B=F×h

---

См. также:

• Примеры решения задач >
• Момент силы относительно точки
• Момент силы относительно оси

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

В этой главе…

• Переходим от поступательного движения к вращательному движению
• Вычисляем тангенциальную скорость и тангенциальное ускорение
• Выясняем связь между угловым ускорением и угловой скоростью
• Разбираемся с моментом силы
• Поддерживаем вращательное движение

Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!

Переходим от прямолинейного движения  к вращательному

Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.

Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:

• ​( v=Delta{s}/Delta{t} )​, где ​( v )​ — это скорость, ​( Delta{s} )​ — перемещение, a ( Delta{t} ) — время перемещения;
• ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
• ​( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 )​, где ​( v_0 )​ — это начальная скорость, ​( t_0 )​ — это начальный момент времени, a ​( t_1 )​ — это конечный момент времени;
• ​( v^2_1-v^2_0=2aDelta{s} )​, где ​( v_1 )​ — это конечная скорость.

По аналогии можно легко вывести основные формулы вращательного движения:

• ​( omega=Delta{theta}/Delta{t} )​, где ​( omega )​ — угловая скорость, ​( Delta{theta} )​ — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
• ​( alpha=Delta{omega}/Delta{t} )​, где ​( alpha )​ — угловое ускорение, ​( Delta{omega} )​ — изменение угловой скорости, ​( Delta{t} )​ — время изменения угловой скорости;
• ​( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 )​, где ​( omega_0 )​ — это начальная скорость;
• ​( omega^2_1-w^2_0=2as )​, где ​( omega_1 )​ — это конечная скорость.

Разбираемся с параметрами вращательного движения

В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.

Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:

Допустим, колеса мотоцикла вращаются с угловой скоростью ​( omega )​, равной 21,5( 21,5pi )​ радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.

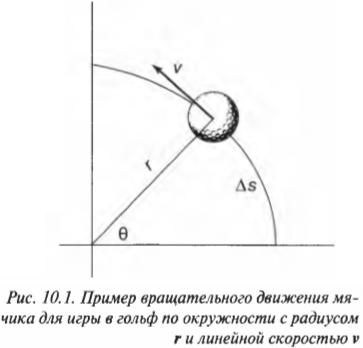
Вычисляем линейную скорость вращательного движения

Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ​( mathbf{r} )​ и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).

Угловая скорость связана с линейной скоростью соотношением ​( v=romega )​, которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.

Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ​( L )​ радиуса ​( r )​ выражается известной формулой ​( L=2pi r )​, а полный угол, который охватывает окружность, равен ​( 2pi )​ радиан. Соответственно, длина дуги окружности длиной ​( Delta s )​, охватывающая угол ​( Deltatheta )​, равна:

Из формулы прямолинейного движения

путем подстановки выражения для ​( Delta s )​ получим:

Поскольку:

где ​( omega )​ — угловая скорость, ​( Delta{theta} )​— угол поворота, ​( Delta{t} )​ — время поворота на угол ( Delta{theta} ), то:

Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5​( pi ) радиан в секунду. Пусть радиус колеса ​( r )​ равен 40 см, тогда достаточно использовать следующую формулу:

Подставляя в нее значения, получим:

Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.

Вычисляем тангенциальное ускорение

Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение

где ​( a )​ — это ускорение, ​( Delta v )​ — изменение скорости, a ​( Delta t )​ — время изменения скорости, с угловым ускорением

где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?

Как мы уже знаем, линейная и угловая скорости связаны равенством

Подставим это выражение в предыдущую формулу линейного ускорения:

Поскольку радиус остается постоянным, то его можно вынести за скобки:

Поскольку угловое ускорение ​( alpha=Deltaomega/Delta t )​, то:

Итак, получаем следующую формулу связи между линейным и угловым ускорением:

Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.

Вычисляем центростремительное ускорение

Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):

Теперь, используя известную формулу связи линейной и угловой скорости ​( v=romega )​, получим:

По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.

Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ​( 2pi )​ радиан. Отсюда получаем угловую скорость Луны:

Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:

После подстановки этого значения в предыдущую формулу получим:

Средний радиус орбиты Луны равен 3,85·10⁸ м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:

Зная это ускорение и массу Луны, которая равна 7,35·10²² кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:

Используем векторы для изучения вращательного движения

В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.

Определяем направление угловой скорости

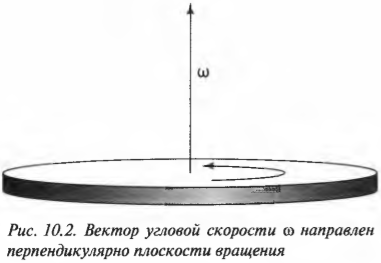
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!

Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ​( omega )​, оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.

Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).

Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.

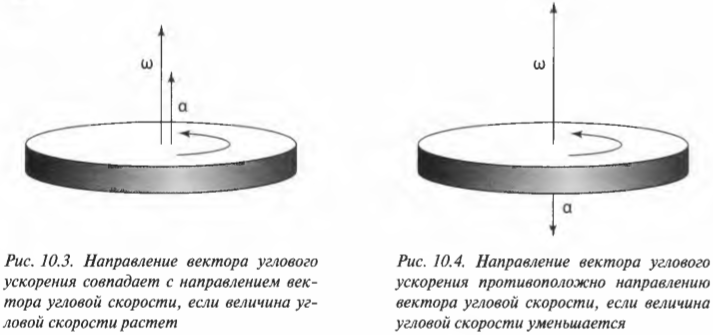
Определяем направление углового ускорения

Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:

где ​( alpha )​ — угловое ускорение, ​( Deltaomega )​ — изменение угловой скорости, ​( Delta t )​— время изменения угловой скорости.

В векторной форме оно имеет следующий вид:

где ​( mathbf{alpha} )​ — вектор углового ускорения, а ​( Deltamathbf{omega} )​ — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.

Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.

А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.

Поднимаем грузы: момент силы

В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.

Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).

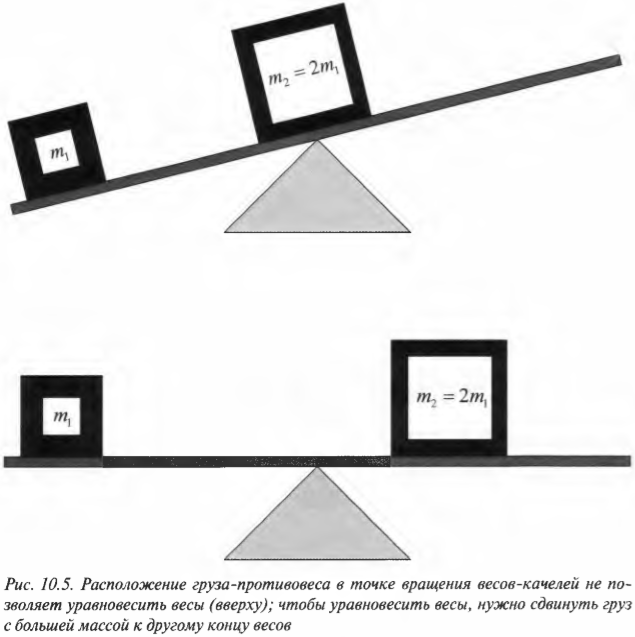
В верхней части рис. 10.5 показаны весы-качели с грузом массы ​( m_1 )​ на одном конце и грузом большей массы ​( m_2=2m_1 )​ посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ​( m_2 )​ к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ​( m_1 )​.

Знакомимся с формулой момента силы

Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.

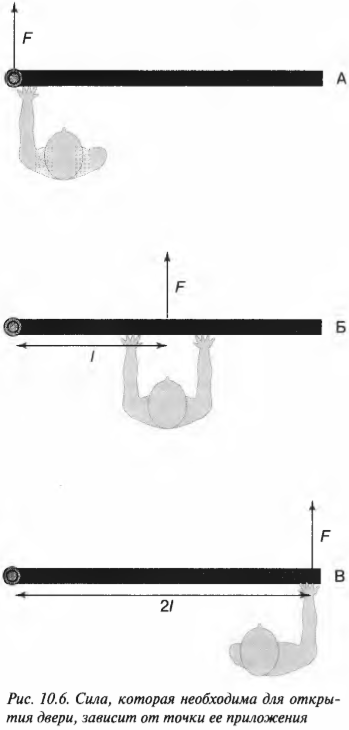
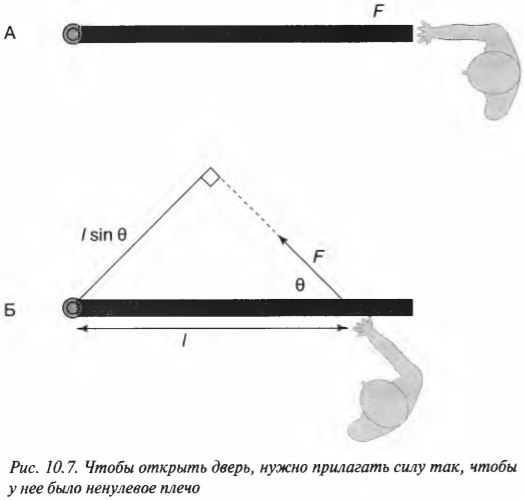
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).

На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ​( F )​ на плечо силы ​( l )​:

Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).

Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ​( l )​ равно 0,5 м и момент силы будет равен:

В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:

Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?

Разбираемся с направлением приложенной силы и плечом силы

Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.

Размышляем над тем, как создается момент силы

Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.

Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ​( theta )​. Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:

Однако в данном случае угол ( theta ) не является прямым.

В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.

Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:

Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).

Итак, получаем для момента силы для схемы Б на рис. 10.7:

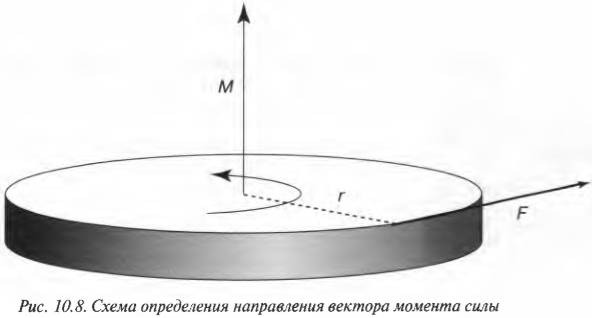
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:

Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.

Определяем направление момента силы

Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.

На рис. 10.8 показан пример силы ​( mathbf{F} )​ с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).

Уравновешиваем моменты сил

В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).

Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:

Иначе говоря, результирующая действующая сила равна нулю.

Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.

Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:

Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.

Простой пример: вешаем рекламный плакат

Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.

Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.

Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:

Иначе говоря:

где ​( mathbf{M_п} )​ — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.

Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:

где ​( m )​ = 50 кг — это масса плаката, ​( mathbf{g} )​ — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ​( mmathbf{g} )​ — сила тяжести плаката, а ​( l_п )​ = 3 м — это плечо силы тяжести плаката.

Подставляя значения, получим:

Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.

Момент силы со стороны болта определяется формулой:

где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.

Подставляя полученные выражения для моментов сил в формулу:

получим, что:

Отсюда с помощью простых алгебраических преобразований получим искомую силу:

Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.

Подставляя значения, получим искомый ответ:

Более сложный пример: учитываем силу трения при расчете равновесия

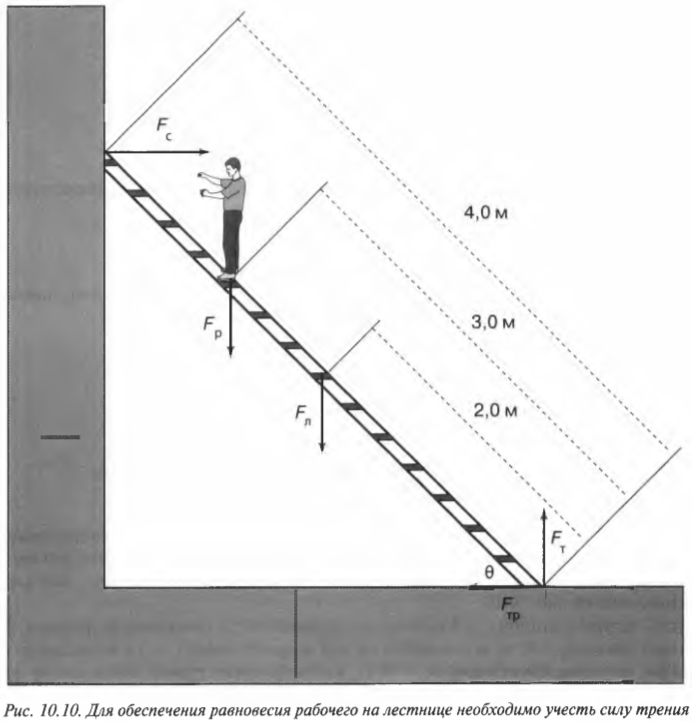
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.

Пусть лестница длиной ​( l_л )​ = 4 м стоит под углом ​( theta )​ = 45° к поверхности тротуара, работник имеет массу ​( m_р )​ = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ​( mu_п )​ = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?

Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:

• ​( mathbf{F_с} )​ — нормальная сила со стороны стены;
• ( mathbf{F_р} ) — вес рабочего;
• ( mathbf{F_л} ) — вес лестницы;
• ( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
• ( mathbf{F_т} ) — нормальная сила со стороны тротуара.

Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:

Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:

или

Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие

Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:

или

Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:

Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ​( mathbf{M_р=[L_р!times! F_р]} )​, весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):

или

или

Поскольку ​( L_р=l_р )​, ​( L_л=l_л/2 )​ (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ​( alpha=360^{circ}-theta )​, ( beta=360^{circ}-theta ) и ​( gamma=theta )​, то получим:

или

Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):

Зададимся вопросом: соблюдается ли условие

Из системы двух уравнений получим:

Итак, остается выяснить, соблюдается ли условие:

После подстановки значений получим:

Поскольку ​( mu_т )​ = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.

Определение

Статика — раздел механики, изучающий условия равновесия тел.

Виды равновесия

Устойчивое равновесие
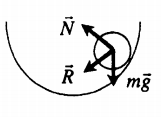	Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min).
Неустойчивое равновесие
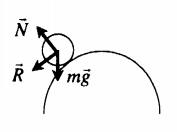	Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max).
Безразличное равновесие
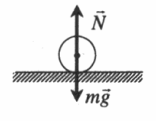	При выведении тела из положения безразличного равновесия дополнительных сил не возникает.

Момент силы

Определение

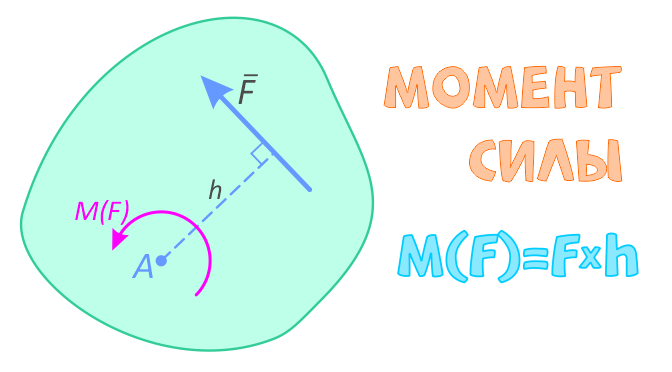
Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:

M = Fd

M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).

Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.

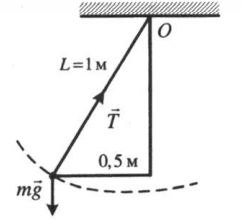
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?

Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:

M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)

Момент силы может быть положительным и отрицательным.

Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:

M₁ = F₁d₁

Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:

M₂ = F₂d₂

Правило моментов

Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

∑Mi=0

Иначе правило моментов можно сформулировать так:

Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.

∑Mпо час. стр.=∑Mпр. час. стр.

Условия равновесия тел

Тело не участвует в поступательном движении:	∑→Fi=0; →vo=0
Тело не участвует во вращательном движении:	∑Mi=0; ω0=0
Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении)	∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0

Простые механизмы

Определение

Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.

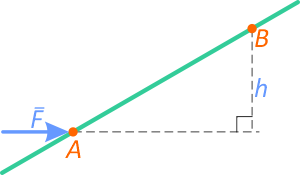
Наклонная плоскость
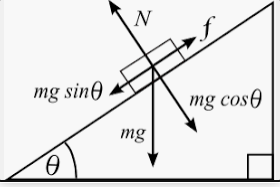	Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsinθ<mg
Рычаг
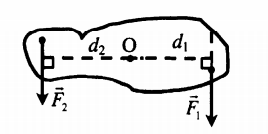
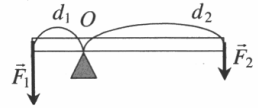	Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2=d2d1
Неподвижный блок
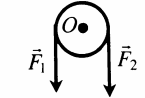	Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2
Подвижный блок
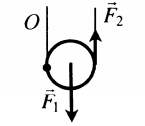	Дает выигрыш в силе в 2 раза: d1 = R d2 = 2R F1 = 2F2
Клин
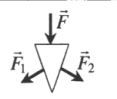	Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2

Золотое правило механики

При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.

Задание EF22660

Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.

---

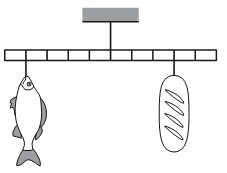
Алгоритм решения

1.Записать исходные данные.

2.Записать правило моментов и выполнить решение в общем виде.

3.Подставить известные данные и вычислить искомую величину.

Решение

Известна лишь масса батона: m₁ = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:

d₁ = 0,3

d₂ = 0,4

Запишем правило моментов:

F₁ d₁ = F₂ d₂

Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:

m₁gd₁ = m₂gd₂

m₁d₁ = m₂d₂

Отсюда масса рыбы равна:

m2=m1d1d2=0,8·0,30,4=0,6 (кг)

Ответ: 0,6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18706

Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения F_тр относительно оси, проходящей через точку О₃ перпендикулярно плоскости чертежа, равно…

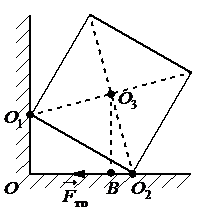
Ответ:

а) 0

б) О₂О₃

в) О₂В

г) О₃В

---

Алгоритм решения

1. Сформулировать определение плеча силы.
2. Найти плечо силы трения и аргументировать ответ.

Решение

Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О₃В.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 9.7k

Чтобы определить, чему равен момент силы, нужно получить произведение вектора силы и радиус-вектора, который проводится к точке приложения силы от оси вращения. Поэтому величину можно назвать характеристикой вращательного воздействия силы на твердое тело.

Термины “крутящий” и “вращающий” моменты в данном случае не являются тождественными. Разница между ними состоит в том, что “вращающий” момент воспринимается как внешнее усилие, которое прикладывают к объекту. Термин “крутящий” же рассматривается как внутреннее усилие, которое появляется при приложении конкретных нагрузок (что делает определение схожим с используемым при изучении сопротивления материалов).

Понятие «момент силы»

Физики воспринимают этот термин в качестве так называемой “вращающей силы”. В соответствии с системой СИ, измеряется данная величина в ньютон-метрах. Иногда в литературе можно также встретить понятие “момент пары сил” (такое определение, например, появляется в исследованиях Архимеда над рычагами).

При использовании простых примеров (например, при приложении силы к рычагу в перпендикулярном отношении к нему) величина рассчитывается как произведение расстояния до оси вращения рычага и непосредственно силы, которая на него воздействует.

Пример: На рычаг оказывает воздействие силы в 3 ньютона, которую прикладывают на расстоянии 2 м от оси вращения рычага. В результате момент силы будет равнозначен силе в 1 ньютон, прикладываемой на расстоянии 6 м по отношению к рычагу.

Как определить, чему равен момент силы

Важно помнить, что в физике энергия воспринимается как скалярная величина. В то же время момент силы считается (псевдо)векторной величиной. Поэтому совпадение размерностей указанных величин никогда не бывает случайным. Например, момент силы в 1 Н/м, приложенный через целый оборот, при выполнении механической работы сообщает энергию в 2 Дж. В математическом отображении эта формула момента силы будет выглядеть так:

[mathbf{E}=mathbf{M} boldsymbol{theta}], где:

• [mathbf{E}] — это энергия;
• [mathbf{M}] — это вращающийся момент;
• [boldsymbol{theta}] — это угол в радианах.

В современных условиях момент силы измеряется при помощи особых датчиков нагрузки, которые могут быть трех типов:

• оптического;
• тензометрического;
• индуктивного.

Применение специальной техники позволяет определить величину предельно точно и избавляет ученых от необходимости производить лишние расчеты.

Момент силы: формулы

У такой формулы момента силы в физике будет один недостаток. С ее помощью не удастся определить, в каком направлении направлен момент силы. Известной станет только его величина. Если сила окажется перпендикулярной вектору, тогда момент рычага окажется равен расстоянию от центра до точки, в которой была приложена сила. В таком случае момент силы достигнет максимального значения:

[vec{T}=vec{r} quad vec{F}]

Если сила совершает какое-либо действие на определенном расстоянии, она параллельно выполняет механическую работу относительно того же объекта. В таком случае в физической практике считается, что и момент силы выполняет работу (при совершении действия через угловое расстояние).

[mathrm{P}=mathrm{M} {omega}]

Международная система измерений предлагает определять мощность в Ваттах, при этом момент силы измеряется в радианах в секунду. Для определения величину угловой скорости используется единица “радианы в секунду”).

Как определяется момент действия нескольких сил

Если на тело действуют одновременно две равные по величине и противоположно направленные силы (не лежащие на одной и той же прямой), оно находится в состоянии равновесия. Такая ситуация связана с тем, что результирующий момент данных сил по отношению к любой из осей не обладает нулевым значением. Ведь обе силы направлены в одну сторону момента и являются парой сил.

Если тело закреплено на оси, оно будет вращаться под влиянием пары сил. Когда же пара сил прилагается по отношению к свободному телу, последнее начнет крутиться вокруг той оси, которая проходит через центр тяжести.

В соответствии с правилом моментов сил в физике, момент пары сил считается одинаковым по отношению к любой оси, перпендикулярной плоскости этой пары. При этом суммарный момент пары M всегда определяется как произведение плеча пары (то есть расстояния l между силами) и одной из этих сил F. Данный расчет производится независимо от типов отрезков, на которые разделяется положение оси.

[mathrm{M}=mathrm{FL}_{1}+mathrm{FL}-2=mathrm{FL}_{1}+mathrm{L}_{2}=mathrm{FL}]

В случае, если равнодействующая момент нескольких сил равняется нулю, он будет одинаковым по отношению ко всем параллельным друг другу осям. Именно поэтому воздействие всех сил на тело можно заменить действием только одной пары сил, имеющих точно такой же момент.

Содержание:

1. Момент силы
2. Момент силы относительно точки (центра)
3. Момент силы относительно оси
4. Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
5. Моменты силы относительно координатных осей
6. Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)

Момент силы (момент силы относительно точки; также: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — эо векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Момент силы

Система сходящихся сил, которая будет рассмотрена в главе 2, является особой среди
систем сил. Только в этой системе линии действия сил имеют одну точку пересечения. Поэтому для ее изучения достаточно основных понятий статики, рассмотренных в разделе 1. Для изучения других систем сил необходимо ознакомиться с понятиями момента силы и пары сил.

Понятие о моменте силы — одно из основных понятий механики, которое широко используется и в теоретических исследованиях и при практических расчетах. К понятию момента силы человечество пришло, рассматривая равновесие и движение тел, имеющих точку или ось вращения (в частности блоков и рычагов, которые использовались в практике еще до нашей эры).

Например, на неподвижный блок (рис. 3.1) действует сила , вращающей его вокруг горизонтальной оси О. Стержень АВ (рис. 3.2), который имеет неподвижную шарнирную опору A, будет вращаться вокруг оси шарнира под действием собственной силы тяжести В обоих примерах сила обуславливает вращательное движение тела. По мере вращательного действия силы на тело является момент силы.

      

Момент силы относительно точки (центра)

Заданная сила , изображена вектором , приложенная к некоторому телу в точке А. Определим момент силы относительно точки О (рис. 3.3). Векторным моментом силы относительно точки О называется вектор, приложенный в точке О, равный векторному произведению радиуса вектора точки приложения силы на вектор силы:

где — радиус-вектор точки приложения силы относительно точки О.

Определим величину (модуль) и направление вектора . Согласно понятиям и свойствам векторного произведения двух векторов, величина (Модуль) момента силы   относительно точки О равна:

Обозначим . Поскольку Тогда:

где (рис. 3.3) — высота  опущенная из вершины В (с точки О) на сторону АВ этого треугольника, совпадает с линией действия силы. Короткое расстояние от точки О до линии действия силы называется плечом силы относительно этой точки. Из этого следует, что модуль (величина) момента силы относительно точки равна произведению величины силы на ее плечо относительно этой точки.

Вектор направляется по правилу векторного произведения: векторный момент силы относительно точки (Центра) является перпендикулярным к плоскости, в которой размещены сила и точка (центр) так, чтобы с его конца было видно попытки силы возвращать тело вокруг точки (Центра) против хода часовой стрелки.
Заметим, что . Поэтому:

Модуль момента силы относительно точки равен удвоенной площади треугольника, вершинами которого является точка и начало и конец вектора

Если линия действия силы проходит через точку (центр), то h = 0, и из формулы (3.2) видно, что момент силы относительно этой точки будет равняться нулю.

Момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, поскольку неизменным остается плечо силы относительно точки (рис. 3.4).

Если на тело действует плоская система сил, то векторы моментов всех сил системы относительно некоторого центра, что лежит в плоскости действия сил, будут перпендикулярны этой плоскости, а следовательно, параллельные и их можно считать скалярными величинами, которые отличаются только величиной и знаками.

В этом случае целесообразно ввести понятие алгебраического момента силы относительно точки (центра), равный взятом со знаком «+» или «-» произведения модуля силы на плечо относительно этой точки (центра)

Будем считать момент положительным, если сила пытается вращать тело вокруг точки (центра) против хода часовой стрелки (рис. 3.5, а), и отрицательным — если по ходу часовой стрелки (рис. 3.5, б). Единицы момента силы:

Момент силы относительно оси

Изучая пространственные системы сил, будем использовать понятие момента силы относительно оси.

Моментом силы относительно оси называется величина, равная  алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Пусть к телу в некоторой точке А приложена сила (Рис. 3.6). определим момент силы  относительно произвольной оси . Проведем плоскость П, перпендикулярную оси .
Точку пересечения плоскости П с осью обозначим А. Спроектируем силу на плоскость П и получим силу 

Согласно определению 

Таким образом, чтобы определить момент силы относительно оси, необходимо:
— спроектировать эту силу на плоскость, перпендикулярную оси;
— найти точку пересечения оси с этой перпендикулярной плоскостью;
— определить алгебраический момент полученной проекции относительно точки пересечения оси с плоскостью.

Из формулы (3.5) следует, что момент силы относительно оси равен нулю, если:
1) сила параллельна оси, тогда
2) линия действия силы пересекает ось, тогда

Эти два условия эквивалентны одному условию: момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости. поскольку момент силы относительно оси , то согласно принятому правилу знаков моментов следует, что момент силы относительно оси положительный, если, смотря с конца оси, видим, что проекция этой силы на плоскость, перпендикулярную оси, пытается вращать тело вокруг оси против часовой стрелки (рис. 3.7, а). если вращение происходит в направлении хода часовой стрелки, то момент силы относительно оси будет отрицательным (рис. 3.7, б). Можно доказать, что момент силы относительно оси не зависит от выбора точки О на этой оси.

Зависимость между моментом силы относительно точки и оси, проходящей через эту точку

Теорема 3.1. Проекция векторного момента силы относительно точки на ось, проходящей через эту точку, равен моменту силы относительно этой оси.

Доказательство. Сила приложена в точке А пространства. Выберем произвольную точку О и проведем оси (рис. 3.8). Определим момент силы относительно оси и относительно точки О на ней.
Известно, что  

где 

Из курса элементарной геометрии известно, что 

где — угол между плоскостями этих треугольников, а следовательно, и угол между перпендикулярами к этим плоскостей.

Поскольку вектор перпендикулярный плоскости, а ось перпендикулярна  к 

Учитывая равенства (3.6), (3.7), получим 

Знак полностью определяется знаком .

Поскольку

что и требовалось доказать.

Моменты силы относительно координатных осей

Пусть на тело действует сила  приложенная в точке А (рис. 3.9). выберем произвольную точку О и из нее проведем оси декартовой системы координат.
Определим момент силы относительно этих осей. Для этого запишем выражение для момента силы относительно точки О.

Согласно (3.1),где — радиус-вектор точки А относительно точки О.
Вектор силы и радиусвектор через проекции на оси координат выражаются:

где  — координаты точки А; — орты выбранной системы координат.

Тогда векторное произведение можно записать в виде определителя:

Раскрывая этот определитель, получим 

Представим векторный момент через его проекции на оси координат:

Сравнивая правые части равенств (3.9) и (3.10), получим:

Поскольку точка О принадлежит осями , то из формул (3.11), учитывая зависимость (3.8), получим выражения:

Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)

Теорема 3.2. Момент равнодействующей пространственной системы сходящихся сил
относительно некоторого центра (точки) равна векторной сумме моментов составляющих сил относительно того же центра (точки).

Доказательство. На тело действует пространственная система сходящихся сил линии действия которых пересекаются в точке В (Рис. 3.10, а). заменим
данную систему сил эквивалентной системой, все силы которой приложенные в точке В
(Рис. 3.10, б). Равнодействующую системы, прилагаемую в той же точке В, обозначим . Найдем момент равнодействующей  относительно точки (центра) О. Согласно формуле (3.1), где — радиус-вектор точки приложения всех сил системы и равнодействующей относительно центра О.

Известно, что . Тогда 

Итак, получили равенство 

Теорема доказана.

Уравнение (3.13) является математическим записи теоремы Вариньона для пространственной системы сходящихся сил.
В случае плоской системы сходящихся сил теорема Вариньона запишется так:

Итак, момент равнодействующей плоской системы сходящихся сил относительно некоторого центра (точки), лежащий в плоскости действия сил, равна алгебраической сумме моментов составляющих сил относительно этого самого центра (точки).

Рассмотрим пример на применение теоремы Вариньона.

Задача. На согнутый под прямым углом стержень АВС действуют силы  и  как показано на рис. 3.11. Найти моменты этих сил относительно точки А, если

Решение.

Для определения момента силы относительно точки используем теорему Вариньона.
Разложим силу  на две составляющие: горизонтальную  и вертикальную .  Величины этих составляющих   Тогда, согласно теоремой 3.2, получим:

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Пара сил
4. Произвольная система сил
5. Плоская произвольная система сил
6. Трение
7. Расчет ферм
8. Расчет усилий в стержнях фермы
9. Пространственная система сил
10. Произвольная пространственная система сил
11. Плоская система сходящихся сил
12. Пространственная система сходящихся сил
13. Равновесие тела под действием пространственной системы сил
14. Естественный способ задания движения точки
15. Центр параллельных сил
16. Параллельные силы
17. Система произвольно расположенных сил
18. Сосредоточенные силы и распределенные нагрузки
19. Кинематика
20. Кинематика твердого тела
21. Движения твердого тела
22. Динамика материальной точки
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки