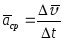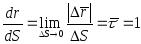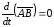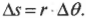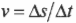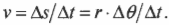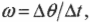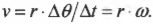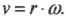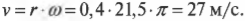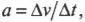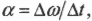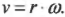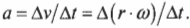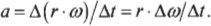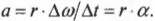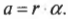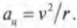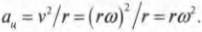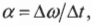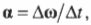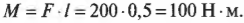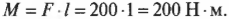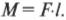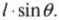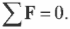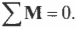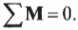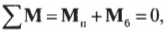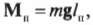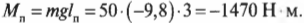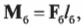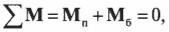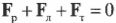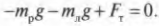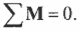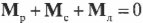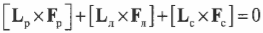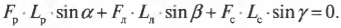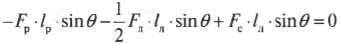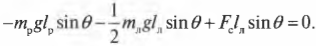Содержание:
Моменты силы относительно точки и оси:
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
Алгебраический момент силы относительно точки
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки.
Рис. 19
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
Плечом 

Обозначим 
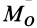
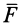

Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке — знак минус.
Алгебраический момент силы представляет собой произведение силы на длину (в 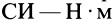
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе 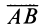
Векторный момент силы относительно точки
При рассмотрении пространственной системы сил, приложенных к твердому телу, применяется понятие векторного момента силы относительно точки.
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
Плечом 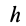

Рис. 20
Условимся векторный момент силы 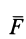


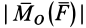
Как и для алгебраического момента, векторный момент силы относительно точки равен удвоенной площади треугольника, построенного на силе и моментной точке:
Справедлива формула
где 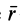

Чтобы убедиться в справедливости формулы (3), достаточно показать, что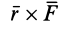

Как показано на рис. 20, 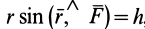
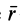
что совпадает с векторным моментом силы относительно точки 
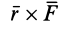
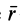
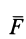
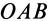

Направление 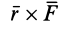

Векторный момент силы относительно точки не изменяется от переноса силы вдоль ее линии действия. Он станет равным
нулю, если линия действия силы пройдет через моментную точку.
Рис. 21
Если сила 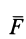
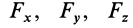
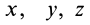
где 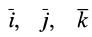
Используя формулу (4), можно выделить проекции 
Модуль векторного момента 
В формулах (6) числовую величину 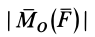
Момент силы относительно оси
Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 22). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси 
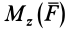
Рис. 22
По определению,
где 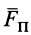
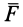





Из определения момента силы относительно оси следует, что введенный выше алгебраический момент силы относительно точки можно считать моментом силы относительно оси, проходящей через эту точку, перпендикулярно плоскости, в которой лежат сила и моментная точка. Момент силы относительно оси можно выразить через площадь треугольника, построенного на проекции силы 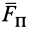

Из формулы (8) можно получить следующие важные свойства момента силы относительно оси:
- Момент силы относительно оси равен нулю, если сила параллельна оси. В этом случае равна нулю проекция силы на плоскость, перпендикулярную оси.
- Момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось. В этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью и, следовательно, равно нулю плечо силы
относительно точки
.
В обоих этих случаях ось и сила лежат в одной плоскости. Объединяя их, можно сказать, что момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.
Связь момента силы относительно оси с векторным моментом силы относительно точки на оси
Используя формулу (8), имеем (рис. 23)
Векторный момент силы 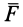



Векторный момент 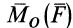
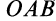
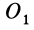
причем векторный момент 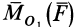
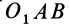
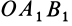
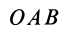
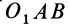

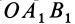

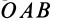
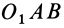
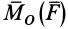
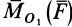
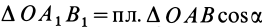
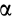
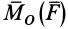

причем знак 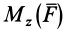
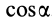
Аналогично,
т. е.
где 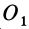

Формулы (11) и (12) отражают искомую связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.
Эту зависимость между моментом силы относительно оси и векторным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
Рис. 23
Формулы для моментов силы относительно осей координат
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов относительно осей координат, если даны проекции силы на оси координат и координаты точки приложения силы. Для оси 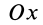
Согласно (5),
следовательно,
Аналогично, для осей 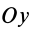
Окончательно
По формулам (13) можно вычислить моменты силы относительно прямоугольных осей координат.
По этим формулам получаются необходимые знаки для 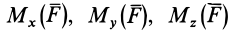
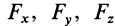
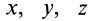
При решении задач момент силы относительно какой-либо оси часто получают, используя его определение, т. е. проецируя силу на плоскость, перпендикулярную оси, и вычисляя затем алгебраический момент этой проекции относительно точки пересечения оси с этой плоскостью.
Момент пары сил. Сложение пар сил. Равновесие пар сил
При изучении теоретической механики необходимо совершенно отчетливо уяснить, что в статике рассматриваются два простейших элемента: сила и пара сил. Любые две силы, кроме сил, образующих пару, всегда можно заменить одной —сложить их (найти равнодействующую). Пара сил нс поддается дальнейшему упрощению, она не имеет равнодействующей и является простейшим элементом.
Действие пары сил на тело характеризуется ее моментом — произведением одной из сил пары на ее плечо (на кратчайшее расстояние между линиями действия сил, образующих пару).
Единицей момента пары сил в Международной системе служит 1 нм (ньютон-метр = 1 н-1ж), а в системе МКГСС (технической)— 1 кГ-м.
Несколько пар сил, действующих на тело в одной плоскости, можно заменить одной парой сил (равнодействующей парой), момент которой равен алгебраической сумме моментов данных пар:
При равновесии пар сил
Если пары сил действуют в одной плоскости, то при решении задач достаточно рассматривать моменты пар как алгебраические величины. Причем знак момента определяется в зависимости от направления вращающего действия пары сил.
Дальнейшее изложение основано на правиле, т. е. считается момент положительным, если пара сил действует против хода часовой стрелки, если же пара сил действует на тело но ходу часовой стрелки, то момент считается отрицательным.
В том случае когда пары сил действуют на тело будучи расположенными в различных плоскостях, гораздо удобнее рассматривать пару сил как вектор, направленный перпендикулярно
к плоскости действия пары сил (рис. 62). Направление вектора в зависимости от направления вращательного действия пары определяется по направлению движения винта с правой нарезкой.
Задача 1.
Определить момент пары сил (рис. 63), если 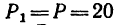
Решение.
1. При определении момента пары сил нужно прежде всего правильно определить плечо пары. При этом необходимо различать следующие понятия: плечо пары сил и расстояние между точками приложения сил нары.
Так как в механике твердого тела сила—скользящий вектор, то действие силы не изменяется при переносе точки ее приложения вдоль линии ее действия. Значит расстояние между точками приложения сил, образующих пару, можно изменять неограниченно. Но плечо пары при этом переносе остается неизменным.
В частном случае расстояние между точками приложения сил, образующих пару, может быть равно плечу.
Чтобы определить плечо данной пары из точки приложения одной из сил, например из точки В, восставим перпендикуляр ВС к линии действия другой силы. Расстояние ВС и есть плечо данной пары сил. Расстояние между точками приложения сил, образующих пару, АВ=0,5 м.
Легко видеть, что
2. Найдем момент пары сил:
Задача 2.
Как изменится момент пары сил 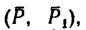
повернуть силы 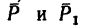
1. Найдем момент пары при заданном положении ее сил (рис. 64, а).
Из точки В восставим перпендикуляр ВС к линиям действия сил 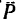
Момент пары при заданном положении сил
2. Повернем силы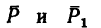
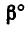
3. Сравнивая полученные результаты, видим, что после поворота сил момент пары увеличивается на 20—14,5 = 5,85 н-м.
4. Легко заметить, что силы 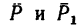
Момент пары сил изменяет свой знак.
Задача 3.
К точкам А, С и В, D, образующим вершины квадрата со стороной 0,5 м (рис. 65, а), приложены равные по модулю силы (Р = 12н) таким образом, что они образуют две пары сил
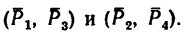
Решение 1.
Плечи у обеих пар сил равны стороне квадрата поэтому
Решение 2.
1. Перенесем силы 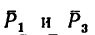
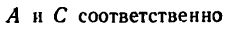
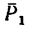
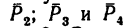
2. Сложим попарно эти силы у каждой из точек В и D. В обоих случаях
3. Силы R, модули которых теперь известны, направлены перпендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил 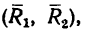
4. Найдем момент пары
и, следовательно,
Эту пару в соответствии со вторым решением можно представить в виде пары 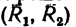
Но можно равнодействующую пару представить и в любом другом виде, например в виде сил Q = 24 и, приложенных к двум любым вершинам квадрата ABCD (рис. 65, в)
- Заказать решение задач по теоретической механике
Задача 4.
На прямоугольник ABCD (рис. 67) вдоль его длинных сторон действует пара сил 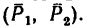
Решение.
1. Момент данной пары сил
необходимо уравновесить парой, момент которой обозначим Л1м. Тогда, согласно условию равновесия,
Откуда
2. Обозначив силы, образующие искомую пару 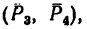
Отсюда
•Значит к прямоугольнику необходимо приложить пару сил с положительным (направленным против хода часовой стрелки) моментом, равным 48 н м. Силы, образующие эту пару, равняются
20 н каждая и одна из них должна действовать вдоль стороны АВ от А к В, вторая — вдоль стороны CD от С к D.
Задача 5.
Прямолинейный стержень АВ должен находиться в равновесии в положении, показанном на рис. 68, а (угол а = 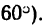
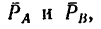
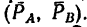
Решение.
1. Пару сил можно уравновесить только парой сил. Поэтому в точках С и D к стержню необходимо приложить две равные силы так, чтобы они образовали пару сил с моментом, равным моменту пары 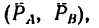
Так как пара 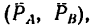
2. Применяем условие равновесия:
Или, подставив значения моментов,
где
Отсюда
Следовательно, в точках С и D необходимо приложить силы 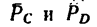
Момент силы относительно точки
Момент силы относительно точки при решении задач по статике, а затем и по динамике имеет не менее важное значение, чем проекции сил. Поэтому нужно уметь определять эту величину безошибочно. Обычно его числовое значение находят неправильно из-за ошибок, допускаемых при определении плеча.
Чтобы не допускать ошибок при определении моментов сил относительно точки, рекомендуется придерживаться следующего порядка:
- Прежде всего нужно научиться «видеть» силу, момент которой определяем, и центр моментов — точку, относительно которой определяем момент (рис. 70 — сила
и центр моментов — точка В).
- Затем из центра момента проводим прямую ВЬ перпендикулярно к линии действия силы DF. Длина перпендикуляра ВС от центра момента до линии действия силы и есть плечо.
- Потом находим знак момента. При этом если сила стремится повернуть плечо вокруг центра момента против хода часовой стрелки, то считаем момент положительным; если по ходу часовой стрелки, то отрицательным (тоже правило, что и при определении знака момента пары сил).
- Находим числовое значение момента силы относительно точки, умножив модуль силы на плечо.
По рис. 70
В частном случае момент силы может равняться нулю. Это происходит тогда, когда центр моментов лежит на линии действия силы, при этом плечо равняется нулю. По рис. 70 момент силы 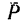
Задача 6.
Определить моменты шести заданных сил (рис. 71) относительно точек А, В и С, если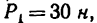
Решение 1 — определение моментов гнести заданных сил относительно точки А (рис. 71, а).
1. Центр моментов в точке А. Через точку А проходят линии действия трех сил 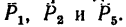
2. Находим момент силы 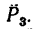
силы 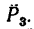
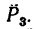
3. Величина момента отрицательная (сила 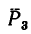
4. Находим момент силы 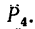
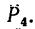
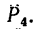
Величина момента положительная (плечо АЕ поворачивается около точки А силой 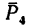
5. Находим момент силы 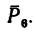
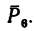
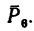
Решение 2 — определение моментов сил относительно точки В (рис. 71, б).
1. Центр моментов в точке В.
2. Через точку В проходят линии действия двух сил: 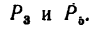
3. Находим момент силы 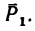
Величина момента отрицательная:
4. Находим момент силы 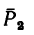
Момент отрицательный:
5. Находим момент силы 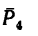
Величина момента положительная:
6. Находим момент силы 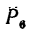
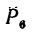
Решение 3 — определение моментов сил относительно точки С (рис. 71, в) рекомендуется выполнить самостоятельно.
Ответ.
В задаче силы расположены так, что либо их плечи определяются очень просто — как катеты прямоугольных треугольников, в которых даны гипотенузы, либо плечи заданы в условии задачи (ВС и АС).
Но иногда некоторые силы заданной системы оказываются расположенными относительно выбранного центра моментов так, что определить длину плеча трудно и требуется, например, предварительно вычислить длины еще одного-двух отрезков. В таких случаях целесообразно силу разложить на две составляющие и применить для определения ее момента теорему Вариньона.
Задача 7.
Определить моменты относительно точки 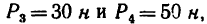

Решение.
1. Относительно точки А моменты сил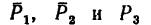
2. Находим момент силы 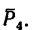
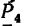
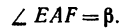
AF = AB — FB.
Величину FB находим из 
следовательно,
И теперь можем определить плечо АЕ:
Раскрываем скобки и заменяем
Момент положительный, следовательно:
Вариант 2-й. Чтобы избежать определения плеча АЕ, которое в данном случае находится после предварительного вычисления двух отрезков (FB и AF), необходимо момент силы 
Разложим силу 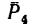
Модуль первой составляющей 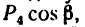
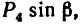
Применяя теорему Вариньона, получаем
Как видно, получено точно такое же значение момента, что и в первом варианте решения:
- Теория пар сил
- Приведение системы сил к простейшей системе
- Условия равновесия системы сил
- Плоская система сил
- Аксиомы и теоремы статики
- Система сходящихся сил
- Плоское движение тела
- Принцип виртуальных перемещений
Содержание:
- Момент силы
- Момент силы относительно точки (центра)
- Момент силы относительно оси
- Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
- Моменты силы относительно координатных осей
- Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Момент силы (момент силы относительно точки; также: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — эо векторная физическая величина, характеризующая действие силы на механический объект, которое может вызвать его вращательное движение.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Момент силы
Система сходящихся сил, которая будет рассмотрена в главе 2, является особой среди
систем сил. Только в этой системе линии действия сил имеют одну точку пересечения. Поэтому для ее изучения достаточно основных понятий статики, рассмотренных в разделе 1. Для изучения других систем сил необходимо ознакомиться с понятиями момента силы и пары сил.
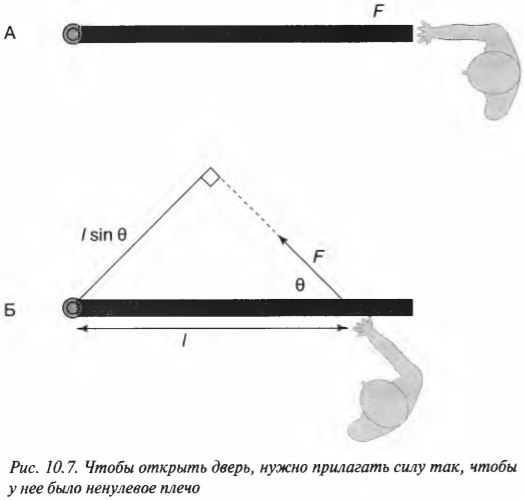
Понятие о моменте силы — одно из основных понятий механики, которое широко используется и в теоретических исследованиях и при практических расчетах. К понятию момента силы человечество пришло, рассматривая равновесие и движение тел, имеющих точку или ось вращения (в частности блоков и рычагов, которые использовались в практике еще до нашей эры).
Например, на неподвижный блок (рис. 3.1) действует сила 


Момент силы относительно точки (центра)
Заданная сила 


где 
Определим величину (модуль) и направление вектора 

Обозначим 

где 

Вектор 
Заметим, что 
Модуль момента силы относительно точки равен удвоенной площади треугольника, вершинами которого является точка и начало и конец вектора
Если линия действия силы проходит через точку (центр), то h = 0, и из формулы (3.2) видно, что момент силы относительно этой точки будет равняться нулю.
Момент силы относительно точки не изменяется при переносе силы вдоль ее линии действия, поскольку неизменным остается плечо силы относительно точки (рис. 3.4).
Если на тело действует плоская система сил, то векторы моментов всех сил системы относительно некоторого центра, что лежит в плоскости действия сил, будут перпендикулярны этой плоскости, а следовательно, параллельные и их можно считать скалярными величинами, которые отличаются только величиной и знаками.
В этом случае целесообразно ввести понятие алгебраического момента силы относительно точки (центра), равный взятом со знаком «+» или «-» произведения модуля силы на плечо относительно этой точки (центра)
Будем считать момент положительным, если сила пытается вращать тело вокруг точки (центра) против хода часовой стрелки (рис. 3.5, а), и отрицательным — если по ходу часовой стрелки (рис. 3.5, б). Единицы момента силы:
Момент силы относительно оси
Изучая пространственные системы сил, будем использовать понятие момента силы относительно оси.
Моментом силы относительно оси называется величина, равная алгебраическому моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Пусть к телу в некоторой точке А приложена сила 



Точку пересечения плоскости П с осью 

Согласно определению
Таким образом, чтобы определить момент силы относительно оси, необходимо:
— спроектировать эту силу на плоскость, перпендикулярную оси;
— найти точку пересечения оси с этой перпендикулярной плоскостью;
— определить алгебраический момент полученной проекции относительно точки пересечения оси с плоскостью.
Из формулы (3.5) следует, что момент силы относительно оси равен нулю, если:
1) сила параллельна оси, тогда
2) линия действия силы пересекает ось, тогда
Эти два условия эквивалентны одному условию: момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости. поскольку момент силы относительно оси 
Зависимость между моментом силы относительно точки и оси, проходящей через эту точку
Теорема 3.1. Проекция векторного момента силы относительно точки на ось, проходящей через эту точку, равен моменту силы относительно этой оси.
Доказательство. Сила 



Известно, что
где
Из курса элементарной геометрии известно, что
где 
Поскольку вектор 


Учитывая равенства (3.6), (3.7), получим
Знак 

Поскольку
что и требовалось доказать.
Моменты силы относительно координатных осей
Пусть на тело действует сила 
Определим момент силы 

Согласно (3.1),

Вектор силы 

где 

Тогда векторное произведение 
Раскрывая этот определитель, получим
Представим векторный момент 
Сравнивая правые части равенств (3.9) и (3.10), получим:
Поскольку точка О принадлежит осями 
Теорема Вариньона для пространственной системы сходящихся сил (Теорема о моменте равнодействующей силы)
Теорема 3.2. Момент равнодействующей пространственной системы сходящихся сил
относительно некоторого центра (точки) равна векторной сумме моментов составляющих сил относительно того же центра (точки).
Доказательство. На тело действует пространственная система сходящихся сил 
данную систему сил эквивалентной системой, все силы которой приложенные в точке В
(Рис. 3.10, б). Равнодействующую системы, прилагаемую в той же точке В, обозначим 



Известно, что 
Итак, получили равенство
Теорема доказана.
Уравнение (3.13) является математическим записи теоремы Вариньона для пространственной системы сходящихся сил.
В случае плоской системы сходящихся сил теорема Вариньона запишется так:
Итак, момент равнодействующей плоской системы сходящихся сил относительно некоторого центра (точки), лежащий в плоскости действия сил, равна алгебраической сумме моментов составляющих сил относительно этого самого центра (точки).
Рассмотрим пример на применение теоремы Вариньона.
Задача. На согнутый под прямым углом стержень АВС действуют силы 

Решение.
Для определения момента силы 
Разложим силу 




Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Центр масс
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки
Для
характеристики вращательного движения
под действием силы вводится понятие
момента силы относительно точки.
Моментом
силы относительно точки называется
вектор

радиуса-вектора
соединяющего центр O с точкой приложения
силы точки А, на саму силу

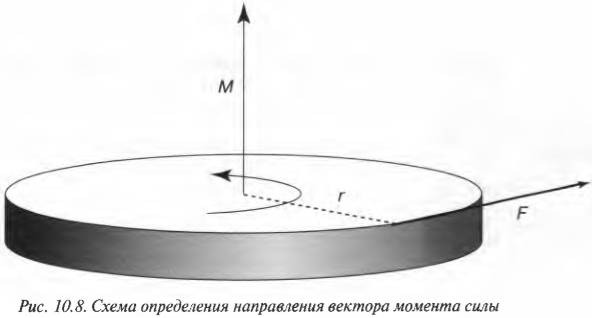
Момент
силы относительно центра в плоскости.
Сила
F
в плоскости XOY

Момент
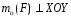

алгебраическое значение момента в
плоскости системы сил и модуль

численно удвоенной площадью ∆ OAB
где
h-плечо
Вычислим

радиус-вектора
Раскроем
векторные произведения по формуле
векторной алгебры:


орты
где


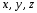
2)
Координатный способ задания движения
Пусть
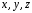
неподвижная декартовая система
координат. Можно задать значения
координат точки для каждого момента
времени.

движения точки в координатной форме
Эти уравнения
являются параметрическими уравнениями
траектории точки
Векторный способ
задания движения
Движение точки
при векторном способе изучения движения
задается радиус-вектором

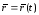
уравнение движения точки
Пусть
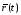
изменении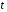
Эта кривая является траекторией точки.
Скорость точки
направлена по касательной к траектории
и вычисляется по формуле
Ускорение:
Экзаменационный
билет №7
-
Момент силы
относительно оси. -
Поступательное
движение твердого тела. Скорость и
ускорение твердого тела.
1) Момент силы относительно оси.
Будем
называть проекцию на эту ось вектора
момента

е.
на
оси

С
помощью формулы (2) момент силы относительно
оси можно вычислить, зная проекции силы
и координаты точки ее приложения.
Зная
момент силы относительно осей

2) Определение
Поступательным
движением твердого тела называется
такое его движение, при котором любой
отрезок, связанный с этим телом, сохраняет
неизменное направление в пространстве.
При поступательном
движении все точки тела имеют в каждый
момент времени одинаковые перемещения.
Траектории,
описываемые точками твердого тела,
одинаковы.
Теорема:
При поступательном движении твердого
тела траектории, скорости и ускорения
всех точек тела одинаковы.
Док-во: выберем
две точки А и В твердого тела радиусы
векторов этих точек удовлетворяют
условию:
Где АВ=const
Продифференцируем
это уравнение:
получим:
Продифференцируем
по времени:


Для описания
поступательного движения тела достаточно
знать движение его одной точки.
Уравнения движения
точки будут уравнениями движения всего
тела. Часто этой одной точкой является
центр масс твердого тела. Движение
точки в пространстве описывается тремя
независимыми уравнениями:
Для плоского
случая:
Поступательное
движение не накладывает условий на
уравнение движения, точки могут описывать
какие угодно траектории—как прямолинейные,
так и криволинейные.
Основное свойство
поступательного движения твердого
тела определяется теоремой:
При поступательном
движении твердого тела все его точки
описывают одинаковые траектории и в
каждый момент времени имеют одинаковые
по величине и направлению скорости и
ускорения.
Экзаменационный
билет №8
-
Аналитический
метод вычисления моментов силы
относительно осей координат. -
Вращательное
движение тело вокруг неподвижной оси.
Кинематические характеристики
вращательного движения.
1)а)если
сила параллельна оси, то её момент
относительно этой оси равна нулю.
F
// z

0
б)
если линия действия силы пересекает
оси, то её моменты относительно этих
осей также равны нулю.
в)
если сила перпендикулярна к оси, например
к оси Y,
и кратчайшее расстояние между линией
действия силы и осью, например осью
x,равно
h,то
момент силы относительно оси х равен
произведению модуля силы на расстояние
между линией действия силы и осью.
г)
если сила старается развернуть твердое
тело вокруг оси против хода часовой
стрелки относительно наблюдателя,
стоящего на этой оси, то момент силы
относительно этой оси положительный
рис.а); если по ходу часовой стрелки-
отрицательный рис. б)
а)
4.
Сложение
параллельных сил, приложенных к твердому
телу направленных в одну сторону.
Найдем
равнодействующую 2х параллельных сил

в точке А и точке В твердого тела
Разложим
силу




силового треугольника рис.(а).Аналогично
найдем
помощью силового треугольника рис.(б)
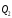
(а и б) соединим в рис. (с) таким образом,
вместо системы 2-х сил
сил
Найдем
равнодействующую из 4-х сил, так как

линии, противоположно направлены, то
они уравновешены и их сумма равна нулю.
Геометрическая
сумма
Равнодействующая
2-х действующих на абсолютно твердое
тело параллельных сил, направленных в
одну сторону равна по модулю сумме
модулей слагаемых сил, им параллельна
и направлена в ту же сторону.
Найдем
линию действия равнодействующей,
проведем через точку О прямую, параллельную
линиям действия слагаемых сил. Точку
пересечения этой прямой с АВ обозначим
С.
Треугольник
АСО подобен силовому треугольнику рис.
(а), так как их стороны параллельны.
∆ ВСО
подобен рис.(б)
Тогда
и
получим
Разделив
почленно первую пропорцию на вторую и
учтя, что 
тогда

Итак
Линия
действия равнодействующей 2-х действующих
на абсолютно твердое тело параллельных
сил, направленных в одну сторону,
проходят между точками приложения
слагаемых сил на расстояниях от этих
точек, обратно пропорционально модулям
этих сил.
2)
Вращением твердого тела вокруг
неподвижной оси называется такое его
движение, при котором две точки тела
остаются неподвижными в течение всего
времени движения. Неподвижными остаются
и все точки тела, расположенные на
прямой, проходящей через его неподвижные
точки. Эта прямая называется осью
вращения.
Через ось вращения
проведем неподвижную плоскость
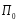
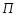
скрепленную с вращающимся телом. Тогда
в момент времени
положение подвижной плоскости и,
следовательно твердого тела определяется
углом между плоскостями
поворота измеряют в радианах. Если
известно число оборотов n за какой-то
промежуток времени, то угол поворота
равен:
φ = 2πn
Положение тела
относительно выбранной системы отсчета
определяется в любой момент времени
ускорением.
За положительное
направление отсчета принимается
вращение против часовой стрелки.
Траектории точек тела при его вращении
вокруг неподвижной оси является
окружность.
Угловая скорость
характеризует быстроту и направление
изменения угла поворота в данный момент
времени. Величина угловой скорости
равна первой производной от угла
поворота по времени:
ω =
Знак производной
определяет направление вращения. Если
ω > 0, то вращение происходит против
хода часовой стрелки.
Если ω < 0, то
вращение – по ходу часовой стрелки.
Угловая скорость
измеряется в рад/сек, в технике угловая
скорость это частота вращения, выраженная
в об/мин.
За 1 минуту тело
повернется на угол

если
число оборотов в минуту.
Угловое ускорение
характеризует быстроту и направление
изменения угловой скорости в данный
момент времени. Величина углового
ускорения равна первой производной от
угловой скорости по времени или второй
производной от угла поворота по времени:
ε =

Знак производной
определяет направление изменения
угловой скорости.
Если ε >0, то
угловое ускорение направлено против
хода часовой стрелки.
Если ε<0 , то
угловое ускорение направлено по ходу
часовой стрелки.
Размерность
углового ускорения
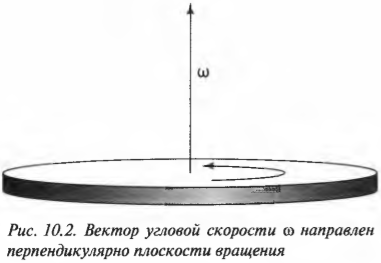
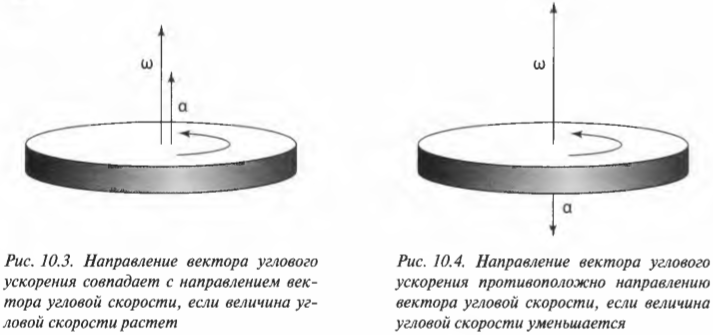
Вектор угловой
скорости —
это вектор, направленный по оси вращения
в ту сторону, откуда оно видно происходящим
против часовой стрелки, с модулем равным
модулю угловой алгебраической скорости

где

единичный вектор оси вращения
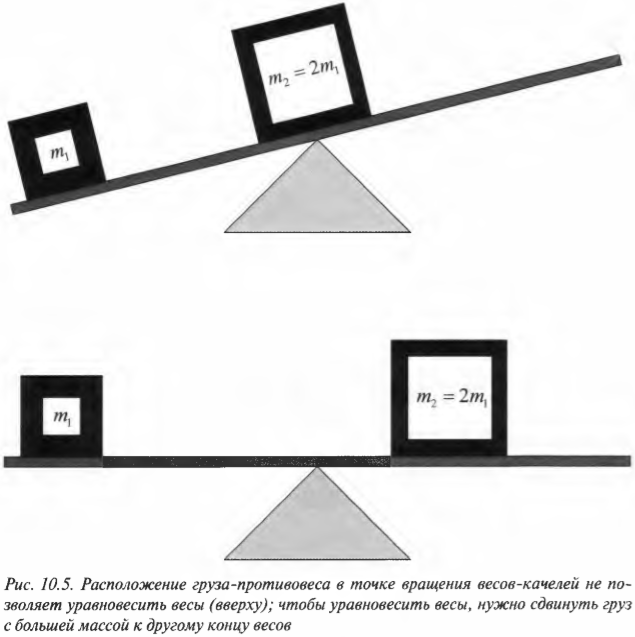
Вектор углового
ускорения
Угловая скорость
и угловое ускорение можно представить
в виде векторов, которые можно приложить
к любой точке на оси вращения, т.е. эти
векторы являются скользящими:
К- единичный вектор
оси OZ. Направление векторов угловых
скорости и ускорения определяются
знаком производных. Угловые скорости
и угловые ускорения являются главными
кинематическими характеристиками
вращательного движения и одинаковы
для всех точек в данный момент времени.
Экзаменационный
билет №9
-
Сложения параллельных
сил приложенных к твердому телу
направленных в одну сторону. -
Определения
скоростей и ускорения точек вращающегося
тела.
1)
Равнодействующая
2-х действующих на абсолютно твердое
тело параллельных сил, направленных в
одну сторону равна по модулю сумме
модулей слагаемых сил, им параллельна
и направлена в ту же сторону.
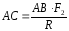
2)
Т.к. траектории точек вращающегося тела
окружности, при определении скоростей
и ускорений удобно воспользоваться
естественным способом задания движения
Дуговая координата
определяющая положение точки на
траектории связана с углом поворота и
радиусом
Для алгебраической
скорости точки М
Модуль скорости
точки М
Вектор скорости
направлен по касательной к траектории
перпендикулярно радиусу.
Вектор скорости
любой точки тела, вращающегося вокруг
неподвижной оси равен по модулю
произведению модуля скорости на
кратчайшее расстояние от точки до оси
и направлен в сторону вращения
перпендикулярно к плоскости
Ускорение точки
М

Угол, образованный
вектором ускорения точки М с радиусом
окружности обозначим

Из формулы следует,
что

Экзаменационный
билет №10
-
Сложения параллельных
сил приложенных к твердому телу
направленных в разные стороны
(антипараллельные силы). -
Векторные выражения
скорости и ускорения точек вращающегося
тела. Равномерное и неравномерное
движения.
1)
Рассмотрим тело, на которое действуют
две параллельные силы


Возьмем
на продолжении
силы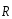
//
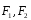
так что
и
удовлетворялось равенство
Сложим
силы
т.е.
равна модулю


0
и их можно отбросить.
=>

равнодействующая.
Определение:
Равнодействующая
2-х антипараллельных сил равна по модулю
разности модулей этих сил, им параллельна
и направлена в сторону большей силы.
Линия действия равнодействующей
проходит вне отрезка соединяющего
точку приложения слагаемых сил, на
расстояниях от этих точек, обратно
пропорционально модулям сил.
2)
Равномерным называется вращение, при
котором угловая скорость постоянна по
модулю и направлению.
Откуда


После интегрирования
получим: (7.1)
Выражение (7.1)
называется законом равномерного
вращения.
При равномерном
вращении угловую скорость можно
определить, если задано число оборотов
в минуту по формуле: (7.2)
где
n
– число оборотов в минуту
Равнопеременным
называют вращение, при котором угловое
ускорение постоянно по величине и
направлению

Откуда
Рис. 1.
Находим
(7.3)
После разделения
переменных и интегрирования
Получим:
Закон равнопеременного вращения.
(7.4)
Если ω
и ε
имеют одинаковые знаки, то вращение
равноускоренное ( рис.1 а). Скорость и
вращательное ускорение направлены в
одну сторону.
Если ω
и ε
имеют разные знаки. То вращение
равнозамедленное. Скорость и вращательное
ускорение направлены в разные стороны.
(рис. 1 б).
Центростремительное
ускорение в обоих случаях направлено
к оси вращения.
Модуль скорости
точки вращающегося тела
равен модулю
векторного произведения
Направление
скорости совпадает векторного
произведения
Следовательно

формула Эйлера
Для получения
векторных формул для ускорений точек
вращающегося тела продифференцируем
это выражение по времени.
Воспользовавшись
определением векторного произведения,
нетрудно убедиться в том, что первое
слагаемое — вращательное, а второе —
центростремительное ускорение.
Т.е.
Экзаменационный
билет №11
-
Пара сил и её
момент. Теорема о моменте сил пары
относительно произвольной точки. -
Плоскопараллельное
движение твердого тела. Уравнение
плоскопараллельного движения.
1)
Определение:
Две
равные, параллельные, но противоположно
направленные силы, приложенные в разных
точках тела, наз парой
сил.
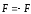

сил
Пара
сил создает вращательное действие на
тело.
Пара
сил характеризуется:
1)плоскостью
действия сил.
2)направлением
вращения пары сил в плоскости.
3)момент
пары сил- это численная характеристика
вращательного действия.
Момент
пары равен произведению одной из сил
пары (модуля) на плечо пары, взятого с
определенным знаком.
Плечо
пары
: кратчайшее расстояние(d)
между линиями действия сил, составляющих
пару.
Момент
пары сил положителен, если пары сил
стремится вращать объект в сторону
противоположную в ращению часовой
стрелки рис.а) и отрицательным, если в
сторону вращения часовой стрелки рис.б)
Вектор
момента
направлен перпендикулярно к плоскости
действия пары сил в такую сторону, чтобы
смотря навстречу этому вектору, видеть
пару сил, стремящейся вращать плоскость
её действия в сторону, обратную вращения
часовой стрелки
Теорема
о моменте сил пары относительно
произвольной точки:
Сумма
моментов сил пары относительно любой
точки, лежащей в плоскости действия
пары равны моменту этой пары.
2)
Определение
Плоским движением
твердого тела называется такое его
движение, при котором каждая точка
движется все время в одной и той же
плоскости.
Плоскости, в которых
движутся отдельные точки ,параллельны
между собой и параллельны одной и той
же неподвижной плоскости.
Звенья большинства
машин и механизмов совершает
плоскопараллельное движение.
Пусть твердое тело
совершает плоское движение параллельной
плоскости По
любая прямая перпендикулярная к этой
плоскости и жестко связанное своими
точками с движущим телом будет двигаться
поступательно, то есть все точки будут
двигаться одинаково. Следовательно,
для изучения движения точек лежащих
на рассмотриваемой прямой достаточно
изучить движение одной точки М.
Примерами
плоскопараллельного движения служат:
1)скольжение стержня
2)качение цилиндра
и т.д.
Положение плоской
фигуры можно задать двумя координатами
полюса и одним углом между отрезком
жестко связанным с телом и направлением
одной из неподвижных осей (х,у,z).
Xа=xа(t)
Yа=yа(t)
Zа=zа(t)
уравнения плоскопараллельного
движения
Вид первых двух
уравнений зависит от выбора полюса.
Закон изменения угла от выбора полюса
не зависит.

y
y’
B
x’
A0
O
x
Экзаменационный
билет №12
-
Эквивалентность
пар сил. -
Определение
скорости точек тело при плоском
движении.
1)
Сформулируем условия эквивалентности
двух пар сил, используя наиболее общую
характеристику пары сил — ее векторный
момент.
Известно,
что пару сил можно поворачивать и
переносить в плоскости её действия. От
этого действие пары сил на твердое тело
не изменяется, если алгебраический
момент пары сил, остается таким же.
Следовательно,
векторный момент пары сил можно
переносить параллельно самому себе в
любую точку твердого тела, лежащую в
плоском действии пары сил. Так как пару
сил можно переносить в параллельную
плоскость, то векторный момент пары
сил можно переносить параллельно самому
себе в любую точку тела, не изменяя
действия пары сил на твердое тело.
Поэтому векторный
момент пары сил, действующий на твердое
тело, есть свободный вектор, т.е. он
характеризуется только величиной и
направлением, а точкой приложения у
него может быть любая точка и, векторный
момент пары сил не обязательно
прикладывается посередине отрезка,
соединяющего точки приложения сил пар.
2)
Теорема:
Ускорение
точки плоской фигуры равно сумме
ускорения полюса и ускорения данной
точки во вращательном движении вокруг
полюса.
Доказательство:
Дано:

Ускорение точки В в её сложном движении:
где относительное
движение-вращение вокруг полюса А.
Переносное движение
– поступательное вместе с полюсом,
Экзаменационный
билет №13
-
Приведение сил к
центру. -
Мгновенный центр
скоростей. Способы нахождения мгновенного
центра скоростей.
1)
Рассмотрим систему состоящую из любого
количества сил, как угодно расположенных
в пространстве. Такую систему сил будем
называть произвольной пространственной
системой сил. Прежде чем перейти к её
преобразованию, приведем вспомогательную
теорему о параллельном переносе сил
Теорема:
Силу, приложенную к абсолютно твердому
телу, можно, не изменяя оказываемого
его действия на тело, переносить
параллельно ей самой в любую точку
тела, добавляя при этом пару с моментом,
равным моменту переносимой силы,
относительно новой точки ее приложения.
Доказательство:
Пусть имеем силу F,
приложенную в точке А. Известно, что
силу, приложенную к твердому телу, можно
переносить вдоль её линии действия, от
чего действие силы на твердое тело не
изменяется. Теперь докажем, что силу
можно переносить на другую параллельную
линию действия. Но этот перенос, следует
компенсировать добавлением соответствующей
пары сил. Приложим в точку В, выбранной
за центр приведения, систему двух равных
по величине, но противоположных по
направлению сил



Система сил
ее можно добавить к любой заданной
системе сил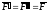

В
A
Тогда


присоединенной парой. Итак вместо силыF,
приложенной в точке А получена сила
F’,
равная ей по величине и направлению,
но приложенная в точке В и присоединенная
пара сил (F,
F’’)
векторный момент которой
Процесс замены
силы
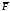

F’’)
называется приведением силы

Итак, если
рассматривается система сил, то все
силы( пользуясь данной теоремой) можно
привести к некоторому центру – в этом
и состоит метод, предложенный Пуансо.
Луи Пуансо (1777-1859
г.) французский математик, механик,
автор геометрической статики (1803 г.).
Ввел в механику понятие момента силы,
пары сил, разработал теорию пар и метод
приведения системы сил. Много сделал
в кинематике, динамике.
2)
Мгновенным
центром скоростей
(МЦС) называется точка Р
плоской
фигуры, скорость которой в данный момент
времени равна нулю. Рассмотрим теперь
различные случаи определения
положения МЦС.
1.
Способ нахождения МЦС по известной
скорости некоторой точки плоской фигуры
и по ее угловой скорости был рассмотрен
выше. 2. Если известны направления
скоростей двух точек плоской фигуры

и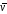
и эти скорости не параллельны друг
другу, то для нахождения МЦС необходимо
из точек А
и В
восставить к этим скоростям перпендикуляры
до их пересечения (рис. 5, а). При этом
ω=

3. Если
скорости двух точек плоской фигуры

и
параллельны друг другу и перпендикулярны
отрезку АВ, то для нахождения МЦС
используется условие пропорциональности
модулей скоростей точек расстояниям
от этих точек до МЦС, что реализуется
при построениях, ясных из рис. 5, б и рис.
5, в.

A

P


B
ω
a)
б)
в)
Рис.5
ω=0 ω=0
а)
б) в)
Рис.6
4. Если
при этом окажется, что

=
(рис.6, а), или если скорости двух точек
плоской фигуры
и
параллельны друг другу и не перпендикулярны
отрезкуАВ
(рис. 6, б), то МЦС располагается в
бесконечности. При этом угловая скорость
тела
ω = 0,
а скорости всех точек тела векторно
равны. Это случай мгновенно поступательного
движения.
5. При
качении какого-либо тела (например,
колеса) по неподвижной поверхности
(рис. 6, в) положение МЦС определяется
из условия отсутствия взаимного
проскальзывания (т. е. равенства скоростей
соприкасающихся точек). МЦС — это точка
соприкосновения тела с поверхностью.
Экзаменационный
билет №14
-
Приведение системы
сил произвольно расположенных к силе
и паре сил. -
Мгновенный центр
ускорения. Способы нахождения мгновенного
центра ускорений.
1)
Теорема: Любую
произвольную систему сил, действующих
на твердое тело, можно в общем случае
привести к силе и паре сил. При этом
сила равна главному вектору системы
сил и приложена в центре приведения, а
пара имеет момент равный главному
моменту системы сил, относительно
центра приведения.
Доказательство:
Пусть дана произвольная система сил

Выберем произвольную
точку О за центр приведения и каждую
силу заданной системы сил приведем к
точке О, добавляя при каждом переносе
присоединенную пару с моментом, равным
моменту данной силы, относительно точки
О. Таким образом система из n
сил заменена системой из 3n
сил, т.е. в точке О приложена система
сходящихся сил

присоединенных пар сил
Векторный момент
присоединенных пар сил можно выразить
через векторные моменты заданных сил
Образованную в
точке О систему сходящихся сил

Заменим одной силой, их равнодействующей,
равной векторной сумме
или
Геометрически
изображается замыкающим вектором
силового многоугольника, построенного
на этих силах.
Для системы
сходящихся сил

– равнодействующая .
Для заданной
системы сил

– векторная сумма или главный вектор
2)
Мгновенным центром ускорений (МЦУ)
называется точка Q плоской фигуры,
ускорение которой в данный момент
времени равно нулю: aQ=0.
Если выбрать в качестве полюса МЦУ , то
теорема о сложении ускорений дает
Ускорение точек
плоской фигуры- это их ускорения в
относительном вращении фигуры вокруг
мгновенного центра ускорений.
Согласно формуле,
получим для модуля ускорения точки
плоской фигуры соотношение:
-ускорения точек
плоской фигуры пропорциональны
расстояниям от этих точек до МЦУ, а
коэффициентом пропорциональности
является

В каждый момент
времени имеет место распределение
ускорений точек плоской фигуры,
показанное на рисунке, где угол

Экзаменационный
билет №15
-
Главный вектор,
главный момент сил. Вычисления главного
вектора и главного момента сил. -
Определение
ускорение точек тело при плоском
движении.
1)
а) Главный вектор.
Для любой системы
сил

вектор, равный сумме этих сил:
Главный вектор
геометрически изображается замыкающей
силового многоугольника, построенного
на заданных силах.
Проектируя обе
части векторного равенства на координате
оси, для произвольной, пространственной
системы сил получаем:
По проекциям
определяем величину главного вектора
и косинусы углов с осями координат.
Для плоской системы
сил, если выбрать ось OZ

векторR
лежит в плоскости OXY
и следовательно

б) Главный
момент сил.
Систему присоединенных
пар сил

заменить одной парой сил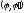


главным моментом.
Главный момент

присоединенных пар
Индекс 0 у величины
главного момента означает, что за центр
приведения взята точка 0.
Итак, главный
момент системы сил является вектором,
замыкающим векторный многоугольник,
образованный при сложении векторных
моментов сил системы относительно
выбранного центра
Проектируя обе
части векторного равенства на
прямоугольные оси координат и используя
связь момента силы относительно оси с
проекциями векторного момента этой
силы относительно точки на оси, имеем:
Величина главного
момента и косинусы его углов с осями
координат
Для плоской системы
сил, если ось OZ

OY
в плоскости действия сил. Главный момент
плоской системы сил

2)
Теорема:
Ускорение
точки плоской фигуры равно сумме
ускорения полюса и ускорения данной
точки во вращательном движении вокруг
полюса.
Доказательство:
Дано:

Ускорение точки В в её сложном движении:
где относительное
движение-вращение вокруг полюса А.
Переносное движение
– поступательное вместе с полюсом,
Экзаменационный
билет №16
-
Лемма Пуансо.
-
Сложное движение.
Основные понятия и определения. Скорость
и ускорение при сложном движении.
1)Лемма
Пуансо.Мы уже выяснили, что силу,
приложенную к ТТ, можно переносить
вдоль линии ее действия. Сейчас мы
увидим, что при определенных условиях
эту силу можно переносить даже параллельно
своему первоначальному положению.
Лемма Пуансо. Действие силы Р, приложенной
к ТТ не изменится, если эту силу перенести
в любую точку О этого тела – центр
приведения, добавив пару сил с моментом,
равным моменту силы Р относительно
центра приведения. Для доказательства
рассмотрим силу Р, приложенную к телу
в точке А (Рис.1а).
Согласно
аксиоме 3 действие силы P⃗ на ТТ не
изменится, если к ней добавить
уравновешенную систему сил:
(P′→,P′′→)∼0.
Выберем
силы этой уравновешенной системы так,
чтобы они были равны по модулю и
параллельны силе P⃗
P′→=P⃗
=−P′′→
Тогда
полученную систему трех сил можно
трактовать как силу P′→ , приложенную
в центре О, и пару сил (P⃗ ,P′′→) с
моментом М(P⃗ ,P′′→)=МО(P⃗ ) :
P⃗
∼(P⃗
,(P′→,P′′→))∼(P′→,(P⃗
,P′′→))
Лемма
доказана.
Сила
P′→, приложенная в точке О, называется
приведенной, а пара (P⃗ ,P′′→) –
присоединенной.
Напомним,
что пару (P⃗ ,P′′→) можно заменить
моментом M⃗ , величина которого равна
моменту силы P⃗ относительно центра
приведения О (Рис.1в), поэтому:
P⃗
∼(P′→,(P⃗
,P′′→))∼(P′→,M⃗
)
2)
Сложным — называется такое движение
точки (тела), которое рассматривается
одновременно в разных системах отсчета.
Например: пассажир,
перемещается в вагоне движущегося
поезда, человек перемещающийся по
лестнице движущегося эскалатора.
При описании
сложного движения точки одну из систем
отсчета считают неподвижной
(её называют основной), другая же
рассматривается как подвижная
.
О,X/,Y/,Z/-основная
система координат.
O,X,Y,Z-
подвижная система координат.
(.) М- движущаяся
точка.
В таком случае
сразу можно рассматривать три движения:
абсолютное, относительное, переносное.
А) Абсолютное
движение —
называется движение точки по отношению
к основной системе отсчета. Соответственно
скорость и ускорение точки по отношению
к основной система отсчета называется
абсолютным ускорением
Относительным
движением
— называется движение точки по отношению
к подвижной системе отсчета. Соответственно
скорость и ускорение точки по отношению
к подвижной системе отсчета называется
относительной скоростью

относительным ускорением
от латинского relativus-
относительный). Положение точки М
относительно неподвижной системы
отсчета определяется радиус вектором
радиус-вектора

Б) Движение подвижной
системы отсчета относительно неподвижной
системы отсчета называется переносным
движением. Движущаяся точка в разные
моменты времени занимает различное
положение в подвижной системе отсчета,
т.е. совпадает с различными ее точками.
Переносной
скоростью

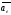
подвижной системы отсчета , с которой
в данный момент времени совпадает
движущаяся точка.
Экзаменационный
билет №17
-
Теорема Пуансо.
Основные теория статики. -
Теорема о сложении
скоростей.
1)
Осн теор статики (теорема Пуансо): Всякую
пространственную систему сил в общем
случае можно заменить эквивалентной
системой, состоящей из одной силы, прило
женной в какой-либо точке тела (центре
приведения) и равной глав ному вектору
данной системы сил, и одной пары сил,
момент которой равен главному моменту
всех сил относительно выбранного центра
приведения.
2)
При сложном движении точки абсолютная
скорость точки равна векторной сумме
относительной и переносной скорости.
Доказательство:
Пусть o1,
x1,
y1,
z1
– неподвижная система отсчета; o,
x,
y,
z
– подвижная система отсчета.x,
y,
z-
координаты движущейся точки М в подвижной
системе отсчета; r,
r0-радиус-векторы
точек М и О в неподвижной системе
отсчета; ρ — радиус-вектор точки М в
подвижной системе отсчета.
из рисунка
i,j,k-орты
подвижной системы
перейдем к записи
для выражения скоростей:
Экзаменационный
билет №18
-
Главный вектор,
главный момент системы сил. Формулы
для их вычисления. -
Теорема о сложении
ускорений.
1)
а) Главный вектор.
Для любой системы
сил
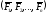
вектор, равный сумме этих сил:
Главный вектор
геометрически изображается замыкающей
силового многоугольника, построенного
на заданных силах.
Проектируя обе
части векторного равенства на координате
оси, для произвольной, пространственной
системы сил получаем:
По проекциям
определяем величину главного вектора
и косинусы углов с осями координат.
Для плоской системы
сил, если выбрать ось OZ

векторR
лежит в плоскости OXY
и следовательно
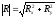
б) Главный
момент сил.
Систему присоединенных
пар сил
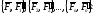
заменить одной парой сил


главным моментом.
Главный момент

присоединенных пар
Индекс 0 у величины
главного момента означает, что за центр
приведения взята точка 0.
Итак, главный
момент системы сил является вектором,
замыкающим векторный многоугольник,
образованный при сложении векторных
моментов сил системы относительно
выбранного центра
Проектируя обе
части векторного равенства на
прямоугольные оси координат и используя
связь момента силы относительно оси с
проекциями векторного момента этой
силы относительно точки на оси, имеем:
Величина главного
момента и косинусы его углов с осями
координат
Для плоской системы
сил, если ось OZ
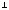
OY
в плоскости действия сил. Главный момент
плоской системы сил

2)
Абсолютное ускорение точки равно
векторной сумме относительного
переносного и Кориолисово ускорение.
Получим теперь
выражение для ускорения движущейся
точки.
1)
2)
3)
Сравнивая три
формулы мы видим, что в выражении для
абсолютного ускорения кроме переносного
и относительного входит ещё одна группа
слагаемых, которая называется кориолисовым
ускорением.
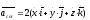
Справка: Густав
Кориолис (1792-1843) французский механик,
описывающий сложное движение точки.
Основные его работы, относятся к
аналитической механике и динамике
машин. Ввел коэффициент ½ в кинетическую
энергию.
Экзаменационный
билет №19
-
Условие равновесия
произвольной пространственной системы
сил. Условия равновесия системы
параллельных сил. -
Теорема Кориолиса.
Ускорение Кориолиса и его анализ.
1)
Условие равновесия пространственной
системы сил.
Произвольной
пространственной системой сил называется
система сил линии действия которых не
лежат в одной плоскости.
Согласно основной
теоремы статики (теореме Пуансо), любую
произвольную систему сил, действующих
на твердое тело, можно заменить
эквивалентной системой, состоящей из
силы (главного вектора системы) и пары
сил (главного момента сил).
Отсюда вытекает
условие равновесия произвольной
пространственной системы сил:
В геометрической
форме: для
равновесия произвольной пространственной
системы сил необходимо и достаточно,
чтобы главный вектор и главный момент
системы равнялись нулю.
В аналитической
форме: для
равновесия произвольной пространственной
системы сил необходимо и достаточно,
чтобы суммы проекций всех сил на три
координатные оси и суммы моментов всех
сил относительно этих осей были равны
нулю.
Условие равновесия
могут быть использованы для решения
задач на равновесие при определении
неизвестных величин (реакций связей).
Чтобы задача была
статистически определимой, число
неизвестных должно быть не более 6.
В частности для
системы параллельных сил условиями
равновесия являются следующие равенства:
2)
Теорема о сложении ускорений (т.Кориолиса)
Абсолютное
ускорение точки равно векторной сумме
относительного переносного и Кориолисово
ускорение.
Получим теперь
выражение для ускорения движущейся
точки.
1)
2)
3)
Сравнивая три
формулы мы видим, что в выражении для
абсолютного ускорения кроме переносного
и относительного входит ещё одна группа
слагаемых, которая называется кориолисовым
ускорением.

Справка: Густав
Кориолис (1792-1843) французский механик,
описывающий сложное движение точки.
Основные его работы, относятся к
аналитической механике и динамике
машин. Ввел коэффициент ½ в кинетическую
энергию.
Экзаменационный
билет №20
-
Вторая и третья
формы условий равновесия. -
Введение в
кинематику. Задачи кинематики.
1)
Уравнения равновесия могут быть записаны
иначе:
∑xi=0;
∑MA=0;
∑MB=0.
Это
вторая форма уравнений равновесия,
причем ось Ox не должна быть перпендикулярна
линии, проходящей через точки A и B
.
∑MA=0;
∑MB=0;
∑MC=0.
Это
третья форма уравнений равновесия,
причем точки A , B и C не должны лежать на
одной прямой.
При
действии на тело плоской системы
параллельных сил одно из уравнений
исчезает и остаются два
уравнения:
∑xi=0;
∑Mo=0.
Для
пространственной системы параллельных
сил могут быть записаны три уравнения
равновесия:
∑zi
=0;
∑Mix=0;
∑Miy=0.
Для
системы сходящихся сил (линии действия
которых пересекаются в одной точке)
можно написать три уравнения для
пространственной системы:
∑xi=0;
∑yi=0;
∑zi=0
и
два уравнения для плоской
системы:
∑xi=0;
∑yi=0.
В
каждом из вышеприведенных случаев
число неизвестных, находимых при решении
уравнений, соответствует числу записанных
уравнений равновесия.
2)
Введение в кинематику. Задачи кинематики.
В кинематике
изучается движение точки или тела
независимо от причин вызывающих или
изменяющих его, т. е. независимо от сил.
Объектом изучения
в кинематике являются:
-
материальная
точка- тело конечной массы, геометрическая
точка, размерами которого можно
пренебречь. -
механическая
система — совокупность материальных
точек -
абсолютно твердое
тело — механическая система, расстояние,
между точками которого не меняется.
Задачи кинематики:
а) задать движение
материальной точки (системы) это значит
дать способ определения положения
точки (системы точек) в любой момент
времени.
б) определение
кинематических характеристик движения
точки (скорость, ускорение) по заданному
закону движения.
Экзаменационный
билет №21
-
Центр параллельных
сил. -
Системы отсчета.
1)Пусть
дана система параллельных сил приложенных
в точках и направленных в одну сторону
(рис. 1.32). Такая система сил может быть
приведена к равнодействующей, параллельной
заданным силам и направленной в ту же
сторону. Так как сила, приложенная к
абсолютно твердому телу, есть вектор
скользящий, то равнодействующую можно
приложить в любой точке на линии ее
действия. Выведем уравнение линии
действия равнодействующей параллельных
сил.
Теорема Вариньона
для системы сходящихся сил (теорема о
моменте равнодействующей).
Теорема:
Момент относительно центра 0
равнодействующей


расположенных в одной плоскости, равен
алгебраической сумме моментов сил
системы относительно того же центра.
Например, момент
силы
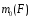
координат по формуле
гдеh
– неизвестно.
Воспользуемся теоремой Вариньона:
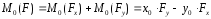
0
2)
Система отсчета.
Пространство, в
котором мы живем, является трехмерным.
Это значит, что положение точки в нем
характеризуется тремя числами. В
двухмерном —
двумя числами.
а) прямоугольная
система координат, в которой тремя
числами

характеризующие положение точки,
являются длины
б) цилиндрическая,
в которой тремя числами
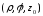


угол
длина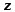
в) сферическая, в
которой тремя числами
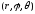


углы
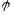
г) прямоугольная,
в которой двумя числами

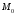

д) полярная, в
которой двумя числами



или расстояние от точки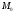
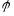
Числа, определяющие
положение точки в некоторой системе
координат, называется координатными
точками.
Экзаменационный
билет №22
-
Центр тяжести
твердого тела. -
Радиус-вектор.
Траектория. Скорость и ускорение точки.
-
Центром
тяжести твердого тела называется
геометрическая точка, жестко связанная
с этим телом, и являющаяся центром
параллельных сил тяжести, приложенных
к отдельным элементарным
частицам.
Радус-вектор:
Для
однородного тела положение центра
тяжести тела не зависит от материала,
а определяется геометрической формой
тела.
2)
Положение точки в пространстве удобно
характеризовать радиус-вектором. Если
начало вектора

то конец вектора опишет кривую наз.
годографом (записыватель пути) векторной
функции. Если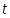
время, то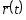
точки. Если радиус-вектор

Траектория
— геометрическое место последовательных
положений движущейся точки называется
траекторией.
Если в интервале
времени

прямолинейное, в противном случае ‒
криволинейное. В частности движение
точки называется круговым, если
траектория точки ‒ окружность.
Скорость точки
Пусть положение
движущейся точки
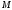
неподвижного центра О.Определяется в
момент времени

который соединяет движущуюся точку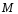
В другой момент
времени
положение
точки
За время
,
радиус-вектор изменится на
Средняя скорость

Средняя скорость
параллельна
и не имеет точки приложения:
вектор скорости
приложенных в точке М, направлен в
сторону ее движения, совпадает с
касательной к траектории в точке М.
Ускорение точки
Пусть движущаяся
точка М в момент времени

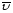
момент времени,
эта точка занимает положение
имея скорость
Чтобы изобразить
приращение скорости
за
времяперенесем вектор скорости
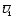
Среднее ускорение
точки

называется отношение
Ускорение точки
в момент времени

Экзаменационный
билет №23
-
Методы определения
центров тяжести. -
Способы задания
движения. Естественный способ задания
движения. Определение скорости при
естественном способе задания движения,
касательное и нормальное ускорение.
1)Наиболее
часто для нахождения центра тяжести
тела или фигуры применяют следующие
методы:
•
метод симметрии;
• метод
разбиения;
• метод
отрицательных масс.
Рассмотрим
приемы, применяемые в каждом из
перечисленных методов.
Метод
симметрии.Представим себе однородное
тело, которое имеет плоскость симметрии.
Выберем такую систему координат, чтобы
оси x и z лежали в плоскости симметрии.В
этом случае каждой элементарной частице
силой тяжести Gi с абсциссой yi = +a
соответствует такая же элементарная
частица с абсциссой yi = -a, тогда:yC =
Σ(Gixi)/ΣGi = 0.вывод: если однородное тело
имеет плоскость симметрии, то центр
тяжести тела лежит в этой плоскости.
Метод
разбиения.Этот метод заключается в
том, что тело разбивают на наименьшее
число частей, силы тяжести и положение
центров тяжести которых известны, после
чего применяют приведенные ранее
формулы для определения общего центра
тяжести тела.Допустим, что мы разбили
тело силой тяжести G на три части G’, G»,
G»’, абсциссы центров тяжести этих частей
x’C, x»C, x»’C известны.
Формула
для определения абсциссы центра тяжести
всего тела:xC = Σ(Gixi)/ΣGi.
Метод
отрицательных масс.Этот метод заключается
в том, что тело, имеющее свободные
полости, считают сплошным, а массу
свободных полостей – отрицательной.
Вид формул для определения координат
центра тяжести тела при этом не
меняется.Таким образом, при определении
центра тяжести тела, имеющего свободные
полости, следует применять метод
разбиения, но считать массу полостей
отрицательной.
2)
Пусть точка движется вдоль пространственной
криволинейной траектории. При естественном
способе задания движения точки задают
а) траекторию точки
б) начало и
направление увеличения дуговой
координаты
в) уравнение
движения как функцию времени
Положение точки
на траектории определяется расстоянием

изменения дуговой координат

закон изменения расстояния
Можно найти
положение точки в любой момент времени


сторону. Примером естественного способа
задания движения является движение
поезда: траектория и направление задано
рельсами, а уравнение движения –
расписанием.
Пусть движение
точки задано естественным способом.
Положение точки М на кривой можно
описать радиус-вектором
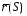
Из определения
скорости точки
умножим и разделим
на
где
как предел отношения
бесконечно малой дуги и хорде
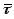
касательной, тогда

алгебраическая скорость точки. Из
определения ускорения

Производная


единичный вектор главной нормали

траектории в данной точке
таким образом:
Вектор ускорения
складывается на две составляющие –
касательное и нормальное

где

ускорения — это проекция вектора
ускорения на касательную, характеризует
изменение скорости по величине

ускорение, проекция вектора ускорения
на нормали, характеризует изменение
скорости по направлению
Экзаменационный
билет №24
-
Предмет статики.
Задачи статики. Сила, точка, эквивалентные
силы. -
Координатный и
векторный способы задания движения.
Скорость и ускорение.
1)
Предмет статики. Задачи статики. Сила,
точка и эквивалентные силы.
Содержанием
курса теоретической механики в
техническом вузе является изучение
равновесия и движения абсолютно твердых
тел, материальных точек и их систем
.Теоретическая механика является базой
для многих технических дисциплин(сопромат,
детали машин, ТММ).Курс теоретической
механики делится на три части:
Статика-раздел
механики, изучающая равновесие тел,
находящиеся под действием внешней
нагрузки.
Кинематика-
рассматривает
движение тел с геометрической стороны
без учета сил, вызывающих это движение
.
Динамика—
изучает движение тел под действием сил
.
Задачи статики
:
1)Упрощение
приложенных систем сил.
2)Установление
условий равновесия системы тел.
Основные понятия
статики :
Равновесием
тел называется состояние покоя или
движение с постоянной скоростью .
Материальной
точкой называется
тело, размерами которого можно
пренебречь.
Система
материальных точек- совокупность
материальных точек , взаимодействующих
между собой.
Абсолютно
твердое тело-система
материальных точек , расстояние между
двумя любыми точками которого остается
неизменным.
Сила является
основной мерой механического
взаимодействия тел.
(F1,F2)-система
тел.
Сила может быть
сосредоточенной (т.е. приложенной к
одной точке) и распределённой (действует
на все точки данного объема или данной
части поверхности)
а)
Р
Сосредоточенная
Сила
q
б)
Распределённая
сила, где
q-интенсивность
нагрузки[H/м]
Сила- величина
векторная и её действие на тело
определяется:
а)точкой приложения
б)числовым значением
в)направлением
Прямая по которой
направлена сила называют линией действия
силы.
За единицу измерения
силы принимают в системе СИ (ньютон)
[Н, кН].
Обозначается 
F,P,Q,R,T…)
Часто в теоретической
механике приходится решать задачи,
когда на тело действует не одна, а
несколько сил произвольно
расположенных.Совокупность нескольких
сил ,действующих на данное тело, называют
системой сил.
S1=(G,T,N)
S2=(T,G)
Если силы ,действующие
на тело или их линия действия сходятся
в одной точке ,то такая система сил
называется сходящейся
.
Если силы или их
линия действия параллельны ,то такая
система сил называется параллельной.
параллельная
система сил
сходящаяся система
сил
Если одну систему
сил действующих на свободное тело
можно заменить другой системой ,но
изменяя при этом состояние покоя или
движение в котором находится тело, то
такие две системы сил называются
эквивалентными.
Система сил под
действием которой тело находится в
равновесии называется уравновешенной
или эквивалентны
нулю.
|F1|=|F2|
{F1,F2)~0
Если данная система
сил эквивалента одной силе ,то эта сила
называют равнодействующая
данной системе .
2)
) Координатный
способ задания движения
Пусть

неподвижная декартовая система
координат. Можно задать значения
координат точки для каждого момента
времени.

движения точки в координатной форме
Эти уравнения
являются параметрическими уравнениями
траектории точки
Векторный способ
задания движения
Движение точки
при векторном способе изучения движения
задается радиус-вектором


уравнение движения точки
Пусть

изменении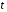
Эта кривая является траекторией точки.
Скорость точки
направлена по касательной к траектории
и вычисляется по формуле
Ускорение:
Экзаменационный
билет №25
-
Аксиомы статики.
-
Поступательное
движение твердого тела. Скорость и
ускорение твердого тела.
1)
Аксиомы статики
а) Аксиома
о равновесии системы двух сил
Если на тело
действуют две силы ,то тело может
находиться в равновесии тогда и только
тогда ,когда эти силы равны по модулю,
лежат на одной прямой и направлены в
противоположные стороны.
б)Аксиома
о добавлении(отбрасывании)системы сил
эквивалентной нулю.
Действие данной
системы сил на тело не изменяется ,если
к ней прибавить или от нее отнять
уравновешенную систему сил(т.е. систему
сил эквивалентную нулю).
(F1,F2,F3,…Fn)~(
F1,F2,F3,…Fn(F1’,F2’))
, если {F1’,F2’}~0
в) Аксиома
параллелограмма сил
Равновесие тела
не изменится ,если две силы ,приложенные
к одной точке заменить одной силой
равной их геометрической сумме.
{R}~{F1,F2}
R=F1+F2
R=
г) Аксиома
равенства действия и противодействия
Всякому действию
соответствует равное и противоположно
направленное противодействие.
д) Аксиома
отвердевания
Если деформированное
тело находится под действием некоторой
системы сил в равновесии, то равновесие
не нарушается ,если это тело отвердеет
,т.е. станет абсолютно твердым.
Из этой аксиомы
следует, что условие равновесия
,являющиеся необходимым и достаточным
для абсолютно твердого тела, являются
необходимыми, но не достаточными для
деформируемого тела.
Достаточные условия
равновесия деформируемых тел
устанавливается в курсе сопромата.
е) Аксиома
связей
всякую связь можно
отбросить и заменить её реакцией –
силой или системой сил.
Тело называется
свободным,
если его
движение в пространстве ничем не
ограничено. В противном случае тело
называется несвободным.
А тела,
ограничивающие перемещение данного
тела называются связями.
Силы, с
которыми связи действуют на данное
тело называются реакциями
связи. Т.е.
связь-это
ограничение, наложенное на движение
тела.
2) Определение
Поступательным
движением твердого тела называется
такое его движение, при котором любой
отрезок, связанный с этим телом, сохраняет
неизменное направление в пространстве.
При поступательном
движении все точки тела имеют в каждый
момент времени одинаковые перемещения.
Траектории,
описываемые точками твердого тела,
одинаковы.
Теорема:
При поступательном движении твердого
тела траектории, скорости и ускорения
всех точек тела одинаковы.
Док-во: выберем
две точки А и В твердого тела радиусы
векторов этих точек удовлетворяют
условию:
Где АВ=const
Продифференцируем
это уравнение:
получим:
Продифференцируем
по времени:


Для описания
поступательного движения тела достаточно
знать движение его одной точки.
Уравнения движения
точки будут уравнениями движения всего
тела. Часто этой одной точкой является
центр масс твердого тела. Движение
точки в пространстве описывается тремя
независимыми уравнениями:
Для плоского
случая:
Поступательное
движение не накладывает условий на
уравнение движения, точки могут описывать
какие угодно траектории—как прямолинейные,
так и криволинейные.
Основное свойство
поступательного движения твердого
тела определяется теоремой:
При поступательном
движении твердого тела все его точки
описывают одинаковые траектории и в
каждый момент времени имеют одинаковые
по величине и направлению скорости и
ускорения.
32
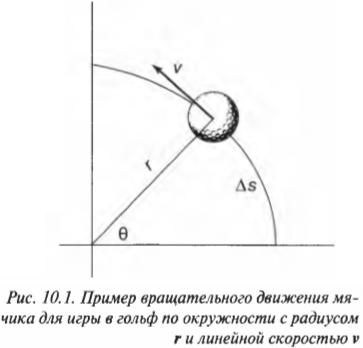
В этой главе…
- Переходим от поступательного движения к вращательному движению
- Вычисляем тангенциальную скорость и тангенциальное ускорение
- Выясняем связь между угловым ускорением и угловой скоростью
- Разбираемся с моментом силы
- Поддерживаем вращательное движение
Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!
Содержание
- Переходим от прямолинейного движения к вращательному
- Разбираемся с параметрами вращательного движения
- Вычисляем линейную скорость вращательного движения
- Вычисляем тангенциальное ускорение
- Вычисляем центростремительное ускорение
- Используем векторы для изучения вращательного движения
- Определяем направление угловой скорости
- Определяем направление углового ускорения
- Поднимаем грузы: момент силы
- Знакомимся с формулой момента силы
- Разбираемся с направлением приложенной силы и плечом силы
- Размышляем над тем, как создается момент силы
- Определяем направление момента силы
- Уравновешиваем моменты сил
- Простой пример: вешаем рекламный плакат
- Более сложный пример: учитываем силу трения при расчете равновесия
Переходим от прямолинейного движения к вращательному
Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.
Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:
- ( v=Delta{s}/Delta{t} ), где ( v ) — это скорость, ( Delta{s} ) — перемещение, a ( Delta{t} ) — время перемещения;
- ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
- ( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( v_0 ) — это начальная скорость, ( t_0 ) — это начальный момент времени, a ( t_1 ) — это конечный момент времени;
- ( v^2_1-v^2_0=2aDelta{s} ), где ( v_1 ) — это конечная скорость.
По аналогии можно легко вывести основные формулы вращательного движения:
- ( omega=Delta{theta}/Delta{t} ), где ( omega ) — угловая скорость, ( Delta{theta} ) — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
- ( alpha=Delta{omega}/Delta{t} ), где ( alpha ) — угловое ускорение, ( Delta{omega} ) — изменение угловой скорости, ( Delta{t} ) — время изменения угловой скорости;
- ( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 ), где ( omega_0 ) — это начальная скорость;
- ( omega^2_1-w^2_0=2as ), где ( omega_1 ) — это конечная скорость.
Разбираемся с параметрами вращательного движения
В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.
Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:
Допустим, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( 21,5pi ) радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.
Вычисляем линейную скорость вращательного движения
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ( mathbf{r} ) и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).
Угловая скорость связана с линейной скоростью соотношением ( v=romega ), которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.
Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ( L ) радиуса ( r ) выражается известной формулой ( L=2pi r ), а полный угол, который охватывает окружность, равен ( 2pi ) радиан. Соответственно, длина дуги окружности длиной ( Delta s ), охватывающая угол ( Deltatheta ), равна:
Из формулы прямолинейного движения
путем подстановки выражения для ( Delta s ) получим:
Поскольку:
где ( omega ) — угловая скорость, ( Delta{theta} )— угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} ), то:
Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5( pi ) радиан в секунду. Пусть радиус колеса ( r ) равен 40 см, тогда достаточно использовать следующую формулу:
Подставляя в нее значения, получим:
Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.
Вычисляем тангенциальное ускорение
Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение
где ( a ) — это ускорение, ( Delta v ) — изменение скорости, a ( Delta t ) — время изменения скорости, с угловым ускорением
где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?
Как мы уже знаем, линейная и угловая скорости связаны равенством
Подставим это выражение в предыдущую формулу линейного ускорения:
Поскольку радиус остается постоянным, то его можно вынести за скобки:
Поскольку угловое ускорение ( alpha=Deltaomega/Delta t ), то:
Итак, получаем следующую формулу связи между линейным и угловым ускорением:
Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.
Вычисляем центростремительное ускорение
Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):
Теперь, используя известную формулу связи линейной и угловой скорости ( v=romega ), получим:
По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.
Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ( 2pi ) радиан. Отсюда получаем угловую скорость Луны:
Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:
После подстановки этого значения в предыдущую формулу получим:
Средний радиус орбиты Луны равен 3,85·108 м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:
Зная это ускорение и массу Луны, которая равна 7,35·1022 кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:
Используем векторы для изучения вращательного движения
В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.
Определяем направление угловой скорости
Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ( omega ), оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.
Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).
Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.
Определяем направление углового ускорения
Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:
где ( alpha ) — угловое ускорение, ( Deltaomega ) — изменение угловой скорости, ( Delta t )— время изменения угловой скорости.
В векторной форме оно имеет следующий вид:
где ( mathbf{alpha} ) — вектор углового ускорения, а ( Deltamathbf{omega} ) — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.
А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.
Поднимаем грузы: момент силы
В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.
Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).
В верхней части рис. 10.5 показаны весы-качели с грузом массы ( m_1 ) на одном конце и грузом большей массы ( m_2=2m_1 ) посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ( m_2 ) к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ( m_1 ).
Знакомимся с формулой момента силы
Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).
На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ( F ) на плечо силы ( l ):
Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).
Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ( l ) равно 0,5 м и момент силы будет равен:
В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:
Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?
Разбираемся с направлением приложенной силы и плечом силы
Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.
Размышляем над тем, как создается момент силы
Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.
Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ( theta ). Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:
Однако в данном случае угол ( theta ) не является прямым.
В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.
Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:
Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).
Итак, получаем для момента силы для схемы Б на рис. 10.7:
Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:
Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.
Определяем направление момента силы
Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.
На рис. 10.8 показан пример силы ( mathbf{F} ) с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).
Уравновешиваем моменты сил
В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).
Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:
Иначе говоря, результирующая действующая сила равна нулю.
Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.
Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:
Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.
Простой пример: вешаем рекламный плакат
Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.
Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.
Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:
Иначе говоря:
где ( mathbf{M_п} ) — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.
Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:
где ( m ) = 50 кг — это масса плаката, ( mathbf{g} ) — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ( mmathbf{g} ) — сила тяжести плаката, а ( l_п ) = 3 м — это плечо силы тяжести плаката.
Подставляя значения, получим:
Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.
Момент силы со стороны болта определяется формулой:
где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.
Подставляя полученные выражения для моментов сил в формулу:
получим, что:
Отсюда с помощью простых алгебраических преобразований получим искомую силу:
Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.
Подставляя значения, получим искомый ответ:
Более сложный пример: учитываем силу трения при расчете равновесия
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.
Пусть лестница длиной ( l_л ) = 4 м стоит под углом ( theta ) = 45° к поверхности тротуара, работник имеет массу ( m_р ) = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ( mu_п ) = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?
Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:
- ( mathbf{F_с} ) — нормальная сила со стороны стены;
- ( mathbf{F_р} ) — вес рабочего;
- ( mathbf{F_л} ) — вес лестницы;
- ( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
- ( mathbf{F_т} ) — нормальная сила со стороны тротуара.
Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:
Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:
или
Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие
Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:
или
Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:
Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ( mathbf{M_р=[L_р!times! F_р]} ), весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):
или
или
Поскольку ( L_р=l_р ), ( L_л=l_л/2 ) (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ( alpha=360^{circ}-theta ), ( beta=360^{circ}-theta ) и ( gamma=theta ), то получим:
или
Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):
Зададимся вопросом: соблюдается ли условие
Из системы двух уравнений получим:
Итак, остается выяснить, соблюдается ли условие:
После подстановки значений получим:
Поскольку ( mu_т ) = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.
Глава 10. Вращаем объекты: момент силы
3.5 (69.52%) 42 votes

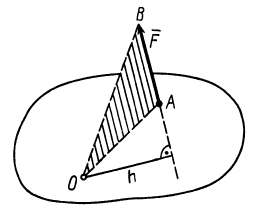

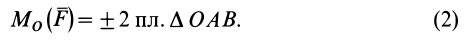
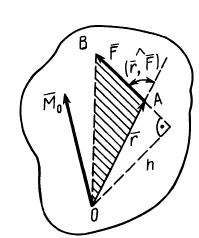
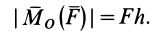
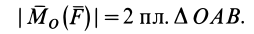

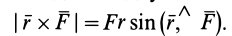
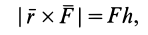
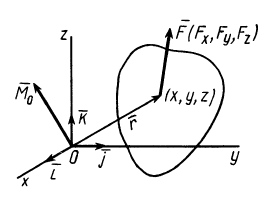
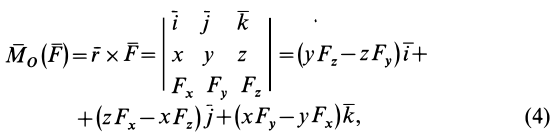
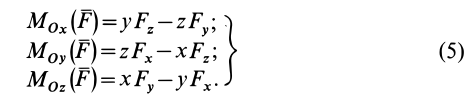
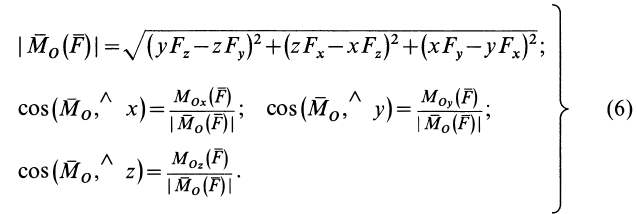
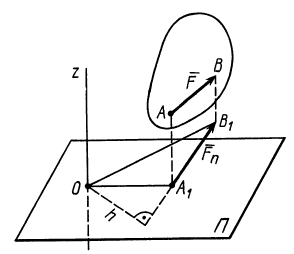
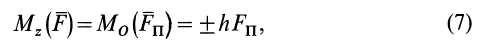
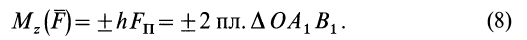
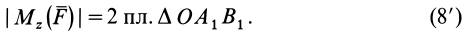
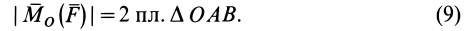
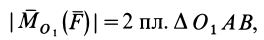
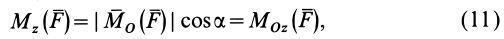
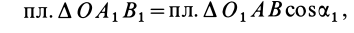
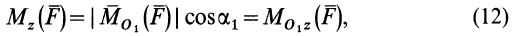
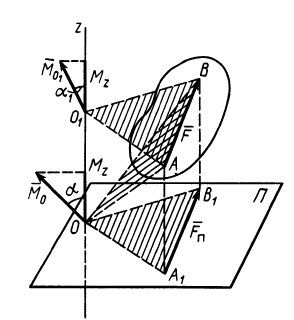
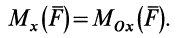
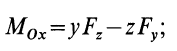
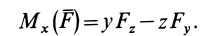
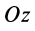
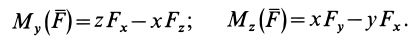
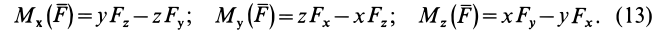
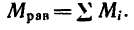
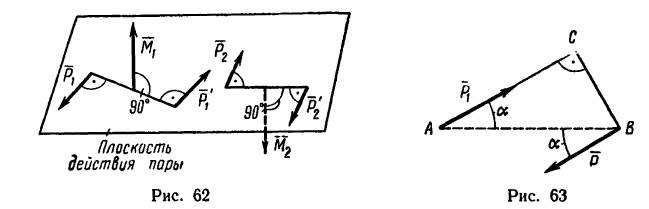
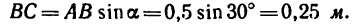
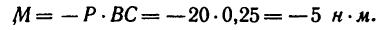
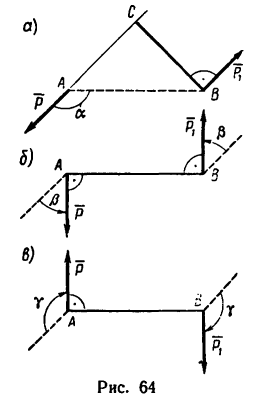
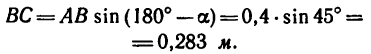
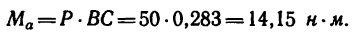
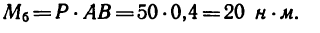
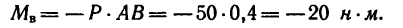
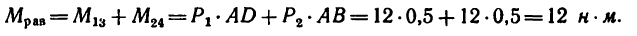
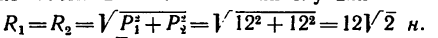
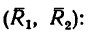
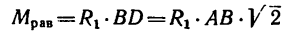
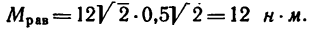
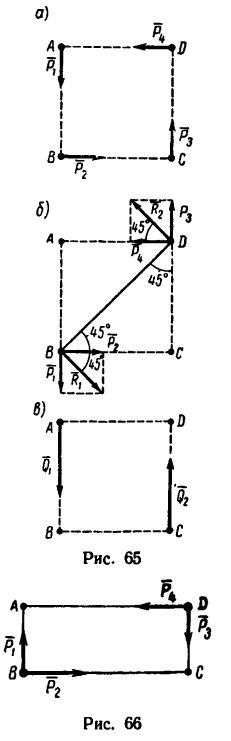
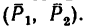
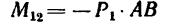
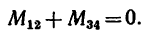
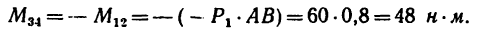
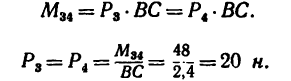
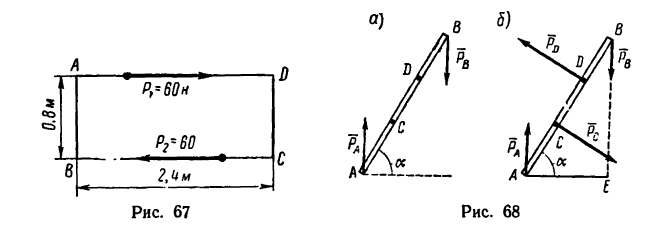
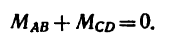
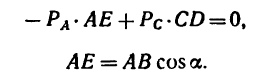
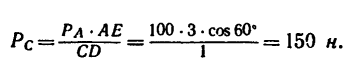
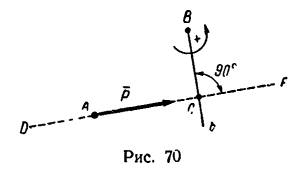
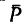 и центр моментов — точка В).
и центр моментов — точка В).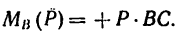
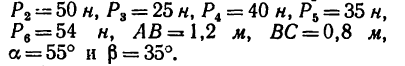
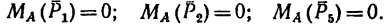
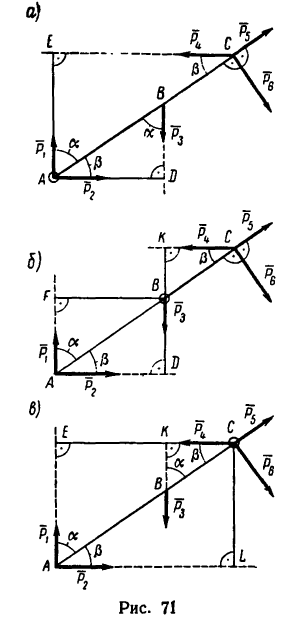
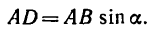
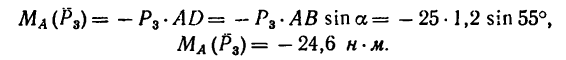
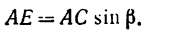
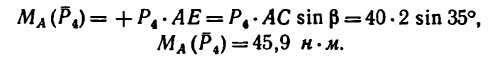
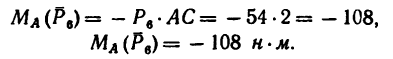
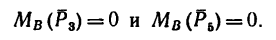
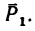
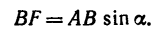
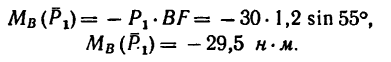
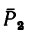
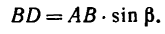
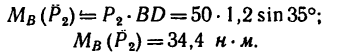
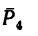
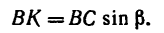
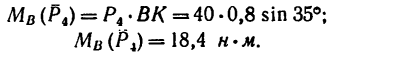
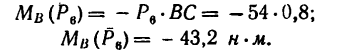
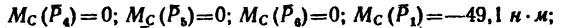
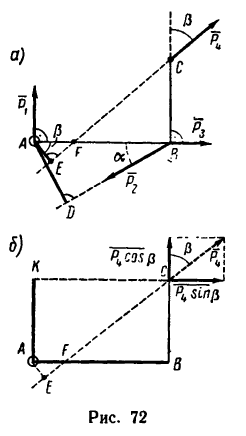
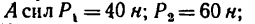
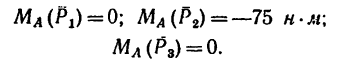
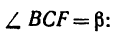
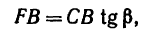
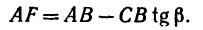
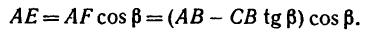
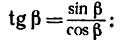
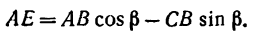
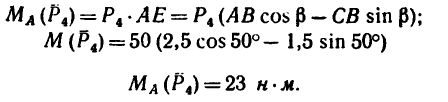
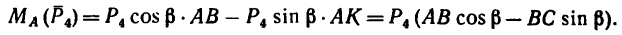
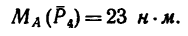
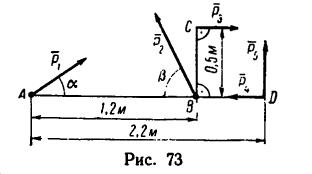


















































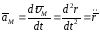









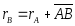












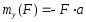

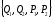
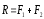
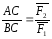





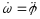











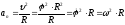
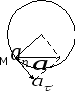

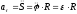
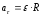






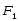



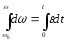





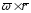



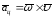
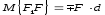









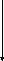



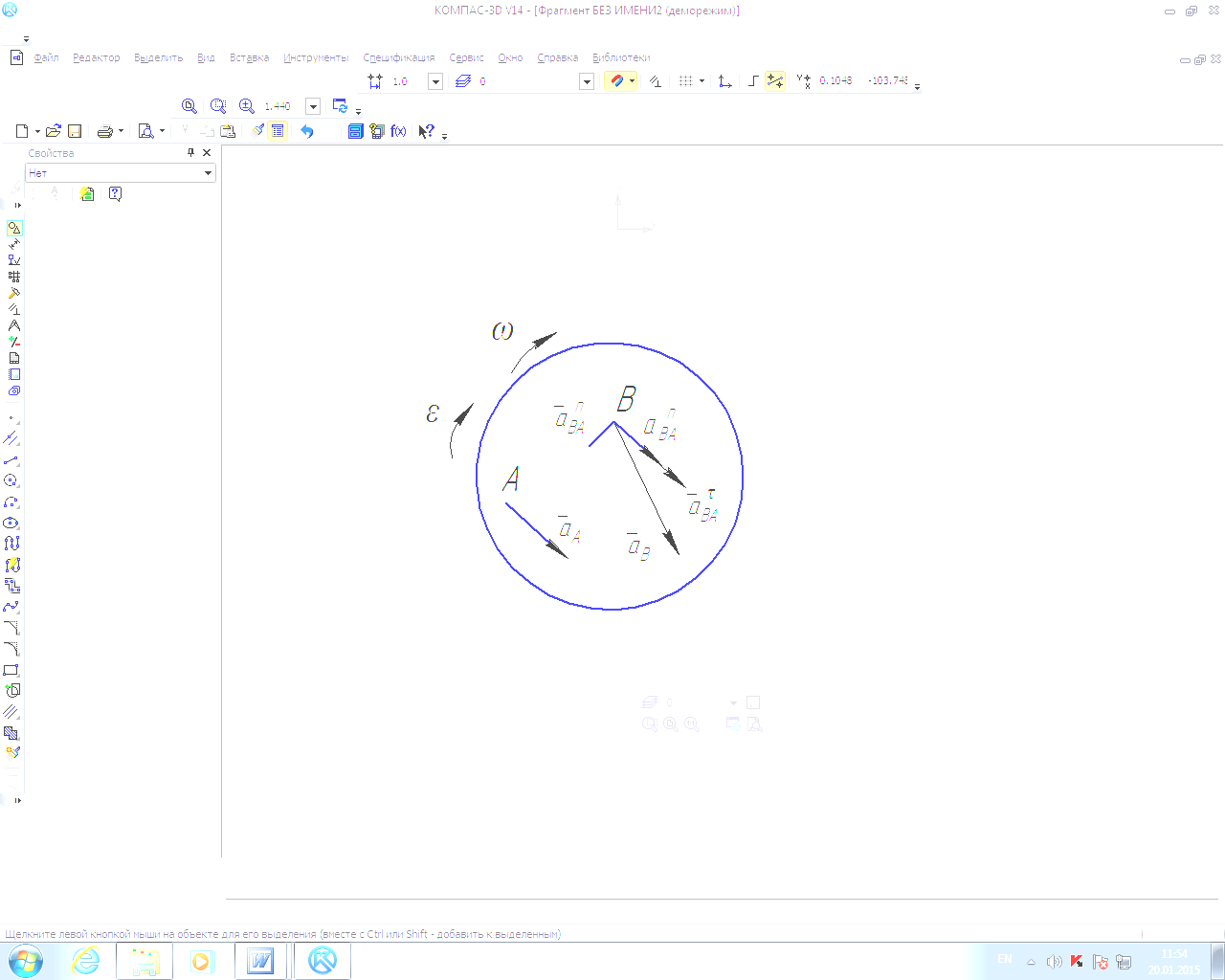



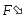













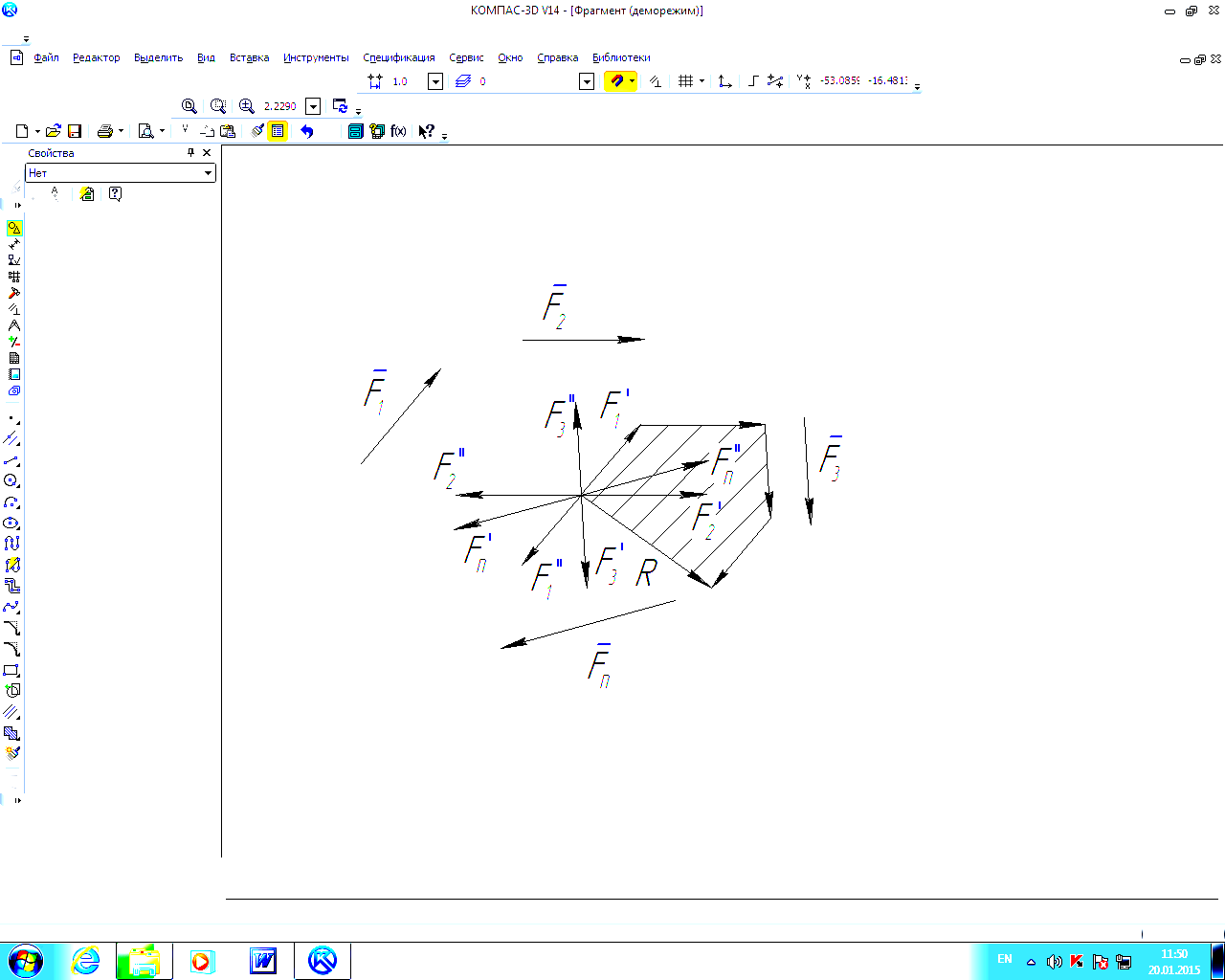



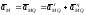



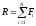
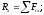




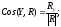


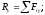





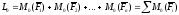









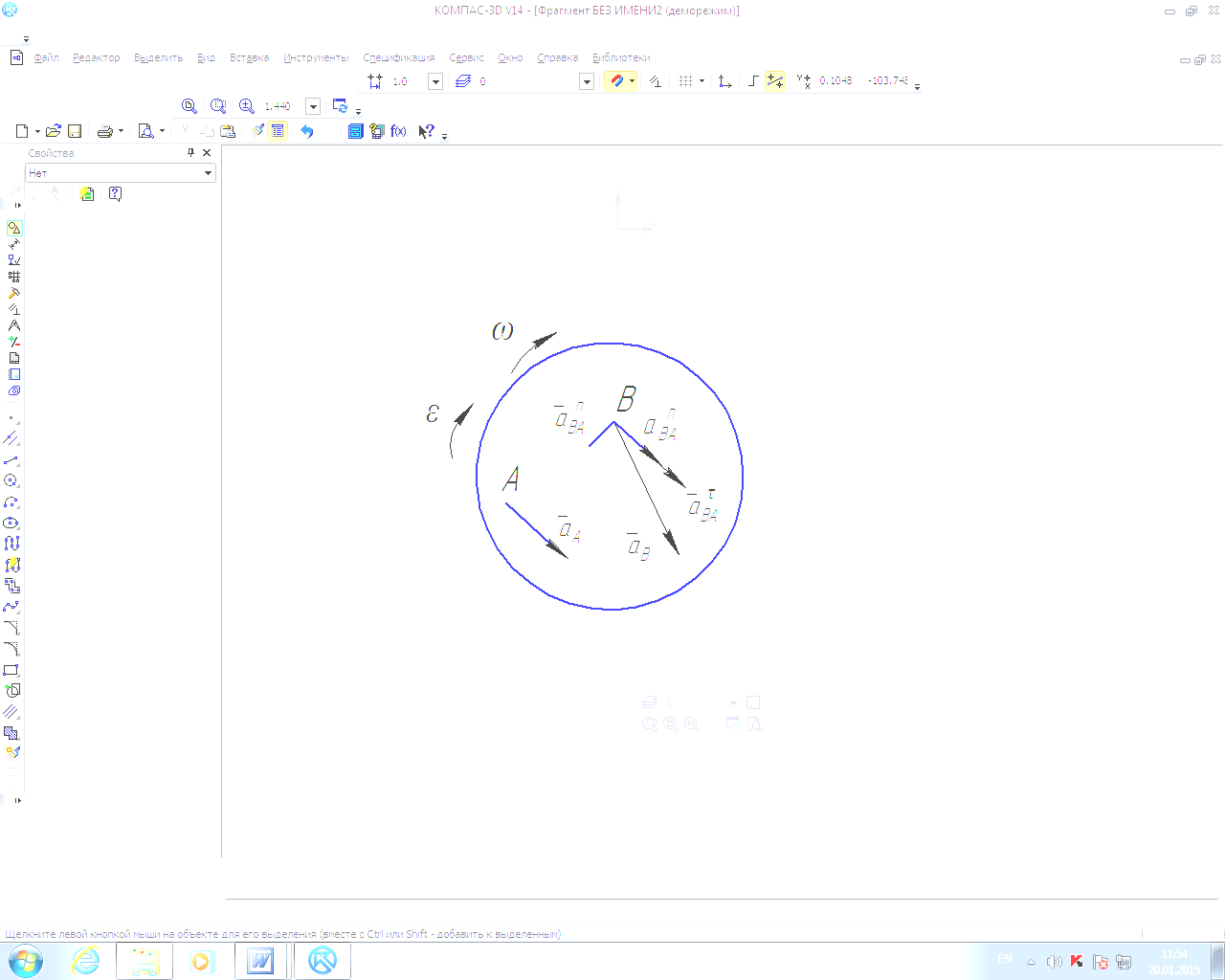

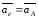







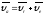
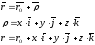

















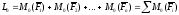


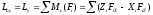
















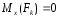

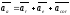
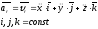

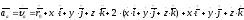
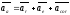


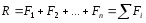



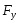



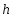






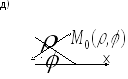

 Для
Для