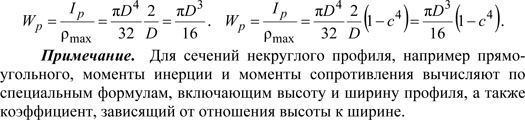13
http//:www.svkspb.nm.ru
Геометрические
характеристики плоских сечений
Площадь:
, dF
— элементарная
площадка.
Статический момент
элемента площади dF
относительно оси 0x  —
—
произведение элемента площади на
расстояние «y» от
оси 0x: dSx
= ydF
Просуммировав
(проинтегрировав) такие произведения
по всей площади фигуры, получаем
статические моменты относительно
осей y и
x:

 ;
;
[см3, м3, т.д.].
Координаты
центра тяжести:
.
Статические моменты относительно
центральных
осей (осей,
проходящих через центр тяжести сечения)
равны нулю. При вычислении статических
моментов сложной фигуры ее разбивают
на простые части, с известными площадями
Fi
и координатами
центров тяжести
xi,
yi.Статический
момент площади всей фигуры = сумме
статических моментов каждой ее части:
.
Координаты
центра тяжести сложной фигуры:
М оменты
оменты
инерции сечения
Осевой
(экваториальный) момент
инерции сечения
— сумма
произведений элементарных площадок dF
на квадраты их расстояний до оси.
;
[см4,
м4,
т.д.].
Полярный момент
инерции сечения относительно некоторой
точки (полюса) —
сумма произведений элементарных площадок
на квадраты их расстояний от этой точки.
 ;
;
[см4,
м4,
т.д.].
Jy
+ Jx
= Jp
.
Центробежный момент инерции
сечения — сумма
произведений элементарных площадок на
их расстояния от двух взаимно
перпендикулярных осей.
.
Центробежный момент инерции сечения
относительно осей, из которых одна или
обе совпадают с осями симметрии, равен
нулю.
Осевые
и полярные моменты инерции всегда
положительны, центробежные моменты
инерции могут быть положительными,
отрицательными или равными нулю.
Момент
инерции сложной фигуры равен сумме
моментов инерции составных ее частей.
Моменты инерции
сечений простой формы
П

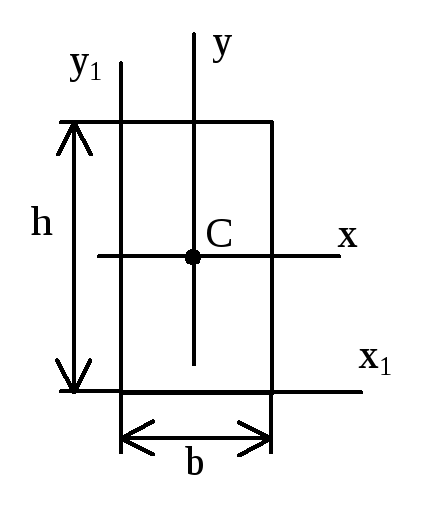
рямоугольное
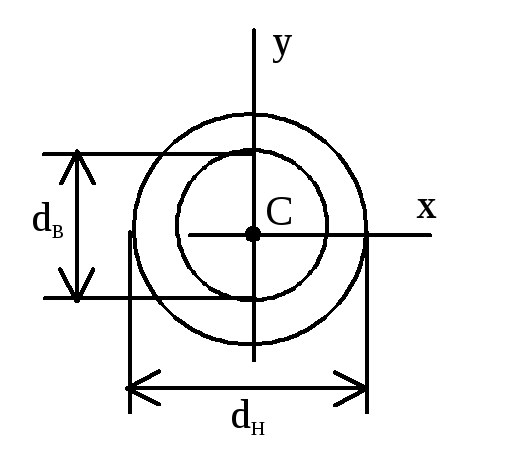
сечение Круг
К


 ольцо
ольцо
Т
р
авнобедренный
Прямоугольный
т
Ч етверть
етверть
круга
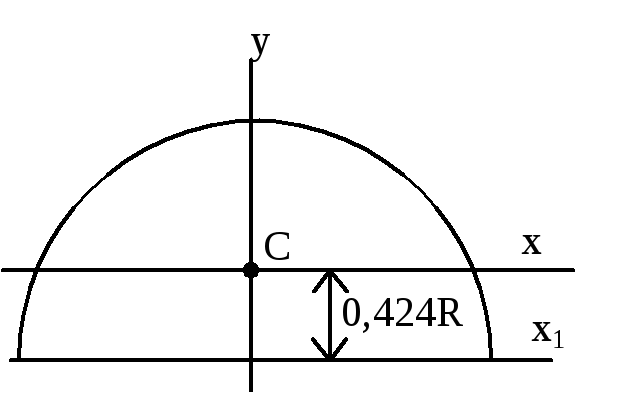
Jy=Jx=0,055R4
Jxy=0,0165R4
на
рис. (—)
Jx0=0,0714R4
Jy0=0,0384R4
Полукруг
М
инерции стандартных профилей находятся
из таблиц сортамента:
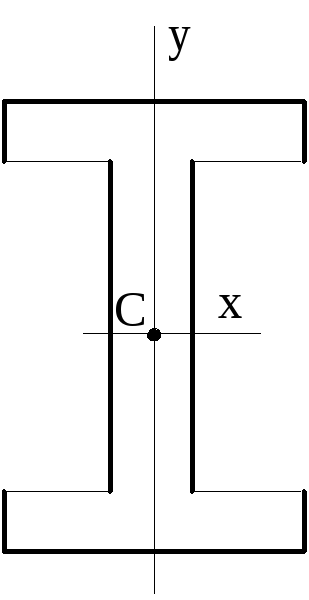
Д
Швеллер
Уголок
М
оменты инерции относительно
параллельных осей
:
J
+ a2F;
Jy1=Jy
+ b2F;
момент
инерции относительно любой оси равен
моменту инерции относительно центральной
оси, параллельной данной, плюс произведение
площади фигуры на квадрат расстояния
между осями. Jy1x1=Jyx
+ abF;
(«a» и
«b»
подставляют
в формулу с учетом их знака).
Зависимость
между моментами
инерции при повороте осей:
J
+ Jysin2
— Jxysin2;
Jy1=Jycos2
+ Jxsin2
+ Jxysin2;
Jx1y1=(Jx
— Jy)sin2
+ Jxycos2
;
Угол
>0,
если
переход
от старой системы координат к новой
происходит против час.стр. Jy1
+ Jx1=
Jy
+ Jx
Экстремальные
(максимальное и минимальное) значения
моментов инерции называются главными
моментами инерции.
Оси, относительно которых осевые моменты
инерции имеют экстремальные значения,
называются главными
осями инерции.
Главные оси инерции взаимно перпендикулярны.
Центробежные моменты инерции относительно
главных осей = 0, т.е. главные оси инерции
— оси, относительно которых центробежный
момент инерции = 0. Если одна из осей
совпадает или обе совпадают с осью
симметрии, то они главные.
Угол,
определяющий положение главных осей:
,
если 0>0
оси поворачиваются против час.стр. Ось
максимума всегда составляет меньший
угол с той из осей, относительно которой
момент инерции имеет большее значение.
Главные оси, проходящие через центр
тяжести, называются главными
центральными осями инерции.
Моменты инерции относительно этих осей:
Jmax
+ Jmin=
Jx
+ Jy.
Центробежный
момент инерции относительно главных
центральных осей инерции равен 0. Если
известны главные моменты инерции, то
формулы перехода к повернутым осям:
Jx1=Jmaxcos2
+ Jminsin2;
Jy1=Jmaxcos2
+ Jminsin2;
Jx1y1=(Jmax
— Jmin)sin2;
Конечной
целью вычисления геометрических
характеристик сечения является
определение главных центральных моментов
инерции и положения главных центральных
осей инерции.
Р
инерции —
; Jx=Fix2,
Jy=Fiy2.
Если
Jx
и Jy
главные моменты инерции, то ix
и iy
— главные
радиусы инерции.
Эллипс, построенный на главных радиусах
инерции как на полуосях, называется
эллипсом
инерции.
При помощи
эллипса инерции можно графически найти
радиус инерции ix1
для любой
оси х1.
Для этого надо провести касательную к
эллипсу, параллельную оси х1,
и измерить расстояние от этой оси до
касательной. Зная радиус инерции,
можно найти момент инерции сечения
относительно оси х1:
.
Для сечений,
имеющих более двух осей симметрии
(например: круг, квадрат, кольцо и др.)
осевые моменты инерции относительно
всех центральных осей равны между собой,
Jxy=0,
эллипс инерции обращается в круг инерции.
Моменты
сопротивления.
Осевой
момент сопротивления
— отношение момента инерции относительно
оси к расстоянию от нее до наиболее
удаленной точки сечения.
[см3,
м3]
Особенно
важны моменты сопротивления относительно
главных центральных осей:
прямоугольник:
;
круг: Wx=Wy=
,
трубчатое
сечение (кольцо): Wx=Wy=

где =
dН/dB.
Полярный
момент сопротивления — отношение
полярного момента инерции к расстоянию
от полюса до наиболее удаленной точки
сечения:
.
Для
круга Wр=
.
Соседние файлы в папке Комплект
- #
- #
- #
- #
В предыдущей статье я рассказывал о моментах инерции, с которыми неразрывно связаны моменты сопротивления. Именно о них сейчас и пойдёт речь. Так что если читатель ещё не читал её — самое время!
А пока нам следует разобраться, что чему сопротивляется. И вообще, является ли организация своего протестного движения моментом сопротивления?
Что такое моменты сопротивления?
В статье про изгиб мы с вами разбирались в том, как найти максимальные напряжения в зоне чистого изгиба
Спойлер:

Где a — максимальное расстояние по интересующей нас оси.
Но чтобы упростить себе расчеты и допускать меньше ошибок, соотношение

Принято называть моментом сопротивления.
Тут может возникнуть вопрос: “Ну так а может не стоило вводить новую величину, а просто оперировать моментами инерции?”
На самом деле так действительно можно сделать, но столкнувшись с большим количеством расчетов читатель и сам наверняка начнет выписывать момент сопротивления. Упрощая алгоритм расчета, мы стремимся исключить возможные ошибки и ускорить сами расчеты. Ведь вместо трехэтажных дробей гораздо удобнее оперировать уже готовым значением.
То есть:
Осевой момент сопротивления – по сути отношение момента инерции к расстоянию до наиболее удаленной от этой оси точки:
По аналогии с полярным моментом инерции для расчетов круглых и близких к ним тел используется полярный момент сопротивления:
Момент сопротивления имеет размерность см3.
Как определить моменты сопротивления простых сечений?
1. Момент сопротивления прямоугольного сечения:
Где Ix:
2. Момент сопротивления квадратного сечения. Частный случай предыдущего пункта:
Где Ix:
3. Момент сопротивления сечения круга:
Где Ix:
4. Момент сопротивления сечения кольцо:
Расчет момента сопротивления сложного сечения
В качестве примера, определим момент инерции и момент сопротивления сечения, изображенного на рисунке ниже:d =20 см, a = 6 см.
1. Определим момент инерции сечения, как разность моментов инерции круга с диаметром d и квадрата со стороной a:
2. Определим момент сопротивления сечения:
3. А теперь давайте попробуем найти разность моментов сопротивления сечения. Будет ли она отличаться от ответа, полученного из двух предыдущих пунктов?
То есть момент сопротивления сечения определяется только через момент инерции! Напрямую складывая/вычитая моменты сопротивления вы получите неправильный ответ!
Подведем небольшой итог:
Момент сопротивления неразрывно связан с моментом инерции.
Моменты сопротивления упрощают расчет нормальных напряжений при изгибе (что особенно важно — максимальных нормальных напряжений), что делает прочностные расчёты при подборе сечения заметно легче и быстрее.
Информация о произведении
Автор: Марк Ершов
Редактор, факт-чекер: К.А.Овчинников
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Список использованных источников
- Александров А.В. Сопротивление материалов: Учеб. для ВУЗов/ А.В. Александров, В.Д. Потапов, Б.П. Державин; под ред. А.В. Александрова – 3-е изд. испр. – М.: Высш. шк., 2003. – 560 с.: ил. ISBN 5-06-003732-0
- Дарков А.В., Шпиро Г.С. Сопротивление материалов – Учеб. для техн. вузов – 5-е изд. перераб. и дополн. – М.: Высш. шк., 1989 – 624 с. ил.
- Г.И. Беликов. Геометрические характеристики поперечных сечений стержней. Учебно-практическое пособие. — Волгоград: ВолгГАСУ, 2015. — 56 с. — ISBN 978-5-98276-752-3
4 909
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
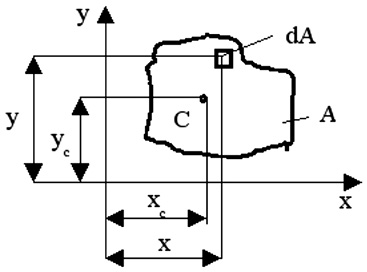
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
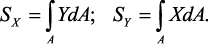
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:
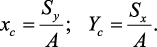
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны
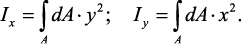
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.
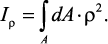
Учитывая, что ρ2 = x2 + y2, получаем Iρ = Ix + Iy.
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).
Полярный момент инерции
Jρ = Jx + Jy;, (6)
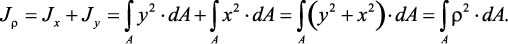
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ2 = y2 + z2) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
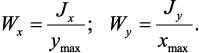
Полярный момент сопротивления
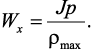
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
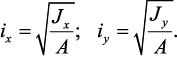
Вычисление геометрических характеристик простых фигур.
Прямоугольное сечение.
Определим осевой момент инерции прямоугольника относительно оси х.
Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:
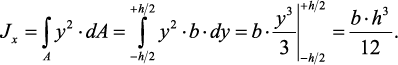
По аналогии запишем
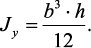
Круглое сечение
Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца 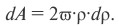
площади кольца в выражение для Jρ и интегрируя, получим:
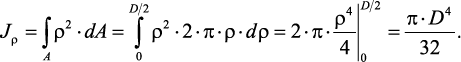
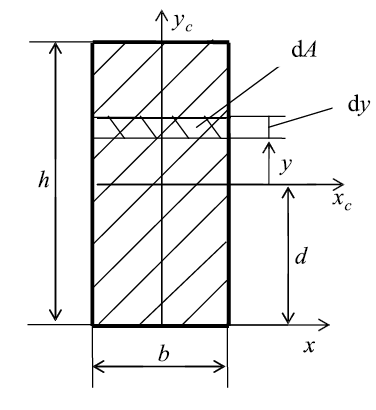
Рис. 11. Прямоугольник
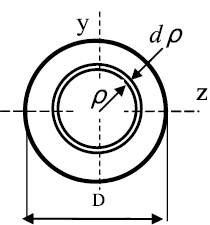
Рис. 12. Круг
Тогда
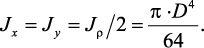
Зачем нужен момент инерции сечения
Несмотря на то, что наука о прочности давно уже шагнула вперёд, и давно уже развиваются многие её направления (строительная механика, механика разрушения, теория упругости и другие), а также несмотря на то, что всё чаще расчеты сложных конструкций выполняются при помощи метода конечного элемента посредством специализированных программных комплексов, прикидочные расчеты на основе методов сопромата не утратили своей актуальности. Ведь именно они, во-первых, позволяют дать оценку прочности конструкции «в полевых условиях» (без трудоёмкого построения конечно-элементной модели, без сложных математических выкладок), а во-вторых — позволяют это сделать достаточно быстро.
В основном, расчеты в сопротивлении материалов имеют целью проверить общую (а не местную) прочность балок. Поэтому расчетная схема принимается упрощенной, и многими конструктивными элементами, даже являющимися концентраторами напряжений, в ней пренебрегают. Тем не менее, несмотря на ряд упрощений в схеме и принятые допущения (гипотезы, принятые для построения теории сопротивления материалов), в этой науке разработаны методы, позволяющие с довольно большой точностью определить опасные сечения и напряжения, возникающие в них.
Вообще, поперечное сечение балки может представлять собой тавр, швеллер, двутавр, круг, прямоугольник, кольцо, полый прямоугольник и т.п. или может быть составным, т.е. составленным из нескольких однотипных или различных профилей. От его формы и размеров зависит прочность и жесткость балки. Площадь поперечного сечения является важной характеристикой, но знать только лишь её достаточно разве что для задач на центральное растяжение. Если же балка испытывает изгиб или кручение, то знать только лишь площадь поперечного сечения оказывается недостаточно. Балка может «проходить» (т.е. обладать достаточной прочностью и жесткостью) с одним типом сечения и «не проходить» с другим типом сечения такой же площади. В процессе решения задач по сопромату, касающихся определения напряжений в балке при её изгибе или кручении, проверке устойчивости сжатых стержней, а также при решении некоторых других задач требуется знать не только площадь, но и другие геометрические характеристики сечения (момент инерции площади сечения, момент сопротивления площади сечения, полярный момент инерции площади сечения). Во-первых, они требуются для решения конкретной задачи об определении напряжений в данной балке с заданными размерами поперечного сечения. Во-вторых, они нужны для выполнения сравнительного анализа разных типов сечений (например, выбора среди нескольких различных сечений с одинаковой площадью именно того сечения, которое будет лучше сопротивляться изгибу или кручению), для подбора оптимального сечения для балки, работающей в конкретно заданных условиях. Поскольку нахождение геометрических характеристик сечения требует определенных знаний и практических навыков, в любом учебнике или справочнике по сопромату выделен раздел, посвященный определению этих характеристик, а в любом задачнике по сопромату приведены задачи по нахождению момента инерции или момента сопротивления сечения.
Что такое момент инерции сечения
Обычно, когда речь идёт о геометрических характеристиках сечения, слово «площадь» опускают, чтобы не было нагромождения слов, и говорят не «момент инерции площади сечения», «момент сопротивления площади сечения», а просто «момент инерции сечения», «момент сопротивления сечения» или даже просто «момент инерции», «момент сопротивления». При этом различают осевой, полярный и центробежный момент инерции площади сечения.
Осевой момент инерции площади фигуры (сечения) — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Другое, менее распространенное его название – экваториальный момент инерции. Величина осевого момента инерции всегда положительна.
Полярный момент инерции площади фигуры (сечения) относительно данной точки (полюса) — это интеграл произведений элементарных площадок на квадраты их расстояний от полюса. Величина полярного момента инерции всегда положительна.
Центробежный момент инерции площади фигуры — это интеграл произведений элементарных площадок на их расстояния от координатных осей. В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. При повороте осей вокруг начала координат на 90 градусов знак центробежного момента инерции меняется на обратный.
Задавая вопросы «в чем измеряется момент инерции», «какова единица измерения момента инерции», «как обозначается момент инерции» необходимо четко представлять, что именно имеется в виду: момент инерции сечения (о котором идёт речь в сопромате и, в частности, в настоящей статье) или же момент инерции тела (который упоминается в физике и в теории механизмов и машин). Размерность момента инерции сечения – это размерность длины в четвертой степени (например, см4, м4, мм4). Моменты инерции сечений стандартных профилей (швеллеров, уголков, тавров, двутавров) приведены в справочных таблицах в размерности «см4». При необходимости, данную в таблице величину можно представить в другой единице измерения. Обычно при решении задач возникает необходимость перевода этой величины в «мм4». Обозначается момент инерции сечения буквой I с нижним индексом, который указывает, относительно какой оси вычислена данная характеристика (например, Ix, Iy). Момент сопротивления сечения обозначается буквой W, также с нижним индексом, указывающим на ось, относительно которой дана эта величина (например, Wx, Wy).
Что такое главные оси
Главные оси инерции — оси, относительно которых центробежный момент инерции равен нулю.
Главные центральные оси — главные оси, проходящие через центр тяжести сечения.
Как найти момент инерции сечения
При вычислении момента инерции сечения можно воспользоваться непосредственно определением момента инерции и вычислить эту характеристику сечения путём нахождения интеграла по площади. Так и поступают при нахождении момента инерции треугольника, круга, прямоугольника, кругового сектора и других простых фигур.
Обозначив характерные размеры сечения через параметры (т.е. буквами) и выполнив соответствующее интегрирование по площади, получают формулы для определения моментов инерции этих сечений. Ход решения показан, например, в учебнике по сопромату Г.С. Писаренко на примере вывода формул для определения момента инерции прямоугольника, треугольника, кругового сектора и эллипса. Такие формулы приведены во многих справочниках по сопромату (например, в книге Писаренко Г.С., Яковлев А.П. Матвеев В.В. Справочник по сопротивлению материалов. – К: Наукова думка, 1975, на страницах 24 — 77) для многих типов сечений (квадрат, полый квадрат, прямоугольник, полый прямоугольник, прямоугольник с круглым отверстием, прямоугольник с двумя отверстиями, прямоугольник с полукруглыми вырезами, повернутый прямоугольник, крестовина, корытное сечение, треугольник, трапеция, круг, кольцо, круговое незамкнутое тонкостенное кольцо, полукруг, четверть круга, круговой сектор, круговой сегмент, полукольцо, сектор кольца, круг с лыской, правильный шестиугольник, правильный многоугольник, круговое сечение с одной или с двумя шпоночными канавками, эллипс, полуэллипс, четверть эллипса, полый эллипс, параболический сегмент, параболический полусегмент, круговой треугольник, сечение железнодорожного рельса). Готовыми формулами из справочника пользоваться намного проще, чем выводить каждый раз нужную формулу самостоятельно путём интегрирования.
В этом же справочнике приведены и формулы для приближенного вычисления геометрических характеристик (F, I, W) сечений стандартных прокатных профилей: уголков (равнобокого и неравнобокого), швеллера, тавра, двутавра, однако на практике этими формулами пользуются весьма редко, т.к. все необходимые характеристики стандартных сечений уже вычислены и приведены в соответствующих нормативных документах (см. ГОСТ 8240-97 для швеллеров, ГОСТ 8509-93 для равнополочных уголков, ГОСТ 8510-86 для неравнополочных уголков, ГОСТ 26020-83 и ГОСТ 8239-89 для двутавров). Выдержки из перечисленных выше стандартов приведены во многих справочниках, учебниках и решебниках по сопромату.
Скачать примеры решения задач, касающиеся того, как найти момент инерции и момент сопротивления, можно здесь (бесплатно, без регистрации):
При вычислении моментов инерции сложных сечений их разбивают на отдельные простые части, моменты инерции которых известны.
Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.
При повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.
Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.
Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения.
Размерность моментов сопротивления – единица длины в кубе (например, см3, м3, мм3).
Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления. Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.
Источники:
- Н.М. Беляев. Сопротивление материалов.
- Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов.
- А.В. Александров, В.Д. Потапов, Б.П. Державин. Сопротивление материалов.
- reshusam.ucoz.ru — Примеры определения моментов инерции сечений.
Дополнительно на Геноне:
- Что такое сопромат
6.3. МОМЕНТ СОПРОТИВЛЕНИЯ
Момент сопротивления – отношение момента инерции к расстоянию до наиболее удаленной точки. В расчетах на прочность при изгибе используют осевые моменты сопротивления Например, для прямоугольника В расчетах на прочность при кручении сечений круглого профиля используют полярный момент сопротивления Так, для круга и кольца соответственно Примечание. Для сечений некруглого профиля, например прямоугольного, моменты инерции и моменты сопротивления вычисляют по специальным формулам, включающим высоту и ширину профиля, а также коэффициент, зависящий от отношения высоты к ширине.

 —
—
 оменты
оменты
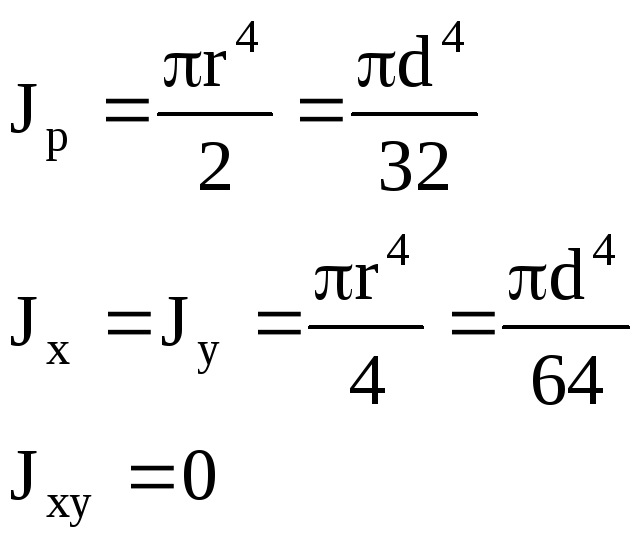
 ольцо
ольцо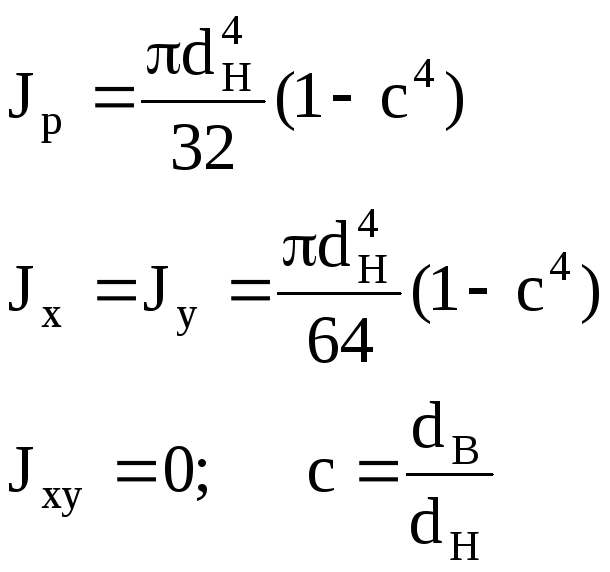
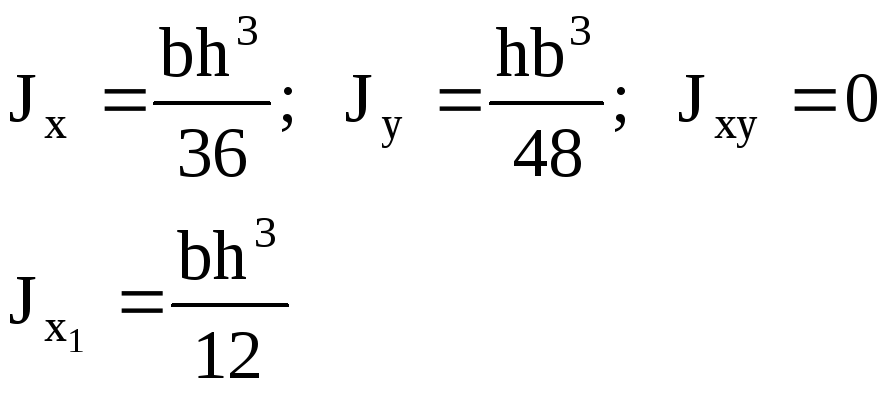

 етверть
етверть