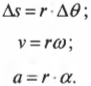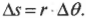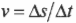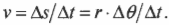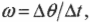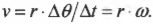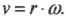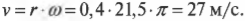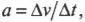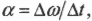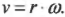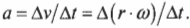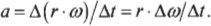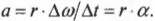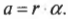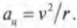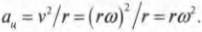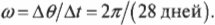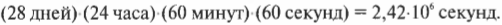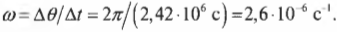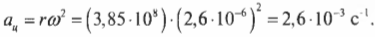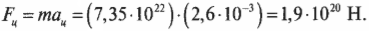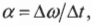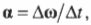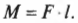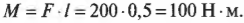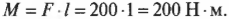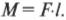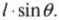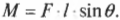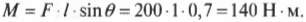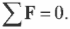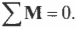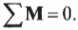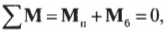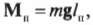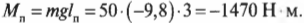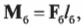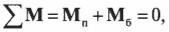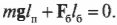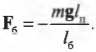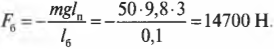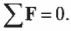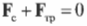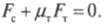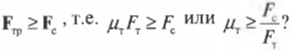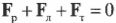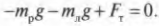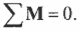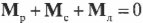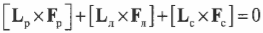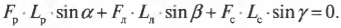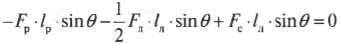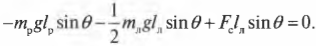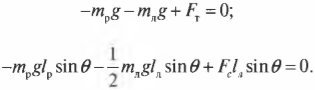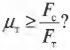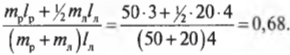Как найти момент вращения колеса

Вращающие моменты и частоты вращения
определяются в последовательности,
задаваемой табл.5 и 6.

Таблица 5

№	Вращающий момент, Н×м	Расчетная зависимость	Результат
1	На валу электродвигателя
2	На конце быстроходного вала
3	На шестерне быстроходного вала
4	На колесе промежуточного вала
5	На шестерне промежуточного вала
6	На колесе тихоходного вала
7	На конце тихоходного вала
В расчетах принять: = 0,98 – к.п.д муфты;= 0,99 – к.п.д подшипников;= 0,97 – к.п.д зубчатого зацепления

Таблица 6

№	Частоты вращения, об/мин.	Расчетная зависимость	Результат
1	Быстроходный вал
2	Промежуточный вал
3	Тихоходный вал

4.3. Определение расчетного контактного напряжения

Для определения коэффициентов концентрации
нагрузки зубчатой передачи необходимо
знать расположение зубчатых колес
относительно опор. Типовые случаи
представлены на рис.3.

Рис. 3

Коэффициенты
иконцентрации нагрузки в зубчатом
зацеплении определяются по графикам
на рис.4 при.

Коэффициенты
идинамической нагрузки для 8-й степени
точности находятся по табл.7 прим/с.

Рис.4

Таблица 7

Твердость поверхностей зубьев	Коэффи-циенты	Окружная скорость V, м/с
1	3	5	8	10
350HB		1,05 1,02	1,15 1,08	1,24 1,10	1,38 1,15	1,48 1,19
	1,10 1,04	1,30 1,12	1,48 1,19	1,77 1,30	1,96 1,38

Примечание: Верхние числа — прямозубые,
нижние – косозубые колеса.

Косозубые передачи имеют преимущество
перед прямозубыми в частности в том,
что в зацеплении постоянно участвуют
не менее двух пар зубьев (рис.5).

Рис.5

Эти контактные линии представляют собой
прямые, наклонно расположенные на
криволинейной поверхности зуба. Однако
нагрузка между ними распределяется
неравномерно, что учитывается при
расчете на контактную и изгибную
прочность коэффициентами
исоответственно. Выбор значений
производится по табл.8.

Таблица 8

Окружная скорость V, м/с	Степень точности
До 5	7 8 9	1,03 1,07 1,13	1,07 1,22 1,35
Св. 5 до 10	7 8	1,05 1,10	1,20 1,30

Контактные напряжения в косозубой
цилиндрической передаче определяют по
формуле

. (2)

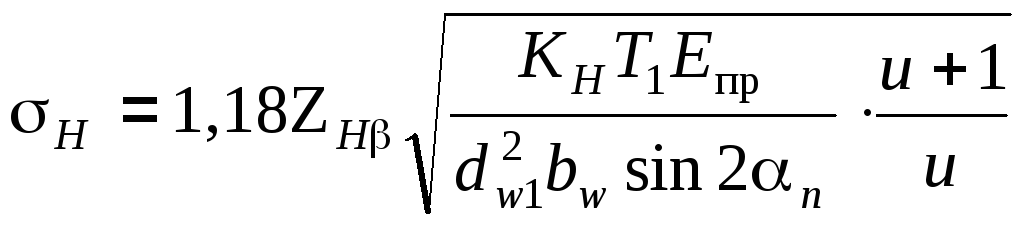
Коэффициент
,
учитывающий особенности расчета
косозубой передачи на контактную
прочность, рассчитывается по табл. 9 по
формуле

.
(3)

Таблица 9

№	Обозн.	Содержание	Зависимость или источник	Резуль-тат
1	2	3	4	5
1		Коэффициент, учитывающий распределение нагрузки между зубьями.	Из табл. 8 с учетом заданной степени точности и V— окружной скорости передачи
2	b	Угол наклона зу-бьев на делительном цилиндре	Из табл. 4
3		Коэффициент торцового перекрытия
4		Формула 3

Коэффициент нагрузки
при расчете на контактную прочность
рассчитывается по табл.10.

Таблица 10

Обозн.	Содержание	Зависимость или источник	Результат
1	2	3	4
	Коэффициент концентрации нагрузки по длине контактных линий	Зависит от: 1) параметра, ; 2) расположения зубчатой передачи относительно опор (см.рис.3); 3) от твердости зубьев (см. рис. 4).

Окончание
таблицы 10

1	2	3	4
	Коэффициент динамичности	Зависит от: 1) V— окружной скорости передачи; 2) степени точности; 3) твердости поверхностей зубьев передачи (см. табл.7).
		=
	Вращающий момент на шестерне рассматриваемой ступени, Н×мм	См. табл. 5.
	Приведенный модуль упругости зубчатой пары, МПа
	Начальный или делительный диаметр шестерни рассматриваемой ступени, мм	См. табл. 4.
	Ширина венца колеса рассматриваемой ступени, мм	См. табл. 4.
	Угол зацепления в нормальной плоскости	Для косозубых передач обычно ==20°.
	Расчетное контактное напряжение, МПа	Формула 2

В этой главе…

• Переходим от поступательного движения к вращательному движению
• Вычисляем тангенциальную скорость и тангенциальное ускорение
• Выясняем связь между угловым ускорением и угловой скоростью
• Разбираемся с моментом силы
• Поддерживаем вращательное движение

Эта и следующая главы посвящены вращательному движению объектов самой разной природы: от космических станций до пращи. Именно такое движение стало причиной того, что наша планета имеет круглую форму. Если вам известны основные свойства прямолинейного движения и законы Ньютона (они подробно описываются в двух первых частях этой книги), то вы сможете быстро овладеть основами вращательного движения. Даже если вы позабыли некоторые сведения из прежних глав, не беда, ведь к ним всегда можно вернуться в случае необходимости. В этой главе представлены основные понятия вращательного движения: угловая скорость угловое ускорение, тангенциальное ускорение, момент силы и т.п. Однако довольно слов, приступим к делу!

Переходим от прямолинейного движения  к вращательному

Для такого перехода нужно изменить уравнения, которые использовались ранее для описания прямолинейного движения. В главе 7 уже упоминались некоторые эквиваленты (или аналоги) из мира прямолинейного и вращательного движения.

Вот как выглядят основные формулы прямолинейного движения, которые подробно описываются в главе 3:

• ​( v=Delta{s}/Delta{t} )​, где ​( v )​ — это скорость, ​( Delta{s} )​ — перемещение, a ( Delta{t} ) — время перемещения;
• ( a=Delta{v}/Delta{t} ), где ( a ) — это ускорение, ( Delta{v} ) — изменение скорости, a ( Delta{t} ) — время изменения скорости;
• ​( Delta{s}=v_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 )​, где ​( v_0 )​ — это начальная скорость, ​( t_0 )​ — это начальный момент времени, a ​( t_1 )​ — это конечный момент времени;
• ​( v^2_1-v^2_0=2aDelta{s} )​, где ​( v_1 )​ — это конечная скорость.

По аналогии можно легко вывести основные формулы вращательного движения:

• ​( omega=Delta{theta}/Delta{t} )​, где ​( omega )​ — угловая скорость, ​( Delta{theta} )​ — угол поворота, ( Delta{t} ) — время поворота на угол ( Delta{theta} );
• ​( alpha=Delta{omega}/Delta{t} )​, где ​( alpha )​ — угловое ускорение, ​( Delta{omega} )​ — изменение угловой скорости, ​( Delta{t} )​ — время изменения угловой скорости;
• ​( theta=omega_0(t_1-t_0)+{}^1!/!_2a(t_1-t_0)^2 )​, где ​( omega_0 )​ — это начальная скорость;
• ​( omega^2_1-w^2_0=2as )​, где ​( omega_1 )​ — это конечная скорость.

Разбираемся с параметрами вращательного движения

В физике движение принято разделять на поступательное и вращательное. При поступательном движении любая прямая, связанная с движущимся объектом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям. Тангенциальным движением называется часть вращательного движения, происходящего по касательной к окружности вращения, а радиальным (или нормальным) движением — часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной, т.е. вдоль радиуса окружности.

Параметры прямолинейного поступательного и вращательного движений можно связать следующими формулами:

Допустим, колеса мотоцикла вращаются с угловой скоростью ​( omega )​, равной 21,5( 21,5pi )​ радиан в секунду. С какой скоростью едет мотоцикл? Чтобы дать ответ на этот вопрос, достаточно воспользоваться простой формулой связи линейной и угловой скорости.

Вычисляем линейную скорость вращательного движения

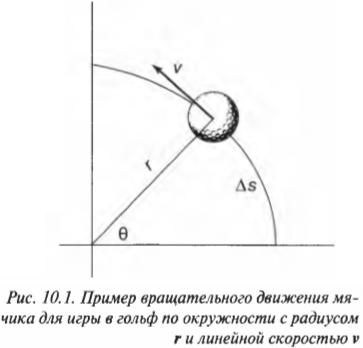
Скорость тангенциального движения материальной точки принято называть линейной скоростью вращательного движения. На рис. 10.1 приведен пример вращения мячика для игры в гольф по окружности с радиусом ​( mathbf{r} )​ и линейной скоростью ( mathbf{v} ). Скорость ( mathbf{v} ) является векторной величиной, т.е. обладает величиной и направлением (подробнее о векторах рассказывается в главе 4), перпендикулярным радиус-вектору ( mathbf{r} ).

Угловая скорость связана с линейной скоростью соотношением ​( v=romega )​, которое легко интуитивно понять. При одинаковой угловой скорости, чем дальше материальная точка от центра окружности вращения, тем больше ее линейная скорость.

Попробуем получить уже упомянутую выше формулу связи линейной и угловой скорости ( v=romega ). Длина окружности ​( L )​ радиуса ​( r )​ выражается известной формулой ​( L=2pi r )​, а полный угол, который охватывает окружность, равен ​( 2pi )​ радиан. Соответственно, длина дуги окружности длиной ​( Delta s )​, охватывающая угол ​( Deltatheta )​, равна:

Из формулы прямолинейного движения

путем подстановки выражения для ​( Delta s )​ получим:

Поскольку:

где ​( omega )​ — угловая скорость, ​( Delta{theta} )​— угол поворота, ​( Delta{t} )​ — время поворота на угол ( Delta{theta} ), то:

Теперь можно легко и просто дать ответ на вопрос, поставленный в конце предыдущего раздела, т.е. определить скорость мотоцикла по угловой скорости вращения его колес. Итак, колеса мотоцикла вращаются с угловой скоростью ( omega ), равной 21,5​( pi ) радиан в секунду. Пусть радиус колеса ​( r )​ равен 40 см, тогда достаточно использовать следующую формулу:

Подставляя в нее значения, получим:

Итак, скорость мотоцикла равна 27 м/с или 97 км/ч.

Вычисляем тангенциальное ускорение

Тангенциальным ускорением называется скорость изменения величины линейной скорости вращательного движения. Эта характеристика вращательного движения очень похожа на линейное ускорение прямолинейного движения (см. главу 3). Например, точки на колесе мотоцикла в момент старта имеют нулевую линейную скорость, а спустя некоторое время после разгона ускоряются до некоторой ненулевой линейной скорости. Как определить это тангенциальное ускорение точки колеса? Переформулируем вопрос: как связать линейное ускорение

где ​( a )​ — это ускорение, ​( Delta v )​ — изменение скорости, a ​( Delta t )​ — время изменения скорости, с угловым ускорением

где ( Deltaomega ) — изменение угловой скорости, ( Delta t ) — время изменения угловой скорости?

Как мы уже знаем, линейная и угловая скорости связаны равенством

Подставим это выражение в предыдущую формулу линейного ускорения:

Поскольку радиус остается постоянным, то его можно вынести за скобки:

Поскольку угловое ускорение ​( alpha=Deltaomega/Delta t )​, то:

Итак, получаем следующую формулу связи между линейным и угловым ускорением:

Иначе говоря, тангенциальное ускорение равно произведению радиуса на угловое ускорение.

Вычисляем центростремительное ускорение

Центростремительнным ускорением называется ускорение, необходимое для удержания объекта на круговой орбите вращательного движения. Как связаны угловая скорость и центростремительное ускорение? Формула для центростремительного ускорения уже приводилась ранее (см. главу 7):

Теперь, используя известную формулу связи линейной и угловой скорости ​( v=romega )​, получим:

По этой формуле можно определить величину центростремительного ускорения по известной угловой скорости и радиусу. Например, для вычисления центростремительного ускорения Луны, вращающейся вокруг Земли, удобно использовать именно эту формулу.

Луна делает полный оборот вокруг Земли за 28 дней, т.е. за 28 дней Луна проходит ​( 2pi )​ радиан. Отсюда получаем угловую скорость Луны:

Чтобы получить значение угловой скорости в привычных единицах, следует преобразовать дни в секунды:

После подстановки этого значения в предыдущую формулу получим:

Средний радиус орбиты Луны равен 3,85·10⁸ м. Подставляя эти значения угловой скорости и радиуса в формулу центростремительного ускорения, получим:

Зная это ускорение и массу Луны, которая равна 7,35·10²² кг, можно определить центростремительную силу, необходимую для удержания Луны на ее орбите:

Используем векторы для изучения вращательного движения

В предыдущих разделах этой главы угловая скорость и угловое ускорение рассматривались как скаляры, т.е. как параметры, характеризующиеся только величиной. Однако эти параметры вращательного движения, на самом деле, являются векторами, т.е. они обладают величиной и направлением (см. главу 4). В этом разделе рассматривается величина и направление некоторых параметров вращательного движения.

Определяем направление угловой скорости

Как нам уже известно, вращающееся колесо мотоцикла имеет не только угловую скорость, но и угловое ускорение. Что можно сказать о направлении вектора угловой скорости? Оно не совпадает с направлением линейной тангенциальной скорости, а… перпендикулярно плоскости колеса!

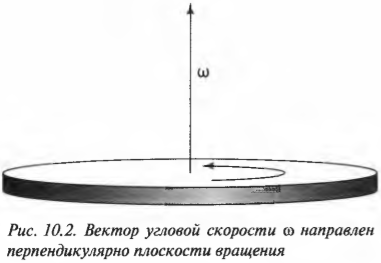
Эта новость всегда приводит к некоторому замешательству среди новичков: угловая скорость ​( omega )​, оказывается, направлена вдоль оси вращающегося колеса (рис. 10.2). Во вращающемся колесе единственной неподвижной точкой является его центр. Поэтому начало вектора угловой скорости принято располагать в центре окружности вращения.

Для определения направления вектора угловой скорости ( omega ) часто используют правило правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление тангенциальной скорости, то вытянутый большой палец укажет направление вектора угловой скорости ( omega ).

Теперь угловую скорость можно использовать так же, как и остальные векторные характеристики движения. Направление вектора угловой скорости можно найти по правилу правой руки, а величину — по приведенной ранее формуле. То, что вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, часто вызывает некоторые трудности у начинающих, но к этому можно быстро привыкнуть.

Определяем направление углового ускорения

Если вектор угловой скорости направлен перпендикулярно плоскости вращательного движения, то куда направлен вектор углового ускорения в случае замедления или ускорения вращения объекта? Как известно (см. предыдущие разделы), угловое ускорение определяется формулой:

где ​( alpha )​ — угловое ускорение, ​( Deltaomega )​ — изменение угловой скорости, ​( Delta t )​— время изменения угловой скорости.

В векторной форме оно имеет следующий вид:

где ​( mathbf{alpha} )​ — вектор углового ускорения, а ​( Deltamathbf{omega} )​ — изменение вектора угловой скорости. Отсюда ясно, что направление вектора углового ускорения совпадает с направлением изменения вектора угловой скорости.

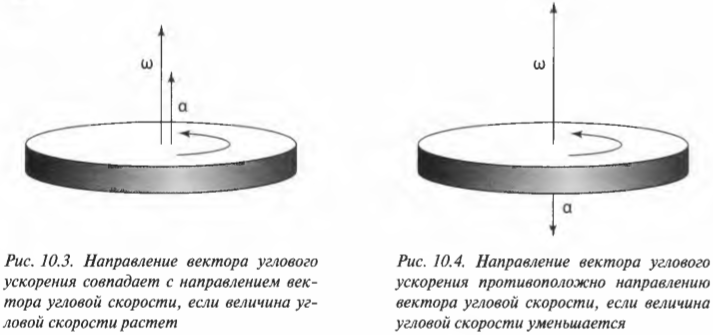
Если вектор угловой скорости меняется только по величине, то направление вектора углового ускорения параллельно направлению вектора угловой скорости. Если величина угловой скорости растет, то направление вектора углового ускорения совпадает с направлением вектора угловой скорости, как показано на рис. 10.3.

А если величина угловой скорости падает, то направление вектора углового ускорения противоположно направлению вектора угловой скорости, как показано на рис. 10.4.

Поднимаем грузы: момент силы

В физике большое значение имеет не только время, но и место приложения силы. Всем когда-либо приходилось пользоваться рычагом для перемещения тяжелых грузов. Чем длиннее рычаг, тем легче сдвинуть груз. На языке физики применение силы с помощью рычага характеризуется понятием момент силы.

Приложение момента силы неразрывно связано с вращательным движением объектов. Если приложить силу к краю карусели, то карусель начнет вращательное движение. Чем дальше точка приложения силы, тем легче раскрутить карусель до заданной угловой скорости (параметры вращательного движения описываются в главе 1 1 ).

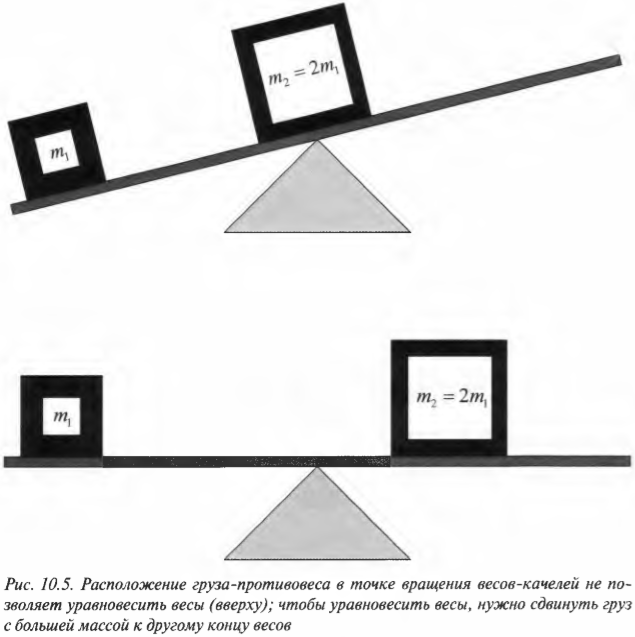
В верхней части рис. 10.5 показаны весы-качели с грузом массы ​( m_1 )​ на одном конце и грузом большей массы ​( m_2=2m_1 )​ посередине. Чтобы уравновесить весы-качели, нужно сместить груз с большей массой ​( m_2 )​ к другому концу весов, как показано в нижней части рис. 10.5. Как известно из опыта, размещение груза в точке вращения весов не приводит к уравновешиванию весов. Чтобы уравновесить весы, нужно сдвинуть груз с большей массой ( m_2=2m_1 ) к другому концу весов на расстояние вдвое меньшее, чем расстояние от точки вращения до второго груза с массой ​( m_1 )​.

Знакомимся с формулой момента силы

Для уравновешивания весов важно не только, какая сила используется, но и где она прикладывается. Расстояние от точки приложения силы до точки вращения называется плечом силы.

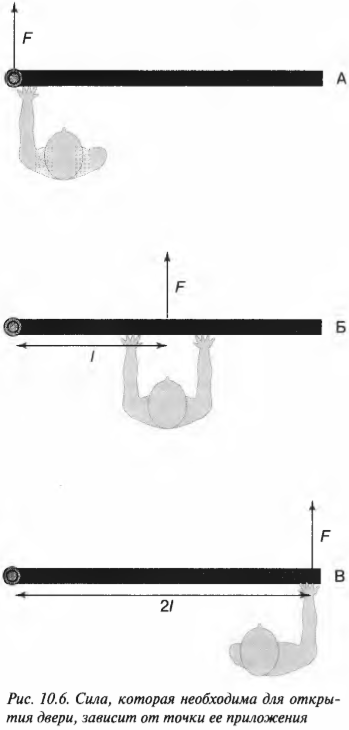
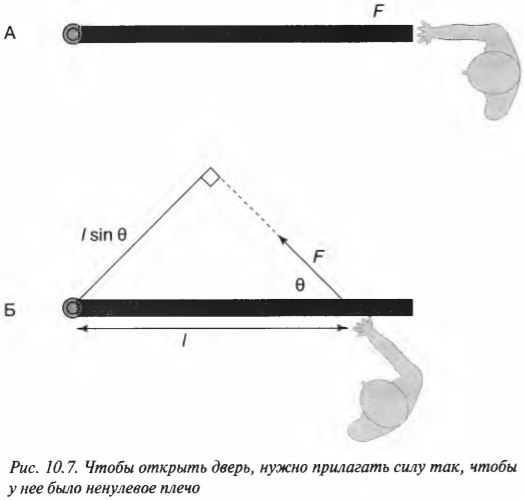
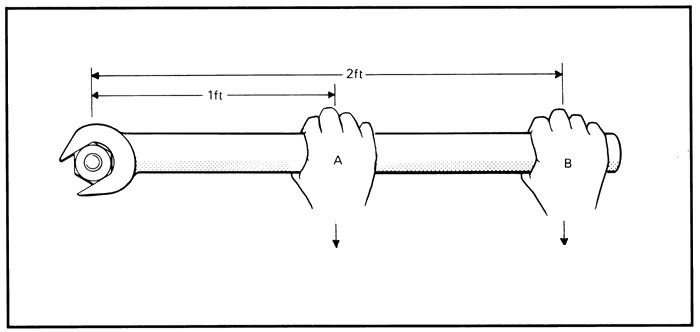
Предположим, что нам нужно открыть дверь, схематически показанную на рис. 10.6. Как известно из опыта, дверь практически невозможно открыть, если прилагать силу вблизи петель (см. схему А на рис. 10.6). Однако, если приложить силу посередине двери, то открыть ее будет гораздо проще (см. схему Б на рис. 10.6). Наконец, прилагая силу у противоположного края двери по отношению к расположению петель, ее можно открыть с еще меньшим усилием (см. схему В на рис. 10.6).

На рис. 10.6 расстояние от мест расположения петель до точки приложения силы и есть плечо силы. Моментом силы называется произведение прилагаемой силы ​( F )​ на плечо силы ​( l )​:

Момент силы в системе СИ измеряется в Н·м, а в системе СГС — в дин·см (подробнее эти системы единиц измерения описываются в главе 2).

Вернемся к примеру на рис. 10.6, где требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н. В случае А (см. рис. 10.6) плечо силы равно нулю и произведение этого плеча на силу любой величины (включая и силу 200 Н) даст нулевой момент силы. В случае Б (см. рис. 10.6) плечо силы равно половине ширины двери, т.е. плечо силы ​( l )​ равно 0,5 м и момент силы будет равен:

В случае В (см. рис. 10.6) плечо силы равно ширине двери, т.е. плечо силы ( l ) равно 1 м и момент силы будет равен:

Итак, увеличение вдвое длины плеча при той же силе дает нам такое же увеличение момента силы. До сих пор сила прилагалась перпендикулярно к линии, соединяющей точку приложения силы и точку вращения. А что будет с моментом силы, если дверь будет немного приоткрыта и направление силы уже будет не перпендикулярным?

Разбираемся с направлением приложенной силы и плечом силы

Допустим, что сила приложена не перпендикулярно к поверхности двери, а параллельно, как показано на схеме А на рис. 10.7. Как известно из опыта, таким образом дверь открыть невозможно. Дело в том, что у такой силы нет проекции, которая бы могла вызвать вращательное движение. Точнее говоря, у такой силы нет ненулевого плеча для создания вращательного момента силы.

Размышляем над тем, как создается момент силы

Момент силы из предыдущего примера требуется создавать всегда для открытия двери независимо от того, какую дверь приходится открывать: легкую калитку изгороди или массивную дверь банковского сейфа. Как вычислить необходимый момент силы? Сначала нужно определить плечо сил, а потом умножить его на величину силы.

Однако не всегда все так просто. Посмотрите на схему Б на рис. 10.7. Как видите, сила прилагается под некоторым углом ​( theta )​. Как в таком случае определить плечо силы? Если бы угол ( theta ) был прямым, то мы могли бы воспользоваться уже известно нам формулой:

Однако в данном случае угол ( theta ) не является прямым.

В таком случае нужно просто помнить следующее правило: плечом силы называется длина перпендикуляра, опущенного из предполагаемой точки вращения на прямую, относительно которой действует сила.

Попробуем применить это правило определения плеча силы для схемы Б на рис. 10.7. Нужно продлить линию, вдоль которой действует сила, а потом опустить на нее перпендикуляр из точки вращения двери. Из полученного прямоугольного треугольника легко определить искомое плечо силы:

Если угол ( theta ) равен нулю, то никакого момента силы не возникает (см. схему А на рис. 10.7).

Итак, получаем для момента силы для схемы Б на рис. 10.7:

Например, если требуется открыть дверь шириной 1 м с помощью силы величиной 200 Н, приложенной под углом ( theta ) = 45°, то создаваемый момент этой силы будет равен:

Как видите, этот момент силы 140 Н·м меньше, чем момент силы 200 Н·м, созданный под прямым углом на схеме В на рис. 10.6.

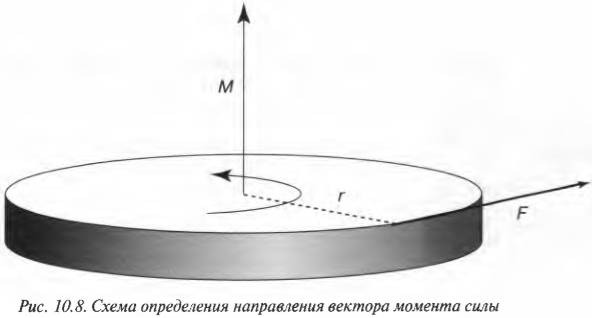
Определяем направление момента силы

Учитывая все приведенные выше сведения о моменте силы, у читателя вполне может возникнуть подозрение, что момент силы обладает направлением. И это действительно так. Момент силы является векторной величиной, направление которой определяется по правилу правой руки. Если охватить ладонью ось вращения, а пальцы свернуть так, чтобы они указывали на направление силы, то вытянутый большой палец укажет направление вектора момента силы.

На рис. 10.8 показан пример силы ​( mathbf{F} )​ с плечом ( mathbf{l} ) и соответствующего вектора момента сил ( mathbf{M} ).

Уравновешиваем моменты сил

В жизни нам часто приходится сталкиваться с равновесными состояниями. Как равновесное механическое состояние определяется с точки зрения физики? Обычно физики подразумевают под равновесным состоянием объекта то, что он не испытывает никакого ускорения (но может двигаться с постоянной скоростью).

Для поступательного движения равновесное состояние означает, что сумма всех сил, действующих на объект равна нулю:

Иначе говоря, результирующая действующая сила равна нулю.

Вращательное движение также может быть равновесным, если такое движение происходит без углового ускорения, т.е. с постоянной угловой скоростью.

Для вращательного движения равновесное состояние означает, что сумма всех моментов сил, действующих на объект, равна нулю:

Как видите, это условие равновесного вращательного движения аналогично условию равновесного поступательного движения. Условия равновесного вращательного движения удобно использовать для определения момента силы, необходимого для уравновешивания неравномерно вращающегося объекта.

Простой пример: вешаем рекламный плакат

Предположим, что у входа в магазин нужно повесить большой и тяжелый рекламный плакат, как показано на рис. 10.9. Хозяин магазина пытался сделать это и раньше, но у него ничего не выходило, поскольку он использовал очень непрочный болт.

Попробуем определить силу, с которой болт должен удерживать всю конструкцию, показанную на рис. 10.9. Пусть плакат имеет массу 50 кг и висит на шесте 3 м от точки опоры шеста, а массу шеста в данном примере будем считать пренебрежимо малой. Болт находится в 10 см от точки опоры шеста.

Согласно условиям равновесия, сумма всех моментов сил должна быть равна нулю:

Иначе говоря:

где ​( mathbf{M_п} )​ — это момент силы со стороны плаката, а ( mathbf{M_б} ) — это момент силы со стороны болта.

Чему равны упомянутые моменты? Момент силы со стороны плаката можно легко определить по формуле:

где ​( m )​ = 50 кг — это масса плаката, ​( mathbf{g} )​ — ускорение свободного падения под действием силы гравитационного притяжения (силы тяжести), ​( mmathbf{g} )​ — сила тяжести плаката, а ​( l_п )​ = 3 м — это плечо силы тяжести плаката.

Подставляя значения, получим:

Обратите внимание, что здесь перед ускорением свободного падения под действием силы гравитационного притяжения стоит знак “минус”. Это значит, что вектор ускорения свободного падения направлен вниз, т.е. в сторону, противоположную выбранному направлению оси координат.

Момент силы со стороны болта определяется формулой:

где ( mathbf{F_б} ) — это искомая сила, с которой болт должен удерживать всю конструкцию, а ( l_б ) = 0,1 м — это ее плечо.

Подставляя полученные выражения для моментов сил в формулу:

получим, что:

Отсюда с помощью простых алгебраических преобразований получим искомую силу:

Как видите сила, с которой болт должен удерживать всю конструкцию, направлена противоположно вектору ускорения свободного падения, т.е. вверх.

Подставляя значения, получим искомый ответ:

Более сложный пример: учитываем силу трения при расчете равновесия

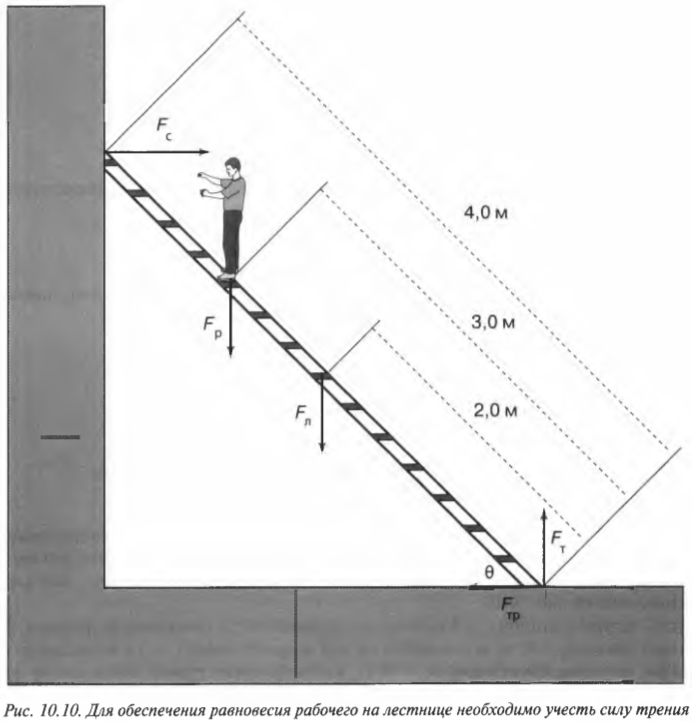
Рассмотрим теперь другую более сложную задачу, в которой для расчета равновесия системы объектов нужно учесть силу трения. Предположим, что работник магазина решил использовать переносную лестницу для монтажа рекламного плаката, как схематически показано на рис. 10.10.

Пусть лестница длиной ​( l_л )​ = 4 м стоит под углом ​( theta )​ = 45° к поверхности тротуара, работник имеет массу ​( m_р )​ = 45 кг и находится на ней на расстоянии ( l_р ) = 3 м от нижнего конца лестницы, лестница имеет массу (m_л ) = 20 кг, а коэффициент трения покоя между поверхностью тротуара и концами лестницы равен ​( mu_п )​ = 0,7. Вопрос: будет ли такая система объектов находиться в состоянии равновесия? Попросту говоря, достаточной ли будет сила трения, чтобы лестница вместе с рабочим не соскользнула и упала?

Итак, для ответа на этот вопрос нам нужно учесть следующие силы, действующие на лестницу:

• ​( mathbf{F_с} )​ — нормальная сила со стороны стены;
• ( mathbf{F_р} ) — вес рабочего;
• ( mathbf{F_л} ) — вес лестницы;
• ( mathbf{F_{тр}} ) — сила трения между поверхностью тротуара и концами лестницы;
• ( mathbf{F_т} ) — нормальная сила со стороны тротуара.

Согласно условиям равновесного поступательного движения, сумма всех сил, действующих на лестницу, должна быть равна нулю:

Это значит, что сумма всех сил вдоль горизонтальной оси, а именно нормальной силы со стороны стены ( mathbf{F_с} ) и силы трения между поверхностью тротуара и концами лестницы ( mathbf{F_{тр}} ), должна быть равна нулю, то есть:

или

Перефразируя поставленный выше вопрос о достаточности силы трения, получим: выполняется ли условие

Кроме того, сумма всех сил вдоль вертикальной оси, а именно веса рабочего ( mathbf{F_р} ), веса лестницы ( mathbf{F_л} ) и нормальной силы со стороны тротуара ( mathbf{F_т} ), должна быть равна нулю, то есть:

или

Согласно условиям равновесного вращательного движения, также необходимо равенство нулю всех моментов сил, действующих на лестницу:

Пусть предполагаемой точкой вращения является нижний конец лестницы, тогда должна быть равна нулю сумма моментов сил, создаваемых весом рабочего ​( mathbf{M_р=[L_р!times! F_р]} )​, весом лестницы ( mathbf{M_л=[L_л!times!F_л]} ) и нормальной силой со стороны стены ( mathbf{M_с=[L_с!times! F_с]} ):

или

или

Поскольку ​( L_р=l_р )​, ​( L_л=l_л/2 )​ (центр тяжести лестницы находится посередине лестницы), ( L_с=l_л ), ​( alpha=360^{circ}-theta )​, ( beta=360^{circ}-theta ) и ​( gamma=theta )​, то получим:

или

Таким образом, мы получили систему из двух уравнений с двумя неизвестными сил ( mathbf{F_с} ) и ( mathbf{F_т} ):

Зададимся вопросом: соблюдается ли условие

Из системы двух уравнений получим:

Итак, остается выяснить, соблюдается ли условие:

После подстановки значений получим:

Поскольку ​( mu_т )​ = 0,7, то упомянутое условие соблюдается, и лестница с рабочим не упадет.

Вращение является типичным видом механического движения, которое часто встречается в природе и технике. Любое вращение возникает в результате воздействия некоторой внешней силы на рассматриваемую систему. Эта сила создает так называемый вращающий момент. Что он собой представляет, от чего зависит, рассматривается в статье.

Процесс вращения

Прежде чем рассматривать концепцию вращающего момента, дадим характеристику систем, к которым может быть применена эта концепция. Система вращения предполагает наличие в ней оси, вокруг которой осуществляется круговое движение или поворот. Расстояние от этой оси до материальных точек системы называется радиусом вращения.

С точки зрения кинематики, процесс характеризуется тремя угловыми величинами:

• углом поворота θ (измеряется в радианах);
• угловой скоростью ω (измеряется в радианах в секунду);
• ускорением угловым α (измеряется в радианах в секунду квадратную).

Эти величины связаны друг с другом следующими равенствами:

ω = dθ/dt;

α = dω/dt.

Примерами вращения в природе являются движения планет по своим орбитам и вокруг своих осей, движения смерчей. В быту и технике рассматриваемое движение характерно для моторов двигателей, гаечных ключей, строительных кранов, открывания дверей и так далее.

Определение момента силы

Теперь перейдем к непосредственной теме статьи. Согласно физическому определению, момент силы представляет собой векторное произведение вектора приложения силы относительно оси вращения на вектор самой силы. Соответствующее математическое выражение можно записать так:

M¯ = [r¯*F¯].

Здесь вектор r¯ направлен от оси вращения к точке приложения силы F¯.

В этой формуле вращающего момента M¯ сила F¯ может быть направлена как угодно относительно направления оси. Тем не менее параллельная оси компонента силы не будет создавать вращения, если ось жестко закреплена. В большинстве задач по физике приходится рассматривать силы F¯, которые лежат в плоскостях перпендикулярных оси вращения. В этих случаях абсолютное значение вращающего момента можно определить по следующей формуле:

|M¯| = |r¯|*|F¯|*sin(β).

Где β является углом между векторами r¯ и F¯.

Что такое рычаг силы?

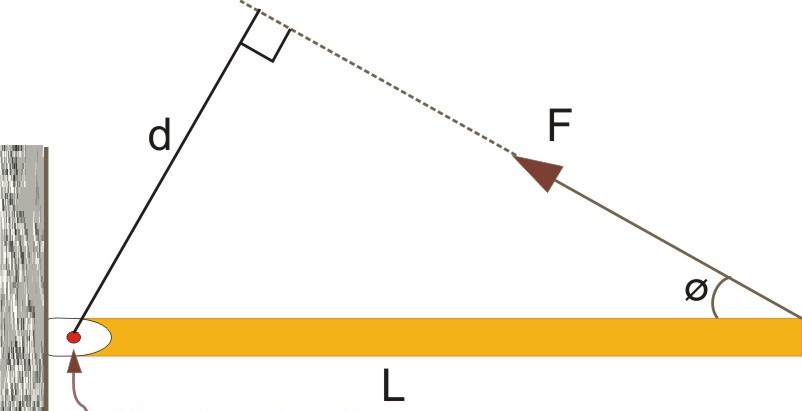
Рычаг силы играет важную роль при определении величины момента силы. Чтобы понять, о чем идет речь, рассмотрим следующий рисунок.

Здесь показан некоторый стержень длиною L, который закреплен в точке вращения одним из своих концов. На другой конец действует сила F, направленная под острым углом φ. Согласно определению момента силы, можно записать:

M = F*L*sin(180^o-φ).

Угол (180^o-φ) появился потому, что вектор L¯ направлен от закрепленного конца к свободному. Учитывая периодичность тригонометрической функции синуса, можно переписать это равенство в таком виде:

M = F*L*sin(φ).

Теперь обратим внимание на прямоугольный треугольник, построенный на сторонах L, d и F. По определению функции синуса, произведение гипотенузы L на синус угла φ дает значение катета d. Тогда приходим к равенству:

M = F*d.

Линейная величина d называется рычагом силы. Он равен расстоянию от вектора силы F¯ до оси вращения. Как видно из формулы, понятием рычага силы удобно пользоваться при вычислении момента M. Полученная формула говорит о том, что вращающий момент максимальный для некоторой силы F будет возникать только тогда, когда длина радиус-вектора r¯ (L¯ на рисунке выше) будет равна рычагу силы, то есть r¯ и F¯ будут взаимно перпендикулярны.

Направление действия величины M¯

Выше было показано, что вращающий момент — это векторная характеристика для данной системы. Куда направлен этот вектор? Ответить на этот вопрос не представляет особого труда, если вспомнить, что результатом произведения двух векторов является третий вектор, который лежит на оси, перпендикулярной плоскости расположения исходных векторов.

Остается решить, будет ли направлен момент силы вверх или вниз (на читателя или от него) относительно упомянутой плоскости. Определить это можно или по правилу буравчика, или с помощью правила правой руки. Приведем оба правила:

• Правило правой руки. Если расположить правую кисть таким образом, чтобы четыре ее пальца двигались от начала вектора r¯ к его концу, а затем от начала вектора F¯ к его концу, то большой палец, оттопыренный, укажет на направление момента M¯.
• Правило буравчика. Если направление вращения воображаемого буравчика совпадает с направлением вращательного движения системы, то поступательное движение буравчика укажет на направление вектора M¯. Напомним, что он вращается только по часовой стрелке.

Оба правила являются равноправными, поэтому каждый может использовать то, которое является для него более удобным.

При решении практических задач разное направление вращающего момента (вверх — вниз, влево — вправо) учитывается с помощью знаков «+» или «-«. Следует запомнить, что за положительное направление момента M¯ принято считать такое, которое приводит к вращению системы против часовой стрелки. Соответственно, если некоторая сила приводит к вращению системы по ходу стрелки часов, то создаваемый ее момент будет иметь отрицательную величину.

Физический смысл величины M¯

В физике и механике вращения величина M¯ определяет способность силы или суммы сил совершать вращение. Поскольку в математическом определении величины M¯ стоит не только сила, но и радиус-вектор ее приложения, то именно последний во многом определяет отмеченную вращательную способность. Чтобы понятнее было, о какой способности идет речь, приведем несколько примеров:

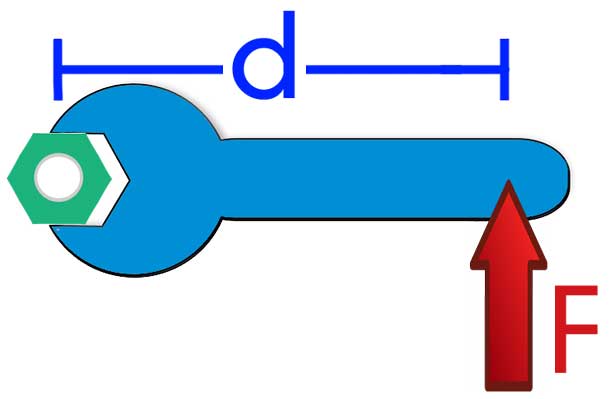
• Каждый человек, хотя бы один раз в жизни пытался открыть дверь, взявшись не за ручку, а толкнув ее недалеко от петель. В последнем случае приходится прилагать значительное усилие, чтобы добиться желаемого результата.
• Чтобы открутить гайку с болта, используют специальные гаечные ключи. Чем длиннее ключ, тем легче открутить гайку.
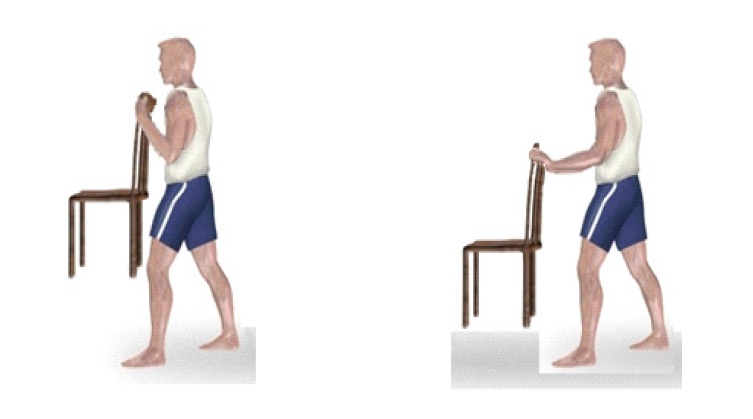
• Чтобы ощутить важность рычага силы, предлагаем читателям проделать следующий эксперимент: взять стул и попытаться удержать его одной рукой на весу, в одном случае руку прислонить к телу, в другом — выполнить задачу на прямой руке. Последнее для многих окажется непосильной задачей, хотя вес стула остался тем же самым.

Единицы измерения момента силы

Несколько слов также следует сказать о том, в каких единицах в СИ измеряется вращающий момент. Согласно записанной для него формуле, он измеряется в ньютонах на метр (Н*м). Однако в этих единицах также измеряется работа и энергия в физике (1 Н*м = 1 джоуль). Джоуль для момента M¯ не применяется, поскольку работа является скалярной величиной, M¯ же — это вектор.

Тем не менее совпадение единиц момента силы с единицами энергии не является случайным. Работа по вращению системы, совершенная моментом M, рассчитывается по формуле:

A = M*θ.

Откуда получаем, что M также может быть выражен в джоулях на радиан (Дж/рад).

Динамика вращения

В начале статьи мы записали кинематические характеристики, которые используются для описания движения вращения. В динамике вращения главным уравнением, которое использует эти характеристики, является следующее:

M = I*α.

Действие момента M на систему, имеющую момент инерции I, приводит к появлению углового ускорения α.

Данную формулу применяют, для определения угловых частот вращения в технике. Например, зная вращающий момент асинхронного двигателя, который зависит от частоты тока в катушке статора и от величины изменяющегося магнитного поля, а также зная инерционные свойства вращающегося ротора, можно определить, до какой скорости вращения ω раскручивается ротор двигателя за известное время t.

Пример решения задачи

Невесомый рычаг, длина которого составляет 2 метра, посередине имеет опору. Какой вес следует положить на один конец рычага, чтобы он находился в состоянии равновесия, если с другой стороны опоры на расстоянии 0,5 метра от нее лежит груз массой 10 кг?

Очевидно, что равновесие рычага наступит, если моменты сил, создаваемые грузами, будут равны по модулю. Сила, создающая момент в данной задаче, представляет собой вес тела. Рычаги силы равны расстояниям от грузов до опоры. Запишем соответствующее равенство:

M₁ = M₂ =>

m₁*g*d₁ = m₂*g*d₂ =>

P₂ = m₂*g = m₁*g*d₁/d₂.

Вес P₂ получим, если подставим из условия задачи значения m₁ = 10 кг, d₁ = 0,5 м, d₂ = 1 м. Записанное равенство дает ответ: P₂ = 49,05 ньютона.

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

  17 слайд

  1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
  Дано:
  I = 245 кг·м2
  = 20 об/c
  t = 1 мин

  Mтр — ?
  N — ?
  Решение
  Запишем уравнение основного закона динамики вращательного движения:
  В проекциях на ось OX:
  Отсюда проекция вектора углового ускорения на ось OX:
  Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Проекция угловой скорости колеса на ось OX:

• 

  18 слайд

  Колесо остановится, поэтому
  Решение (продолжение)
  Величина (модуль) вектора углового ускорения:
  1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
  Для модулей векторов:

• 

  19 слайд

  Величина углового перемещения колеса изменяется как
  Решение (продолжение)
  Из двух кинематических уравнений движения получаем систему уравнений:
  Величину углового ускорения ε получим из второго уравнения и подставим в первое:
  1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.

• 

  20 слайд

  1. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/c. Через время t = 1 мин после того, как на колесо перестал действовать момент сил М, оно остановилось. Найти момент сил трения Мтр и число оборотов N, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском.
  Решение (продолжение)
  Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения:
  После подстановки получим:
  Отсюда полное число оборотов колеса до остановки:
  Ответ: Мтр = 513 H·м, N = 600.

• 

  21 слайд

  5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
  Дано:
  I = 245 кг·м2
  = 20 об/c
  N = 1000

  Mтр — ?
  t — ?
  Решение
  Запишем уравнение основного закона динамики вращательного движения:
  В проекциях на ось OX:
  Отсюда проекция вектора углового ускорения на ось OX:
  Величина углового ускорения постоянна, векторы углового ускорения и угловой скорости направлены противоположно. Угловое перемещение колеса

• 

  22 слайд

  5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
  Величина угловой скорости колеса изменяется как
  Колесо остановится, поэтому
  Решение (продолжение)
  Из двух кинематических уравнений движения получаем систему уравнений:
  Величину углового ускорения ε получим из второго уравнения и подставим в первое:

• 

  23 слайд

  5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
  Величину углового перемещения φ выразим через число оборотов, сделанных до остановки, а начальную угловую скорость – через начальную частоту вращения:
  Решение (продолжение)
  После подстановки получим:
  Откуда время движения до остановки:

• 

  24 слайд

  5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
  Решение (продолжение)
  Теперь вернёмся к динамическому уравнению движения и найдём величину момента сил трения. Для проекций на ось OX:
  Величина момента сил трения
  Или, для краткости,
  Как было получено ранее,
  Теперь

• 

  25 слайд

  5. Маховое колесо, момент инерции которого I = 245 кг·м2, вращается с частотой  = 20 об/с. После того как на колесо перестал действовать вращающий момент, оно остановилось, сделав N = 1000 об. Найти момент сил трения Мтр и время t, прошедшее от момента прекращения действия вращающегося момента до остановки колеса.
  Решение (продолжение)
  Ответ: t = 100 c; Мтр = 308 H·м.

• 

  26 слайд

  2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
  Дано:
  m = 0,5 кг
  I = 0,1 кг·м2
  R = 20 cм
  h0 = 1 м

  t — ?
  Ек — ?
  Т — ?
  Решение
  Прежде всего, запишем динамическое уравнение движения груза. Из второго закона Ньютона:
  Для проекций на ось OY:
  Если учесть, что груз опускается, то
  где a — величина (модуль) проекции ускорения на ось OY.
  a = const., начальная скорость груза равна нулю, следовательно кинематическое уравнение движения можно записать так:

• 

  27 слайд

  2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
  Решение (продолжение)
  Через время t груз окажется на земле (y = 0), поэтому
  Величину ускорения можно определить из уравнения второго закона Ньютона
  но для этого нужно знать величину силы натяжения нити T.
  Запишем уравнение основного закона динамики вращательного движения для барабана:
  В проекциях на ось OZ, перпендикулярную плоскости рисунка:
  Из третьего закона Ньютона

• 

  28 слайд

  2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
  Решение (продолжение)
  Величину углового ускорения ε можно выразить через величину линейного ускорения a:
  Теперь можно записать систему уравнений, из которой можно определить a и T:

• 

  29 слайд

  2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
  Решение (продолжение)
  Найдём величину линейного ускорения a:
  Подставим выражение для a в формулу для времени движения груза:

• 

  30 слайд

  2. На барабан радиусом R = 20 см, момент инерции которого I = 0,1 кгм2, намотан шнур, к концу которого привязан груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом h0 = 1 м. Через какое время t груз опустится до пола? Найти кинетическую энергию Ек груза в момент удара о пол и силу натяжения нити Т. Трением пренебречь.
  Ответ: t = 1,1 c; Ek = 0,82 Дж; Т = 4,1 H.
  Решение (продолжение)
  Кинетическая энергия груза
  Скорость груза
  где

• 

  31 слайд

  3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что блок вращается с угловым ускорением  = 2,36 рад/c2. Блок считать однородным диском.
  Дано:
  Mтр = 98,1 Н·м
  I = 50 кг·м2
  R = 20 cм
  e = 2,36 рад/c2

  Т2 – Т1 — ?
  Решение
  Вращательное движение блока описывается основным законом динамики вращательного движения.
  Запишем для блока:
  Для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.
  Согласно третьему закону Ньютона

• 

  32 слайд

  3. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т1 – Т2 по обе стороны блока, если известно, что блок вращается с угловым ускорением  = 2,36 рад/c2. Блок считать однородным диском.
  Решение (продолжение)
  Из этого уравнения получаем:
  Ответ: T2 – T21 =1,08 кН.

• 

  33 слайд

  3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
  Дано:
  Mтр = 98,1 Н·м
  I = 50 кг·м2
  R = 20 cм
  m1 = 1 кг
  m2 = 1,5 кг

  Т2 – Т1 — ?
  Решение
  Поступательное движение гирь описывается вторым законом Ньютона, а вращательное движение блока – основным законом динамики вращательного движения.
  Запишем для гирь и блока:
  Перепишем систему уравнений. Для этого первое и второе уравнения запишем для проекций на вертикальную ось OY, а третье – для проекций на ось OZ, направленную перпендикулярно плоскости рисунка.

• 

  34 слайд

  Решение (продолжение)
  Согласно третьему закону Ньютона
  Величину углового ускорения ε можно выразить через величину линейного ускорения a:
  Нить нерастяжима, поэтому
  3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.

• 

  35 слайд

  Решение (продолжение)
  Система уравнений приобретает вид:
  Вычтем из второго уравнения первое и выполним элементарные преобразования в третьем:
  3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.

• 

  36 слайд

  Решение (продолжение)
  3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.
  Разделим первое уравнение на второе:

• 

  37 слайд

  Решение (продолжение)
  3А. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого I = 50 кгм2 и радиус R = 20 см. Момент сил трения вращающегося блока Мтр = 98,1 Нм. Найти разность сил натяжения нити Т2 – Т1 по обе стороны блока, если известно, что массы гирь m1 = 1 кг, m2 = 1,5 кг. Блок считать однородным диском.

• 

  38 слайд

  4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
  Решение
  Дано:
  h = 0,5 м
  0 = 0

  v — ?
  Задачу решим с помощью закона сохранения энергии. Любое из трёх перечисленных в условии тел участвует в двух движениях – поступательном с скоростью v и вращательном вокруг своего центра масс. Поэтому кинетическая энергия тела складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения.
  В системе действуют только консервативные силы (трения нет), поэтому изменение полной механической энергии равно нулю.

• 

  39 слайд

  4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
  Решение (продолжение)
  потенциальная энергия тела в поле силы тяжести уменьшилась.
  кинетическая энергия поступательного движения тела увеличилась.
  кинетическая энергия вращательного движения тела увеличилась. Здесь ω — угловая скорость вращения тела.

• 

  40 слайд

  4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
  Решение (продолжение)
  Любое из тел катится без проскальзывания, поэтому
  По этой общей формуле можно найти скорость любого из трёх тел, для этого достаточно подставить выражение для момента инерции соответствующего тела.

• 

  41 слайд

  4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
  Решение (продолжение)
  1. Шар:
  2. Диск:

• 

  42 слайд

  4. Найти линейные скорости  движения центров шара, диска и обруча, скатывающихся без проскальзывания с наклонной плоскости. Высота наклонной плоскости h = 0,5 м, начальная скорость всех тел 0 = 0. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
  Ответ: 1 = 2,65 м/c, 2 = 2,56 м/c, 3 = 2,21 м/c;  = 3,13 м/c.
  Решение (продолжение)
  3. Обруч:
  4. Для тела, соскальзывающего без вращения по наклонной плоскости

• 

  43 слайд

  6. Маховое колесо начинает вращаться с угловым ускорением  = 0,5 рад/c2 и через время t1 = 15 с после начала движения приобретает момент импульса L1 = 73,5 кгм2/c. Найти кинетическую энергию T колеса через время t2 = 20 с после начала движения.
  Решение
  Дано:
   = 0,5 рад/c2
  ω0 = 0
  t1 = 15 с
  t2 = 20 с
  L1 = 73,5 кгм2/c

  Т — ?
  Кинетическую энергию вращающегося колеса можно найти как
  где I – момент инерции колеса, ω2 – угловая скорость колеса в момент времени t2.
  Колесо вращается равноускоренно, начальная угловая скорость вращения равна нулю.
  Величина (модуль) момента импульса колеса
  Отсюда

• 

  44 слайд

  6. Маховое колесо начинает вращаться с угловым ускорением  = 0,5 рад/c2 и через время t1 = 15 с после начала движения приобретает момент импульса L1 = 73,5 кгм2/c. Найти кинетическую энергию T колеса через время t2 = 20 с после начала движения.
  Ответ: T=490 Дж.
  Решение (продолжение)
  Подставим в формулу для кинетической энергии полученные выражения для момента инерции и угловой скорости.

• 

  45 слайд

  7. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы?
  Решение
  Дано:
  m = 5 кг
  ω0 = 0
  t = 5 с
  F = 19,6 Н

  Т — ?
  Кинетическую энергию вращающегося диска можно найти как
  где I – момент инерции диска, ω – угловая скорость колеса в момент времени t.
  Сила F создаёт постоянный вращающий момент, что приводит к равноускоренному вращению диска. Основной закон динамики вращательного движения можно записать так:
  Для проекций на ось OX (см. рисунок):
  Диск вращается равноускоренно, начальная угловая скорость вращения равна нулю,

• 

  46 слайд

  7. К ободу диска массой m = 5 кг приложена касательная сила F = 19,6 Н. Какую кинетическую энергию T будет иметь диск через время t = 5 с после начала действия силы?
  Ответ: T=1,92 кДж.
  Решение (продолжение)
  Момент инерции диска относительно данной оси вращения

• 

  47 слайд

  8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость  надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
  Дано:
  l = 85 см

  v — ?
  Решение
  Если мы сообщим нижнему концу стержня некоторую скорость, он сможет совершить полный оборот вокруг оси, проходящей через точку О.
  Если эта скорость минимальная из всех возможных, при которых стержень совершит оборот, то в верхней точке скорость стержня будет очень близка к нулю (рис. 2).
  Для определения минимальной скорости, при которой возможен полный оборот стержня применим закон сохранения энергии. Трение в системе отсутствует, поэтому можно считать, что все силы, действующие в системе консервативны.
  Изменение потенциальной энергии в поле сил тяжести определим по изменению положения центра тяжести стержня, который совпадает с его геометрическим центром.

• 

  48 слайд

  8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость  надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
  Решение (продолжение)
  Потенциальная энергия стержня в поле сил тяжести увеличилась.
  Кинетическая энергия стержня уменьшилась, так как в верхней точке он практически остановился.
  Здесь ω — начальная угловая скорость стержня.
  Момент инерции стержня относительно точки O

• 

  49 слайд

  8. Однородный стержень длиной l = 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую минимальную скорость  надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
  Ответ: =7,1 м/c.
  Решение (продолжение)

• 

  50 слайд

  9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека  точечной массой. Трения нет.
  Решение
  Дано:
  m = 100 кг
  m0 = 60 кг
  n1 = 10 об/мин

  n2 — ?
  На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
  Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ:
  В случае, когда человек стоит на краю платформы, момент инерции системы

• 

  51 слайд

  9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека  точечной массой. Трения нет.
  В случае, когда человек стоит в центре платформы, его момент инерции относительно рассматриваемой оси равен нулю, а момент инерции системы
  Решение (продолжение)
  Подставим выражения для моментов инерции в закон сохранения момента импульса:
  Угловая скорость связана с частотой вращения соотношением:

• 

  52 слайд

  9. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой 2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека  точечной массой. Трения нет.
  Ответ: 2 = 22 об/мин.
  Решение (продолжение)

• 

  53 слайд

  10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кгм2? Считать платформу однородным диском. Трения нет.
  Решение
  Дано:
  m = 80 кг
  R = 1 м
   1 = 20 об/мин
  I1=2,94 кгм2
  I2=0,98 кгм2

  n2 — ?
  На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
  Направлены моменты импульса системы одинаково. Для проекций на вертикальную ось OZ:
  Угловая скорость связана с частотой вращения соотношением:

• 

  54 слайд

  10. Горизонтальная платформа массой m=80 кг и радиусом R=1 м вращается с частотой 1=20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1=2,94 кгм2 до I2=0,98 кгм2? Считать платформу однородным диском. Трения нет.
  Решение (продолжение)
  Частота вращения после изменения момента инерции
  Момент инерции системы
  Момент инерции диска

• 

  55 слайд

  10. Горизонтальная платформа массой m = 80 кг и радиусом R = 1 м вращается с частотой 1 = 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой 2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от I1 = 2,94 кг·м2 до I2 = 0,98 кгм2? Считать платформу однородным диском. Трения нет.
  Ответ: 2=21 об/мин.
  Решение (продолжение)

• 

  56 слайд

  11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.
  Решение
  Дано:
  m0 = 60 кг
  m = 100 кг
  0 = 4 км/ч
  R = 10 м

  n — ?
  На рассматриваемую систему не действуют внешние моменты сил, следовательно её момент импульса сохраняется.
  В лабораторной системе отсчёта
  — момент импульса системы до начала движения человека;
  — момент импульса системы после начала движения человека.
  В лабораторной системе отсчёта
  — момент импульса платформы;
  — момент импульса человека.

• 

  57 слайд

  Решение (продолжение)
  Направлены моменты импульса человека и платформы в противоположные стороны. Для проекций на вертикальную ось OZ:
  В уравнение входит величина проекции скорости человека в лабораторной системе отсчёта, а в условии дана скорость относительно платформы. Найдём величину скорости в лабораторноё системе отсчёта.
  Как только человек начнёт движение, платформа начнёт вращаться в противоположном направлении (см. рисунок). Поэтому по закону сложения скоростей
  Величина линейной скорости края платформы
  11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.

• 

  58 слайд

  Решение (продолжение)
  Величина линейной скорости человека в лабораторной системе отсчёта
  Подставим выражение для величины линейной скорости человека в лабораторной системе отсчёта в уравнение закона сохранения момента импульса:
  Теперь осталось определить угловую скорость вращения платформы из последнего уравнения.
  11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.

• 

  59 слайд

  Решение (продолжение)
  Напомним, что I – момент инерции платформы, которая имеет форму диска.
  11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.

• 

  60 слайд

  Ответ:  = 3,6 об/мин.
  Решение (продолжение)
  Угловая скорость связана с частотой вращения соотношением:
  11. Человек массой m0 = 60 кг находится на неподвижной платформе массой m = 100 кг. С какой частотой  будет вращаться платформа, если человек начнет движение по краю платформы вокруг оси вращения? Скорость движения человека относительно платформы 0 = 4 км/ч. Радиус платформы R = 10 м. Считать платформу однородным диском, а человека  точечной массой. Трения нет.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 266 071 материал в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»

• Курс повышения квалификации «Экономика и право: налоги и налогообложение»

• Курс повышения квалификации «Введение в сетевые технологии»

• Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»

• Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»

• Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»

• Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»

• Курс повышения квалификации «Организация маркетинга в туризме»

• Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»

• Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»

• Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.

СКОРОСТЬ — это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.

ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.

УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение — это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения. Если объект движется с постоянной скоростью — ускорение отсутствует.

СИЛА — Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.

Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).

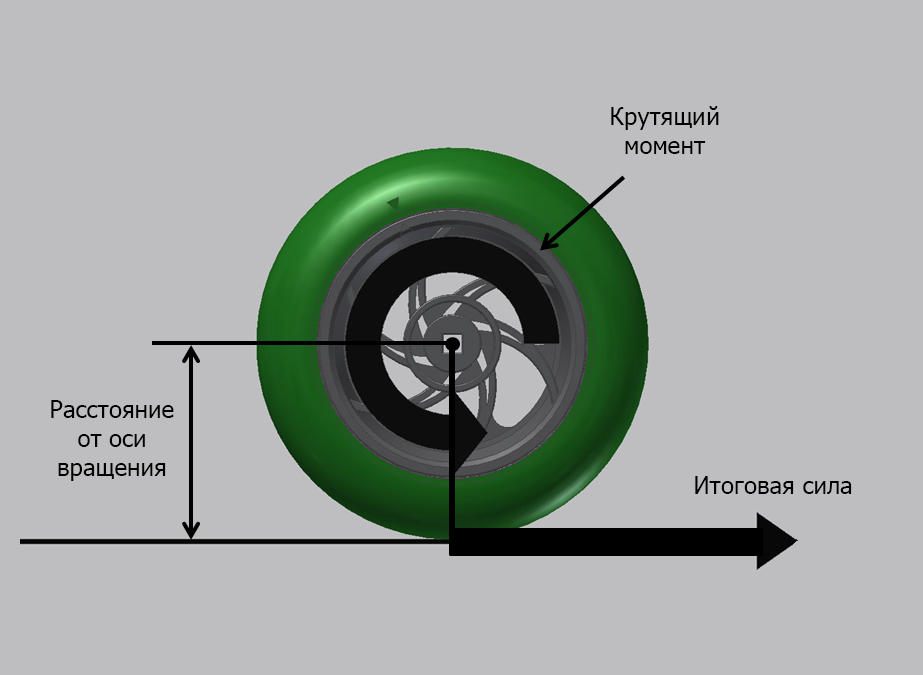
КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент — это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент — как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.

В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.

Сила = Крутящий момент/Радиус колеса

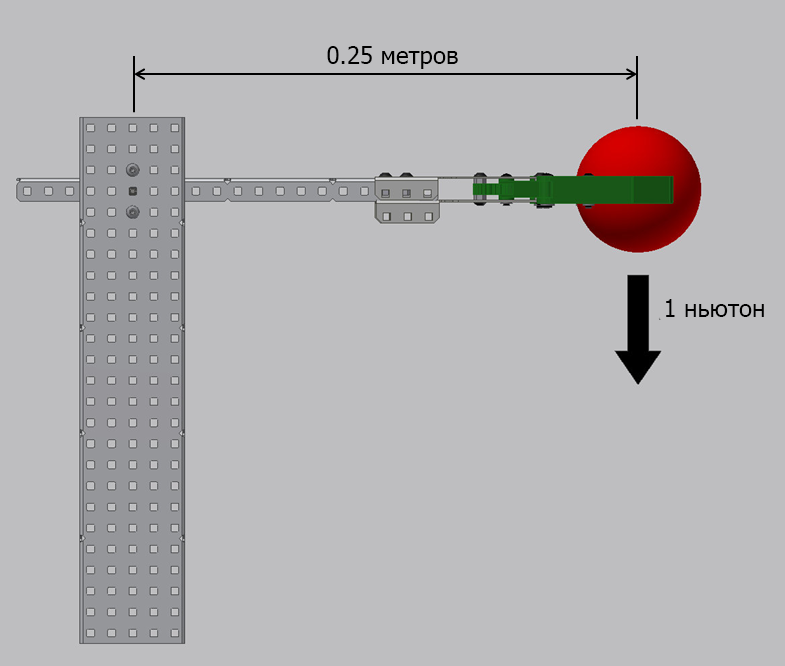
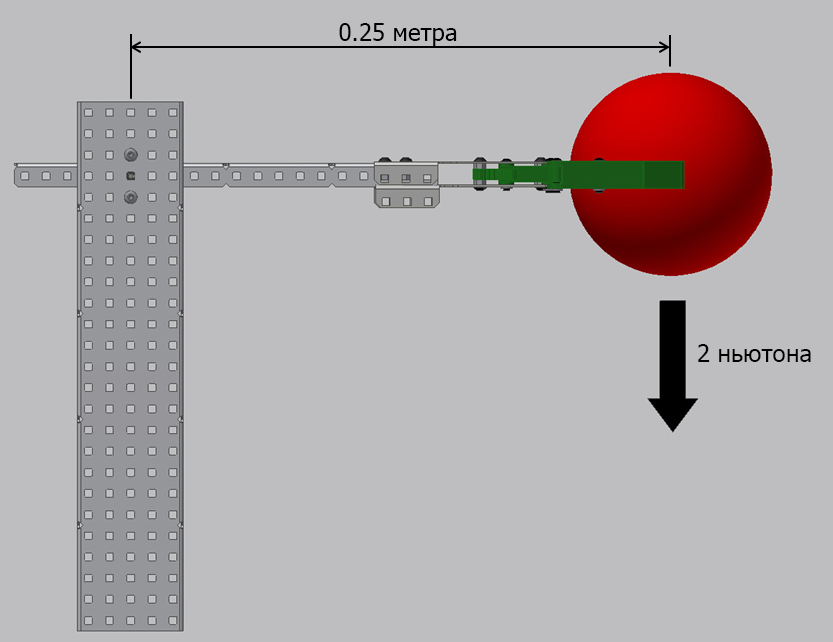
В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда

Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.

Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.

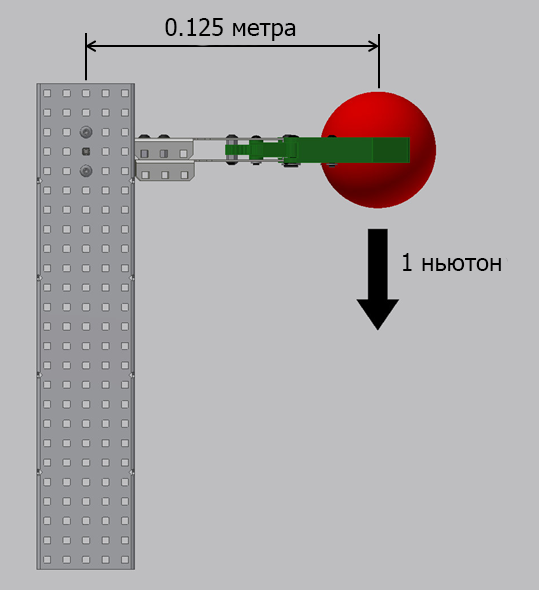
Пример 7.2

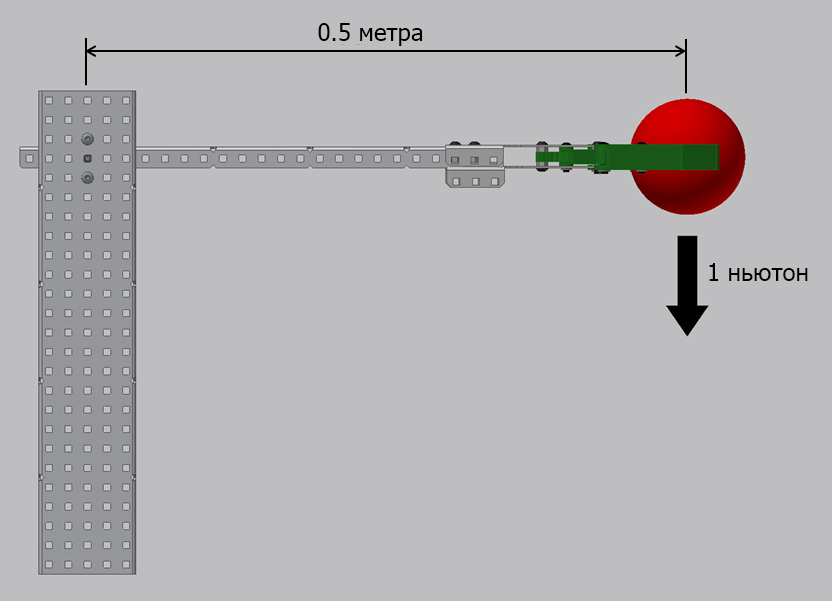
Пример 7.3

Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.

Пример 7.2 — Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.

Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.

Пример 7.3 — Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.

Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.

Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.

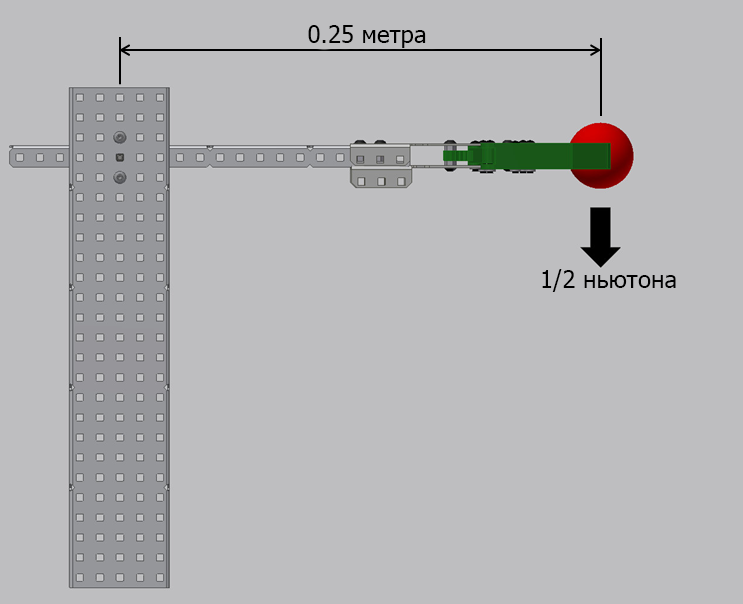
Пример 7.4

Пример 7.5

Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?

Пример 4 — Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.

Пример 5 — Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.

Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.

Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.

РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.

МОЩНОСТЬ — Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.

Мощность — это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?

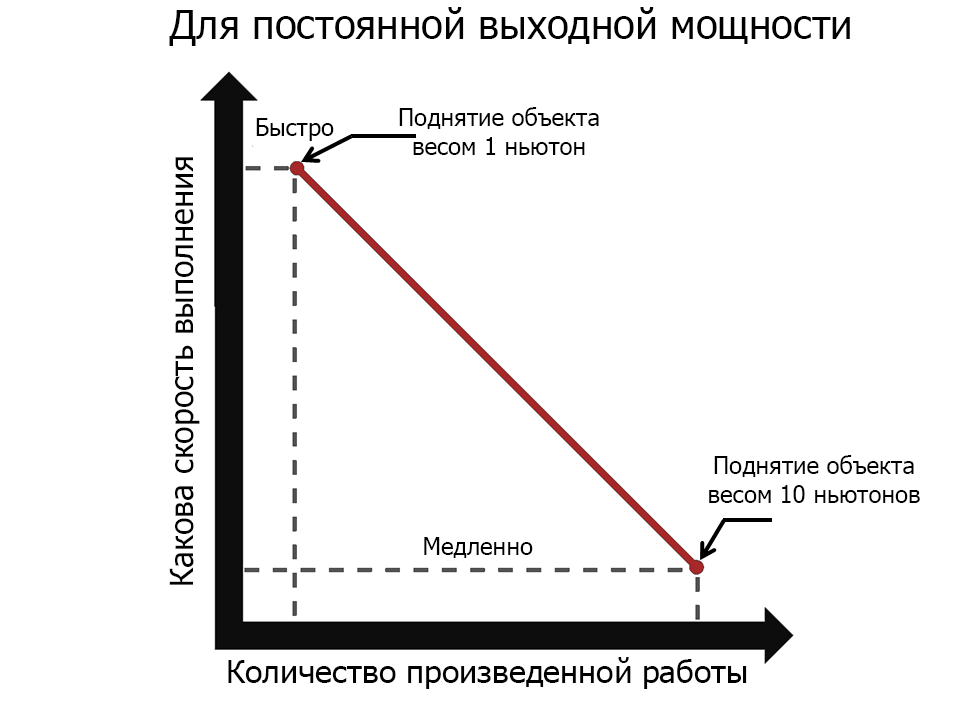
В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).

Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.

Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]

1 Ватт = 1 (Ньютон х Метр) / Секунда

Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.

Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.