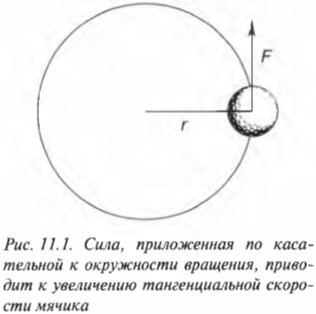
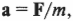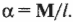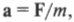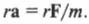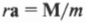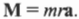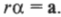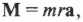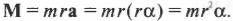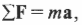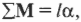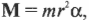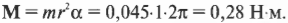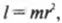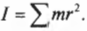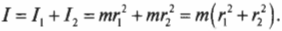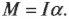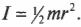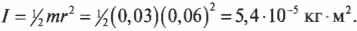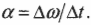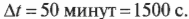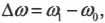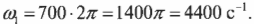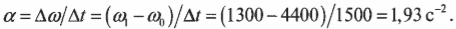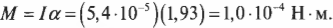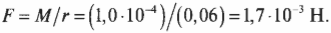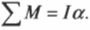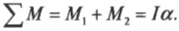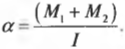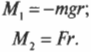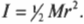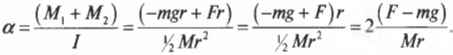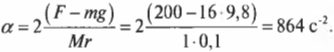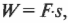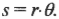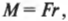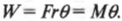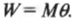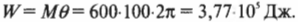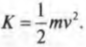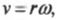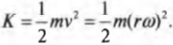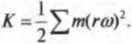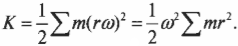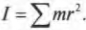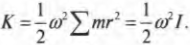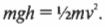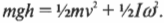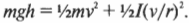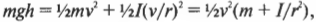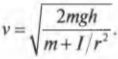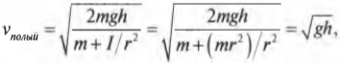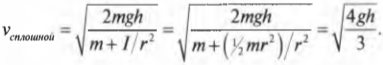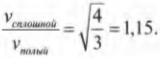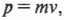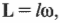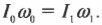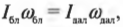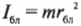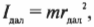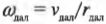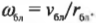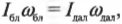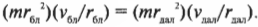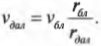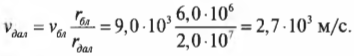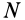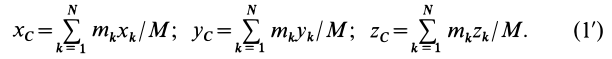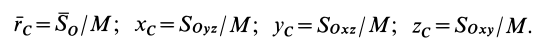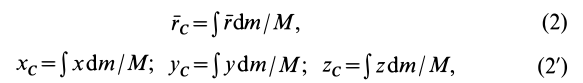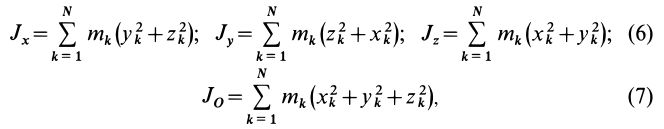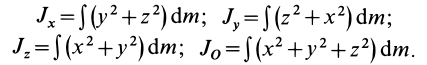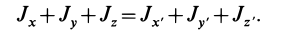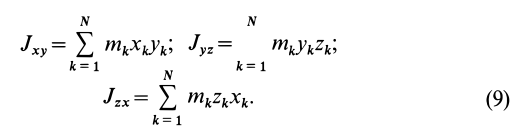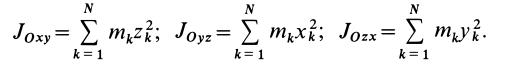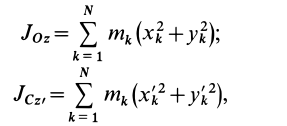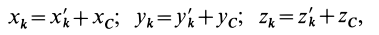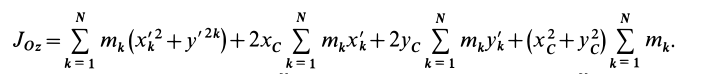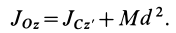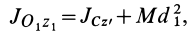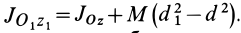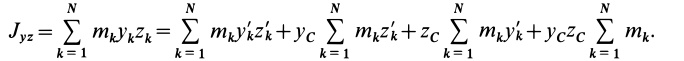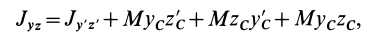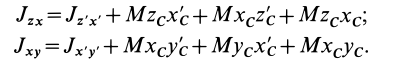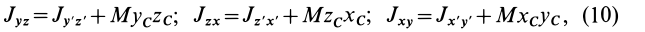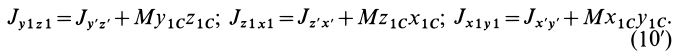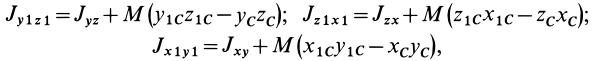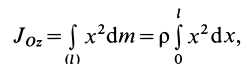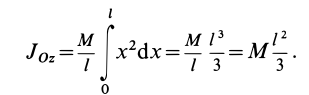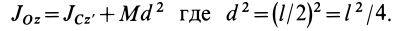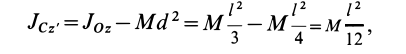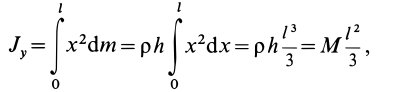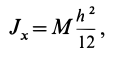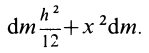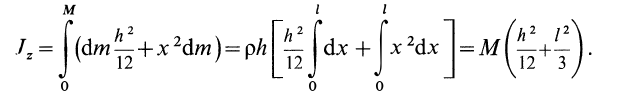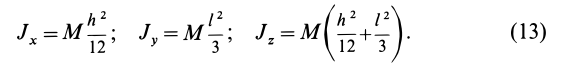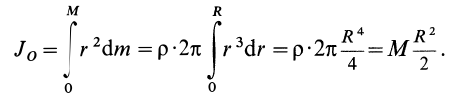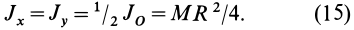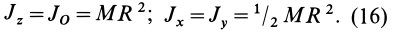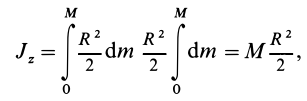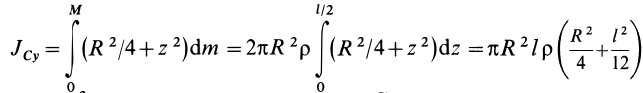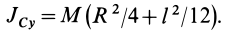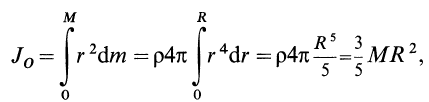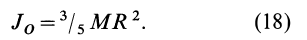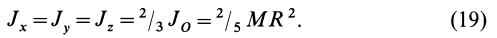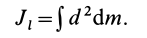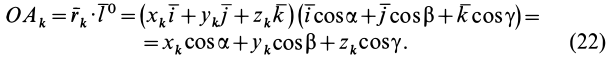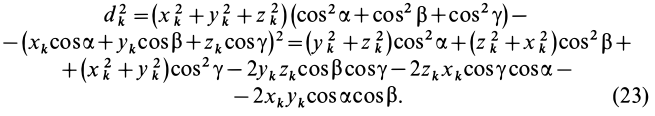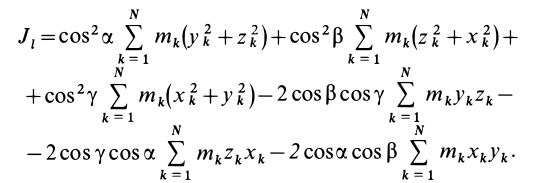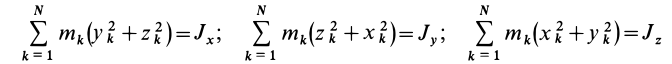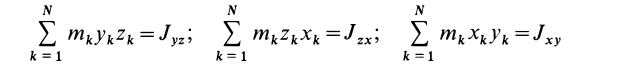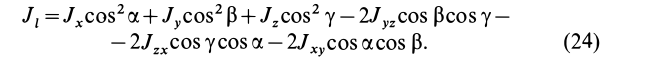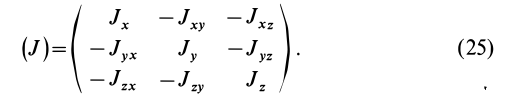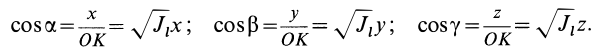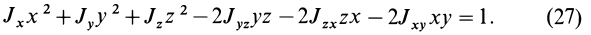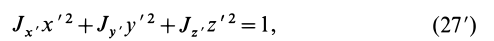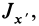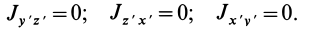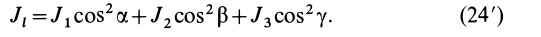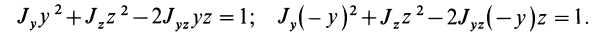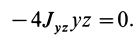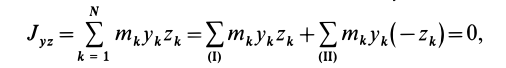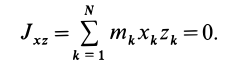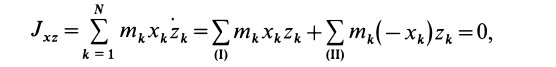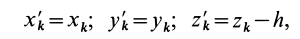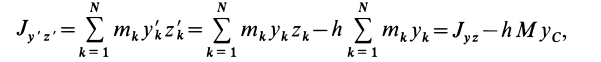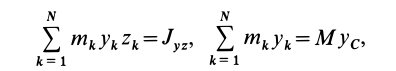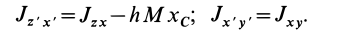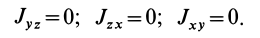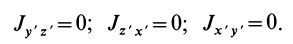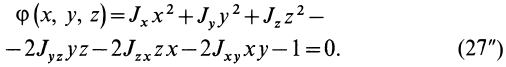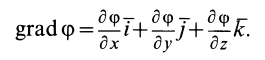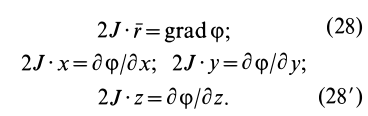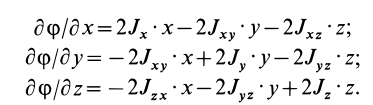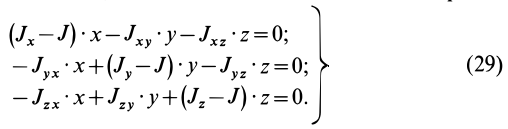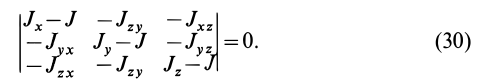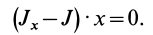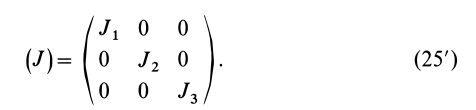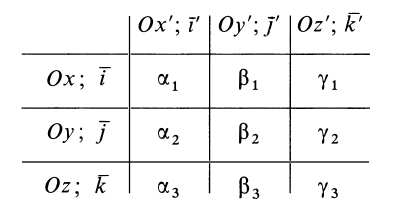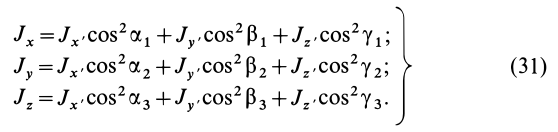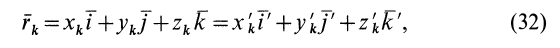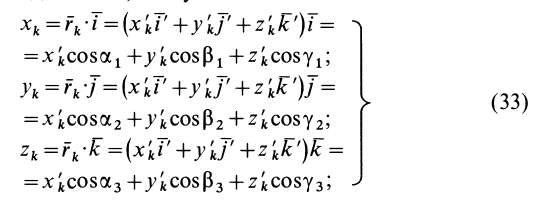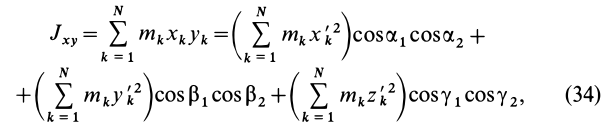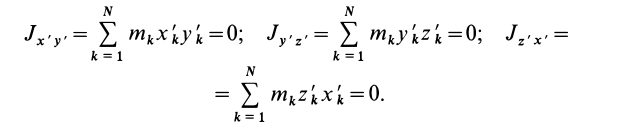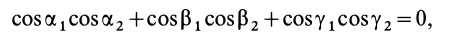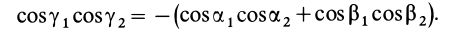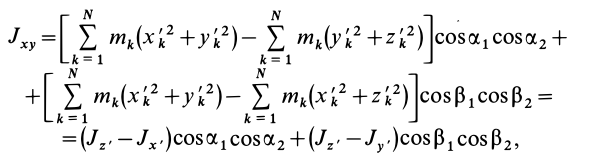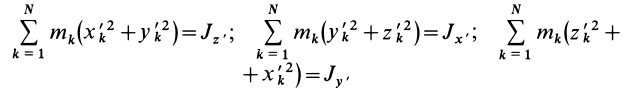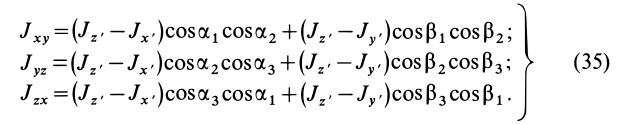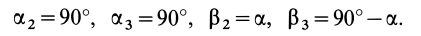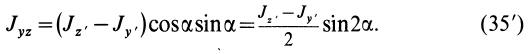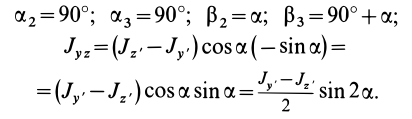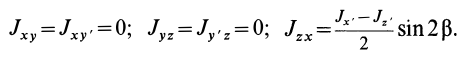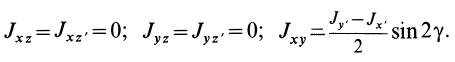Зачем нужен момент инерции сечения
Несмотря на то, что наука о прочности давно уже шагнула вперёд, и давно уже развиваются многие её направления (строительная механика, механика разрушения, теория упругости и другие), а также несмотря на то, что всё чаще расчеты сложных конструкций выполняются при помощи метода конечного элемента посредством специализированных программных комплексов, прикидочные расчеты на основе методов сопромата не утратили своей актуальности. Ведь именно они, во-первых, позволяют дать оценку прочности конструкции «в полевых условиях» (без трудоёмкого построения конечно-элементной модели, без сложных математических выкладок), а во-вторых — позволяют это сделать достаточно быстро.
В основном, расчеты в сопротивлении материалов имеют целью проверить общую (а не местную) прочность балок. Поэтому расчетная схема принимается упрощенной, и многими конструктивными элементами, даже являющимися концентраторами напряжений, в ней пренебрегают. Тем не менее, несмотря на ряд упрощений в схеме и принятые допущения (гипотезы, принятые для построения теории сопротивления материалов), в этой науке разработаны методы, позволяющие с довольно большой точностью определить опасные сечения и напряжения, возникающие в них.
Вообще, поперечное сечение балки может представлять собой тавр, швеллер, двутавр, круг, прямоугольник, кольцо, полый прямоугольник и т.п. или может быть составным, т.е. составленным из нескольких однотипных или различных профилей. От его формы и размеров зависит прочность и жесткость балки. Площадь поперечного сечения является важной характеристикой, но знать только лишь её достаточно разве что для задач на центральное растяжение. Если же балка испытывает изгиб или кручение, то знать только лишь площадь поперечного сечения оказывается недостаточно. Балка может «проходить» (т.е. обладать достаточной прочностью и жесткостью) с одним типом сечения и «не проходить» с другим типом сечения такой же площади. В процессе решения задач по сопромату, касающихся определения напряжений в балке при её изгибе или кручении, проверке устойчивости сжатых стержней, а также при решении некоторых других задач требуется знать не только площадь, но и другие геометрические характеристики сечения (момент инерции площади сечения, момент сопротивления площади сечения, полярный момент инерции площади сечения). Во-первых, они требуются для решения конкретной задачи об определении напряжений в данной балке с заданными размерами поперечного сечения. Во-вторых, они нужны для выполнения сравнительного анализа разных типов сечений (например, выбора среди нескольких различных сечений с одинаковой площадью именно того сечения, которое будет лучше сопротивляться изгибу или кручению), для подбора оптимального сечения для балки, работающей в конкретно заданных условиях. Поскольку нахождение геометрических характеристик сечения требует определенных знаний и практических навыков, в любом учебнике или справочнике по сопромату выделен раздел, посвященный определению этих характеристик, а в любом задачнике по сопромату приведены задачи по нахождению момента инерции или момента сопротивления сечения.
Что такое момент инерции сечения
Обычно, когда речь идёт о геометрических характеристиках сечения, слово «площадь» опускают, чтобы не было нагромождения слов, и говорят не «момент инерции площади сечения», «момент сопротивления площади сечения», а просто «момент инерции сечения», «момент сопротивления сечения» или даже просто «момент инерции», «момент сопротивления». При этом различают осевой, полярный и центробежный момент инерции площади сечения.
Осевой момент инерции площади фигуры (сечения) — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Другое, менее распространенное его название – экваториальный момент инерции. Величина осевого момента инерции всегда положительна.
Полярный момент инерции площади фигуры (сечения) относительно данной точки (полюса) — это интеграл произведений элементарных площадок на квадраты их расстояний от полюса. Величина полярного момента инерции всегда положительна.
Центробежный момент инерции площади фигуры — это интеграл произведений элементарных площадок на их расстояния от координатных осей. В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. При повороте осей вокруг начала координат на 90 градусов знак центробежного момента инерции меняется на обратный.
Задавая вопросы «в чем измеряется момент инерции», «какова единица измерения момента инерции», «как обозначается момент инерции» необходимо четко представлять, что именно имеется в виду: момент инерции сечения (о котором идёт речь в сопромате и, в частности, в настоящей статье) или же момент инерции тела (который упоминается в физике и в теории механизмов и машин). Размерность момента инерции сечения – это размерность длины в четвертой степени (например, см4, м4, мм4). Моменты инерции сечений стандартных профилей (швеллеров, уголков, тавров, двутавров) приведены в справочных таблицах в размерности «см4». При необходимости, данную в таблице величину можно представить в другой единице измерения. Обычно при решении задач возникает необходимость перевода этой величины в «мм4». Обозначается момент инерции сечения буквой I с нижним индексом, который указывает, относительно какой оси вычислена данная характеристика (например, Ix, Iy). Момент сопротивления сечения обозначается буквой W, также с нижним индексом, указывающим на ось, относительно которой дана эта величина (например, Wx, Wy).
Что такое главные оси
Главные оси инерции — оси, относительно которых центробежный момент инерции равен нулю.
Главные центральные оси — главные оси, проходящие через центр тяжести сечения.
Как найти момент инерции сечения
При вычислении момента инерции сечения можно воспользоваться непосредственно определением момента инерции и вычислить эту характеристику сечения путём нахождения интеграла по площади. Так и поступают при нахождении момента инерции треугольника, круга, прямоугольника, кругового сектора и других простых фигур.
Обозначив характерные размеры сечения через параметры (т.е. буквами) и выполнив соответствующее интегрирование по площади, получают формулы для определения моментов инерции этих сечений. Ход решения показан, например, в учебнике по сопромату Г.С. Писаренко на примере вывода формул для определения момента инерции прямоугольника, треугольника, кругового сектора и эллипса. Такие формулы приведены во многих справочниках по сопромату (например, в книге Писаренко Г.С., Яковлев А.П. Матвеев В.В. Справочник по сопротивлению материалов. – К: Наукова думка, 1975, на страницах 24 — 77) для многих типов сечений (квадрат, полый квадрат, прямоугольник, полый прямоугольник, прямоугольник с круглым отверстием, прямоугольник с двумя отверстиями, прямоугольник с полукруглыми вырезами, повернутый прямоугольник, крестовина, корытное сечение, треугольник, трапеция, круг, кольцо, круговое незамкнутое тонкостенное кольцо, полукруг, четверть круга, круговой сектор, круговой сегмент, полукольцо, сектор кольца, круг с лыской, правильный шестиугольник, правильный многоугольник, круговое сечение с одной или с двумя шпоночными канавками, эллипс, полуэллипс, четверть эллипса, полый эллипс, параболический сегмент, параболический полусегмент, круговой треугольник, сечение железнодорожного рельса). Готовыми формулами из справочника пользоваться намного проще, чем выводить каждый раз нужную формулу самостоятельно путём интегрирования.
В этом же справочнике приведены и формулы для приближенного вычисления геометрических характеристик (F, I, W) сечений стандартных прокатных профилей: уголков (равнобокого и неравнобокого), швеллера, тавра, двутавра, однако на практике этими формулами пользуются весьма редко, т.к. все необходимые характеристики стандартных сечений уже вычислены и приведены в соответствующих нормативных документах (см. ГОСТ 8240-97 для швеллеров, ГОСТ 8509-93 для равнополочных уголков, ГОСТ 8510-86 для неравнополочных уголков, ГОСТ 26020-83 и ГОСТ 8239-89 для двутавров). Выдержки из перечисленных выше стандартов приведены во многих справочниках, учебниках и решебниках по сопромату.
Скачать примеры решения задач, касающиеся того, как найти момент инерции и момент сопротивления, можно здесь (бесплатно, без регистрации):
При вычислении моментов инерции сложных сечений их разбивают на отдельные простые части, моменты инерции которых известны.
Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.
При повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.
Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.
Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения.
Размерность моментов сопротивления – единица длины в кубе (например, см3, м3, мм3).
Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления. Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.
Источники:
- Н.М. Беляев. Сопротивление материалов.
- Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов.
- А.В. Александров, В.Д. Потапов, Б.П. Державин. Сопротивление материалов.
- reshusam.ucoz.ru — Примеры определения моментов инерции сечений.
Дополнительно на Геноне:
- Что такое сопромат
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
13
http//:www.svkspb.nm.ru
Геометрические
характеристики плоских сечений
Площадь:
, dF
— элементарная
площадка.
Статический момент
элемента площади dF
относительно оси 0x  —
—
произведение элемента площади на
расстояние «y» от
оси 0x: dSx
= ydF
Просуммировав
(проинтегрировав) такие произведения
по всей площади фигуры, получаем
статические моменты относительно
осей y и
x:

 ;
;
[см3, м3, т.д.].
Координаты
центра тяжести:
.
Статические моменты относительно
центральных
осей (осей,
проходящих через центр тяжести сечения)
равны нулю. При вычислении статических
моментов сложной фигуры ее разбивают
на простые части, с известными площадями
Fi
и координатами
центров тяжести
xi,
yi.Статический
момент площади всей фигуры = сумме
статических моментов каждой ее части:
.
Координаты
центра тяжести сложной фигуры:
М оменты
оменты
инерции сечения
Осевой
(экваториальный) момент
инерции сечения
— сумма
произведений элементарных площадок dF
на квадраты их расстояний до оси.
;
[см4,
м4,
т.д.].
Полярный момент
инерции сечения относительно некоторой
точки (полюса) —
сумма произведений элементарных площадок
на квадраты их расстояний от этой точки.
 ;
;
[см4,
м4,
т.д.].
Jy
+ Jx
= Jp
.
Центробежный момент инерции
сечения — сумма
произведений элементарных площадок на
их расстояния от двух взаимно
перпендикулярных осей.
.
Центробежный момент инерции сечения
относительно осей, из которых одна или
обе совпадают с осями симметрии, равен
нулю.
Осевые
и полярные моменты инерции всегда
положительны, центробежные моменты
инерции могут быть положительными,
отрицательными или равными нулю.
Момент
инерции сложной фигуры равен сумме
моментов инерции составных ее частей.
Моменты инерции
сечений простой формы
П

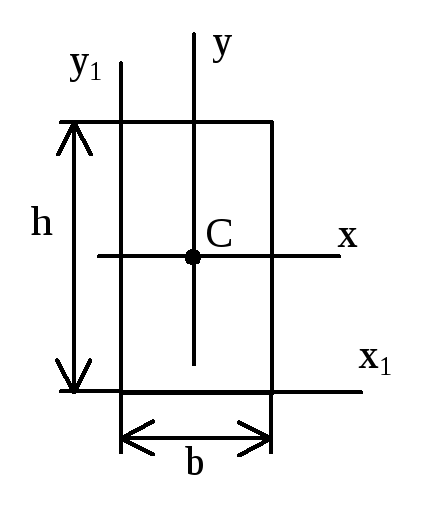
рямоугольное
сечение Круг
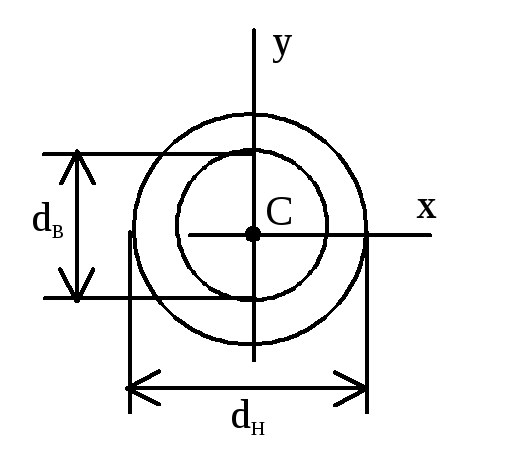
К


 ольцо
ольцо
Т
р
авнобедренный
Прямоугольный
т
Ч етверть
етверть
круга
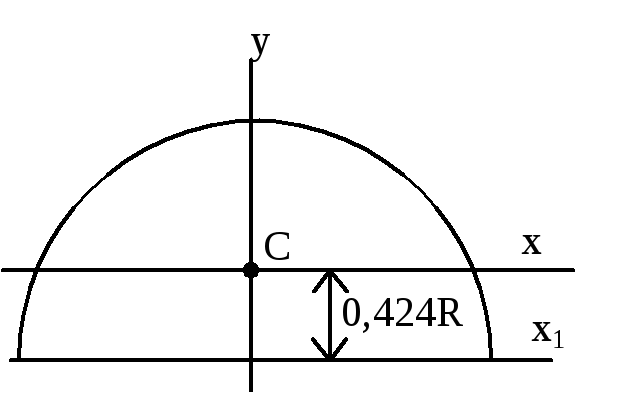
Jy=Jx=0,055R4
Jxy=0,0165R4
на
рис. (—)
Jx0=0,0714R4
Jy0=0,0384R4
Полукруг
М
инерции стандартных профилей находятся
из таблиц сортамента:
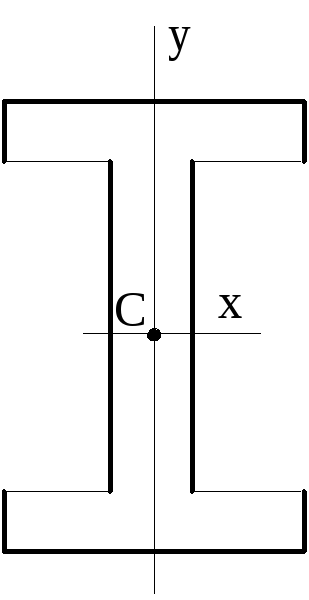
Д
Швеллер
Уголок
М
оменты инерции относительно
параллельных осей
:
J
+ a2F;
Jy1=Jy
+ b2F;
момент
инерции относительно любой оси равен
моменту инерции относительно центральной
оси, параллельной данной, плюс произведение
площади фигуры на квадрат расстояния
между осями. Jy1x1=Jyx
+ abF;
(«a» и
«b»
подставляют
в формулу с учетом их знака).
Зависимость
между моментами
инерции при повороте осей:
J
+ Jysin2
— Jxysin2;
Jy1=Jycos2
+ Jxsin2
+ Jxysin2;
Jx1y1=(Jx
— Jy)sin2
+ Jxycos2
;
Угол
>0,
если
переход
от старой системы координат к новой
происходит против час.стр. Jy1
+ Jx1=
Jy
+ Jx
Экстремальные
(максимальное и минимальное) значения
моментов инерции называются главными
моментами инерции.
Оси, относительно которых осевые моменты
инерции имеют экстремальные значения,
называются главными
осями инерции.
Главные оси инерции взаимно перпендикулярны.
Центробежные моменты инерции относительно
главных осей = 0, т.е. главные оси инерции
— оси, относительно которых центробежный
момент инерции = 0. Если одна из осей
совпадает или обе совпадают с осью
симметрии, то они главные.
Угол,
определяющий положение главных осей:
,
если 0>0
оси поворачиваются против час.стр. Ось
максимума всегда составляет меньший
угол с той из осей, относительно которой
момент инерции имеет большее значение.
Главные оси, проходящие через центр
тяжести, называются главными
центральными осями инерции.
Моменты инерции относительно этих осей:
Jmax
+ Jmin=
Jx
+ Jy.
Центробежный
момент инерции относительно главных
центральных осей инерции равен 0. Если
известны главные моменты инерции, то
формулы перехода к повернутым осям:
Jx1=Jmaxcos2
+ Jminsin2;
Jy1=Jmaxcos2
+ Jminsin2;
Jx1y1=(Jmax
— Jmin)sin2;
Конечной
целью вычисления геометрических
характеристик сечения является
определение главных центральных моментов
инерции и положения главных центральных
осей инерции.
Р
инерции —
; Jx=Fix2,
Jy=Fiy2.
Если
Jx
и Jy
главные моменты инерции, то ix
и iy
— главные
радиусы инерции.
Эллипс, построенный на главных радиусах
инерции как на полуосях, называется
эллипсом
инерции.
При помощи
эллипса инерции можно графически найти
радиус инерции ix1
для любой
оси х1.
Для этого надо провести касательную к
эллипсу, параллельную оси х1,
и измерить расстояние от этой оси до
касательной. Зная радиус инерции,
можно найти момент инерции сечения
относительно оси х1:
.
Для сечений,
имеющих более двух осей симметрии
(например: круг, квадрат, кольцо и др.)
осевые моменты инерции относительно
всех центральных осей равны между собой,
Jxy=0,
эллипс инерции обращается в круг инерции.
Моменты
сопротивления.
Осевой
момент сопротивления
— отношение момента инерции относительно
оси к расстоянию от нее до наиболее
удаленной точки сечения.
[см3,
м3]
Особенно
важны моменты сопротивления относительно
главных центральных осей:
прямоугольник:
;
круг: Wx=Wy=
,
трубчатое
сечение (кольцо): Wx=Wy=

где =
dН/dB.
Полярный
момент сопротивления — отношение
полярного момента инерции к расстоянию
от полюса до наиболее удаленной точки
сечения:
.
Для
круга Wр=
.
Соседние файлы в папке Комплект
- #
- #
- #
- #
В этой главе…
- Переходим от динамики поступательного движения к динамике вращательного движения
- Вычисляем момент инерции
- Определяем работу вращательного движения
- Находим связь между работой и изменением кинетической энергии
- Изучаем закон сохранения момента импульса
Эта глава посвящена динамике вращательного движения, т.е. описанию сил и их влияния на характер вращательного движения. Здесь рассматриваются основные законы динамики вращательного движения по аналогии с законами динамики поступательного движения. Например, описывается аналог второго закона Ньютона (см. главу 5), представлено новое понятие “момент инерции”, исследуется связь между работой и кинетической энергией и т.п.
Содержание
- Применяем второй закон Ньютона для вращательного движения
- Преобразуем тангенциальное ускорение в угловое
- Пример: вычисляем момент силы для обеспечения углового ускорения
- Вычисляем момент инерции протяженного объекта
- Пример: замедление вращения компакт-диска
- Еще один пример: поднимаем груз
- Вычисляем энергию и работу при вращательном движении
- Работа при вращательном движении
- Изучаем кинетическую энергию вращательного движения
- Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
- Не можем остановиться: момент импульса
- Сохраняем момент импульса
- Пример закона сохранения момента импульса: вычисляем скорость спутника
Применяем второй закон Ньютона для вращательного движения
Согласно второму закону Ньютона (см. главу 5), ускорение объекта под действием силы пропорционально величине силы и обратно пропорционально массе объекта:
где ( mathbf{a} ) — это вектор ускорения, ( mathbf{F} ) — вектор силы, а ( m ) — масса объекта. Подробнее о векторах рассказывается в главе 4. Соблюдается ли этот закон для вращательного движения?
В главе 10 мы уже познакомились характеристиками вращательного движения, которые являются эквивалентами (аналогами) некоторых характеристик поступательного движения. А как будет выглядеть аналог у второго закона Ньютона? Похоже, что во вращательном движении роль ускорения ( mathbf{a} ) играет угловое ускорение ( alpha ), а роль силы ( mathbf{F} ) — момент силы ( mathbf{M} )? Не вдаваясь в подробности, скажем лишь, что это действительно так. А что же с массой? Оказывается, что для этого используется новое понятие — момент инерции ( l ). Известно, что второй закон Ньютона для вращательного движения принимает следующий вид:
Рассмотрим простой пример. Пусть привязанный нитью мячик для игры в гольф вращается по окружности, как показано на рис. 11.1. Допустим, что к мячику приложена направленная по касательной к окружности тангенциальная сила, которая приводит к увеличению тангенциальной скорости мячика. (Обратите внимание, что речь идет не о нормальной силе, направленной вдоль радиуса окружности вращения. Более подробно нормальная и тангенциальная скорости, а также нормальное и тангенциальное ускорения рассматриваются в главе 10.)
Поскольку:
то, умножая обе части этой формулы на радиус окружности ( r ), получим:
Поскольку ( rmathbf{F}=mathbf{M} ) то
или
Таким образом, частично совершен переход от второго закона Ньютона для поступательного движения к его аналогу для вращательного движения. (Следует отметить, что это выражение справедливо для материальной точки, т.е. объекта, размерами которого можно пренебречь по сравнению с величиной радиуса окружности ( r ). Для протяженного объекта следует использовать другие формулы, которые описываются далее в этой главе. — Примеч. ред.)
Преобразуем тангенциальное ускорение в угловое
Чтобы полностью перейти от описания поступательного движения к описанию вращательного движения, необходимо использовать связь между угловым ускорением ( alpha ) и тангенциальным ускорением ( mathbf{a} ). Как нам уже известно из главы 10, они связаны следующим соотношением:
Подставляя это выражение в приведенную выше формулу
получим:
Итак, мы получили связь момента силы, действующей на материальную точку, и ее углового ускорения. Коэффициент пропорциональности между ними, ( l=mr^2 ), называется моментом инерции материальной точки. Таким образом, мы получили эквивалент второго закона Ньютона для вращательного движения, где роль силы играет момент силы, роль ускорения — угловое ускорение, а роль массы — момент инерции.
Пример: вычисляем момент силы для обеспечения углового ускорения
Если на объект действует несколько сил, то второй закон Ньютона имеет следующий вид:
где ( mathbf{sum!F} ) обозначает векторную сумму всех сил, действующих на объект.
Аналогично, если на объект действует несколько моментов сил, то второй закон Ньютона имеет вид:
где ( mathbf{sum! M} ) обозначает векторную сумму всех моментов сил, действующих на объект. Аналог массы, т.е. момент инерции, измеряется в кг·м2.
Помните, что аналогом второго закона Ньютона при описании вращательного движения является формула ( mathbf{sum! M}=lalpha ), т.е. угловое ускорение прямо пропорционально сумме всех моментов сил, действующих на вращающийся точечный объект, и обратно пропорционально моменту инерции.
Пусть мячик из предыдущего примера (см. рис. 11.1) имеет массу 45 г, а длина нити равна 1 м. Какой момент сил необходимо приложить, чтобы обеспечить угловое ускорение — ( 2pi с^{-2} )? Подставляя значения в уже известную нам формулу
получим:
Как видите, для решения этой задачи достаточно было поступить, как при определении силы, необходимой для обеспечения ускорения поступательного движения (где нужно было бы умножить массу на ускорение), т.е. умножить угловое ускорение на момент инерции.
Вычисляем момент инерции протяженного объекта
Момент инерции легко вычисляется для очень маленького (точечного) объекта, если все точки объекта расположены на одинаковом расстоянии от точки вращения. Например в предыдущем примере, если считать, что мячик для игры в гольф гораздо меньше длины нити, то все его точки находятся на одинаковом расстоянии от точки вращения, равном радиусу окружности вращения ( r ). В таком случае момент инерции имеет знакомый вид:
где ( r ) — это расстояние, на котором сосредоточена вся масса мячика ( m ).
Однако такая идеальная ситуация имеет место далеко не всегда. А чему равен момент инерции протяженного объекта, например стержня, вращающегося относительно одного из своих концов? Ведь его масса сосредоточена не в одной точке, а распределена по всей длине. Вообще говоря, для определения момента инерции протяженного объекта нужно просуммировать моменты инерции всех материальных точек объекта:
Например, момент инерции ( l ) системы из двух “точечных” мячиков для игры в гольф с одинаковой массой ( m ) на расстояниях ( r_1 ) и ( r_2 ) равен сумме их отдельных моментов инерции ( l_1=mr_1^2 ) и ( l_2=mr_2^2 ):
А как определить момент инерции диска, вращающегося относительно своего центра? Нужно мысленно разбить диск на множество материальных точек, вычислить момент инерции каждой такой точки и просуммировать полученные моменты инерции. Физики научились вычислять моменты инерции для многих объектов со стандартной формой. Некоторые из них приведены в табл. 11.1.
Попробуем вычислить моменты инерции нескольких предметов с простой геометрией.
Пример: замедление вращения компакт-диска
Компакт-диски могут вращаться с разными угловыми скоростями. Это необходимо для обеспечения одинаковой линейной скорости считывания информации на участках, находящихся на разных расстояниях от центра вращения. Пусть диск массой 30 г и диаметром 12 см сначала вращается со скоростью 700 оборотов в секунду, а спустя 50 минут — со скоростью 200 оборотов в секунду. Какой средний момент сил действует на компакт-диск при таком уменьшении скорости? Связь момента сил и углового ускорения имеет вид:
Момент инерции диска с радиусом ( r ), вращающегося относительно своего центра в плоскости диска, выражается формулой:
Подставляя значения, получим:
Теперь нужно определить угловое ускорение, которое определяется следующей формулой:
Изменение угловой скорости ( Deltaomega ) произошло за промежуток времени:
В данном примере изменение угловой скорости:
где ( omega_1 ) — конечная, а ( omega_0 ) — начальная угловая скорость компакт-диска.
Чему они равны? Начальная скорость 700 оборотов в секунду означает, что диск за секунду 700 раз проходит ( 2pi ) радиан:
Аналогично, конечная скорость 200 оборотов в секунду означает, что диск за секунду 200 раз проходит ( 2pi ) радиан:
Подставляя значения в формулу углового ускорения, получим:
Подставляя значения момента инерции и углового ускорения в итоговую формулу момента силы, получим:
Итак, средний момент равен 10-4 Н·м, а чему будет равна сила для создания такого момента, если она приложена к краю диска? Ее величину легко вычислить по следующей формуле:
Оказывается, для такого замедления компакт-диска нужно приложить не такую уж и большую силу.
Еще один пример: поднимаем груз
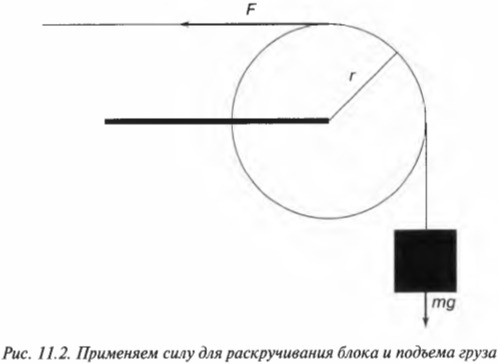
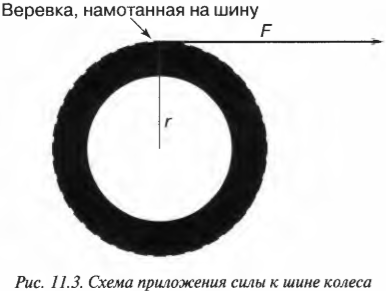
Вращательное движение порой внешне выглядит не так очевидно, как вращение ком- пакт-диска. Например подъем груза с помощью блока также является примером вращательного движения. Хотя канат и груз движутся поступательно, но сам блок вращается (рис. 11.2). Пусть радиус блока равен 10 см, его масса равна 1 кг, масса груза равна 16 кг, а к веревке прилагается сила 200 Н. Попробуем вычислить угловое ускорение блока.
В данном примере нужно вычислить сумму всех моментов сил ( mathbf{sum! M} ), которые действуют на веревку:
В данном примере на веревку действует два момента сил: один ( M_1 ) со стороны груза весом ( mg ), а другой ( M_2 ) — со стороны горизонтальной силы ( F ):
Отсюда получаем формулу для углового ускорения:
Эти моменты ( M_1 ) и ( M_2 ) имеют одинаковое плечо, равное радиусу блока ( r ), поэтому:
Поскольку блок имеет форму диска, то из табл. 11.1 находим его момент инерции:
Подставляя выражения для ( l ), ( M_1 ) и ( M_2 ) в формулу для углового ускорения, получим:
Подставляя значения, получим:
Вычисляем энергию и работу при вращательном движении
При изучении поступательного движения в главе 8 мы познакомились с понятием работа. Она равна произведению силы на перемещение под действием этой силы. Можно ли выразить работу при вращательном движении на основе его характеристик? Конечно можно, и для этого потребуется преобразовать силу в момент силы, а перемещение — в угол. В этом разделе демонстрируется такое преобразование, а также связь работы с изменением энергии.
Работа при вращательном движении
Допустим, что инженеру в области автомобилестроения необходимо рассчитать параметры революционно новой шины колеса. Для начала он решил оценить работу, которую необходимо выполнить для ускоренного раскручивания этой шины. Как связать работу при поступательном движении и работу при вращательном движении? Инженер предложил простую, как все гениальное, идею: “связать” шину веревкой. Точнее говоря, он предложил намотать веревку на шину, потянуть за веревку с помощью внешней силы и раскрутить шину. Так, приравнивая работу внешней силы при поступательном движении веревки и работу ускорения вращательного движения шины, можно, образно говоря, “связать” их веревкой.
Пусть шина имеет радиус ( r ) и для ее вращения используется сила ( F ), как показано на рис. 11.3.
Чему равна работа этой силы? Применим знакомую нам формулу:
где ( s ) — это перемещение веревки под действием этой силы. В данном примере перемещение ( s ) равно произведению радиуса ( r ) на угол поворота шины ( theta ):
Подставляя это выражение в формулу работы, получим:
Поскольку момент ( M ), создаваемой этой силой, равен:
то получаем для работы:
Таким образом, работа при вращательном движении равна произведению момента силы и угла поворота. Она измеряется в тех же единицах, что и работа при поступательном движении, т.е. в джоулях.
Учтите, что для описания вращательного движения в этих формулах работы угол нужно указывать в радианах.
Вот еще один пример. Пусть пропеллер самолета совершает 100 поворотов с постоянным моментом силы 600 Н·м. Какую работу выполняет двигатель самолета? Для ответа на этот вопрос начнем с уже известной нам формулы:
Полный оборот соответствует повороту на угол ( 2pi ). Подставляя значения в формулу, получим:
Что происходит с выполненной таким образом работой? Она преобразуется в кинетическую энергию вращательного движения.
Изучаем кинетическую энергию вращательного движения
Из главы 8 нам уже известно, что объект массы ( m ), движущийся поступательно со скоростью ( v ), обладает кинетической энергией:
А как получить формулу кинетической энергии для вращающегося объекта? Нужно применить данную формулу для всех его частичек.
При описании вращательного движения аналогом массы является момент инерции, а аналогом скорости — угловая скорость.
Как известно (см. главу 10), тангенциальная скорость ( v ) и угловая скорость ( omega ) связаны соотношением:
где ( r ) — это радиус окружности вращения.
Подставляя это соотношение в предыдущую формулу, получим:
Однако эта формула справедлива только для бесконечно малой материальной точки. Чтобы определить кинетическую энергию протяженного объекта, нужно просуммировать кинетические энергии всех его мельчайших материальных точек, т.е. вычислить сумму:
Как можно было бы упростить эту формулу? Предположим, что все составляющие частички протяженного объекта вращаются с одинаковой угловой скоростью. Тогда угловую скорость можно вынести за знак суммирования и получим:
Здесь начинается самое интересное. Ранее в этой главе уже приводилась формула момента инерции:
Теперь совсем нетрудно сделать подстановку в предыдущей формуле кинетической энергии:
Итак, кинетическая энергия вращательного движения вычисляется аналогично кинетической энергии поступательного движения, если вместо массы использовать момент инерции, а вместо тангенциальной скорости — угловую скорость. Примеры кинетической энергии вращательного движения окружают повсюду. Спутник на космической орбите и бочка пива, которую скатывают по наклонной плоскости, обладают определенной кинетической энергией вращательного движения. Особенности вращательного движения бочки пива более подробно описываются в следующем разделе.
Измеряем кинетическую энергию бочки, катящейся по наклонной плоскости
Итак, нам уже известно, что объекты могут двигаться поступательно и вращательно, причем двигаться так, что без знания строгих законов физики порой трудно понять их поведение. Да ну? Действительно, если бочка скользит вниз по наклонной плоскости, то ее потенциальная энергия превращается в кинетическую энергию поступательного движения (см. главу 8). А если бочка скатывается вниз по наклонной плоскости, то ее потенциальная энергия превращается не только в кинетическую энергию поступательного движения, но и в кинетическую энергию вращательного движения.
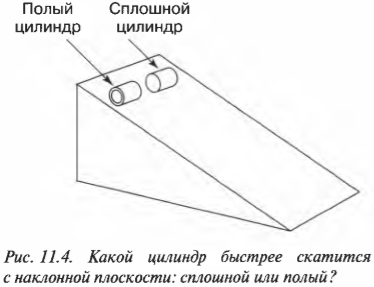
На рис. 11.4 показан случай, когда с наклонной плоскости высотой ( h ) скатываются сплошной и полый цилиндры с одинаковой массой ( m ). Какой цилиндр достигнет нижнего конца наклонной плоскости?
Иначе говоря: какой цилиндр будет обладать большей скоростью в конце наклонной плоскости? Поскольку действующие на цилиндры силы постоянны, то постоянны и их ускорения, а значит, большая скорость в конце пути означает меньшее время его прохождения. В случае только поступательного движения цилиндра и при отсутствии трения уменьшение потенциальной энергии ( mgh ) преобразуется в увеличение кинетической энергии только поступательного движения ( {}^1!/!_2mv^2 ), т.е.:
Однако в данном примере эта формула не годится, потому что цилиндры скатываются без проскальзывания. Это значит, что часть уменьшения потенциальной энергии будет преобразовываться в увеличение кинетической энергии поступательного движения ( {}^1!/!_2mv^2 ), а часть — в кинетическую энергию вращательного движения ( {}^1!/!_2Iomega ^2 ). Тогда предыдущее равенство принимает следующий вид:
Сделаем подстановку ( omega=v/r ) и получим:
Путем несложных алгебраических преобразований получим:
откуда легко получить выражение для скорости цилиндра:
Для обоих цилиндров все параметры одинаковы, кроме момента инерции ( I ). Как это повлияет на скорость цилиндров? Согласно данным из табл. 11.1, полый цилиндр имеет момент инерции ( mr^2 ), а сплошной — ( {}^1!/!_2mr^2 ).
Итак, для полого цилиндра получим:
а для сплошного цилиндра:
А их отношение равно:
Как видите, скорость сплошного цилиндра в 1,15 раза больше скорости полого цилиндра, а значит, сплошной цилиндр быстрее достигнет конца наклонной плоскости.
Как на пальцах объяснить полученный результат? Все очень просто. В полом цилиндре вся масса сосредоточена на расстоянии радиуса цилиндра, а в сплошном цилиндре значительная часть масса распределена ближе радиуса. Это значит, что при одинаковой угловой скорости в полом цилиндре больше материала будет обладать большей тангенциальной скоростью, а для этого потребуется потратить больше энергии.
Не можем остановиться: момент импульса
Допустим, нам нужно остановить космический корабль с массой 40 т, который находится на околоземной орбите. Для этого потребуется затратить немалые усилия. Почему? Все дело во вращательном импульсе космического корабля.
В главе 9 подробно описывается понятие импульс материальной точки, который выражается следующей формулой:
где ( m ) — это масса, a ( v ) — скорость материальной точки.
По аналогии, при описании вращательного движения физики используют понятие вращательный импульс (который в русскоязычной научной литературе чаще называют моментом импульса материальной точки. — Примеч. ред.):
где ( l ) — это момент инерции, а ( omega ) — угловая скорость материальной точки.
Следует помнить, что момент импульса (или вращательный импульс) является вектором, направление которого совпадает с направлением вектора угловой скорости.
Момент импульса в системе СИ измеряется в кг·м2·с-1 (более подробно системы единиц измерения описываются в главе 2). Одним из наиболее важных свойств момента импульса является закон сохранения момента импульса.
Сохраняем момент импульса
Закон сохранения момента импульса гласит: момент импульса сохраняется, если равна нулю сумма всех моментов внешних сил. Этот закон проявляется во многих обыденных ситуациях. Например часто приходится видеть, как мастера фигурного катания на льду вращаются с широко разведенными в стороны руками, а затем резко приближают их к своему телу и сильно ускоряют свое вращение. Дело в том, что таким образом они уменьшают свой момент инерции и, согласно закону сохранения момента импульса, увеличивают свою угловую скорость. Зная начальную угловую скорость вращения фигуриста ( omega_0 ) и его моменты инерции в позе с разведенными руками ( I_0 ) и в позе с сомкнутыми руками ( I_1 ), легко найти конечную угловую скорость ( omega_1 ) по формуле:
Однако этот закон удобно использовать не только в таких простых ситуациях. Возвращаясь к примеру с космическим кораблем на околоземной орбите, следует отметить, что его орбита далеко не всегда является строго круглой. Чаще всего орбиты спутников Земли и других планет имеют эллиптическую форму. Поэтому без закона сохранения момента импульса было бы гораздо сложнее определять параметры их орбитального движения.
Пример закона сохранения момента импульса: вычисляем скорость спутника
Предположим, что космический корабль вращается на эллиптической орбите вокруг Плутона. Причем в самой близкой к Плутону точке орбиты спутник находится на расстоянии 6·106 м от центра Плутона и имеет скорость 9·103 м/с. Вопрос: какой будет скорость спутника в самой далекой точке эллиптической орбиты на расстоянии 2·107 м от центра Плутона?
Для ответа на этот вопрос нужно воспользоваться законом сохранения момента импульса, поскольку на спутник не действуют никакие внешние моменты сил (сила гравитационного притяжения направлена параллельно радиусу и не создает момента). Однако закон сохранения момента импульса нужно преобразовать так, чтобы вместо угловых скоростей в его формулировке фигурировали тангенциальные скорости.
Итак, рассмотрим формулу закона сохранения момента импульса:
где ( I_{бл} ) — это момент инерции спутника в самой близкой точке, ( I_{дал} ) — это момент инерции спутника в самой далекой точке, ( omega_{бл} ) — угловая скорость спутника в самой близкой точке, а ( omega_{дал} ) — угловая скорость спутника в самой далекой точке.
Предположим, что размеры спутника гораздо меньше расстояния до центра Плутона и спутник можно считать материальной точкой. Тогда его моменты инерции равны:
и
где ( r_{бл} ) — это расстояние от спутника до центра Плутона в самой близкой точке эллиптической орбиты, а ( r_{дал} ) — это расстояние от спутника до центра Плутона в самой далекой точке эллиптической орбиты.
Кроме того:
и
Подставляя все перечисленные соотношения в формулу закона сохранения момента импульса
получим:
Отсюда путем несложных алгебраических преобразований, получим:
Подставляя значения, получим:
Итак, в ближайшей к Плутону точке орбиты спутник будет иметь скорость 9000 м/с, а в самой дальней — 2700 м/с. Этот результат мы легко получили только благодаря знанию закона сохранения момента импульса.
Глава 11. Раскручиваем объекты: момент инерции
3.1 (61.38%) 29 votes
Содержание:
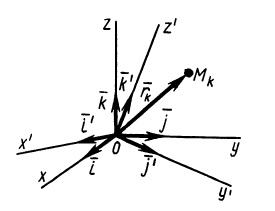
Геометрия масс:
Центр масс
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек
где 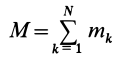
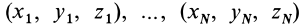
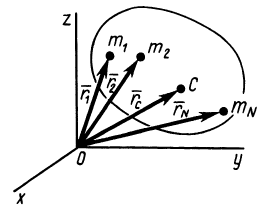
Рис. 21
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Векторная величина 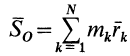
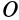
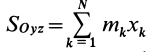
массы относительно координатной плоскости 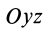
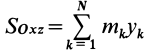
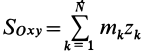
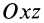
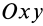
Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 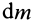
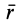
Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму
где 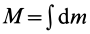
Для однородных сплошных тел 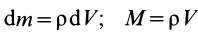
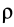
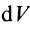
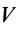
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 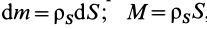
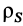
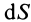
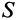
Для тонкой проволоки, которую можно принять за отрезок линии, 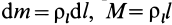
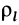
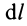
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Моменты инерции относительно точки и оси
Моментом инерции механической системы, состоящей из 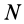
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем
где 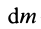
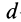
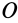
Моментом инерции 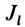
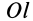
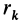
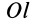
Рис. 22
В частном случае сплошного тела сумму следует заменить интегралом:
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 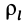
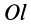
где 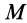
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.
Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины 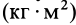
Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.
Моменты инерции относительно осей координат
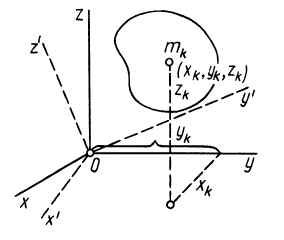
Моменты инерции относительно декартовых осей координат 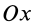
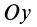
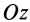
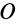
где 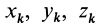
Из приведенных формул следует зависимость
Если через точку 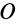
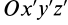
Из сравнения (8) и (8′) следует, что
Рис. 23
Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.
Для осей координат 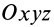
Центробежные моменты инерции часто называют произведениями инерции.
Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.
Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.
Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 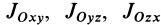
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
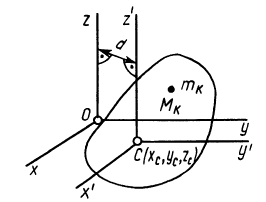
Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 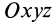
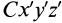
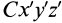
Рис. 24
По определению момента инерции относительно оси имеем
где 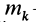
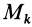
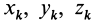
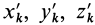
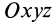
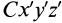
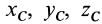
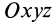
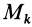
Подставим эти значения координат в выражение момента инерции 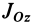
В этом соотношении 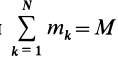
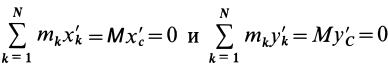
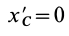
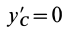
того, что по условию центр масс находится в начале координат этой системы координат.
Величина 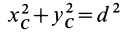
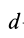
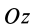
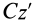
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.
Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.
Если взять ось 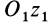
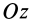
где 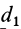
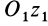
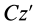
Исключая момент инерции 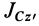
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем
Учитывая, что 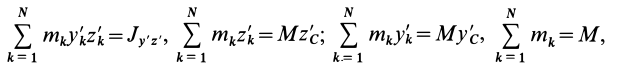
где 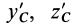
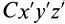
Так как начало системы координат 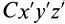
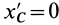
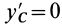
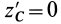
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).
Если производится параллельный перенос осей 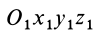
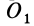
Исключая из (10) и (10′) центробежные моменты инерции Л’з» Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 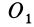
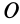
где 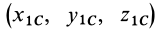
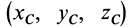
Моменты инерции простейших однородных тел
Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.
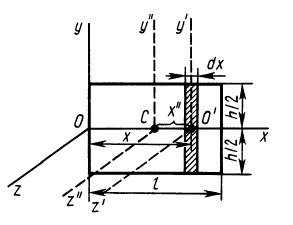
Однородный стержень
Имеем однородный стержень длиной 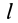
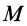
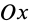
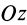
так как 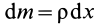
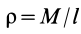
Вычисляя интеграл, получаем
Рис. 25
Таким образом,
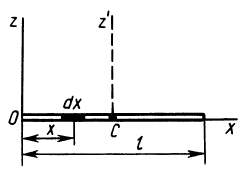
Момент инерции стержня относительно оси 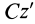
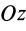
Следовательно,
т. е.
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры 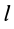
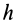
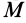
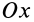
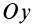
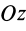
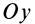
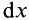
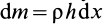
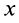
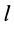
так как 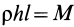
Аналогичные вычисления для оси 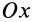
так как эта ось 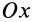
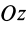
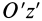
Рис. 26
Интегрируя это выражение в пределах от 0 до 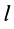
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:
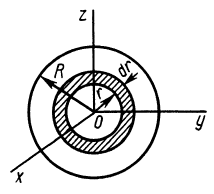
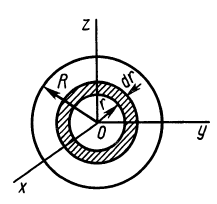
Круглый диск
Имеем тонкий однородный диск радиусом 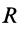
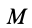
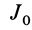
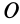
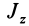
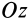
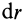
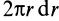
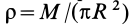
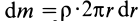
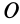
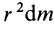
Таким образом,
Рис. 27
Для осей координат 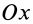
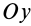
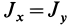
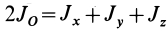
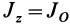
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем
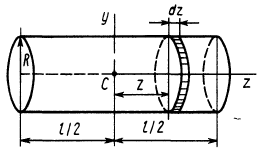
Круглый цилиндр
Рис. 28
Для круглого однородного цилиндра, масса которого 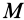
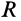
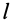
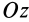
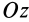
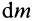
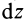
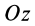
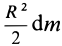
т.е.
Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 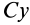
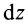
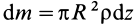
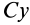
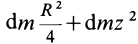
Чтобы получить момент инерции всего цилиндра относительно оси 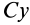
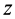
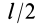
Но 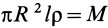
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.
Шар
Пусть масса шара 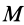
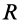
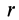
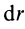
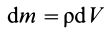
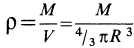
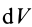
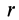
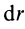
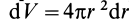
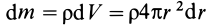
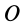
т.е.
Рис. 29
Для осей координат, проходящих через центр шара, в силу симметрии 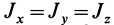
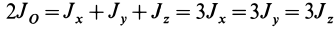
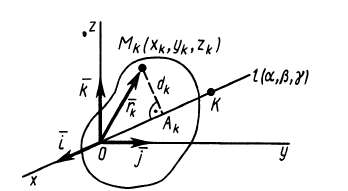
Моменты инерции относительно осей, проходящих через заданную точку
В заданной точке 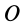
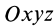
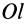
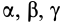
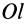
или для сплошных тел
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 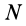
Из прямоугольного треугольника 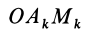
где 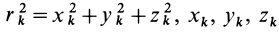
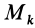
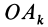
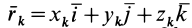
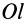
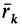
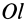
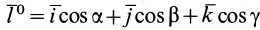
Умножая в (21) 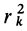
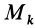
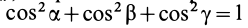
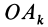
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем
Учитывая, что
— моменты инерции относительно осей координат, а
— центробежные моменты инерции относительно тех же осей, получим
Для определения момента инерции 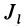
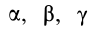

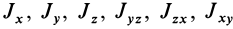
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке 
Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.
Рис. 30
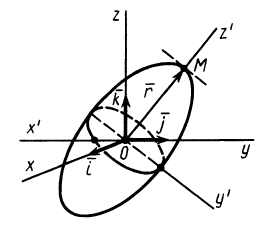
Эллипсоид инерции
Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 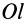

Геометрическое место концов отрезков 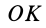
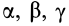
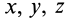
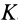
Подставляя эти значения косинусов углов в (24) и сокращая на 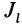
Это действительно уравнение эллипсоида, так как отрезок 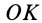

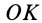
Для каждой точки 
В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям 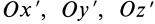
где 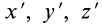
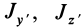
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.
Главные моменты инерции часто обозначают 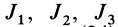
- Заказать решение задач по теоретической механике
Свойства главных осей инерции
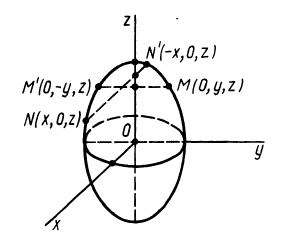
Теорема 1. Если одна из декартовых осей координат, например 

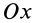
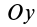

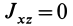
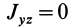
Главная ось инерции 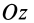
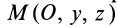
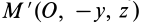
Вычитая из первого уравнения второе, имеем
Так как всегда можно выбрать точки, для которых 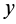
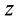
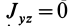
Рис. 31
Аналогичные рассуждения для двух симметричных относительно оси 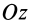
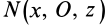
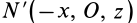
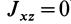
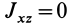
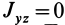

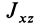
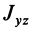


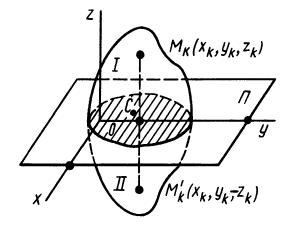
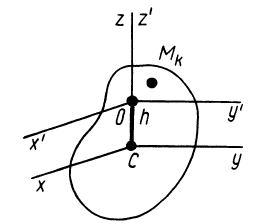
Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.
Рис. 32
Для доказательства теоремы выберем в плоскости симметрии 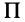

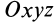

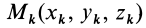
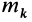
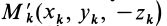
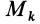
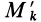
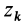
Для центробежного момента инерции 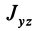
так как часть тела (I), соответствующая точкам с положительными координатами 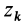
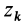
Так как центробежные моменты инерции 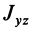
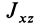



Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.
Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.
Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.
Теорема доказывается аналогично предыдущей. Для каждой точки тела 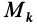
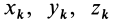
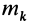
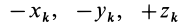

так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты 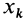
Аналогично доказывается, что 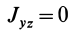
Таким образом, ось 
Теорема 4. Главные оси инерции для точки 
Выберем в точке 
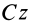
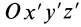
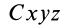
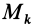
где 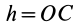
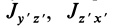
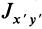
так как
где 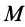
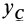
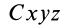
Если 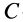
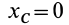
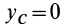
Используя полученные формулы при этих условиях, имеем:
Рис. 33
Следовательно, оси 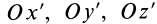
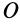
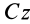
Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 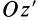
Определение главных моментов инерции и направления главных осей
Пусть известны компоненты тензора инерции в точке 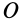
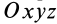
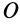
Если оси координат 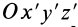
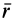
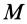
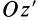
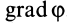
Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 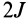
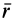
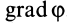
Рис. 34
В этих уравнениях 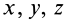
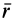
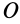
Для частных производных из (27′) получаем:
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 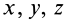
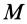
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 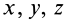
Это кубическое уравнение для определения 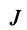
В общем случае имеется три различных действительных корня кубического уравнения 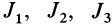
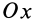
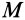
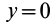
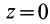
Так как 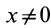
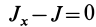
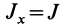
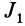
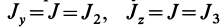
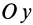
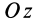
Подставляя в (29) 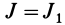
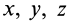
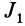
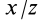
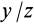
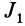
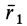
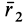
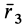
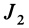
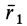
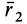
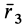
Таким образом, если известен тензор инерции для осей 
Выражение компонентов тензора инерции через главные моменты инерции
Определим компоненты тензора инерции в точке 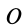

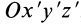
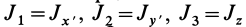

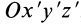
Осевые моменты инерции относительно осей 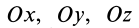
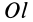
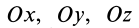
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки 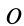

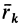
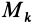
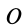
где 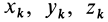
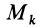
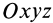
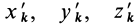
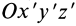
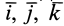
Рис. 35
Используя (33) для центробежного момента инерции 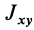
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.
Оси координат 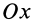
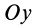
или
Используя это соотношение для исключения величины 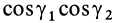
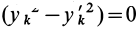
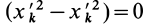
где
— главные моменты инерции. Аналогично получаются выражения для 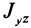
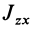
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 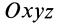
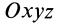
Если ось 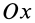
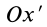
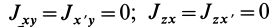
Из (35) имеем
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 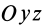
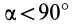
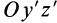
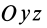
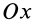
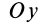
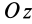
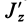
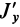
Рис. 36
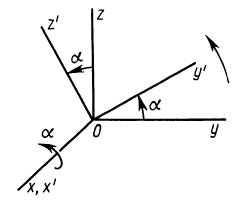
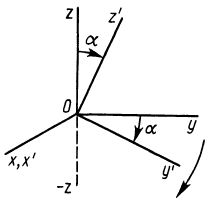
Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 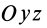
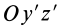
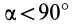
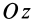
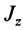
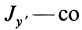
= 90°; р2 = а; Р3 = 90° + а;
Рис. 37
Аналогично при совпадении осей 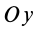
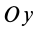
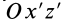
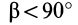
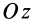
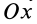
При совпадении осей 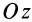
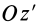
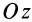
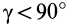
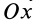
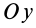
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки










 —
—
 оменты
оменты
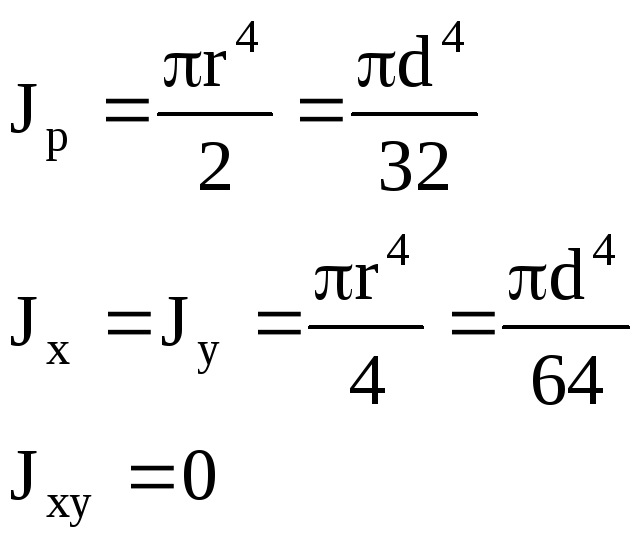
 ольцо
ольцо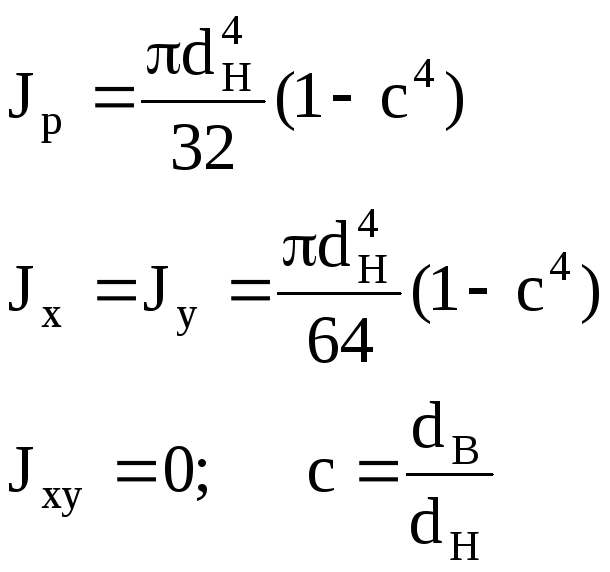
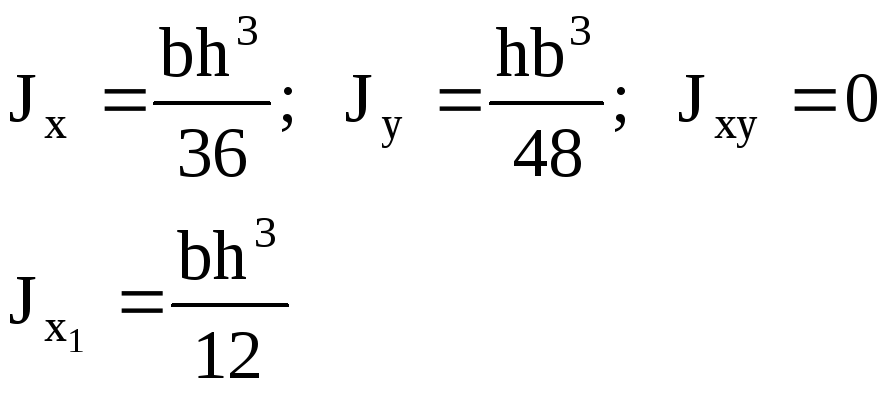

 етверть
етверть