Как найти моменты инерции относительно главных осей

Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ

Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.  

Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
 

 

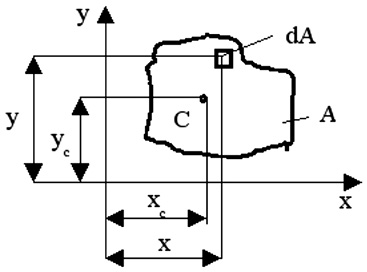
Рис. 10. Площадь А в системе координат х, у

Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:

 

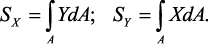
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:

(3)

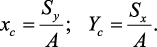
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны

(4)

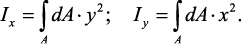
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.

(5)

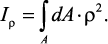
Учитывая, что ρ² = x² + y², получаем I_ρ = I_x + I_y.

Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.

Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).

Полярный момент инерции

J_ρ = J_x + J_y;, (6)

 

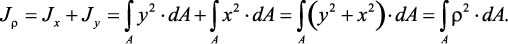
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ² = y² + z²) до этой точки, взятая по всей площади сечения А.

Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки

 

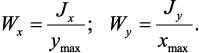
Полярный момент сопротивления

 

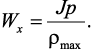
Осевой и полярный моменты сопротивления имеют размерность м3.

Радиус инерции

Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:

 

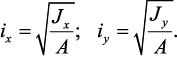
Вычисление геометрических характеристик простых фигур.

Прямоугольное сечение.

Определим осевой момент инерции прямоугольника относительно оси х.

Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:

 

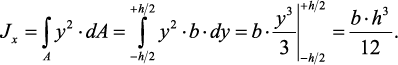
По аналогии запишем

 

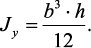
Круглое сечение

Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.

Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца 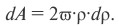. Подставляя выражение для
площади кольца в выражение для Jρ и интегрируя, получим:

 

 

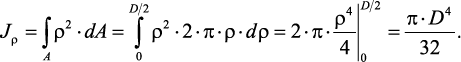
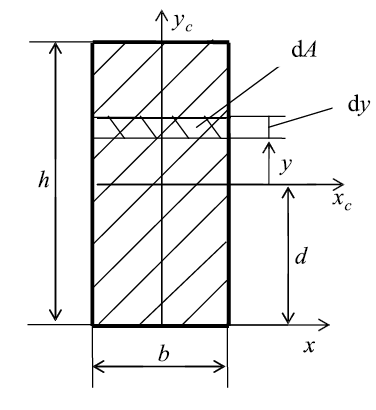
Рис. 11. Прямоугольник
 

 

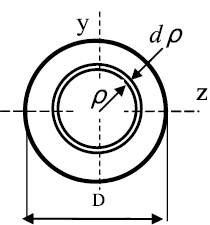
Рис. 12. Круг

Тогда

 
 

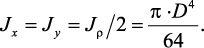
Вычислим моменты инерции фигуры
произвольной формы относительно осей,
повернутых относительно заданных осей
ина угол(Рис.4.14)

Рис.4.14

Пусть моменты инерции относительно
осей
иизвестны. Выберем произвольную площадкуи выразим ее координаты в системе осейичерез координаты в прежних осяхи:

,. (4.27)

Найдем осевые и центробежный моменты
инерции фигуры относительно повернутых
осей
и:

.
(4.28)

Принимая во внимание, что

;и,

получим:

.
(4.28)

Таким же образом установим:

.
(4.29)

Центробежный момент инерции принимает
вид:

или

.
(4.30)

Выразим осевые моменты через синус и
косинус двойного угла. Для этого введем
следующие функции:

. (4.31)

Подставляя (4.31) в формулы (4.27) и (4.28),
получим:

.
(4.32)

.
(4.33)

Если сложить выражения для осевых
моментов инерции (4.32) и (4.33), то получим:

.
(4.34)

Условие (4.34) представляет условие
инвариантности суммы осевых моментов
инерции относительно двух взаимно
перпендикулярных осей, т.е. сумма
осевых моментов инерции относительно
двух взаимно перпендикулярных осей не
зависит от величины угла поворота осей
и является величиной постоянной.Ранее это условие было получено на том
основании, что сумма осевых моментов
инерции относительно двух взаимно
перпендикулярных осей равнялась величине
полярного момента инерции относительно
точки пересечения этих осей.

Исследуем уравнение для момента инерции
на экстремум и найдем такое значение
угла,
при котором момент инерции достигнет
экстремальной величины. Для этого
возьмем первую производную от момента
инерциипо углу(выражение (4.32)) и результат приравняем
нулю. При этом положим.

(4.35)

Выражение в скобках представляет собой
центробежный момент инерции относительно
осей, наклоненных к оси
под углом.
Относительно этих осей центробежный
момент инерции равен нулю:

,
(4.36)

а это
означает, что новые оси являются главными
осями.

Ранее было определено, что главными
осями инерции являются оси, относительно
которых центробежный момент инерции
равен нулю. Сейчас это определение можно
расширить – это оси, относительно
которых осевые моменты инерции имеют
экстремальные значения. Моменты
инерции относительно этих осей называютсяглавными моментами инерции.

Найдем положение главных осей инерции.
Из выражения (4.36) можно получить:

.
(4.37)

Полученная формула дает для угла
два значения:и.

Следовательно, существуют две взаимно
перпендикулярные оси, относительно
которых моменты инерции имеют экстремальные
значения. Как уже отмечалось выше, такие
оси называются главными осями инерции.
Остается установить, относительно какой
из осей момент инерции достигает
максимального значения, а относительно
какой – минимального значения. Решить
эту задачу можно путем исследования
второй производной от выражения (4.32) по
углу
.
Подставив в выражение для второй
производной значение углаилии исследуя знак второй производной,
можно судить о том, какой из углов
соответствует максимальному моменту
инерции, какой – минимальному. Ниже
будут приведены формулы, которые дадут
однозначное значение угла.

Найдем экстремальные значения для
моментов инерции. Для этого преобразуем
выражение (4.32) , вынося за скобку
:

.
(4.38)

Используем известную из тригонометрии
функцию и подставим в нее выражение
(4.37), получим:

.
(4.39)

Подставляя в формулу (4.38) выражение
(4.39) и производя необходимые вычисления,
получаем два выражения для экстремальных
моментов инерции, которые не включают
в себя угол наклона осей
:

;
(4.40)

. (4.41)

Из формул (4.40) и (4.41) видно, что величины
главных моментов инерции определяются
непосредственно через моменты инерции
относительно осей
и.
Поэтому их можно определять, не зная
положения самих главных осей.

Зная экстремальные значения моментов
инерции
иможно помимо формулы (4.37) определять
положение главных осей инерции.

Приведем без вывода формулы, позволяющие
находить углы
имежду осьюи главными осями:

;(4.42)

Угол
определяет положение оси, относительно
которой момент инерции достигает
максимальной величины (),
уголопределяет положение оси, относительно
которой момент инерции достигает
минимальной величины ().

Введем еще одну геометрическую
характеристику, которая называется
радиусом инерции сечения. Обозначается
эта характеристика буквой
и может быть вычислена относительно
осейиследующим образом:

;(4.43)

Радиус инерции находит широкое применение
в задачах сопротивления материалов и
его применение будет рассмотрено в
следующих разделах курса.

Рассмотрим несколько примеров расчетов
конструкций с учетом поворота осей и с
использованием радиуса инерции сечения.

Пример 4.7. Моменты инерции сечения
прямоугольной формы относительно
главных осей равны соответственносм⁴,см⁴.
При повороте на 45⁰моменты инерции
относительно новых осей оказались
одинаковыми. Чему равна их величина?

Решение:

Для решения задачи воспользуемся
выражением (4.28) с учетом того, что
центробежный момент инерции относительно
главных осей равен нулю:

.
(а)

Подставим в формулу (а) численные значения
для моментов инерции и угла поворота
осей:

см⁴.

Пример
4.8. У которой
из фигур (Рис.4.15), имеющих одинаковую
площадь, радиус инерции относительно
оси
,
будет
наибольшим?
Определить
наибольший радиус инерции сечения
относительно оси
.

Решение:

1. Найдем площадь каждой из фигур и
размеры сечений. Площадь фигур равняется
для третьей фигуры
см².

Диаметр первого сечения найдем из
выражения:

см.

Размер стороны квадрата:

см.

Основание треугольника:

см.

Рис.4.15

2. Находим моменты и радиусы инерции
каждого из сечений относительно
центральной оси
.

Для сечения круглой формы:

см⁴;см.

Для сечения квадратной формы:

см⁴;см.

Для сечения прямоугольной формы:

;

Для сечения треугольной формы:

см⁴;см.

Наибольший радиус инерции оказался у
сечения прямоугольной формы и равен он

см.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

6.6. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

При изменении угла α значения Iz1, Iy1, Iz1y1 (6.13) изменяются, и при некотором значении угла α0 они принимают экстремальные значения. Взяв первую производную по углу α от формул (6.13) и приравняв ее нулю, получим: Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции. Их вычисляют следующим образом: Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны; для симметричных сечений оси симметрии являются главными. Главные оси, проходящие через центр тяжести фигуры, называют главными центральными осями инерции. Пример 6.4. Определить, каким образом изменяется момент инерции квадратного сечения при его повороте. Решение. Момент инерции относительно повернутой оси: Поскольку оси z, y квадрата являются осями симметрии, то есть главными, то центробежный момент инерции относительно них Izy = 0: Выводы. 1. Моменты инерции квадратного сечения с изменением положения центральных осей остаются постоянными. 2. В квадрате и других правильных многоугольниках (треугольниках, пятиугольниках) любая центральная ось является и главной. Такие фигуры называют фигурами равного сопротивления. Пример 6.5. Для фигуры, представленной в примере 6.1, определить главные центральные моменты инерции. Решение. Расстояния между центральной осью составной фигуры и собственными центральными осями элементов Моменты инерции относительно центральных осей, параллельных основанию и высоте a1= y1 – yC = 5 – 3,5 = 1,5 см; a2= y2 – yC = 1 – 3,5 = –2,5 см; b1= z1 – zC = 1 – 2,5 = –1,5 см; b2= z2 – zC = 5 – 2,5 = 2,5 см. Центробежный момент инерции Направления главных осей инерции Угол α0 (положительный) откладываем против хода часовой стрелки от оси с большим моментом инерции, то есть zC . Величины главных центральных моментов инерции