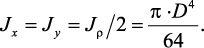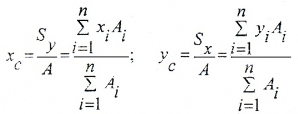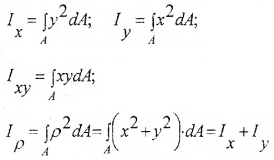Д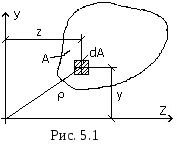
определения этим геометрическим
характеристикам для сечения произвольной
формы (рис. 5.1).
Статическим
моментом площади относительно некоторой
оси называется взятый по всей его площади
интеграл от произведения площади
элементарного участка dA
на расстояние от его центра тяжести до
рассматриваемой оси.
(5.1)
Статические
моменты выражаются в см3
и м3.
Статический
момент площади составной фигуры
относительно какой-либо оси равен сумме
статических моментов площадей отдельных
фигур относительно этой же оси.
Статический
момент площади может быть положительным,
отрицательным или равным нулю. Он
равняется нулю тогда, когда рассматриваемая
ось проходит через центр тяжести площади
сечения.
Осевым
(экваториальным) моментом инерции
сечения относительно некоторой оси
называется взятый по всей его площади
А интеграл от произведения площади
элементарного участка dA
на квадрат расстояния от его центра
тяжести до рассматриваемой оси:
(5.4)
Полярным
моментом инерции сечения относительно
некоторой точки (полюса) называется
взятый по всей его площади А интеграл
от произведения площади элементарного
участка dA
на квадрат расстояния от его центра
тяжести до рассматриваемой точки
(полюса):
(5.5)
Центробежным
моментом инерции сечения относительно
некоторых двух взаимно перпендикулярных
осей называется взятый по всей его
площади А интеграл от произведения
площади элементарного участка dA
на расстояния от его центра тяжести до
рассматриваемых осей:
(5.6)
Моменты
инерции измеряются в см4
и м4.
Осевые и полярные моменты инерции всегда
положительны. Центробежные моменты
инерции могут быть положительными,
отрицательными или равными нулю.
Центробежный
момент инерции сечения относительно
осей, из которых одна или обе совпадают
с его осями симметрии, равен нулю.
23.Зависимость между моментами инерции относительно параллельных осей. Вычисление моментов инерции сложных сечений.
Определим
момент инерции фигуры относительно
какой-либо оси
(рис. 3.4).
Пусть
— центральная ось и момент инерции
известен. Из чертежа видно
.
Следовательно
Первый
интеграл дает площадь поперечного
сечения. Второй интеграл, представляющий
статический момент относительно
центральной оси
равен рулю.
Рис.
3.4. Параллельный перенос осей
Третий
интеграл представляет собой момент
инерции
относительно оси
.
Таким образом
(3.13)
и
относительно ортогональной оси
. (3.14)
Момент
инерции относительно любой оси равен
моменту инерции относительно центральной
оси, параллельной данной, плюс произведение
площади фигуры на квадрат расстояния
между осями.
Из
формул (4.13) и (3.14) видно, что момент инерции
относительно центральной оси меньше,
чем момент инерции относительно любой
нецентральной оси, которая параллельно
центральной.
Момент
инерции относительно центральной оси
называется центральным моментом инерции.
Положение
главных центральных осей и величины
главных центральных моментов инерции
для симметричных сечений определяются
в следующем порядке:
1. Сложное
сечение разбивается на простые фигуры
(круг, прямоугольник, двутавр, уголок и
т.п.) и проводятся их центральные
оси Zi
и Yi
(как правило – горизонтально и
вертикально).
2.
Определяется по формулам (5.3) положение
центра тяжести всего сечения и через
эту точку проводятся его центральные
оси Z и Y. При наличии двух осей симметрии
центр тяжести всего сечения находится
в точке их пересечения.
Если
сечение обладает только одной осью
симметрии, то по формулам (5.3) определяется
только одна координата центра тяжести.
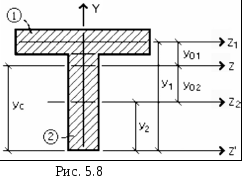
Поясним это для фигуры, показанной на
рис. 5.8:
а)
оси Z’ и Y’ выбираем так, чтобы ось Y’ совпала
с осью симметрии фигуры, а ось Z’ – чтобы
было удобно определить расстояние до
этой оси от центральных осей простых
фигур;
б) определяем
статический момент площади сечения
относительно произвольной оси Z’
по формуле:
= А1у1 + А2у2,
где
Аi
– площади сечений простых фигур; уi
– расстояния от произвольной оси Z’
до центральных осей простых фигур Zi.
Расстояния уi
необходимо брать с учетом знаков;
в) определяем
координату уC
центра тяжести по формуле (5.3):
=
г) на
расстоянии уC
от оси Z
проводим вторую центральную ось Z.
Первой центральной осью является ось
симметрии Y.
3. Моменты
инерции относительно главных центральных
осей Z
и Y
(рис. 5.8) определяем по формулам (5.9),
которые в развернутом виде запишутся
так:
так
как одна из рассматриваемых осей
(ось
Y) является осью симметрии.
В
этих формулах:
–осевые
моменты инерции простых фигур относительно
своих центральных осей (собственные
моменты инерции), которые определяются
по формулам (5.10)–(5.19) или по таблицам
сортаментов для прокатных элементов;
–расстояния
от общих центральных осей сечения Z
и Y
до центральных осей простых фигур. В
рассматриваемом примере
и
показаны на рис. 5.8;
Ai
– площади простых фигур. Если простой
фигурой является фигура, вырезанная от
общей, т.е. «пустая» фигура, то в
соответствующие формулы площади таких
фигур A
и их собственные моменты инерции
подставляются со знаком «минус».
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этом уроке посмотрим, как определяются осевые моменты инерции для сложного сечения (состоящего из простых фигур).
Условие задачи
В качестве примера возьмём симметричное сечение, имеющее две оси симметрии:

Определение положения центра тяжести
Первым делом, необходимо определить положение центра тяжести сечения. Как это делается, можешь посмотреть в отдельном уроке, перейдя по указанной ссылке. Здесь же, я приведу только расчёт.
Подготовим сечение к расчёту:
- разобьём сечение на простейшие фигуры;
- обозначим центры тяжести отдельных фигур;
- введём вспомогательные координатные оси (y0, x0).

Площадь сечения
Используя эту страничку, найдём площади отдельных фигур:

Расстояния от центров тяжести отдельных фигур до вспомогательных осей
Статические моменты

Координаты центра тяжести
Покажем центр тяжести всего сечения:

Как видишь, центр тяжести находится ровно посередине сечения. Это свойство симметричного сечения. У такого сечения, которое имеет две оси симметрии, центр тяжести находится на пересечении этих осей. Поэтому для симметричного сечения можно и НЕ рассчитывать положение центра тяжести.
Расчёт осевых моментов инерции
Для выполнения дальнейшего расчёта следует обозначить центральные оси для всего сечения (x, y), а также собственные оси для каждой отдельной фигуры, которые формируют сечение:

Как определить моменты инерции относительно центральных осей?
Осевые моменты инерции (Ix, Iy) относительно центральных осей (x, y) можно определить по следующим формулам:

где Ixi, Iyi – моменты инерции отдельных фигур относительно собственных осей;
Ai – площади отдельных фигур;
yci, xci – расстояния от центров тяжести отдельных фигур до соответствующей центральной оси.
Определение моментов инерции для каждой фигуры
Определим осевые моменты инерции каждой отдельной фигуры, пользуясь справочной информацией:
Определение расстояний от центров тяжести каждой фигуры до центральных осей
Определение моментов инерции относительно центральных осей
Другие уроки, на проекте – ssopromat.ru, по расчёту геометрических характеристик можно найти здесь.
Рассмотрим формулы для определения геометрических характеристик плоских сечений: статического момента площади фигуры, осевых моментов инерции и радиуса инерции сечения.
При расчете элементов конструкций на прочность, жесткость и устойчивость приходится кроме общеизвестной характеристики – площади поперечного сечения A, оперировать такими геометрическими характеристиками сечений, как статический момент площади, момент инерции, момент сопротивления, радиус инерции.
Статический момент площади
Интегралы вида:
называются статическими моментами площади сечения A относительно осей X и Y соответственно.
В тех случаях, когда сечение может быть разделено на простейшие фигуры площади Ai и координаты центров тяжести xi и yi которых известны, статические моменты площади сложной фигуры определяются через суммирование
Статические моменты площади имеют размерность [м3] и могут принимать любые числовые значения. Для осей XC, YC, проходящих через центр тяжести сечения C (центральные оси), статические моменты равны нулю:
Координаты центров тяжести сечения определяются относительно так называемых вспомогательных осей по формулам:
Если сечение имеет ось симметрии, то центр тяжести находится на этой оси и его положение определяется одной координатой.
При наличии двух и более осей симметрии центр тяжести совпадает с точкой пересечения этих осей.
Моменты инерции
Моментами инерции площади сечения называют интегралы вида:
где:
Ix, Iy — осевые моменты инерции площади сечения относительно осей OX, OY соответственно;
Ixy — центробежный момент инерции;
Iρ — полярный момент инерции.
Размерность момента инерции [м4], Ix, Iy, I ρ всегда положительны, Ixy может принимать любые значения, при этом, если хотя бы одна из осей является осью симметрии, Ixy=0.
Зависимости между моментами инерции относительно параллельных осей выражаются формулами:
где a, b – расстояния между осями X, XC и Y, YC.
Оси, относительно которых Ixy=0, называют главными, а осевые моменты инерции относительно них – главными моментами инерции.
Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а соответствующие им моменты инерции – главными центральными моментами инерции.
Главные оси характерны тем, что их моменты инерции принимают экстремальные значения (Imax, Imin).
Момент инерции сложного сечения относительно какой-либо оси находится суммированием моментов инерции составляющих его частей относительно той же оси:
Радиусы инерции
Величины
называют радиусами инерции сечения относительно осей OX и OY соответственно.
Эллипс, построенный в главных осях, с полуосями, равными главным радиусам инерции
называют эллипсом инерции.
Лекции по сопромату >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Лекция 4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ СТЕРЖНЯ
Математические определения геометрических характеристик плоских
фигур: статические моменты, осевые моменты инерции и центробежный,
полярный момент инерции. Центральные оси. Главные оси. Определение
положения центра тяжести элементарных сечений и составленного из
элементарных фигур. Нахождение геометрических характеристик сечений
относительно центральных осей.
Различают следующие характеристики сечений: площадь А, статические
моменты площади, моменты инерции площади, центробежный момент инерции
площади.
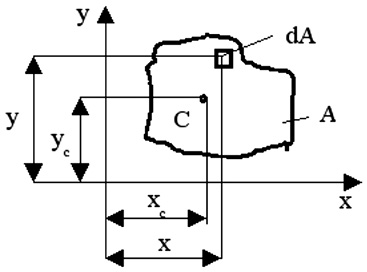
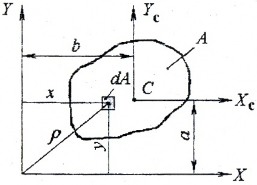
Рис. 10. Площадь А в системе координат х, у
Под статическим моментом площади относительно некоторой оси
понимается сумма произведений площадей элементарных площадок на
расстояния от их центра тяжести до соответствующей оси:
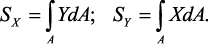
Определение центра тяжести сечения. Статические моменты сечения
относительно осей проходящих через центр тяжести равны нулю, поэтому их
используют для определения координат центров тяжести сечения. Для этого
проводят вспомогательные оси x и y и координаты центра тяжести сечения
определяют по зависимостям:
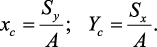
Моменты инерции сечения. Осевым моментом инерции сечения I
называется интеграл по площади произведения элементарной площадки на
квадрат расстояния до оси. Осевые моменты инерции сечения относительно
осей x и y будут соответственно равны
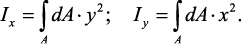
Полярным моментом инерции сечения Iρ называется интеграл по
площади произведения элементарной площадки на квадрат расстояния до
начало координат.
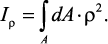
Учитывая, что ρ2 = x2 + y2, получаем Iρ = Ix + Iy.
Полярный момент инерции сечения равен сумме осевых моментов инерции сечения.
Оси, относительно которых центробежный момент инерции равен нулю,
называются главными центральными осями, осевые моменты инерции
относительно их принимают свои экстремальные значения (максимум
и минимум).
Полярный момент инерции
Jρ = Jx + Jy;, (6)
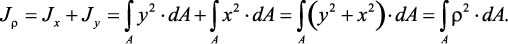
Полярный момент инерции относительно данной точки – сумма
произведений элементарных площадей dA на квадраты их расстояний
(ρ2 = y2 + z2) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления. Осевой момент сопротивления относительно
рассматриваемой оси – величина равная моменту инерции относительно той
же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
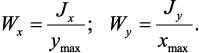
Полярный момент сопротивления
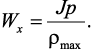
Осевой и полярный моменты сопротивления имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
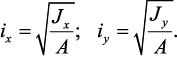
Вычисление геометрических характеристик простых фигур.
Прямоугольное сечение.
Определим осевой момент инерции прямоугольника относительно оси х.
Разобьем площадь прямоугольника на элементарные площадки
с размерами b (ширина) и dy (высота) (рис. 11). Тогда площадь такого
элементарного прямоугольника (заштрихована)равна dA = b•dy. Подставляя
значение dA в формулу для определения осевого момента инерции, получим:
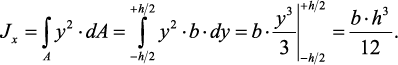
По аналогии запишем
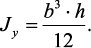
Круглое сечение
Вначале целесообразно найти полярный момент инерции. Затем,
учитывая, что для круга Jx = Jy, а Jρ = Jx + Jy, найдем Jx = Jy = Jρ/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ
(рис. 12); площадь такого кольца 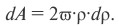
площади кольца в выражение для Jρ и интегрируя, получим:
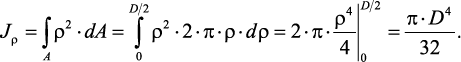
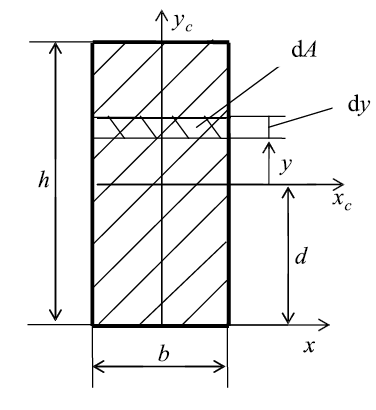
Рис. 11. Прямоугольник
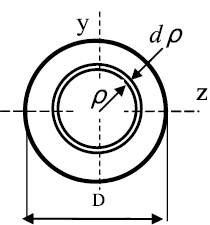
Рис. 12. Круг
Тогда