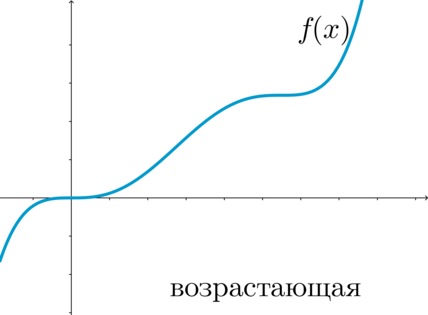
Общие сведения
Функцией вида р = f(r) называется зависимость ее значения от переменной величины «r» или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.
Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) <= f(r2) или f(r1) >= f(r2) соответственно. Кроме того, нужно учитывать, что r1 < r2 или r1 <= r2. Необходимо отметить, что точки r1 и r2 должны принадлежать (а;b).
Когда f(r) является строгой (только убывающей или возрастающей — постоянство), тогда знак «<=» или «>=» следует заменить на строгий «<» или «>»: f(r1) < f(r2) или f(r1) > f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:
- Возрастающая: ∀ r1, r2 ∈ (a;b): r1 < r2 ⇒ f(r1) <= f(r2). Расшифровывается запись таким образом: для любых (∀) точек r1 и r2, принадлежащих (∈) интервалу (a;b), при условии, что r1 < r2, следует (⇒) выполнение неравенства f(r1) <= f(r2).
- Строго возрастающая: ∀ r1, r2 ∈ (a;b): r1 < r2 ⇒ f(r1) < f(r2).
- Убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) >= f(r2).
- Строго убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) > f(r2).
Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.
Теорема о пределе
Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.
Чтобы доказать утверждение, следует задать некоторую функцию, которая является монотонной. Кроме того, она должна возрастать на некотором интервале [а;b]. После этого нужно выбрать любую точку r0 ∈ (a;b]. В результате этого для ∀ r ∈ [a;r0) ⇒ f(r) <= f(r0) ⇒ f(r) ограничена сверху на [a;r0) ⇒ при существующих (∃ — знак существования) верхних границах (sup) функции f(r) = M <= f(r0). По определению для ∀ r ∈ [a;r0) ⇒ f(r) <= M.
Следует предположить, что существует некоторая переменная «e», которая больше нуля. Она также определена на текущем интервале. Следовательно, выполняется неравенство М — е < f(e). Пусть q = r0 — e и t — значение r0 c левой границей 0 — q. Если выполняется условие ∀ r ∈ (е;r0) = (t;r0), то f(e) <= f(r). В итоге получается, что ∀ е > 0 ∃ q > 0 для r ∈ (t;r0): М — е < f(e) < f(r) <= M < M + e. Следовательно, |f(r) — M| < e. Левый предел, в котором х стремится к точке r0: lim [f(r)] |(r -> r0 — 0) = M. Отсюда следует такое соотношение: f(r0 — 0) = sup f(r), a <= r < r0.
Таким же образом доказывается правосторонний предел в точке r0 ∈ [a;b). Получается такое соотношение: f(r0 + 0) = inf f(r), r0 < r <= b. Теорема доказана. Кроме того, существуют следствия, полученные при доказательстве утверждения о пределе:
- Возрастание: f(r0 — 0) = lim [f(r)] |(r -> r0 — 0) <= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).
- Убывание: f(r0 — 0) = lim [f(r)] |(r -> r0 — 0) >= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).
Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.
Критерии возрастания и убывания
Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:
- Для убывающей и возрастающей.
- Если является строго убывающей или строго возрастающей.
- Определение по точке, производной и интервалу.
Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) <= 0, а также возрастающей при f'(r) >= 0 соответственно (при r ∈ данному интервалу).
Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) < 0 и производная f'(r) также не равна нулевому значению на указанном промежутке. Третья теорема позволяет определить характер монотонности p = f(r) в заданной точке r0 ∈ (а;b). Существует два варианта соотношений: для убывающей f'(r0) < 0 и возрастающей: f'(r0) > 0.
Основные свойства
Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:
- Сумма двух убывающих (возрастающих) k = f(t) и l = f(v) является возрастающим (убывающим) выражением.
- Если k = f(t) возрастает, то -k = f(t) (противоположная) будет убывать. При убывании первой вторая будет возрастать соответственно.
- Когда у k = f(t) есть обратная вида k2 = 1 / f(t), тогда при убывании первой вторая будет возрастать. Если первая возрастает, то вторая убывает.
- Результатом произведения двух убывающих (возрастающих) является убывающая функция. Также должны выполняться такие условия: k = f(t) >= 0 и l = f(v) >= 0.
- Если k = f(t) возрастает или убывает на (а;b), а l = f(t) возрастает или убывает на (c;d), и (а;b) входит в (c;d), то композиция функций к∘ l (k(l(t))) также возрастает или убывает.
После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.
Базовые знания
Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:
- Найти производную первого порядка — f'(r).
- Приравнять выражение, полученное в первом пункте, к 0.
- Найти критические точки, решив уравнение во втором пункте.
- Определить знак f'(r) на промежутках, полученных в результате разбиения критическими точками. Найти промежутки убывания и возрастания.
Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.
Нахождение производной
Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.
Рисунок 1. Дифференциалы простых выражений.
Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:
- Сумма: [k(t) + l(t)]’ = k'(t) + l'(t).
- Разность: [k(t) — l(t)]’ = k'(t) — l'(t).
- Произведение: [k(t) * l(t)]’ = k'(t) * l(t) + l'(t) * k(t).
- Частное: [k(t) / l(t)]’ = [k'(t) * l(t) — l'(t) * k(t)] / (l(t))^2.
- Сложная: [k(l(t))]’ = l'(t) * k'(t).
Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.
Корни уравнений и критические точки
Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.
Первый тип решается по очень простому алгоритму: следует перенести неизвестные в одну часть, а известные — в другую. Для решения квадратного уравнения (aw^2 + bw + c = 0) нужно его упростить, разложить на множители или вычислить дискриминант. Последний вычисляется по следующей формуле: D = b^2 — 4ac. Количество корней зависит от значения D и определяется по таким формулам:
- Два решения при D > 0: w1 = (-b — [D]^(1/2)) / 2a и w2 = (-b + [D]^(1/2)) / 2a.
- D = 0 (одно): w = (-b) / 2a.
- Нет корней, когда D < 0.
Используя метод разложения на множители, можно решить без D. Например, в выражении x(x-1)(x-4) = 0 рассматривается три уравнения: x1 = 0, х2 -1 = 0 и х3 — 4 = 0. Решение кубических и биквадратных равенств с неизвестной осуществляется методом разложения на множители. При этом понижается степень до 2, а дальше находятся его корни.
Для нахождения корней других уравнений следует воспользоваться заменой, а затем свести к линейному или квадратному. Следует отметить, что решая трансцендентные (логарифмы и показатели), следует знать правила логарифмирования и свойства степени. Корни также находятся при помощи замены.
Критическими называются точки, в которых функция меняет свое поведение (четность, периодичность, экстремумы и т. д.). При исследовании они записываются в специальную таблицу поведения в виде промежутков.
Пример решения
Задачи бывают нескольких типов. В одних следует найти промежутки монотонности, а во-вторых — доказать на основании теорем, что она возрастает или убывает на заданном промежутке. Например, необходимо найти промежутки монотонности функции z(y) = (y^2 + 1) / y. Следует отметить, что она является дифференцируемой. Ее область определения D(z) = (-бесконечность;0) U (0;+бесконечность). Решать ее нужно по алгоритму:
- Производная: [(y^2 + 1) / y]’ = (y^2 — 1) / y.
- Приравнять к 0: (y^2 — 1) / y = 0.
- Найти корни — критические точки (y — 1)(y + 1) / y = 0: y1 не равен 0, y2 = 1 и у3 = — 1.
- Построить таблицу.
| y | (-infinity;-1) | (-1;0) | (0;1) | (1;+infinity) |
| z’ | — | + | — | + |
| z | У | В | У | В |
Таблица 1. Интервалы монотонности.
Если функция является четной, то эта особенность не влияет на результат, поскольку ее производная может быть с отрицательным знаком. Примером является обычный тригонометрический косинус.
Таким образом определение монотонности функции на заданном промежутке является одним из элементов исследования ее поведения. Для осуществления этой операции применяются специальный алгоритм, теоремы и свойства.
НЕМНОГО О МОНОТОННОСТИ
Монотонные
функции
Определение
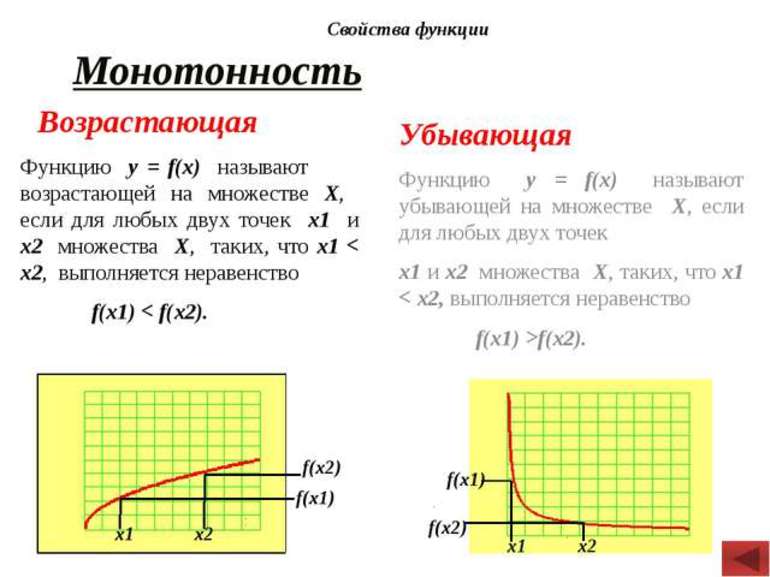
1. Функция f(x)
называется возрастающей на некотором промежутке X, если для любых x1
и x2
из этого промежутка таких, что x1<x2,
выполняется неравенство f(x1)<f(x2).
Так, например,
возрастающей на множестве неотрицательных действительных чисел является функция
.
Определение
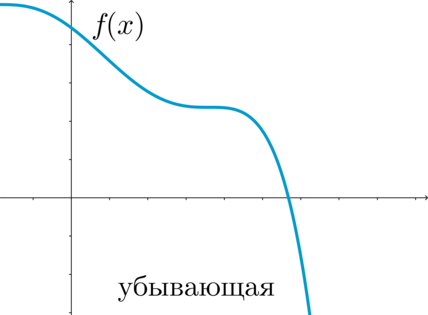
2. Функция f(x)
называется убывающей на некотором промежутке X, если для любых x1
и x2
из этого промежутка таких, что x1<x2,
выполняется неравенство f(x1)>f(x2).
Примером такой
функции может стать функция y=x10,
убывающая на луче .
Определение
3. Функция, обладающая одним из перечисленных свойств на
промежутке X, называется монотонной на этом промежутке.
Следует отметить,
что, отвечая на вопрос о промежутках монотонности функций в задачах,
следует указывать максимально возможные промежутки возрастания и убывания
функции, то есть промежутки, на которых функция обладает указанным свойством, а
на любом его расширении функция этим свойством уже не обладает.
Замечание.
Функция f(x) монотонная на множествах X1
и X2,
может не быть монотонной на объединении этих множеств. Так, например, хорошо
известная функция является убывающей на каждом из
промежутков: (−∞;0) и (0;+∞), но не является убывающей на объединении этих
промежутков, то есть на множестве (−∞; 0)∪(0;+∞).
Действительно, например, возьмём x1=-1,
а x2=1.
Тогда x1< x2,
и -1=f(x1)<f(x2)=1.
Свойства
монотонных функций:
1. Если
функция f(x) возрастает на множестве X, то для любого числа c функция f(x)+c
тоже возрастает на множестве X.
2. Если
функция f(x) возрастает на множестве X, то для любого положительного числа c
функция с· f(x) тоже возрастает на множестве X.
3. Если
функция f(x) возрастает на множестве X, то функция -f(x) убывает на этом
множестве.
4. Если
функция f(x) возрастает на множестве X и сохраняет знак на этом множестве, то
функция убывает на этом множестве.
5. Если
функции f(x) и g(x) возрастают (убывают) на множестве X,
то функция также возрастает (убывает) на этом множестве;
6. Если
функции f (x) и g(x) возрастают (убывают) на множестве X
и, кроме того, для всех значений x
из этого множества, то функция также возрастает
(убывает) на X;
7. Композиция
одинаково монотонных функций, монотонна в том же смысле. То есть, если функции
f(x) и g(x) являются возрастающими функциями, то функция f(g(x)) тоже является
возрастающей.
Всякая монотонная функция принимает каждое свое значение ровно один раз. А
стало быть, равенство значений такой функции возможно лишь в случае равенства
значений её аргумента, то есть справедливо следующее утверждение:
Утверждение 1. Если функция f(x) монотонна
на множестве всех действительных чисел, то уравнение f(g(x))=f(h(x))
равносильно уравнению g(x)=h(x).
Задание
1. Функция f(x),
определенная на множестве всех действительных чисел, является возрастающей на
этом множестве. Решите уравнение f(sinx—cosx)=f(2-2cosx).
Решение. По условию задачи, функция f(x), определенная
на множестве всех действительных чисел, является возрастающей на этом множестве.
Поэтому, согласно утверждению 1, заданное уравнение равносильно уравнению sinx—cosx=2-2cosx,
множество решений которого пусто.
Ответ.
Ø.
Утверждение 2. Если функция f(x)
является монотонной в области определения, то уравнение f(g(x))=f(h(x))
равносильно уравнению g(x)=h(x)
на области определения первого уравнения.
Задание
2. Функция g(x),
определенная на множестве отрицательных действительных чисел, является
убывающей на этом множестве. Решите уравнение .
Найдите корни этого уравнения, принадлежащие промежутку .
Решение.
Так как, согласно условию, функция g(x),
определенная на множестве отрицательных действительных чисел, является
убывающей на этом множестве, то заданное уравнение равносильно смешанной
системе:
Заметим, что в этой системе одно из двух неравенств является
избыточным («лишним»), его можно не писать, так как оно легко получается из двух
других соотношений системы. Поскольку второе неравенство системы решается
намного проще первого, то оставляем именно его, и заданное уравнение становится
равносильным следующей системе:
Ответ.
Ярким примером тому, насколько важным порой бывает освободиться от избыточного
(«лишнего») неравенства, является, на мой взгляд, уравнение
.
Задание
3. Решите уравнение и
найдите его корни, принадлежащие интервалу , если
известно, что .
Решение.
Функция , определённая
на множесте положительных действительных чисел, является возрастающей на этом
множестве, как сумма двух возрастающих на нём функций и
(смотри свойство 5
монотонных функций). А значит, согласно утверждению 2, заданное уравнение
равносильно смешанной системе:
Заметим, что одно из неравенств этой системы является избыточным
(лишним), его можно не писать, так как оно получается из двух других
соотношений системы. Поскольку второе неравенство системы решается намного проще
первого, то оставляем именно его, и заданное уравнение становится
равносильным следующей системе:
Далее…
Ответ
Задание
4. а) Решите уравнение, где
;
б)
Найдите корни этого уравнения, принадлежащие отрезку .
Решение.
а) Функция , определенная на
множестве всех действительных чисел, является убывающей на этом множестве,
так как для всех x () выполняется неравенство
, причем производная
не равна тождественно нулю ни на каком
интервале множества R. Поэтому, на основании утверждения 1, заданное уравнение
равносильно уравнению .
б)
Ответ:
а) б)
Задание 5. Решите уравнение . Если:
а) ; б)
. В каждом случае найдите корни заданного
уравнения, принадлежащие отрезку .
Решение. Предлагаю
каждому учащемуся начать с решения наиболее сложного, с его точки зрения,
уравнения. Отвечают на вопросы: 1) Почему именно это уравнение Вы посчитали
наиболее сложным? 2) Чем осложнено это уравнение?
Ответ.
Задание
6. а) Решите уравнение б)
Найдите корни этого уравнения, принадлежащие отрезку .
Решение.
а) Заметим, что заданное уравнение можно переписать
в виде , где
.
Функция f(x) определена на множестве всех действительных чисел и является
возрастающей на этом множестве, как сумма двух возрастающих на нём функций
y=x3
и y=x.
Именно поэтому, заданное уравнение равносильно уравнению .
б)
Ответ.
а) б)
Задание
7*. Найдите сумму корней уравнения , принадлежащих отрезку
, если
.
Решение.
Согласно теореме о монотонности сложной функции и теореме о
монотонности суммы двух монотонных функций, функция f(x), определённая на
множестве всех действительных чисел, является монотонной на этом множестве. А
значит, согласно утверждению 1, заданное уравнение равносильно уравнению . Перепишем это
уравнение следующим образом: и
рассмотрим функцию . Функция
p(x) является четной, а значит на любом симметричном относительно нуля
промежутке сумма корней (если они существуют) уравнения равна
нулю. Заметим, что на концах отрезка
функция p(x) принимает значения разных
знаков, а значит внутри этого отрезка существует, по крайней мере, один нуль непрерывной
функции p(x). Поэтому на промежутке уравнение имеет корни
и сумма этих корней равна нулю. Осталось рассмотреть функцию p(x) на
полуинтервале . На этом промежутке функция y=sinx
принимает лишь положительные значения, поэтому p(x) можно переписать следующим
образом: . Производная
на итервале
отрицательная, так как на этом интервале
выполняются неравенства sin3x>0
и cosx<0.
А значит, согласно достаточному условию убывания функции, функция p(x) убывает
на промежутке , достигая наименьшего значения
в точке . Поскольку это значение больше нуля

заданное уравнение корней не имеет.
Ответ.
0.
Задание
8*. Найдите значения параметра a, при которых
уравнение имеет четыре корня.
Решение.
Перепишем заданное уравнение следующим образом: .
Теперь, нетрудно заметить, что заданное уравнение имеет вид: , где
—
монотонная на множестве R функция. По утверждению 1 исходное уравнение
равносильно уравнению .
Ответ.
Задание
9*. Найдите все значения параметра a,
при каждом из которых уравнение аимеет ровно одно
решение.
Решение.
Выполняя серию преобразований, последовательно получаем:
Из последнего равенства следует, что заданное уравнение можно переписать
следующим образом: . Поскольку функция f(x) определена
на множестве всех действительных чисел и является возрастающей на нем, то
исходное уравнение равносильно квадратному уравнению ,
которое будет иметь одно решение тогда и только тогда, когда его дискриминант
равен нулю.
Ответ.
Утверждение 3. Если
функция f(x), определенная на множестве всех действительных чисел, монотонна на
множестве X и множества значений функций g(x)
и h(x)
являются подмножествами множества X, то уравнение f(g(x))=f(h(x))
равносильно уравнению g(x)=h(x).
Задание
10. Решите уравнение .
Решение.
Заметим, что заданное уравнение можно переписать в виде , где
. Функция
f(x), определеная на множестве всех действительных чисел, является убывающей
на отрезке [-1; 1], так как она непрерывна на этом отрезке и имеет
отрицательную производную в каждой его
внутренней точке. Поскольку множеством значений функции y=cos2x служит отрезок
[-1; 1], а множеством значений функции y=sin2x
– отрезок [0; 1], причем [0; 1]Ì [-1; 1], то, согласно
замечанию 3, заданное уравнение равносильно уравнению .
Ответ.
Задание
10.1* Решите уравнение , сводящееся к уравнению
серией преобразований. Найдите сумму
корней этого уравнения, принадлежащих полуинтервалу .
Решение.
Смотрите решение задания 7*.
Ответ.
Снова 0.
Задание
11. Составьте (придумайте) задание аналогичное
заданию 10 и решите задание, составленное соседом по парте.
Практически в каждом из выше рассмотренных заданий, мы
преобразовывали уравнение к виду, позволяющему выделить по обе стороны от знака
равенства одну и туже внешнюю, для каждой из двух композиций, функцию. После
чего, пользуясь монотонностью этой функции, мы её отделяли, заменяя решение
одной задачи решением эквивалентной ей более простой задачи. Именно поэтому,
такой метод решения естественно назвать методом ДЕКОМПОЗИЦИИ.
Декомпозиция (Википедия) —
разделение целого на части. Также декомпозиция — это научный метод,
использующий структуру задачи и позволяющий заменить решение одной большой
задачи решением серии меньших задач, пусть и взаимосвязанных, но более простых.
Задания
для самостоятельного решения
Задание 1. Решите
уравнение . Найдите корни уравнения, принадлежащие
отрезку .
Задание 2. а)
Решите уравнение , где
б)
Найдите корни этого уравнения, принадлежащие отрезку .
Задание 3. а) Решите
уравнение б) Найдите все корни этого уравнения,
принадлежащие отрезку .
Задание 4. а) Решите
уравнение ;
б) Найдите корни этого
уравнения, принадлежащие отрезку .
Задание 5. Дана функция . Решите уравнение

Найдите корни уравнения, принадлежащие отрезку .
Задание
6. Решите уравнение .
Задание 7. При всех
значениях параметра a решите уравнение
.
Задание 8. Найдите все
значения параметра a, при каждом из которых уравнение не
имеет действительных решений.
Задание
9. Дана
функция .
1)
Запишите уравнение в обычном виде.
2)
Посмотрите в интернете свойства показательной функции .
3) Решите уравнение и найдите все его корни, принадлежащие
промежутку .
Задание
10. Дана
функция .
1)
Запишите уравнение .
2)
Посмотрите в интернете свойства показательной функции .
3)
Решите уравнение и найдите все его корни,
принадлежащие отрезку .
Задание
11. Дана
функция .
1)
Запишите уравнение в привычном для Вас виде.
2)
Посмотрите в интернете свойства логарифмической функции .
3) Решите уравнение и найдите его корни, принадлежащие
промежутку .
Задание
12.
Дана функция .
1)
Запишите уравнение в обычном виде.
2)
Посмотрите в интернете свойства логарифмической функции .
3)
3) Решите уравнение и найдите все его корни,
принадлежащие промежутку .
Задание
13. Решите
уравнение .
Сложная
функция (композиция функций)
Термин сложная
функция в действительности в математическом языке является
«чисто рабочим»: так называют функцию, если она задана в виде у=f(g(x)) с
внешней функцией f и внутренней функцией g. Из самого задания этой функции
ясно, что для вычисления значения у сложной функции к значению аргумента х
сначала применяется функция g, а затем к полученному значению g(x) применяется
функция f — тогда и получается значение f(g(x)), то есть композиция
функций (суперпози́ция фу́нкций) — это
применение одной функции к результату другой.
-
Понятие сложной функции. Правило вычисления производной сложной функции.
Сложная
функция – функция от функции. Если z –
функция от у,
т.е. z(y),
а у,
в свою очередь, – функция от х,
т.е. у(х),
то функция f(x)
= z(y(x))
называется сложной
функцией (или композицией,
или суперпозицией
функций)
от х.
В
такой функции х – независимая,
а у – промежуточная
переменная.
При этом сложная функция определена
для тех значений независимой переменной,
для которых значения промежуточной
функции у входят
в область определения функции z(y).
Правило.
Если
функция f имеет производную в точке x0,
а функция g имеет производную в
точке y0 = f(x0),
то сложная функция h(x) = g(f(x)) также имеет
производную в точке x0.
6) Теорема
Ро́лля (теорема
о нуле производной)
утверждает, что Если вещественная
функция непрерывна на отрезке [a;b]
и дифференцируема на интервале (a;b),
принимает на концах этого интервала
одинаковые значения, то на этом интервале
найдётся хотя бы одна точка, в которой
производная функции равна нулю.
Геометрический
смысл
Теорема
утверждает, что если ординаты обоих
концов гладкой кривой равны, то на кривой
найдется точка, в которой касательная
к кривой параллельна оси абсцисс.
Следствие
Если
непрерывная функция обращается в ноль
в n различных
точках, то ее производная обращается в
ноль по крайней мере в n −
1 различных точках[1],
причем эти нули производной лежат в
выпуклой оболочке нулей исходной
функции. Это следствие легко проверяется
для случая действительных корней, однако
имеет место и в комплексном случае.
Теорема
Лагранжа
Пусть
функция f(x):
-
непрерывна
на отрезке [a, b]; -
дифференцируема
в интервале (a, b).
Тогда
существует точка с О (a,b)такая,
что
|
f(b) |
(1) |
Формула
(1) называется формулой
Лагранжа,
или формулой
конечных приращений
7) Определение монотонной функции. Достаточное условие монотонности функции на промежутке .
Моното́нная
фу́нкция — это функция, приращение которой
не меняет знака, то есть либо всегда
неотрицательное, либо всегда
неположительное. Если в дополнение
приращение не равно нулю, то функция
называется стро́го моното́нной.
Монотонная функция — это функция,
меняющаяся в одном и том же направлении.
Функция
возрастает, если большему значению
аргумента соответствует большее значение
функции. Функция убывает, если большему
значению аргумента соответствует
меньшее значение функции.
Достаточное
условие.
Если
функция f(x) дифференцируема на (a,b) и f/(x)≥0 (f/(x)≤0) на (a,b),
то f(x) не
убывает (не возрастает)
на (a,b).
Доказательство
Рассмотрим
случай когда f/(x)≥0.
Рассмотрим две точки x1,x2∈(a,b) и
применим формулу Лагранжа.
На[x1,x2] функция f(x) удовлетворяет
всем условиям этой теоремы. Следует,
чтоx1<x2:
f(x2)−f(x1)=f/(c)(x2−x1), где c∈(x1,x2) и
правая часть больше нуля,
значит f(x2)−f(x1)≥0 илиf(x2)≥f(x1) при x2>x1,
функция не убывает.
Теорема
доказана.
 Экстремум функции
Экстремум функции
Экстре́мум в
математике
— максимальное или минимальное значение функции на
заданном множестве.
Точка, в которой достигается экстремум,
называется точкой
экстремума.
Соответственно, если достигается минимум
— точка экстремума называется точкой
минимума, а
если максимум — точкой
максимума.
В математическом
анализевыделяют
также понятие локальный
экстремум (соответственно минимум или
максимум).
Определения
Пусть
дана функция
и
—
внутренняя точка области определения f.
Тогда
-
x0
называется точкой локального максимума
функции f,
если существует проколотая
окрестность
такая,
что
-
x0
называется точкой локального минимума
функции f,
если существует проколотая
окрестность
такая,
что
Если
неравенства выше строгие, то x0
называется точкой строгого локального
максимума или минимума соответственно.
-
x0
называется точкой абсолютного
(глобального) максимума, если
-
x0
называется точкой абсолютного минимума,
если
Значение
функции f(x0)
называют (строгим) (локальным) максимумом
или минимумом в зависимости от ситуации.
Точки, являющиеся точками (локального)
максимума или минимума, называются
точками (локального) экстремума.
Необходимые
условия существования локальных
экстремумов
-
Лемма
Ферма.
Пусть функция
дифференцируема
в точке локального экстремума x0.
Тогда:
.
-
Если
в точке экстремума существует первая
частная производная (по какому-либо
аргументу), то она равна нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Монотонность функций
(blacktriangleright) Функция (f(x)) называется возрастающей на промежутке (X), если для любых (x_1, x_2in
X), таких что (x_1<x_2), выполнено (f(x_1)<f(x_2)).
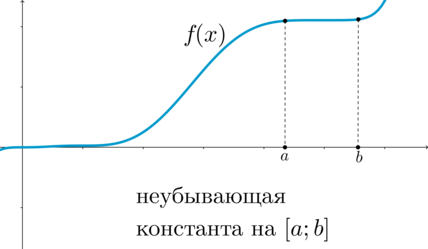
Функция называется неубывающей на промежутке (X), если для любых (x_1, x_2in X), таких что (x_1<x_2), выполнено (f(x_1)leq f(x_2)).
(blacktriangleright) Функция (f(x)) называется убывающей на промежутке (X), если для любых (x_1, x_2in X), таких что (x_1<x_2), выполнено (f(x_1)>f(x_2)).
Функция называется невозрастающей на промежутке (X), если для любых (x_1, x_2in X), таких что (x_1<x_2), выполнено (f(x_1)geq f(x_2)).
(blacktriangleright) Возрастающие и убывающие функции называют строго монотонными, а невозрастающие и неубывающие — просто монотонными.
(blacktriangleright) Основные свойства:
I. Если функция (f(x)) — строго монотонна на (X), то из равенства (x_1=x_2) ((x_1,x_2in X)) следует (f(x_1)=f(x_2)), и наоборот.
Пример: функция (f(x)=sqrt x) является строго возрастающей при всех (xin [0;+infty)), поэтому из равенства (sqrt x=sqrt 4) следует (x=4).
II. Если функция (f(x)) — строго монотонна на (X), то уравнение (f(x)=c), где (c) — некоторое число, всегда имеет не более одного решения на (X).
Пример: функция (f(x)=x^2) является строго убывающей при всех (xin
(-infty;0]), поэтому уравнение (x^2=9) имеет на этом промежутке не более одного решения, а точнее одно: (x=-3).
функция (f(x)=-dfrac 1{x+1}) является строго возрастающей при всех (xin (-1;+infty)), поэтому уравнение (-dfrac 1{x+1}=0) имеет на этом промежутке не более одного решения, а точнее ни одного, т.к. числитель левой части никогда не может быть равен нулю.
III. Если функция (f(x)) — неубывает (невозрастает) и непрерывна на отрезке ([a;b]), причем на концах отрезка она принимает значения (f(a)=A, f(b)=B), то при (Cin [A;B]) ((Cin
[B;A])) уравнение (f(x)=C) всегда имеет хотя бы одно решение.
Пример: функция (f(x)=x^3) является строго возрастающей (то есть строго монотонной) и непрерывной при всех (xinmathbb{R}), поэтому при любом (Cin (-infty;+infty)) уравнение (x^3=C) имеет ровно одно решение: (x=sqrt[3]{C}).
Задание
1
#3153
Уровень задания: Легче ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [27x^6+(a-x)^3+3x^2=x-a]
имеет ровно два корня.
Перепишем уравнение в виде: [(3x^2)^3+3x^2=(x-a)^3+(x-a)] Рассмотрим функцию (f(t)=t^3+t). Тогда уравнение перепишется в виде: [f(3x^2)=f(x-a)] Исследуем функцию (f(t)). [f'(t)=3t^2+1>0] Следовательно, функция (f(t)) возрастает при всех (t). Значит, каждому значению функции (f(t)) соответствует ровно одно значение аргумента (t). Следовательно, для того, чтобы уравнение имело корни, нужно: [3x^2=x-a quadLeftrightarrowquad 3x^2-x+a=0] Чтобы полученное уравнение имело два корня, нужно, чтобы его дискриминант был положительным: [D=1-12a>0 quadRightarrowquad a<dfrac1{12}]
Ответ:
(left(-infty;dfrac1{12}right))
Задание
2
#2653
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при которых уравнение [7^{ax^2-2x}-7^{x^2-1}=sqrt[7]{2x-ax^2}-sqrt[7]{1-x^2}]
имеет два корня.
(Задача от подписчиков.)
Сделаем замену: (ax^2-2x=t), (x^2-1=u). Тогда уравнение примет вид: [7^t-7^u=sqrt[7]{-t}-sqrt[7]{-u} quadLeftrightarrowquad 7^t+sqrt[7]t=7^u+sqrt[7]u] Рассмотрим функцию (f(w)=7^w+sqrt[7]w). Тогда наше уравнение примет вид: [f(t)=f(u).]
Найдем производную [f'(w)=7^wln7+dfrac1{7cdot sqrt[7]{w^6}}.] Заметим, что при всех (wne 0) производная (f'(w)>0), т.к. (7^w>0), (w^6>0). Заметим также, что сама функция (f(w)) определена при всех (w). Т.к. к тому же (f(w)) непрерывна, то мы можем сделать вывод, что (f(w)) возрастает на всем (mathbb{R}).
Значит, равенство (f(t)=f(u)) возможно тогда и только тогда, когда (t=u). Вернемся к изначальным переменным и решим полученное уравнение:
[ax^2-2x=x^2-1quadLeftrightarrowquad (a-1)x^2-2x+1=0] Для того, чтобы данное уравнение имело два корня, оно должно быть квадратным и его дискриминант должен быть положительным:
[begin{cases} a-1ne 0\
4-4(a-1)>0end{cases} quadLeftrightarrowquad
begin{cases}ane1\a<2end{cases}]
Ответ:
((-infty;1)cup(1;2))
Задание
3
#3921
Уровень задания: Равен ЕГЭ
Найдите все положительные значения параметра (a), при которых уравнение
[5((ax-2)^3-(x^2-2)^3+3e^{ax}-3e^{x^2})=\
=6e^{x^2}cdot sin{2x^2} — 6e^{ax}cdot sin{2ax} +
3e^{x^2}cdot cos{2x^2} — 3e^{ax}cdot cos{2ax}]
имеет как минимум (2) решения.
Перенесем все слагаемые, содержащие (ax), влево, а содержащие (x^2) – вправо, и рассмотрим функцию
[f(t)=5(t-2)^3+15e^t+6e^tcdot sin{2t} +3e^tcdot cos{2t}]
Тогда исходное уравнение примет вид:
[f(ax)=f(x^2)]
Найдем производную:
[f'(t)=15(t-2)^2+15e^tcdot (1+cos{2t})]
Т.к. ((t-2)^2 geqslant 0, e^t>0, 1+cos{2t} geqslant 0), то (f'(t)geqslant 0) при любых (tin mathbb{R}).
Причем (f'(t)=0), если ((t-2)^2=0) и (1+cos{2t}=0) одновременно, что не выполняется ни при каких (t). Следовательно, (f'(t)> 0) при любых (tin mathbb{R}).
Таким образом, функция (f(t)) строго возрастает при всех (tin
mathbb{R}).
Значит, уравнение (f(ax)=f(x^2)) равносильно уравнению (ax=x^2).
Уравнение (x^2-ax=0) при (a=0) имеет один корень (x=0), а при (ane 0) имеет два различных корня (x_1=0) и (x_2=a).
Нам нужно найти значения (a), при которых уравнение будет иметь не менее двух корней, учитывая также то, что (a>0).
Следовательно, ответ: (ain (0;+infty)).
Ответ:
((0;+infty)).
Задание
4
#1232
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [2^{ax-sqrt{x+1}}cdot
log_{frac{1}{3}}{sqrt{ax+2}}+log_9{(sqrt{x+1}+2)}=0]
имеет единственное решение.
Домножим правую и левую части уравнения на (2^{sqrt{x+1}}) (т.к. (2^{sqrt{x+1}}>0)) и перепишем уравнение в виде: [2^{ax}cdot log_{frac{1}{9}}{(ax+2)}=2^{sqrt{x+1}}cdot
log_{frac{1}{9}}{(sqrt{x+1}+2)}]
Рассмотрим функцию (y=2^tcdot log_{frac{1}{9}}{(t+2)}) при (tgeqslant 0) (т.к. (sqrt{x+1}geqslant 0)).
Производная (y’=left( -2^tcdot
log_9{(t+2)}right)’=-dfrac{2^t}{ln9}cdot left( ln 2cdot
ln{(t+2)}+dfrac{1}{t+2}right)).
Т.к. (2^t>0, dfrac{1}{t+2}>0, ln{(t+2)}>0) при всех (tgeqslant 0), то (y'<0) при всех (tgeqslant 0).
Следовательно, при (tgeqslant 0) функция (y) монотонно убывает.
Уравнение можно рассматривать в виде (y(t)=y(z)), где (z=ax,
t=sqrt{x+1}). Из монотонности функции следует, что равенство возможно только в том случае, если (t=z).
Значит, уравнение равносильно уравнению: (ax=sqrt{x+1}), которое в свою очередь равносильно системе: [begin{cases}
a^2x^2-x-1=0\
ax geqslant 0
end{cases}]
При (a=0) система имеет одно решение (x=-1), которое удовлетворяет условию (axgeqslant 0).
Рассмотрим случай (ane 0). Дискриминант первого уравнения системы (D=1+4a^2>0) при всех (a). Следовательно, уравнение всегда имеет два корня (x_1) и (x_2), причем они разных знаков (т.к. по теореме Виета (x_1cdot x_2=-dfrac{1}{a^2}<0)).
Это значит, что при (a<0) условию (axgeqslant 0) подходит отрицательный корень, при (a>0) условию подходит положительный корень. Следовательно, система всегда имеет единственное решение.
Значит, (ain mathbb{R}).
Ответ:
(ain mathbb{R}).
Задание
5
#1234
Уровень задания: Равен ЕГЭ
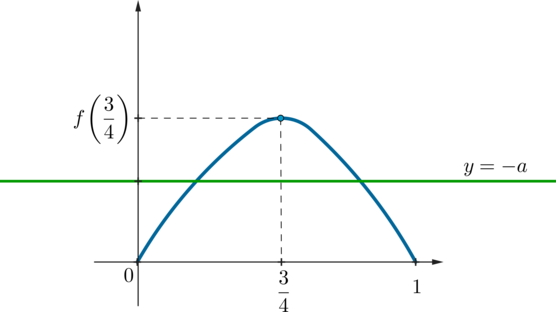
Найдите все значения параметра (a), при каждом из которых уравнение [2x^3-3x(ax+x-a^2-1)-3a-a^3=0]
имеет хотя бы один корень из отрезка ([-1;0]).
Рассмотрим функцию (f(x)=2x^3-3x(ax+x-a^2-1)-3a-a^3) при некотором фиксированном (a). Найдем ее производную: (f'(x)=6x^2-6ax-6x+3a^2+3=3(x^2-2ax+a^2+x^2-2x+1)=3((x-a)^2+(x-1)^2)).
Заметим, что (f'(x)geqslant 0) при всех значениях (x) и (a), причем равна (0) только при (x=a=1). Но при (a=1):
(f'(x)=6(x-1)^2 Rightarrow f(x)=2(x-1)^3 Rightarrow) уравнение (2(x-1)^3=0) имеет единственный корень (x=1), не удовлетворяющий условию. Следовательно, (a) не может быть равно (1).
Значит, при всех (ane 1) функция (f(x)) является строго возрастающей, следовательно, уравнение (f(x)=0) может иметь не более одного корня. Учитывая свойства кубической функции, график (f(x)) при некотором фиксированном (a) будет выглядеть следующим образом:
Значит, для того, чтобы уравнение имело корень из отрезка ([-1;0]), необходимо: [begin{cases}
f(0)geqslant 0\
f(-1)leqslant 0
end{cases} Rightarrow
begin{cases}
a(a^2+3)leqslant 0\
(a+2)(a^2+a+4)geqslant 0
end{cases} Rightarrow
begin{cases}
aleqslant 0\
ageqslant -2
end{cases} Rightarrow -2leqslant aleqslant 0]
Таким образом, (ain [-2;0]).
Ответ:
(ain [-2;0]).
Задание
6
#13005
Уровень задания: Легче ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [(sin^2x-5sin x-2a(sin x-3)+6)cdot (sqrt2a+8xsqrt{2x-2x^2})=0]
имеет корни.
(Задача от подписчиков)
ОДЗ уравнения: (2x-2x^2geqslant 0 quadLeftrightarrowquad xin
[0;1]). Следовательно, для того, чтобы уравнение имело корни, нужно, чтобы хотя бы одно из уравнений [sin^2x-5sin x-2a(sin x-3)+6=0 quad {small{text{или}}}quad
sqrt2a+8xsqrt{2x-2x^2}=0] имело решения на ОДЗ.
1) Рассмотрим первое уравнение [sin^2x-5sin x-2a(sin x-3)+6=0 quadLeftrightarrowquad
left[begin{gathered}begin{aligned}
&sin x=2a+2\
&sin x=3\
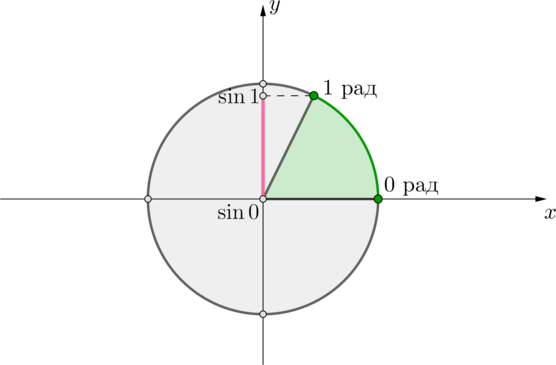
end{aligned} end{gathered}right. quadLeftrightarrowquad sin x=2a+2] Данное уравнение должно иметь корни на ([0;1]). Рассмотрим окружность:
Таким образом, мы видим, что для любых (2a+2in [sin 0;sin 1]) уравнение будет иметь одно решение, а для всех остальных – не будет иметь решений. Следовательно, при (ain left[-1;-1+0,5sin
1right]) уравнение имеет решения.
2) Рассмотрим второе уравнение [sqrt2a+8xsqrt{2x-2x^2}=0 quadLeftrightarrowquad 8xsqrt{x-x^2}=-a]
Рассмотрим функцию (f(x)=8xsqrt{x-x^2}). Найдем ее производную: [f'(x)=-4cdot dfrac{x(4x-3)}{sqrt{x-x^2}}] На ОДЗ производная имеет один ноль: (x=frac34), который к тому же является точкой максимума функции (f(x)).
Заметим, что (f(0)=f(1)=0). Значит, схематично график (f(x)) выглядит так:
Следовательно, для того, чтобы уравнение имело решения, нужно, чтобы график (f(x)) пересекался с прямой (y=-a) (на рисунке изображен один из подходящих вариантов). То есть нужно, чтобы [0leqslant -aleqslant fleft(dfrac34right) quadRightarrowquad
-dfrac{3sqrt3}2leqslant aleqslant 0]
3) Таким образом, изначальное уравнение будет иметь решения при (ain left[-1;-1+0,5sin 1right]) или (ain
left[-dfrac{3sqrt3}2;0right]). Объединяя эти решения, получим [ain left[-dfrac{3sqrt3}2;0right].]
Ответ:
(ain left[-dfrac{3sqrt3}2;0right])
Задание
7
#2704
Уровень задания: Равен ЕГЭ
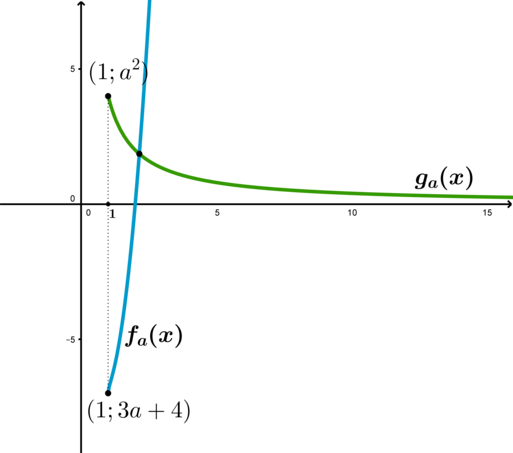
Найдите все значения параметра (a), при каждом из которых уравнение [sqrt{x-1}+5x^2-9x+3a+8=dfrac{a^2}{x}]
имеет ровно одно решение.
Рассмотрим семейства функций (f_a(x)=sqrt{x-1}+5x^2-9x+3a+8,
g_a(x)=dfrac{a^2}{x}).
ОДЗ уравнения: (xgeqslant 1). При этих (x):
Функция (y_1=sqrt{x-1}) является строго возрастающей. Графиком функции (y_2=5x^2-9x) является парабола, вершина которой находится в точке (x=dfrac{9}{10}). Следовательно, при всех (xgeqslant 1) функция (y_2) также строго возрастает (правая ветвь параболы). Т.к. сумма строго возрастающих функций есть строго возрастающая, то (f_a(x)) – строго возрастает (константа (3a+8) не влияет на монотонность функции).
Функция (g_a(x)=dfrac{a^2}{x}) при всех (xgeqslant 1) представляет собой часть правой ветви гиперболы и является строго убывающей.
Решить уравнение (f_a(x)=g_a(x)) — значит найти точки пересечения функций (f) и (g). Из их противоположной монотонности следует, что уравнение может иметь не более одного корня.
При (xgeqslant 1) (f_a(x)geqslant 3a+4,
0<g_a(x)leqslant a^2). Следовательно, уравнение будет иметь единственное решение в том случае, если:
[3a+4leqslant a^2 Rightarrow ain (-infty;-1]cup[4;+infty)]
Ответ:
(ain (-infty;-1]cup[4;+infty)).
Подготовка к Единому государственному экзамену по математике зачастую вызывает особые затруднения у выпускников. Есть множество сложных заданий, которым уделяется недостаточно внимания в общеобразовательной программе. В их числе нахождение интервалов монотонности функций и точек экстремума. Как показывает практика последних лет, многие выпускники сталкиваются с проблемами в решении подобных заданий. Поэтому стоит сделать акцент на их повторении, чтобы легко справляться даже с задачами повышенного уровня сложности. В этом вам поможет наш онлайн-сервис.
Подготовка к экзаменационному испытанию вместе со «Школково» — залог вашего успеха!
Наш образовательный портал позволит вам быстро и эффективно подготовиться к предстоящему итоговому тестированию по математике. Наши преподаватели собрали, систематизировали и оформили информацию по тематике в максимально простой и понятной форме. Поэтому ученики смогут быстро воспринимать материалы. Благодаря особому методу они уже через несколько дней будут решать даже те задания, которые казались невыполнимыми.
Начните с повторения правил и формул, которые могут понадобиться при исследовании монотонности функций. Для этого перейдите в раздел «Теоретическая справка». Вы вспомните виды и свойства функций, как определить знак производной, найти критические точки и многое другое. В каталогах представлены как типовые примеры по тематике, так и задания повышенного уровня сложности, которые могут встретиться в ЕГЭ. Их список постоянно обновляется и дополняется, поэтому выпускники будут ежедневно получать новые задания без повторений. Дети научатся находить количество значений необходимых параметров, работать с различными видами тригонометрических функций, а также справляться с уравнениями, в которых встречаются корни различной степени и логарифмы.
Если у школьника возникнут сложности с решением примера, он может добавить задание в «Избранное» и вернуться к нему позже.
Для того чтобы занятия проходили максимально результативно, советуем начать с самых простых заданий, где нужно указать промежутки монотонности функций y=f(x), и постепенно переходить к более трудным. Так ученики смогут выявить свои самые слабые стороны и сделать упор на решении конкретных типов упражнений.
Чтобы получить большие результаты, рекомендуем обращаться к нашему порталу ежедневно. Начните подготовку к итоговому тестированию уже сегодня вместе с онлайн-сервисом «Школково»!
Обучающие материалы доступны всем желающим подтянуть знания по математике. Вы можете сохранить результаты и отслеживать свой прогресс. Для этого зарегистрируйтесь в системе на нашем официальном сайте shkolkovo.net.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Монотонность функции. Возрастание и убывание
Возрастающая и убывающая функции в промежутке
ОПРЕДЕЛЕНИЕ
Функция называется возрастающей в промежутке , если большому значению аргумента соответствует большее значение функции, то есть для любой пары
таких, что
справедливо неравенство
ОПРЕДЕЛЕНИЕ
Функция называется убывающей в промежутке , если большому значению аргумента соответствует меньшее значение функции, то есть для любой пары
таких что
справедливо
Монотонная функция
ОПРЕДЕЛЕНИЕ
Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает.
Достаточное условие монотонности функции.Пусть функция определена и дифференцируема в промежутке
. Для того чтобы функция была возрастающей в промежутке
, достаточно, чтобы
для всех
Для убывания функции достаточно, чтобы для всех
Для исследования функции на монотонность необходимо:
- найти её производную
;
- найти критические точки функции как решения уравнения
;
- определить знак производной на каждом из промежутков, на которые критические точки разбивают область определения функции;
- согласно достаточному условию монотонности функции определить промежутки возрастания и убывания.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Нужна помощь с
решением задач?
Более 500 авторов онлайн и готовы помочь тебе прямо сейчас! Цена от 20 рублей за задачу. Сейчас у нас проходит акция, мы дарим 100 руб
на первый заказ.












 Экстремум функции
Экстремум функции