Как найти мощность если ток переменный - Исправление недочетов и поиск решений вместе с Examum.ru

Исследуем и рассчитываем мощность в цепи переменного тока

Содержание

1 Виды тока
2 Зачем нужно знать мощность электрооборудования
3 Виды мощности
4 Как измерить косинус «фи»
5 Как узнать мощность
6 Видео по теме

В процессе эксплуатации электрооборудования важную роль играет соответствие требуемой мощности и возможностей сети электропитания. Чтобы выполнить предварительные расчёты, необходимо понимать, какова природа электрической мощности и чем определяется её величина.

Виды тока

Техника может работать с использованием постоянного или переменного электрического тока. В первом случае сила тока на протяжении эксплуатации не меняется. Во втором она периодически меняется по абсолютной величине и знаку.

Наиболее часто переменный ток изменяется по синусоидальному закону, однако в некоторых случаях импульсы могут иметь другую, например, прямоугольную форму. В бытовых и производственных условиях часто для питания электроприборов требуется наличие однофазного или трехфазного переменного тока.

На представленном выше графике сила тока для активной мощности обозначена красным цветом. Для реактивной использованы обозначения с индексами L и C. На этом графике показан сдвиг фаз. Здесь видно, что ёмкостный ток отстаёт, а индуктивный опережает активный. При проведении расчетов для выбора автотрансформатора или других электроприборов важно правильно учитывать имеющиеся смещения.

Зачем нужно знать мощность электрооборудования

Каждый подключенный электроприбор для обеспечения своей работы будет потреблять часть мощности электросети. Если их работает одновременно несколько, то мощности складываются. Важно при расчете потребляемой электроэнергии учитывать:

Мощность в цепи переменного тока или постоянного, которая обеспечивается поставщиком.
Параметры защитных приборов, с помощью которых осуществляется регулирование рабочих характеристик оборудования.
Конструкцию системы проводов и удлинителей.
Наличие автотрансформатора или аналогичных устройств.

Если подаваемая мощность недостаточна, это способствует появлению перебоев в поставке электроэнергии. Защитные приборы должны быть настроены таким образом, чтобы при возникновении аварийной ситуации прерывать поступление электричества. Для этого в них должны быть заложены данные о том, какая величина мощности в цепях переменного или постоянного тока считается нормальной, а какая свидетельствует о возникновении проблемной ситуации.

Провода, удлинители и другие элементы электропроводки рассчитаны на определённые предельные значения. При их превышении они будут плавиться или перегорать. Перед подключением автотрансформатора или других электроприборов нужно предварительно узнать, соответствует ли требуемая им мощность имеющимся возможностям электросети.

Виды мощности

Полная мощность на участке цепи определяется как работа, выполняемая в течение единицы времени. Её также можно рассматривать как отношение используемой энергии к продолжительности интервала времени, на протяжении которого это происходит.

При работе электрического прибора часть мощность частично тратится на получение полезного эффекта. Такую мощность называют активной. Электрическая энергия при этом превращается в другой вид. Например, речь может идти о том, что она выделится в виде света или тепла.

Переменный ток при наличии в схеме ёмкости и индуктивности создаёт реактивную мощность. Она не расходуется, а преобразуется из одной формы в другую. Реактивная мощность, выделяемая в конкретной цепи переменного тока, считается паразитной. Если ее величина незначительная, то вся используемая энергия является активной.

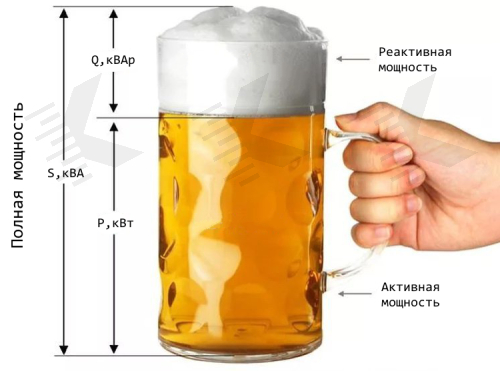
Реактивная и активная мощности — это составляющие полной электрической мощности. Сложение осуществляется по векторным правилам. Чтобы рассчитать полную мощность, следует применить теорему Пифагора.

На приведённом рисунке длина гипотенузы выражает полную мощность, горизонтально расположенный катет — активную составляющую, а вертикально — реактивную. Как известно, квадрат гипотенузы — это сумма квадратов катетов.

В приведённой формуле используются следующие обозначения:

С левой стороны знака равенства указана полная мощность.
В качестве P рассматривается активная мощность.
С помощью Q обозначена реактивная мощность.

Соотношение активной и реактивной мощности выражается через косинус угла «фи». Этот угол представляет собой фазовый сдвиг между электротоком и электронапряжением. Чтобы оценить реальную мощность работы оборудования, косинус «фи» часто указывают в технической документации электроприбора, как коэффициент мощности. Он полезен для определения особенностей использования автотрансформатора или других приборов.

Единицей измерения активной мощности является ватт. Для реактивной применяется вольт-ампер реактивный (вар). Полная мощность измеряется вольт-амперами.

Используется еще и такое понятие, как мгновенная мощность, которая постоянно меняется. Например, она может иметь нулевое значение в тех точках, где сила электротока также равняется нулю. На практике мгновенная мощность используется редко, но применяется её среднее значение за период.

Как измерить косинус «фи»

Обычно эта информация содержится в технической документации прибора. Если она не указана, то ее измеряют с помощью специального прибора — фазометра.

Чем больше рассматриваемая величина, тем выше будет эффективность электрооборудования. Если косинус небольшой, то выгодно улучшить ситуацию, используя компенсацию реактивной мощности переменного тока. Чтобы понять принцип работы, следует вспомнить, что реактивная мощность возникает из-за наличия ёмкости и индуктивности в электроцепи.

Для компенсации используют регулируемый узел, действующий противоположно реактивной составляющей электромощности. Например, регулировка может осуществляться при помощи дросселя с высокой индуктивностью. Его подключают последовательно с нагрузкой.

Как узнать мощность

Один из наиболее простых способов — измерение мощности с помощью ваттметра. Существуют различные виды таких устройств. Поскольку в быту не требуется особенно высокой точности, можно использовать довольно простые приборы.

Также можно провести вычисления, измерив напряжение, силу тока и сопротивление. Расчёт мощности осуществляется с помощью двух из этих трёх величин.

При использовании постоянного тока определение активной мощности выполняется с помощью следующего выражения:

Если нужно определить мощность однофазного переменного тока, используется формула:

Если ток трёхфазный, тогда мощность можно рассчитать по формуле:

Указанная выше формула мощности применяется при симметричном трёхфазном распределении. Если оно является асимметричным, тогда для каждой фазы мощность переменного тока вычисляется отдельно, а затем найденные значения складываются. Средняя мощность для переменного тока определяется интегральным исчислением.

Для определения реактивной мощности используют формулу:

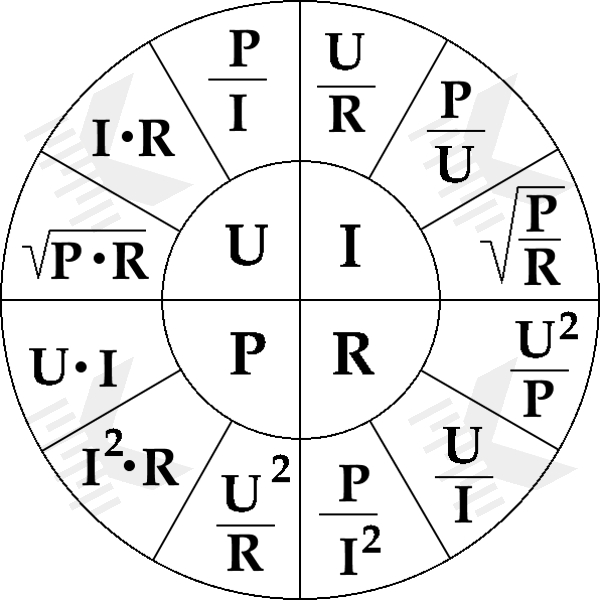
Знание электрической мощности не только полезно само по себе, но оно помогает вычислить различные характеристики используемого электрооборудования. Обычно значение мощности и косинуса «фи» можно получить из технической документации. Например, зная напряжение, можно вычислить силу электрического тока, чтобы учесть её при подключении и обеспечении безопасности использования оборудования.

На представленной выше схеме во внутреннем круге указаны величины, которые требуется определить. Вдоль окружности приведены формулы, которыми следует воспользоваться для вычисления.

Сказанное можно пояснить на следующем примере. Допустим, нужно определиться с мощностью. В этом случае следует обратить внимание на левый нижний сектор чертежа. Зная две из трёх величин, через которые выражается мощность (напряжение, силу тока и сопротивление), можно подобрать подходящую формулу для вычисления.

Если требуется найти, чему равна сила тока, то это выполняется аналогичным образом. Разница состоит в том, что теперь следует работать с правым верхним сектором. Здесь потребуется знать две из следующих трёх величин: мощность, сопротивление и напряжение. Нужно подобрать подходящую формулу и выполнить соответствующие вычисления.

Видео по теме

Источник

Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.

Понятие электрической мощности и способы ее расчета

С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования. Это и обуславливает столкновение носителей заряда, электроэнергия переходит в другие виды и выделяется в виде излучения, тепла или механической энергии в окружающее пространство. Преобразование одного вида в другой и есть потребляемая мощность прибора или участка электрической цепи.

В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.

Через напряжение и ток

Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I

Где:

P – активная мощность;
U – напряжение приложенное к участку цепи;
I — сила тока, протекающего через соответствующий участок.

Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи. Чтобы найти мощность вам нужно выполнить произведение силы тока на напряжение. Обе величины должны находиться в одних единицах измерения – Вольты и Амперы, тогда результат также получится в Ваттах. Можно использовать и другие способы кВ, кА, мВ, мА, мкВ, мкА и т.д., но и параметр мощности пропорционально изменит свой десятичный показатель.

Через напряжение и сопротивление

Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома для участка цепи, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:

I = U/R

Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:

P = U*(U/R)=U²/R

Где,

P – величина нагрузки;
U – приложенная разность потенциалов;
R – сопротивление нагрузки.

Через ток и сопротивление

Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.

Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:

U=I*R

после того как выражение подставить в формулу мощности, получим:

P = (I*R)*I =I²*R

Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.

Полная мощность в цепи переменного тока

Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:

Где,

S – полная мощность
P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.

Также составляющие вычисляются через тригонометрические функции, так:

P = U*I*cosφ

Q = U*I*sinφ

что активно используется в расчете электрических машин.

Рис. 1. Треугольник мощностей

Пример расчета полной мощности для электродвигателя

Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.

Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:

S = 3*U_ф*I_ф

В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:

Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.

Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.

Рис. 2. Шильд электродвигателя

Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:

полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
напряжение, при соединении обмоток треугольником составит 220 В;
сила тока при том же способе соединения – 13,3 А.

С таким перечнем характеристик можно воспользоваться несколькими способами:

S = 1,732*220*13,3 = 5067 Вт

Чтобы найти искомую величину, сначала определяем активную составляющую:

P = P_{полезная} / КПД = 3000/0.8 = 3750 Вт

Далее полную по способу деления активной на коэффициент cos φ:

S = P/cos φ = 3750/0.74 = 5067 Вт

Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.

Примеры задач

Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.

Рис. 3. Последовательная расчетная цепь

Как видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:

P = U²/R = 81 / (10+20+30) = 1.35 Вт

Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:

Рис. 4. Параллельная схема подключения

Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:

R_общ = (R₁*R₂) / (R₁+R₂) = (10*15) / (10+15) = 6 Ом

Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:

P = I²*R = 25*6 = 150 Вт

Видео по теме

Источник

С помощью калькулятора мощности вы можете самостоятельно выполнить расчет мощности по току и напряжению для однофазных (220 В) и трехфазных сетей (380 В). Программа также рассчитывает мощность через сопротивление и напряжение, или через ток и сопротивление согласно закону Ома. Значение cos φ принимается согласно указаниям технического паспорта прибора, усредненным значениям таблиц ниже или рассчитываются самостоятельно по формулам. Без необходимости рекомендуем не изменять коэффициент и оставлять равным 0.95. Чтобы получить результат расчета, нажмите кнопку «Рассчитать».

Смежные нормативные документы:

СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
СП 76.13330.2016 «Электротехнические устройства»
ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
ГОСТ Р 50571.1-93 «Электроустановки зданий»

Формулы расчета мощности

Мощность — это физическая величина, равная отношению количества работы ко времени совершения этой работы.
Мощность электрического тока (P) — это величина, характеризующая скорость преобразования электрической энергии в другие виды энергии. Международная единица измерения — Ватт (Вт/W).

— Мощность по току и напряжению (постоянный ток): P = I × U
— Мощность по току и напряжению (переменный ток однофазный): P = I × U × cos φ
— Мощность по току и напряжению (переменный ток трехфазный): P = I × U × cos φ × √3
— Мощность по току и сопротивлению: P = I² × R
— Мощность по напряжению и сопротивлению: P = U² / R

I – сила тока, А;
U – напряжение, В;
R – сопротивление, Ом;
cos φ – коэффициент мощности.

Расчет косинуса фи (cos φ)

φ – угол сдвига между фазой тока и напряжения, причем если последний опережает ток сдвиг считается положительным, если отстает, то отрицательным.

cos φ – безразмерная величина, которая равна отношению активной мощности к полной и показывает насколько эффективно используется энергия.

Формула расчета косинуса фи: cos φ = S / P

S – полная мощность, ВА (Вольт-ампер);
P – активная мощность, Вт.

Активная мощность (P) — реальная, полезная, настоящая мощность, эта нагрузка поглощает всю энергию и превращает ее в полезную работу, например, свет от лампочки. Сдвиг по фазе отсутствует.

Формула расчета активной мощности: P (Вт) = I × U × cos φ

Реактивная мощность (Q) — безваттная (бесполезная) мощность, которая характеризуется тем, что не участвует в работе, а передается обратно к источнику. Наличие реактивной составляющей считается вредной характеристикой цепи, поскольку главная цель существующего электроснабжения — это сокращение издержек, а не перекачивание ее туда и обратно. Такой эффект создают катушки и конденсаторы.

Формула расчета реактивной мощности: P (ВАР) = I × U × sin φ

Полная мощность электроприбора (S) — это суммарная величина, которая включает в себе как активную, так и реактивную составляющие мощности.

Формула расчета полной мощности: S (ВА) = I × U или S = √( P² + Q²)

Косинус фи для различных потребителей – таблица

Наименование электроприбора	cos φ
Бойлер	1
Болгарка	0.8
Вакуумный насос	0.85
Индукционные печи	0.85
Компрессор	0.7
Компьютер	0.95
Кофеварка	1
Лампы газоразрядные	0.4-0.6
Лампы люминисцентные	0.95
Лампы накаливания	1
Обогреватель	1
Перфоратор	0.85
Пылесос	0.9
СВЧ-печь	1
Стиральная машина	0.9
Телевизор	1
Утюг	1
Фен	1
Холодильник	0.95
Электродрель	0.85
Электромоторы	0.7-0.8
Электроплита	1
Электросварка дуговая	0.3-0.6
Электрочайник	1

Источник

Мощность переменного тока

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Мощность тока через резистор
Мощность тока через конденсатор
Мощность тока через катушку
Мощность тока на произвольном участке

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

$P= I_0 frac{displaystyle dA}{displaystyle dt vphantom{1^a}} = UI.$ (1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: P > 0 . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: P < 0 . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

к оглавлению ▴

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение P_0 нашей мощности связано с амплитудами тока и напряжения привычными формулами:

$P_0=U_0 I_0 = I_0^2 R = frac{displaystyle U_0^2}{displaystyle R vphantom{1^a}}.$

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и P_0 . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение P_0/2 ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно 1/2

Итак, для среднего значения bar{P} мощности тока на резисторе имеем:

$bar{P}= frac{displaystyle P_0}{displaystyle 2 vphantom{1^a}} = frac{displaystyle U_0 I_0}{displaystyle 2 vphantom{1^a}} = frac{displaystyle I_0^2 R}{displaystyle 2 vphantom{1^a}} = frac{displaystyle U_0^2}{displaystyle 2R vphantom{1^a}}.$ (3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

$bar{U}= frac{displaystyle U_0}{displaystyle sqrt(2) vphantom{1^a}}, bar{I}= frac{displaystyle I_0}{displaystyle sqrt(2) vphantom{1^a}}.$ (4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

$bar{P}=bar{U} bar{I} = bar{I}^2 R = frac{displaystyle bar{U}^2}{displaystyle R vphantom{1^a}}.$

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые 220 вольт из розетки — это действующее значение напряжения бытовой электросети.

к оглавлению ▴

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

$I = I_0 sin left ( omega t + frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = I_0 cos omega t.$

Для мгновенной мощности получаем:

$P = UI = U_0 I_0 sin omega t cos omega t = frac{displaystyle 1}{displaystyle 2 vphantom{1^a}}U_0 I_0 sin2 omega t = P_0 sin2 omega t.$

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

к оглавлению ▴

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на pi/2 :

$I = I_0 sin left ( omega t - frac{displaystyle pi}{displaystyle 2 vphantom{1^a}} right ) = -I_0 cos omega t.$

Для мгновенной мощности получаем:

$P = UI = -U_0 I_0 sin omega t cos omega t = -frac{displaystyle 1}{displaystyle 2 vphantom{1^a}}U_0 I_0 sin2 omega t = -P_0 sin2 omega t.$

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

к оглавлению ▴

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз alpha . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

$sin x sin y = frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} (cos (x-y) - cos (x+y)).$

В результате получим:

$P = U_0 I_0 frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} ( cos alpha - cos (2 omega t - alpha)).$ (6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

$bar{P} = U_0 I_0 frac{displaystyle 1}{displaystyle 2 vphantom{1^a}} cos alpha.$ (7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Установка автоматических выключателей, выбор сечения провода, подбор нового электроприбора для домашних целей – все это требует знания и умения манипулировать основными характеристиками электрического тока. Напряжение, сила тока, мощность неразрывно связаны между собой, изменение одного оказывает влияние на остальные величины. Эту взаимосвязь, а также определение разных характеристик рассмотрим в этой статье.

Как узнать ток, зная мощность и напряжение?
Как узнать напряжение, зная силу тока?
Как рассчитать мощность, зная силу тока и напряжения?
Как определить потребляемую мощность цепи, имея тестер, который мерит сопротивление?
Формула расчета сечения провода и как определяется сечение провода

Как узнать ток, зная мощность и напряжение?

В металлах, из которых сделаны провода, находятся свободные электроны, участвующие в работе. На клеммах источника тока создается сила, заставляющая заряды перемещаться по проводнику. Эта сила называется электродвижущей (э. д. с.). В постоянных цепях электроны выходят из источника с одной клеммы и «втягиваются» другой. При движении электронов совершается какая-то работа, зависящая от напряжения и тока. Связь силы тока с мощностью и напряжением видна в формуле:

P = UI,

где P – мощность, Вт; U – напряжение, В; I – ток, А.

Что такое ток? Для наглядности возьмем несколько рек, вода в которых течет с одинаковой скоростью. Однако русло у всех разное: одни реки широкие, другие узкие, какие-то глубокие или мелкие. Понятно, что объем воды, проходящий через контрольную точку, у всех будет разным. Выходит, что чем глубже или шире река, тем большее воды проходит по ней.

То же самое относится к электронам – чем больше их проходит через точку на проводнике, тем больший ток мы имеем. В отличие от рек, которые в половодье могут разливаться, избыток носителей заряда не может выходить за пределы провода. Как рассчитать пропускную способность кабеля рассмотрим в последнем подзаголовке.

Сравним зависимость силы тока от мощности и напряжения. Для этого воспользуемся приведенной выше формулой.

Внимание! Эта формула предназначена для постоянного тока. Отличие от переменного напряжения будет рассмотрено в следующем подзаголовке.

Сначала все значения следует привести к единой системе. Если мощность выражена в киловаттах или милливаттах, их нужно перевести в ватты. В одном киловатте 1 000 ватт. В одном ватте содержится 1 000 милливатт. То же самое относится и к напряжению. Если переделать формулу в такой вид: I = , то можно рассчитать ток. Например, есть утюг мощностью 1,2 кВт, как узнать ток?

Вольтметром измеряем напряжение в розетке, если прибора нет, можно считать его равным 220 В. Киловатты утюга переводим в ватты, получаем 1 200 ватт. Эти значения вставляем в формулу:

Как узнать напряжение, зная силу тока?

Снова поговорим о постоянном напряжении. Напряжение – это сила, действующая на заряженные частицы, заставляющая их двигаться. Вернемся к реке. Даже если она будет широкой и глубокой, но вода в ней не будет двигаться, она не сможет совершать какую-то работу. Движение воды происходит из-за перепада уровней поверхности земли. Чем больше разница между уровнями дна на каком-то участке, тем быстрее будет поток, и тем большую работу может совершать вода.

Напряжение в каком-то смысле можно сравнить с таким перепадом: чем выше напряжение при одном и том же токе, тем большей мощностью обладает энергия, проходящая по проводнику. При постоянном напряжении электроны движутся всегда в одном направлении, но существуют более сложные схемы изменения напряжения или тока:

переменный;
периодический;
синусоидальный;
квазистационарный;
высокочастотный;
пульсирующий;
однонаправленный.

Эти разновидности часто сопутствуют друг другу. Так в домашней сети применяются сразу три разновидности: переменный, периодический, синусоидальный. Переменное напряжение указывает на противоположные знаки напряжения в течение одного периода. Происходит это следующим образом: напряжение от ноля поднимается до максимального положительного значения, затем опускается до ноля и опускается до максимального отрицательного значения. Поскольку такие изменения происходят за равный промежуток времени, их называют периодическими. Плавные переходы носят синусоидальный вид, что соответствует названию такого тока.

Переменное напряжение может быть:

однофазным;
двухфазным;
трехфазным.

В первом случае есть фазный и нулевой провод. При подключении нагрузки электроны движутся то в одном направлении, то в другом. Чтобы определить соотношение напряжения и мощности в переменном токе используют среднеквадратическое значение. Оно определяется по нагреванию нагрузки одного и того же номинала. Сначала пропускают постоянный ток одного напряжения в течение определенного времени и замеряют температуру нагрева испытуемого тела. Затем опытным путем подбирают такое переменное напряжение, при котором за то же время происходит такое же нагревание.

Для однофазного переменного тока оно будет меньше в от амплитудного значения. То есть в сети вольтметр показывает 220 В среднеквадратическое значение, а амплитудное будет составлять 311 В.

Пояснение! На переменное напряжение сильное влияние оказывает емкость и индуктивность, снижая полезную мощность, но в этой статье мы подробно это не будем разбирать.

Двухфазный ток может быть либо сдвинутым, как, например, взятые две фазы у трехфазной сети, либо противоположным. В последнем случае фазы работают таким образом, что максимальное положительное значение одной фазы, соответствует максимальному отрицательному значению другой.

Для создания вращающегося магнитного поля применяют трехфазную сеть. Обычно к ней подключают электродвигатели. Если обмотки соединены по схеме треугольника, то суммарная мощность каждой фазы будет равна линейной. При подключении по схеме звезда суммарная мощность будет в больше линейной. Схема подключения электродвигателя указана на его шильдике (табличке).

Определение напряжения при известном токе и мощности, осуществляется по той же формуле. Если определяется трехфазное напряжение, то следует учитывать схему подключения нагрузки и добавлять или нет коэффициент .

Как рассчитать мощность, зная силу тока и напряжения?

Разобравшись с током и напряжением, уже будет легче посчитать мощность, используя все ту же формулу. Однако для переменного тока различают несколько мощностей:

мгновенная;
активная;
реактивная;
полная.

Мгновенная мощность рассчитывается в момент измерения и может сильно отличаться от полной мощности. Активной называют полезную мощность, которая определяется по формуле:

Косинус фи в синусоидальном токе является коэффициентом мощности, выражается в процентах от 0 до 100 или цифрах от 0 до 1. Показывает сдвиг фаз между током и напряжением. Для трехфазной сети общая активная мощность складывается из отдельных фазных мощностей.

Реактивная мощность учитывает расход энергии на реактивную нагрузку (индуктивность, конденсатор, обмотка электродвигателя), которая снова возвращается к источнику. Для этого используется формула:

Полная мощность состоит из активной и реактивной, причем реактивная может иметь отрицательный или положительный знак.

Как определить потребляемую мощность цепи, имея тестер, который мерит сопротивление?

Кроме перечисленных формул, есть еще и другие, например, такие:

С их помощью можно узнать мощность, не имея данных о напряжении или токе. Стоит отметить, что сопротивление измеряется в Омах.

Осторожно! При измерении сопротивления цепи в ней не должно быть электричества.

Если сопротивление известно, тогда можно узнать, как рассчитать нагрузку по току. Для этого

где R – сопротивление нагрузки, P – мощность нагрузки, I – ток нагрузки. Однако нагрузки, содержащие емкость или индуктивность, таким способом нельзя рассчитать. Также не получится узнать мощность лампы накаливания, измерив сопротивление ее нити, потому что вольфрам при нагревании увеличивает свое сопротивление.

Формула расчета сечения провода и как определяется сечение провода

Раньше уже говорилось, что чрезмерный ток недопустим для проводов. Это связано с их перегревом. Поэтому каждый проводник способен пропускать через себя ограниченный ток. Почему провода греются? Любой материал в нормальных условиях имеет собственное сопротивление. Проходящий через него ток производит работу по нагреву металла. Этот нагрев допускается до определенной температуры, после чего начинается его плавление.

Рекомендуем прочитать: Принцип работы регулятора напряжения

Существуют специальные таблицы, помогающие подобрать сечение провода в зависимости от рабочего тока. Сечение – это площадь проволоки в разрезе. Как правило, такой разрез имеет вид круга. Чтобы найти сечение, необходимо найти площадь этого круга. Можно воспользоваться формулой:

где S – площадь круга или сечение в мм²; П – постоянное число равное 3,14159265; r – радиус круга. Для определения радиуса диаметр делят на два, затем подставляют в формулу.

Интересно! Многожильный и одножильный провод с одинаковым диаметром способны пропускать разную силу тока.

Мощность, напряжение, сила тока – это основные величины, зависящие друг от друга. Используя одну из приведенных формул, можно найти необходимую величину.

Понравилась статья? Расскажите друзьям:

Оцените статью, для нас это очень важно:

Проголосовавших: 5 чел.
Средний рейтинг: 5 из 5.

Источник