Как найти мощность множества истинности предиката - Исправление недочетов и поиск решений вместе с Examum.ru

Логика предикатов

Предикаты вслед за высказываниями являются следующим важным предметом, исследуемым математической логикой. Понятие предиката обобщает понятие высказывания, а теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний, для изучения закономерностей процессов умозаключения и логического следования, составляющих предмет математической логики. В настоящей главе рассматриваются основы теории предикатов.

Понятие предиката

В высказывании все четко: это — конкретное утверждение о конкретных объектах — истинное или ложное. Предикат — предложение, похожее на высказывание, но все же им не являющееся: о нем нельзя судить, истинно оно или ложно. Дадим точное определение.

Определение 18.1. Определенным на множествах M_1,M_2,ldots,M_n n-местным предикатом называется предложение, содержащее переменных x_1,x_2,ldots,x_n , превращающееся в высказывание при подстановке вместо этих переменных любых конкретных элементов из множеств M_1,M_2,ldots,M_n соответственно.

Для n-местного предиката будем использовать обозначение P(x_1,x_2,ldots,x_n) . Переменные называют предметными, а элементы множеств M_1,M_2,ldots,M_n , которые эти переменные пробегают, — конкретными предметами. Всякий n-местный предикат P(x_1,x_2,ldots,x_n) , определенный на множествах , представляет собой функцию п аргументов, заданную на указанных множествах и принимающую значения в множестве всех высказываний. Поэтому предикат называют также функцией-высказыванием.

Рассмотрим пример. Предложение «Река впадает в озеро Байкал» является одноместным предикатом, определенным над множеством всех названий рек. Подставив вместо предметной переменной название «Баргузин», получим высказывание «Река Баргузин впадает в озеро Байкал». Это высказывание истинно. Подставив вместо предметной переменной название «Днепр», получим ложное высказывание «Река Днепр впадает в озеро Байкал».

Другой пример. Предложение (выражение) « x^2+y^2 leqslant 9 » является двухместным предикатом, заданным над множествами mathbb{R},mathbb{R} . Множества, на которых задан двухместный предикат, совпадают (говорят, что «двухместный предикат задан на множестве $mathbb{R}^2$ «). Пара действительных чисел 2, 2 превращает данный предикат в истинное высказывание: « 2^2+2^2 leqslant 9 «, а пара чисел 2, 3 — в ложное: « 2^2+3^2 leqslant 9 «.

Отметим еще один подход к понятию предиката. Как отмечалось, предикат P(x_1,x_2,ldots,x_n) , определенный на множествах M_1,M_2,ldots,M_n , превращается в конкретное высказывание , если вместо предметных переменных подставить в него конкретные предметы (элементы a_1,a_2,ldots,a_n ) из множеств соответственно. Это высказывание может быть либо истинным, либо ложным, т. е. его логическое значение равно 1 или 0. Следовательно, данный предикат определяет функцию аргументов, заданную на множествах M_1,M_2,ldots,M_n принимающую значение в двухэлементном множестве {0;1} . Иногда эту функцию и называют предикатом.

Классификация предикатов

Определение 18.2. Предикат P(x_1,x_2,ldots,x_n) , заданный на множествах M_1,M_2,ldots,M_n , называется:

а) тождественно истинным, если при любой подстановке вместо переменных x_1,x_2,ldots,x_n любых конкретных предметов a_1,a_2,ldots,a_n из множеств M_1,M_2,ldots,M_n соответственно он превращается в истинное высказывание P(a_1,a_2,ldots,a_n) ;

б) тождественно ложным, если при любой подстановке вместо переменных x_1,x_2,ldots,x_n любых конкретных предметов из множеств M_1,M_2,ldots,M_n соответственно он превращается в ложное высказывание;

в) выполнимым (опровержимым), если существует по меньшей мере один набор конкретных предметов a_1,a_2,ldots,a_n из множеств M_1,M_2,ldots,M_n соответственно, при подстановке которых вместо соответствующих предметных переменных в предикат P(x_1,x_2,ldots,x_n) последний превратится в истинное (ложное) высказывание P(a_1,a_2,ldots,a_n) .

Приведем примеры предикатов.

Одноместный предикат «Город расположен на берегу реки Волги», определенный на множестве названий городов, является выполнимым, потому что существуют города, названия которых превращают данный предикат в истинное высказывание, или, иначе, удовлетворяют этому предикату (например, Ульяновск, Саратов и т. д.). Но данный предикат не будет тождественно истинным, потому что существуют города, названия которых превращают его в ложное высказывание, или, иначе, не удовлетворяют этому предикату (например, Прага, Якутск и т.д.). Этот же предикат являет собой пример опровержимого, но не тождественно ложного предиката (продумайте!).

В другом примере одноместный предикат « sin^2x+cos^2x=1 «, определенный на множестве действительных чисел, тождественно истинный. Наконец, двухместный предикат « x^2+y^2<0 «, заданный также на множестве действительных чисел, является тождественно ложным предикатом, потому что любая пара действительных чисел превращает его в ложное высказывание (не удовлетворяет ему).

Отметим некоторые достаточно очевидные закономерности взаимосвязей между предикатами различных типов (рекомендуется осмыслить их):

1) каждый тождественно истинный предикат является выполнимым, но обратное неверно;
2) каждый тождественно ложный предикат является опровержимым, но обратное неверно;
3) каждый не тождественно истинный предикат будет опровержимым, но, вообще говоря, не будет тождественно ложным;
4) каждый не тождественно ложный предикат будет выполнимым, но, вообще говоря, не будет тождественно истинным.

Множество истинности предиката

Определение 18.3. Множеством истинности предиката P(x_1,x_2,ldots,x_n) , заданного на множествах M_1,M_2,ldots,M_n , называется совокупность всех упорядоченных n-систем (a_1,a_2,ldots,a_n) , в которых a_1in M_1,a_2in M_2,ldots,a_nin M_n , таких, что данный предикат обращается в истинное высказывание P(a_1,a_2,ldots,a_n) при подстановке x_1=a_1,x_2=a_2,ldots,x_n=a_n . Это множество будем обозначать $P^{+}$ . Таким образом,

$P^{+}= bigl{(a_1,a_2,ldots,a_n)colon, lambda bigl(P(a_1,a_2, ldots, a_n)bigr)= 1bigr}.$

Множество $P^{+}$ истинности «-местного предиката P(a_1,a_2,ldots,a_n) представляет собой n-арное отношение между элементами множеств M_1,M_2,ldots,M_n . Если предикат P(x) — одноместный, заданный над множеством , то его множество истинности $P^{+}$ является подмножеством множества $Mcolon, P^{+}subseteq M$ .

Например, множеством истинности двухместного предиката «Точка принадлежит прямой «, заданного на множестве всех точек плоскости и на множестве всех прямых этой плоскости, является бинарное отношение принадлежности (инцидентности) между точками и прямыми плоскости. Другой пример. Множество истинности двухместного предиката S(x,y)colon~ x^2+y^2=9 , заданного на множестве $mathbb{R}^2$ , есть множество всех таких пар действительных чисел, которые являются координатами точек плоскости, образующими окружность с центром в начале координат и радиуса 3. Наконец, если A(x)colon « |a|>2 » — одноместный предикат над mathbb{R} , то $A^{+}= (-infty;-2)cup(2;+infty)$ , или $A^{+}= mathbb{R} setminus[-2;2]$ .

В терминах множества истинности легко выразить понятия, связанные с классификацией предикатов (определение 18.2). В самом деле, n-местный предикат P(x_1,x_2,ldots,x_n) , заданный на множествах M_1,M_2,ldots,M_n , будет:

а) тождественно истинным тогда и только тогда, когда $P^{+}=M_1times M_2times ldotstimes M_n$ ;
б) тождественно ложным тогда и только тогда, когда $P^{+}=varnothing$ ;
в) выполнимым тогда и только тогда, когда $P^{+}nevarnothing$ ;
г) опровержимым тогда и только тогда, когда $P^{+}ne M_1times M_2times ldotstimes M_n$ .

На языке множеств истинности еще более отчетливо проясняются закономерности взаимосвязей между предикатами различных типов, отмеченные в конце предыдущего пункта. Проанализируйте их еще раз.

Равносильность и следование предикатов

Определение 18.4. Два n-местных предиката P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n) , заданных над одними и теми же множествами M_1,M_2,ldots,M_n , называются равносильными, если набор предметов (элементов) a_1in M_1, a_2in M_2, ldots, a_nin M_n превращает первый предикат в истинное высказывание P(a_1,a_2,ldots,a_n) в том и только в том случае, когда этот набор предметов превращает второй предикат в истинное высказывание Q(a_1,a_2,ldots,a_n) .

Другими словами (на языке множеств истинности), предикаты P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n) равносильны тогда и только тогда, когда их множества истинности совпадают. $P^{+}=Q^{+}$ .

Утверждение о равносильности двух предикатов и символически будем записывать так: PLeftrightarrow Q . Отношение равносильности предикатов является отношением эквивалентности, так что совокупность всех n-местных предикатов, определенных на множествах M_1,M_2,ldots,M_n , распадается на непересекающиеся классы равносильных предикатов (все они определяют одну и ту же функцию, заданную на множествах и принимающую значения в двухэлементном множестве {0;1} ). Переход от предиката P_1 к равносильному ему предикату P_2 называется равносильным преобразованием первого. Это понятие очень важно для школьной математики, потому что изучаемые в ней уравнения и неравенства представляют собой частные виды предикатов. Решение уравнения и неравенства есть поиск их множеств истинности. При таком поиске мы проделываем над уравнением и неравенством различные преобразования, и здесь важно, чтобы эти преобразования были равносильными, т. е. чтобы найденное множество оказалось бы множеством истинности именно исходного уравнения или неравенства. Аналогична ситуация при решении систем уравнений или неравенств.

Рассмотрим простой пример. Пусть требуется решить уравнение (найти множество истинности предиката): 4x-2=-3x-9 . Преобразуем его равносильным образом:

4x-2=-3x-9quad Leftrightarrowquad 4x+3x=-9+2quad Leftrightarrowquad x=-1

Ответ: {-1} — множество всех решений данного уравнения (множество истинности данного предиката).

Отметим следующее немаловажное обстоятельство: может быть так, что два предиката равносильны, если их рассматривать над одним множеством, и неравносильны, если их рассматривать над другим (в частности, объемлющим первое) множеством. Такова, например, ситуация с предикатами: sqrt{xcdot y}=15 и sqrt{x}cdotsqrt{y}=15 .

Определение 18.5. Предикат Q(x_1,x_2, ldots,x_n) , заданный над множествами M_1,M_2, ldots, M_n , называется следствием предиката P(x_1,x_2,ldots,x_n) , заданного над теми же множествами, если он превращается в истинное высказывание на всех тех наборах значений предметных переменных из соответствующих множеств, на которых в истинное высказывание превращается предикат P(x_1,x_2,ldots,x_n) .

Другими словами (в терминах множеств истинности), можно сказать, что предикат является следствием предиката тогда и только тогда, когда $P^{+}subseteq Q^{+}$ .

Утверждение о том, что предикат является следствием предиката , будем символически записывать так: PRightarrow Q .

Например, одноместный предикат, определенный на множестве натуральных чисел, « делится на 3″ является следствием одноместного предиката, определенного на том же множестве, « делится на 6″. Из двух предикатов, упомянутых перед последним определением, первый будет следствием второго, если считать, что оба предиката заданы на множестве mathbb{Z} целых чисел.

Язык множеств истинности позволяет установить взаимосвязь между понятиями равносильности и следования предикатов: два предиката, определенные на одних и тех же множествах, равносильны тогда и только тогда, когда каждый из них является следствием другого. Кроме того, этот же язык дает возможность без труда установить следующие простые теоремы.

Теорема 18.6. Каждые два тождественно истинных (тождественно ложных) предиката, заданных на одних и тех же множествах, равносильны. Обратно, всякий предикат, равносильный тождественно истинному (тождественно ложному) предикату, сам является тождественно истинным (тождественно ложным) предикатом.

Теорема 18.7. Каждый тождественно истинный n-местный предикат является следствием любого другого n-местного предиката, определенного на тех же множествах. Каждый n-местный предикат является следствием любого тождественно ложного n-местного предиката, определенного на тех же множествах.

Теорема 18.8. Пусть P(x_1,x_2,ldots,x_n) и Q(x_1,x_2,ldots,x_n) — два n-местных предиката, определенные на одних и тех же множествах, такие, что Q(x_1, x_2, ldots, x_n) есть следствие . Тогда:

а) если P(x_1,x_2,ldots,x_n) тождественно истинный (выполнимый), то и Q(x_1, x_2, ldots, x_n) тождественно истинный (выполнимый);

б) если Q(x_1,x_2,ldots,x_n) тождественно ложный (опровержимый), то и P(x_1, x_2, ldots, x_n) тождественно ложный (опровержимый).

Доказательство теоремы 18.8:

а) Поскольку PRightarrow Q , поэтому $P^{+}subseteq Q^{+}$ . Если теперь тождественно истинный предикат, то

$P^{+}= M_1times M_2times ldotstimes M_n$ (где M_1,M_2,ldots,M_n — множества, на которых определены n-местные предикаты и ).

Но $Q^{+}subseteq M_1times M_2times ldotstimes M_n$ . Поэтому $Q^{+}= M_1times M_2times ldotstimes M_n$ , а, значит, предикат — тождественно истинный предикат. Если же — выполнимый предикат, то $P^{+}nevarnothing$ . Но $P^{+}subseteq Q^{+}$ . Тогда $Q^{+}nevarnothing$ и — выполнимый предикат.

б) Пусть — тождественно ложный предикат. Тогда $Q^{+}=varnothing$ . Но $P^{+}subseteq Q^{+}$ , поэтому $P^{+}=varnothing$ . Следовательно, предикат — тождественно ложный. Наконец, пусть — опровержимый предикат. Тогда $Q^{+}ne M_1times M_2times ldotstimes M_n$ . Поскольку, кроме того,

$P^{+}subseteq Q^{+}$ и $P^{+}subseteq M_1times M_2times ldotstimes M_n$ , то $P^{+}ne M_1times M_2times ldotstimes M_n$ .

Следовательно, предикат — опровержимый.

Отыщите самостоятельно в настоящем и предыдущем пунктах данной лекции утверждения, обосновывающие остальные сформулированные теоремы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

§ 1.Понятия предиката. Логические и кванторные операции над предикатами.

Определение 1. Одноместным предикатом
Р(х)называется всякая функция одного
переменного, а которой аргументхпробегает значение из некоторого
множества М, а функция при этом одно
их двух значений; истина или ложь.

Множество М, на котором задан предикат,
называется областью определения
предиката.

Множество IМ,
на котором предикат принимает только
истинные значения, называется областью
истинности предиката Р(х).

Предикат Р(х) называется тождественным
истинным( тождественно ложным) на
множестве М, еслиI=М
(I=).

Определение 2. n—
местным предикатом называется
всякая функцияn
переменныхQ(),
определенная на множестве М= Мх
Мх…х
Ми принимающая на этом множестве одно
из двух значений: истина или ложь.

Как и для одноместных предикатов, для
n- местных предикатов
можно определить область истинности,
понятие тождественно истинного и
тождественно ложного предиката.

Говорят, что предикат Р(х) является
следствием предиката Q(х) (Q(х)Р(х)), еслиII:
и предиката Р(х) иQ(х)равносильны(Q(х)Р(х)), еслиII.

Пример 1.Среди следующих предложений
выделить предикаты и для каждого их них
указать область истинности, еслиМ=Rдля одноместных предикатов иМ= R
x Rдля двухместных предикатов:

х +5=1;
при х = 2 выполняется равенствох-1=0;
х-2+1=0;
существует такое число х , что
х-2х+1=0;
х + 2 < Зх — 4;
однозначное число х кратно 3;
(х+ 2)-(3х — 4);

Решение.

1) предложение является одноместным
предикатом Р(х), IР = {-4};

2) предложение не является предикатом.
Это ложное высказывание;

3) предложение является одноместным
предикатом Р(х), IР = {1};

4) предложение не является предикатом.
Это истинное высказывание;

5) предложение является одноместным
предикатом Р(х) , IР = (3;+;

6) предложение является одноместным
предикатом Р(х), IР =
{0;3;6;9};

7) предложение не является предикатом;

предложение является двухместным
предикатом Q(x,y),=RxR{(0,0)}.

Пример 2. Выяснить, какие из следующих
предикатов являются тождественно
истинными:

1)
;
2)
;

3) sin2x+cos2x=l;
4)

Решение. Очевидно, предикаты 1), 3),
4) являются тождественно истинными.
В предикате 2) при х=0,y=0
неравенство нарушается, а в предикате
5) неравенство нарушается при всех
положительных значенияхx.
Следовательно, предикаты 2) и 5) не
тождественно истинны.

Так как предикаты
могут принимать два значения 1 и 0, то к
ним применимы все операции алгебры
высказываний.

Например,
конъюнкцией двух предикатов Р(х)
и
Q(x)
называется
новый предикат
,
который
принимает значение 1 при тех и только
тех значениях
x
,
при которых каждый из предикатов Р(х)и
Q(x)
принимает
значение 1
и
принимает значение 0 во всех остальных
случаях. Очевидно, что

.

Аналогично
определяются операции дизъюнкция,
импликация, эквивалентность двух
предикатов и отрицание предиката.
Легко видеть, что
,
,_.

Ясно, что при
выполнении логических операций над
предикатами к ним применимы и равносильности
алгебры логики.

Пример
3.
Пусть даны предикаты: Р(х):
«х — четное
число» и Q(x):
« x
кратно
3», определенные на множестве N. Найти
области истинности предикатов:

1)
;
2)
;
3)
P(x);
4)
.

Решение.
Так как

,
,то

1)
;

2);

3)
;

4)
.

Сказанное
позволяет находить области истинности
более
сложных предикатов, полученных в
результате применения к исходным
предикатам логических операций.

Пример
4.
Пусть даны предикаты А(х,у)
и
В(х,у),
определенные
на множестве
. Найти множество истинности предиката
и
изобразить ее с помощью кругов
Эйлера-Венна.

Решение.
Так как

=,
то
.
изображена
заштрихованной частью рисунка.

Можно рассматривать
и обратную задачу: Зная область
истинности предиката, полученного в
результате применения логических
операций к некоторым предикатам,
записать этот предикат.

Пример
5.
Записать предикат, полученный в
результате логических операций над
предикатами Р(х),
Q(x)
и

,
область истинности которого I
заштрихована
на рисунке.

Решение.
Так как здесь

,
то искомый предикат имеет вид
.

Пусть
имеется предикат Р(х),
определенный на множестве М.
Если
,
то
подстановка а
вместо
х
в
предикат Р(х)
превращает
этот предикат в высказывание Р(a).
Такое
высказывание называется единичным.
Наряду
с образованием из предикатов единичных
высказываний в логике предикатов
рассматривается еще две операции,
которые превращают одноместный предикат
в высказывание.

Определение
3.
Пусть Р(х) — предикат, определенный
на множестве М.
Под
выражением

понимают
высказывание, истинное, когда Р(х)
тождественно
истинный на множестве М
предикат
и ложное в противном случае. Это
высказывание уже не зависит от х.
Соответствующее
ему словесное выражение будет «Для
всякого х
Р(х)
истинно». Символ
насыпаютквантором
всеобщности. Переменную
х
в
предикате Р(х)
называют свободной (ей можно придавать
различные значения из M),
в высказывании
переменнуюx
называют
связанной квантором V.

Определение
4.
Пусть P(х)
— предикат, определенный на множестве
М.
Под
выражением
понимают высказывание, которое
является истинным, если существует хотя
бы один элемент
, для
которого Р(х)
истинно,
и ложным в противном случае. Это
высказывание уже не зависит от х.
Соответствующее
ему словесное выражение будет: «Существует
х,
при
котором Р(х)
истинно».
Символ
называюткванторам
существования. В
высказывании

переменная
х
связана
квантором 3,

Пример
6.
Даны предикаты
и,
определенные на множествеR.
Требуется установить, какие из
следующих высказывании истинны и какие
ложны:

;
2);3);4).

Решение.
Так как
при всех
х,,
то
будут истинны высказывания
и. Так как уравнениеимеет только два действительных корнях₁
= 3
и х₂
= 1,
то предикат Q(x)
принимает
значение 1 только при х
= 3 и х
= 1
и О в остальных случаях. Но тогда
высказывание
ложно, а высказываниеистинно.

Нетрудно
видеть, что когда предикат

определен
на конечном множестве
,
то

,
а

то есть кванторные
операции обобщают операции конъюнкции
и дизъюнкции на случай бесконечных
областей.

Кванторные
операции применяются и к многоместным
предикатам. Так, применение к двухместному
предикату Q(x,y)
квантора
всеобщности по переменной х
дает
одноместный предикат

зависящий
от у.
К
этому предикату можно применить
кванторную операцию по переменной
у.
В
результате получим или высказывание

или
высказывание
.

Таким
образом, может быть получено одно из
восьми высказываний:
,
,,,,,xyQ(x,y),
.

Легко показать,
что перестановка любых кванторов
местами, вообще говоря, изменяет
логическое значение высказывания.

Пример
7.
Пусть предикат Q(x,y):
«x:y
»
определен на множестве
.
Показать, что высказыванияи

имеют
различные логические значения.

Решение.
Так как высказывание

означает,
что для всякого натурального числа у
существует
натуральное число х
такое, что у
является
делителем х,
то это высказывание истинно.

Высказываниеозначает,
что есть натуральное число х,
которое делится на любое натуральное
число у.
Это
высказывание, очевидно, ложно.

3.1.
Среди следующих предложений выделите
предикаты, для каждого из предикатов
укажите одну из возможных областей
определения и в соответствии с ней
область истинности:

1) Луна есть спутник
Венеры;

2)
Планеты х и у
принадлежат
Солнечной системе;

3)
;

5);

6) Любое
простое число р
не
имеет делителей, отличных от себя и
1;

7)
Натуральное число п
не
меньше 1;

Треугольник ABC
равен
треугольнику A₁B₁C₁

9)
;

10)

;

11)
.

3.2.
Даны предикаты Р(х)
:
«»
иQ(x):
«».
Найдите области истинности этих
предикатов, если их область определения
есть: 1)R;
2) N.

3.3. На
множестве
заданы два предикатаР(х):
«х — простое
число», Q(x):
«x
—
нечетное число». Составьте их таблицы
истинности. Равносильны ли предикаты
Р(х)
и
Q(x)
на
множестве
,?

3.4.
Будут ли следующие предикаты равносильны
или один из них является следствием
другого? (Предметные переменные в
предикатах принадлежат R).

1)

и
;

2)
и;

3)
и
;

4)

и

y
= x
;

5)
и
;

6)
x
+ y
= z
и

;

7) х³
+ у³
=
0 и

3.5.
Найти области истинности предикатов:

1)
;
2)

3)
4)

3.6.
Изобразите на декартовой плоскости
области истинности предикатов:

1);
2);
3)
;

4)
;
б)6).

3.7.
На множестве М
= {1,2,3,…,20}
заданы предикаты:

А(х):
«х не
делится на 5»;

В(х):
«х — четное
число»;

С(х):
«х — число
простое»;

D(x):
«х кратно
3».

Найдите множества
истинности следующих предикатов:

1)
A(x)&
B(x)
; 2) C(x)&
B(x);

3)
C(x)& D(x)
; 4) B(x)&
D(x);

(x)&
D(x)
; 6) A(x)&
(x);

7)
(x)&
(x)
;
A(x)&
B(x)& D(x) ;,

9)
A(x)
V B(x)
; 10) B(x)
V C(x)
;

11)
C(x)
V D(x)
; 12) B(x)
V
D(x)
;

13)
(x)
V D(x)
; 14) B
(x)
v
(x)
;

15)
A(x)
V B(x)
V
D(x)
; 16) C(x)
→
А(x);

17)
D(x)
→
(x)
;
18) A(x) → B(x);

19)
(A(x)&
C(x))
→
(x)
;

20) (A(x)&D(x))
→
(x).

3.8.
Изобразите на диаграммах Эйлера-Венна
области истинности для следующих
предикатов:

(х)&(х);

(х)

↔
(х);

3)
(Р(х)
→
Q(x))
v
R(x)&
(х);

4) P(x)

→
(Q(x)
v
(x))
;

5)
Р(х)&Q(х)
→
(x)
.

3.9.
Изобразите на координатной плоскости
области истинности предикатов:

1);

2)
;

3)

;

4)

;

5)

.

3.10.
Записать предикаты, полученные в
результате логических операций над
предикатами Р(х),
Q(x)
и
,
области истинности которых
заштрихованы
на следующих рисунках:

3.11.
Установить, какие из следующих
высказываний истинны, а какие ложны,
при условии, что область определения
предикатов М
совпадает
с R:

1)
;

2)

;

3)
;

4)
;

5)
;

6)

;

7)
;

;

9)
.

3.12.
Приведите примеры таких значений а,
для
которых данное высказывание: а) истинно;
б) ложно.
.

1)

;

2)
.

3)

;

4)

.

Источник

Информатика. 10 класса. Босова Л.Л. Оглавление

§ 18. Алгебра логики

Из курса информатики основной школы вы знаете, что для компьютерных наук большое значение имеет математическая логика, а точнее, её часть, называемая алгеброй логики.

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.

Джордж Буль (1815-1864) — английский математик, основоположник алгебры логики. Дж. Буль изучал логику мышления математическими методами и разработал алгебраические методы решения традиционных логических задач. В 1854 году он опубликовал работу, в которой изложил суть алгебры логики, основанной на трёх операциях: and, or, not. Долгое время алгебра логики была известна достаточно узкому классу специалистов. В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейноконтактных и электронно-ламповых схем.

18.1. Логические высказывания и переменные

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно.

Например, высказывание «Джордж Буль — основоположник алгебры логики» истинно, а высказывание «2 + 2 = 5» ложно.

Что вы можете сказать об истинности или ложности предложения «Данное высказывание — ложь»?

Из имеющихся высказываний можно строить новые высказывания. Для этого используются логические связки — слова и словосочетания «не», «и», «или», «если …, то», «тогда и только тогда» и др.

Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым).

Например, из двух простых высказываний «Алгебра логики является основой строения логических схем компьютеров» и «Алгебра логики служит математической основой решения сложных логических задач» можно получить составное высказывание «Алгебра логики является основой строения логических схем компьютеров и служит математической основой решения сложных логических задач».

Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики. Эти вопросы решаются теми науками, к сфере которых относятся элементарные высказывания. Такое сужение интересов позволяет обозначать высказывания символическими именами (например, А, В, С). Так, если обозначить элементарное высказывание «Джордж Буль — основоположник алгебры логики» именем А, а элементарное высказывание «2 + 2 = 5» именем В, то составное высказывание «Джордж Буль — основоположник алгебры логики, и 2 + 2 = 5» можно записать как «А и В». Здесь А, В — логические переменные, «и» — логическая связка.

Логическая переменная — это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».

Для логических значений «истина» и «ложь» могут использоваться следующие обозначения:

Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

18.2. Логические операции

Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Из курса информатики основной школы вам известны логические операции отрицание, конъюнкция и дизъюнкция. Их таблицы истинности представлены ниже.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны, называется конъюнкцией или логическим умножением.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, называется дизъюнкцией или логическим сложением.

Логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному, называется отрицанием или инверсией.

При построении отрицания простого высказывания:

• используется оборот «неверно, что» или к сказуемому добавляется частица «не»;
• в высказывании, содержащем слово «все», это слово заменяется на «некоторые» и наоборот.

Рассмотрим несколько новых логических операций.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся ложным тогда и только тогда, когда первое высказывание (посылка) истинно, а второе (следствие) — ложно, называется импликацией или логическим следованием.

Операция импликации обозначается символом ? и задаётся следующей таблицей истинности:

В разговорной речи импликации соответствуют предложения, содержащие связку «если …, то». Эту связку мы используем тогда, когда хотим показать наличие причинно-следственной связи, иначе говоря, зависимость одного события от другого. Например, пусть некоторый человек сказал: «Если завтра будет хорошая погода, то я пойду гулять». Ясно, что человек окажется лжецом лишь в том случае, если погода действительно будет хорошей, а гулять он не пойдёт. Если же погода будет плохой, то, независимо от того, пойдёт он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.

Результат операции импликации, как и других логических операций, определяется истинностью или ложностью логических переменных, а не наличием причинно-следственных связей между высказываниями. Например, абсурдное с житейской точки зрения высказывание «Если 2 > 3, то существуют ведьмы» является истинным с точки зрения алгебры логики.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным тогда и только тогда, когда только одно из двух высказываний истинно, называется строгой (исключающей) дизъюнкцией.

Строгая дизъюнкция обозначается символом ? и задаётся следующей таблицей истинности:

В русском языке строгой (разделительной) дизъюнкции соответствует связка «либо». В отличие от обычной дизъюнкции (связка «или») в высказывании, содержащем строгую дизъюнкцию, мы утверждаем, что произойдёт только одно событие.

Например, высказывая утверждение «На сегодняшнем матче Петя сидит на трибуне А либо на трибуне Б», мы считаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б, и что сидеть одновременно на двух трибунах Петя не может.

Логическая операция, ставящая в соответствие двум высказываниям новое, являющееся истинным, когда оба исходных высказывания истинны или оба исходных высказывания ложны, называется эквиваленцией или равнозначностью.

В логике эквиваленция обозначается символом и задаётся следующей таблицей истинности:

В разговорной речи для выражения взаимной обусловленности используется связка «тогда и только тогда, когда», а в математике — «необходимо и достаточно».

Рассмотрим высказывание «Денис пойдёт в бассейн тогда и только тогда, когда он выучит уроки».

Это высказывание истинно (договорённость соблюдается), если истинны оба элементарных высказывания («Денис пойдёт в бассейн», «Денис выучит уроки»). Высказывание истинно (договорённость не нарушается) и в том случае, если оба элементарных высказывания ложны («Денис не пойдёт в бассейн», «Денис не выучит уроки»). Если же одно из двух высказываний ложно («Денис пойдёт в бассейн, хотя и не выучит уроки», «Денис выучит уроки, но не пойдёт в бассейн»), то договорённость нарушается, и составное высказывание становится ложным.

А сейчас посмотрите внимательно на таблицы истинности строгой дизъюнкции и эквиваленции: если на некотором наборе логических переменных результатом строгой дизъюнкции является истина, то на этом же наборе результатом эквиваленции всегда будет ложь, и наоборот.

Можно сделать выводы:

• операция эквиваленции есть отрицание операции строгой дизъюнкции

• операция строгой дизъюнкции есть отрицание операции эквиваленции

На сегодняшний день в алгебре логики не существует унифицированной символики для обозначения логических операций. В таблице 4.1 представлены логические операции и их наиболее распространённые обозначения, используемые как в алгебре логики, так и в некоторых языках программирования. Здесь же приведены речевые обороты, соответствующие логическим операциям.

Таблица 4.1

Логические операции и их обозначения

Операция отрицания выполняется над одним операндом. Такие операции называются одноместными или унарными. Все остальные логические операции, представленные в таблице 4.1, выполняются над двумя операндами и называются двуместными или бинарными.

18.3. Логические выражения

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (О, 1), логических переменных, знаков логических операций и скобок.

Для логического выражения справедливо:

1) всякая логическая переменная, а также логические константы (О, 1) есть логическое выражение;
2) если А — логическое выражение, то и 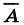— логическое выражение;
3) если А и В — выражения, то, связанные любой бинарной операцией, они также представляют собой логическое выражение.

При преобразовании или вычислении значения логического выражения логические операции выполняются в соответствии с их приоритетом:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Как и в арифметике, скобки меняют порядок выполнения операций.

Пример 1. Выясним, какие из приведённых слов удовлетворяют логическому условию (первая буква согласная ? вторая буква согласная) & (последняя буква гласная ? предпоследняя буква гласная):

1) ОЗОН;
2) ИГРА;
3) МАФИЯ;
4) ТРЕНАЖ.

Вычислим значение логического выражения для каждого из данных слов:

Итак, заданному условию удовлетворяют первое и четвёртое слова.

Решение логического уравнения — это один или несколько наборов значений логических переменных, при которых логическое уравнение становится истинным выражением.

Пример 2. Решим логическое уравнение

Дизъюнкция ложна в том и только в том случае, когда ложно каждое из образующих её высказываний. Иными словами, наше уравнение соответствует системе уравнений:

Таким образом, значение переменной D уже найдено. Импликация равна нулю в единственном случае — когда из истины следует ложь. Иначе говоря, в нашем случае: А = 1 и С = 0.

Подставим найденные значения переменных в уравнение

Ответ: А = 1, В = 1, С = 0, D = 0.

Логические уравнения могут иметь не одно, а несколько и даже очень много решений. Зачастую требуется, не выписывая все решения уравнения, указать их количество.

Пример 3. Выясним, сколько различных решений имеет логическое уравнение

Дизъюнкция истинна, если истинно хотя бы одно из образующих её высказываний. Решение данного логического уравнения равносильно совокупности, состоящей из двух уравнений:

Первое равенство будет выполняться только при А = 1, В = 1 и С = 0. Поскольку D в этом уравнении не задействовано, оно может принимать любое из двух значений (0 или 1). Таким образом, всего первое уравнение имеет два решения.

Самостоятельно выясните, сколько решений имеет второе уравнение (из совокупности двух уравнений).

Сколько решений имеет исходное уравнение?

Пример 4. Выясним, сколько решений имеет очень простое с виду логическое уравнение х₁ & х₂ ? х₃ & х₄ = 1.

Введём замену переменных. Пусть t₁ = х₁ & х₂, t₂ = х₃ & х₄. Тогда исходное уравнение примет вид: t₁ ? t₂ = 1.

На t₁ никаких ограничений нет, эта переменная может принимать значения 0 и 1. Импликация равна 0 только в случае, когда из истины (1) следует ложь (0). Исключим этот вариант. Построим дерево решений, представив на нём значения переменных t₁ и t₂ при которых t₁ ? t₂ = 1.

Получаем для t₁ и t₂ три набора значений: 00, 01, 11. Первая двоичная цифра в каждом из этих трёх наборов — результат выражения х₁ & х₂, вторая — х₃ & х₄. Рассмотрим первый набор: существует три набора х₁ и х₂ таких, что х₁ & х₂ = 0, другими словами, первый 0 мы можем получить тремя способами. Второй О в этом наборе мы также можем получить тремя способами.

Из курсов информатики и математики основной школы вам известно одно из основных правил комбинаторики — правило умножения. Согласно ему, если элемент А можно выбрать n способами, и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами.

Согласно правилу умножения, пару 00 можно получить 3 • 3 = 9 способами.

Что касается пары 01, то первый 0 мы можем получить тремя способами, а для получения 1 существует единственный вариант (х₃ & х₄ = 1 при х₃ = 1 и х₄ = 1). Следовательно, есть ещё три набора переменных х₁, х₂, х₃, х₄, являющихся решением исходного уравнения.

Самостоятельно доведите решение этой задачи до конца.

18.4. Предикаты и их множества истинности

Равенства, неравенства и другие предложения, содержащие переменные, высказываниями не являются, но они становятся высказываниями при замене переменной каким-нибудь конкретным значением. Например, предложение х < 12 становится истинным высказыванием при х = 5 (5 < 12 — истина) и ложным при x: = 15 (15 < 12 — ложь). Предложения такого рода называют высказывательными формами или предикатами.

Предикат — это утверждение, содержащее одну или несколько переменных.

Выделим некоторый предикат Р(х) и рассмотрим множество всевозможных объектов I, к которым он относится, — область определения предиката. Можно выделить такое подмножество Р множества I, что на всех его элементах предикат Р(х) будет превращаться в истинное высказывание. Определённое таким образом Р называется множеством истинности предиката Р(х).

Рассмотрим множество учеников некоторого класса. Известно, что в этом классе два отличника — Иван и Саша. Предикат «Он отличник» будет истинным высказыванием только по отношению к этим двум ученикам и ложным по отношению ко всем остальным.

Предикаты позволяют задать множество, не перечисляя всех его элементов. Например, множество истинности предиката Р(х) = (х < 0) — множество отрицательных чисел; множество истинности предиката Р(х, у) = (х² + у² = 1) — множество точек окружности единичного радиуса с центром в начале координат. Следует отметить, что многие задания, выполняемые вами на уроках математики, прямо связаны с предикатами. Например, стандартное задание «Решить квадратное уравнение x² — 3x + 2 = 0» фактически означает требование найти множество истинности предиката Р(х) = (x² — 3x + 2 = 0).

Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Пусть А и В соответственно являются множествами истинности предикатов А(х) и В(х). Тогда пересечение множеств А и В будет являться множеством истинности для предиката А(х) & В(х), а объединение множеств А и В будет множеством истинности для предиката А(х) ? В(х).

Пример 5. Найдём все целые числа 2, превращающие предикат

P(z) = (z > 5) & (z — 2 < 15) в

истинное высказывание. Другими словами, требуется найти множество истинности предиката P(z), заданного на множестве целых чисел I.

Предикат P(z) состоит из двух предикатов, соединённых операцией конъюнкции: P(z) = A(z) & B(z). Рассмотрим каждый из них в отдельности.

Множеством истинности предиката A(z) = (z > 5) являются целые числа 6, 7, 8 и т. д. Множеством истинности предиката В(z) = (z — 2 < 15) являются все целые числа, меньшие 17.

Множество истинности исходного предиката — пересечение (общие элементы) множеств истинности образующих его предикатов:

Р = А ? В = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}.

Его мощность |Р| = 11.

Пример 6. Рассмотрим предикат (50 < х²) ? (50 > (х + 1)²), определённый на множестве целых чисел. Найдём множество истинности этого предиката.

Зачастую задания такого рода формулируют несколько иначе.

Например, так: «Найдите все целые числа х, для которых истинно высказывание (50 < х2) ? (50 > (х + 1)2)».

Проанализируем отдельно каждый из элементарных предикатов (50 < х²) и (50 > (x + 1)²), решив соответствующие неравенства:

Определим значение исходного предиката на каждом из полученных подмножеств, причём отдельно рассмотрим значение х = -8 (оно попадает в два подмножества) и значение х = 7 (оно не попадает ни в одно подмножество):

Итак, множеством истинности исходного предиката являются целые числа, принадлежащие отрезку [-8; 7]. Наименьшим элементом этого множества является число -8, наибольшим — число 7; мощность множества равна 16.

САМОЕ ГЛАВНОЕ

Высказывание — это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными (сложными). Высказывание, никакая часть которого не является высказыванием, называется элементарным (простым). Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).

Составное логическое высказывание можно представить в виде логического выражения (формулы), состоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.

Логические операции имеют следующий приоритет:

1) отрицание;
2) конъюнкция;
3) дизъюнкция, строгая дизъюнкция;
4) импликация, эквиваленция.

Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.

Предикат — это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Вопросы и задания

1. Из данных предложений выберите те, которые являются высказываниями. Обоснуйте свой выбор.

2. Из каждых трёх выберите два высказывания, являющихся отрицаниями друг друга:

3. Рассмотрите следующие элементарные высказывания: А = «Река Днепр впадает в Чёрное море», В = «45 — простое число», С = «Вена — столица Австрии», D = «0 — натуральное число».

4. Представьте каждую пословицу в виде сложного логического высказывания, построенного на основе простых высказываний. Ответ обоснуйте при помощи таблиц истинности.

5. Подберите вместо А, В, С, D такие высказывания, чтобы полученные сложные высказывания имели смысл

6. Вычислите: 1) 1 v X & O;

7. Сколько из приведённых чисел Z удовлетворяют логическому условию: ((Z кратно 4) v (Z кратно 5)) ? (Z кратно 6)?

8. Найдите все целые числа Z, для которых истинно высказывание:

9. Какие из высказываний А, В, С должны быть истинны и ка кие ложны, чтобы были ложны следующие высказывания?

10. Даны три числа в различных системах счисления:

11. Логическое отрицание восьмиразрядного двоичного числа записанное в десятичной системе счисления, равно 217 Определите исходное число в десятичной системе счисления,

12. Определите логическое произведение и логическую сумм} всех двоичных чисел в диапазоне от 16₁₀ до 22₁₀, включая границы. Ответ запишите в восьмеричной системе счисления.

13. Сколько различных решений имеет логическое уравнение?

14. Сколько решений имеет логическое уравнение х₁ & х₂ v х₃ & x₄ = 1?

15. Изобразите в декартовой прямоугольной системе координат множества истинности для следующих предикатов:

16. Предикат ((8x — 6) < 75) ? (х(x — 1) > 65) определён на множестве целых чисел. Найдите его множество истинности. Укажите наибольшее целое число х, при котором предикат превращается в ложное высказывание.

§ 17. Некоторые сведения из теории множеств
§ 18. Алгебра логики
§ 19. Таблицы истинности

Источник

Известия Института математики и информатики УдГУ

2017. Том 50

УДК 510.635, 517.988.52, 519.833, 517.977 © Д. А. Серков

К ПОСТРОЕНИЮ МНОЖЕСТВА ИСТИННОСТИ ПРЕДИКАТА1

В работе развит подход, именуемый «размыкание предиката», сводящий задачу поиска множества истинности предиката к задаче поиска множества неподвижных точек некоторого отображения (далее — размыкающее отображение). Предлагаемая техника дает дополнительные возможности анализа задач и построения решений путем систематического привлечения результатов теории неподвижных точек. Даны формальное определение операции размыкания предиката, способы построения и исчисления размыкающих отображений и их основные свойства. В случае когда область определения предиката частично упорядочена, указаны способы построения размыкающих функций, обладающих свойством сужаемости. Это позволило получить представления интересующих элементов решения в виде итерационных пределов. Вместе с тем эффективность полученного решения зависит от специфики рассматриваемой задачи и выбранного варианта реализации метода. В качестве иллюстраций рассмотрены процедуры построения и дальнейшего использования размыкающих отображений для предикатов «быть нэшевским равновесием» и «быть неупреждающим селектором».

Б01: 10.20537/2226-3594-2017-50-06 § 1. Введение

Под термином «размыкание предиката» понимается сведение задачи поиска и/или изучения свойств множества истинности заданного предиката к задаче поиска и/или изучения свойств неподвижных точек некоторого отображения. Понятно, что размыкание предиката, если оно осуществлено, дает (как минимум дополнительную) возможность анализа его области истинности и построения элементов этой области с теми или иными дополнительными свойствами. Имеется несколько нетривиальных примеров размыкания предиката: в теории игр — при исследовании седловых точек (см. [1]) и равновесий Нэша (см. [2,3]); в динамических играх — при построении стабильных (слабоинвариантных) множеств (см. [4,5]) и неупреждающих селекторов многозначных отображений (см., например, [6,7]).

Во многих случаях, например при изучении дифференциальных уравнений и дифференциальных включений, «размыкающее» отображение (то есть отображение, имеющее своими неподвижными точками решения соответствующего уравнения) возникает естественным образом из поставленной задачи. И тогда для доказательства теорем существования и/или единственности остается «только» найти подходящую теорему о неподвижных точках.

В отмеченных выше примерах из теории игр вид размыкающего отображения не вытекает столь очевидно из постановки задачи и выдается как готовый продукт: способ построения такого отображения остается за рамками рассмотрения.

В настоящей статье излагается формальный подход к построению размыкающих отображений, намеченный в работах [8,9]: приведены определение размыкания предиката, способы построения и исчисления размыкающих отображений, их основные свойства. В качестве иллюстрации показано, как с помощью предложенной техники удается построить размыкающие отображения для некоторых известных задач и при этом получить теоремы существования более общего вида. Описываемый подход далек от универсальности, но по крайней мере приложим во многих интересных случаях.

В § 2 приводятся обозначения и определения общего характера, а также отдельные утверждения из теории неподвижных точек, используемые в дальнейших приложениях. В § 3 рассмотрены свойства размыкающих отображений и операции над ними. В §4 дается вывод размыкающего отображения для предиката «быть равновесием Нэша» в игре с произвольным числом участников и соответствующее представление множества равновесий. Наконец, в § 5 этот

1 Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 16-0Ю0649.

подход используется для описания наибольшего неупреждающего селектора заданной мульти-функции.

§ 2. Определения и вспомогательные сведения §2.1. Обозначения и определения общего характера

В дальнейшем используется теоретико-множественная символика (кванторы, пропозициоч с1е£ с1е£

нальные связки, 0 — пустое множество); = — равенство по определению; ^ — эквивалентность по определению. Принимаем аксиому выбора. Семейством называем множество, все элементы которого — множества. Через Р(Т) (через Р&(Т)) условимся обозначать семейство всех (всех непустых) п/м произвольного множества Т; семейство Р(Т) именуем также булеаном множества Т. Если А и В — непустые множества, то ВА есть множество всех отображений из множества А в множество В (см. [10, с. 77]). Если при этом / € ВА и С € Р&(А), то (/1 С) € Вс есть сужение / на множество С: (/1 С)(ж) = /(ж) Уж € С. Полагаем, также

/(С) есть образ множества С € Р(А) при отображении /: /(С) = {/(ж) : ж € С}. В случае когда / € Р(В)А, будем также называть / многозначным отображением (м/о) или мультифункцией (м/ф) из А в В. В случае когда ^ € Р&(ВА), полагаем | С) = {(/ | С) : / € ^}. Если / € Вто обозначим /-1 м/ф из Р(А)В гада /-1(Ь) = {а € А | Ь = /(а)} УЬ € В. В случае когда / € Р(В)А, то есть / — м/ф, полагаем /-1(Ь) = {а € А | Ь € /(а)} УЬ € В. Для произвольной м/ф / € Р(В)А обозначим через С(/) подмножество из А х В, являющееся графиком функции /: С(/) = {(а, Ь) € А х В | Ь € /(а)}. Понятно, что при этом для любого а € А, /(а) = {ь € В | (а,Ь) € С(/)} и С(/-1) = {(Ь,а) € В х А | (а,Ь) € С(/)}. Для М/Ф / € Р(В)А обозначим ч ерез dom(/) подмножеств о из А, на котором значения / непусты: асш(/)= {а € А | /(а) = 0}.

Для функции / € X— обозначим ч ерез Е1х(/) множество всех ее неподвижных точек: Е1х(/) = {ж € X | /(ж) = ж} В случае когда / — м/ф, множество Е1х(/) определяется как

Пх(/) = {ж € X | ж € /(ж)}. Если Е € Р(Х-) и Р(Р(Х), то положим Е1х(Е) = П/eFЕix(/) и назовем Еix(Е) множеством общих неподвижных точек семейства Е.

Назовем частично упорядоченное множество (ЧУМ) направленным, если каждое конечное его подмножество имеет мажоранту. Всякое линейно упорядоченное подмножество ЧУМ назовем цепью. Для У € Р(Х) обозначим через Ту и ±у наибольший и наименьший элементы множества У соответственно, если они существуют. Назовем ЧУМ (X, строго индуктивным,, если всякая его непустая цепь С имеет нижнюю грань т£ С € X. Назовем ЧУМ (X, с-полным (сЬат сотр^е), если всякая его цепь С (в том числе и пустая) имеет нижнюю грань т£ С € X. Отметим, что в с-полном ЧУМ существует наибольший элемент — нижняя грань пустой цепи.

Пусть (X, — ЧУМ и / € X-. Назовем функцию / сужающей на (X, если /(ж) ^ ж Уж € X; назовем / изотопной на (X, если (ж ^ ж&) (/(ж) ^ /(ж&)) Уж, ж& € X.

Будем обозначать через ОКО класс порядковых чисел (ординалов). Запись а € ОКО будем рассматривать как сокращение высказывания «а есть порядковое число» («а есть ординал»). Отношение порядка (строгого порядка) на классе ОКО будем обозначать как ^

Для всякого а € ОКО обозначим через W(а) = {1 € ОКО | 1 а} (а) = W(а) и {а}) множество всех ординалов меньших (не больших), чем а. Для всяких множества X и а € ОКО назовем а-последовательностыо в X (а+-последовательност,ью в X) и обозначим как (ж1 )-^(а) ((ж,)^+(«)) всякое отображение W(a) Э 1 ^ ж1 € X (W^-(a) Э 1 ^ ж1 € X) из множества отображений X(X^+(а)). В случае когда это не вызывает двусмысленности, будем также называть а-последовательностью множество {ж1 : 1 € W(a)} членов этой последовательности. В частности, будем говорить, что некоторая а-последовательность (ж1)^(«) есть (образует) цепь, если соответствующее множество {ж1 : 1 € W(a)} является цепью (линейно упорядочено). При этом отображение W(a) Э 1 ^ ж1 € X, вообще говоря, не предполагается изотопным. Первое бесконечное предельное порядковое число (бесконечный предельный ординал) обозначим как си. Для всякого множества X обозначим через |X| класс эквивалентности множеств, равномощных множеству X (кардинал X). Обозначим через |X| + наименьший среди ординалов п обладающих тем свойством, что |X| < п Отношение порядка (строгого порядка) на классе кардиналов будем обозначать как <= (<).

Предикат P на непустом множестве X будем отождествлять с одноименной функцией из {0,1}X. Будем говорить, что для x € X выполняется предикат P, и записывать это через P(x), если и только если P(x) = 1. Множество всех x € X, для которых выполняется

PP ратного отображения будем обозначать это множество как P-1(1). Множество всех предикатов на X обозначим как pR(X). Обозначим через T (F) предикат тождественно истинный (ложный) на X T-1(1) = X (F-1(0) = X). Таким образом, для любого P € PR(X) выполняется P = TP = F V P .

нием предиката P операцию поиска и/или построения отображения Fp € P(X)X такого, что Fix(Fp) = Pотображение Fp, обладающее указанным свойством, будем называть размыкающим (для предиката P). Обозначим через UM(P) множество (из P&(P(X)X) всех размыкающих отображений предиката P: UM(P) = {/ € P(X)X | Fix(f) = P-1(1)}. Исключение функций из размыкающих отображений условно: всякая функция /, удовлетворяющая Fix(/) = P-1(1), представлена в UM(P) мультифункцией Ff гада Ff(x) = {/(x)}. Поэтому далее мы будем писать / € UM(P), подразумевая Ff € UM(P).

§ 2.2. Вспомогательные результаты о неподвижных точках

В § 4 мы воспользуемся утверждениями о неподвижных точках, опирающимися на топологические свойства. Введем обозначения. Пусть Z — непустое множество и F € P(Z)Z — многозначное отображение. По заданному отображению F определим отображение F € P(Z)P(Z) следующим образом:

F(Y) = ( U F(у) J П Y = U F(у) П Y.

\y€Y J y

Заметим, что множество F(Y) является множеством «кандидатов» из множества Y во мноY

в F(Y), заведомо не принадлежат Fix(F).

Обозначим через O(Z) множество всех покрытий Z, то есть всех подмножеств (Ок)к С P(Z) таких, что UkSkОк = Z. Пусть т(Z) — некоторая топология в Z (множество всех открытых множеств). Обозначим через Ofo(Z) (Ofc(Z)) множество всех конечных открытых (замкнутых) Z

Fix(F)= П U F(Ok) = П U F^(Ok). (2.1)

(ok)keOfo(z) кек (Ok),eOfC(z) кек

V(Ok)k € Ofc(Z) Ж € K, F(Os) = 0. (2.2)

нимает вид

VS > 0 € Z, d(Z^, F(Zs)) < S. (2.3)

Следующие утверждения о неподвижных точках используют структуры порядка и будут нам полезны в §5. Пусть X = 0 и (X, — строго индуктивное ЧУМ, a F € P(XX) — произвольно заданное непустое множество сужающих отображений. Пусть а € ORD и ф =

= (/в)eew+ (a) G FW(a) — произвольно выбранная а+-последовательпость во множестве F. Определим а+-последовательпость (фв )eew+ (а) G (Xх )w+(a) композиций первых в отображений из а+-последовательпости ф. Проведем построение индуктивно.

I. При а равном 0 положим ф0(х) = x для всех x G X.

Пусть вообще в G ORD таково, что в = 0 и для каждого n G W(e) определена композиция фп G X х первых n отображений из ф.

II. Если в имеет предшественника (пусть это 7), положим фв = /в о ф7.

III. Если в — предельное порядковое число ив = 0, положим

фв(x) = /в (inf {фп(x): n G W(в)}) Vx G X.

В силу принципа трансфинитной индукции (см. [10, гл. VII, § 1, теорема 4; гл. VII, §4, теорема 1]) для любых а G ORD, а+-последовательности ф = (/в)eew+(a) G Fw+(a) и в G W+(a) однозначно определено отображение фв G XВ частности, при в = а определено отображение фа — композиция всех отображений из а+-последовательпости ф в заданном порядке.

щего отображения / G Xх оиределена а-итерация /a G Xх отображения /: для F = {/} и единственной а+-последовательпости ф G FW+(а) положим /а = фа.

Леииа2.1. Пусть (X, — непустое строго индуктивное ЧУМ, F G P(Xх) — непустое множество сужающих отображении. Тогда для любых а G OR^ ф = (/в^ew+M G F^^ выполняются неравенства фа(x) ^ фв (x) Vx G X Vв G W+ (а); в частносmu, фа — сужающее на (X, отображение.

Л е м м а 2.2. Пусть (X, — непустое строго индуктив ное ЧУМ, F G P(Xх) — непустое множество сужающих изотопных отображении, а G ORD и ф = (/в^ew+M G F^^. Тогда, для, всякого в G W+ (а) отображение фв также изотопное.

Пусть (X, — непустое строго индуктивное ЧУМ, а G ORD и F G P&(XX) — непустое множество сужающих в (X, отображений. Через ITERa[F] обозначим подмножество

из P&(Xх) гада ITERa[F] = {фв : ф G Fw+(a), в G W+ (а)} и для люб ого x G X положим

ITERq[F](x) = {ф^) : ф G ITERq[F]}.

Предложение 2.1. Пусть (X, — непустое строго индуктив ное ЧУМ, F G P(XX) — непустое множество отображений, сужающих на (X, Тогда,

(i) для, любо го x G X выполнено нераве нет,во Fix(F) П ITER|x|+ [F](x) = 0;

(ii) в частное mu, Fix(F) = 0.

Следствие 2.1. Пусть (X, — непустое индуктивное ЧУМ, / G Xх — сужающее отображение на, (X, и а G ORD выбрано из условия |X|+ ^ а. Тогда Fix(/) = = {/a(x): x G X}.

§ 3. Исчисление размыкающих отображений § 3.1. Структура порядка, сужение, логические операции

На множестве P(X )х введем частичный по рядок полагая (g ^ /) ^ (g(x) С / (x) Vx G X), V/, g G P(X)х. Иными словами, (g ^ /) ^ (G(g) С G(/)) для всех /,g G P(X)х. Заметим, что для любых /,g G P(X)х выполняется /-1,g-1 G P(X)х, и, в силу очевидных соотношений (G(g) С G(/)) ^ (G(g-1) С G(/-1)), имеем

(g ^ /) ^ (g-1 ^ /-1)- (3.1)

Легко проверить, что ЧУМ (Р(Х)х, — полная решетка. Для любого Р € Р^Я(Х) обозначим через Тр и -р м/ф из Р(Х)х вида

Тр(х) = /Х& Р(Х)- -р(ж) = |{Х)& Р(Х)& Ух € X.

\Х \{ж}, -Р(ж), \0, -Р(ж),

Для предикатов Т, в частности, имеем Тт(ж) = X -т(ж) = {ж}, Т#(ж) = X \ {ж} -#(ж) = 0 Ух € X При этом в силу равенств С(ТР) = X х X \ {(ж, ж) € X | -Р(ж)} Р) = {(ж, ж) € € X | Р(ж)} имеем соотношения

Тр = (Тр )-1, -р = (-р )-1. (3.2)

Лемма3.1. Для любого Р € ) справедливы соотношения

Тр, -р € им(Р), (3.3)

тр = Тяот(р )> -Р = -яот(р )• (3-4)

То есть, ЧУМ (ЯМ(Р), образует «отрезок» в (Р^)х, а значит — полную подрешетку:

иМ(Р) = {/ € Р(^х | -р ^ / ^ Тр}. (3.5)

Доказательство. Включения (3.3) следуют из определений. Соотношения (3.4) проверяются от противного. Покажем, что для любого / € Р^)х верны импликации

(/ ^ Тр) ^ (Пх(/) С Р-1(1)), (-Р ^ /) ^ (Р-1(1) С Пх(/)).

Пусть / таково, что / ^ Тр. Тогда для произвольного ж € X с учетом (3.3) имеем импликации

(ж € /(ж)) ^ (ж € Тр(ж)) ^ Р(ж).

Таким образом,

Пх(/) С Р-1(1). (3.6)

Напротив, если -р ^ /, то для любого ж € X в силу (3.3) выполняется

Р(ж) ^ (ж € -р(ж)) ^ (ж € /(ж)).

Следовательно,

Р-1(1) С Пх(/). (3.7)

Совокупность вложений (3.6), (3.7) дает включение / € ЯМ(Р). Так как / было выбрано произвольно, имеем вложение ЯМ(Р) I {/ € Р^)х | -р ^ / ^ Тр}. Обратное вложение выполняется в силу определений наибольшего и наименьшего элементов и равенств (3.4). Этим завершается доказательство.

Из (3.1), (3.2) и (3.5) сразу следует эквиваленция (/ € ЯМ(Р)) ^ (/-1 € ЯМ(Р)). Отметим еще одну форму размыкающего отображения, следующую из (3.5): Рр(ж) = Р-1(1) ж € X.

Приведем конструкцию размыкающего отображения для сужения предиката на подмножество области определения. Для любых ф € Р^)х и У € Р&^) обозначим через [ф | У] отображение из Р(У)у вида

[ф | У](у) = У П ф(у) Уу € У.

Напомним, что при этом для всякого Р € ) отображение (Р | У) € ) = {0,1}^

определено равенствами (Р | У)(у) = Р(у) у € У.

Л е м м а 3.2. Для любых Р € ) У € Р&^) выполняется равенство

иМ((Р | У)) = {[ф | У]: ф € ЦМ(Р)}. (3.8)

Доказательство. Фиксируем Р € фЭТ^) и У € Р&^). Тогда для любых у € У и ф € ЯМ(Р)

(у € Пх([ф | У])) ^ (у € [ф | У](у)) ^ (у € ф(у)) ^ (у € Пх(ф)) ^ Р(у) ^ (Р | У)(у).

ции. Так как у выбиралось произвольно, имеем включение [ф | У] € ИМ((Р | У)). В силу проф

{[ф | У] : ф € ЯМ(Р)} С иМ((Р | У)). (3.9)

Для обоснования обратного вложения фиксируем произвольное отображение фу € ЯМ((Р | У)) и обозначим через фх отображение из Р^)х вида

фх(2) = 2 € У&

\р-1(1), 2 € У.

Проверяется, что фу = [фх | У]• Представив множество истинности Р-1(1) предиката Р в виде суммы (Р-1(1) П У) и (Р-1(1) \ У) получим, что Е1х(фх) = Р-1(1) То есть фх € ИМ(Р). Таким образом, выполнено вложение, обратное (3.9). Доказательство закончено.

Далее приводится построение размыкающих отображений для выражений логики высказываний на основе размыкающих отображений входящих в них предикатов.

Л е м м а 3.3. Пусть Р, д € ). Тогда выполняются равенства

иМ(-Р) = {/ € Р^)х | 3д € иМ(Р) : /(ж) = X \ д(ж) Уж € X}, (3.10)

ЯМ(Рд) = {/ € Р^)х | 3д € ЯМ(Р) 3д € ИМ(д) : /(ж) = д(ж) П д(ж) Уж € X}, (3.11) ИМ(Р V д) = {/ € Р^)х | 3д € им(р) 3д € ИМ(д) : /(ж) = д(ж) и д(ж) Уж € X}. (3.12)

Доказательство. Докажем, например, равенство (3.11). Фиксируем Р, д € фЭТ^) и ф € ЯМ(Рд). Тогда для любого ж € X

(ж € ф(ж)) ^ (ж € Р-1(1) П д-1(1)). (3.13)

Положим

= I ф(2) и {2}, 2 € р-1 (1) \ д-1(1), ( = I ф(2) и {2}, 2 € д-1(1) \ Р-1(1),

1 ф(2), 2 € р-1 (1) \ д-1(1), фд(2) 1ф(2), 2 € д-1(1) \ р-1(1).

Так как X \ (Р-1(1) \ д-1(1)) = (Р-1(1) П д-1(1)) и (X \ Р-1(1)) в силу выбора ф (см. (3.13)) имеем (ж € фр(ж)) ^ Р(ж). Следовательно, фр € ИМ(Р). Аналогично получаем включение фд € ЯМ(д). Легко проверяется, что ф(ж) = фр(ж) П фд(ж) Уж € X. Так как ф было выбрано произвольно, имеем вложение

ЯМ(РВД С {/ € Р^)х | 3д € ИМ(Р) 3д € ИМ(^) : /(ж) = д(ж) П д(ж) Уж € X}.

Докажем обратное вложение. Пусть д € ЯМ(Р) и д € ЯМ(д) и / € Р^)х таково, что / (ж) = д(ж) П д(ж) Уж € X Тогда для любого ж € X имеем

(ж € Пх(/)) ^ (ж € /(ж)) ^ (ж € д(ж) П д(ж)) ^ (ж € Пх(д) П Пх(д)) ^ (Р(ж)д(ж)).

То есть / € ЯМ(Рд). Так как д и д выбирались произвольно, имеем искомое вложение:

ЯМ(РВД I {/ € Р^)х | 3д € ЯМ(Р) 3д € ИМ(^) : /(ж) = д(ж) П д(ж) Уж € X}.

Таким образом, выполнено (3.11). Соотношения (3.10) и (3.12) доказываются аналогично. Доказательство закончено.

Замечание2. На основе указанных соотношений понятным образом строятся размыкающие отображения для других выражений логики высказываний.

Следствие 3.1. Для любых Р € ), / € ЯМ(Р), Т € ЯМ(Т) и ^ € ЯМ(3) отображения /т, /^ € Р(Х)х вида

/т(ж) == Т(ж) П /(ж), /^(ж) == ^(ж) и /(ж) Уж € X (3.14)

суть размыкающие отображения, для Р:

/т/ € ЯМ(Р). (3.15)

Доказательство опирается па лемму 3.3 и равенства Р = РТ = Р V 3 выполненные для всех Р € ).

В случае, когда X — ЧУМ, можно переходить от размыкающей м/фк размыкающей функции, обладающей при этом свойством сужаемости. Такой переход позволяет использовать теоремы о представлении множества неподвижных точек, наибольших и наименьших неподвижных точках. Для произвольного ЧУМ (2, <) определим отображение ЬЕ^ € Р(2как

ЬЕ^(г) = {у € 2 | у < г}, г € Я. (3.16)

Л е м м а 3.4. Пусть (X, — непустое ЧУМ, Р € ), / € ЯМ(Р). Пусть для м/ф

д € Ху определяется как

С € Р(Х )х вида, С (ж) = ЬЕх (ж)П / (ж) ж € X выполняется, раве нство ^ш(С) = Хм функция

д(ж) = ТС(С() Уж € X. (3.17)

[у € с (ж), -атС(Л),

Тогда, д — сужающее отображение на (X, и д € ЯМ(Р).

Доказательство. Из (легко проверяемого) включения ЬЕх € ИМ(Т), соотношений (3.14) и (3.15) следует, что С € ЯМ(Р). Кроме того, по построению (см. (3.16)) выполнены неравенства

у < ж Уу € С(ж), Уж € X. (3.18)

С учетом определений (3.17) имеем

д(ж) € С(ж) Уж € X. (3.19)

Из (3.18) и (3.19) получаем неравенства д(ж) ^ ж Уж € X. То есть д — сужающее отображение па (X,

Из включения (3.19) следует, что Е1х(д) С Е1х(С). Покажем обратное вложение. Пусть ж € С(ж). Тогда из (3.18) следуют неравенства у ^ ж Уу € С(ж). Это означает, что ж = ТС(5). Следовательно (см. (3.17)), д(ж) = ж. То есть ж € Е1х(д). В силу произвольного выбора ж имеем вложение Е1х(С) С Е1х(д). Итак, Е1х(д) = Е1х(С). С учетом С € ЯМ(Р) получим равенство Е1х(д) = Р-1(1). Доказательство закончено. □

§ 3.2. Размыкание предиката на прямом произведении

Пусть имеются непустые множества I, (X,,)1ех и

X = П XI. (3.20)

Обозначим через ж1 ¿-ую компоненту элемента ж € X: ж1 = (ж | {¿}) € X,.. Обозначим через (у,ж-1) элемент из X, который получается подстановкой элемента у € X,, вместо ¿-й компоненты элемента ж € X:

(у,ж-4), = |у& 3 = Уж € X Уу € XI У1 €1. (3.21)

3 €1\{1Ь

ЗамечаниеЗ. В случае когда индексное множество I состоит из одного элемента, определение (3.21) дает тождество

(у, ж-) = у Уж € X Уу € XI VI € I. (3.22)

Пусть Р € ). Зададим отображения € Р(Х4)х, С1 € Р(Х)х вида

В(ж) = {у € XI | Р((у,ж-4))} Уж € X VI € I, (3.23)

С1(ж)=£ {2 € X | 2 €Д.(ж)} Уж € X VI €1. (3.24)

3 а м е ч а н и е 4. Сразу отметим следующий из определений вид этих отображений в случае, когда I — синглетон (см. (3.22)): В1(ж) = С1(ж) = {у € X | Р(у)} Уж € X VI € I.

Л е м м а 3.5. Для любого 1 € I выполняется включение С1 € ЯМ(Р).

Доказательство. Зафиксируем 1 € I. Пусть ж € X такой, что ж € Е1х(С1). Тогда по определению имеем ж € С.(ж). Воспользуемся представлением (см. (3.21)) ж = (ж1,ж-1). Из (3.24) получим ж1 € В.(ж). Значит (см. (3.23)), Р((ж1,ж-1)). Еще раз пользуясь равенством ж = (ж1,ж-1 ), получим Р(ж) И следовательно, ж лежит в Р-1(1). Так как ж был выбран произвольно, получаем вложение

Пх(С1) С {ж € X | Р(ж)}. (3.25)

Проверим обратное вложение. Пусть ж € X такой, что Р(ж). Тогда Р((ж1 ,ж-1)). Значит, ж1 € В. (ж). Откуда следует ж € С.(ж), то есть ж € Е1х(С.). Так как ж был выбран произвольно, получаем вложение {ж € X | Р(ж)} С Е1х(С1) С учетом (3.25) получим Е1х(С1) = {ж € X | Р(ж)}.

кончено. □

§ 3.3. Размыкание конъюнкции предикатов на прямом произведении

Часто условия (предикаты) на множестве отображений формулируются как поточечные условия: для каждого аргумента требуется выполнение того или иного условия на значение отображения в данной точке. Такие высказывания естественно рассматривать как конъюнкции предикатов (проиндексированных множеством определения) на произведении областей значений этих отображений при соответствующих аргументах. Далее приводится построение размыкающего отображения для произвольной конъюнкции предикатов над произвольным произведением множеств.

Пусть для непустого множества индексов 3 задано семейство Р, € фЭТ^), ? € 3, предикатов на прямом произведении X (см. (3.20)). Пусть предикат Р € фЭТ^) имеет вид

Р(ж) » (Р,(ж) У? € 3), ж € X. (3.26)

Условие 3.1. Мощность множества (предикатов) 3 не превосходит мощности множества I (сомножителей в X).

Пусть выполняется условие 3.1 и д € I ^ — некоторая инъекция из 3 в I. Зададим отображения В, € )х вида

В» = {у € XI | Р,((у,ж-1))} Уж € X У1 € I У? €3 (3.27)

и отображения В, € )х вида

В(ж) = /В19-1(1)(ж)((у,ж-1))}, 1 € д(3), Уж € X У1 € I.

1 () 1X1, 1 € д(3),

Зададим м/ф ^р € Р^)х следующим образом:

(ж) = П В1(ж) Уж € X. (3.29)

Л е м м а 3.6. Справедливо равенство ^»р € ЯМ(Р).

Доказательство. На основе отображений В^, построим отображения С,, С1 € € Р(Х)х, полагая

Су(ж) = (г € X | € Ву(ж)}, ^(ж) = (г € X | € В^ж)} Уж € X V* € I У? € ^.

Из леммы 3.5 следует, что для любых 1 € I ] € ^ верно включение С, € ЯМ(Р,). Тогда с учетом равенств С1(ж) = XI € 9(^0 (см- (3.28), (3.30)), имеем

р| С4(ж) = р| ^-^(ж) = р| С,0),(ж) Уж € X.

¿е! ¿е?(^)

Из (3.11) следует, что для отображения О(ж) = ПСд(,),(ж) Уж € X выполняется включение О € ЯМ(Р). Для завершения доказательства теперь достаточно проверить равенство

П С1(ж) = П В1 (ж) Уж € X. (3.31)

¿е! ¿е!

С учетом определения С1 для любых ] € I и г € X имеем равенство ( П1ех С.(г) | (,?}) = В,(г).

Следовательно, для любого у € X верно

(у € П ад) ^ (у, € ( П ¿¿(ж) | Ы) Ч? € I) ^ (у, € В,(ж) У? € I) ^ (у € П »¿(ж)).

¿е! ¿е! ¿е!

Доказательство закончено. □

Пример 3.1. Выполним размыкание предиката В, — «быть седловой точкой». Пусть и, V — непустые множества и па произведении X = И х V задана функция исходов ^: И х V ^ М. Игрок, выбирающий и € И, минимизирует, а игрок, выбирающий V € V, максимизирует исход. Элемент ж* = (и*^*) € X называется седловой точкой, если выполнено условие (предикат Р,)

В,(ж*) ^ (^>(и*^) ^ ^>(и*,v*) ^ ^(и, V*) У(и, V) € И х V). (3.32)

Из (3.32) следует, что В, есть конъюнкция двух предикатов:

Ри(ж*) ^ (^(и*, V*) ^ ^(и, V*) Уи € И), Ву(ж*) ^ (<^(и*^) ^ <^(и*^*) Vv € V).

Так как сомножителей в произведении два и предиката два, то выполняется условие 3.1 и имеется две возможности установить соответствие д: (Pи,Pv) ^ (И, V) и (Pи,Pv) ^ (V, И). Определения предикатов Ри, Pv указывают па первый вариант, как более простой. Используя выбранный вариант инъекции д, построим в соответствии с (3.27) (3.28) м/ф Ви € Р(И)Х,

Ви(ж*) = argmin ^(и, V*), Bv(ж*) = argmax ^(и* ,v). «еи vеv

Здесь значением операции argmin (а^тах) является пустое множество, если минимизирующие (максимизирующие) элементы отсутствуют. Из отображений Ви, Bv согласно (3.29) строим отображение € )х:

Рр3(и, V) = argmin^>(и&^) х argmax<^(и, V&), (и, V) € X. и&еи v&еv

Итак, в силу леммы 3.6 имеем равенство ^р, € ЯМ(В,).

§ 4. Равновесия Нэша для произвольного множества игроков

§4.1. Формулировка задачи и определение размыкающей м/ф

Обратимся к задаче поиска равновесий Нэша. Пусть (X, J) — игра с I игроками в нормальной форме, а именно:

xх, J=(JiW,

где X — множество состояний игры, Xt — множество стратегий ¿-го игрока, a J( — функция выигрыша ¿-го игрока: Jt : X ^ R, ¿ € I. Обозначим через pn € PR(X) предикат «быть

pn (x) ^ (Jt(z, x-) < Jt(x) Vz € Xt V¿ € I) Vx € X.

Понятно, что предикат pn представлен конъюнкцией предикатов P? € PR(X), j € I, вида

P?(x) ^ (J?(z, x—) ^ J?(x) Vz € X?) Vx € X.

В силу формулировки задачи количество предикатов совпадает с количеством сомножителей в произведении X, то есть выполнено условие 3.1. Положим ^(¿) = ¿ € I, и, используя выбранный вариант инъекции q, построим в соответствии с (3.27) (3.28) м/ф BL € P(Xt)X:

B(x)= {y € Xi | Pi((y,x-i))} =

= {y € Xi | Ji(z,x-i) < Ji(y,x-i), Vz € Xi} =

= {y € Xi | sup Ji(z,x-i) ^ Ji(y,x-i)} = argmax Jt(y,x-.).

zeXi yeXi

Тогда в силу (3.29) для отображения FpN € P(X)X имеем

Fpn (x)=J| Bi(x) = Y\ argmax Jt(y,x—) Vx € X. (4.1)

Отображение FpN по построению удовлетворяет условиям леммы 3.6 и, следовательно, является размыкающим для предиката pn FpN € UM(pn )• Воспользуемся этим фактом для описания множества равновесий Нэша в случае, когда множества Xt суть компакты.

§4.2. Использование размыкающей м/ф для предиката Нэша

Пусть множество стратегий Xt ¿-го игрока — топологическое пространство. Тогда полага-X

Воспользуемся равенством (4.1) и теоремой 2.1 для описания множества равновесий Нэша.

Теорема 4.1. Пусть Xi; ¿ € I, — компактные хаусдорфовы пространства, для любого ¿ € I функция Ji полунепрерывна сверху на X, функция Jt(z, ■) полунепрерывна снизу на, Х— при любом z € Xt. При этих условиях для множества P—*(1) равновесий Нэша выполняются равенства

P-&(1)= п u^Pn (oK)= п u^Pn (oK).

(Ok)keOfo(x) кек (ok)keofc(x) кек

В частности, равновесие Нэша достигается тогда и только тогда, когда в произвольном покрытии (Ок)к € Ofc(X) найдется множество Ок € (Ок)к, содержащее два, последовательных приближения Курно:

V(ok)к € Ofc(X) Зк € K 3x,x& € Ок, x& € (x). (4.2)

нимает вид (2.3): V£ > 0 3x^ € X d(x^,FpN(x^)) ^ Здесь d(x^,FpN(x^)) обозначает расстояние в X от точки x^ до множества FpN (x^).

Отметим также, что в теоремах [11, Theorem 4, 5] неверно сформулированы условия на функции р и Jf. при таких условиях приведенные доказательства некорректны. Правильные условия сформулированы выше, в теореме 4.1; для функции р эти условия эквивалентны требованию непрерывности.

Доказательство. В силу леммы 3.6 имеем равенство P—1(1) = Fix(FpN).

Для обоснования утверждений теоремы 4.1 остается проверить применимость равенств (2.1) к отображению FpN, то есть выполнение условий теоремы 2.1. Компактность и хаусдорфовость пространства X следует из компактности и хаусдорфовости порождающих его пространств Xt и из свойств топологии тихоновского произведения [12, теоремы 2.3.11, 3.2.4].

Проверим замкнутость графика отображения FpN. Отметим, что для любых x € X и i € I в силу полунепрерывности сверху Jt и компактно сти Xt множество argmaxyex J с (y,x_) определено и непусто. Значит, для любого х € X определено и непусто множество FpN (х). График G(FpN) отображения FpN представляется пересечением графиков G(Ct) отображений Ct (см. (3.24), (3.31)):

G(Fpn) = f| G(Ci).

Следовательно, в силу аксиом семейства замкнутых множеств замкнутость множеств G(Ct) влечет замкнутость G(FpN). С другой стороны, для любого i € I графи к G(Ct) можно представить в виде

G(Ci) = {(z,w) € X2 | w € Ci(z)} = {(z,w) € X2 | wt € B.(z)} =

= {(z,w) € X2 | wt € argmax Jt((y,z_t))} = {(z,w) € X2 | Jt((wt,z_t)) ^ max Jt((y,z_t))} =

= {((zt,x_t), (xt,z_t)) : (z € X)(Jt((xt,x_J) ^ max Jt((y,x_t)))}.

Исходя из полунепрерывности снизу па X_t функции Jt(y, ■) при каждом y € Xt проверяется (см. [13, предложение 1.5]), что функция x ^ maxyex Jt((y,x_)) полунепрерывна снизу па X. Тогда с учетом полунепрерывности сверху па X функции Jt получаем, что множество H = {x € X | Jt((xt,x_t)) ^ maxygx, Jt((y,x_t))} замкнуто в X. Следовательно, G(Ct) гомеоHX

Значит, множество G(Ct) замкнуто. Этим завершается доказательство теоремы. □

§ 5. Задача о неупреждающем селекторе м/ф

В работах [6,7,14,15] множества неупреждающих селекторов заданной м/ф представлены в виде неподвижных точек специального отображения (обозначенного как Г). То есть в этих работах выполнено размыкание предиката «быть неупреждающим сектором».

Вместе с тем процесс нахождения размыкающего отображения остался за рамками рассмотрения. В этом пункте, на основе конструкций из указанных работ и следуя схеме (3.26)^(3.29), мы реализуем «рутинное» построение этого размыкающего отображения и с его помощью дадим описание множества неупреждающих селекторов заданной м/ф при ослабленных условиях.

§ 5.1. Неупреждаемость, селектор

1. Всюду в дальнейшем фиксируем непустое множество I и непустое множество X. Полагаем D = I х X. Выберем множество C € P&(X1), элементы которого будут рассматриваться в качестве реализаций управления. Фиксируем непустые множества Y и П € P&(Y1). Элементы ш € П будем использовать в качестве реализаций неопределенных факторов. Введем множество M = P(C)n всех м/ф на П со значениями в C: а(ш) С C при ш € П, а € M.

2. Введем па M частичный порядок С, полагая (ф С ф) ^ (ф(ш) С ф(ш) Vw € П) Уф, ф € M.

Проверим, что ЧУМ (M, С) образует полную решетку. В самом деле, пусть Ф € P(M), то

есть ф(ш) € P(C) для всех ф € Ф и ш € П. Обозначим Ф*(ш) = (Jф(ш), Ф*(ш) = ПфеФ ф(ш),

ш € П. Тогда при любом ш € П выполнены включения Ф*(ш) € Р(С), Ф*(ш) € Р(С). Значит, отображения ш ^ Ф*(ш) и ш ^ Ф*(ш) принадлежат М. С другой стороны, легко проверить, что Ф* С ф С Ф* Уф € Ф. То есть Ф* = ±ф, Ф* = Тф Так как Ф выбиралось произвольно, утверждение доказано.

Для любых ф, ф € М назовем ф селектором ф, если ф С ф.

3. Выберем и зафиксируем произвольное непустое семейство Х € Р(1). Назовем м/ф ф € М Х-неупреждающей, если выполняется условие

(ш& € П(ш | А)) ^ ((ф(ш) | А) С (ф(ш&) | А) У А € X Уш, ш& € П. (5.1)

Замечание 6. Импликации (5.1) в силу эквиваленций

(ш& € П(ш | А)) ^ (ш € П(ш& | А)) ^ ((ш | А) = (ш& | А)) УА €Х Уш, ш& € П.

и соображений симметрии равносильны импликациям

((ш | А) = (ш& | А)) ^ ((ф(ш) | А) = (ф(ш&) | А)) УА € X Уш, ш& € П,

4. Многие задачи сводятся к построению наибольшего Х-неупреждающего селектора некоторой заданной м/ф ф € М, то есть к построению Х-неупреждающей м/ф ф € М, для которой выполняется неравенство ф С ф, и при вся кой Х-неупреждаю щей в € М такой, ч то в С ф, выполняется неравенство в С ф.

Зафиксируем для дальнейшего изложения некоторое многозначное отображение М € М, для которого и будем решать указанную задачу поиска наибольшего Х-неупреждающего селектора. С этой целью введем следующие обозначения: для произвольных А € X Ф С П, ш € П, Н С С, Ь € Си ф € М положим

Ф(ш | А) = {V € Ф | (V | А) = (ш | А)}, Н(Ь | А) = {/ € Н | (/ | А) = (Ь | А)}, (5.2)

Ф(-ш | А)=Ф(ш | А) \{ш}, (5.3)

[ф](ш | А)= П (Ф(v) I А, (5-4)

Vеп(ш | А)

[ф](-ш | А)= П (Ф(V) I А. (5.5)

veП(-ш|А)

А также в соответствии с (5.1) определим предикат Рпа € «быть Х-неупреждающим

отображением»:

Ргаа(ф) ^ ((ш& € П(ш | А)) ^ ((ф(ш) | А) С (ф(ш&) | А)) УА € Х Уш, ш& € П) , ф € М. (5.6)

§ 5.2. Размыкание предиката неупреждаемости

Представим М как прямое произведение П экземпляров множества Р(С). Из определения (5.6) следует представление предиката Рпа в форме конъюнкции предикатов вида

(ф) » ((ш& € П(ш | А)) ^ ((ф(ш) | А) С (ф(ш&) | А)) УА € Х) , ш € П, ф € М. (5.7)

Как видно, индексное множество в конъюнкции предикатов, представляющей Ргаа, совпадает

I = д = П и определим 9(ш) = ш Уш € П. Тогда имеем

= = р(с), ш € П, М = X = ПXI = П Р(С),

¿е! шеп

Bi = Bw g P(P(C))M, Fpna(ф) = п Bw(Ф) g P(P(C)) = P(M)M.

Мы привели этот список «действующих лиц и исполнителей» для удобства отслеживания схемы (3.20)^(3.29). В дальнейших выкладках мы не будем переходить к обозначениям пункта 3 для сохранения более наглядной связи с содержательной стороной задачи. Модернизируем определение (5.7), используя обозначения (5.4).

Л е м м а 5.1. Справедливо утверждение

Pw (Ф) ^ ([ф](ш | A) = ^ф(ш) | A) VA eX) , ш G Q, ф G M. (5.8)

Доказательство. Фиксируем A G X, ш G Q и ф G M. Легко видеть (достаточно в правой части (5.4) рассмотреть v = ш), что всегда выполняются вложения

[ф](ш | A) с (ф(ш) | A). (5-9)

(h | A) G П (Ф(ш&) I A) =[ф](ш | A).

w&en(w | A)

В силу произвольного выбора h получаем включение (ф(ш) | A) С [ф](ш | A). С учетом (5.9) имеем равенство [ф](ш | A) = (ф(ш) | A). Значит, справедлива импликация

((ш& G П(ш | A)) ^ ((ф(ш) | A) С (ф(ш&) | A))) ^ ([Ф](ш | A) = (ф(ш) | A)). (5.Ю)

Пусть теперь выполняется следствие в (5.10). Тогда при ш& G 0(ш | A) в силу равенства [ф](ш | A) = (ф(ш) | A) имеем (см. (5.4)) (ф(ш) | A) С (ф(ш&) | A). В силу произвольного выбора ш& выполняются импликации (ш& G 0(ш | A)) ((ф(ш) | A) С (ф(ш&) | A)), то есть посылка из соотношений (5.10). Таким образом, в (5.10) посылка и следствие эквивалентны. Так как A, ш и ф выбирались произвольно, установлена эквиваленция (5.8). Доказательство завершено. □ Итак, интересующий нас предикат Pna имеет вид (см. (5.8))

ргаа(ф) ^ (рш(ф) Vш G Q) ^ ([ф](ш | A) = (ф(ш) | A) VA GXVw G Q) Vф G M. (5.11)

Воспользуемся (3.28) для построения отображений Bw G P(P(C))M (в качестве q, как отмечалось, используем тождественное отображение):

Bw(ф) = {L G P(C) | Pw((L, ф-w))} Vш G Q Vф G M. (5.12)

Напомним (см. (3.21)), что для любых L G PP(C), ф G M и ш G Q м/ф (L, ) G M определена соотношениями

(L, ф-w)(v) = |L& V = ш& (5.13)

1 ^ \ф(v), v G Q \{ш}. 1 }

Преобразуем (5.12), используя представление (5.8):

Bw(ф) = {L G P(C) | [(L, ф-w)](ш | A) = ((L, ф-w)(ш) | A) VA G X}. С учетом (5.4) и (5.13) имеем (продолжаем равенства)

= {L G P(C) | f| ((L, ф-w)(v) | A) = (L | A) VA GX}.

ven(w | A)

Заметим, что в пересечении (при V = ш) встречается множество (Ь | А), поэтому последнее выражение можно преобразовать следующим образом (см. (5.3), (5.5)):

= {Ь е Р(С) | (ь | А) с р| ((Ь,ф-Ш) (V) | А У А ех} =

= {Ь е Р(С) | (Ь | А С р| (Ф^) | А) VA е X} =

Vеп(-ш|А)

= {Ь е Р(С) | (Ь | А с [ф](-ш | А) УА еХ}.

ства):

= {Ь е Р(С) | Ь с У С(Ь | А) УА еХ}.

Лес (Л | А)е[ф](-ш | А)

Наконец, реализуем конъюнкцию по А е X и воспользуемся определением булеана Р (продолжаем равенства):

{Ь е Р(С) | Ь с р| У С(Ь | А)} = Р

Аех Лес

(Л | А)е[ф](-ш | А)

П и С(Л | А)

Аех Лес \ (Л | А)е[ф](-ш | А)

Итак, имеем

Вш (Ф) = Р

П и С(Л | А)

Аех Лес \ (Л | А)е[ф](-ш | А)

Уш е П УФ е М.

Следуя (3.29), запишем размыкающее отображение ^р>„а е Р(М)м для предиката неупре-ждаемости (5.11):

(Ф) = П в- (Ф) = П Р

П и С(Л | А)

Аех Лес \ (Л | А)е[ф](-ш | А) )

УФ е М.

Согласно лемме 3.6 имеем ^р>„а е ЯМ(Ргаа).

§ 5.3. Выделение наибольшего неупреждающего селектора

Возвращаясь к исходной задаче, найдем среди неподвижных точек отображения (5.14) наибольшую, содержащуюся в ЧУМ (Мм, Е), где Мм = {Ф е М | Ф С М}. Так же как и для ЧУМ (М, С), проверяется, что ЧУМ (Мм, С) образует полную решетку.

Определим (см. (3.8)) размыкающее отображение ^(рпа |мм) Для сужения (Ргаа | Мм) предиката Ргаа на непустое подмножество Мм С М. Имеем для всех Ф е Мм

^(рпа |Мм)(Ф) = [^р„а | Мм](Ф) = Мм№па(Ф) = Мм П П Р

П Р(мм) п П р

Ушеп ) шеп

( \ П и С(Л | А)

Аех Лес \ (Л | А)е[ф](-ш | А) )

П и С(Л | А)

шеп Аех Лес

\ (Л | А)е[ф](-ш | А) )

( \ П Р П и М(ш)(Л | А)

шеп Аех Лес

\ (Л | А)е[ф](-ш | А) )

Воспользуемся леммой 3.4 для построения однозначного селектора м/ф ^(рпа | мм)- Заметим, эта лемма применима, так как ЧУМ (Мм, Е) образует полную решетку (и тем более индуктивное ЧУМ). Напомним, что в рассматриваемом случае отображение ЬЕмм (см. (3.16)) имеет вид ЬЕмм(а) = ЛР(а(ш)), а € Мм- Построим в соответствии с условиями леммы 3.4 отображение 7 € Р(Мм)Мм: для всех ф € Мм

7(Ф) = F(pna | mm) (Ф) П LEMM (Ф) = П P

(h | A)e[*](-w | A)

U M(W)(h | A)

п*(ФМ)

(h | А)е[ф](-ш | A)

IJ ф(и) nM(w)(h | A)

(h | А)е[ф](-ш | A)

U ФИ(Ь I A)

В выкладках используются равенство Р(Х)ПР(У) = Р(ХПУ), справедливое для произвольных множеств также свойства декартова произведения [10, гл. IV, § 5]. Заметим, что в силу

включения 0 € Р(Х), где X — любое множество, при всяком ф € Мм выполнено неравенство

7 (Ф) = 0Рассмотрим отображение 7 € (Мм)Мм гада 7(0) = вир(мм,с) 7(0) У0 € Мм- Преобразуем его, используя равенства У = 8ир(р(х),с) Р(У), справедливые для произвольных множеств X и К таких, что У С X:

7(ф) = sup(MM,c) 7(ф)

suP(mm,q гг P

(h | A)e[*](-w | A)

U Ф(^)(Ь I A)

П suP(P(c),c) P

п u фи(л i a)

Aex hec \ (h | A)e[*](-w | A)

пп u ФИ(Л I A). (5-15)

wen Aex hec

(h | A)e[*](-w | A)

Из представления (5.15) следует, что для любого ф € Мм выполнено включение 7(ф) € 7(ф), то есть 7(ф) = Т7(ф) Уф € Мм. В силу леммы 3.4 получаем, что 7 — сужающая функция и 7 € ЯМ((Р„а | Мм))Наконец, воспользуемся подходящими утверждениями теории неподвижных точек для описания искомого наибольшего элемента. Так как 7 — сужающее отображение, действующее Мм

ждающих селекторов м/ф М как множества истинности предиката (Рпа | Мм) •

Предложение 5.1. Пусть а € ORD таково, нто |Мм| равенство

(Ргаа | Мм)-1(1) = (7а(^) : Ф € Мм}.

а. Тогда, выполняется

Представление (5.15) указывает па изотонность функции 7 в (Мм, Е) для всех ф, ф € Мм выполняются импликации (ф = ф) ^ (7(Ф) Е Y(Ф))- Отсюда в силу леммы 2.2 следует, что при любом а € ORD функция 7″ также изотопна. Из этого следует (см. теорему Тарско-го [16, Theorem 1]), что множество Fix(7) = (Pna | Мм)-1(1) образует полную подрешетку в (Мм, =)• В частности, множество Fix(7) содержит T(pna |mm)-i(1) — наибольшего неупре-ждающего селектора м/ф M. Воспользуемся изотонностью 7″ и представлением (5.16) для описания наибольшего селектора м/ф M:

Предложение 5.2. Пусть а € OR^ |Мм|+ а. Тогда T(Pna | mm)-1(1) = 7°(M).

Утверждение следует из соотношений T(pna | mm)-i(1) = TFix(7) = 7°(Tmm) = 7°(M), в которых второе равенство опирается на изотонность 7″ и представление (5.16).

5.4. Г и y

В координатной форме y имеет вид

y(^)M = р| (J | A) Уф е Mm Vw е Q. (5.17)

(h | A)e[*|(-w | A)

Элиминируя в (5.17) обозначения (5.2), (5.4), получим равенства Г(ф)(ш) = y(Ф)(ш), ф е M, w е П, для итератора Г, определенного в работах [6,7,14,15]:

Г(ф)(ш) = {/ е ФМ | VA eXVw& е Q(w | A) (/ | A) е (ф(ш&) | A)} Уф е M Vw е Q.

Предложение 5.2 обобщает представление [6, теорема 6.1], где используется а = ш (наименьший бесконечный ординал). В предложенном описании большая мощность итераций компенсирует отсутствие условий топологического характера на Q, С и M.

Список литературы

1. Kakutani S. A generalization of Brouwer&s fixed point theorem // Duke Math. J. 1941. Vol. 8. No. 3. P. 457-459. DOI: 10.1215/S0012-7094-41-00838-4

2. Nash J. Non-cooperative games // Annals of Mathematics. 1951. Vol. 54. No. 2. P. 286-295. DOI: 10.2307/1969529

3. Nikaido H. On von Neuman&s minimax theorem // Pacific Journal of Mathematics. 1954. Vol. 4. No. 1. P. 65-72. DOI: 10.2140/pjm.l954.4.65

4. Ченцов А.Г. О структуре одной игровой задачи сближения // Доклады АН СССР. 1975. Т. 224. № 6. С. 1272-1275.

5. Ченцов А.Г. К игровой задаче наведения // Доклады АН СССР. 1976. Т. 226. № 1. С. 73-76.

6. Ченцов А.Г. Неупреждаюгцие селекторы многозначных отображений // Дифференциальные уравнения и процессы управления. 1998. № 2. С. 1-64.

7. Ченцов А.Г. Наследственные мультиселекторы многозначных отображений и их построение итерационными методами // Дифференциальные уравнения и процессы управления. 1999. № 3. С. 1-54.

8. Серков Д.А. Об одном подходе к анализу множества истинности: размыкание предиката // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. 2016. Т. 26. Вып. 4. С. 525-534. DOI: 10.20537/vml60407

9. Serkov D.A. Unlocking of predicate: application to constructing a non-anticipating selection // Вестник Удмуртского университета. Математика. Механика. Компьютерные науки. 2017. Т. 27. Вып. 2. С. 283-291. DOI: 10.20537/vml70211

10. Куратовский К., Мостовский А. Теория множеств. М.: Мир, 1970. 416 с.

11. Serkov D.A. On fixed point theory and its applications to equilibrium models // Вестн. ЮУрГУ. Сер. Матем. моделирование и программирование. 2016. Т. 9. № 1. С. 20-31. DOI: 10.14529/mmpl60102

12. Энгелькинг Р. Общая топология. М.: Мир, 1986. 752 с.

13. Обен Ж.-П. Нелинейный анализ и его экономические приложения. М.: Мир, 1988.

14. Ченцов А.Г. Неупреждаюгцие многозначные отображения и их построение с помощью метода программных итераций. I // Дифференциальные уравнения. 2001. Т. 37. № 4. С. 470-480.

15. Ченцов А.Г. Неупреждаюгцие многозначные отображения и их построение с помощью метода программных итераций. II // Дифференциальные уравнения. 2001. Т. 37. № 5. С. 679-688.

16. Tarski A. A lattice-theoretical fixpoint theorem and its applications // Pacific Journal of Mathematics. 1955. Vol. 5. No. 2. P. 285-309. DOI: 10.2140/pjm. 1955.5.285

Поступила в редакцию 10.10.2017

Серков Дмитрий Александрович, д. ф.-м.н., ведущий научный сотрудник, Институт математики и механики им. Н. Н. Красовского УрО РАН, 620990, Россия, г. Екатеринбург, ул. С. Ковалевской, 16; профессор, кафедра вычислительных методов и уравнений математической физики, Институт радиоэлектроники и информационных технологий, Уральский федеральный университет, 620002, Россия, г. Екатеринбург, ул. Мира, 32. E-mail: serkov@imm.uran.ru

D. A. Serkov

On the construction of a predicate truth set

Citation: Izv. Inst. Mat. Inform. Udmurt. Gos. Univ., 2017, vol. 50, pp. 45-61 (in Russian). Keywords: truth set of predicate, fixed points, Nash equilibrium, nonanticipating mappings. MSC2010: 06E30, 47J25, 47H04, 47H10, 91B50 DOI: 10.20537/2226-3594-2017-50-06

We provide an approach to constructing a predicate truth set, which we refer to as unlocking of predicate. The approach reduces the problem of searching for a predicate truth set to searching for a set of fixed points of some mappings (hereinafter «unlocking mappings»). Unlocking of predicate gives an extra opportunity to analyze the truth set and to build its elements with desired properties. In this paper, we outline how to build unlocking mappings for some general types of predicates: we give a formal definition of the predicate unlocking operation, rules for the construction and calculation of unlocking mappings and their basic properties. As an illustration, we routinely construct unlocking mappings for predicates «be a Nash equilibrium» and «be non-anticipating mapping»; then on this basis we provide expressions for corresponding truth sets.

REFERENCES

1. Kakutani S. A generalization of Brouwer&s fixed point theorem, Duke Math. J., 1941, vol. 8, no. 3, pp. 457-459. DOI: 10.1215/S0012-7094-41-00838-4

2. Nash J. Non-cooperative games, Annals of Mathematics, 1951, vol. 54, no. 2, pp. 286-295. DOI: 10.2307/1969529

3. Nikaido H. On von Neumann&s minimax theorem, Pacific Journal of Mathematics, 1954, vol. 4, no. 1, pp. 65-72. DOI: 10.2140/pjm.l954.4.65

4. Chentsov A.G. On the structure of a game problem of convergence, Sov. Math. Dokl., 1975, vol. 16, no. 5, pp. 1404-1408.

5. Chentsov A.G. On a game problem of guidance, Sov. Math. Dokl., 1976, vol. 17, pp. 73-77.

6. Chentsov A.G. Non-anticipating selections of multivalued mappings, Differ. Uravn. i Protsessy Upr., 1998, no. 2, pp. 1-64 (in Russian).

7. Chentsov A.G. Hereditary multiselectors of multivalued mappings and their construction by iterative methods, Differ. Uravn. i Protsessy Upr., 1999, no. 3, pp. 1-54 (in Russian).

8. Serkov D.A. An approach to analysis of the set of truth: unlocking of predicate, Vestn. Udmurt. Univ. Mat. Mekh. Komp&yut. Nauki, 2016, vol. 26, issue 4, pp. 525-534 (in Russian). DOI: 10.20537/vml60407

9. Serkov D.A. Unlocking of predicate: application to constructing a non-anticipating selection, Vestn. Udmurt. Univ. Mat. Mekh. Komp&yut. Nauki, 2017, vol. 27, issue 2, pp. 283-291. DOI: 10.20537/vml70211

10. Kuratowski K., Mostowski A. Set theory, Amsterdam: North-Holland, 1967, 417 p. Translated under the title Teoriya mnozhestv, Moscow: Mir, 1970, 416 p.

11. Serkov D.A. On fixed point theory and its applications to equilibrium models, Bulletin of the South Ural State University, Series Mathematical Modelling, Programming and Computer Software, 2016, vol. 9, issue 1, pp. 20-31. DOI: 10.14529/mmpl60102

12. Engelking R. General topology, Warszawa: PWN, 1985, 752 p. Translated under the title Obshchaya topologiya, Moscow: Mir, 1986, 752 p.

13. Aubin J.-P. L&analyse non lineaire et ses motivations economiques, Paris, Masson, 1984, 214 p. Translated under the title Nelineinyi analiz i ego ekonomicheskie prilozheniya, Moscow: Mir, 1988.

14. Chentsov A.G. Nonanticipating multimappings and their construction by the method of program iterations: I, Differential Equations, 2001, vol. 37, issue 4, pp. 498-509. DOI: 10.1023/A:1019275422741

15. Chentsov A.G. Nonanticipating multimappings and their construction by the method of program iterations: II, Differential Equations, 2001, vol. 37, issue 5, pp. 713-723. DOI: 10.1023/A:1019224800877

16. Tarski A. A lattice-theoretical fixpoint theorem and its applications, Pacific Journal of Mathematics, 1955, vol. 5, no. 2, pp. 285-309. DOI: 10.2140/pjm.l955.5.285

Received 10.10.2017

Serkov Dmitrii Aleksandrovich, Doctor of Physics and Mathematics, Leading Researcher, N. N. Krasovskii Institute of Mathematics and Mechanics, Ural Branch of the Russian Academy of Sciences, ul. S. Kovalevskoi, 16, Yekaterinburg, 620990, Russia;

Professor, Ural Federal University, ul. Mira, 32, Yekaterinburg, 620002, Russia. E-mail: serkov@imm.uran.ru

МНОЖЕСТВО ИСТИННОСТИ ПРЕДИКАТА НЕПОДВИЖНЫЕ ТОЧКИ РАВНОВЕСИЕ НЭША НЕУПРЕЖДАЮЩИЕ ОТОБРАЖЕНИЯ truth set of predicate fixed points nash equilibrium nonanticipating mappings

Источник