Как найти мощность множества примеры - Исправление недочетов и поиск решений вместе с Examum.ru

Введение в теорию множеств

Время на прочтение
12 мин

Количество просмотров 95K

Концепция бесконечности идеологически далека от обычной математической терминологии — ни одна другая тема не выходит за пределы математики так, что превращается из практического, аналитического инструмента в явление мифического порядка. Понятие бесконечности на короткой ноге с такими культурными темами, как религия и философия, и окутана загадочной аурой божественности.

Когда-то давным давно во всех академических дисциплинах было заложено фундаментальное убеждение — существует единственная бесконечность.

Но 1874 году довольно малоизвестный математик провёл серию революционных наблюдений, подвергавших сомнению это всеми принятое и глубоко укоренившееся убеждение. Георг Кантор в своей (теперь уже ставшей легендарной) публикации On a Property of the Collection of All Real Algebraic Numbers доказал, что множество вещественных чисел «более многочисленно», чем множество алгебраических чисел. Так он впервые показал, что существуют бесконечные множества разных размеров (не волнуйтесь — для прояснения этого мы вскоре подробно изучим его статью).

«Множество — это большое количество, которое позволяет воспринимать себя как одно» — Георг Кантор

С 1874 по 1897 год Кантор неистово публиковал статью за статьёй, разворачивая свою теорию абстрактных множеств в расцветающую дисциплину. Однако она была встречена упорным сопротивлением и критикой; многие педанты считали, что его теории перешли в область философии и нарушили принцип религии.

Однако когда начали находиться практические применения математического анализа, отношение к теории изменилось, а идеи и результаты Кантора начали получать признание. К первому десятилению 20-го века его наблюдения, теории и публикации достигли своей кульминации — признания современной теории множеств новой, совершенно уникальной областью математики:

Теория множеств — это математическая теория о точно определённых наборах (множествах) отдельных объектов, называемых членами или элементами множества.

Сколько чисел есть между 0 и 1?

Первая публикация Кантора, состоящая из четырёх с половиной страниц, является великолепным примером краткости. Она разделена на два отдельных доказательства, совместно приводящих к выводу о существовании по крайней мере двух уникальных видов множеств.

В первой части теории исследуется множество вещественных алгебраических чисел и доказывается, что это бесконечное счётное множество. Здесь не стоит путать — «счётное» не обязательно значит, что счёт ведётся строго в целых числах; в контексте теории множеств «счётное» означает, что множество, пусть даже состоящее из бесконечного числа элементов, можно описать повторяющимся рядом, например упорядоченной многочленной функцией. Кантор назвал это свойство бесконечного набора чисел соответствия «один к одному» с рядом, наличием взаимно однозначного соответствия.

Если говорить вкратце, то набор, или множество всех вещественных алгебраических чисел можно вывести с помощью какого-то теоретического ряда многочленов с различными степенями и коэффициентами; следовательно, множество всех вещественных алгебраических чисел является бесконечным счётным множеством.

Во второй части труда Кантора анализируется роль вещественных комплексных чисел, также называющихся трансцендентными числами. Транцендентные числа (лучшие примеры которых — это пи и e) имеют любопытное свойство: математически невозможно вывести их с помощью многочленной функции — они не являются алгебраическими. Вне зависимости от величин, количества частей, степеней или коэффициентов, никакой ряд никогда не может посчитать пи в своём наборе бесконечного счётного множества.

Затем Кантор указывает, что в любом замкнутом интервале [a,b] существует хотя бы одно транцендентное число, которое никогда нельзя будет подсчитать в бесконечном счётном множестве. Поскольку одно такое число существует, то предполагается, что в семействе вещественных чисел существует бесконечное количество транцендентных чисел.

Таким образом он доказал очень чёткое различие между множеством непрерывных, идущих потоком несчётных чисел и набора счётных чисел, которые можно представить как ряд, например, всех вещественных алгебраических чисел.

Далее: запись и операции

Первая публикация Кантора завершилась на этом потрясающем подтверждении существования по крайней мере двух разных видов бесконечности. После его первой статьи появился шквал дополнений, медленно, но верно прокладывавших путь к современной теории множеств.

Стоит также поделиться интересным наблюдением: большинство людей, использующих теорию множеств на практике, ценят скорее не эту конкретную теорему, а заданный ею обобщённый язык. Благодаря своей абстрактной природе теория множеств скрытно влияет на множество областей математики. В математическом анализе, который требует дифференциального и интегрального исчисления, необходимо понимание пределов и непрерывности функций, окончательно закреплённых в теории множеств. В алгебре логики логические операции «и», «или» и «не» соответствуют операциям пересечения, объединения и разности в теории множеств. И последнее, но не менее важное — теория множеств закладывает основы топологии — исследования геометрических свойств и пространственных отношений.

Вооружившись базовым пониманием истории множеств и совершив кратковременное погружение в глубины его влияния, мы можем приступать к знакомству с основами системы обозначений теории множеств.

Часть вторая. Краткий обзор операций, обозначений и диаграмм Венна.

Как сказано в предыдущей части, одно из фундаментальных преимуществ теории множеств произрастает не из какой-то конкретной теории, а из созданного ею языка. Именно поэтому основная часть этого раздела будет посвящена обозначениям, операциям и визуальному представлению теории множеств. Давайте начнём с объяснения базовых символов обозначения множества — соответствующих ему элементов. В таблице ниже показан пример одного множества A с тремя элементами:

A — это множество с элементами «1», «2» и «3»

«1» — элемент множества A

В первой строке показано множество A с тремя отдельными элементами (A = {1,2,3}); во второй строке показан правильный способ обозначения отдельного конкретного элемента 1, принадлежащего множеству A. Пока всё довольно просто, но теория множеств становится существенно интереснее, когда мы добавляем второе множество — начинается путешествие по стандартным операциям.

Для показанной выше таблицы давайте введём два дополнительных множества B и C, содержащие следующие элементы: B = {3,A,B,C,D,E}, C = {1,2}. Хоть мы и создали три множества (A,B и C), в показанных ниже примерах операции выполняются одновременно только с двумя множествами, поэтому внимательно следите за тем, какие множества указаны в самом левом столбце. В показанной ниже таблице представлено пять самых распространённых операндов множеств:

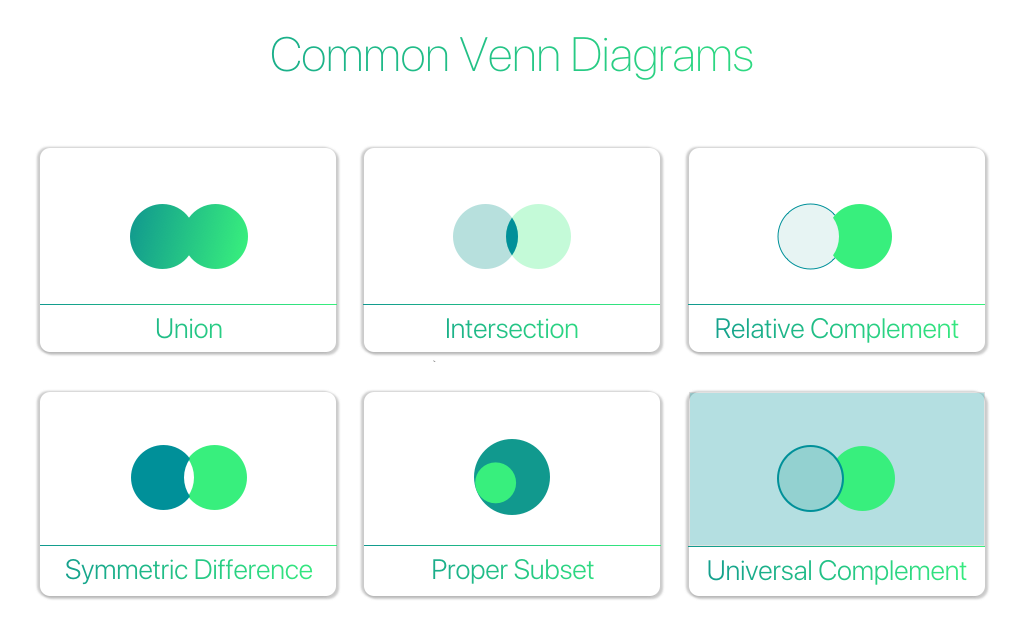
Операции: пересечение (intersection) — множество элементов, принадлежащих множеству A и множеству B;

объединение (union) — множество элементов, принадлежащих множеству A или множеству B;

подмножество (subset) — C является подмножеством A, множество C включено во множество A;

собственное (истинное) подмножество — C является подмножеством A, но C не равно A;

относительное дополнение (relative complement) — множество элементов, принадлежащих к A и не к B.

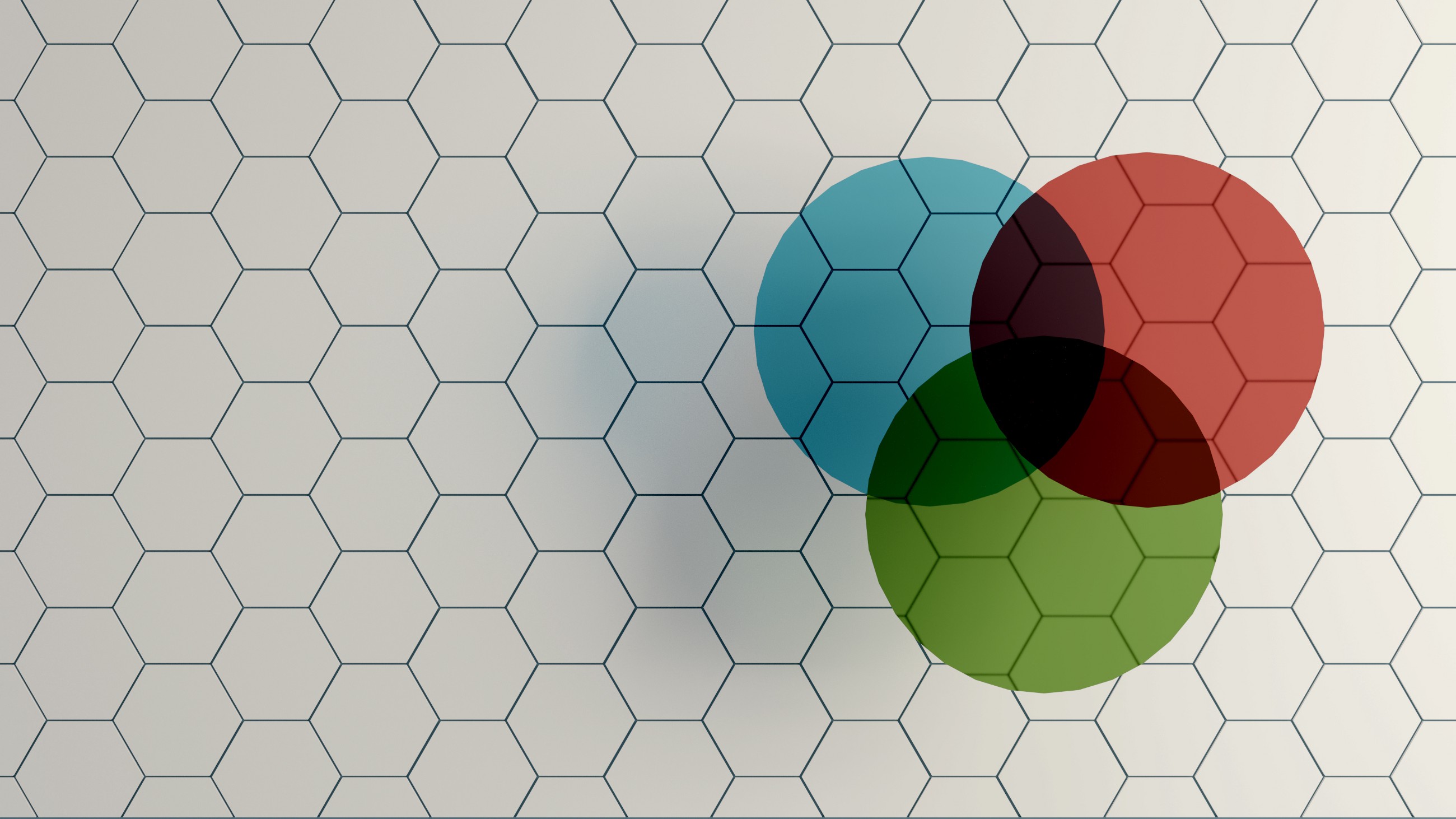
Вот и они, самые распространённые операции в теории множеств; они довольно популярны и в областях за пределами чистой математики. На самом деле, высока вероятность того, что вы уже видели подобные типы операций в прошлом, хоть и не совсем с такой терминологией, и даже пользовались ими. Хорошая иллюстрация: попросите любого студента описать диаграмму Венна из двух пересекающихся групп, и он интуитивно придёт к правильному результату.

Ещё раз взгляните на последнюю строку, относительное дополнение — какое необычное сочетание слов, правда? Относительное к чему? Если относительное дополнение A — B определяется как A и не B, то как нам обозначить всё, что не является B?

Универсальное множество — пустое множество

Оказывается, если мы хотим получить значимый ответ, то для начала нужно предоставить генеральной совокупности нашей задачи множеств некий контекст. Он часто явным образом задаётся в начале задачи, когда допустимые элементы множества ограничиваются некоторым фиксированным классом объектов, в котором существует универсальное множество, являющееся общим множеством, содержащим все элементы для этой конкретной задачи. Например, если мы хотели бы работать со множествами только из букв английского алфавита, то наше универсальное множество U состояло бы из 26 букв алфавита.

Для любого подмножества A множества U дополнение множества A (обозначаемое A′ или U − A) определяется как множество всех элементов в генеральной совокупности U, которое не находится в A. Если вернуться к поставленному выше вопросу, то дополнением множества B является всё в пределах универсального множества, что не принадлежит B, в том числе и A.

Прежде чем мы двинемся дальше, надо упомянуть ещё одно принципиальное множество, которое достаточно важно для базового понимания: нулевое или пустое множество. Учтите, что существует единственное пустое множество, поэтому никогда не говорят «пустые множества». Хотя мы не будем рассматривать в этой статье эквивалентность, основная теория гласит, что два множества эквивалентны, если они имеют одинаковые элементы; следовательно, может быть только одно множество без элементов. Поэтому существует единственное пустое множество.

Диаграммы Венна и остальное

Диаграммы Венна, официально изобретённые в 1880 году Джоном Венном, являются именно тем, что вы и представляете, хотя их научное определение звучит примерно так:

Схематичное изображение всех возможных отношений нескольких множеств

Ниже показано изображение шести самых распространённых диаграмм Венна, и почти во всех показаны недавно изученные нами операнды:

Объединение (union), пересечение (intersection), относительное дополнение (relative complement), симметрическая разность (symmetric difference), собственное множество (proper subset), абсолютное дополнение (universal дополнение).

Начав с очень простых обозначений множества и его элементов, мы узнали затем о базовых операциях, позволивших нарисовать эту визуальную подсказку. Мы рассмотрели все операции, за исключением симметрической разности (внизу слева). Чтобы не оставлять пробелов в знаниях, скажем, что симметрическая разность, также называемая дизъюнктивным объединением — это просто множество элементов, которые находятся в любом из множеств, но не входят в их пересечение.

Закончим мы этот раздел введением понятия мощности (кардинального числа). Мощность множества, обозначаемая символом абсолютного значения — это просто количество уникальных элементов, содержащихся в определённом множестве. Для показанного выше примера мощность трёх множеств равна: |A| = 3, |B| =6, |C| = 2.

Прежде чем двигаться дальше, дам вам пищу для размышлений — какова связь между мощностью и количеством возможных подмножеств?

Часть 3. Мощность и показательные множества

В предыдущих двух частях мы разобрались с основами теории множеств. В третьей части мы укрепим своё понимание, сосредоточившись на самом важном свойстве любого множества: общем количестве содержащихся в нём уникальных элементов.

Количество уникальных элементов во множестве, также известное как мощность, предоставляет нам фундаментальную опорную точку для дальнейшего, более глубокого анализа этого множества. Во-первых, мощность — это первое из рассматриваемых нами уникальных свойств, позволяющее нам объективно сравнивать различные виды множеств, проверяя, существует ли биекция (это, с небольшими оговорками, просто более изысканный термин для function ) одного множества на другое. Ещё один способ применения мощности, а также тема этой части статьи — мощность позволяет оценить все возможные подмножества, существующие в данном множестве. Что достаточно буквально можно применять в повседневных задачах распределения решений, будь то планирование бюджета на поездку в продуктовый магазин или оптимизация портфеля акций.

Примеры мощности множеств

Например, в таблице выше показаны пять отдельных множеств с их указанной справа мощностью. Как мы уже говорили, символ мощности напоминает символ абсолютного значения — значение, заключённое между двумя вертикальными линиями. Все примеры понятны, за исключением, возможно, последней строки, которая подчёркивает тот факт, что на мощность влияют только уникальные элементы множества.

Помните подмножества из предыдущей части статьи? Оказывается, что мощность некоторого множества A и количество возможных подмножеств множества A имеют удивительную связь. Ниже показано, что количество подмножеств, которые можно составить из некоторого подмножества, увеличивается с порядком мощности на предсказуемую величину:

Количество возможных подмножеств в C= 2^|C|

Давайте подробно рассмотрим показанный ниже пример. Однако для начала поразмыслим над формулой. Представим мощность как общее количество «позиций», которое представляет множество. При создании некоторого подмножества для каждой возможной позиции принимается булево решение (да/нет). Это означает, что каждый уникальный элемент, добавляемый к множеству (то есть увеличивающий мощность на единицу) увеличивает количество возможных подмножеств на множитель два. Если вы программист или учёный, то можете уяснить эту логику немного глубже, если поймёте, что все подмножества множества можно вычислить с помощью таблицы двоичных чисел.

Показательное множество (булеан)

Прежде чем мы вычислим все подмножества для примера множества C, я хотел бы ввести последнее понятие — булеан.

Булеан обозначается заглавной буквой S, за которой в скобках указывается исходное множество S(С). Булеан — это множество всех подмножеств C, включая пустое множество и само множество C. В таблице ниже показан булеан S(С) со всеми перестановками возможных подмножеств для множества C, содержащихся в одном большом множестве.

Для удобства форматирования я убрал запятые между множествами***

Чем может быть полезен булеан? На самом деле, вы скорее всего много раз интуитивно использовали булеаны, даже об этом не догадываясь. Каждый раз, когда вы выбираете подмножество элементов из более крупного множества, вы выбираете элемент булеана. Например ребёнок внимательно изучающий кондитерский магазин с купюрой в 5 долларов — какой элемент булеана множества всех доступных сладостей он выберет? Или если взять более технический пример: вам, как разработчику ПО может потребоваться запросить всех возможных пользователей базы данных, также обладающих свойством X и Y — ещё один случай, в котором одно подмножество выбирается из всех возможных подмножеств.

Эквивалентность и биективная функция

Теперь мы понимаем, что такое мощность множества, почему оно важно, и его связь с булеаном. Поэтому вернёмся ненадолго к тому, что упоминали в самом начале: что конкретно определяет эквивалентность в теории множеств?

Очевидно, что два множества с одинаковой мощностью имеют некое общее свойство, но на этом сходства заканчиваются — что если в одном из множеств есть многократно повторяющийся элемент? Что если два множества имеют одинаковую мощность и количество элементов? Нельзя отрицать, что они в какой-то степени «эквивалентны», но даже в этом случае всё равно есть возможность различий, потому что каждое множество может иметь разные элементы, повторяющиеся одинаковое количество раз. Смысл здесь в том, что концепция эквивалентности в теории множеств немного чужда другим областям математики. Установление эквивалентности в этом мире требует знакомства с этой концепцией и нового языка. В последней части этой статьи мы введём понятие эквивалентности, а также таких базисных свойств, как инъективные, биективные и сюръективные функции.

Часть 4. Функции.

В этой части мы подробнее расскажем о функциях в пределах теории множеств. Как и в случае с предыдущими понятиями, терминология стандартных функций в теории множеств слегка отличается от других областей математики, а потому требует объяснения. Терминологии довольно много, так что давайте сразу приступим к делу! В первой таблице внизу отражены понятия области определения, области значений и значения функции:

Функция в мире теории множеств — это просто соответствие некоторых (или всех) элементов из Множества A некоторым (или всем) элементам Множества B. В показанном выше примере набор всех возможных элементов A называется областью определения; элементы A, используемые в качестве входных значений, в частности называются аргументами. Справа набор всех возможных выходных значений (называющихся в других областях математики «областью значений»), называется кообластью; набор настоящих выходных элементов B, соответствующих A, называется образом.

Пока особо ничего сложного, только новый способ задания параметров функций. Далее мы расскажем о том, как описывать поведения этих функций соответствия при помощи обычных типов функций.

Инъекции, сюръекции и биекции

В теории множеств для классификации соответствия множеств обычно используются три понятия: инъекция, сюръекция и биекция. К сожалению, эти понятия имеют несколько разных названий, усиливающих неразбериху, поэтому мы сначала рассмотрим каждое определение, а затем изучим визуальные примеры. Все три термина описывают способ, которым отображаются аргументы на образы:

Функция является инъективной (или «один к одному»), если каждый элемент в кообласти отображается не более чем на один элемент в области определения.
Функция является сюръективной, если каждый элемент в кообласти отображается не менее чем на один элемент в области определения. (то есть образ и кообласть функции эквивалентны.)
Функция является биективной, если каждый элемент кообласти отображается ровно на один элемент области определения.

Вишенкой на торте этих сложных определений стали возможные дополнительные значения слов «инъективный», «сюръективный» и «биективный». Когда они используются для описания функции (соответствия), верным будет представленное выше значение; однако также верно будет идентифицировать функции (соответствия) исключительно по этим характеристикам. То есть функция с инъективным поведением называется инъекцией, функция с сюръективным поведением — сюръекцией, а функция с биективным поведением — биекцией.

Прочитайте заново представленный выше список пунктов. Биекция — это просто функция, удовлетворяющая обоим предыдущим требованиям; то есть, функция инъективна и сюръективна. Инъективная функция не должна быть сюръективной, а сюръективная — инъективной. Ниже показан визуальный пример, в котором эти три классификации привели к созданию функций множеств, определяемых четырьмя возможными комбинациями инъективных и сюръективных свойств:

Биекция (инъекция + сюръекция), инъекция (инъекция + не-сюръекция), сюръекция (не-инъекция + сюръеция), без классификации (не-инъекция + не-сюръекция)

Вот и всё! Теперь мы обладаем элементарным пониманием самых часто встречаемых соотношений, встречающихся в мире множеств. Однако это ни в коем случае не конец нашего пути: напротив, это самое начало.

Фундаментальные основы теории множеств — ключ к пониманию более высокоуровневых областей математики. Чтобы продолжить наше движение вверх, к этим различным областям, далее нужно будет, пользуясь своими знаниями о теории множеств, уяснить одну из самых революционных теорий в истории математики: систему аксиом Цермело-Френкеля.

Источник

2.1. Мощность. Счетные множества

Количество
элементов конечных множеств может быть
выражено неотрицательным целым числом.
Для оценки количества элементов в
бесконечных множествах вводится
обобщенное понятие числа — мощность,
которая для конкретного множества А
обозначается как 
А.
На конечных множествах она совпадает
с числом элементов, ее можно определить
простым подсчетом.

Пример 1. a,b,c=3;
1,…,10}=10.

Для
исследования мощности бесконечных
множеств используют отображения.

Определение. Множества
А
и В
называют эквивалентными
(имеющими одинаковую мощность),
если между ними можно установить взаимно
однозначное отображение. Обозначают
как: | А|=|
В|.

Для
конечных множеств эквивалентность
означает равенство чисел элементов.

Рассмотрим
самый простой вид бесконечных множеств.

Определение. Cчетными
называют все множества, эквивалентные
множеству N
натуральных чисел. Мощность N
обозначают ₀
(алеф нуль, алеф – первая буква
древнееврейского алфавита):
N
= ₀.

Основное свойство
счетных множеств заключается в том, что
их элементы можно пронумеровать числами
натурального ряда. Это позволяет
использовать различные алгоритмы их
последовательной обработки.

Вопрос о допустимости
использования в математике бесконечных
величин и множеств занимал умы мыслителей
еще с древности. Уже тогда признавалось
существование потенциальной
бесконечности,
под которой понимается отсутствие
предела у возрастающих числовых
последовательностей, например у
натурального ряда N.

В то же время,
многие видные ученые, начиная с античности
(Аристотель) до второй половины XIX
века (Лейбниц, Гаусс, Коши и др.), выступали
против признания и использования в
математике актуальной
бесконечности,
при которой бесконечные множества в
символьном виде вводятся в формулы,
подобно обычным конечным, и с ними
допускается выполнение различных
действий.

Переворот совершил
в конце XIX
века немецкий математик Георг Кантор,
который вопреки существовавшему мнению,
ввел в математику актуально-бесконечные
множества, доказав целый ряд теорем,
раскрывающих их свойства.

Пример 2. Найдем
мощность множества N₂всех четных
положительных чисел (делящихся без
остатка на 2).

Решение. Все
числа в N₂
имеют вид:
n₂=2n,
где nN.
Отображение f:NN₂,
задаваемое этой зависимостью, является
линейным с ненулевым линейным коэффициентом
(С₀=2).
Как доказано ранее, оно взаимно однозначно.
По определению множества N₂
и N
эквивалентны.
Таким образом,
множество N₂так же
счетно, как и N,
N₂
=N
= ₀.

Пример 3. Найти
мощность множества Z
всех целых чисел
в интервале (– ;
+ ).

Решение. Аналогично
доказываем Z₀
путем построения взаимно однозначного
отображения
f
: Z
N. Разобьем
Z
на два подмножества: N,
N_—,
где N_——
неположительные целые числа (0 и все
отрицательные). Обозначим через N₂
множество натуральных четных чисел,
через
— множество натуральных нечетных чисел
({1,3,5,7,…}).

Искомое
отображение f
строим из двух отдельных взаимно
однозначных отображений следующим
образом:

N
N₂; n₂= 2n;

N_—;n_₂= –2n_—+1.

И
первая и вторая части построенного
отображения являются линейными с
ненулевыми линейными коэффициентами
(С₀=2,

–2),
следовательно,
они взаимно однозначны. Так как
Z
= NN_—;
N=N₂,
то искомое взаимно однозначное отображение
построено. Следовательно, Z=N
=₀.

Замечание. Взаимно
однозначное отображение может быть
построено различными способами. В
примере 3 его можно указать, например,
следующим образом:

A:
0 1 2 –1
–2 3 4 …

       …

N:
1 2 3 4 5
6 7 …

Пример 4. Найти
мощность множества A
рациональных чисел в сегменте [0,1].

Решение. По
определению рациональными являются
числа, которые могут быть представлены
в виде a =

n /
m, где n,
m — целые
числа, n ≥
0, m >
0. На сегменте [0,1]
n 
m. Упорядочить
данные числа можно следующим образом.
В первой строке расположить числа, где
после сокращения числителя и знаменателя
знаменатель равен 1; во второй —
несократимые числа со знаменателем 2,
не вошедшие в строку 1; в третьей —
несократимые числа со знаменателем
3,не
вошедшие в строки 1 и 2, и т.д.

В итоге получаем
таблицу:

m=1:
0/1, 1/1;

m=2:
1/2;

m=3:
1/3,2/3;

m=4:
1/4, 3/4;

…

Таблица
содержит все числа из А,
причем каждое входит ровно один раз.
Если задать порядок по строкам таблицы
сверху вниз и внутри строк слева направо,
то каждому ее элементу можно взаимно
однозначно поставить в соответствие
свой порядковый номер — натуральное
число:

0/1

1, 1/1 
2, 1/23,
1/34,
2/35,
1/46,
3/47,…

Отсюда
следует, что построено взаимно однозначное
отображение
f
: AN
,

₀.

Пример 5. Найти
мощность множества A
рациональных чисел на всей числовой
оси (–;
+).

Решение. Рациональные
числа в А
можно представить в виде a
= 
n /
m,
где n, m —
целые неотрицательные числа (m

0). Упорядочиваем их аналогично рациональным
числам из [0,1], рассматривая вместо
знаменателей веса чисел W
= n
+ m.
Таблица будет иметь вид:

W=1:
0/1;

W=2:
+1/1; –1/1;

W=3:
+2/1; +1/2; –1/2; –2/1;

…

Вводя
пересчет элементов по аналогии с примером
4, также можно показать, что в данном
случае 

₀.

Для
практического определения счетной
мощности
множеств можно использовать следующие
утверждения.

Теорема
2.1. Любое
подмножество B
счётного множества А
конечно или счётно.

Доказательство.
Упорядочим элементы множества А
= {a₁,
a₂,
…} и удалим
из него все элементы, не входящие в В.
При этом всегда будет получено
упорядоченное конечное или бесконечное
(счетное) множество элементов, составляющее
подмножество B.

Теорема
2.2. Объединение
любого конечного или счётного числа
счетных множеств тоже всегда является
счётным множеством.

Доказательство.
Допустим, есть конечное или счётное
число множеств А₁,
А₂,
А₃,
… .
Объединение
их обозначим через А.
В общем случае А₁,
А₂,
А₃,
… могут
пересекаться, поэтому перейдем к
непересекающимся множествам В₁= А₁;
В₂= (A₂ A₁);
В₃= (A₃ (A₁
A₂))
и т. д.
Очевидно, 
B_i= = 
A_i= A.
Мощность числа элементов в каждом
множестве B_i
не превышает счётную. Поэтому их можно
записать в виде упорядоченной
последовательности (b_i₁,
b_i₂,
…).
Объединяя
такие записи множеств B₁,B₂,…,
получим запись элементов всего исходного
множества А
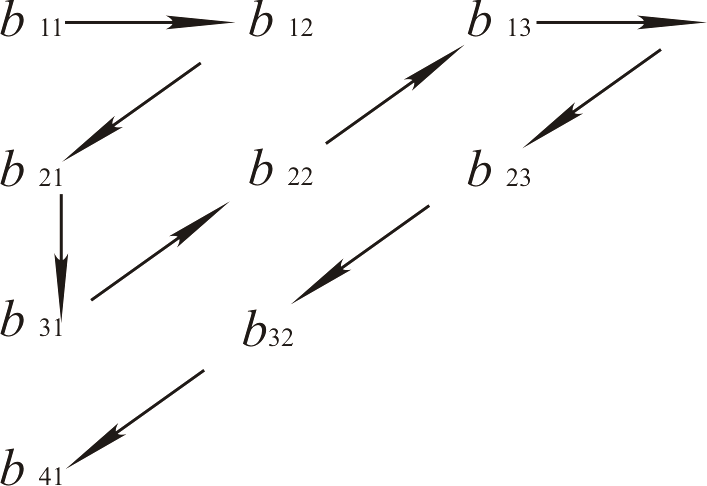
в виде таблицы:

b₁₁b₁₂b₁₃…

b₂₁b₂₂ b₂₃…

b₃₁
b₃₂
b₃₃…

…

В
этой таблице все элементы А
присутствуют ровно один раз. Для
доказательства счетности множества А
графически укажем на рис.2.1 способ
упорядочения его элементов (сопоставления
их числам из натурального ряда).

Рис. 2.1

Данный
способ упорядочения задает взаимно
однозначное отображение множества А
на N. Отсюда
следует: ₀.

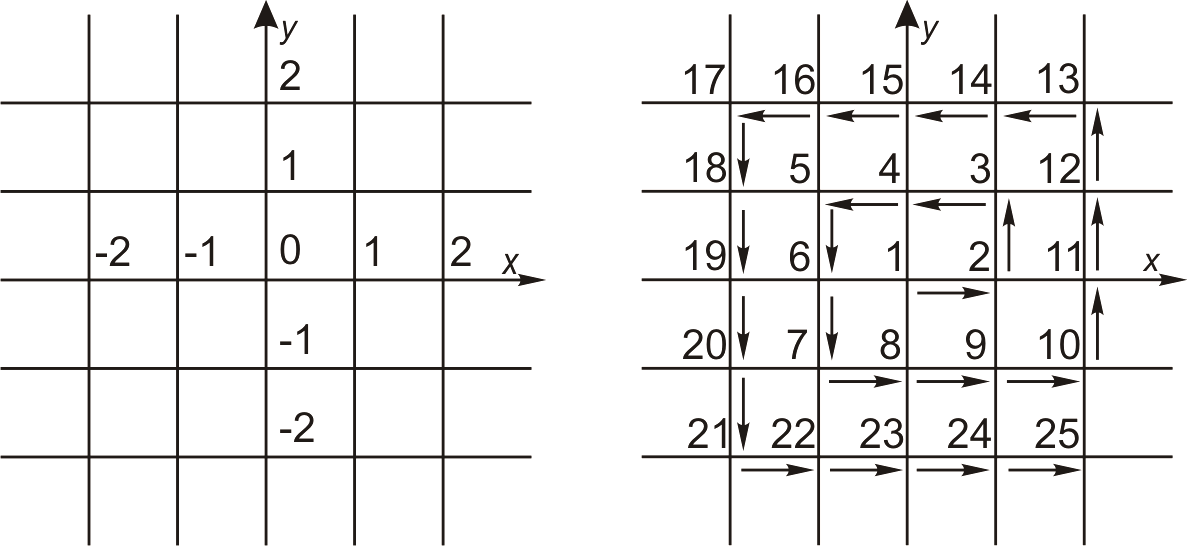
Пример 6. На
плоскости (x,
y) задана
ортогональная сетка с шагом 1 (рис.2.2).
Найти мощность множества А
узлов сетки.

Решение. Мощность
множества горизонтальных линий равна
мощности множества всех целых чисел Z.
Выше показано, что оно счетно. Также
счетно множество вертикальных линий.
По доказанной ранее теореме о счетной
сумме счетных множеств получим:
А
= ₀.

Рис.
2.2 Рис. 2.3

Замечание.
Задачу можно решить, непосредственно
указав взаимно однозначное отображение
f:
A
N.
Например, так, как показано на рис. 2.3.

Для практического
сравнения мощностей множеств также
может быть использована теорема,
сформулированная Кантором и доказанная
Шредером и Бернштейном.

Теорема
2.3. Кантора-Бернштейна.
Пусть А
и В
— некоторые произвольные множества.
Если А
эквивалентно некоторому подмножеству
В₁
множества В,
а В
— некоторому подмножеству А₁
из А,
то А
эквивалентно В:А=В.

Доказательство
производится путем построения взаимно
однозначного отображения между А
и В.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Достаточно часто в математической науке возникает ряд трудностей и вопросов, причем многие ответы не всегда проясняются. Не исключением стала такая тема, как мощность множеств. По сути, это не что иное как численное выражение количества объектов. В общем смысле множество является аксиомой, у него нет определения. В основе лежат любые объекты, а точнее их набор, который может носить пустой, конечный или бесконечный характер. Кроме этого, он содержит числа целые или натуральные, матрицы, последовательности, отрезки и прямые.

О существующих переменных

Нулевой или пустой набор, не имеющий собственного значения, считается элементом мощности, так как это подмножество. Сбор всех подмножеств непустого множества S является множеством множеств. Таким образом, набор мощности заданного множества считается многим, мыслимым, но единым. Это множество называется множеством степеней S и обозначается P (S). Если S содержит N элементов, то P (S) содержит 2 ^ n подмножеств, так как подмножество P (S) является либо ∅, либо подмножеством, содержащим r элементов из S, r = 1, 2, 3, … Составленное из всего бесконечного множества M называется степенным количеством и символически обозначается P (M).

Элементы теории множеств

Эта область знаний была разработана Джорджем Кантором (1845-1918 годы жизни). Сегодня она используется почти во всех отраслях математики и служит ее фундаментальной частью. В теории множеств элементы представлены в форме списка и заданы типами (пустой набор, одноэлементный, конечные и бесконечные множества, равные и эквивалентные, универсальные), объединение, пересечение, разность и дополнение чисел. В повседневной жизни часто говорится о коллекции таких объектов, как куча ключей, стая птиц, пачка карточек и т. д. В математике 5 класса и не только, встречаются натуральные, целые, простые и составные числа.

Можно рассмотреть следующие множества:

натуральные числа;
буквы алфавита;
первичные коэффициенты;
треугольники с разными значениями сторон.

Видно, что эти указанные примеры представляют собой четко определенные множества объектов. Рассмотрим еще несколько примеров:

пять самых известных ученых мира;
семь красивых девушек в обществе;
три лучших хирурга.

Эти примеры мощности множества не являются четко определенными коллекциями объектов, потому, что критерий «наиболее известных», «самых красивых», «лучших» варьируется от человека к человеку.

Наборы

Это значение представляет собой четко определенное количество различных объектов. Предположив, что:

набор слов является синонимом, агрегатом, классом и содержит элементы;
объекты, члены являются равными по значению терминами;
наборы обычно обозначаются прописными буквами A, B, C;
элементы набора представлены маленькими буквами a, b, c.

Если «a» — элемент множества A, то говорится, что «a» принадлежит A. Обозначим фразу «принадлежит» греческим символом «∈» (epsilon). Таким образом, выходит, что a ∈ A. Если ‘b’ — элемент, который не принадлежит A, это представляется как b ∉ A. Некоторые важные наборы, используемые в математике 5 класса, представляют, используя три следующих метода:

заявки;
реестров или табличные;
правило создания построения.

При детальном рассмотрении форма заявления основана на следующем. В этом случае задано четкое описание элементов множества. Все они заключены в фигурные скобки. Например:

множество нечетных чисел, меньших 7 — записывается как {меньше 7};
набор чисел больше 30 и меньше 55;
количество учеников класса, вес которых больше, чем учителя.

В форме реестра (табличной) элементы набора перечислены в паре скобок {} и разделены запятыми. Например:

Пусть N обозначает множество первых пяти натуральных чисел. Следовательно, N = → форма реестра
Набор всех гласных английского алфавита. Следовательно, V = {a, e, i, o, u, y} → форма реестра
Множество всех нечетных чисел меньше 9. Следовательно, X = {1, 3, 5, 7} → форма реестра
Набор всех букв в слове «Математика». Следовательно, Z = {M, A, T, H, E, I, C, S} → Форма реестра
W — это набор последних четырех месяцев года. Следовательно, W = {сентябрь, октябрь, ноябрь, декабрь} → реестр.

Стоит отметить, что порядок, в котором перечислены элементы, не имеет значения, но они не должны повторяться. Установленная форма построения, в заданном случае правило, формула или оператор записываются в пару скобок, чтобы набор был корректно определен. В форме set builder все элементы должны обладать одним свойством, чтобы стать членом рассматриваемого значения.

В этой форме представления набора элемент множества описывается с помощью символа «x» или любой другой переменной, за которой следует двоеточие («:» или «|» используется для обозначения). Например, пусть P — множество счетных чисел, большее 12. P в форме set-builder написано, как — {счетное число и больше 12}. Это будет читаться определенным образом. То есть, «P – множество элементов x, такое, что x является счетным числом и больше 12».

Решенный пример с использованием трех методов представления набора: количество целых чисел, лежащих между -2 и 3. Ниже приведены примеры различных типов наборов:

Пустой или нулевой набор, который не содержит какого-либо элемента и обозначается символом ∅ и считывается как phi. В форме списка ∅ имеет написание {}. Пустым является конечное множество, так как число элементов 0. Например, набор целых значений меньше 0.
Очевидно, что их не должно быть <0. Следовательно, это пустое множество.
Набор, содержащий только одну переменную, называется одноэлементным множеством. Не является ни простым, ни составным.

Конечное множество

Множество, содержащее определенное число элементов, называется конечным либо бесконечным множеством. Пустое относится к первому. Например, набор всех цветов в радуге.

Бесконечное количество – это набор. Элементы в нем не могут быть перечислены. То есть, содержащий подобные переменные, называется бесконечным множеством. Примеры:

мощность множества всех точек в плоскости;
набор всех простых чисел.

Но стоит понимать, что все мощности объединения множества не могут быть выражены в форме списка. К примеру, вещественные числа, так как их элементы не соответствуют какой-либо конкретной схеме.

Кардинальный номер набора – это число различных элементов в заданном количестве A. Оно обозначается n (A).

Например:

A {x: x ∈ N, x <5}. A = {1, 2, 3, 4}. Следовательно, n (A) = 4.
B = набор букв в слове ALGEBRA.

Эквивалентные наборы для сравнения множеств

Две мощности множества A и B являются таковыми, если их кардинальное число одинаково. Символом для обозначения эквивалентного набора является «↔». Например: A ↔ B.

Равные наборы: две мощности множества A и B, если они содержат одни и те же элементы. Каждый коэффициент из A является переменной из B, и каждый из B является указанным значением A. Следовательно, A = B. Различные типы объединения множеств в мощности и их определения объясняются с помощью указанных примеров.

Сущность конечности и бесконечности

Каковы различия между мощностью конечного множества и бесконечного?

Для первого значения характерно следующее название, если оно либо пустое, либо имеет конечное число элементов. В конечном множестве переменная может быть указана, если она имеет ограниченный счет. Например, с помощью натурального числа 1, 2, 3. И процесс листинга заканчивается на некотором N. Число различных элементов, отсчитываемых в конечном множестве S, обозначается через n (S). А также называется порядком или кардинальным. Символически обозначается по стандартному принципу. Таким образом, если множество S является русским алфавитом, то оно содержит в себе 33 элемента. Также важно запомнить, что элемент не встречается более одного раза в наборе.

Бесконечное количество в множестве

Множество называется бесконечным, если элементы не могут быть перечислены. Если оно имеет неограниченное (то есть несчетное) натуральное число 1, 2, 3, 4 для любого n. Множество, которое не является конечным, называется бесконечным. Теперь можно обсудить примеры рассматриваемых числовых значений. Варианты конечного значения:

Пусть Q = {натуральные числа меньше 25}. Тогда Q — конечное множество и n (P) = 24.
Пусть R = {целые числа между 5 и 45}. Тогда R — конечное множество и n (R) = 38.
Пусть S = {числа, модуль которых равен 9}. Тогда S = {-9, 9} является конечным множеством и n (S) = 2.
Набор всех людей.
Количество всех птиц.

Примеры бесконечного множества:

количество существующих точек на плоскости;
число всех пунктов в сегменте линии;
множество положительных целых чисел, кратных 3, является бесконечным;
все целые и натуральные числа.

Таким образом, из приведенных выше рассуждений понятно, как различать конечные и бесконечные множества.

Мощность множества континуум

Если провести сравнение множества и других существующих значений, то к множеству присоединено дополнение. Если ξ – универсальное, а A – подмножество ξ, то дополнение к A является количеством всех элементов ξ, которые не являются элементами A. Символически обозначается дополнение A относительно ξ как A’. К примеру, 2, 4, 5, 6 являются единственными элементами ξ, которые не принадлежат A. Следовательно, A’= {2, 4, 5, 6}

Множество с мощностью континуум имеет следующие особенности:

дополнением универсального количества является пустое рассматриваемое значение;
эта переменная нулевого множества является универсальным;
количество и его дополнение являются непересекающимися.

Например:

Пусть количество натуральных чисел является универсальным множеством и А – четное. То, тогда A ‘{x: x – множество нечетное с такими же цифрами}.
Пусть ξ = множество букв в алфавите. A = набор согласных. Тогда A ‘= количество гласных.
Дополнением к универсальному множеству является пустое количество. Можно обозначить через ξ. Тогда ξ ‘= Множество тех элементов, которые не входят в ξ. Пишется и обозначается пустое множество φ. Поэтому ξ = φ. Таким образом, дополнение к универсальному множеству является пустым.

В математике «континуум» иногда используется для обозначения реальной линии. И в более общем плане, для описания подобных объектов:

континуум (в теории множеств) — вещественная линия или соответствующее кардинальное число;
линейный — любое упорядоченное множество, которое разделяет определенные свойства реальной прямой;
континуум (в топологии) — непустое компактное связное метрическое пространство (иногда хаусдорфово);
гипотеза о том, что никакие бесконечные множества больше целых чисел, но меньшие, чем действительные числа;
мощность континуума — кардинальное число, представляющее размер множества действительных чисел.

По существу дела, континуум (измерение), теории или модели, которые объясняют постепенные переходы из одного состояния в другое без каких-либо резких изменений.

Проблемы объединения и пересечения

Известно, что пересечение двух или более множеств – это количество, содержащее все элементы, которые являются общими в этих значениях. Задачи Word на множествах решаются, чтобы получить основные идеи о том, как использовать свойства объединения и пересечения множеств. Решенные основные проблемы слов на множествах выглядят так:

Пусть A и B – два конечных множества. Они представляют собой такие, что n (A) = 20, n (B) = 28 и n (A ∪ B) = 36, находится n (A ∩ B).

Связь в наборах с использованием диаграммы Венна:

Объединение двух множеств может быть представлено заштрихованной областью, представляющей A ∪ B. A ∪ B, когда A и B – непересекающиеся множества.
Пересечение двух множеств может быть представлено диаграммой Венна. С затененной областью, представляющей A ∩ B.
Разность двух наборов может быть представлена диаграммами Венна. С заштрихованной областью, представляющей A — B.
Связь между тремя наборами, использующими диаграмму Венна. Если ξ представляет универсальное количество, то A, B, C – три подмножества. Здесь все три набора являются перекрывающимися.

Обобщение информации о множестве

Мощность множества определяется как общее количество отдельных элементов в наборе. А последнее указанное значение описывается как количество всех подмножеств. При изучении подобных вопросов требуются методы, способы и варианты решения. Итак, у мощности множества примерами могут служить следующие:

Пусть A = {0,1,2,3}| | = 4, где | A | представляет мощность множества A.

Теперь можно найти свой набор мощности. Это тоже довольно просто. Как уже сказано, набор мощности установлен из всех подмножеств заданного количества. Поэтому нужно в основном определить все переменные, элементы и другие значения A, которые {}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, { 2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}.

Теперь мощность выясняет P = {{}, {0}, {1}, {2}, {3}, {0,1}, {0,2}, {0,3}, {1,2}, {1,3}, {2,3}, {0,1,2}, {0,1,3}, {1,2,3}, {0,2,3}, {0,1,2,3}}, который имеет 16 элементов. Таким образом, мощность множества A = 16. Очевидно, что это утомительный и громоздкий метод решения этой проблемы. Однако есть простая формула, по которой, непосредственно, можно знать количество элементов в множестве мощности заданного количества. | P | = 2 ^ N, где N — число элементов в некотором A. Эта формула может быть получена применением простой комбинаторики. Таким образом, вопрос равен 2 ^ 11, поскольку число элементов в множестве A равно 11.

Итак, множеством является любое численно выраженное количество, которое может быть всевозможным объектом. К примеру, машины, люди, числа. В математическом значении это понятие шире и более обобщенное. Если на начальных этапах разбираются числа и варианты их решения, то в средних и высших стадиях условия и задачи усложнены. По сути, мощность объединения множества определена принадлежностью объекта к какой-либо группе. То есть один элемент принадлежит к классу, но имеет одну или несколько переменных.

Источник

Мо́щность мно́жества, кардина́льное число́ мно́жества (лат. cardinalis ← cardo «главное обстоятельство; стержень; сердцевина») — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.

В основе этого понятия лежат естественные представления о сравнении множеств:

Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность).
Обратно: множества, равные по мощности, должны допускать такое взаимно-однозначное соответствие.
Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).

До построения теории мощности множеств множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.

Мощность множеств позволяет сравнивать бесконечные множества.
Например, счётные множества являются самыми «маленькими» бесконечными множествами.

Мощность множества обозначается через |A| .
Иногда встречаются обозначения , и .

Содержание

1 Определение
2 Связанные определения
3 Примеры
4 Свойства
5 Арифметика кардинальных чисел
- 5.1 Следующее по порядку кардинальное число
- 5.2 Сложение кардинальных чисел
  - 5.2.1 Вычитание
- 5.3 Умножение кардинальных чисел
  - 5.3.1 Деление
- 5.4 Возведение кардинальных чисел в степень
  - 5.4.1 Извлечение корней
  - 5.4.2 Логарифмы
6 Континуум-гипотеза
7 См. также
8 Примечания
9 Литература

Определение

При соблюдении аксиомы выбора мощность множества формально определяется как наименьшее порядковое число alpha , при котором между и alpha можно установить биективное соответствие. Данное определение также называется распределением кардинальных чисел по фон Нейману. Если мы не принимаем аксиому выбора, требуется иной подход. Самое первое определение мощности множества (оно неявно присутствует в работах Кантора и явным образом сформулировано у Фреге, а также в Principia Mathematica) представляет собой класс [X] всех множеств, равномощных . В аксиоматических системах, основанных на теории ZFC, такое определение неприменимо, поскольку при непустом такая совокупность слишком велика, чтобы подходить под определение множества. Точнее, если , то существует инъективное отображение универсального множества в [X] , при котором каждое множество переходит в , откуда, в силу аксиомы ограничения размера следует, что [X] — собственный класс. Данное определение можно использовать в теории типов и «новых основаниях», а также в связанных с ними аксиоматических системах. В случае ZFC определение можно использовать, если ограничить коллекцию [X] равномощными множествами с наименьшим рангом (этот приём, предложенный Даной Скоттом, работает благодаря тому, что совокупность объектов, обладающих заданным рангом, является множеством).

Формальный порядок среди кардинальных чисел вводится следующим образом: означает, что множество можно инъективно отобразить на . Согласно теореме Кантора — Бернштейна, из пары неравенств и следует, что |X|=|Y| . Аксиома выбора эквивалентна утверждению о том, что для любых множеств и выполняется, по крайней мере, одно из неравенств или .

Множество называется бесконечным по Дедекинду, если в нём существует такое собственное подмножество , что |X|=|Y| . В противном случае множество называется конечным по Дедекинду. Конечные кардинальные числа совпадают с обычными натуральными числами — иначе говоря, множество конечно тогда и только тогда, когда при некотором натуральном . Все остальные множества бесконечны. При соблюдении аксиомы выбора можно доказать, что определения по Дедекинду совпадают со стандартными. Кроме того, можно доказать, что мощность множества натуральных чисел aleph_0 (алеф-нуль, или алеф-0 — название образовано от первой буквы еврейского алфавита aleph ) представляет собой наименьшее бесконечно большое кардинальное число, то есть в любом бесконечном множестве есть подмножество мощности aleph_0 . Следующее по порядку кардинальное число обозначается aleph_1 и так далее, число алефов бесконечно. Любому порядковому числу alpha соответствует кардинальное число $aleph _{alpha }$ , причём таким образом можно описать любое бесконечно большое кардинальное число.

Связанные определения

Для мощностей, как и в случае конечных множеств, имеются понятия: «равенство», «больше», «меньше». То есть для любых множеств и возможно только одно из трёх:
1. , или и равномощны;
2. , или мощнее , то есть содержит подмножество, равномощное , но и не равномощны;
3. , или мощнее — в этом случае содержит подмножество, равномощное , но и не равномощны.

Примеры

Множество называется счётным, если оно равномощно множеству всех натуральных чисел . Счётными множествами являются:

Бесконечные множества, неравномощные множеству , называются несчётными. По теореме Кантора несчётным является множество бесконечных последовательностей, составленных из цифр 0 и 1. Мощность этого множества называется континуум.

Мощность множества вещественных чисел равна континууму.

Свойства

Арифметика кардинальных чисел

Обычные арифметические операции над числами натурального ряда можно обобщить на случай кардинальных чисел. Можно также показать, что в случае конечных кардинальных чисел эти операции совпадают с соответствующим арифметическими действиями над числами. Помимо этого, операции над кардинальными числами сохраняют многие свойства обычных арифметических операций.

Следующее по порядку кардинальное число

При соблюдении аксиомы выбора для каждого кардинального числа kappa можно определить следующее за ним число $kappa ^{+}>kappa$ , причём между kappa и $kappa ^{+}$ нет других кардинальных чисел. Если kappa конечно, то следующее кардинальное число совпадает с . В случае бесконечных kappa следующее кардинальное число отличается от следующего порядкового числа.

Сложение кардинальных чисел

Если множества и не имеют общих элементов, то сумма мощностей определяется мощностью их объединения. При наличии общих элементов исходные множества можно заменить непересекающимися множествами той же мощности — например, заменить на , а на .

Нейтральность нуля относительно сложения:

Ассоциативность:

Коммутативность:

Монотонность (неубывание) сложения по обоим аргументам:

kappa leq mu rightarrow kappa +nu leq mu +nu .

kappa leq mu rightarrow nu +kappa leq nu +mu .

Сумму двух бесконечных кардинальных чисел можно легко вычислить при соблюдении аксиомы выбора. Если одно из чисел kappa или бесконечно, то

Вычитание

При соблюдении аксиомы выбора для любого бесконечного кардинального числа sigma и произвольного кардинального числа существование kappa , при котором , эквивалентно неравенству . Такое kappa единственно (и совпадает с sigma ) тогда и только тогда, когда .

Умножение кардинальных чисел

Произведение двух кардинальных чисел выражается через декартово произведение множеств:

Свойства нуля:

kappa cdot mu =0rightarrow kappa =0lor mu =0

Нейтральность единицы относительно умножения:

Ассоциативность:

(kappa cdot mu )cdot nu =kappa cdot (mu cdot nu )

Коммутативность:

Монотонность (неубывание) умножения по обоим аргументам:

kappa leq mu rightarrow kappa cdot nu leq mu cdot nu .

kappa leq mu rightarrow nu cdot kappa leq nu cdot mu .

Дистрибутивность умножения относительно сложения:

kappa cdot (mu +nu )=kappa cdot mu +kappa cdot nu

(mu +nu )cdot kappa =mu cdot kappa +nu cdot kappa

По аналогии со сложением произведение двух бесконечных кардинальных чисел можно легко вычислить при соблюдении аксиомы выбора. Если числа kappa и отличны от нуля и хотя бы одно из них бесконечно, то

Деление

При соблюдении аксиомы выбора для любой пары кардинальных чисел и , где бесконечно, а не равно нулю, существование kappa , при котором , эквивалентно неравенству . Такое kappa единственно (и совпадает с ) тогда и только тогда, когда mu <pi .

Возведение кардинальных чисел в степень

Возведение в степень определяется следующим образом:

$|X|^{{|Y|}}=|X^{Y}|$

где $X^{Y}$ обозначает множество всех функций из в .

$kappa ^{0}=1$

(в частности, $0^{0}=1$

), см. Пустая функция

$1leq mu rightarrow 0^{mu }=0$

$1^{mu }=1$

$kappa ^{1}=kappa$

$kappa ^{{mu +nu }}=kappa ^{mu }cdot kappa ^{nu }$

$kappa ^{{mu cdot nu }}=(kappa ^{mu })^{nu }$

$(kappa cdot mu )^{nu }=kappa ^{nu }cdot mu ^{nu }$

Монотонность:

$1leq nu land kappa leq mu rightarrow nu ^{kappa }leq nu ^{mu }$

$kappa leq mu rightarrow kappa ^{nu }leq mu ^{nu }$

Заметим, что $2^{{|X|}}$ представляет собой мощность булеана и, следовательно, $2^{{|X|}}>|X|$ для любого множества (см. Диагональный метод Кантора). Отсюда следует, что среди кардинальных чисел нет наибольшего (поскольку для любого кардинального числа kappa можно указать большее число $2^{kappa }$ ). В действительности класс всех кардинальных чисел является собственным (хотя в некоторых аксиоматизациях теории множество этого доказать нельзя — к таковым, например, относится система «Новых оснований»).

Все последующие утверждения, приведенные в этом разделе, опираются на аксиому выбора.

Если kappa и — конечные числа, большие 1, а — бесконечное кардинальное число, то $kappa ^{nu }=mu ^{nu }$
Если кардинальное число kappa бесконечно, а конечно и отлично от нуля, то $kappa ^{mu }=kappa$ .

Если и , причём хотя бы одно из них бесконечно, то

$max{kappa ,2^{mu }}leq kappa ^{mu }leq max{2^{kappa },2^{mu }}$

Используя теорему Кёнига, можно доказать, что для любого бесконечного кардинального числа kappa выполняются неравенства:

$kappa <kappa ^{{cf(kappa )}}$

$kappa <cf(2^{kappa })$

где обозначает конфинальность kappa .

Извлечение корней

При условии соблюдения аксиомы выбора для любого бесконечного кардинала kappa и конечного кардинала mu >0 существует кардинальное число , при котором $nu ^{mu }=kappa$ , причём .

Логарифмы

При соблюдении аксиомы выбора кардинальное число lambda , удовлетворяющее условию $mu ^{lambda }=kappa$ , при заданном бесконечном kappa и конечном mu >1 , существует не всегда. Если же такое lambda существует, то оно бесконечно и меньше kappa , причём любое конечное кардинальное число nu >1 также будет удовлетворять равенству $nu ^{lambda }=kappa$ .

Логарифмом бесконечного кардинального числа kappa называется наименьшее кардинальное число , удовлетворяющее условию $kappa leq 2^{mu }$ . Несмотря на то, что логарифмы бесконечно больших кардинальных чисел лишены некоторых свойств, характерных для логарифмов положительных вещественных чисел, они оказываются полезными в некоторых областях математики — в частности, при изучении кардинальных инвариантов топологических пространств.

Континуум-гипотеза

Согласно утверждению континуум-гипотезы, между aleph_0 и $2^{aleph_0}$ не существует других кардинальных чисел. Кардинальное число $2^{aleph_0}$ также обозначается и представляет собой мощность континуума (то есть множества вещественных чисел). В данном случае $2^{{aleph _{0}}}=aleph _{1}$ . Обобщённая континуум-гипотеза отрицает существование кардинальных чисел, заключённых строго между |X| и $2^{{|X|}}$ , для любого бесконечного множества . Континуум-гипотеза является независимой от стандартной аксиоматизации теории множеств, то есть системы аксиом Цермело-Френкеля в сочетании с аксиомой выбора (см. Теория множеств Цермело-Френкеля).

См. также

Порядковое число

Примечания

Литература

А. А. Болибрух, Проблемы Гильберта (100 лет спустя), Глава 2 Первая проблема Гильберта: континуум-гипотеза, Библиотека «Математическое просвещение», Выпуск 2
Р. Курант, Г. Роббинс, Что такое математика? Глава II, § 4.
Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 109-110. — 383 с. — ISBN 5-09-001287-3.
Брудно А. Л. Теория функций действительного переменного. — М.: Наука, 1971. — 119 с.

Источник