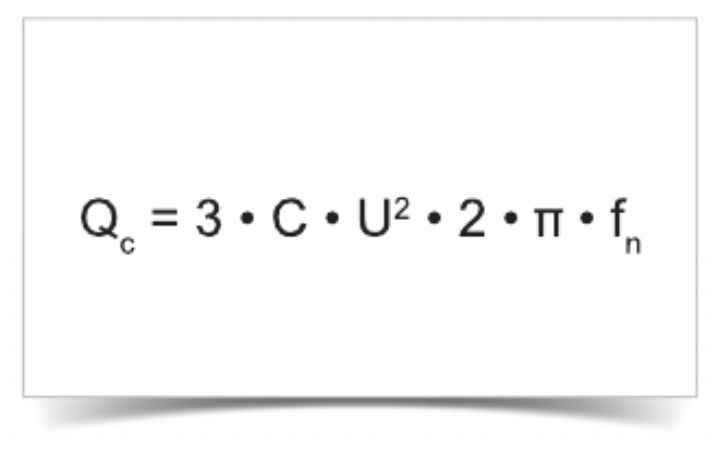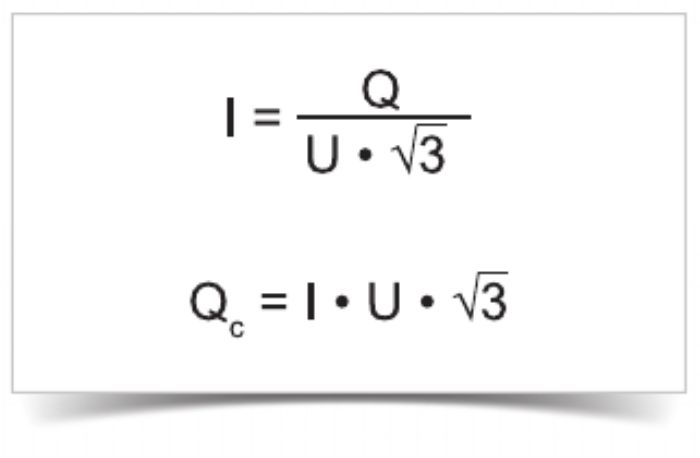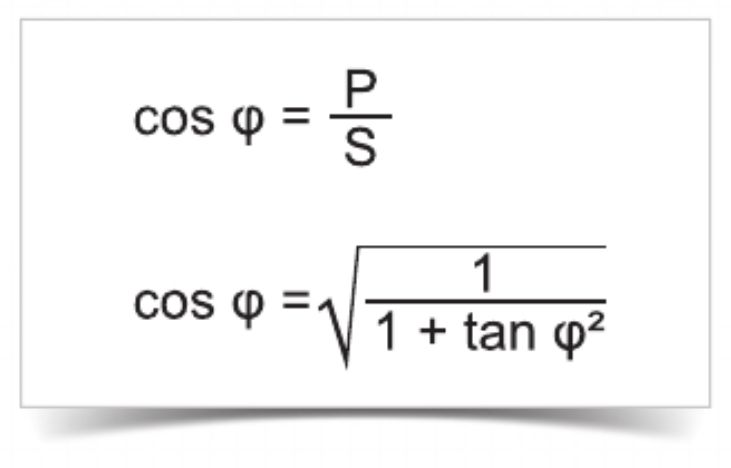Как найти мощность потребляемую конденсатором

Формулы для расчета конденсатора

Реактивная мощность конденсатора однофазная

Пример: 66.5 кА с 400 В / 50 Гц

0.0000665 · 400² · 2 · 3.14 · 50 = 3,340 ВАр = 3.34 кВАр

   

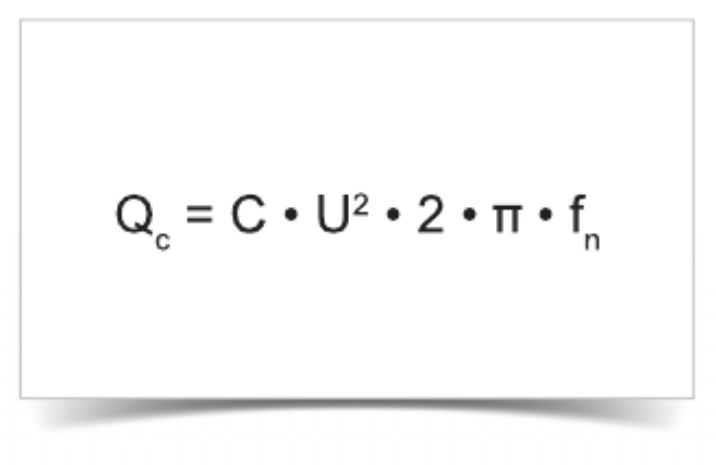
Реактивная мощность конденсатора при соединении треугольником

Пример: 3 х 57 кА с 480 В / 50 Гц

3 · 0.000057 · 4802 · 2 · 3.14 · 50 = 12,371 ВАр = 12.37 кВАр

  

Реактивная мощность конденсатора при соединении звездой

Пример: 3 х 33,2 кА с 400 В / 50 Гц

3 · 0.0000332 · (400 / 1.73)2 · 2 · 3.14 · 50 = 1670 ВАр = 1.67 кВАр

 

 Ток конденсатора в фазовом проводнике

Пример: 24 кВАр с 400 В

25,000 / (400 · 1.73) = 36 A

 

 Частота последовательного резонанса (fr) и коэффициента расстройки (p) у конденсаторов, перестраиваемых постоянным напряжением

 Пример: p = 0,07 (расстройка 7 %) в сети 50 Гц

   

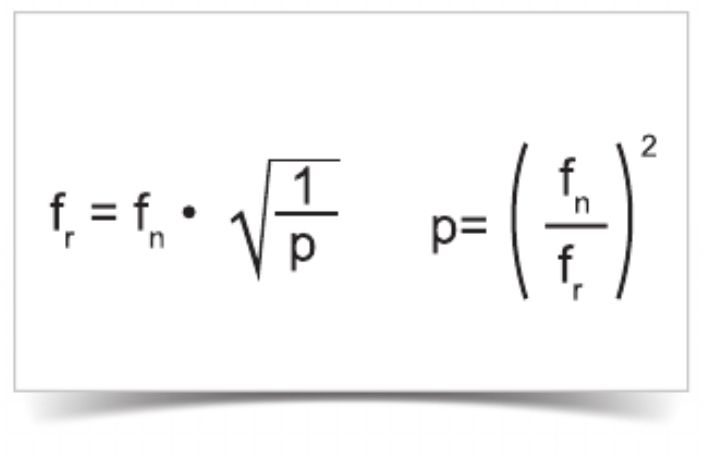
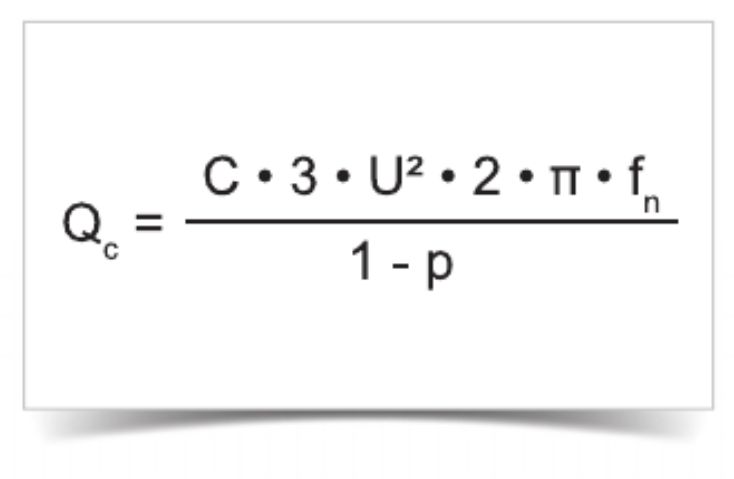
Необходимая номинальная трехфазная мощность конденсатора в варианте с расстройкой

Пример: 3 x 308 мкФ при 400 В / 50 Гц с p = расстройка 7 % 0,000308 · 3 · 4002 · 2 · 3,14 · 50 / (1 — 0,07) = 50 кВАр

Какой конденсатор нужно для этого использовать?

Это значит, что для ступени 50 кВАр необходим конденсатор 440 В 56 кВАр

    

  Коэффициент мощности и пересчет cos в tan

   

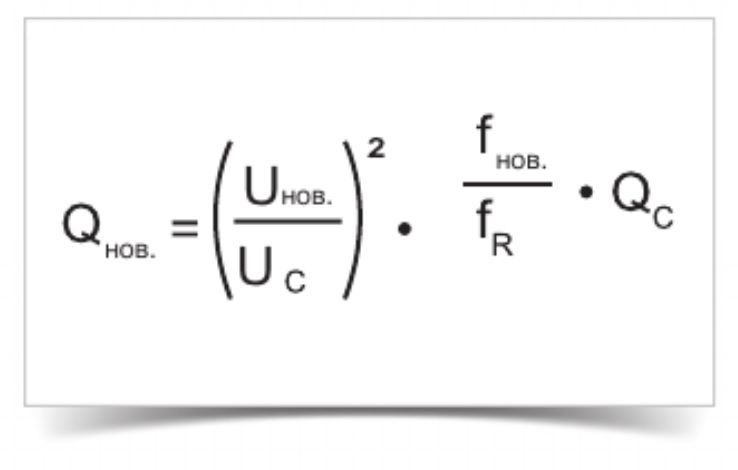
  Пересчет реактивной мощности конденсатора в зависимости от напряжения в сети

Расчет реактивной мощности Q_нов. · C – константа.

Пример:

Сеть: 400 В, 50 Гц, 3-фазный

Номинальные характеристики конденсатора: 480 В, 70 кВАр, 60 Гц, 3-фазный,

треугольный, незапертый

Вопрос: чему равна результирующая номинальная мощность конденсатора?

   Результирующая компенсационная мощность этого 480-вольтного конденсатора, подключенного к сети 400 В 50 Гц, составляет всего 40,5 кВАр.

Обозначения

Q_C Номинальная мощность конденсатора

P Коэффициент фильтрации

U_C Напряжение конденсатора

U_N Номинальное напряжение

N_C Эффективность фильтрования Qнов. Новая реактивная мощность Uнов. Новое напряжение

f_new Новая частота

f_R Номинальная частота конденсатора

Мощность переменного тока

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.

Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.

Пусть и — мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени — настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины и можно считать постоянными в течение интервала .

Пусть за время через наш участок прошёл заряд (в соответствии с правилом выбора знака для силы тока заряд считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу

Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:

(1)

Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.

Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.

1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).

2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.

Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).

Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.

к оглавлению ▴

Мощность тока через резистор

Пусть переменный ток протекает через резистор сопротивлением . Напряжение на резисторе, как нам известно, колеблется в фазе с током:

Поэтому для мгновенной мощности получаем:

(2)

График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.

Рис. 1. Мощность переменного тока через резистор

Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:

На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между и . Где же именно?

Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?

Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:

среднее значение квадрата синуса (или косинуса) за период равно .

Этот факт иллюстрируется рисунком 2.

Рис. 2. Среднее значение квадрата синуса равно

Итак, для среднего значения мощности тока на резисторе имеем:

(3)

В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):

(4)

Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:

Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением , то в обоих случаях лампочка будет гореть одинаково ярко.

Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.

к оглавлению ▴

Мощность тока через конденсатор

Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на :

Для мгновенной мощности получаем:

График зависимости мгновенной мощности от времени представлен на рис. 3.

Рис. 3. Мощность переменного тока через конденсатор

Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.

Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).

Рис. 4. Напряжение на конденсаторе и сила тока через него

Рассмотрим последовательно все четыре четверти периода.

1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.

Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.

2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.

Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).

3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.

Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.

4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.

Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.

Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.

к оглавлению ▴

Мощность тока через катушку

Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на :

Для мгновенной мощности получаем:

Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).

Рис. 5. Напряжение на катушке и сила тока через неё

Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.

В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.

Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.

к оглавлению ▴

Мощность тока на произвольном участке

Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .

Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:

Тогда для мгновенной мощности имеем:

(5)

Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:

В результате получим:

(6)

Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:

(7)

Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:

Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки , и средняя мощность равна нулю.

Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.

С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.

Расчет емкости конденсатора

> Теория > Расчет емкости конденсатора

Конденсаторы – это компоненты, способные хранить электрозаряд или электрическую энергию. Простейшая форма элемента – это две пластины из металла с диэлектриком между ними, не допускающим электрического соединения обкладок. При подаче напряжения в межобкладочном пространстве образуется электрическое поле, с положительным зарядным знаком на одной пластине и с отрицательным – на другой. Распределение заряда одинаково с обеих сторон.

Различные типы конденсаторов

Емкость конденсатора

Для конденсаторного элемента емкость – это потенциальная мера хранения энергии. Она имеет символ С и рассчитывается в фарадах (Ф). Наиболее часто можно встретить единицы, масштабированные в меньшую сторону: микро-, нано-, пикофарады.

Емкость конденсатора можно выразить через заряд (q) и напряжение (V):

C = q/V = (I x t)/V, где:

Емкость определяется также структурными размерами конденсатора:

C = (ε x ε0 x S)/d.

Из этой формулы получается, что емкость тем больше, чем:

• больше поверхность пластины S;
• меньше расстояние между ними d;
• лучше дипольное образование в изоляторе (больше диэлектрическая проницаемость ε):

ε0 = 8,85 х 10 ( в -12 степени), Ф/м – диэлектрическая проницаемость в вакууме.

Для увеличения емкости плоского конденсатора надо увеличить плоскость его пластин, уменьшить межобкладочное расстояние или применить для изолятора материал с большим значением ε.

Формулы емкости для различных конденсаторов

Элементы обладают фиксированной емкостью, определенной производителем, значение которой нельзя изменить.

Конденсаторы с переменной емкостью

Емкость конденсатора: формула

Для этих элементов характерна способность менять емкость. Простейший из них состоит из нескольких половин дисков (одной), фиксированных и электрически связанных друг с другом.

Другая группа аналогичных половин диска установлена на общей оси. При вращении вала фиксированная на нем половина диска устанавливается между неподвижными половинами, и происходит изменение емкости.

Конденсатор с переменной емкостью

Характеристики конденсатора

1. Диэлектрическая постоянная ε является мерой того, как изолирующий материал влияет на емкость конденсатора;
2. Диэлектрическая прочность определяет самое высокое напряжение, которое может быть приложено к конденсаторному элементу.

   В случае его превышения происходит пробой;

3. Температурная зависимость. В фильтрах и резонансных схемах важную роль играет температурный коэффициент ТК. В зависимости от температуры, меняется отдаваемая мощность. Изменение может быть со знаком «плюс» и «минус».

   Некоторые схемы требуют точности расчета конденсатора.

Соединение конденсаторов

Измеритель емкости конденсаторов

В электрических цепях нередко производят подключения, состоящие из нескольких конденсаторов, имеющих разные типы соединений.

Последовательное соединение

Если левая пластина первого конденсатора несет заряд со знаком «плюс», правая из-за электростатической индукции получит его со знаком «минус». При этом он будет смещен от левой обкладки второго конденсатора, что, в свою очередь, положительно зарядит ее и т. д.

Последовательное соединение конденсаторных элементов

Напряжение, приложенное к общей емкости конденсаторов, будет складываться из напряжений на каждом из них:

V = V1 + V2 + V3 + …

Так как:

• V1 = q/С1;
• V2 = q/С2;
• V3 = q/С3,

а для всей батареи последовательных элементов:

V = q/С,

то q/С = q/С1 + q/С2 + q/С3.

Количество электричества в последовательной цепи одинаково, значит допустимо разделить обе части уравнения на q.

Рассчитать емкость элементов, собранных в последовательную цепь, можно по формуле:

1/С = 1/С1 + 1/С2 + 1/С3 + …

Важно! Величина, обратная суммарной емкости конденсаторных элементов, соединенных в последовательную цепь, составляет сумму обратных величин емкостей отдельных компонентов.

Параллельное соединение

Когда емкость конденсаторов мала, они включаются параллельно. Как рассчитать общую емкость такой цепи, определяется теми же зависимостями, но с учетом того, что напряжение на конденсаторных пластинах будет одинаковым:

V = V1 = V2 = V3 = …

Параллельное соединение конденсаторных элементов

Количество электричества на каждом конденсаторе составит:

q1 = V x C1, q2 = V x C2, q3 = V x C3.

Общий заряд конденсаторной батареи:

q = q1 + q2 + q3 = V/C1 + V/C2 + V/C3 = V x (C1 + C2 + C3), а С = С1 + С2 + С3.

Важно! При параллельном соединении конденсаторных элементов каждый из них подключен на полное напряжение электроцепи, а общая емкость суммируется.

В сети есть сайты, имеющие калькулятор для расчета конденсатора при разных конфигурациях электросхемы, а также позволяющих определить емкость, задавая свои структурные параметры, как для плоских, так и для цилиндрических элементов.

Расчет конденсатора для электродвигателя

Приборы для измерения емкости аккумулятора

Трехфазный электромотор можно подключить к однофазной линии, которая позволит управлять им с помощью конденсатора. При этом надо произвести расчет емкости конденсатора.

Чтобы узнать значение в микрофарадах, которое нужно получить от конденсаторного элемента, и найти оптимальный пусковой момент в однофазной линии, надо знать технические характеристики мотора.

Схемы включения электромотора с конденсатором

1. Активная мощность определяется:

Р = √3 x V x I x соsφ.

Она может быть указана на таблице, прикрепленной к мотору. Напряжение – 220 В в однофазном режиме. Величина соsφ также указывается производителем (обычно для электродвигателей соsφ = 0,8-0,85).

1. Отсюда можно найти силу тока:

I = P/(√3 x V x  соsφ).

1. Емкость конденсатора для соединенных звездой двигательных обмоток Сраб = 4800 x I /V, для соединенных в Δ – Сраб = 2800 x I/V;
2. Для пускового конденсаторного элемента Спуск = 2,5 С.

Сетевой калькулятор онлайн производит и такой тип расчетов. Для этого вводятся параметры электромотора и питающей сети, в результате получается емкостное значение.

Источник: https://elquanta.ru/teoriya/raschet-emkosti-kondensatora.html

Конвертер величин

Постоянная времени определяется по формуле

Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой

где C — емкость в фарадах и V — напряжение в вольтах.

Максимальный ток I определяется по закону Ома:

Максимальный заряд Q определяется по формуле

где C — емкость в фарадах и V — напряжение в вольтах.

Фильтрующие электролитические конденсаторы на системной плате компьютера

Применение

Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе

Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор.

Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.

Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.

Резистивно-емкостные фильтры нижних частот

Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра

Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.

Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале.

У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.

Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.

В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки.

В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее.

Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.

Простой пассивный RC-фильтр верхних частот

Фильтры верхних частот пропускают только высокочастотные составляющие сигналов и ослабляют низкочастотные составляющие. Фильтры верхних частот используются, например, в разделительных фильтрах звуковых частот (кроссоверах) для подавления низкочастотных составляющих в сигналах, подаваемых на высокочастотные динамики («пищалки»), которые не могут воспроизводить такие сигналы и к тому же обладают малой мощностью по сравнению с мощностью низкочастотных сигналов.

Активный фильтр верхних частот с операционным усилителем

Фильтры верхних частот часто используются для блокировки постоянной составляющей сигналов в тех случаях, когда она нежелательна.

Например, в профессиональных микрофонах очень часто используется «фантомное» питание постоянным напряжением, которое подается по микрофонному кабелю. В то же время микрофон записывает переменные сигналы, такие как человеческий голос или музыка.

Постоянное напряжение не должно появляться на выходе микрофона и не должно поступать на вход микрофонного усилителя, поэтому для его блокировки используется фильтр верхних частот.

Если фильтр нижних частот и фильтр верхних частот стоят друг за другом, они образуют полосовой фильтр, который пропускает частоты только в определенной полосе частот и не пропускает частоты за пределами этой полосы. Такие фильтры широко используются в радиоприемниках и радиопередатчиках.

В приемниках полосовые фильтры используются только для селективного пропускания и усиления сигналов радиостанции в требуемой узкой полосе частот. При этом сигналы других радиостанций за пределами этой полосы подавляются. Передатчики могут передавать радиосигналы только в определенном разрешенном для них диапазоне частот.

Поэтому в них используются полосовые фильтры для ограничения полосы передаваемого сигнала таким образом, что он вписывался в допустимые пределы.

Постоянная времени определяется по формуле

Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой

где C — емкость в фарадах и V — напряжение в вольтах.

Максимальный ток I определяется по закону Ома:

Максимальный заряд Q определяется по формуле

где C — емкость в фарадах и V — напряжение в вольтах.

Фильтрующие электролитические конденсаторы на системной плате компьютера

Конденсатор

Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).

Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).

Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).

• 1nF = 0.000000001 = 10-9 F

• 1pF = 0.000000000001 = 10-12 F

Плоский конденсатор

Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Заряд конденсатора. Напряжение

В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.

На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.

Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.

Формула для нахождения тока конденсатора во время переходного периода:

• ΔVc/Δt – Изменение напряжения на конденсаторе за отрезок времени

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Устройство конденсатора. От чего зависит емкость?

Емкость плоского конденсатора зависит от трех основных факторов:

• Расстояние между пластинами – d

• Относительная диэлектрическая проницаемость вещества между пластинами — ɛ

Площадь пластин

Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.

Расстояние между пластинами

Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).

Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость ɛ. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

• Порошки оксидов металлов – от 6 до 20

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В.

Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В.

Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.

Ток утечки

Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.

Источник: http://hightolow.ru/capacitor1.php

Накачка и сброс — больше энергии, чем вы ожидали!

В

Разработчики часто сталкиваются с трудностями при создании высокоэффективных преобразователей мощности. Причина — необходимость уменьшить тепловыделение в ограниченной области, чтобы обеспечить другие подсистемы большей входной мощностью или сберечь электроэнергию из соображений экологичности.

Что же должен сделать разработчик, когда от него требуется обеспечить выходную мощность, превосходящую входную мощность на 50 или 100%? Эта на первый взгляд невыполнимая задача может быть решена, хотя и с некоторыми ограничениями. Некоторые виды нагрузки требуют большие мощности лишь в относительно короткие периоды времени продолжительностью в миллисекунды, секунды или даже минуты.

В статье рассматривается, как этого можно добиться, заряжая блок конденсаторов для накопления энергии (накачка), пока она не потребуется, и разряжая конденсаторы на нагрузку контролируемым образом (сброс).
Все источники подводимого электропитания имеют ограниченные предельные значения тока, напряжения или мощности.

Из-за наличия внутреннего сопротивления выходное напряжение батарей падает при большой нагрузке, тем самым косвенно устанавливая наибольший выходной ток для стабилизации напряжения на нагрузке. Практически все адаптеры питания рассчитаны на наибольший уровень выходной мощности. При превышении этого уровня адаптер питания может перейти в режим защиты от перегрузки по току, либо может даже сработать предохранитель для защиты источника входного питания.

Интерфейс USB используется как источник питания с напряжением 5 В с выходным током всего 0,1A, но при необходимости может обеспечивать максимальный выходной ток до 0,5 A. Такая величина тока ограничивает мощность этого чрезвычайно распространенного источника питания величиной всего 2,5 Вт. Дополнительную выходную мощность можно получить только от источника накопленной энергии, например от конденсатора или батареи.

Тип нагрузки имеет значение

Передача тока в нагрузку от заряженного конденсатора определяется переносом требуемого количества заряда в течение определенного периода времени. В терминах подводимой мощности этот процесс можно определить с помощью уравнения:

P = 0,5Cbulk(Vi2 – Vf2),       (1)

где Cbulk — емкость заряжаемого конденсатора; Vi — начальное напряжение конденсатора, а Vf — конечное напряжение после разряда.
Эта концепция проста в реализации: следует зарядить конденсатор большой емкости до начального высокого напряжения и дать ему разрядиться до заданного уровня; при этом ток подается в нагрузку в условиях временной перегрузки по току.

В конце цикла разряда на конденсаторе останется напряжение Vf, и потребуется повторный заряд конденсатора до напряжения Vi. Мощность, которую должен поддерживать конденсатор большой емкости, равна подводимой к нагрузке мощности за вычетом мощности, которая обеспечивается входным источником питания во время разряда. При расчете КПД всех импульсных преобразователей не следует занижать требуемую величину емкости конденсатора.

Уравнение (1) представляет собой выражение для напряжения на конденсаторе при подаче постоянной мощности на нагрузку. Однако это является наихудшей ситуацией, поскольку не всякая нагрузка требует постоянной мощности.Примером нагрузки постоянной мощности служит вход регулируемого импульсного источника питания. Для поддержания постоянной мощности по мере уменьшения входного напряжения импульсного источника питания входной ток должен возрастать.

Нагрузка может быть резистивной или проявлять себя как источник постоянного тока. На рисунке 1 показаны разрядные характеристики трех типов нагрузки. Все характеристики начинаются в одной точке, соответствующей начальному напряжению, но затем они расходятся. Ток постоянного сопротивления изменяется противоположно току постоянной мощности и снижается при уменьшении напряжения, постепенно стабилизируясь по мере разряда.

Разряд на нагрузку в режиме постоянного тока происходит линейно до нулевого напряжения, причем обеспечивается одинаковый ток, независимо от напряжения на конденсаторе. Разряд в режиме постоянной мощности, в свою очередь, происходит быстрее всего из-за резкого возрастания разрядного тока по мере уменьшения напряжения.

В зависимости от типа нагрузки необходимая емкость может существенно изменяться, поэтому всегда полезно знать характер конкретной нагрузки.

При использовании блока конденсаторов разработчик должен также решить, до каких пределов его можно будет разряжать. Существуют два возможных способа. Первый состоит в непосредственном подключении нагрузки к блоку конденсаторов.

Перепад напряжения на конденсаторах должен находиться в допустимых для нагрузки эксплуатационных пределах. Обычная полупроводниковая нагрузка допускает отклонение лишь 3—5% от номинального напряжения. Это существенно ограничивает допустимое падение напряжения и принуждает использовать конденсаторы большой емкости. В этом случае не требуется дополнительной стабилизации напряжения.

Второй способ допускает большие перепады напряжения и использует дополнительный стабилизатор между конденсатором и нагрузкой. Стабилизатор может быть понижающим, повышающим или даже SEPIC-преобразователем, в зависимости от размаха напряжения на входе, выходе и конденсаторе. При большом перепаде напряжения на конденсаторе более эффективно используется запасенная энергия, что минимизирует величину необходимой емкости. Уменьшение требуемой емкости может снизить общие затраты, даже с учетом расходов на дополнительный стабилизатор.

Некоторые суперконденсаторы оказываются несовершенными

Преимущество суперконденсаторов — плотность энергии, которая в 1000—10000 раз превышает плотность энергии электролитических конденсаторов. В настоящее время часто используются конденсаторы с номинальным значением емкости 100 Ф и более. Многие из них предназначены для приложений с малым потреблением тока, например для резервных запоминающих устройств.

Конденсаторы таблеточного типа часто имеют эквивалентное последовательное сопротивление (equivalent series resistance — ESR) 100 Ом и более. Разработчик должен определить максимальное допустимое ESR исходя из разрядного тока и падения напряжения. Современные типы суперконденсаторов имеют очень малую величину ESR, сравнимую с аналогичным показателем для керамических конденсаторов.

На схеме, представленной на рисунке 2, были выбраны суперконденсаторы с малым ESR, поскольку они должны служить источником тока в сотни миллиампер. Питание схемы осуществляется от порта USB с предельным значением входной мощности 2,5 Вт. Выходное напряжение преобразователя составляет 7 В на импульсной нагрузке 4,2 Вт в течение 4 с, а затем 0,7 Вт в течение 15 с.

Изолированный обратноходовой преобразователь с контроллером TPS40210 использован для заряда блока суперконденсаторов до напряжения 13,5 В во время режима малой нагрузки. Допускается разряд конденсатора приблизительно до 9,5 В через 4 с режима большой нагрузки. В течение этого периода входной ток стабилизируется на уровне не более 0,5 A (2,5 Вт) и измеряется резистором с помощью операционного усилителя.

Во время импульса тока нагрузки 0,6 А (нижняя кривая) напряжение на суперконденсаторе (верхняя кривая) снижается приблизительно до 4 В. Это значение является входным напряжением для синхронного понижающего DC/DC-преобразователя типа TPS62110, стабилизирующего выходное напряжение на уровне 7 В (средний сигнал). Когда выходной ток нагрузки при напряжении 7 В уменьшается до 0,1 A, блок конденсаторов повторно полностью заряжается до 13,5 В.

Во время этих ступенчатых изменений режимов нагрузки и больших перепадов входного напряжения выходное напряжение остается стабильным с небольшими отклонениями. На рисунке 4 показаны сигналы в момент подачи напряжения 4,5 В на вход USB. При включении блок конденсаторов первоначально разряжен, а обратноходовой преобразователь немедленно переключается в режим ограничения входного тока, поскольку выходная нагрузка ведет себя как короткозамкнутая.

Блок конденсаторов медленно заряжается до напряжения 13,5 В со скоростью, которая определяется ограничением по входной мощности 2,5 Вт и потерями, связанными с КПД обратноходового преобразователя. Когда напряжение достигает 13,5 В, вторичный контур принимает управление на себя, позволяя уменьшить входной ток. В этом примере выходная нагрузка отсутствует, хотя для полного заряда конденсаторов требуется приблизительно 18 с. Время запуска будет еще более продолжительным, если подключить внешнюю нагрузку. Это является одним из недостатков, связанных с наличием накопительного конденсатора большой емкости.  

Заключение

Схема, представленная в этой статье, обеспечивает построение изолированного источника питания, мощность которого больше мощности входного источника питания. Хранение энергии в конденсаторе большой емкости имеет свои недостатки, в частности, высокую стоимость суперконденсаторов и продолжительное время запуска. Тип нагрузки непосредственно влияет на величину необходимой емкости для длительной поддержки требуемой величины напряжения.

Нагрузка с постоянной мощностью, например такая как стабилизирующий импульсный преобразователь, представляет собой наиболее тяжелый вид нагрузки и может разрядить накопительный конденсатор быстрее, чем резистивная нагрузка или нагрузка по постоянному току.

Однако если в схеме предусмотреть возможность значительного снижения напряжения на накопительном конденсаторе, после которого включен импульсный стабилизатор, то можно удовлетворить потребности в энергии для самой большой нагрузки.

Литература

Вы можете скачать эту статью в формате pdf здесь.

Источник: http://www.russianelectronics.ru/developer-r/review/micro/doc/48636/

Расчет конденсатора для светодиодов

Необходимость подключить светодиод к сети – частая ситуация. Это и индикатор включения приборов, и выключатель с подсветкой, и даже диодная лампа.

Существует множество схем подключения маломощных индикаторных LED через резисторный ограничитель тока, но такая схема подключения имеет определённые недостатки. При необходимости подключить диод, с номинальным током 100-150мА, потребуется очень мощный резистор, размеры которого будут значительно больше самого диода.

Вот так бы выглядела схема подключения настольной светодиодной лампы. А мощные десяти ваттные резисторы при низкой температуре в помещении можно было бы использовать в качестве дополнительного источника отопления.

Применение в качестве ограничителя тока конде-ров позволяет значительно уменьшить габариты такой схемы. Так выглядит блок питания диодной лампы мощностью 10-15 Вт.

Принцип работы схем на балластном конденсаторе

В этой схеме конде-р является фильтром тока. Напряжение на нагрузку поступает только до момента полного заряда конде-ра, время которого зависит от его ёмкости. При этом никакого тепловыделения не происходит, что снимает ограничения с мощности нагрузки.

Чтобы понять, как работает эта схема и принцип подбора балластного элемента для LED, напомню, что напряжение – скорость движения электронов по проводнику, сила тока – плотность электронов.

Для диода абсолютно безразлично, с какой скоростью через него будут «пролетать» электроны. Расчет конде-ра основан на ограничении тока в цепи. Мы можем подать хоть десять киловольт, но если сила тока составит несколько микр оампер, количества электронов, проходящих через светоизлучающий кристалл, хватит для возбуждения лишь крохотной части светоизлучателя и свечения мы не увидим.

В то же время при напряжении несколько вольт и силе тока десятки ампер плотность потока электронов значительно превысит пропускную способность матрицы диода, преобразовав излишки в тепловую энергию, и наш LED элемент попросту испарится в облачке дыма.

Расчет гасящего конденсатора для светодиода

Разберем подробный расчет, ниже сможете найти форму онлайн калькулятора.

Расчет емкости конденсатора для светодиода:

С(мкФ) = 3200 * Iсд) / √(Uвх² — Uвых²)

С мкФ – ёмкость конде-ра. Он должен быть рассчитан на 400-500В;
Iсд – номинальный ток диода (смотрим в паспортных данных);
Uвх – амплитудное напряжение сети  — 320В;
Uвых – номинальное напряжение питания LED.

Можно встретить еще такую формулу:

C = (4,45 * I) / (U — Uд)

Она используется для маломощных нагрузок до 100 мА и до 5В.

Расчет конденсатора для светодиода (калькулятор онлайн):

Для наглядности проведём расчёт нескольких схем подключения.

Подключение одного светодиода

Для расчета емкости конде-ра нам понадобится:

• Максимальный ток диода – 0,15А;
• напряжение питания диода – 3,5В;
• амплитудное напряжение сети  — 320В.

Для таких условий параметры конде-ра: 1,5мкФ, 400В.

Подключение нескольких светодиодов

При расчете конденсатора для светодиодной лампы необходимо учитывать, что диоды в ней соединены группами.

• Напряжение питания для последовательной цепочки – Uсд * количество LED в цепи;
• сила тока – Iсд * количество параллельных цепочек.

Для примера возьмём модель с шестью параллельными линиями из четырёх последовательных диодов.

Напряжение питания – 4 * 3,5В = 14В;
Сила тока цепи – 0,15А * 6 = 0,9А;

Для этой схемы параметры конде-ра: 9мкФ, 400В.

Простая схема блока питания светодиодов с конденсатором

Разберём устройство без трансформаторного блока питания для светодиодов на примере фабричного драйвера LED ламы.

• R1 – резистор на 1Вт, который уменьшает значимость перепадов напряжения в сети;
• R2,C2 – конде-р служит в качестве токоограничителя, а резистор для его разрядки после отключения от сети;
• C3 – сглаживающий конде-р, для уменьшения пульсации света;
• R3 – служит для ограничения перепадов напряжения после преобразования, но более целесообразно вместо него установить стабилитрон.

Какой конденсатор можно использовать для балласта?

В качестве гасящих конденсаторов для светодиодов используются керамические элементы рассчитанные на 400-500В. Использование электролитических (полярных) конденсаторов недопустимо.

Меры предосторожности

Безтрансформаторные схемы не имеют гальванической развязки. Сила тока цепи при появлении дополнительного сопротивления, например прикосновение рукой с  оголённому контакту в цепи, может значительно увеличится, став причиной электротравмы.

Оцените, пожалуйста, статью. Мы старались:) (13 4,77 из 5)
Загрузка…

Источник: https://SvetodiodInfo.ru/texnicheskie-momenty/raschet-kondensatora-dlya-svetodioda.html

4.5.1. Общие сведения

Когда
конденсатор подключен к переменному
синусоидальному напряжению, в нем
возникает синусоидальный ток, опережающий
напряжение на 90^о(рис. 4.5.1).

Рис. 4.5.1

Мгновенная
мощность, потребляемая конденсатором
(как и любой другой цепью) определяется
как произведение напряжения и тока:

p
= ui

График изменения этой мощности можно
построить, перемножая попарно ординаты
графиков u(t)
иi(t), взятые
в один и тот же момент времени. Полученная
таким образом кривая (рис. 4.5.1) представляет
собой синусоиду двойной частоты с
амплитудой.

Q_C
= U_Cm

I_Cm /2
= U_C

I_C.

Когда p>0, конденсатор
заряжается, потребляя энергию и запасая
ее в электрическом поле. Когдаp<0,
он отдает ее другим элементам цепи,
являясь источником энергии. ВеличинаQ_Cявляется максимальной мощностью,
потребляемой или отдаваемой конденсатором,
и называетсяемкостной реактивной
мощностью.

Средняя (активная)
мощность, потребляемая конденсатором,
равна нулю.

4.5.2. Экспериментальная часть Задание

Выведите
кривые тока и напряжения конденсатора
на экран виртуального осциллографа,
перенесите их на график и постройте
кривую изменения мгновенных значений
мощности перемножением мгновенных
значений напряжения и тока.

Порядок выполнения эксперимента

• Соберите
  цепь согласно схеме (рис. 4.5.2), подсоедините
  к ней регулируемый источник синусоидального
  напряжения с параметрами: U
  = 5Bиf= 1 кГц.

Рис. 4.5.2

• Включите
  виртуальные приборы V0,A1 и осциллограф.

• «Подключите»
  два входа осциллографа к приборам V0
  иA1, а остальные отключите.

• Установите
  параметры развёртки осциллографа так,
  чтобы на экране было изображение
  примерно одного-двух периодов напряжения
  и тока.

• Включите
  блок «Приборы II», выберите
  из меню функции «Активная мощность» и
  «Реактивная мощность», подключите их
  кV1 иA1,
  запишите значения реактивной мощностиQ_Cи убедитесь, что активная мощность
  близка к нулю.

• Занесите
  данные осциллографирования напряжения
  и тока конденсатора в табл. 4.5.1
  соответственно указанным моментам
  времени. Выполните вычисления мгновенных
  значений мощности.

Таблица 4.5.1

Время t, мс	Ток iC, мА	Напряжение uC, В	p = uCiC, мВт
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0

• Перенесите
  данные табл. 4.5.1 на график (рис.4.5.3).

Рис. 4.5.3

• По графику
  p(t) определите
  максимальное значение (реактивную
  мощность) и сравните ее с реактивной
  мощностью, измеренной варметром.

По осциллограмме: Q_C= …… мВт;

По варметру: Q_C= …… ВАр.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #