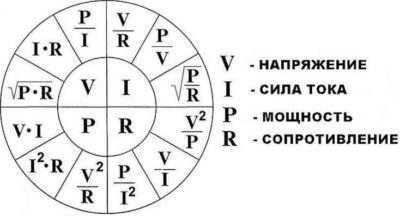
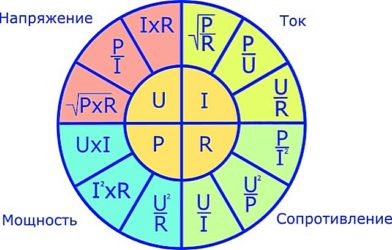
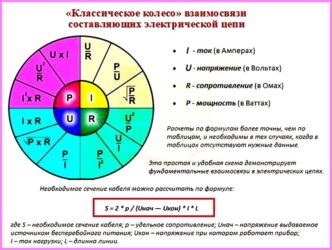
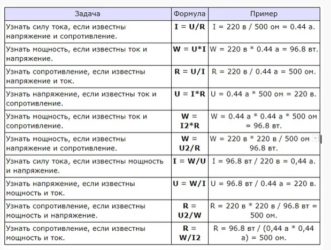
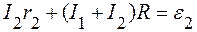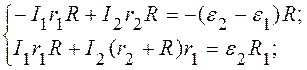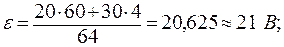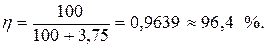Мощность тока на лампе:
P₁ = I²·R₁ = 0,16 · 3 = 0,48 (Bт)
Мощность тока на реостате:
P₂ = I²·R₂ = 0,16 · 2 = 0,32 (Bт)
————————————
Или так:
Напряжение на лампе:
U₁ = I·R₁ = 0,4 · 3 = 1,2 (B)
Напряжение на реостате:
U₂ = I·R₂ = 0,4 · 2 = 0,8 (B)
Мощность тока на лампе:
P₁ = U₁²/R₁ = 1,44 : 3 = 0,48 (Bт)
Мощность тока на реостате:
P₂ = U₂²/R₂ = 0,64 : 2 = 0,32 (Bт)
 |
Резистор, сопротивление которого постоянно, и реостат подсоединены к источнику постоянного напряжения, как показано на рисунке. При силе тока в цепи I1 = 2 A на реостате выделяется мощность P1 = 48 Вт, а при силе тока I2 = 5 A на нем выделяется мощность P2 = 30 Вт.
|
Решение
1. Пусть в первом случае сопротивление реостата равно R1, во втором — равно R2. По закону Ома имеем систему:
где:
| R2 = | P2 | = | 6 | Ом. |
| I22 | 5 |
Решая систему (1), получим:
| U = | P1I22 − P2I12 | = 36 B, |
| I1I2(I2 − I1) |
| r = | P1I2 − P2I1 | = 6 Ом. |
| I1I2(I2 − I1) |
2. Если сопротивление реостата равно нулю, то:

или
где IU — мощность, развиваемая источником. На рисунке представлена зависимость PR(I). Эта парабола, вершина которой соответствует Pmax при силе тока:
Следовательно:
| Pmax = | U2 | = | U2Rм | => Rм = r. |
| 4r | (Rм + r)2 |
Итак,
Далее: максимальная сила тока в предохранителе [тема: задачи на минимум и максимум]
Теги:
- задачи с решениями
- электродинамика
- законы постоянного тока
Содержание
- 1 Рассчитать мощность по сопротивлению и напряжению. Расчет мощности по току и напряжению
- 1.1 Негативное воздействие реактивной нагрузки
- 1.2 Расчет потребляемой мощности
- 1.3 Калькулятор мощности онлайн
- 1.4 Способы расчета сопротивления по математическим формулам
- 2 Расчет мощности
- 2.1 Что такое мощность электроэнергии
- 2.2 Мгновенное значение электрической мощности
- 2.3 Расчеты мощности для электроцепей переменного тока
- 2.4 Расчет мощности в цепи с активной нагрузкой
- 2.5 Расчет реактивной мощности
- 3 Расчет мощности сопротивления резистора — Все об электричестве
- 3.1 Формула параллельного соединения резисторов
- 3.2 Пример №1
- 3.3 Пример расчета №2
- 3.4 Как рассчитать сложные схемы соединения резисторов
- 3.5 Ток, протекающий в цепи параллельно соединенных резисторах
- 3.6 Параллельное соединение резисторов — онлайн калькулятор
- 3.7 Подведем итог
- 3.8 Мощность при параллельном и последовательном соединении резисторов
- 3.9 Свойства и технические характеристики резисторов
- 4 Формула напряжение ток мощность – Формула сопротивления тока. Как найти, вычислить электрическое сопротивление по закону Ома. Как найти сопротивление формула через мощность и силу тока
- 4.1 Что такое мощность электрического тока
- 4.2 По какой формуле вычисляется мощность электрического тока
- 4.3 От чего зависит мощность тока
- 4.4 Мощность электрического тока — Основы электроники
Рассчитать мощность по сопротивлению и напряжению. Расчет мощности по току и напряжению
Расчет электрической мощности
В прошлой статье мы с вами вывели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на силу тока в «амперах», мы получаем мощность в «ваттах». Давайте применим ее к следующей схеме:
В этой схеме есть две известные нам величины: напряжение батареи составляет 18 вольт, а сопротивление лампы — 3 ома. Используя Закон Ома мы определим третью величину — силу тока:
Теперь, зная силу тока, мы можем умножить ее значение на напряжение и получить мощность:
Это означает что лампа рассеивает 108 ватт энергии в форме сета и тепла.
Давайте в этой же схеме увеличим напряжение батареи и посмотрим что произойдет. Интуиция подсказывает нам, что при увеличении напряжения и неизменном сопротивлении, сила тока в цепи также увеличится. А это значит, что увеличится и мощность:
В этой схеме напряжение батареи изменено и составляет 36 вольт вместо прежних 18. Сопротивление лампы не изменилось, и равно 3 омам. Сила тока теперь будет равна:
Давайте обсудим полученное значение. Если I=U/R, и мы удваиваем значение напряжения (U), оставляя неизменным сопротивление, то по логике вещей сила тока у нас тоже должна удвоиться. Действительно, сила тока в данной схеме имеет значение 12 ампер вместо прежних 6. А сейчас давайте вычислим мощность:
Обратите внимание, что мощность у нас также увеличилась по сравнению с предыдущим примером, и увеличилась она значительнее, чем увеличилась сила тока. Почему так получилось? Ответ на этот вопрос прост. Мощность является функцией напряжения умноженного на силу тока, а так как обе эти величины удвоились по сравнению с предыдущими значениями, то мощность увеличилась в 2х2 или в 4 раза. Вы можете проверить эту цифру разделив 432 ватта на 108 ватт и увидев, что соотношение между ними равно 4.
При проектировании любых электрических цепей выполняется расчет мощности. На его основе производится выбор основных элементов и вычисляется допустимая нагрузка. Если расчет для цепи постоянного тока не представляет сложности (в соответствии с законом Ома, необходимо умножить силу тока на напряжение — Р=U*I), то с вычислением мощности переменного тока — не все так просто. Для объяснения потребуется обратиться к основам электротехники, не вдаваясь в подробности, приведем краткое изложение основных тезисов.
В цепях переменного тока расчет мощности ведется с учетом законов синусоидальных изменений напряжения и тока. В связи с этим введено понятие полной мощности (S), которая включает в себя две составляющие: реактивную (Q) и активную (P). Графическое описание этих величин можно сделать через треугольник мощностей (см. рис.1).
Под активной составляющей (Р) подразумевается мощность полезной нагрузки (безвозвратное преобразование электроэнергии в тепло, свет и т.д.). Измеряется данная величина в ваттах (Вт), на бытовом уровне принято вести расчет в киловаттах (кВт), в производственной сфере – мегаваттах (мВт).
Реактивная составляющая (Q) описывает емкостную и индуктивную электронагрузку в цепи переменного тока, единица измерения этой величины Вар.
Рис. 1. Треугольник мощностей (А) и напряжений (В)
В соответствии с графическим представлением, соотношения в треугольнике мощностей можно описать с применением элементарных тригонометрических тождеств, что дает возможность использовать следующие формулы:
- S = √P 2 +Q 2, — для полной мощности;
- и Q = U*I*cos φ , и P = U*I*sin φ — для реактивной и активной составляющих.
Эти расчеты применимы для однофазной сети (например, бытовой 220 В), для вычисления мощности трехфазной сети (380 В) в формулы необходимо добавить множитель – √3 (при симметричной нагрузке) или суммировать мощности всех фаз (если нагрузка несимметрична).
Для лучшего понимания процесса воздействия составляющих полной мощности давайте рассмотрим «чистое» проявление нагрузки в активном, индуктивном и емкостном виде.
Возьмем гипотетическую схему, в которой используется «чистое» активное сопротивление и соответствующий источник переменного напряжения. Графическое описание работы такой цепи продемонстрировано на рисунке 2, где отображаются основные параметры для определенного временного диапазона (t).
Рисунок 2. Мощность идеальной активной нагрузки
Мы можем увидеть, что напряжение и ток синхронизированы как по фазе, так и частоте, мощность же имеет удвоенную частоту. Обратите внимание, что направление этой величины положительное, и она постоянно возрастает.
Как видно на рисунке 3, график характеристик емкостной нагрузки несколько отличается от активной.
Рисунок 3. График идеальной емкостной нагрузки
Частота колебаний емкостной мощности вдвое превосходит частоту синусоиды изменения напряжения. Что касается суммарного значения этого параметра, в течение одного периода гармоники оно равно нулю. При этом увеличения энергии (∆W) также не наблюдается. Такой результат указывает, что ее перемещение происходит в обоих направлениях цепи. То есть, когда увеличивается напряжение, происходит накопление заряда в емкости. При наступлении отрицательного полупериода накопленный заряд разряжается в контур цепи.
В процессе накопления энергии в емкости нагрузки и последующего разряда не производится полезной работы.
Представленный ниже график демонстрирует характер «чистой» индуктивной нагрузки. Как видим, изменилось только направление мощности, что касается наращения, оно равно нулю.
Негативное воздействие реактивной нагрузки
В приведенных выше примерах рассматривались варианты, где присутствует «чистая» реактивная нагрузка. Фактор воздействия активного сопротивления в расчет не принимался. В таких условиях реактивное воздействие равно нулю, а значит, можно не принимать его во внимание. Как вы понимаете, в реальных условиях такое невозможно. Даже, если гипотетически такая нагрузка бы существовала, нельзя исключать сопротивление медных или алюминиевых жил кабеля, необходимого для ее подключения к источнику питания.
Реактивная составляющая может проявляться в виде нагрева активных компонентов цепи, например, двигателя, трансформатора, соединительных проводов, питающего кабеля и т.д. На это тратится определенное количество энергии, что приводит к снижению основных характеристик.
Реактивная мощность воздействует на цепь следующим образом:
- не производит ни какой полезной работы;
- вызывает серьезные потери и нештатные нагрузки на электроприборы;
- может спровоцировать возникновение серьезной аварии.
Именно по этому, производя соответствующие вычисления для электроцепи, нельзя исключать фактор влияния индуктивной и емкостной нагрузки и, если необходимо, предусматривать использование технических систем для ее компенсации.
Расчет потребляемой мощности
В быту часто приходится сталкиваться с вычислением потребляемой мощности, например, для проверки допустимой нагрузки на проводку перед подключением ресурсоемкого электропотребителя (кондиционера, бойлера, электрической плиты и т.д.). Также в таком расчете есть необходимость при выборе защитных автоматов для распределительного щита, через который выполняется подключение квартиры к электроснабжению.
В таких случаях расчет мощности по току и напряжению делать не обязательно, достаточно просуммировать потребляемую энергию всех приборов, которые могут быть включены одновременно. Не связываясь с расчетами, узнать эту величину для каждого устройства можно тремя способами:
При расчетах следует учитывать, что пусковая мощность некоторых электроприборов может существенно отличаться от номинальной. Для бытовых устройств этот параметр практически никогда не указывается в технической документации, поэтому необходимо обратиться к соответствующей таблице, где содержатся средние значения параметров стартовой мощности для различных приборов (желательно выбирать максимальную величину).
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами.
Отцом же науки об электричестве считается французский ученый Кулон — именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор.
Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно — расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество? Если коротко, то это — направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве — закон Ома .
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению:
сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах.
Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах.
Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах.
Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом .
Вся остальная электротехника «пляшет» от этого.
А теперь — о мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление .
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так — ничего сложного!
Каждый человек ежедневно пользуется бытовыми приборами, которые имеют электрическую цепь. Онлайн расчет нагрузки в Амперах и Ватах. Это определенная «дорога» для электрического тока, вырабатываемая энергия передается агрегату и запускает его действие.
Все устройства условно разделяются на три группы как источники электроэнергии (первичные и вторичные), преобразующие агрегаты (осветительные и тепловые приборы), а также элементы вспомогательного назначения – коммутаторы, провода, измерительное оборудование, обеспечивающие работу цепи в реальных условиях.
Все эти приборы входят в общий электромагнитный процесс и имеют свой класс электрической цепи, которая создается для обеспечения эффективной функциональности устройства, требуемого режима работы. Быстро узнать сколько Ват в Ампере поможет сервис расчета мощности.
Калькулятор мощности онлайн
Это надежный помощник в работе при расчете мощности электрической цепи, позволяющий за несколько секунд получить готовый 99,9% результат. Пользователь может за считанные минуты продумать массу вариантов и выбрать наиболее оптимальный. Вероятность ошибки сводится к минимуму.J = U/R; U = R×J; R = U/J; P=U²/R
Чтобы осуществить расчет электрических цепей онлайн необходимо вести в готовую таблицу два значения, напряжение (В) и ток (А). А после нажать на кнопку «Вычислить» и получить сиюминутный результат данных сопротивления (Ом) и мощности (Вт) при заданных пользователем параметрах.
Данный онлайн калькулятор мощности для расчета электрических цепей является автоматической, нужно быть внимательными при введении всех показателей. Если число состоит из целой и дробной части, то разделять их нужно точкой, а не запятой.
Способы расчета сопротивления по математическим формулам
Чтобы сделать расчет сопротивления электрических цепей можно применить всем известную формулу Закона Ома
Источник: https://enbima.ru/calculate-the-power-by-resistance-and-voltage-calculation-of-current-and-voltage.html
Расчет мощности
> Теория > Расчет мощности
Современная структура общества такова, что на бытовом и промышленном уровне повсеместно используется электроэнергия. Генераторные установки, вырабатывающие электроэнергию, преобразующие подстанции работают для того, чтобы передать ее потребителям на бытовые электрические приборы и промышленные электроустановки.
Общая схема передачи электроэнергии потребителям с учетом мощностей
Что такое мощность электроэнергии
В электросетях, по которым передается энергия, существует ряд основных параметров, которые обязательно учитываются при проектировании и эксплуатации электроустановок.
Одним из таких показателей является электрическая мощность, под этим подразумевается способность электроустановки генерировать, передавать или преобразовывать определенную величину электроэнергии за определенный период времени. Преобразованием считается процесс изменения электрической энергии в тепло, механические движения или другой вид энергии. Чтобы сделать расчет мощности, надо знать, как минимум, величины тока, напряжения и ряда других параметров.
Расчет тока и напряжения, мощности иногда не делают, а измеряют параметры на месте. Но такая возможность не всегда предоставляется. Надо знать, как рассчитать мощность, когда цепь обесточена, при проектировании электроустановок, уметь пользоваться таблицей законов Ома и рассчитать силу тока по известным значениям параметров. Рассчитывать мощность нагрузки и ток нагрузки приходится для того, чтобы правильно выбрать сечение проводов в цепи, величину тока срабатывания для защитных автоматов и других нужд.
Законы Ома наглядно показывают, как посчитать ток по мощности и напряжению
Физический смысл электрической мощности в цепях переменного и постоянного тока одинаковый, но от условий нагрузки в цепи мощность может выражаться разными соотношениями. Для стандартизации закономерности явлений вводится понятие мгновенное значение, что указывает на зависимость скорости преобразований электроэнергии от фактора времени.
Электрическая мощность – это величина, выражающая скорость преобразования энергии электричества в другой вид энергии, обозначается буквой «Р».
Мгновенное значение электрической мощности
Определение – электрическая мощность тесно связана с другими параметрами цепи, током и напряжением, при изменении величины одного из них изменяются другие. Поэтому показания мощности фиксируются в короткий промежуток времени – ∆t.
Расчет мощности трехфазной сети
Напряжение в данном случае обозначают буквой «U» – это выражает разность потенциалов зарядов, перемещенных электрическим полем из одной точки в другую за промежуток времени ∆t.
Сила тока обозначается буквой «I» – это поток, переносимый магнитным полем зарядов, другими словами заряд, перенесенный во временной интервал ∆t.
Исходя из этих определений, просматривается пропорциональная зависимость между этими параметрами:
Р = UxI.
При расчетах можно учитывать зависимость мощности от сопротивления нагрузки «R». По законам Ома для участка цепи с постоянным током мощность выражается как:
Р = I2xR или P = U2|R.
Если поставить в схему питания амперметр и вольтметр, то не придется думать, как вычислить силу тока.
Обратите внимание! Амперметр ставится последовательно в цепь по отношению к сопротивлению нагрузки, а вольтметр – параллельно.
В качестве источника питания используется аккумулятор, как нагрузка установлен прожектор. В данном случае не делается расчет силы тока, параллельно нагрузке подключен вольтметр, для измерения напряжения в Вольтах. Амперметр подключается последовательно для измерения тока в Амперах. Зная показания напряжения и тока по формулам, показанным выше, легко рассчитывается мощность.
Для участков цепи с переменным током формулы расчетов сложнее – необходимо учитывать характер нагрузки.
Расчеты мощности для электроцепей переменного тока
Переменный ток и напряжение имеют синусоидальный вид, при различных нагрузках происходит смещение фазы между ними на определенный угол. По этой причине направление тока иногда может быть противоположным, от нагрузки к источнику питания.
Это бывает в электродвигателях, когда обмотка начинает генерировать энергию, это негативно сказывается на эффективности работы оборудования, снижается мощность.
При большом количестве потребителей в электросети характер нагрузки имеет смешанный вид, в идеале выделяют три типа нагрузки:
- Активная нагрузка, ее представляют такие электроприборы, как лампы накаливания, нагревательные тэны, спиральные электроплиты;
- Емкостная нагрузка – это конденсаторы в оборудовании различного назначения;
- Индуктивная нагрузка представлена катушками в электродвигателях, обмотках электромагнитов, дросселями и трансформаторами, другими приборами, где ток протекает через обмотки.
Емкостные и индуктивные виды выделяют как реактивную энергию в электросетях. Зная вид нагрузки, расчет потребляемой мощности делается точнее.
Расчет мощности в цепи с активной нагрузкой
Это классический случай в однофазной сети 220 В, в качестве нагрузки можно использовать обычные резисторы. Мощность рассчитывается как произведение действующих значений тока и напряжения, умноженное на соsϕ. В данном случае ϕ – угол смещения между фазами тока и напряжения.
Р = UI cos ϕ
График зависимости мощности по току и напряжению при активной нагрузке
Из графика можно узнать, что колебания тока и напряжения одинаковы по частоте и фазе, мощность всегда положительная с частотой в два раза больше.
Активная электрическая мощность характеризует процесс преобразования в сетях с переменным током энергии в тепло, механические движения, излучение света, в любой вид другой энергии. Измеряется активная нагрузка в Вт, кВт.
Расчет реактивной мощности
Как найти мощность в цепях с индуктивной и емкостной нагрузками? Это делается аналогичным образом. Расчет потребляемой мощности, как и в случае с активной нагрузкой, означает, что действующие напряжение и ток перемножаются, и результат умножается на sin ϕ. Где ϕ – угол сдвига фаз тока и напряжения.
Р = UI sin ϕ
Диаграмма, показывающая взаимосвязь параметров цепи при индуктивной нагрузке
График показывает, что мощность может принимать отрицательные значения, в этот момент энергия отдается в сторону источника питания, фактически она бесполезна и расходуется на нагрев.
Реактивная составляющая энергии характеризует работу нагрузки в виде электронного оборудования, электротехнических схем, моторов с наличием емкостной и индуктивной нагрузки. Единица измерения реактивной мощности при подсчете измеряется в Вар, это (Вольт-Ампер реактивный), обозначается буквой «Q».
Треугольник, отображающий отношение мощностей в сети
Зависимость мощности в цепи переменного тока от реактивной и активной составляющих с учетом угла сдвига фаз хорошо отображается на диаграмме, которую называют треугольником мощностей.
Формула расчета полной мощности обозначается буквой «S»
В этом случае учитывается полный импеданс рассчитываемой мощности электрического тока (комплексное сопротивление нагрузки). Тем, кому вычислением заниматься сложно даже на калькуляторе, можно воспользоваться онлайн калькуляторами на сайте https://www.fxyz.ru с вычислением мощности в цепях с различной нагрузкой. Вычисляется все мгновенно, достаточно заполнить таблицу с исходными параметрами. Когда такой калькулятор под рукой, я вычислю быстро нужные мне параметры.
Источник: https://elquanta.ru/teoriya/raschet-moshhnosti.html
Расчет мощности сопротивления резистора — Все об электричестве
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
Пример №1
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
Отправить сообщение об ошибке.
Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
Мощность при параллельном и последовательном соединении резисторов
Все известные виды проводников обладают определенными свойствами, в том числе и электрическим сопротивлением. Это качество нашло свое применение в резисторах, представляющих собой элементы цепи с точно установленным сопротивлением.
Они позволяют выполнять регулировку тока и напряжения с высокой точностью в схемах. Все подобные сопротивления имеют свои индивидуальные качества. Например, мощность при параллельном и последовательном соединении резисторов будет различной.
Поэтому на практике очень часто используются различные методики расчетов, благодаря которым возможно получение точных результатов.
Свойства и технические характеристики резисторов
Как уже отмечалось, резисторы в электрических цепях и схемах выполняют регулировочную функцию. С этой целью используется закон Ома, выраженный формулой: I = U/R. Таким образом, с уменьшением сопротивления происходит заметное возрастание тока. И, наоборот, чем выше сопротивление, тем меньше ток. Благодаря этому свойству, резисторы нашли широкое применение в электротехнике. На этой основе создаются делители тока, использующиеся в конструкциях электротехнических устройств.
Помимо функции регулировки тока, резисторы применяются в схемах делителей напряжения. В этом случае закон Ома будет выглядеть несколько иначе: U = I x R. Это означает, что с ростом сопротивления происходит увеличение напряжения. На этом принципе строится вся работа устройств, предназначенных для деления напряжения. Для делителей тока используется параллельное соединение резисторов, а для делителей напряжения – последовательное.
На схемах резисторы отображаются в виде прямоугольника, размером 10х4 мм. Для обозначения применяется символ R, который может быть дополнен значением мощности данного элемента. При мощности свыше 2 Вт, обозначение выполняется с помощью римских цифр. Соответствующая надпись наносится на схеме возле значка резистора.
Современные технологии позволяют изготавливать данные элементы с довольно точными значениями сопротивления.
Важным параметром резистора считается отклонение сопротивления. Его измерение осуществляется в процентах от номинала. Стандартный ряд отклонений представляет собой значения в виде: +20, +10, +5, +2, +1% и так далее до величины +0,001%.
Большое значение имеет мощность резистора. По каждому из них во время работы проходит электрический ток, вызывающий нагрев. Если допустимое значение рассеиваемой мощности превысит норму, это приведет к выходу из строя резистора. Следует учитывать, что в процессе нагревания происходит изменение сопротивления элемента. Поэтому если устройства работают в широких диапазонах температур, применяется специальная величина, именуемая температурным коэффициентом сопротивления.
Источник: https://contur-sb.com/raschet-moschnosti-soprotivleniya-rezistora/
Формула напряжение ток мощность – Формула сопротивления тока. Как найти, вычислить электрическое сопротивление по закону Ома. Как найти сопротивление формула через мощность и силу тока
- Мощность электрического тока: формула
- Мощность электрического тока — Основы электроники
- физические формулы, использующие мощность и напряжение
- Формула напряжения тока. Как найти, вычислить электрическое напряжение.
-
- Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.
-
- Как узнать ток зная мощность и напряжение
- формулы расчета мощности в проводнике
- Зависимость мощности от силы тока, формула мощности, физический смысл
- А теперь, перейдем к главному.
- О мощности электрического тока
- Что такое мощность электрического тока
- По какой формуле вычисляется мощность тока
- От чего зависит мощность тока
Прежде чем рассматривать электрическую мощность, следует определиться, что же представляет собой мощность вообще, как физическое понятие. Обычно, говоря об этой величине, подразумевается определенная внутренняя энергия или сила, которой обладает какой-либо объект.
Это может быть мощность устройства, например, двигателя или действия (взрыв). Ее не следует путать с силой, поскольку это различные понятия, хотя и находящиеся в определенной зависимости между собой. Любые физические действия совершаются под влиянием силы. С ее помощью проделывается определенный путь, то есть выполняется работа. В свою очередь, работа А, проделанная в течение определенного времени t, составит значение мощности, выраженное формулой: N = A/t (Вт = Дж/с).
Другое понятие мощности связано со скоростью преобразования энергии той или иной системы. Одним из таких преобразований является мощность электрического тока, с помощью которой также выполняется множество различных работ. В первую очередь она связана с электродвигателями и другими устройствами, выполняющими полезные действия.
Что такое мощность электрического тока
Мощность тока связана сразу с несколькими физическими величинами. Напряжение (U) представляет собой работу, затрачиваемую на перемещение 1 кулона. Сила тока (I) соответствует количеству кулонов, проходящих за 1 секунду. Таким образом, ток, умноженный на напряжение (I x U), соответствует полной работе, выполненной за 1 секунду. Полученное значение и будет мощностью электрического тока.
Приведенная формула мощности тока показывает, что мощность находится в одинаковой зависимости от силы тока и напряжения. Отсюда следует, что одно и то же значение этого параметра можно получить за счет большого тока и малого напряжения и, наоборот, при высоком напряжении и малом токе. Это свойство позволяет передавать электроэнергию на дальние расстояния от источника к потребителям. В процессе передачи ток преобразуется с помощью трансформаторов, установленных на повышающих и понижающих подстанциях.
Существует два основных вида электрической мощности – активная и реактивная. В первом случае происходит безвозвратное превращение мощности электрического тока в механическую, световую, тепловую и другие виды энергии. Для нее применяется единица измерения – ватт. 1Вт = 1В х 1А. На производстве и в быту используются более крупные значения – киловатты и мегаватты.
К реактивной мощности относится такая электрическая нагрузка, которая создается в устройствах за счет индуктивных и емкостных колебаний энергии электромагнитного поля. В переменном токе эта величина представляет собой произведение, выраженное следующей формулой: Q = U х I х sin(угла).
Синус угла означает сдвиг фаз между рабочим током и падением напряжения. Q является реактивной мощностью, измеряемой в Вар – вольт-ампер реактивный.
Данные расчеты помогают эффективно решить вопрос, как найти мощность электрического тока, а формула, существующая для этого, позволяет быстро выполнить вычисления.
Обе мощности можно наглядно рассмотреть на простом примере. Какое-либо электротехническое устройство оборудовано нагревательными элементами – ТЭНами и электродвигателем. Для изготовления ТЭНов используется материал, обладающий высоким сопротивлением, поэтому при прохождении по нему тока, вся электрическая энергия преобразуется в тепловую. Данный пример очень точно характеризует активную электрическую мощность.
Что касается электродвигателя, то внутри него расположена медная обмотка, обладающая индуктивностью, которая, в свою очередь, обладает эффектом самоиндукции. Благодаря этому эффекту, происходит частичный возврат электричества обратно в сеть. Возвращаемая энергия характеризуется небольшим смещением в параметрах напряжения и тока, оказывая негативное влияние на электрическую сеть в виде дополнительных перегрузок.
Такие же свойства имеют и конденсаторы из-за своей электрической емкости, когда накопленный заряд отдается обратно. Здесь также смещаются значения тока и напряжения, только в противоположном направлении.
Данная энергия индуктивности и емкости, со смещением по фазе относительно значений действующей электросети, как раз и есть реактивная электрическая мощность.
Благодаря противоположному эффекту индуктивности и емкости в отношении сдвига фазы, становится возможным выполнить компенсацию реактивной мощности, повышая, тем самым, эффективность и качество электроснабжения.
По какой формуле вычисляется мощность электрического тока
Правильное и точное решение вопроса чему равна мощность электрического тока, играет решающую роль в деле обеспечения безопасной эксплуатации электропроводки, предупреждения возгораний из-за неправильно выбранного сечения проводов и кабелей. Мощность тока в активной цепи зависит от силы тока и напряжения.
Для измерения силы тока существует прибор – амперметр. Однако не всегда возможно воспользоваться этим прибором, особенно когда проект здания еще только составляется, а электрической цепи просто не существует. Для таких случаев предусмотрена специальная методика проведения расчетов.
Силу тока можно определить по формуле при наличии значений мощности, напряжения сети и характера нагрузки.
Существует формула мощности тока, применительно к постоянным значениям силы тока и напряжения: P = U x I. При наличии сдвига фаз между силой тока и напряжением, для расчетов используется уже другая формула: P = U x I х cos φ. Кроме того, мощность можно определить заранее путем суммирования мощности всех приборов, которые запланированы к вводу в эксплуатацию и подключению к сети. Эти данные имеются в технических паспортах и руководствах по эксплуатации устройств и оборудования.
Таким образом, формула определения мощности электрического тока позволяет вычислить силу тока для однофазной сети: I = P/(U x cos φ), где cos φ представляет собой коэффициент мощности.
При наличии трехфазной электрической сети сила тока вычисляется по такой же формуле, только к ней добавляется фазный коэффициент 1,73: I = P/(1,73 х U x cos φ). Коэффициент мощности полностью зависит от характера планируемой нагрузки.
Если предполагается использовать лишь лампы освещения или нагревательные приборы, то он будет составлять единицу.
При наличии реактивных составляющих в активных нагрузках, коэффициент мощности уже считается как 0,95. Данный фактор обязательно учитывается в зависимости от того, какой тип электропроводки используется. Если приборы и оборудование обладают достаточно высокой мощностью, то коэффициент составит 0,8. Это касается сварочных аппаратов, электродвигателей и других аналогичных устройств.
Для расчетов при наличии однофазного тока значение напряжения принимается 220 вольт. Если присутствует трехфазный ток, расчетное напряжение составит 380 вольт. Однако с целью получения максимально точных результатов, необходимо использовать в расчетах фактическое значение напряжения, измеренное специальными приборами.
От чего зависит мощность тока
Мощность тока, различных приборов и оборудования зависит сразу от двух основных величин – силы тока и напряжения. Чем выше ток, тем больше значение мощности, соответственно, при повышении напряжения, мощность также возрастает. Если напряжение и сила тока увеличиваются одновременно, то мощность электрического тока будет возрастать как произведение той и другой величины: N = I x U.
Очень часто возникает вопрос, в чем измеряется мощность тока? Основной единицей измерения этой величины является 1 ватт (Вт). Таким образом, 1 ватт является мощностью устройства, потребляющего ток силой в 1 ампер, при напряжении 1 вольт. Подобной мощностью обладает, например, лампочка от обычного карманного фонарика.
Расчетное значение мощности позволяет точно определить расход электрической энергии. Для этого необходимо взять произведение мощности и времени. Сама формула выглядит так: W = IUt где W является расходом электроэнергии, произведение IU – мощностью, а t – количеством отработанного времени. Например, чем больше продолжается работа электрического двигателя, тем большая работа им совершается. Соответственно возрастает и потребление электроэнергии.
electric-220.ru
Мощность электрического тока — Основы электроники
Обычно электрический ток сравнивают с течением жидкости по трубке, а напряжение или разность потенциалов — с разностью уровней жидкости.
В этом случае поток воды, падающий сверху вниз, несет с собой определенное количество энергии. В условиях свободного падения эта энергия растрачивается бесполезно для человека. Если же направить падающий поток воды на лопасти турбины, то последняя начнет вращаться и сможет производить полезную работу.
Работа, производимая потоком воды в течение определенного промежутка времени, например, в течение одной секунды, будет тем больше, чем с большей высоты падает поток и чем больше масса падающей воды.
Точно так же и электрический ток, протекая по цепи от высшего потенциала к низшему, совершает работу. В каждую данную секунду времени будет совершаться тем больше работы, чем больше разность потенциалов и чем большее количество электричества ежесекундно проходит через поперечное сечение цепи.
Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы.
Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи.
Для измерения мощности электрического тока принята единица, называемая ватт (Вт).
Мощностью в 1 Вт обладает ток силой в 1 А при разности потенциалов, равной 1 В.
Для вычисления мощности постоянного тока в ваттах нужно силу тока в амперах умножить на напряжение в вольтах.
Если обозначить мощность электрического тока буквой P, то приведенное выше правило можно записать в виде формулы
P = I*U. (1)
Воспользуемся этой формулой для решения числового примера. Требуется определить, какая мощность электрического тока необходима для накала нити радиолампы, если напряжение накала равно 4 в, а ток накала 75 мА
Определим мощность электрического тока, поглощаемую нитью лампы:
Р= 0,075 А*4 В = 0,3 Вт.
Мощность электрического тока можно вычислить и другим путем. Предположим, что нам известны сила тока в цепи и сопротивление цепи, а напряжение неизвестно.
В этом случае мы воспользуемся знакомым нам соотношением из закона Ома:
U=IR
и подставим правую часть этого равенства (IR) в формулу (1) вместо напряжения U.
Тогда формула (1) примет вид:
P = I*U =I*IR
или
Р = I2*R. (2)
Например, требуется узнать, какая мощность теряется в реостате сопротивлением в 5 Ом, если через него проходит ток, силой 0,5 А. Пользуясь формулой (2), найдем:
P= I2*R = (0,5)2*5 =0,25*5 = 1,25 Вт.
Наконец, мощность электрического тока может быть вычислена и в том случае, когда известны напряжение и сопротивление, а сила тока неизвестна. Для этого вместо силы тока I в формулу (1) подставляется известное из закона Ома отношение U/R и тогда формула (1) приобретает следующий вид:
Р = I*U=U2/R (3)
Например, при 2,5 В падения напряжения на реостате сопротивлением в 5 Ом поглощаемая реостатом мощность будет равна:
Р = U2/R=(2,5)2/5=1,25 Вт
Таким образом, для вычисления мощности требуется знать любые две из величин, входящих в формулу закона Ома.
Мощность электрического тока равна работе электрического тока, производимой в течение одной секунды.
P = A/t
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник: https://ikeacover.ru/raznoe/formula-napryazhenie-tok-moshhnost-formula-soprotivleniya-toka-kak-najti-vychislit-elektricheskoe-soprotivlenie-po-zakonu-oma-kak-najti-soprotivlenie-formula-cherez-moshhnost-i-silu-toka.html
Экстремальные задачи по физике практически отсутствуют в задачниках и мало извечтны большинству учащихся. Решение таких задач с физическим содержанием способствует углублению межпредметных связей физики и математики. Эти задачи физически интересны, их можно решать как с применением производной, так и методами элементарной математики. В данной работе показано применение разных способов решения для одной из таких задач, а именно для решения задачи из части С ЕГЭ (С4 демо,2010 г)
Скачать:
| Вложение | Размер |
|---|---|
| ekstremalnaya_zadacha_chasti_s_ege.doc | 389 КБ |
Предварительный просмотр:
ЭКСТРЕМАЛЬНАЯ ЗАДАЧА ЧАСТИ С ЕГЭ
Оркина Виктория Евгеньевна
Научный руководитель: Газизуллина А.Ф., учитель физики и информатики
МБОУ СОШ с. Райманово Туймазинского района
Экстремальные задачи по физике практически отсутствуют в задачниках и мало известны большинству учащихся. Решение таких задач с физическим содержанием способствует углублению межпредметных связей физики и математики. Эти задачи физически интересны, их можно решать как с применением производной, так и методами элементарной математики. В моей работе я показал применение этих способов решения для одной из таких задач, а именно для решения задачи из части С ЕГЭ (С4 Демо 2010г).
Цель работы: исследовать зависимость мощности тока в резисторе от сопротивления резистора.
1. математический расчёт
(рассмотрение математических приемов элементарного решения экстремальных задач );
2. построение графиков;
3. анализ полученных данных.
Задачи: рассмотреть способы решения задачи и выбрать наиболее простое решение сложных заданий части С.
Задача
Какую наибольшую полезную мощность тока Рмах может обеспечить источник с ЭДС ε и внутренним сопротивлением r?
P= I*U = I*(ε – I*r) = ε *I – r*I² = ε²/4r – r*(I – ε/2r) ²
Значит, максимум мощности Рмах = ε²/4r при
Сравнивая с законом Ома ,
видим, что этот максимум достигается при R = r.
Рассмотрим равенство P = ε *I – r*I² как квадратное уравнение относительно I:
ε *I – r*I² + P = 0, откуда I1,2= ε±
Следовательно, Р≤ ε²/4r, т.е. Рмах = ε²/4r
При решении с помощью производной за независимую переменную проще выбрать ток I, а не внешнее сопротивление R.
По закону Ома для полной цепи, ток,
мощность, выделяемая во внешней цепи:
Дифференцируем P по R:
Найдем критические точки из условия
Имеем две критические точки R = — r и R = r. Но, так как R>0, то
R = -r не имеет смысла. Производная мощности меняет знак с
«+» на «-» в точке R = r, следовательно, R = r – точка минимума.
Таким образом, мощность максимальна, если R = r, т.е.
внутреннее сопротивление источника тока равно внешнему сопротивлению. Это означает, что применительно к задаче максимум мощности наблюдается при R = r.
Формула для мощности тока в резисторе:
Закон Ома для полной цепи:
Объединив две формулы, получим:
Электрическая цепь состоит из источника тока и реостата. ЭДС источника ε = 6 В, его внутреннее сопротивление r = 2 Ом. Сопротивление реостата можно изменять в пределах от 1 Ом до 5 Ом. Чему равна максимальная мощность тока, выделяемая на реостате?
ε = 6 В, r = 2 Ом, R = [1; 5] Ом
Согласно проведенному мной исследованию зависимости мощности тока в резисторе от сопротивления, мощность тока, выделяемая на реостате, максимальна при R= r=2 Ом.
Мощность определим по формуле:
Подставим числовые значения
Из графиков и таблицы следует, что при равенстве внешнего и внутреннего сопротивлений мощность тока во внешней части цепи достигает максимальной величины. Эта зависимость проявляется как в первом, так и во втором опытах. (Приложение1) График зависимости мощности от сопротивления приведен в приложении 2. Действительно максимум мощности достигается при R=2 Ом.
В случае, когда проводник неподвижен и химических превращений в нем не происходит, то работа тока целиком расходуется на нагревание проводника. Количество теплоты, выделяющееся в проводнике за конечный промежуток времени при прохождении постоянного тока I, рассчитывается по формуле
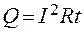
Формула (2.7) выражает закон Джоуля-Ленца для участка цепи постоянного тока: количество теплоты, выделяемое постоянным электрическим током на участке цепи, равно произведению квадрата силы тока на время его прохождения и электрическое сопротивление этого участка цепи.
Так как IR = U, то формулу (2.7) можно переписать в виде
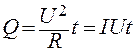
Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t, вычисляется по формуле
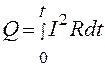
Закон Джоуля-Ленца в дифференциальной форме (для данной точки проводника с током) имеет вид
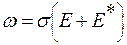
где ω − плотность тепловой мощности; σ − удельная электропроводность; Е− напряженность электрического поля в данной точке проводника; Е * − напряженность поля сторонних сил.
Примеры решения задач
Задача 1. За время τ = 20 с при равномерно возраставшей силе тока от нуля до Io в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Найти Io.
| Io – ? | Решение: Так как ток равномерно возрастает, то зависимость силы тока от времени имеет вид 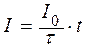 . (1) . (1) |
| τ = 20 с R = 5 Ом Q = 4 кДж |
По закону Джоуля-Ленца за время dt в проводнике выделится количество тепла
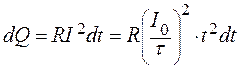
Полное количество тепла за время от 0 до τ
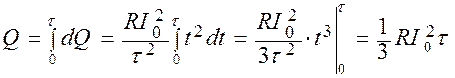
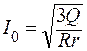
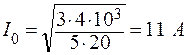
Задача 2. При включении электромотора в сеть с напряжением U = 220 В он потребляет ток I = 5 А. Определить мощность, потребляемую мотором, и его КПД, если сопротивление обмотки мотора R = 6 Ом.
| Pп – ? η – ? | Решение: Полная мощность, потребляемая мотором: 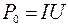 , Р0 = 1100 Вт. , Р0 = 1100 Вт. |
| U = 220 В I = 5 А R = 6 Ом |
Мощность, выделяющаяся в виде тепла:
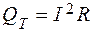
Полезная мощность (механическая)
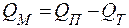
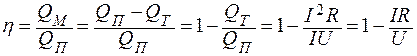
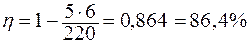
Задача 3. Источник тока с ЭДС замкнут на реостат. При силе тока I1 = 0,2 А и I2 = 2,4 А на реостате выделяется одинаковая мощность. Найти:
1) при какой силе тока на реостате выделяется максимальная мощность?
2) чему равна сила тока короткого замыкания?
где R1 и R2 – сопротивления реостата в каждом случае. По условию P1 = P2, поэтому
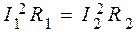
По закону Ома для полной цепи
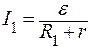
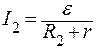
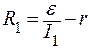
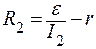
подставив их в (1), получаем:
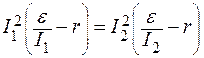
Отсюда находим отношение 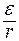
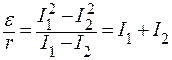
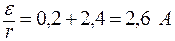
Максимальная мощность выделяется при условии R = r, при этом ток
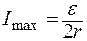
Ток короткого замыкания
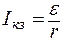
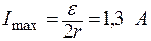
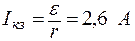
Задача 4. При изменении внешнего сопротивления с R1 = 6 Ом до R2 = 21 Ом. КПД схемы увеличился вдвое. Чему равно внутреннее сопротивление источника тока r ?
| r − ? | Решение: При сопротивлении R1 КПД источника тока 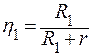 , а при сопротивлении R2 , а при сопротивлении R2 |
| R1 = 6 Ом R2 = 21 Ом η2 = 2η1 |
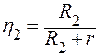
Так как по условию задачи η2=2η1, то
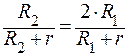
Отсюда выражаем r:
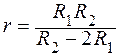
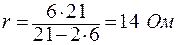
Ответ: r = 14 Ом.
Задача 5. Две батареи с ЭДС ε1 = 20 В и ε2 = 30 В и внутренними сопротивлениями r1 = 4 Ом и r2 = 60 Ом соединены параллельно и подключены к нагрузке R = 100 Ом. Найти: 1) мощность, которая выделяется в нагрузке; 2) параметры ε и r генератора, которым можно заменить батареи без изменения тока в нагрузке; 3) КПД этого генератора.
| P – ? ε, r – ? η – ? | Решение: 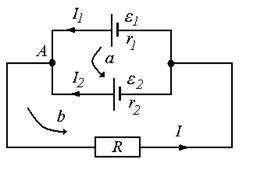 Рис. 52 Рис. 52 |
| ε1 = 20 В ε2 = 30 В r1 = 4 Ом r2 = 60 Ом R = 100 Ом |
Используя правила Кирхгофа, найдем токи I1, I2, I в узле A:
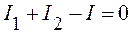
Для контура a с обходом против часовой стрелки
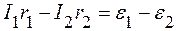
Для контура b с обходом против часовой стрелки
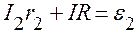
Решим систему линейных уравнений (1) – (3) относительно I1, I2, I.
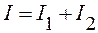
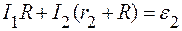
Умножая уравнение (2) на R, а уравнение (5) – на r1, и складывая их, получаем:
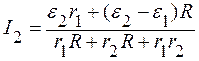
Подставляя (6) в выражение (2), находим I1:
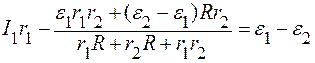
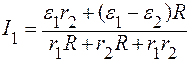
Подставляя выражения (6) и (7) в (4), находим I:
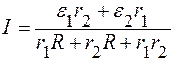
В нагрузке выделяется мощность:
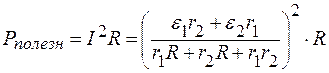
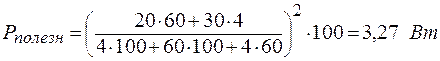
Находим параметры генератора. Если данные в задаче батареи заменить на одну с ЭДС ε и внутренним сопротивлением r, то через сопротивление R потек бы ток
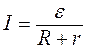
Преобразуем выражение (8), поделив числитель и знаменатель дроби на (r1+r2), получим
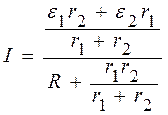
Для того чтобы эти выражения были одинаковыми, необходимо выполнение условий:
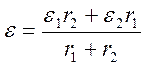
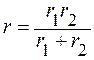
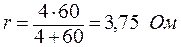
КПД этого генератора в данной схеме
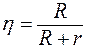
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9405 — 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Установите соответствие между графиками зависимости физических величин от сопротивления реостата и величинами, которые эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите выбранные цифры под соответствующими буквами.
Объект авторского права ООО «Легион»
Вместе с этой задачей также решают:
В идеальном колебательном контуре увеличили индуктивность катушки. Как при этом изменятся собственная частота колебаний в контуре и амплитуда колебаний силы тока в нём?
Установите соответствие между единицами измерения и физическими величинами.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите выбранн…
Пучок света переходит из воздуха в стекло. Частота световой волны ν, скорость света в воздухе c, показатель преломления стекла относительно воздуха n. Чему равны длина волны и скор…
На каком графике правильно изображена зависимость
Калькулятор мощности – расчет по току, напряжению, сопротивлению
Перемотайте вниз чтобы НАЧАТЬ (место для вашего контента)
С помощью калькулятора мощности вы можете самостоятельно выполнить расчет мощности по току и напряжению для однофазных (220 В) и трехфазных сетей (380 В). Программа также рассчитывает мощность через сопротивление и напряжение, или через ток и сопротивление согласно закону Ома. Значение cos φ принимается согласно указаниям технического паспорта прибора, усредненным значениям таблиц ниже или рассчитываются самостоятельно по формулам. Без необходимости рекомендуем не изменять коэффициент и оставлять равным 0.95. Чтобы получить результат расчета, нажмите кнопку «Рассчитать».
Смежные нормативные документы:
- СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
- СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
- СП 76.13330.2016 «Электротехнические устройства»
- ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
- ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
- ГОСТ Р 50571.1-93 «Электроустановки зданий»
Формулы расчета мощности
Мощность — это физическая величина, равная отношению количества работы ко времени совершения этой работы. Мощность электрического тока (P) — это величина, характеризующая скорость преобразования электрической энергии в другие виды энергии. Международная единица измерения — Ватт (Вт/W).
— Мощность по току и напряжению (постоянный ток): P = I × U — Мощность по току и напряжению (переменный ток однофазный): P = I × U × cos φ — Мощность по току и напряжению (переменный ток трехфазный): P = I × U × cos φ × √3 — Мощность по току и сопротивлению: P = I 2 × R — Мощность по напряжению и сопротивлению: P = U 2 / R
- I – сила тока, А;
- U – напряжение, В;
- R – сопротивление, Ом;
- cos φ – коэффициент мощности.
Мощность ток напряжение, расчёты для однофазной сети 220 В
Сила тока I (в амперах, А) подсчитывается по формуле:
I = P / U,
где
P – электрическая полная нагрузка (обязательно указывается в техническом паспорте устройства), Вт (ватт)
U – напряжение электрической сети, В (вольт)
Ниже в таблице представлены величины нагрузки типичных бытовых электроприборов и потребляемый ими ток (для напряжения 220 В).
Сила тока, АСтиральная машина2000 – 25009,0 – 11,4Джакузи2000 – 25009,0 – 11,4Электроподогрев пола800 – 14003,6 – 6,4Стационарная электрическая плита4500 – 850020,5 – 38,6СВЧ печь900 – 13004,1 – 5,9Посудомоечная машина2000 — 25009,0 – 11,4Морозильники, холодильники140 — 3000,6 – 1,4Мясорубка с электроприводом1100 — 12005,0 — 5,5Электрочайник1850 – 20008,4 – 9,0Электрическая кофеварка6з0 — 12003,0 – 5,5Соковыжималка240 — 3601,1 – 1,6Тостер640 — 11002,9 — 5,0Миксер250 — 4001,1 – 1,8Фен400 — 16001,8 – 7,3Утюг900 — 17004,1 – 7,7Пылесос680 — 14003,1 – 6,4Вентилятор250 — 4001,0 – 1,8Телевизор125 — 1800,6 – 0,8Радиоаппаратура70 — 1000,3 – 0,5Приборы освещения20 — 1000,1 – 0,4
Различные потребители электроэнергии подключаются через соответствующие автоматы к электросчётчику и далее общему автомату, который должен быть рассчитан на нагрузку приборов, которыми будет оборудована квартира. Провод, который подводит питание также должен удовлетворять нагрузке энергопотребителей.
Расчет косинуса фи (cos φ)
φ – угол сдвига между фазой тока и напряжения, причем если последний опережает ток сдвиг считается положительным, если отстает, то отрицательным.
cos φ – безразмерная величина, которая равна отношению активной мощности к полной и показывает насколько эффективно используется энергия.
Формула расчета косинуса фи: cos φ = S / P
- S – полная мощность, ВА (Вольт-ампер);
- P – активная мощность, Вт.
Активная мощность (P) — реальная, полезная, настоящая мощность, эта нагрузка поглощает всю энергию и превращает ее в полезную работу, например, свет от лампочки. Сдвиг по фазе отсутствует.
Формула расчета активной мощности: P (Вт) = I × U × cos φ
Реактивная мощность (Q) — безваттная (бесполезная) мощность, которая характеризуется тем, что не участвует в работе, а передается обратно к источнику. Наличие реактивной составляющей считается вредной характеристикой цепи, поскольку главная цель существующего электроснабжения — это сокращение издержек, а не перекачивание ее туда и обратно. Такой эффект создают катушки и конденсаторы.
Формула расчета реактивной мощности: P (ВАР) = I × U × sin φ
Полная мощность электроприбора (S) — это суммарная величина, которая включает в себе как активную, так и реактивную составляющие мощности.
Формула расчета полной мощности: S (ВА) = I × U или S = √( P 2 + Q 2 )
Источник
Определение мощности электродвигателя по потребляемому току
Мощность двигателя можно определить по потребляемому им току. Для измерения силы тока будем использовать токоизмерительные клещи.
Перед началом измерений предварительно отключаем подачу напряжения на электродвигатель. После этого снимаем крышку с клеммной коробки и расправляем токопроводящие жилы, чтобы обеспечить удобный доступ к ним.
Затем подаем напряжение на двигатель и даем поработать в режиме номинальной нагрузки в течение нескольких минут. Устанавливаем предел измерений на значение «200 А» и токовыми клещами выполняем измерение потребляемого тока на одной из фаз. Далее замеряем напряжение на обмотках с помощью щупов, входящих в комплект токоизмерительных клещей.
Как найти мощность двигателя зная сопротивление
Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.
В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.
Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению
Так записывается основная формула:
Путем преобразования основной формулы можно найти и другие две величины:
Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
Формула мгновенной электрической мощности:
Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.
Применение закона Ома на практике
На практике часто приходится определять не силу тока I
, а величину сопротивления
R
. Преобразовав формулу Закона Ома, можно рассчитать величину сопротивления
R
, зная протекающий ток
I
и величину напряжения
U
.
Величину сопротивления может понадобится рассчитать, например, при изготовлении блока нагрузок для проверки блока питания компьютера. На корпусе блока питания компьютера обычно есть табличка, в которой приведен максимальный ток нагрузки по каждому напряжению. Достаточно в поля калькулятора ввести данные величины напряжения и максимальный ток нагрузки и в результате вычисления получим величину сопротивления нагрузки для данного напряжения. Например, для напряжения +5 В при максимальной величине тока 20 А, сопротивление нагрузки составит 0,25 Ом.
Определение мощности электродвигателя без бирки
При отсутствии техпаспорта или бирки на двигателе возникает вопрос: как узнать мощность электродвигателя без таблички или технической документации? Самые распространенные и быстрые способы, о которых мы расскажем в статье:
- По диаметру и длине вала
- По габаритам и крепежным размерам
- По сопротивлению обмоток
- По току холостого хода
- По току в клеммной коробке
- С помощью индукционного счетчика (для бытовых электродвигателей)
Определение мощности двигателя по диаметру вала и длине
Простейшие способы определения мощности и марки двигателя – габаритные размеры – вал или крепежные отверстия. В таблице указаны длины и диаметры валов (D1) и длина (L1) для каждой модели асинхронного промышленного трехфазного мотора. Перейти к подробным габаритным размерам электродвигателей АИР
| Р, кВт | 3000 об. мин | 1500 об. мин | 1000 об. мин | 750 об. мин | ||||
| D1, мм | L1, мм | D1, мм | L1, мм | >D1, мм | L1, мм | D1, мм | L1, мм | |
| 1,5 | 22 | 50 | 22 | 50 | 24 | 50 | 28 | 60 |
| 2,2 | 24 | 28 | 60 | 32 | 80 | |||
| 3 | 24 | 32 | 80 | |||||
| 4 | 28 | 60 | 28 | 60 | 38 | |||
| 5,5 | 32 | 80 | 38 | |||||
| 7,5 | 32 | 80 | 38 | 48 | 110 | |||
| 11 | 38 | 48 | 110 | |||||
| 15 | 42 | 110 | 48 | 110 | 55 | |||
| 18,5 | 55 | 60 | 140 | |||||
| 22 | 48 | 55 | 60 | >140 | ||||
| 30 | 65 | |||||||
| 37 | 55 | >60 | 140 | 65 | 75 | |||
| 45 | 75 | 75 | ||||||
| 55 | 65 | 80 | 170 | |||||
| 75 | 65 | 140 | 75 | 80 | 170 | |||
| 90 | 90 | |||||||
| 110 | 70 | 80 | 170 | 90 | ||||
| 132 | 100 | 210 | ||||||
| 160 | 75 | 90 | 100 | 210 | ||||
| 200 | ||||||||
| 250 | 85 | 170 | 100 | 210 | ||||
| 315 | — | — |
Проверить мощность по габаритам и крепежным размерам
Таблица подбора мощности двигателя по крепежным отверстиям на лапах (L10 и B10):
Источник
Как найти мощность тока — формулы с примерами расчетов
Формулы, позволяющие выполнить расчет мощности, зная силу тока и напряжение либо сопротивление и напряжение. Пример расчетных работ.
В физике достаточно много внимания уделено энергии и мощности устройств, веществ или тел. В электротехнике эти понятия играют не менее важную роль чем в других разделах физики, ведь от них зависит насколько быстро установка выполнит свою работу и какую нагрузку понесут линии электропередач. Исходя из этих сведений подбираются трансформаторы для подстанций, генераторы для электростанций и сечение проводников передающих линий. В этой статье мы расскажем, как найти мощность электрического прибора или установки, зная силу тока, напряжение и сопротивление. Содержание:
- Определение
- Формулы для расчётов цепи постоянного тока
- Для переменного тока
- Пример расчёта полной мощности для электродвигателя
- Расчет для параллельного и последовательного подключения
- Заключение
Потребляемая энергия
Расчёт потребляемой энергии для дома или квартиры не представляет особой сложности. Для этого требуется выполнить следующий алгоритм действий:
- составить таблицу всех электроприборов, используемых в доме, включая и лампы освещения;
- в отдельные графы вынести: мощность прибора, часы работы в сутки;
- для каждого потребителя энергии посчитать (путём умножения мощности на время работы) среднесуточное потребление;
- просуммировать все полученные величины мощности.
Такой расчёт даст реальную картину потребления электроэнергии. Пользуясь этими данными, можно контролировать расход и корректировать потребляемую суточную мощность каждого прибора.
Не важно, каким способом рассчитывается или измеряется потребляемая мощность. Главная задача процесса – грамотно подобрать сечение проводников для устройства проводки, подвода питающих кабелей и обеспечить срабатывание автоматической защиты. Кабель, подводящий напряжение в помещение, должен выдерживать одновременное включение всех потребителей, расположенных в нём длительное время. Его выбор напрямую зависит от точности определения мощности потребителей.
Определение
Мощность – это скалярная величина. В общем случае она равна отношению выполненной работы ко времени:
Простыми словами эта величина определяет, как быстро выполняется работа. Она может обозначаться не только буквой P, но и W или N, измеряется в Ваттах или киловаттах, что сокращенно пишется как Вт и кВт соответственно.
Электрическая мощность равна произведению тока на напряжение или:
Как это связано с работой? U – это отношение работы по переносу единичного заряда, а I определяет, какой заряд прошёл через провод за единицу времени. В результате преобразований и получилась такая формула, с помощью которой можно найти мощность, зная силу тока и напряжение.
Электроприбор для измерения силы тока
Для измерения силы электротока используют специальный прибор под названием амперметр. Если требуется измерить токи самых разных сил, то прибегают к использованию миллиамперметров и макроамперметров. Чтобы измерить им требуемую величину, его подключают в цепь последовательно. Ток, который проходит через устройство, будет изменяться им, и данные будут выведены на цифровой дисплей или аналоговые шкалы.
Важно! Стоит помнить, что включать амперметр можно на любом участке сети, поскольку сила тока в простой замкнутой цепи без ответвлений одинакова во всех точках. Современные тестеры и мультиметры содержат функцию измерения силы электротока, поэтому нет необходимости прибегать к габаритным приборам, предназначенным для промышленного использования
Современные тестеры и мультиметры содержат функцию измерения силы электротока, поэтому нет необходимости прибегать к габаритным приборам, предназначенным для промышленного использования
Таким образом, сила электротока – это основополагающая характеристика движущихся частиц. Она не только дает понять, какое в сети напряжение и сопротивление, но и определяет другие важные величины по типу ЭДС и т. д.
Формулы для расчётов цепи постоянного тока
Проще всего посчитать мощность для цепи постоянного тока. Если есть сила тока и напряжение, тогда нужно просто по формуле, приведенной выше, выполнить расчет:
Но не всегда есть возможность найти мощность по току и напряжению. Если вам они не известны – вы можете определить P, зная сопротивление и напряжение:
Также можно выполнить расчет, зная ток и сопротивление:
Последними двумя формулами удобен расчёт мощности участка цепи, если вы знаете R элемента I или U, которое на нём падает.
Работа электрического тока
Проходя по цепи, ток совершает работу. Как например, водный поток направить течь, на лопасти генератора, то пон будет совершать работу, вращая лопасти. Так же и ток совершает работу, двигаясь по проводнику. И эта работа тем выше, чем больше величина сила тока и напряжения. Работа электрического тока, совершаемая на участке цепи, прямо пропорциональна силе тока, напряжению и времени действия тока. Работа электрического тока обозначается латинским символом A. Так как, произведение I×U есть мощность, то формулу работы электрического тока можно записать: A = P×t
Будет интересно➡ Закон Джоуля Ленца — самая полная теория
Единицей измерения работы электрического тока, является ватт в секундах или в джоулях. Поэтому, если мы хотим вычислить, какую работу осуществил ток, идя по цепи в течение временного интервала, мы должны умножить мощность на время Рассмотрим практический пример, через реостат с сопротивлением 5 Ом идет ток силой 0,5 А. Нужно вычислить, какую работу совершит ток в течение четырех часов. Работа в течение одной секунды будет: P=I2R = 0,52×5= 0,25×5 =1,25 Вт,
Тогда за 4 часа t=14400 секунд. Следовательно: А = Р×t= 1,25×14 400= 18 000 вт-сек. Ватт-секунда или один джоуль считаетсяя слишком малой велечиной для измерения работы. Поэтому на практике применяют единицу, называемую ватт-час (втч). Один ватт-час это эквивалентно 3 600 Дж. В электротехнике используются и еще большие единицы, гектоваттчас (гвтч) и киловаттчас (квтч): 1 квтч =10 гвтч =1000 втч = 3600000 Дж, 1 гвтч =100 втч = 360 000 Дж, 1 втч = 3 600 Дж.
Как рассчитать сопротивление и мощность
Допустим, требуется подобрать токоограничивающий резистор для блока питания схемы освещения. Нам известно напряжение питания бортовой сети «U», равное 24 вольта и ток потребления «I» в 0,5 ампера, который нельзя превышать. По выражению (9) закона Ома вычислим сопротивление «R». R=24/0,5=48 Ом. На первый взгляд номинал резистора определен. Однако, этого недостаточно. Для надежной работы семы требуется выполнить расчет мощности по току потребления.
Согласно действию закона Джоуля — Ленца активная мощность «Р» прямо пропорционально зависит от тока «I», проходящего через проводник, и приложенного напряжения «U». Эта взаимосвязь описана формулой Р=24х0,5=12 Вт.
Проведенный расчет мощности резистора по току его потребления показывает, что в выбираемой схеме надо использовать сопротивление величиной 48 Ом и 12 Вт. Резистор меньшей мощности не выдержит приложенных нагрузок, будет греться и со временем сгорит. Этим примером показана зависимость того, как на мощность потребителя влияют ток нагрузки и напряжение в сети.
Интересно почитать: все о законе Ома.
Для переменного тока
Однако для электрической цепи переменного тока нужно учитывать полную, активную и реактивную, а также коэффициент мощности (соsФ). Подробнее все эти понятия мы рассматривали в этой статье: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html.
Отметим лишь, что чтобы найти полную мощность в однофазной сети по току и напряжению нужно их перемножить:
Результат получится в вольт-амперах, чтобы определить активную мощность (ватты), нужно S умножить на коэффициент cosФ. Его можно найти в технической документации на устройство.
Для определения реактивной мощности (вольт-амперы реактивные) вместо cosФ используют sinФ.
Или выразить из этого выражения:
И отсюда вычислить искомую величину.
Найти мощность в трёхфазной сети также несложно, для определения S (полной) воспользуйтесь формулой расчета по току и фазному напряжению:
А зная Uлинейное:
1,73 или корень из 3 – эта величина используется для расчётов трёхфазных цепей.
Тогда по аналогии чтобы найти P активную:
Определить реактивную мощность можно:
На этом теоретические сведения заканчиваются и мы перейдём к практике.
Мощность тока
Разобравшись с понятием механической мощности, перейдём к рассмотрению электрической мощности (мощность электрического тока). Как Вы должны знать U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока.
Активная электрическая мощность (это мощность, которая безвозвратно преобразуется в другие виды энергии — тепловую, световую, механическую и т.д.) имеет свою единицу измерения — Вт (Ватт). Она равна произведению 1 вольта на 1 ампер. В быту и на производстве мощность удобней измерять в кВт (киловаттах, 1 кВт = 1000 Вт). На электростанциях уже используются более крупные единицы — мВт (мегаватты, 1 мВт = 1000 кВт = 1 000 000 Вт).
Будет интересно➡ Фантомное питание для микрофона: схема подключения
Реактивная электрическая мощность — это величина, которая характеризует такой вид электрической нагрузки, что создаются в устройствах (электрооборудовании) колебаниями энергии (индуктивного и емкостного характера) электромагнитного поля. Для обычного переменного тока она равна произведению рабочего тока I и падению напряжения U на синус угла сдвига фаз между ними: Q = U*I*sin(угла). Реактивная мощность имеет свою единицу измерения под названием ВАр (вольт-ампер реактивный). Обозначается буквой «Q».
Простым языком активную и реактивную электрическую мощность на примере можно выразить так: у нас имеется электротехническое устройство, которое имеет нагревательные тэны и электродвигатель. Тэны, как правило, сделаны из материала с высоким сопротивлением. При прохождении электрического тока по спирали тэна, электрическая энергия полностью преобразуется в тепло. Такой пример характерен активной электрической мощности.
Электродвигатель этого устройства внутри имеет медную обмотку. Она представляет собой индуктивность. А как мы знаем, индуктивность обладает эффектом самоиндукции, а это способствует частичному возврату электроэнергии обратно в сеть. Эта энергия имеет некоторое смещение в значениях тока и напряжения, что вызывает негативное влияние на электросеть (дополнительно перегружая её).
Похожими способностями обладает и ёмкость (конденсаторы). Она способна накапливать заряд и отдавать его обратно. Разница ёмкости от индуктивности заключается в противоположном смещении значений тока и напряжения относительно друг друга. Такая энергия ёмкости и индуктивности (смещённая по фазе относительно значения питающей электросети) и будет, по сути, являться реактивной электрической мощностью.
Более подробно о свойствах реактивной мощности мы поговорим в соответствующей статье, а в завершении этой темы хотелось сказать о взаимном влиянии индуктивности и ёмкости. Поскольку и индуктивность, и ёмкость обладают способностью к сдвигу фазы, но при этом каждая из них делает это с противоположным эффектом, то такое свойство используют для компенсации реактивной мощности (повышение эффективности электроснабжения). На этом и завершу тему, электрическая мощность, мощность электрического тока.
Пример расчёта полной мощности для электродвигателя
Мощность у электродвигателей бывает полезная или механическая на валу и электрическая. Они отличаются на величину коэффициента полезного действия (КПД), эта информация обычно указана на шильдике электродвигателя.
Отсюда берём данные для расчета подключения в треугольник на Uлинейное 380 Вольт:
Тогда найти активную электрическую мощность можно по формуле:
P=Pна валу/n=160000/0,94=170213 Вт
Теперь можно найти S:
Именно её нужно найти и учитывать, подбирая кабель или трансформатор для электродвигателя. На этом расчёты окончены.