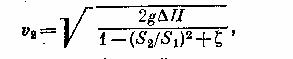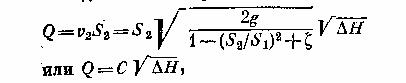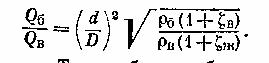Как найти мощность течения

From Wikipedia, the free encyclopedia

Stream power
Water flowing in creek
Common symbols	Ω, ω
SI unit	Watts
In SI base units	kg m² s⁻³
Derivations from other quantities	Ω=ρgQS
Dimension	M L² T⁻³

Stream power, originally derived by R. A. Bagnold in the 1960s, is the amount of energy the water in a river or stream is exerting on the sides and bottom of the river.^[1] Stream power is the result of multiplying the density of the water, the acceleration of the water due to gravity, the volume of water flowing through the river, and the slope of that water. There are many forms of the stream power formula with varying utilities, such as comparing rivers of various widths or quantifying the energy required to move sediment of a certain size. Stream power is closely related to other criteria such as stream competency and shear stress. Stream power is a valuable measurement for hydrologists and geomorphologists tackling sediment transport issues as well as for civil engineers, who use it in the planning and construction of roads, bridges, dams, and culverts.

History[edit]

Although many authors had suggested the use of power formulas in sediment transport in the decades preceding Bagnold’s work,^[2]^[3] and in fact Bagnold himself suggested it a decade before putting it into practice in one of his other works,^[4] it wasn’t until 1966 that R. A. Bagnold tested this theory experimentally to validate whether it would indeed work or not.^[1] This was successful and since then, many variations and applications of stream power have surfaced. The lack of fixed guidelines on how to define stream power in this early stage lead to many authors publishing work under the name «stream power» while not always measuring the entity in the same way; this led to partially failed efforts to establish naming conventions for the various forms of the formula by Rhoads two decades later in 1986.^[5]^[6] Today stream power is still used and new ways of applying it are still being discovered and researched, with a large integration into modern numerical models utilizing computer simulations.^[5]^[7]^[8]^[9]

Derivation[edit]

It can be derived by the fact that if the water is not accelerating and the river cross-section stays constant (generally good assumptions for an averaged reach of a stream over a modest distance), all of the potential energy lost as the water flows downstream must be used up in friction or work against the bed: none can be added to kinetic energy. Therefore, the potential energy drop is equal to the work done to the bed and banks, which is the stream power.

We know that change in potential energy over change in time is given by the equation:

${frac {Delta PE}{Delta t}}=mg{frac {Delta z}{Delta t}}$

where water mass and gravitational acceleration are constant. We can use the channel slope and the stream velocity as a stand-in for : the water will lose elevation at a rate given by the downward component of velocity $u_{z}$ . For a channel slope (as measured from the horizontal) of alpha :

${frac {Delta z}{Delta t}}=u_{z}=usin(alpha )approx uS$

where is the downstream flow velocity. It is noted that for small angles, . Rewriting the first equation, we now have:

${frac {Delta PE}{Delta t}}=mguS$

Remembering that power is energy per time and using the equivalence between work against the bed and loss in potential energy, we can write:

$Omega ={frac {Delta PE}{Delta t}}$

Finally, we know that mass is equal to density times volume. From this, we can rewrite the mass on the right hand side

where is the channel length, is the channel width (breadth), and is the channel depth (height). We use the definition of discharge

where is the cross-sectional area, which can often be reasonably approximated as a rectangle with the characteristic width and depth. This absorbs velocity, width, and depth. We define stream power per unit channel length, so that term goes to 1, and the derivation is complete.

Various Forms[edit]

(Total) Stream power[edit]

Stream power is the rate of energy dissipation against the bed and banks of a river or stream per unit downstream length. It is given by the equation:

where Ω is the stream power, ρ is the density of water (1000 kg/m³), g is acceleration due to gravity (9.8 m/s²), Q is discharge (m³/s), and S is the channel slope.^[5]

Total Stream Power[edit]

Total stream power often refers simply to stream power, but some authors use it as the rate of energy dissipation against the bed and banks of a river or stream per entire stream length. It is given by the equation:

where Ω is the stream power, per unit downstream length and L is the length of the stream.^[7]^[5]

Unit (or Specific) Stream power[edit]

Unit stream power is stream power per unit channel width, and is given by the equation:

$omega ={frac {rho gQS}{b}}$

where ω is the unit stream power, and b is the width of the channel. Normalizing the stream power by the width of the river allows for a better comparison between rivers of various widths.^[5] This also provides a better estimation of the sediment carrying capacity of the river as wide rivers with high stream power are exerting less force per surface area than a narrow river with the same stream power, as they are losing the same amount of energy but in the narrow river it is concentrated into a smaller area.

Critical Unit Stream Power[edit]

Critical unit stream power is the amount of stream power needed to displace a grain of a specific size, it is given by the equation:

${displaystyle omega _{0}=tau _{0}nu _{0}}$

where τ₀ is the critical shear stress of the grain size that will be moved which can be found in the literature or experimentally determined while v₀ is the critical mobilization speed.^[10]^[11]

Relationships to other variables[edit]

Size of displaced sediment[edit]

Critical stream power can be used to determine the stream competency of a river, which is a measure to determine the largest grain size that will be moved by a river. In rivers with large sediment sizes the relationship between critical unit stream power and sediment diameter displaced can be reduced to:^[12]^[13]

${displaystyle omega _{0}=0.030D_{i}^{1.69}}$

While in intermediate-sized rivers the relationship was found to follow:^[12]

${displaystyle omega _{0}=0.130D_{i}^{1.438}}$

Shear stress[edit]

Shear stress is another variable used in erosion and sediment transport models representing the force applied on a surface by a perpendicular force, and can be calculated using the following formula

Where τ is the shear stress, S is the slope of the water, ρ is the density of water (1000 kg/m³), g is acceleration due to gravity (9.8 m/s²).^[14]
Shear stress can be used to compute the unit stream power using the formula

Where V is the velocity of the water in the stream.^[14]

Applications[edit]

Landscape evolution[edit]

An example of a map displaying a stream power index (SPI) alongside an index displaying how wet the ground is (TWI)

Stream power is used extensively in models of landscape evolution and river incision. Unit stream power is often used for this, because simple models use and evolve a 1-dimensional downstream profile of the river channel. It is also used with relation to river channel migration, and in some cases is applied to sediment transport.^[1]

Predicting flood plain formation[edit]

By plotting stream power along the length of a river course as a second-order exponential curve, you are able to identify areas where flood plains may form and why they will form there.^[15]

Sensitivity to erosion[edit]

Stream power has also been used as a criterion to determine whether a river is in a state of reshaping itself or whether it is stable. A value of unit stream power between 30 and 35 W m⁻² in which this transition occurs has been found by multiple studies.^[7]^[16]^[17] Another technique gaining popularity is using a gradient of stream power by comparing the unit stream power upstream to the local unit stream power ( ${displaystyle Delta omega =omega _{local}-omega _{upstream}}$ ) to identify patterns such as sudden jumps or drops in stream power, these features can help identify locations where the local terrain controls the flow or widens out as well as areas prone to erosion.^[7]^[8]

Bridge and culvert design[edit]

Stream power can be used as an indicator of potential damages to bridges as a result of large rain events and how strong bridges should be designed in order to avoid damage during these events.^[9] Stream power can also be used to guide culvert and bridge design in order to maintain healthy stream morphology in which fish are able to continuing traversing the water course and no erosion processes are initiated.^[18]

References[edit]

^ ^a ^b ^c Bagnold, Ralph A. (1966). «An approach to the sediment transport problem from general physics». Professional Paper. doi:10.3133/pp422i. ISSN 2330-7102.
^ Rubey, W. W. (1933). «Equilibrium-conditions in debris-laden streams». Transactions, American Geophysical Union. 14 (1): 497. doi:10.1029/tr014i001p00497. ISSN 0002-8606.
^ Knapp, Robert T. (1938). «Energy-balance in stream-flows carrying suspended load». Transactions, American Geophysical Union. 19 (1): 501. doi:10.1029/tr019i001p00501. ISSN 0002-8606.
^ Bagnold, Ralph A. (1956-12-18). «The flow of cohesionless grains in fluids». Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. 249 (964): 235–297. doi:10.1098/rsta.1956.0020. ISSN 0080-4614. S2CID 124012787.
^ ^a ^b ^c ^d ^e Gartner, John (2016-01-01). «Stream Power: Origins, Geomorphic Applications, and GIS Procedures». Water Publications.
^ Rhoads, Bruce L. (May 1987). «Stream Power Terminology». The Professional Geographer. 39 (2): 189–195. doi:10.1111/j.0033-0124.1987.00189.x. ISSN 0033-0124.
^ ^a ^b ^c ^d Bizzi, S.; Lerner, D. N. (January 2015). «The Use of Stream Power as an Indicator of Channel Sensitivity to Erosion and Deposition Processes: SP AS AN INDICATOR OF EROSION AND DEPOSITION». River Research and Applications. 31 (1): 16–27. doi:10.1002/rra.2717. S2CID 129164405.
^ ^a ^b Gartner, John D.; Dade, William B.; Renshaw, Carl E.; Magilligan, Francis J.; Buraas, Eirik M. (November 2015). «Gradients in stream power influence lateral and downstream sediment flux in floods». Geology. 43 (11): 983–986. doi:10.1130/G36969.1. ISSN 0091-7613.
^ ^a ^b Anderson, Ian; Rizzo, Donna M.; Huston, Dryver R.; Dewoolkar, Mandar M. (May 2017). «Stream Power Application for Bridge-Damage Probability Mapping Based on Empirical Evidence from Tropical Storm Irene». Journal of Bridge Engineering. 22 (5): 05017001. doi:10.1061/(ASCE)BE.1943-5592.0001022. ISSN 1084-0702.
^ Wilcock, Peter R. (April 1993). «Critical Shear Stress of Natural Sediments». Journal of Hydraulic Engineering. 119 (4): 491–505. doi:10.1061/(asce)0733-9429(1993)119:4(491). ISSN 0733-9429.
^ Petit, F.; Gob, F.; Houbrechts, G.; Assani, A. A. (2005-07-01). «Critical specific stream power in gravel-bed rivers». Geomorphology. 69 (1): 92–101. doi:10.1016/j.geomorph.2004.12.004. ISSN 0169-555X.
^ ^a ^b Petit, F.; Gob, F.; Houbrechts, G.; Assani, A. A. (2005-07-01). «Critical specific stream power in gravel-bed rivers». Geomorphology. 69 (1): 92–101. doi:10.1016/j.geomorph.2004.12.004. ISSN 0169-555X.
^ COSTA, JOHN E. (1983-08-01). «Paleohydraulic reconstruction of flash-flood peaks from boulder deposits in the Colorado Front Range». GSA Bulletin. 94 (8): 986–1004. doi:10.1130/0016-7606(1983)94<986:PROFPF>2.0.CO;2. ISSN 0016-7606.
^ ^a ^b Gartner, John (2016-01-01). «Stream Power: Origins, Geomorphic Applications, and GIS Procedures». Water Publications.
^ Jain, V.; Fryirs, K.; Brierley, G. (2008-01-01). «Where do floodplains begin? The role of total stream power and longitudinal profile form on floodplain initiation processes». Geological Society of America Bulletin. 120 (1–2): 127–141. doi:10.1130/B26092.1. ISSN 0016-7606.
^ Orr, H.G.; Large, A.R.G.; Newson, M.D.; Walsh, C.L. (August 2008). «A predictive typology for characterising hydromorphology». Geomorphology. 100 (1–2): 32–40. doi:10.1016/j.geomorph.2007.10.022.
^ Brookes, Andrew (1987). «The distribution and management of channelized streams in Denmark». Regulated Rivers: Research & Management. 1 (1): 3–16. doi:10.1002/rrr.3450010103. ISSN 1099-1646.
^ Kosicki, Andrzej J.; Davis, Stanley R. (January 2001). «Consideration of Stream Morphology in Culvert and Bridge Design». Transportation Research Record: Journal of the Transportation Research Board. 1743 (1): 57–59. doi:10.3141/1743-08. ISSN 0361-1981. S2CID 109792586.

Источник

Вода, двигаясь в
реках под действием сил тяжести, свершает
работу. Для двух сечений 1-1 и 2-2 реки на
участке длиной L,
согласно уравнению Д. Бернулли, удельная
энергия потока равна:

Е₁= z₁
+
+

Е₂= z₂
+
+

потенциальная
часть или энергия положения и давления
состоит:

z
– геометрическая высота (м),

— пьезометрическая
высота (м);

кинетическая часть
или скоростной напор —

(м).

где: γ = ρ*g
— объемный вес (кг/м³)

при этом плотность
воды ρ = 1000 (кг*с²/м⁴),
g
= 9,81 (м/с²)

α – коэффициент
кинетической энергии потока (коэффициент
Кориолиса), учитывающий неравномерность
распределения скоростей по сечению.
Для равномерного турбулентного потока
по экспериментальным данным α = 1,03 –
1,1

Разность
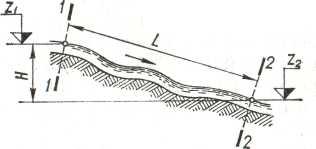
удельных энергий потока в сечениях
1—1 и 2—2
представляет
собой работу
(срабатываемый напор Н),
которую совершает
1 кг
воды
при его перемещении
из первого сечения во второе:

Рисунок 1. Схема к
определению работы речного потока.

Н
= (z₁
+
+
)
– (z₂
+
+
),
м.

Предполагая,
что давления и
кинетические энергии потока в
рассматриваемых сечениях равны, поэтому
работу, совершаемую весовым расходом
ρgQ
в
единицу
времени, определяют по формуле:

N
= ρgQ(z₁
– z₂)
= ρgQH,
Вт.

Величина
расхода равна произведению скорости
потока и площади сечения: Q
= v*s,
м³/с.

Подставляя
γ = ρ*g
= 1000*9,81 (кг/м³)
и выражая мощность в кВт, получим:

Nпотока
=
= 9,81QH,
кВт.

Эта
мощность речного потока в естественном
состоянии расходуется на преодоление
сил трения о ложе реки, взаимное гашение
энергии потока и т.д. Для использования
энергии данного участка реки в целях
получения электроэнергии, необходимо
искусственно сконцентрировать падение
этого участка в одном каком-либо месте,
т.е. создать разность уровней воды,
которую называют статическим
напором.

Путем
строительства на реках гидроэлектростанций
и установкой
в здании ГЭС гидроагрегатов гидравлическая
энергия потока, рассредоточенная
на определенном участке реки,
концентрируется в
одном месте и преобразуется в электрическую.

1.3.3 Схемы и компоновка гидроузлов.

Рисунок.
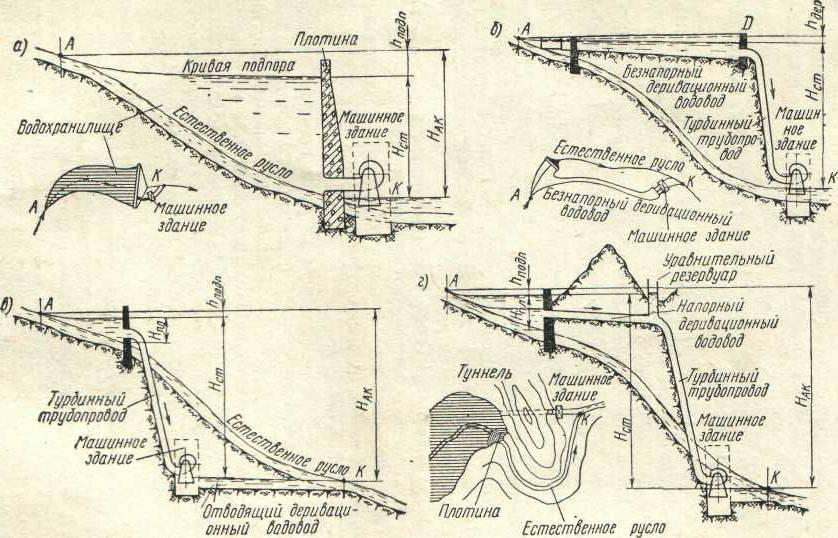
2. Схемы создания напора в приплотинных
и деривационных ГЭС.

В
практике гидроэнергетического
строительства применяют различные
технические схемы использования водной
энергии.
В зависимости от местных условий,
концентрация напора на ГЭС достигается
при помощи гидротехнических сооружений,
образующих
следующие технические схемы: плотинную,
деривационную и
плотинно-деривационную.

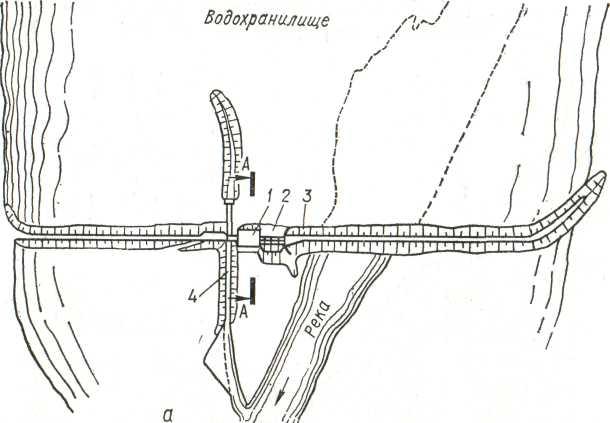
Плотинная
схема
(рис. 2а). Эта схема характеризуется
наличием плотины, которая создает
разность отметок уровней перед плотиной
(верхний бьеф) и за плотиной (нижний
бьеф). Поверхность воды в верхнем
бьефе перед плотиной в разрезе вдоль
потока образует так называемую кривую
подпора. Вследствие этого используемый
статический напор Н_ст
получается несколько меньше разности
отметок подпертого участка реки Н_ак
между пунктами А и К на величину
h_подп.

В
плотинных схемах гидроузлов здание
машинного зала располагается рядом с
плотиной или в плотине, при этом в
зависимости от величины напора и размеров
гидротурбин гидростанции могут быть
двух типов — русловые
и приплотинные.

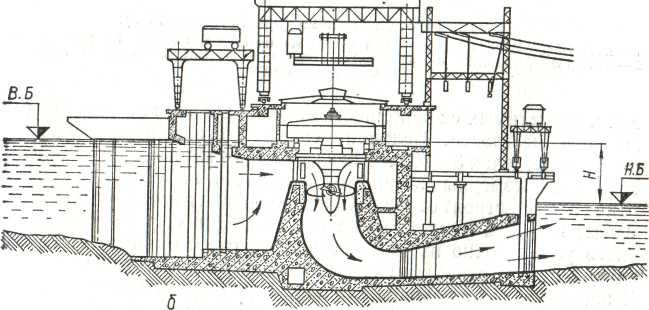
Русловые
— здание
ГЭС входит в состав сооружений, создающих
напор (рис.3), и полностью воспринимает
сдвигающие и опрокидывающие усилия,
действующие на него со стороны воды.
ГЭС такого типа строят при напорах 3 —
40 м и устанавливают на них, главным
образом, осевые гидротурбины.

Рисунок
3. Плотинная схема. Русловая ГЭС.

а –
план сооружений, б – поперечный разрез
по зданию. 1 – здание ГЭС. 2 – водосливная
плотина. 3 – земляная плотина. 4 – шлюз.

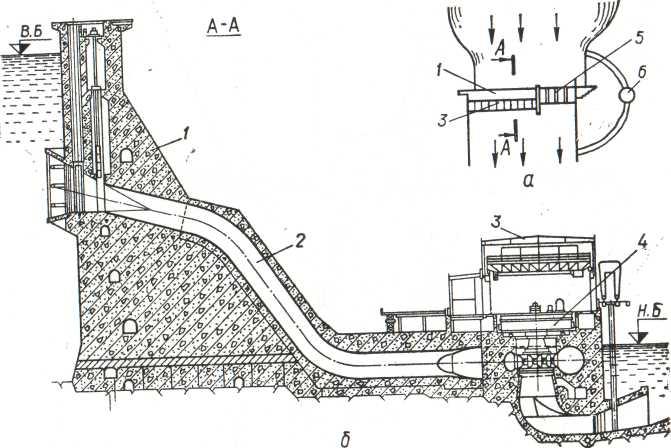
Приплотинные
— здание ГЭС находится непосредственно
за плотиной (рис. 4а).
Такие ГЭС строят при средних и высоких
напорах (Н = 40 – 300 м). Подвод воды к
турбинам осуществляется при помощи
водоприемников и турбинных водоводов.
Устанавливаемые типы турбин: осевые
или диагональные поворотно-лопастные
и радиально-осевые, в зависимости от
величины напора, графика нагрузки и
требований, предъявляемых к установке
турбин на ГЭС.

Рисунок 4. Плотинная схема. Приплотинная
ГЭС.

а – план сооружений; б — поперечный
разрез по плотине и зданию.

1 — плотина глухая; 2 – водоводы; 3 —
здание ГЭС; 4 — гидроагрегат; 5 —
плотина водосливная; 6 — судоподъемник.

Пример русловой
станции – Майнская ГЭС, приплотинной
– Саяно-Шушенская ГЭС.

Напор,
создаваемый плотиной, обычно небольшой,
но он может доходить до 230 м; например,
на Нурекской ГЭС на реке Вахш высота
плотины около 300 м. (Саяно-Шушенская ГЭС:
Н_пл
= 242 м, Н_расч=194
м) Высота плотины и создаваемый ею напор
определяются топографическими условиями
местности, расположенной выше плотины,
и допустимыми пространствами
затопления.

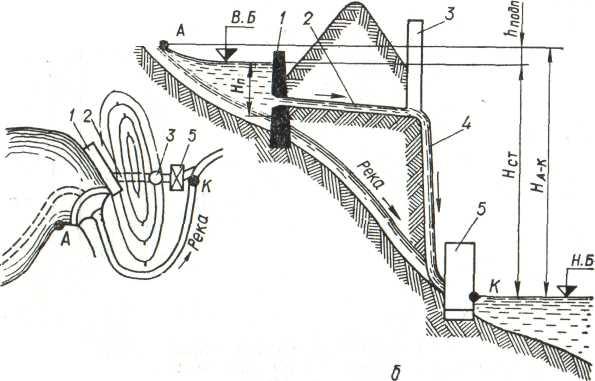
Деривационная
схема (рис
2б,
2в).
При больших уклонах рек с относительно
малыми расходами воду отводят в так
называемую деривацию (канал или
туннель). Гидравлический уклон деривации
выбирают минимальным, обеспечивающим
необходимый расход. Таким образом,
значительный перепад реки, в естественном
состоянии рассредоточенный на большом
протяжении, при помощи деривации
концентрируют в одном месте, где
строят здание ГЭС и устанавливают
гидроагрегаты. Трасса деривации
должна быть по возможности кратчайшей,
чтобы избежать дополнительных потерь
напора. Деривация может быть подводящей
(рис 2б) или отводящей (рис. 2в). Одна из
возможных схем указана на рис. 5.

Р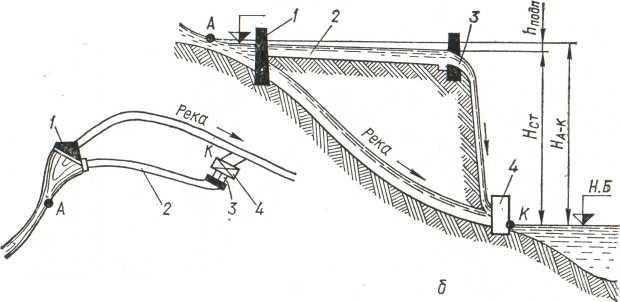ис.
5. Деривационная схема:

а —
план сооружений; б — вертикальный
разрез: / — плотина; 2
—
деривация; 3 — турбинные
водоводы;
4
— здание
ГЭС.

Напоры,
создаваемые при помощи деривации,
находятся в пределах Н = 200 – 2000 м и
зависят от природных и других условий.
На деривационных ГЭС применяют следующие
типы турбин: радиально-осевые (Н < 650
м) или ковшовые (Н > 300 м).

Плотинно-деривационная
схема
(рис. 4г). Напор на станции создается
при помощи плотины и деривации
одновременно. Если река на верхнем
участке имеет малый уклон, там целесообразно
построить плотину и создать
водохранилище, которое будет использовано
для регулирования расхода на ГЭС.
Основная часть напора создается, как
правило, деривацией. Величина напоров
и используемое турбинное оборудование
такие же, как и в случае деривационной
схемы.

Рис. 5.
Плотинно-деривационная схема:

а
— план сооружений; 6 — вертикальный
разрез: 1 — плотина; 2 — деривация; 3 —
уравнительный резервуар; 4 — турбинные
водоводы; 5 — здание ГЭС.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

6-я лекция, 2010 г.

6. Кинематика и
динамика жидкости

(продолжение пятой
лекции)

6.1 Уравнение Бернулли для потока реальной (вязкой) жидкости.

6.2 Мощность потока.

6.3 Коэффициент Кориолиса.

6.4 Гидравлические потери (общие сведения).

6.5 Местные потери.

6.6. Потери энергии на трение по длине

6.7.Примеры использования уравнения Бернулли в технике

6.1Уравнение Бернулли
для потока реальной (вязкой) жидкости.

При переходе от струйки
элементарной идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему
конечные размеры и ограниченному стенками, необходимо учесть неравномерность
распределения скоростей по сечению, а
также потери энергии. То и другое является следствием вязкости жидкости.

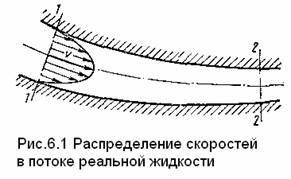
При движении
вязкой жидкости вдоль твердой стенки в
трубе, происходит торможение потока из-за влияния вязкости, а также из-за
действия сил молекулярного сцепления между жидкостью и стенкой. Поэтому наибольшего значения скорость
достигает в центральной части потока, а по мере приближения к стенке она уменьшается
почти до нуля. Получается распределение скоростей подобное тому которое показано
на рис. 6.1.

Неравномерное
распределение скоростей означает скольжение (сдвиг) одних слоев по другим, вследствие
чего возникают касательные напряжения (напряжения трения). Кроме того, движение
вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием. Это
требует затрат энергии, поэтому удельная
энергия движущейся вязкой жидкости не остается постоянной, как в случае
идеальной жидкости, а постепенно расходуется на преодоление сопротивления и,
следовательно, уменьшается вдоль потока.

Из-за неравномерного
распределения скоростей при выводе уравнения Бернулли потока вязкой жидкости приходится
вводить в рассмотрение среднюю по сечению скорость (см. лекцию №5), а также
среднее значение удельной энергии жидкости в данном сечении. Измерения средней
скорости потока практически выполнить проще и они могут быть сделаны с большей
точностью.

Прежде чем приступить
к рассмотрению уравнения Бернулли для потока вязкой жидкости сделаем следующее
допущение: будем считать, что в пределах рассматриваемых поперечных сечений
потока справедлив основной закон гидростатики, например, в первой форме, т. е. гидростатический
напор в пределах рассматриваемых сечений
есть величина одинаковая для всех точек данного сечения:

Предполагаем, что
при движении жидкости отдельные струйки
оказывают одна на другую в поперечном направлении такое же давление, как слои
жидкости в неподвижном состоянии. Это может быть доказано в том случае, когда
течение в данных поперечных сечениях является
параллельно струйным. Поэтому
именно такие (или близкие к ним) поперечные сечения и будем рассматривать.

6.2. Мощность потока

Введем понятие
мощности потока. Мощностью потока в данном сечении будем называть полную энергию,
которую проносит поток через это сечение в единицу времени. Так как в различных
точках поперечного сечения потока частицы жидкости обладают различной энергией,
сначала выразим элементарную мощность (мощность элементарной струйки) в виде
произведения полной удельной энергии жидкости в данной точке на элементарный
массовый расход dQ_m:

Рассмотрим
мощность, как частное от деления работы на время. Выразим работу, как
произведение давления на площадь, например гидроцилиндра, и путь, который проделывает
поршень под действием этой силы.

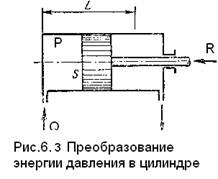
Пусть площадь поршня
равна s, его
ход L, избыточное
давление жидкости в левой полости цилиндра необходимое для преодоления силы F равно Р = F/S, избыточное давление по другую
сторону поршня равно нулю. Преодолевая силу F при перемещении поршня из левого
положения, давление совершает работу А = РSL. Расход жидкости, которую
необходимо подвести к цилиндру для совершения этой работы за время t ,
равен объему цилиндра, т. е. Q t = W
=SL.Работа, выполняемая
гидроцилиндром

A = pSL = PQ.

N = F/dt = (p*f*S)/dt = p*Q – выражение для определения мощности
гидравлического потока под действие силы Р.

Возьмем теперь третью форму уравнения Бернулли

gН= gz + p/(ρ) + (v²/2), (6.1)

умножим
его на изменение массового расхода dQ_m .

Наличие в составе
dQ_m плотности ρ преобразует третью форму у-я Бернулли(энергетическую)
во вторую форму в виде суммы давлений, в
результате получаем элементарную мощность потока.

dN = gH*dQ_m = (gz + p/ρ + v²/2)*ρ* v*dS = P*Q (6.2)

Мощность всего
потока найдем, как интеграл от предыдущего выражения по площади S:

N = ρ (6.3)

Или, учитывая,
сделанные допущения

N = ρ (6.4)

Третья степень
под интегралом получается при умножении квадрата скорости в сумме на скорость в
первой степени.

6.3 Коэффициент
Кориолиса

Найдем среднее по сечению значение полной
удельной мощности жидкости делением этой величины на массовый расход, используя выражение для
среднего массового расхода – ρQ = , Q=vср*S.), получим

(6.5)

Поскольку среднюю
скорость проще измерять, используем ее значение, умножив и разделив последний
член на V , и получим, переходя
к напорам, третья степень в знаменателе получается умножением на скорость в
составе расхода

(6.6)

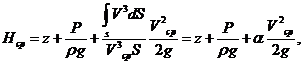
где α –
безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения
скоростей и равный

(6.7)

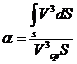
Если умножить
числитель и знаменатель выражения (6.7) на ρ/2, можно убедиться, что
коэффициент α представляет собой отношение действительной кинетической
энергии потока в данном сечении к кинетической энергии того же потока и в том
же сечения, но при равномерном распределении скоростей, поскольку произведение dm = ρ*vdS –есть масса.

Для для течения
вязкой жидкости скоростей (см. рис.6.1) коэффициент α не является
величиной постоянной.

Возьмем два сечения
реального потока, первое и второе, и обозначим средние значения полного напора
жидкости в этих сечениях соответственно Н_ср1 и Н_ср2.
Тогда

Н_ср1 = Н_ср2 + Σh_п,

где Σh_п — суммарная потеря полного напора на участке
между рассматриваемыми сечениями.

Используя формулу
для Нср,
предыдущее уравнение можно переписать так:

(6.8)

Это и есть
уравнение Бернулли для потока вязкой жидкости. От аналогичного уравнения для
элементарной струйки идеальной жидкости полученное уравнение отличается членом,
представляющее собой потерю полного напора, и коэффициентами, учитывающим
неравномерность распределения скоростей. Кроме того, скорости,
входящие в это уравнение, являются средними по сечениям.

Уравнение
Бернулли (6.8) и его формы применимы не только для жидкостей, но для газов при
условии, что скорость их движения значительно меньше скорости звука.

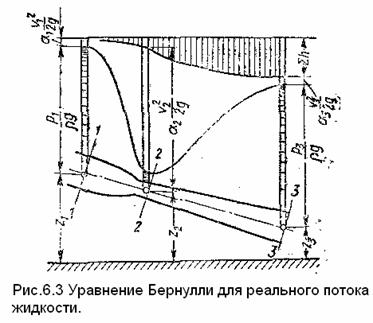
Графически это
уравнение можно представить диаграммой подобно тому, как это делали для идеальной жидкости, но с учетом потери
напора. Последняя является некоторой высотой, которая неуклонно возрастает
вдоль потока (рис. 1.27).

Для струйки
идеальной жидкости уравнение Бернулли представляет собой закон
сохранения механической энергии.

Для потока
реальной жидкости уравнение Бернулли является уравнением баланса
энергии с учетом потерь.
Энергия, теряемая жидкостью на рассматриваемом участке течения, разумеется, не
исчезает бесследно, превращаясь в другую
форму — тепловую. Так как удельная теплоемкость жидкостей обычно велика по
сравнению с потерями удельной энергии, а также ввиду того, что тепловая энергия
непрерывно рассеивается, повышение температуры часто бывает практически
малозаметным. Этот процесс преобразования механической энергии в тепловую
является необратимым, т. е. таким, обратное течение которого (превращение
тепловой энергии в механическую) невозможно

Уменьшение
среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к
единице его длины, называется гидравлическим уклоном.

Изменение
удельной потенциальной энергии жидкости, отнесенное к единице длины, называется
пьезометрическим уклоном. Очевидно, что в трубе постоянного диаметра с
неизменным распределением скоростей указанные уклоны одинаковы.

6.4 Гидравлические
потери (общие сведения).

Потери удельной
энергии (напора), — гидравлические потери, зависят от формы и размеров трубопровода,
скорости течения и вязкости жидкости.

При
турбулентном движении гидравлические потери пропорциональны скорости во второй
степени,

h _п =
ζ V²_ср /(2g), (6.9)

или в единицах
давления

p_п =
ρgh_п
= ζρ V²_ср /2.
(6.9‘)

В это выражение
входит безразмерный ζ коэффициент потерь,
или коэффициент
сопротивления.

Коэффициент
потерь, таким образом, есть отношение величины потерянного напора к скоростному
напору.

Гидравлические
потери разделяют на местные потери и потери на трение по длине.

6.5.Местные потери энергии вызваны
изменениями формы и размера трубопровода, вызывающими деформацию потока. Жидкости,
протекая через местные сопротивления изменяет скорость и образует вихри. После
отрыва потока от стенок вихри образуют области, в которых частицы жидкости движутся
в основном по замкнутым траекториям.

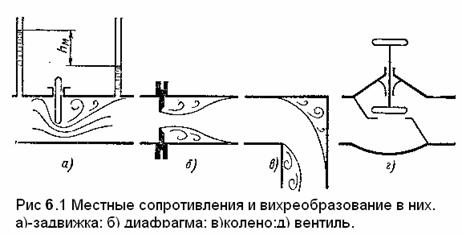
Примерами местных
сопротивлений устройства, изображенные на рис. 6.1. Здесь же показаны отрывы
потока и вихреобразование.

Если диаметр трубы и, следовательно, скорость в ней изменяются по
длине, то за расчетную скорость удобнее принимать большую из скоростей, т.е.
ту, которая соответствует меньшему диаметру трубы.

Каждое местное
сопротивление характеризует значение коэффициента сопротивления ζ, которое приближенно можно считать постоянным
для данной формы местного сопротивления.

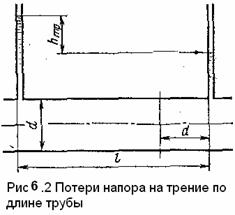
6.6. Потери энергии на трение по длине возникают в прямых трубах постоянного
сечения, при равномерном течении, и возрастают пропорционально длине трубы
(рис. 7. 2).

Эти потери
обусловлены внутренним трением в жидкости.
Потери напора на трение можно выразить по общей формуле (6.1) для гидравлических
потерь, т. е.

h _тр
= ζ _тр v²/(2g).

Однако, удобнее
коэффициент ζтр связать
с относительной длиной трубы l/d.

Обозначим
коэффициент потерь участка круглой трубы длиной l =d равной
ее диаметру и обозначим его через λ. Для всей трубы длиной l и диаметром d не равным длине трубы,
коэффициент потерь будет в l/d раз больше:

ζ _тр = λ* l/d .

В результате
формула (7.1) примет вид

(6.10)

или в единицах
давления

р_тр =
λ* . (6.11)

Формулу (6.10)
называют формулой Вейсбаха — Дарси.

Коэффициент,
входящий в выражение (6.2) называется коэффициент
потерь на трение по длине λ, или коэффициентом Дарси.

(Физический смысл
коэффициента λ. При равномерном движении в трубе длиной l и диаметром d, имеет место
равновесие сил, действующих на объем: сил давления и силы трения. Это
равновесие выражается равенством

πd²p_тр/4 — πdlτ₀ = 0,

где τ₀
— напряжение трения на стенке трубы.

Если учесть
формулу (6.10), то

λ= ,

λ есть величина, пропорциональная
отношению напряжения от силы трения на стенке трубы к динамическому давлению,
определяемому по средней скорости.

Ввиду постоянства
объемного расхода несжимаемой жидкости
вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также
остаются.

6.6.
Применение уравнения Бернулли в технике

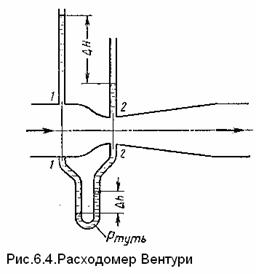
Расходомер
Вентури — устройство, устанавливаемое в
трубопроводах и выполняющее сужение потока — дросселирование (рис.6.4).

Расходомер
состоит из двух участков — плавно сужающегося сопла и постепенно расширяющегося
диффузора. Скорость потока в суженном месте возрастает, а давление падает.
Возникает перепад давлений, который измеряется двумя пьезометрами или дифференциальным
U-образным манометром.
Эта разность связана с расходом.

В
сечении 1-1 перед сужением скорость потока равна V₁,
давление Р₁, площадь сечения
S₁ , а в cечении 2-2: V₂, P₂ ,S₂,разность показаний пьезометров,
присоединенных к сечениям ΔН.

Запишем
для сечений 1-1 и 2-2 потока уравнение Бернулли и уравнение расхода, считая
распределение скоростей равномерным.

где
hм — потеря напора
между сечениями 1-1 и 2-2.

Учитывая, что

найдем
из этой системы уравнений одну из
скоростей, например,

отсюда
объемный расход

где
С — величина постоянная для данного расходомера.

Зная
величину С, можно найти расход в трубопроводе по формуле. Коэффициент С можно определить теоретически, но лучше
найти его экспериментально при тарировании расходомера.

Вместо
пьезометров для измерения перепада давлений в расходомере применяют
дифференциальный манометр. Принимая что над ртутью в трубках находится та же жидкость,
плотностью ρ, можно записать

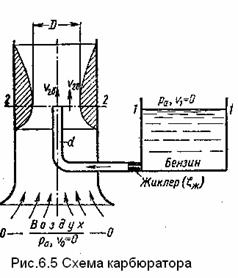
Карбюратор
поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешивания
его с потоком воздуха (рис. 6.5). Поток воздуха
засасываемого в двигатель,
сужается в том месте, где установлен
распылитель бензина (обрез трубки диаметром d). Скорость воздуха этом сечении возрастает, а давление по
закону Бернулли падает. Благодаря пониженному
давлению бензин вытекает в поток воздуха.

Надем
соотношение между массовыми расходами бензина Qб и воздуха Qв при заданных размерах D и d и коэффициентах сопротивления
воздушного канала (до сечения 2-2) и жиклера ζж (сопротивлением
бензотрубки пренебрегаем).

Записав
уравнение Бернулли для потока воздуха (сечение 1-1 и 2-2), а затем для потока
бензина (сечение 1-1 и 2-2), получим (при z₁= z₂‚ и α=
1):

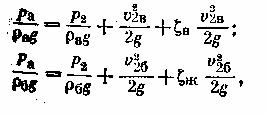
откуда

Учитывая, что
массовые расходы

получим

Таким образом,
обеспечивается постоянство соотношения расходов бензина и воздуха. Однако, следует
иметь в виду приближенный характер данного решения.

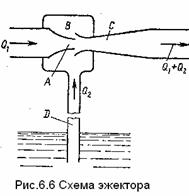
Струйный насос
(эжектор) состоит из плавно сходящегося насадка А (рис.6.6), осуществляющего сжатие
потока, и постепенно расширяющейся трубки С, установленной на некотором
расстоянии от насадка в камере В.

Вследствие увеличения скорости потока в струе
на выходе из насадка и по всей камере В значительно понижается. В расширяющейся
трубке скорость уменьшается, а давление возрастает приблизительно до
атмосферного (если жидкость вытекает в
атмосферу), следовательно в камере В давление обычно меньше
атмосферного, т. е. возникает разрежение (вакуум). Под действием разрежения
жидкость из нижнего резервуара всасывается по трубе D в камеру В, где происходят слияние и
дальнейшее перемешивание двух потоков.

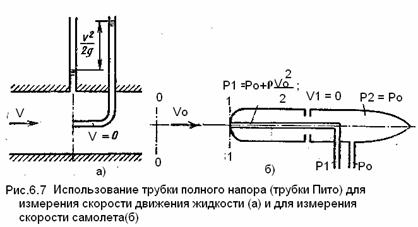
Трубка полного
напора ( трубка Пито) служит для измерения скорости в трубе (рис. 1.34). Если
установить в этом потоке трубку, повернутую под углом 90°, отверстием навстречу
потоку и пьезометр, то жидкость в этой трубке поднимается над уровнем в пьезометре
на высоту равную скоростному напору.

Объясняется это тем, что скорость v частиц жидкости,
попадающих в отверстие трубки, уменьшается до нуля, а давление, следовательно,
увеличивается на величину скоростного напора. Измерив разность высот подъема жидкости в трубке Пито
и пьезометре, легко определить скорость жидкости в данной точке. На этом же
принципе основано измерение скорости полета самолета. На рис.1.35 показана
схема самолетной скоростной трубки (насадка) для измерения малых по сравнению
со скоростью звука скоростей полета.

Запишем уравнение
Бернулли для струйки , которая набегает на трубку вдоль ее оси, а затем растекается по ее
поверхности. Для сечений 0-0 (невозмущенный поток) и 1-1 (где v =0), получаем

Так как боковые
отверстия трубки приближенно воспринимают давление невозмущенного потока, р₂≈ р₀ , следовательно, из предыдущего имеем

Источник

6-я лекция.

23.03.12

6. КИНЕМАТИКА И ДИНАМИКА РЕАЛЬНОЙ ЖИДКОСТИ-2

6.1 Уравнение Бернулли для потока реальной (вязкой) жидкости.

6.2 Мощность потока.

6.3 Коэффициент Кориолиса.

6.4 Гидравлические потери (общие сведения).

6.5 Местные потери.

6.6. Потери энергии на трение по длине

Расчеты параметров ГЭС

Для справки.
Теоретическая мощность «идеальной» ГЭС можно посчитать по формуле:

N= p * Q,
где N — мощность, в ваттах
p — давление перед турбиной, в паскалях
Q — расход воды, в м3 в секунду.

Давление 10 метрового столба воды составляет 1 атмосферу или 100 000 паскалей.
1 литр составляет 1/1000 м3

Например,
ГЭС, потребляющая 45 литров в секунду (0,045 м3/сек) и работающая на
перепаде 2 метра (20 000 паскалей), по вышеуказанной формуле может
выдать 900 Ватт.

Реальные турбинные колёса небольших мощностей выдают 30-50% от теоретического значения.

От данной отправной точки можно строить свои предположения. хватит ли Вам
вашего ручейка только на светодиодные лампочки или всё же на
электроинструмент и бетономешалку…

«Бесплотинные ГЭС

— их мощность можно примерно оценить как

N = 120* V(куб)*D (квадрат)

где N — мощность, ватт, V- скорость течения, в метрах в секунду, а D — диаметр колеса, в метрах.
Это
— для хорошо сделанного винта. Для колес по типу старых водяных мельниц
мощность считается по площади сечения лопаток, которая омывается водой.

Как
мне кажется, безплотинные ГЭС можно использовать при скоростях где-то
от 0,7-1 м/с, а такие скорости в центральной России встречаются довольно
редко (почти нигде). А если и встречаются, то там может оказаться
мелко. То есть, должно крупно повезти, чтобы была возможность
пользоваться такой установкой. Но я, например, знаю людей, которым
повезло.»

http://ecovillage.narod.ru/energy/energy.htm

За правильность формулы не ручаюсь (она, в отличии от плотинной ГЭС скорее эмпирическая), но сайт вполне адекватный.

Путём
модельного расчёта при скорости течения в 1 м/c (бОльшие скорости —
скорее экзотика для большинства рек) получаем на 1 кВт мощности станции
диаметр колеса ГЭС в 2,9 метра.

А вот если Вам повезло и скорость
течения у Вас в ручье уже хотя бы 2 м/с, то диаметр колеса киловаттной
станции ужмётся до 1 метра. Можно и плотину не ставить — а просто отобрать достаточный для Вашей ГЭС поток воды в обычную трубу.

Называется всё это чудо «Деривационная ГЭС».

Вот схемка: http://bse.sci-lib.com/particle007175.html

Используются
такие ГЭС в основном в горных районах, где, кроме функции получения
электроэнергии, служат ещё и для регуляции паводкового и ливневого
стока.

Например, на Западной Украине сейчас, по моим сведениям,
стоит брошенными около 70 малых ГЭС, построенных во время Сталина. При
желании могу найти человека с явками и паролями для интересующихся
возродить там любую из таких ГЭС.

На формулу расчёта мощности
способ подвода воды к гидроагрегату влияния не оказывает. Скорее, подвод
в трубе немного уменьшит напорный уровень ГЭС за счёт трения воды в
трубе.

Охрана подающих труб, безусловно, находится в ведении владельца ГЭС.

Так, например, при уклоне в 5% длина подводящего канала деривационной ГЭС с перепадом в 2 метра составит 40 метров. Проблема в том, реки обычно не текут «по уклонам», а уже заранее выбрали весьма извилистые пути с минимальными уклонами.

Например,
в районе Днепропетровска река Днепр имеет отметку +51 метр при
расстоянии от устья в 480 км. А теперь посчитайте уклон в процентах…

И такую ситуацию Вы получите в 95% малых рек и ручьёв в европейской части России и Украины — за исключением Карпат и Кавказа.

Источник

History[edit]

Derivation[edit]

Various Forms[edit]

(Total) Stream power[edit]

Total Stream Power[edit]

Unit (or Specific) Stream power[edit]

Critical Unit Stream Power[edit]

Relationships to other variables[edit]

Size of displaced sediment[edit]

Shear stress[edit]

Applications[edit]

Landscape evolution[edit]

Predicting flood plain formation[edit]

Sensitivity to erosion[edit]

Bridge and culvert design[edit]

See also[edit]

References[edit]

1.3.3 Схемы и компоновка гидроузлов.

Рекомендуемые материалы

Расчеты параметров ГЭС

«Бесплотинные ГЭС