Найти мощность источника ЭДС
- Главная
- /
- Физика
- /
- Найти мощность источника ЭДС
Чтобы найти мощность источника ЭДС воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
ЭДС источника: ε =В
Сила тока: I =A
Мощность источника ЭДС: P =
0
Вт
Теория
Если электрическая цепь содержит источник ЭДС, то поглощаемая* на нём или отдаваемая** им электрическая мощность равна:
Формула
P = I ⋅ ε , где P — мощность источника ЭДС, I — сила тока, ε — ЭДС
Пример
Если ЭДС источника ε = 12 В, а сила тока I = 5 А, то:
мощность источника ЭДС P = 12 ⋅ 5 = 60 Вт
* Если ток внутри ЭДС течёт от плюса к минусу (противонаправлен градиенту потенциала), то мощность поглощается источником ЭДС из сети (электродвигатель, заряд аккумуляторной батареи).
** Если ток внутри ЭДС течёт от минуса к плюсу (сонаправлен), то мощность отдаётся источником ЭДС в сети (батарея, генератор).
См. также
На этой странице вы узнаете
- Где самое большое сопротивление в теле человека?
- Какой ученый променял бильярд на физику?
- К чему может привести авария среди электронов?
Весь современный мир держится на электричестве. Наряду с глобальной интернет-сетью, наш мир «опутан» сетью электрических проводов. Что такого происходит в этих тоненьких проводах, что от них зависит жизнь целого города? Давайте поближе познакомимся с электрическим током и узнаем, откуда он появляется.
Мы с вами уже познакомились с электрическими схемами в теме «Законы постоянного тока», где выяснили, какие приборы существуют и как используются в схемах. В этой статье мы поговорим о том, как в элементарных электрических цепях появляется ток. Начало положено, сопротивление бесполезно.
Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.
Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение.
Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока).
Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?
Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.
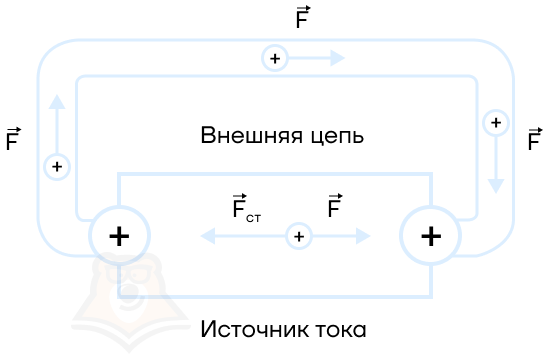
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_{ст})), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)).
Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_{ст})), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда.
После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.
Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.
Основные параметры источника тока
Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление.
ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_{ст})), затраченную на перемещение зарядов (q) внутри источника.
(ε) – ЭДС источника тока (В);
(А_{ст})– работа сторонних сил (Дж);
(q) – заряд, помещенный внутри источника (Кл).
Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока.
Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление.

Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.
Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.
Закон Ома для участка цепи
Георг Ом рос в небогатой семье. Также он был довольно азартным человеком, любил играть в бильярд в компании друзей. В университетские годы Ом был лучшим игроком в бильярд среди студенческой молодежи, показывал прекрасные результаты в конькобежном спорте.
Но его очень манили точные науки: физика и математика. Однажды он смог собрать всю свою волю «в кулак» и начать проводить опыты в лаборатории обычной школы, где работал учителем. И так он окончательно вжился в статус ученого-физика. После этого он играл в бильярд только для получения удовольствия, а не использовал его как способ заработка.
Дальше мы с вами поговорим о напряжении на элементах электрической цепи, и, в частности, на источнике тока. Поэтому вспомним, что такое напряжение из темы «Законы постоянного тока». Напряжение – физическая величина, которая показывает, какую работу сторонние силы должны приложить, чтобы перенести заряд от одной точки до другой.
Так как у источника тока имеется внутреннее сопротивление, значит, внутри него также будет и напряжение. Чтобы найти его, воспользуемся законом Ома — умножим внутреннее сопротивление источника тока r на сам ток I и получим:
Ur = Ir.
Также мы можем найти напряжение, которое будет выделяться на внешней цепи. Для этого снова умножим ток I на общее сопротивление цепи R:
UR = IR.
Оказывается, что не вся энергия источника тока уходит в цепь. Как раз таки та часть энергии, которая уходит на преодоление внутреннего сопротивления, и будет характеризовать потери. Тогда мы можем записать еще одну формулу для нахождения ЭДС источника тока:
ε – ЭДС источника тока (В);
UR – напряжение на самой электрической цепи (В);
Ur – напряжение внутри источника тока (В).
Теперь давайте подставим вместо напряжений полученные формулы через токи и сопротивления и выразим силу тока. Так мы получим закон Ома для полной цепи:
I – ток в цепи (А);
ε – ЭДС источника тока (В);
R – сопротивление в цепи (Ом);
r – внутреннее сопротивление источника (Ом).
Сила тока в цепи с заданным источником тока (при неизменной ЭДС и с постоянным внутренним сопротивлением) зависит только от сопротивления внешней цепи R.
Самое большое электрическое сопротивление на теле человека — поверхность верхнего рогового слоя кожи человека. Оно может достигать 40000–100000 Ом. Но это не значит, что можно хвататься за оголенные провода голыми руками! Этого сопротивления далеко не достаточно, чтобы защитить человека от опасного электрического тока.
Резко уменьшают сопротивление человека потливость кожного покрова, переутомление, нервное возбуждение. Значение снижается до 800–1000 Ом. Поэтому даже самое небольшое напряжение может вызвать ожог кожи.
Задачи на данную тему встречаются в №12 ЕГЭ. Давайте рассмотрим один пример.
Задача. Найдите внутреннее сопротивление источника ЭДС, если сопротивление в цепи R = 4 Ом, а ЭДС ε=10 В. Сила тока в цепи 2 А.
Решение.Воспользуемся законом Ома для полной цепи и выразим из него внутреннее сопротивление источника ЭДС:
(I=frac{ε}{R + r}),
(r=frac{ε}{I}-R=frac{10}{2}-4=1) (Ом).
Ответ: 1 Ом
Короткозамкнутая цепь
Рассмотрим частный случай электрической цепи, в котором источник тока будет подключен сам на себя. Иначе говоря, он будет короткозамкнутым.
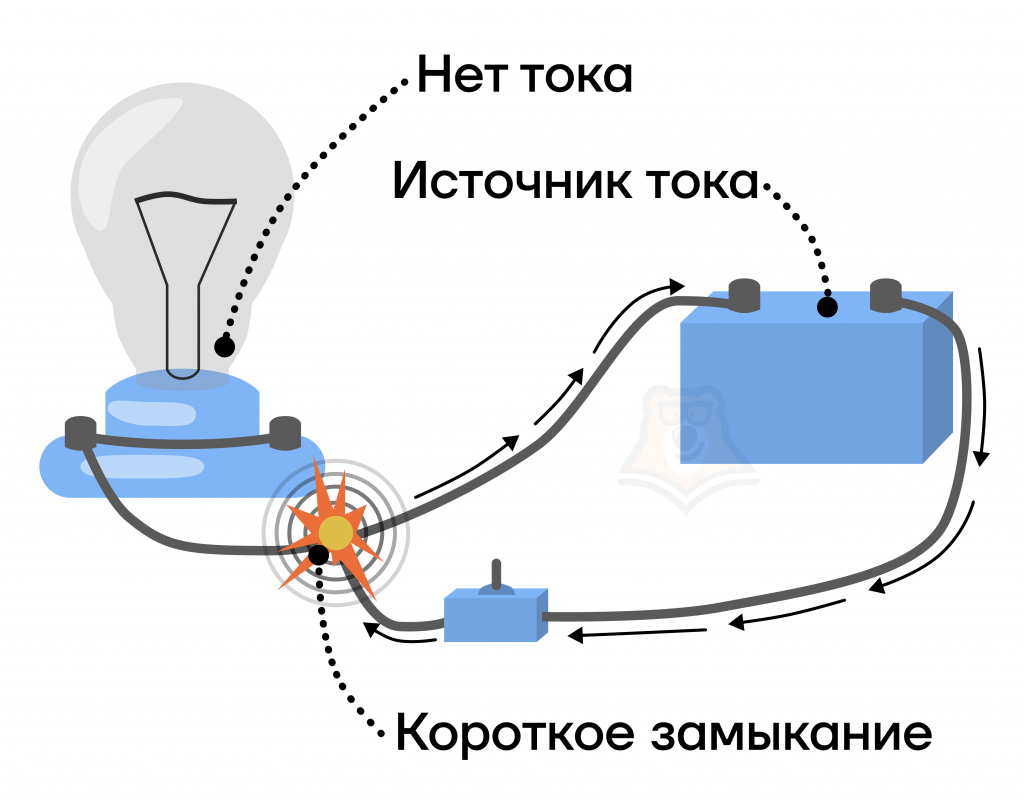
В этом случае отсутствует сопротивление внешней цепи и закон Ома для цепи будет выглядеть так:
(I_{кз}) – ток короткого замыкания (А);
(ε) – ЭДС источника тока (В);
(r) – сопротивление источника ЭДС (Ом).
Короткое замыкание — это такой случай соединения проводов, при котором практически весь ток проходит по пустому проводу и возвращается в источник тока.
Короткое замыкание приводит к сильному нагреву, расплавлению металлов, а иногда и к пожарам.
Если сравнить поток электронов с потоком машин, то ток короткого замыкания – это авария на автодороге. Один поток машин решил влезть в другой. В результате на дороге образовалась авария. Но машины продолжают налетать одна на другую (как в метель в Норильске).
При коротком замыкании сила тока будет увеличиваться до тех пор, пока отключающие механизмы не прекратят поступление силы тока.
Теперь, когда мы уже рассмотрели основные характеристики источника тока, можем перейти к мощности и КПД источника тока.
Мощность и КПД источника тока
Мы уже не раз говорили о том, что при протекании тока выделяется энергия. Источники тока не исключение. При подключении их к цепи на них выделяется энергия. При этом энергия выделяется и в самой цепи.
Чтобы найти мощность передачи энергии (P), выделяемой источником тока, необходимо умножить силу тока на ЭДС этого источника тока. Тогда получим:
(P_{ист}) – мощность источника тока (Вт);
(ε) – ЭДС источника тока (В);
(I) – сила тока (А).
При этом часть этой мощности уходит на элементы внешней цепи, а другая часть – на преодоление внутреннего сопротивления источника тока:
(εI = I^2R + I^2r).
Тогда мощность, выделяемая на внешней цепи:
(P_R=I^2R).
А мощность, которая теряется на внутреннее сопротивление источника тока:
(P_r=I^2r).
Теперь давайте рассмотрим коэффициент полезного действия (КПД, ) источника тока. Как мы уже говорили ранее, часть ЭДС источника тока уходит на внутреннее сопротивление, а часть – на внешнюю цепь. При этом вспомним, что КПД – это отношение полезной мощности к затраченной.
Запишем формулы для мощности:
(P_{ист}=εI=I^2(R+r)),
(P_R=IU =I^2R).
Тогда КПД:
(eta) – КПД источника тока;
(ε) – ЭДС источника тока (В);
(U) – напряжение на внешней цепи (В);
(I) – сила тока (А):
(R) – сопротивление на внешней цепи (Ом);
(r) – сопротивление источника тока (Ом).
Также задачи на тему ЭДС встречаются и в №16 ЕГЭ. Сложность данных задач заключается в установлении правильной зависимости величин друг от друга.
Задача.Определите, как изменятся сила тока (А) в цепи и сопротивление резистора (Б), если ЭДС источника тока заменить на такую же ЭДС, но с большим внутренним сопротивлением.
1) увеличится
2) уменьшится
3) не изменится
Решение.
Б) Внешнее сопротивление никак не зависит от источника тока. Поэтому оно не изменится — выбираем ответ 3.
А) Запишем закон Ома для полной цепи:
(I=frac{ε}{R + r})
При увеличении внутреннего сопротивления знаменатель увеличится. Следовательно, сила тока уменьшится, так что вариант 2 тоже нам подходит.
Ответ: 23
Мы с вами выяснили, что источники тока – элементы электрической цепи, без которых самой цепи не существовало бы. Хотя, конечно, она бы существовала, но была бы бесполезной. Однако и они «не без греха», так как существует опасное внутреннее сопротивление, которое является головной болью для многих инженеров. А все потому, что оно снижает КПД источников тока. Дальше вы можете ознакомиться с полноценными электрическими схемами и посмотреть, как ток ведет себя за пределами источника тока.
Термины
Напряжение – произведение сопротивления элемента и протекающего через него тока.
Резистор (или резистивный элемент) – элемент электрической цепи, который может только потреблять энергию и не может ее создавать.
Сторонние силы — это все внешние силы, воздействующие на заряд.
Электростатическое поле — невидимое поле, создаваемое постоянными электрическими зарядами.
Фактчек
- ЭДС источника тока (ε) — это физический параметр, который характеризует работу, затраченную на перемещение зарядов внутри источника сторонними силами: (ε =frac{А_{cт}}{q}).
- Внутреннее сопротивление (r) — определяет количество потерь энергии при прохождении тока через источник тока.
- Закон Ома для полной цепи: Сила тока в замкнутой цепи равна отношению ЭДС цепи к ее полному сопротивлению: (I =frac{ε}{R + r}).
- Предельное значение силы тока для данного источника тока называется током короткого замыкания: (I_{кз} =frac{ε}{r}).
- Полная мощность цепи — это есть мощность источника тока: (P_ист=εI).
Проверь себя
Задание 1.
Как рассчитывается ЭДС источника тока?
- (ε =frac{А_{ст}}{q})
- (ε =frac{U}{q})
- (ε =frac{А_{ст}}{I})
- (ε =frac{А_{ст}}{qt})
Задание 2.
Короткое замыкание — это:
- Соединение концов участка цепи проводником, сопротивление которого очень мало по сравнению с сопротивлением участка цепи.
- Соединение концов участка цепи проводником, сопротивление которого очень велико по сравнению с сопротивлением участка цепи.
- Соединение концов участка цепи проводником, сопротивление которого не зависит от сопротивления участка цепи.
- Отсутствие электрического тока в цепи.
Задание 3.
Чему равно ЭДС источника тока?
- (ε = U_R- U_r)
- (ε = U_R+ U_r)
- (ε = U_R U_r)
- (ε = U_R)
Задание 4.
От чего зависит сила тока в цепи с заданным источником тока?
- от внутреннего сопротивления цепи
- от внутреннего сопротивления источника тока
- от внешнего сопротивления цепи
- не зависит ни от каких величин
Задание 5.
Где самое большое сопротивление в человеке?
- в сердце
- в пищеварительной системе
- на коже
- в голове
Ответы: 1. — 1; 2. — 1; 3. — 2; 4. — 3; 5. — 3.
При упорядоченном движении заряженных частиц в проводнике электрическое поле совершает работу. Ее принято называть работой тока.
Рассмотрим произвольный участок цепи. Это может быть однородный проводник, к примеру, обмотка электродвигателя или нить лампы накаливания. Пусть за время ∆t через поперечное сечение проводника проходит заряд ∆q. Тогда электрическое поле совершит работу:
A=ΔqU
Но сила тока равна:
I=ΔqΔt
Выразим заряд:
Δq=IΔt
Тогда работа тока равна:
A=IUΔt
Работа тока на участке цепи равна произведению силы тока, напряжения и времени, в течение которого совершалась работа.
Выражая через закон Ома силу тока и напряжение, получим следующие формулы для вычисления работы тока:
A=I2RΔt=U2RΔt
Работа тока измеряется в Джоулях (Дж).
Пример №1. Определите работу тока, совершенную за 10 секунд на участке цепи напряжением 200В и силой тока 16 А.
A=IUΔt=16·220·10=35200 (Дж)=35,2 (кДж)
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Закон Джоуля—Ленца
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Q=I2RΔt
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Используем закон Ома и закон Джоуля—Ленца:
Q=I2RΔt=(UR)2Δt=U2RΔt=1222=72 (Дж)
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Определение
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
P=AΔt
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P=IU=I2R=U2R
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P=I2R=0,32·10=0,9 (Вт)
Выразив силу тока через заряд, прошедший за единицу времени, получим:
P=qUt
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P=(εR+r)2R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
Pmax=(εr+r)2r=ε24r
Мощность тока внутренней цепи:
Pвнутр=I2r=(εR+r)2r
Полная мощность:
Pполн=I2(R+r)=ε2R+r
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P=(εR+r)2R
Применим закон Ома для полной цепи:
I=εR+r
Выразим сопротивление внешней цепи:
R=εI−r
Отсюда:
P=(εεI−r+r)2(εI−r)=I2(εI−r)=Iε−rI2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
rI2−Iε+P=0
I2−1I+0,75=0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
| Объем проводника цилиндрической формы |
V=Sl |
| Масса проводника цилиндрической формы |
m=ρV=ρSl |
| Количество теплоты и изменение температуры |
Q=cmΔT |
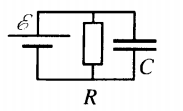
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
| Электроемкость, заряд и напряжение |
C=qU |
| Напряженность и напряжение |
E=Ud |
| Энергия конденсатора |
W=q22C=CU22 |
| Количество теплоты |
Q=ΔW |
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
I=εR+r
Применим закон Ома:
I=UR
Приравняем правые части выражений и получим:
εR+r=UR
Отсюда напряжение на конденсаторе равно:
U=εRR+r
Напряженность электрического поля равна:
E=Ud=εRd(R+r)=9·80,002(8+1)=720,018=4000 (Вм)
Задание EF17564
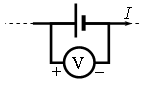
Ответ:
а) 5 Дж
б) 4 Дж
в) 3 Дж
г) 1 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу для нахождения количества теплоты, выделенной внутри источника тока.
3.Выполнить решение в общем виде.
4.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• ЭДС источника тока: ε = 3 В.
• Внутреннее сопротивление источника тока: r = 1 Ом.
• Сила тока в цепи: I = 2 А.
• Напряжение на внешней цепи: U = 5 В.
Количество теплоты, выделенной внутри источника тока, равно:
Q=I2rt=22·1·1=4 (Дж)
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17573
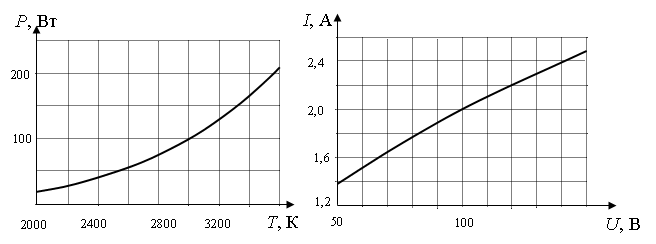
При нагревании спирали лампы накаливания протекающим по ней электрическим током основная часть подводимой энергии теряется в виде теплового излучения. На рисунке изображены графики зависимости мощности тепловых потерь лампы от температуры спирали P=P(T) и силы тока от приложенного напряжения I=I(U). При помощи этих графиков определите примерную температуру спирали лампы при силе тока I=2 A.
Ответ:
Алгоритм решения
1.Записать исходные данные.
2.С помощью графика зависимости силы тока от напряжения вычислить мощность.
3.С помощью графика зависимости мощности от температуры спирали определить ее температуру.
Решение
Нас интересует сила тока, равная 2 А. По графику зависимости силы тока от напряжения этому значение соответствует U = 100 В. Мощность определяется формулой:
P=IU=2·100=200 (Вт)
Этой мощности соответствует температура, равная около 3600 К.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17608
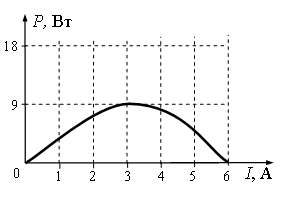
Какое из утверждений соответствует результатам опыта?
А. При коротком замыкании в цепи сила тока будет равна 6 А.
Б. При силе тока в цепи 3 А на реостате выделяется минимальная мощность.
Ответ:
а) только А
б) только Б
в) и А, и Б
г) ни А, ни Б
Алгоритм решения
- Проверить истинность каждого из утверждений.
- Выбрать верный ответ.
Решение
Согласно первому утверждению, при коротком замыкании в цепи сила тока будет равна 6 А. Это действительно так, потому что при этом значении силы тока мощность равна нулю. А это значит, что сопротивление на внешней цепи было нулевым.
Согласно второму утверждению, при силе тока в цепи 3 А на реостате выделяется минимальная мощность. Это не так. На графике этой силе тока соответствует максимальная мощность.
Верно только первое утверждение «А».
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 8.4k
Как определить мощность источника тока
Содержание
- 1 Виды мощности
- 2 Активная и реактивная мощность
- 3 Как определяется мощность
- 4 Мощность источника питания
- 5 Видео по теме
Источники питания используются повсеместно. Их основная задача — преобразование параметров электроэнергии, поступающей из сети, в такие, которые необходимы для конкретного электротехнического устройства. Способность ИП выполнять данную задачу зависит от его мощности. Она является главной характеристикой любого блока питания. Чтобы оценить эффективность устройства, необходимо понимать, как найти мощность, если известны различные характеристики электрической цепи.
Виды мощности
При вычислении мощности возможны следующие ситуации:
- Мгновенная мощность вычисляется для очень малого промежутка времени. Это значение важно знать в тех случаях, когда в разные моменты времени эта величина меняется. Проведение замеров позволит мастеру получить целостное представление об используемой мощности. Для постоянного тока данная характеристика постоянна.
- Активное значение мощности применяется для определения постоянной величины, которая фактически является средним значением при наличии переменного тока. При этом мгновенные значения будут изменяться, а активная мощность будет в среднем характеризовать происходящие процессы. Активная мощность — это показатель выполнения полезной работы электрическим оборудованием.
- Реактивная мощность относится к работе индуктивных и емкостных элементов электрических приборов. Она циклически переходит из одной формы в другую. При этом происходит перемещение зарядов, то есть, осуществляется электрическая работа, которая обычно не является полезной.
Активная и реактивная мощность
При работе электрического оборудования следует рассматривать полную мощность. Она показывает работу, которая проводится в единицу времени (в СИ в этом качестве рассматривается 1 секунда). При этом нужно помнить, что полная мощность складывается из активной и реактивной мощности.
Это разделение связано с используемым сопротивлением. Если электрические заряды преодолевают активное сопротивление, мощность также является активной. Она, как правило, относится к выполнению полезной работы.
При наличии переменного тока в электрической цепи присутствует реактивное сопротивление. Оно связано с работой электромагнитного поля и фактически сводится к периодическим изменениям, при которых энергия регулярно перетекает из одной формы в другую, практически не расходуясь.
В бытовых приборах и промышленном оборудовании в большинстве случаев присутствуют оба вида мощности. Активная играет основную роль при использовании постоянного тока или в тех случаях, когда её доля в общей мощности относительно высока.
Обычно в технической документации указывается параметр cosφ. Он может принимать значения от 0 до 1 включительно. Его величина показывает долю активной мощности в полной. Она будет высокой, например, в электронагревательных приборах, где значительная часть энергии тратится на выполнение полезной работы по обогреву помещения.
Надо учитывать, что наличие реактивной мощности оказывает разрушительное действие на прибор. Это может быть, например, связано с разрушением изоляции проводов и кабелей, с повышением риска возникновения короткого замыкания или с порчей оболочек электроприводов или трансформаторов.
Для получения полной мощности применяется векторное сложение активной и реактивной мощности. Её величину вычисляют по теореме Пифагора как длину гипотенузы прямоугольного треугольника, в котором катетами являются активная и реактивная мощности.
Как определяется мощность
Эта величина определяется на основе работы, выполненной при перемещении заряда. Мощность равна частному от деления её величины на потраченное для этого время. Из курса физики известно, что работу можно выразить как произведение разности потенциалов на перемещаемый заряд. Для вычисления заряда можно применить следующую формулу:
На основе сказанного можно привести такое равенство:
Из формулы видно, что мощность можно выразить как произведение напряжения и силы тока. Её можно преобразовать с использованием закона Ома:
Подставив это выражение в формулу мощности, выводят эквивалентные формы, которые могут быть более удобными в некоторых ситуациях.
Например, при рассмотрении последовательного соединения удобной будет формула с использованием силы тока и напряжения. Это связано с тем, что сила электротока на рассматриваемом участке является одинаковой.
При параллельном соединении одинаковым на различных участках будет электронапряжение. В данном случае производить вычисления проще с использованием формулы, которая выражает мощность через разницу потенциалов и сопротивление.
В международной системе измерений для мощности используется ватт. Иногда применяют эквивалентную единицу вольт*ампер. Широко используются значения, которые выражаются в единицах, кратных ваттам. В качестве примера можно привести киловатт и мегаватт, которые соответствуют тысяче и миллиону ватт соответственно.
У большинства электроприборов, используемых в быту, мощность находится в определённых пределах, которые примерно соответствуют значениям, указанным в следующей таблице:
В прошлом в качестве единицы измерения мощности активно использовалась лошадиная сила. Для ее выражения через ватты нужно применять следующую формулу:
Хотя классической единицей измерения энергии или выполненной работы является джоуль, для электрических приборов чаще используется ватт*час.
При описании электрических устройств или деталей часто указывают предельную мощность. В технической документации также может быть указана номинальная мощность оборудования. Режим работы устройства в этом случае считается оптимальным. Если реальная мощность будет выше, то это означает, что прибор эксплуатируется очень интенсивно.
Сказанное можно пояснить на следующем примере. Допустим, речь идёт о резисторе на 500 Ом. Пусть в технической документации сказано, что предельно допустимая мощность при его использовании составляет 10 Вт. В этом случае предельно допустимое напряжение определяется по формуле:
Из этого выражения можно найти напряжение. Для него будет правильным следующее равенство:
Подставляя конкретные значения, получаем, что квадратный корень нужно извлечь из произведения 500 * 10 = 5000. Он будет примерно равен 70.7. Таким образом, предельно допустимым напряжением для этого резистора будет 70.7 В.
Иногда возникает необходимость практически измерить мощность. Это можно сделать с помощью ваттметра.
Для определения мощности также используют амперметр и вольтметр. Первый присоединяют последовательно, второй — параллельно. Получив значения силы тока и напряжения, на их основе производят вычисления для определения мощности.
Мощность источника питания
В предыдущем разделе было рассмотрено понятие мощности и относящиеся к ней характеристики в применении к различным электрическим узлам или приборам. При рассмотрении источника элетротока потребуется учитывать имеющиеся в этом случае особенности.
Используемый ИП должен соответствовать параметрам электрической цепи, которую он питает. При этом необходимо обратить внимание на следующее:
- Значение полной мощности электрической цепи.
- ЭДС источника.
- Внутренне сопротивление ИП.
- Потери энергии внутри источника питания.
- Значение полезной мощности.
Мощность источника тока должна превосходить мощность электроприбора не меньше, чем на 5-10%. Это позволит обеспечить электропитание даже в условиях интенсивного использования прибора. Энергия источника питания будет расходоваться на совершение полезной работы, а также на потери.
Для понимания особенностей работы источника питания важно знать разницу между электронапряжением на клеммах и электродвижущей силой. Практически в работающей цепи электроны перемещаются по замкнутому пути. Они переходят от отрицательной клеммы через электрическую цепь к положительной. Попадая внутрь батареи под воздействием электродвижущей силы, электроны будут вновь перемещаться на отрицательную клемму.
Нужно учитывать, что величина ЭДС не является независимой от нагрузки. Её точное значение можно узнать при измерении на холостом ходу. Чтобы вычислить мощность источника питания, можно воспользоваться формулой, которая выражает её через ЭДС и сопротивление. Для этого потребуется выполнить следующие действия:
- Нужно определить величину электродвижущей силы (E) источника питания. Для этого замеряют разность потенциалов на клеммах на холостом ходу.
- Далее требуется подключить нагрузку, которая имеет известное сопротивление (R).
- Затем в электрической цепи измеряют силу тока (I), а также напряжение (U).
- Теперь есть возможность узнать падение напряжения (U0) внутри источника тока. Оно представляет собой разность между электродвижущей силой и напряжением в цепи.
- Внутреннее сопротивление (R0) вычисляется по формуле R0 = U0 / I.
Подставив полученные значения в формулу, выраженную через напряжение и сопротивление, можно определить мощность источника тока.
Полную мощность ИП можно представить как Рполн = Рполезн + Рпотерь.
Для определения полезной мощности используется одна из трех формул:
Мощность потерь, возникающая во внутренней цепи, то есть, в источнике тока, расходуется лишь на процессы, происходящие в самом ИТ и не может использоваться для каких-либо других целей. Ее вычисляют по формуле:
Для определения полной мощности можно воспользоваться одной из трех формул:
Используя приведённый здесь алгоритм, можно определить полезную мощность, которая создаётся рассматриваемым источником тока. Чтобы составить представление о зависимости полезной мощности и той, которая расходуется на нагрев ИТ, можно воспользоваться графиком. Из него видно, что полезная мощность сначала возрастает, а затем начинает убывать. Максимума она достигает в точке, в которой сопротивление нагрузки равно внутреннему сопротивлению источника электротока, то есть, R = r.
КПД при таком условии будет равен 50%. В общем случае коэффициент полезного действия находят по формуле:
Максимальная полезная мощность равняется половине полной. Следовательно
Из сказанного видно, что при подборе наиболее подходящего источника питания для электрического устройства нужно стремиться к тому, чтобы внутреннее сопротивление источника питания было равно сопротивлению нагрузки. Если оно значительно меньше, то существенная часть мощности в процессе эксплуатации будет рассеиваться в виде тепла. Приведённое требование соответствия величин называют условием согласования.
Важно отметить, что в качестве устройства питания не обязательно может использоваться батарея или аккумулятор. Отмеченная здесь закономерность будет действовать и в том случае, если речь идёт об использовании усилителя.
В качестве примера использования указанного правила можно привести подключение акустической системы к усилителю. В этом случае выходной импеданс последнего должен подбираться таким образом, чтобы быть примерно равным входному импедансу подключённых динамиков. На практике в технической документации усилителя указывают границы, в которых должна находиться соответствующая характеристика подключённых устройств.
Видео по теме
При прохождении тока в цепи электрическое поле совершает работу по перемещению заряда. В этом случае работу электрического поля называют работой электрического тока.
При прохождении заряда (q) по участку цепи электрическое поле будет совершать работу: (A=qcdot U), где (U) — напряжение электрического поля, (A) — работа, совершаемая силами электрического поля по перемещению заряда (q) из одной точки в другую.
Для выражения любой из этих величин можно использовать приведённый ниже рисунок.
Рис. (1). Зависимость между работой, напряжением и зарядом
Количество заряда, прошедшее по участку цепи, пропорционально силе тока и времени прохождения заряда:
q=I⋅t
.
Работа электрического тока на участке цепи пропорциональна напряжению на её концах и количеству заряда, проходящего по этому участку:
A=U⋅q
.
Работа электрического тока на участке цепи пропорциональна силе тока, времени прохождения заряда и напряжению на концах участка цепи:
A=U⋅I⋅t
.
Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком.
Рис. (2). Зависимость между работой, силой тока и временем прохождения заряда
Единицы измерения величин:
работа электрического тока ([A]=1) Дж;
напряжение на участке цепи ([U]=1) В;
сила тока, проходящего по участку ([I]=1) А;
время прохождения заряда (тока) ([t]=1) с.
Для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображённую на рисунке. Вольтметром измеряется напряжение на лампе, амперметром — сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.
Рис. (3). Схема и часы для измерения
Например:
I = 1,2 АU = 5 Вt = 1,5 мин = 90 сА = U⋅I⋅t = 5⋅1,2⋅90 = 540 Дж
Обрати внимание!
Работа чаще всего выражается в килоджоулях или мегаджоулях.
(1) кДж = 1000 Дж или (1) Дж = (0,001) кДж;
(1) МДж = 1000000 Дж или (1) Дж = (0,000001) МДж.
Для потребителей электрической энергии существуют приборы, позволяющие в пределах ошибки измерения получать числовые данные о ее расходе в единицу времени.
Рис. (4). Электросчетчик
Механическая мощность численно равна работе, совершённой телом в единицу времени:
N = Аt
. Чтобы найти мощность электрического тока, надо поступить точно также, т.е. работу тока,
A=U⋅I⋅t
, разделить на время.
Мощность электрического тока обозначают буквой (Р):
. Таким образом:
Мощность электрического тока равна произведению напряжения на силу тока:
P=U⋅I
.
Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведённый ниже рисунок.
Рис. (5). Зависимость между мощностью, напряжением и силой тока
За единицу мощности принят ватт: (1) Вт = (1) Дж/с.
Из формулы
P=U⋅I
следует, что
(1) ватт = (1) вольт ∙ (1) ампер, или (1) Вт = (1) В ∙ А.
Обрати внимание!
Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
(1) гВт = (100) Вт или (1) Вт = (0,01) гВт;
(1) кВт = (1000) Вт или (1) Вт = (0,001) кВт;
(1) МВт = (1 000 000) Вт или (1) Вт = (0,000001) МВт.
Пример:
Измерим силу тока в цепи с помощью амперметра, а напряжение на участке — с помощью вольтметра.
Рис. (6). Схема
Так как мощность тока прямо пропорциональна напряжению и силе тока, протекающего через лампочку, то перемножим их значения:
.
Ваттметры измеряют мощность электрического тока, протекающего через прибор. По своему назначению и техническим характеристикам ваттметры разнообразны.
В зависимости от сферы применения у них различаются пределы измерения.
|
Аналоговый ваттметр |
Аналоговый ваттметр |
Аналоговый ваттметр |
Цифровой ваттметр |
|
|
|
|
|
Рис. (7). Приборы для измерения
Подключим к цепи по очереди две лампочки накаливания, сначала одну, затем другую и измерим силу тока в каждой из них. Она будет разной.

Рис. (8). Лампы различной мощности в цепи
Сила тока в лампочке мощностью (25) ватт будет составлять (0,1) А. Лампочка мощностью (100) ватт потребляет ток в четыре раза больше — (0,4) А. Напряжение в этом эксперименте неизменно и равно (220) В. Легко можно заметить, что лампочка в (100) ватт светится гораздо ярче, чем (25)-ваттовая лампочка. Это происходит оттого, что её мощность больше. Лампочка, мощность которой в (4) раза больше, потребляет в (4) раза больше тока. Значит:
Обрати внимание!
Мощность прямо пропорциональна силе тока.
Что произойдёт, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение (110) В и (220) В.


Рис. (8). Лампа, подключенная к источнику тока с различным напряжением
Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае её мощность будет больше. Следовательно:
Обрати внимание!
Мощность зависит от напряжения.
Рассчитаем мощность лампочки в каждом случае:
| I=0,2АU=110ВP=U⋅I=110⋅0,2=22Вт | I=0,4АU=220ВP=U⋅I=220⋅0,4=88Вт. |
Можно сделать вывод о том, что при увеличении напряжения в (2) раза мощность увеличивается в (4) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно, ток через нить накала и её расчётное сопротивление) указывается только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).
Рис. (9). Маркировка
В таблице дана мощность, потребляемая различными приборами и устройствами:
Таблица (1). Мощность различных приборов
|
Название |
Рисунок |
Мощность |
| Калькулятор |
|
(0,001) Вт |
| Лампы дневного света |
|
(15 — 80) Вт |
| Лампы накаливания |
|
(25 — 5000) Вт |
| Компьютер |
|
(200 — 450) Вт |
| Электрический чайник |
|
(650 — 3100) Вт |
| Пылесос |
|
(1500 — 3000) Вт |
| Стиральная машина |
|
(2000 — 4000) Вт |
| Трамвай |
|
(150 000 — 240000) Вт |
Источники:
Рис. 1. Зависимость между работой, напряжением и зарядом. © ЯКласс.
Рис. 3. Схема и часы для измерения. © ЯКласс.
Рис. 5. Зависимость между мощностью, напряжением и силой тока. © ЯКласс.
Рис. 6. Схема. © ЯКласс.
Таблица 1. Мощность различных приборов. Компьютер. Указание авторства не требуется, 2021-08-14, Pixabay License, https://pixabay.com/ru/photos/яблоко-стул-компьютер-1834328/.