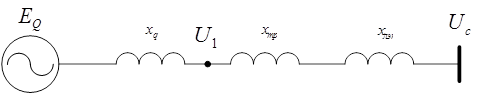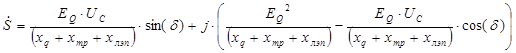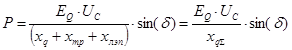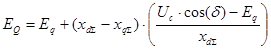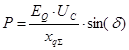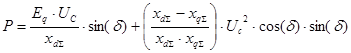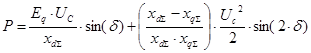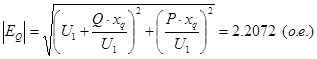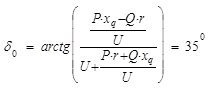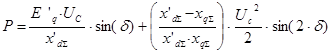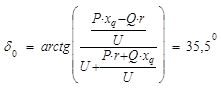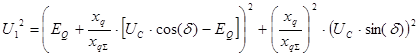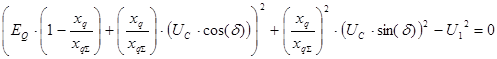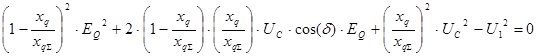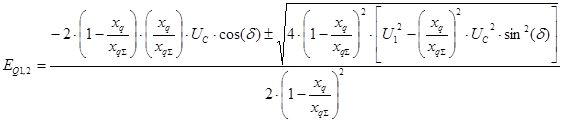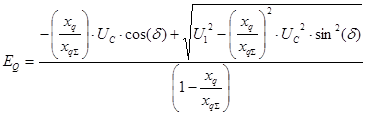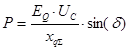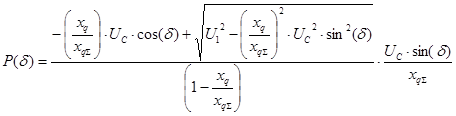Как найти мощность угловую

Вывод формулы угловой характеристики активной мощности.

Как было установлено
выше, мощность синхронной машины Р
зависит от
угла нагрузки 6 между векторами э. д. с.
£ и напряжения (]
машины.
Зависимость Р
= f (б) при Е
= const и U
= const называется
угловой характеристикой активней
мощности синхронной машины. Изучение
этой зависимости позволяет выяснить
ряд важных свойств синхронной машины.
Выведем математическое выражение для
угловой характеристики мощности, приняв
г_а
= О, так как
это сопротивление весьма мало влияет
на вид угловой характеристики.

Спроектируем на
рис. 33-3 векторы э. д. с, напряжений и
падений напряжения на направление
вектора £ и на направление, перпендикулярное
ему. Тогда получим

Равенство (35-4) и является искомым
математическим выражением угловой
характеристики мощности, согласно
которому Р — = / (Е, U, 8, x_d,
Хд). Электромагнитный момент М =
P/Q = = рР/со пропорционален мощности
Р, и поэтому зависимость М = — f (E,
U, 0, x_d, x_q)
имеет подобный же вид.

В выражение (35-4) необходимо подставлять
насыщенные значения x_d
и x_q, соответствующие
величине результирующей э. д. с. £б при
данном режиме, и значение Е по
спрямленной насыщенной х. х. х.,
соответствующей этому же значению Е&.
Учитывая, что значение х_оа1
относительно мало, можно принять Е&
да U. Равенством (35-4) можно
пользоваться также тогда, когда под U
понимается напряжение не на зажимах
машины, а в какой-нибудь более удаленной
точке линии, соединенной с машиной
(например, за повышающим трансформатором,
на приемном конце линии и т. д.). В этом
случае в величины x_d и
х_д нужно включить
также индуктивное сопротивление линии
до рассматриваемой точки. Угол нагрузки
8 во всех случаях измеряется между э. д.
с. от поля возбуждения генератора Е и
рассматриваемым напряжением U.

Неявнополюсная
машина. Понятие о статической устойчивости.
Далее будем предполагать, что
машина работает параллельно с сетью
бесконечной мощности и поэтому U =
const, / = const и ток возбуждения генератора
не изменяется. Для простоты предположим
также, что ц_с = const и, следовательно,
x_d = const и x_q
= = const.

У неявнополюсной машины x_q
= x_d и на основании
выражения (35-4)

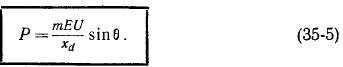
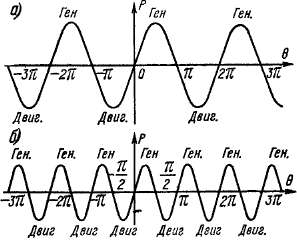
При указанных предположениях Р = /
(8), согласно равенству (35-5), представляет
собой синусоиду (рис. 35-8, а). Полуволны
Р > 0 соответствуют генераторному
режиму работы и полуволны Р < 0 —
двигательному. Как следует из рис. 35-8,
а, при беспрерывном изменении 8
синхронная машина попеременно переходит
из генераторного режима работы в
двигательный и обратно. Такое изменение
8 означает, что ротор машины вращается
несинхронно — несколько быстрее или
несколько медленнее поля реакции якоря.
Зависимость Р = f (в) на рис. 35-8, а
при этом действительна только при
бесконечно медленном изменении 8, когда
в результате несинхронного вращения
ротора в цепях индуктора не индуктируется
никаких токов.

Изменение угла 8 на величину 2я означает,
что ротор машины передвинулся относительно
поля статора на два полюса. Режим

работы машины при этом, как это ясно из
физических соображений, равенств (35-4),
(35-5) и рис. 35-8, а, не изменяется. Поэтому
достаточно рассмотреть угловую
характеристику в пределах — я sS; е <
я. Диапазон — я sc; б «S 0 соответствует
двигательному, а диапазон 0 ==с 6 «S л —
генераторному режиму. Так как полупериоды
синусоидальной кривой симметричны, то
свойства синхронной машины в двигательном
и генераторном режимах аналогичны.
Поэтому ниже рассмотрим режим генератора
(рис. 35-9). Согласно рис. 35-9, при увеличении
Р от нуля угол 6 будет расти от 6 = 0 и
при критическом угле нагрузки 6_кр
= 90° достигается максимальная мощность
Р — Р_т, которую способен
развить генератор. На основании выражения
(35-5) для неявнопо-люсной машины

Как видно из равенства (35-6), Р_т
тем больше, чем больше Е или ток
возбуждения машины, чем больше U и
чем меньше*<*. По этой причине-с целью
уменьшения x_d в синхрон-

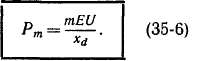
Рис 35-8 Угловые
характеристики активной мощности
неявнополюсной (а) и реактивной (б)
синхронной
машины

ных машинах зазор выполняется больше,
чем в асинхронных машинах.

В установившемся режиме работы генератора
механическая’ мощность Р_п
д, развиваемая первичным
двигателем, равна электрической мощности
Р, отдаваемой генератором в сеть,
т. е. Р_{п д} = Р.
При этом под Р_п. _д следует
понимать мощность первичного двигателя
за вычетом механических и магнитных
потерь в генераторе (при г_а
= О электрические потери в якоре равны
нулю). Мощность Р_{п д}
не зависит от угла б и поэтому изображена
на рис. 35-9 горизонтальной прямой, которая
пересекается с характеристикой
электрической мощности Р — f (6) в
точках / и 2. В этих точках Р_п.
_д = Р, и, следовательно, обе они
могли бы соответствовать нормальному
установившемуся режиму работы. Однако
устойчивой является только работа в
точке /.

Действительно, если при работе в точке
/ рис. 35-9 в результате небольшого
случайного преходящего возмущения угол
8 увеличится на Де, то электрическая
мощность генератора превысит

мощность первичного
двигателя на АР. Вследствие этого на
валу будет действовать избыточный
тормозящий электромагнитный момент

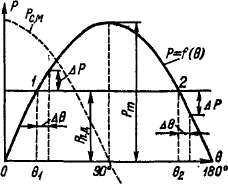
Рис. 35-9. Угловая
характеристика

активной мощности
неявнополюс-

ного синхронного
генератора

и ротор генератора
будет притормаживаться. Угол е будет
уменьшаться, и восстановится устойчивый
установившийся режим работы в точке /.
Если при работе в точке 1
угол 6 в
результате случайного возмущения
уменьшится, то при прекращении действия
этого возмущения генератор также
вернется в режим работы в точке 1.

Если же при работе
в точке 2 рис.
35-9 угол е увеличится на Дб, то мощность
генератора будет на АР
меньше
мощности турбины, ротор будет ускоряться,
угол 8 возрастет еще больше и т. д. В
результате генератор выйдет из синхронизма
или при благоприятных условиях перейдет
в устойчивый режим работы на последующих
положительных полуволнах кривой рис.
35-8, а после
«проскальзывания» ротора на четное
число полюсных делений. Если же при
работе в точке 2
угол 6
уменьшится,

то вследствие
нарушения баланса мощностей этот угол
будет уменьшаться и далее, пока этот
баланс не восстановится в точке 1.

Таким образом,
работа неявнополюсного генератора
устойчива в области 0 •< 6 <С 90° и
неустойчива в области 90° < 6 < 180°.

Аналогичным образом
можно установить, что неявнополюс-ный
синхронный двигатель работает устойчиво
в области 0 > 8 > —90°.

Рассмотренные
здесь вопросы относятся к области так
называемой статической устойчивости
синхронной машины.

Режим работы
определенной установки называется
статически устойчивым, если при наличии
весьма небольших возмущений режима
работы (небольшое изменение U,
Р_п-
д,
if и
т. д.) изменения режима работы (величина
9, Рит. д.) также будут небольшими и при
прекращении действия этих возмущений
восстановится прежний режим работы. Из
сказанного

выше следует, что режим работы синхронной
машины статически устойчив, если

Невозбужденная явнополюсная машина.
Если if = 0, то и Е = О,

так как в нормальных машинах э д с. от
остаточного магнитного потока пренебрежимо
мала. В этом случае на основании выражения
(35-4)

Зависимость Р = f (б), согласно равенству
(35-10), представляет собой синусоиду с
удвоенной частотой (рис. 35-8, б).

Из равенства (35-10) и рис. 35-8, б следует,
что явнополюсная машина в состоянии
развивать мощность при синхронном
режиме

работы также без возбуждения. Устойчивая
работа в режиме генератора происходит
при 0 < е < 45°, а в режиме двигателя —
при — 45° < 6 < 0°. Пределу устойчивой
работы соответствует е _кр = ± 45°
вместо 8_кр = ± 90° в предыдущем
случае.

В рассматриваемом случае в машине
существует только поток реакции якоря.
При цилиндрическом

Рис 35-10 Картины
магнитного поля невозбужденной синхронной
машины

р

роторе (рис. 35-10, а), когда x<i — x_q,
положение ротора относительно
вращающегося поля реакции якоря
безразлично, поэтому машина не развивает
электромагнитного момента и мощности.
В явнополюсной машине ротор стремится
занять по отношению к вращающемуся полю
положение, при котором сопротивление
магнитному потоку и энергия магнитного
поля минимальны. Если при этом приложенный
к валу момент М_ст = 0, то 6=0 (рис.
35-10, б) и электромагнитный момент,
действующий на ротор, также равен нулю.
При этом, согласно равенству (35-10), также
Р — 0. Если вал нагружен внешним
моментом, то положение ротора относительно
поля смещается, 9 Ф 0

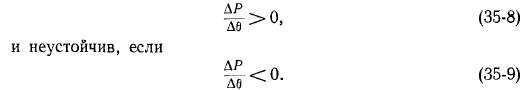
и в машине развиваются электромагнитный
момент и активная мощность (рис. 35-10, в).
Так как сам ротор не намагничен, то
поворот ротора относительно поля на
180° не приводит к изменению режима, как
это и следует из рис. 35-8, б.

У невозбужденной явнополюсной машины
электромагнитный момент развивается
исключительно вследствие действия поля
реакции якоря при наличии неравномерности
воздушного зазора (х_а
=£■ Хд) и называется поэтому реактивным
(см. также § 25-4).

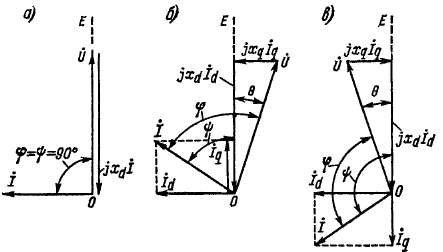
Рис. 35-11. Векторные
диаграммы реактивной синхронной машины
при работе на холостом ходу (а), в режиме
генератора (б) и двигателя (в)

Реактивный режим работы может возникнуть,
например, в случае, когда при параллельной
работе с сетью явнополюсный генератор
по какой-либо причине теряет возбуждение
(неисправность возбудителя, ложное
срабатывание автомата гашения поля и
т. д.) и был при этом слабо загружен.
Последнее обстоятельство существенно
потому, что предельная мощность, которую
может развить генератор в этом режиме,
невелика. Действительно, по формуле
(35-10) в относительных единицах получим

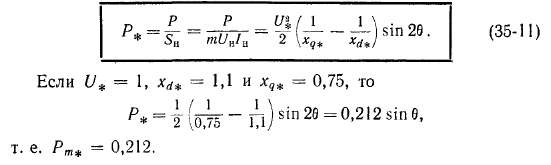
Машина в этом
режиме потребляет большой реактивный
ток для создания магнитного поля. На
холостом ходу (6=0)

/ = U/x_d

и, например,, при U* = 1 и x_d*
= 1,1 будет /* = 0,91.

Строятся также синхронные двигатели
малой мощности, лишенные обмотки
возбуждения и называемые реактивными
(см. § 41-3).

На рис. 35-11 изображены векторные диаграммы
явно-полюсной машины при работе без
возбуждения, причем штриховой линией
показано направление э. д с. Е, которая
индуктировалась бы при наличии
возбуждения. При этом, как и в гл. 33, на
диаграммах представлены токи, отдаваемые
машиной в сеть. В соответствии с этим
на рис 35-11, как и в режиме недовозбуждения
(Е < U), ток опережает напряжение.
Возбужденная явнополюс-ная машина. В
этом случае оба члена равенства (35-4)
отличны от нуля и машина развивает
мощность как за счет электромагнитного
момента, создаваемого с участием потока
возбуждения,

так и за счет реактивного электромагнитного
момента. На рис. 35-12 изображены кривые
1 и 2 обеих составляющих мощности и
кривая 3 суммарной мощности.

Максимальная мощность и предел
устойчивости работы в данном случае
наступают при критическом угле б_кр.
значение которого определяется равенством

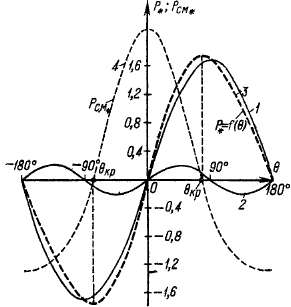
Рис 35-12 Угловая
характеристика активной мощности
возбужденного явнополюс-ного генератора
при Е^ =
1,87, £/„ = 1, *<**= 1-1. *?* = 0,75

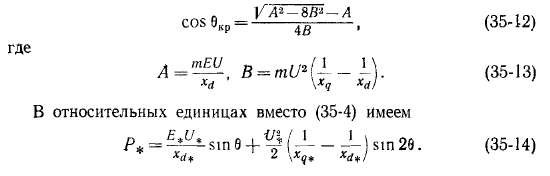
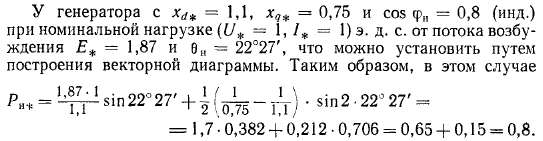
Вторая составляющая мощности в данном
случае равна 19% от всей мощности. Таким
образом, в нормальных режимах работы
эта составляющая сравнительно мала. У
генератора с приведенными данными при
£„. = 1,87 и U% = 1 критический угол
нагрузки 8_кр = 77° и предельная
мощность Р_т* = 1,75, т.
,е. примерно в два раза больше номинальной
активной мощности (/>„ = 0,8).

Угловая
характеристика реактивной
мощности. Наряду с рассмотренными
выше^характеристиками активной мощности
представляют интерес также угловые
характеристики реактивной мощности Q.

Реактивная мощность

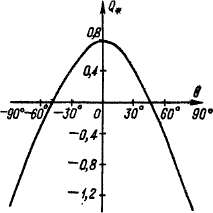
Рис. 35-13. Угловая
характеристика реактивной мощности
явнополюсного генератора

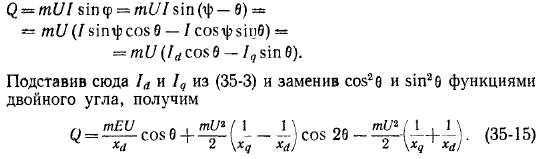
Так как косинус — функция четная, то
при прочих равных условиях эта
характеристика для режимов генератора
и двигателя одинакова.

Кривая Q# — f (б) по формуле (35-15) для
перевозбужденной синхронной машины
при Е* — 1,87, £/„ = 1, х_а*
= 1,1, х_?* = = 0,75 изображена на рис.
35-13. Из этой кривой видно, что если при
6=0 генератор отдает в сеть реактивную
мощность, то с увеличением 6 величина Q
начинает падать и при некотором б
изменяет знак, т. е. машина начинает
потреблять реактивную мощность из сети.
Это является следствием того, что при
Е = const и U = const в случае увеличения
активной нагрузки вектор / непрерывно

поворачивается против часовой стрелки
и при некотором 8 начинает опережать 0.
Такой характер изменения / следует
из рассмотрения векторных диаграмм
рис. 33-2, 33-3 и др.

Рассмотренные выше выражения угловых
характеристик дают правильные результаты,
если в них подставляются насыщенные
значения параметров. Поскольку эти
значения в большинстве случаев неизвестны,
то расчеты по этим выражениям часто
выполняются при подстановке ненасыщенных
значений параметров. При этом значения
максимальной мощности получаются
заниженными на 8—12%, а значения углов
б_кр — завышенными на 8—15%. Значение
угла 9 при Р = Р_н также получается
завышенным.

§ 35-4. Синхронизирующая мощность,
синхронизирующий момент и статическая
перегружаемость синхронных машин

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рассмотрим простейшую схему электропередачи, состоящую из генератора электростанции, повышающего трансформатора, линии электропередачи и шин приемной системы. Введем допущение о том, что приемная система обладает бесконечной  мощностью, так что любое изменение режима рассматриваемой электропередачи не вызовет изменения напряжения на шинах приемной системы и частоты. Дополнительно к выше написанному допущению пренебрежем активным сопротивлением элементов электропередачи, емкостью линии и токами намагничивания трансформаторов.

Рис.1. Расчетная схема

Режим работы генератора в установившемся режиме работы описывается следующим уравнением:

,

где  — вспомогательная ЭДС;

— синхронная ЭДС статора.

Рис.2. Схема замещения расчетной цепи

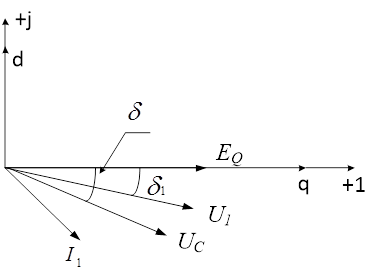
Построим векторную диаграмму для соответствующей схемы замещения.

Рис.3. Векторная диаграмма

При выполнении расчетом в дальнейшем за вещественную ось выбрана ось q, а за мнимую — ось d.

Полная электрическая мощность выдаваемая в сеть от генератора определяется по формуле:

     (о.е.)

Примечание: В именованных единицах формулы для определения мощности выглядит следующим образом: (и.е.), однако при выводе последующих формул используется формула , которая связывает параметры в относительных единицах. В качестве базисных величин выбраны следующие переменные: линейное напряжение и фазный ток. В результате при переводе формулы из именованных единиц в относительные единицы получим запись: (о.е.).

Преобразуем формулу для определения полной мощности к зависимости передаваемой мощности от параметров схемы замещения, значений напряжений в узлах расчетной схемы и взаимного угла между векторами напряжения (δ).

Ток, который передается от генератора можно определить исходя из второго закона Кирхгофа:

,

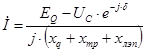
где .

Подставляю в формулу для мощности выражение для определения сопряженного тока, получим следующую запись:

В результате после преобразования была получена формула для определения активной и реактивной мощности от режимных параметров. Рассмотрим выражение для определения активной мощности:

В полученное выражение для мощности входит переменная , которая не имеет физического смысла. В зависимости от исходной системы возбуждения генератора последнее выражение переписывается в различных формах в зависимости от принятых исходных условий:

— постоянство синхронной ЭДС статора ();

— постоянство потокосцепления контура возбуждения ( );

— постоянное напряжение на зажимах генератора ( ).

а. Угловая характеристика мощности синхронной машины при постоянстве синхронной ЭДС статора ()

Переменная E_Q, которая входит в уравнения для определения активной мощности , может быть переписана через переменную E_q  следующим образом:

.

Найдем выражение для определения тока . Для этого рассмотрим следующее выражение:

Выразим ток  подставляя в ранее полученное выражение уравнения, которые описывают установившийся режим работы синхронной машины (, ). В результате подстановки получим:

;

.

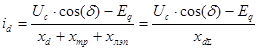
Подставим полученное выражение для определения   в уравнение E_Q с учетом соотношения . В результате подстановки получим:

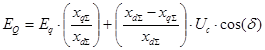
Полученное выражение определяет закон изменения ЭДС E_Q при условии постоянства синхронной ЭДС статора.

Далее преобразуем выражение для определения активной мощности  с помощью полученного выражения :

Полученное выражение носит название угловой характеристика мощности синхронной машины при постоянстве синхронной ЭДС статора.

Полученная формула показывает, что в общем случае при  характеристика мощности содержит кроме основной синусоидальной составляющей мощности также составляющую двойного угла. Амплитуда составляющей мощности двойного угла обычно не велика. Так, например, при работе машины непосредственно на шины бесконечной мощности при , , , , составляющая двойного угла равна 18% от амплитуды основной составляющей. Наличие реактивности внешней сети заметно уменьшает эту цифру: если  то указанное соотношение составляет 13%, 10% и 7,1 %.

Рассмотрим в качестве примера турбогенератор со следующими параметрами:

МВт, , кВ

, , , 

Для данной модели генератора определим зависимость электромагнитной мощности от угла δ при сопротивлении  (о.е.). В качестве базисных величин будем использовать полную мощность генератора и генераторное напряжение. Перед построением угловой характеристики мощности необходимо определить значение параметра E_q и угол δ при заданных номинальных параметров генератора.

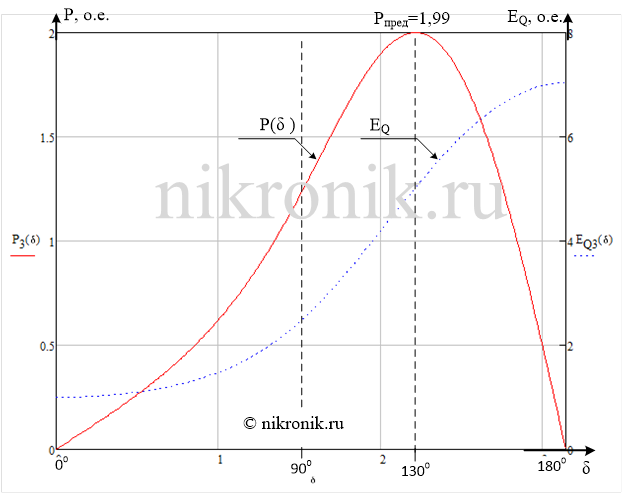
Зависимость электромагнитной мощности от угла  при имеет вид представленный на рис.4.

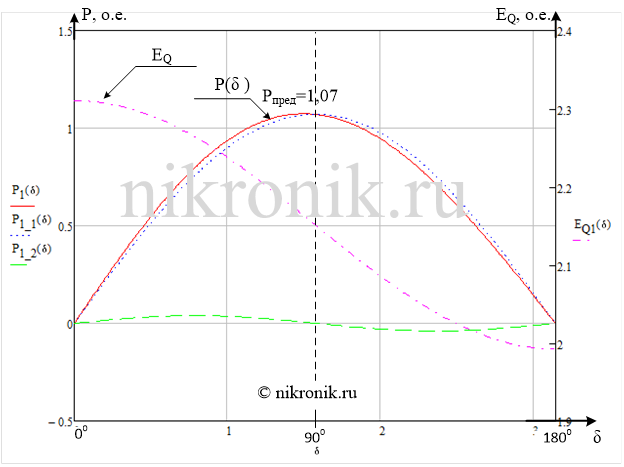
Рис.4. Угловая характеристика мощности при постоянстве синхронной ЭДС статора, а также зависимость изменения E_Q.

Как видно из рисунка, максимальная мощность соответствует углу несколько меньшему, чем 90 градусов и мало отличатся от мощности, определяемой основной синусоидальной составляющей. Поэтому при ориентировочных расчетах обычно пренебрегают влиянием неявнополюности машины.

Для данного рассматриваемого случая получили, что изменение активной мощности в диапазоне от 0 до 1,07 до 0  (о.е.), а вспомогательной ЭДС  E_Q  меняется от значения 2,31 до значения 1,99 (о.е.).

б. Угловая характеристика мощности синхронной машины при постоянстве потокосцепления контура возбуждения ()

Переменная , которая входит в уравнения для определения активной мощности , может быть переписана через переменную  следующим образом:

.

Поскольку данная формула полностью аналогична формуле записанной ранее для определения , то выражение для мощности можно записать следующее (делая соответствующие замены параметров  и  на новые  и  соответственно):

Полученное выражение определяет закон изменения ЭДС E_Q при постоянстве потокосцепления контура возбуждения..

Полученное выражение носит название угловой характеристика мощности синхронной машины при постоянстве потокосцепления контура возбуждения.

Поскольку вторая составляющая выражения при углах от 0 до пи/2 отрицательна, то максимум угловой характеристики в случае  достигается при угле больше пи/2 и превышает максимальное значение мощности, отвечающее условию .

Рассмотрим в качестве примера турбогенератор со следующими параметрами (аналогично предыдущему случаю):

МВт, , кВ

, , , 

Для данной модели генератора определим зависимость электромагнитной мощности от угла δ при сопротивлении (о.е.). В качестве базисных величин будем использовать полную мощность генератора и генераторное напряжение. Перед построением угловой характеристики мощности необходимо определить значение параметра E’_q и угол δ при заданных номинальных параметров генератора.

Зависимость электромагнитной мощности от угла  при имеет вид представленный на рис.5.

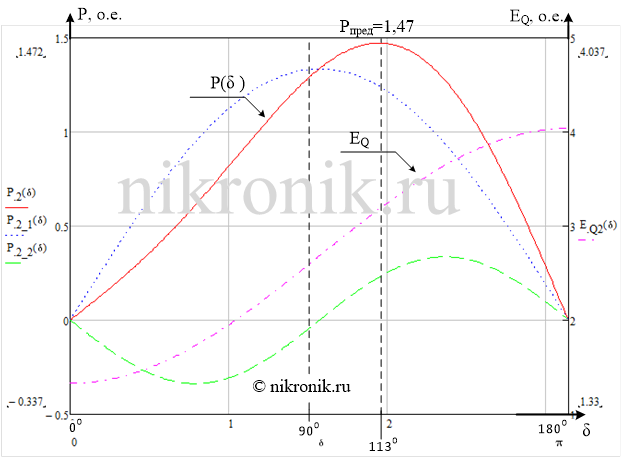
Рис.5. Угловая характеристика мощности при постоянстве потокосцепления контура возбуждения, а также зависимость изменения E_Q.

Как видно из рисунка, максимальная мощность соответствует углу большему, чем 90 градусов.

Для данного рассматриваемого случая получили, что изменение активной мощности в диапазоне от 0 до 1,47 до 0  (о.е.), а вспомогательной ЭДС  E_Q  меняется от значения 1,33 до значения 4,03 (о.е.).

в. Угловая характеристика мощности синхронной машины при постоянном напряжении на зажимах генератора ()

Для представленной ранее схемы замещения можно записать следующую систему уравнений:

П.1. Первое уравнение  из записанной системы можно переписать в следующем виде:

Полученное выражение в комплексной форме можно разложить на следующую равносильную систему уравнений:

Для того, чтобы избавиться от угла , возведем данную систему уравнений в квадрат и сложим оба уравнения:

Определим токи  и , для этого рассмотрим следующие уравнение (см. П.2).

П.2. Второе уравнение из записанной системы можно переписать в следующем виде:

В результате получим следующую систему уравнений:

Из данной системы уравнений выразим токи  и  :

П.3.Подставим полученные значения  и  в уравнение, полученное по П.1.:

В результате преобразований получили квадратное уравнение относительно переменной E_Q. Корни квадратного уравнения  определяются по формуле:

В данном случае неизвестная E_Q определяется следующим образом:

После аналитического преобразования, а также с учетом того, что физический смысл имеет только знак «+» получаем следующее выражение:

Полученное выражение дает закон изменения вспомогательной ЭДС  E_Q, необходимый для поддержания напряжения на шинах генератора .

Далее преобразуем выражение для определения активной мощности  с помощью полученного выражения E_Q:

Полученное выражение носит название угловой характеристика мощности синхронной машины при постоянном напряжении на зажимах генератора.

Рассмотрим в качестве примера турбогенератор со следующими параметрами (аналогично предыдущему случаю):

МВт, , кВ

, , , 

Для данной модели генератора определим зависимость электромагнитной мощности от угла δ при сопротивлении (о.е.). В качестве базисных величин будем использовать полную мощность генератора и генераторное напряжение.

Зависимость электромагнитной мощности от угла δ при постоянном напряжении на зажимах генератора имеет вид представленный на рис.6.

Рис.6. Угловая характеристика мощности при постоянном напряжении на зажимах генератора, а также зависимость изменения E_Q.

Как видно из рисунка, максимальная мощность соответствует углу намного большему, чем 90 градусов.

Для данного рассматриваемого случая получили, что изменение активной мощности происходит в диапазоне от 0 до 1,99 до 0  (о.е.), а вспомогательной ЭДС  E_Q  меняется от значения 1 до значения 7,04 (о.е.).

Общие выводы

Как видно из полученных расчетов, в зависимости от принятых условий, предел передаваемой мощности и угол  различен.  Следует отметить, что каждый рассмотренный случай соответствует своему типу регулирования синхронной машины:

— Постоянство синхронной ЭДС статора говорит о неизменном токе возбуждения (в установившемся режиме работы), что в свою очередь соответствует случаю отсутствия на эквивалентном генераторе автоматического регулятора возбуждения. 

— Постоянство потокосцепления контура возбуждения соответствует случаю, когда на эквивалентном генераторе установлен автоматический регулятор возбуждения пропорционального действия. 

— Постоянство напряжении на зажимах генератора обеспечивается за счет применения на эквивалентном генераторе автоматического регулятора возбуждения сильного действия. Данный регулятор (АРВ СД) отличается от АРВ ПД тем, что в закон регулирования возбуждения вводятся производные изменения параметров режима, которые обеспечивают расширение области устойчивости до еще больших значений угла δ, чем при пропорциональном регулировании.