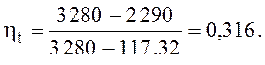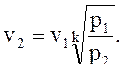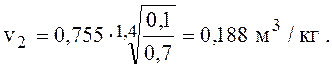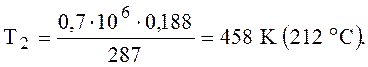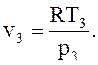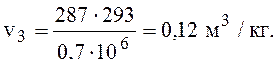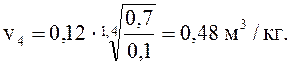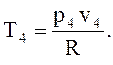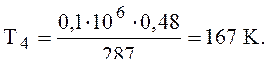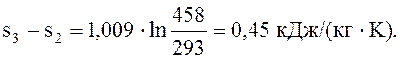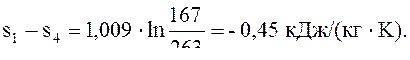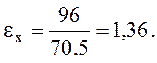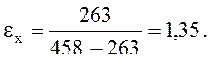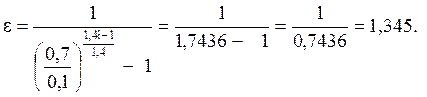Как найти мощность в цикле ренкина - Исправление недочетов и поиск решений вместе с Examum.ru

В
этом разделе пособия вначале рассматривается
схема простой паротурбинной установки
(ПТУ) и соответствующий ей цикл Ренкина,
а затем — способы повышения термического
КПД циклов ПТУ и более сложные схемы и
циклы, с помощью которых реализуются
эти способы.

4.1. Установка, работающая по циклу Ренкина

Задача.
Паротурбинная
установка работает по циклу Ренкина
при начальных параметрах пара р₁= 60 бар и
t₁= 600°С.
Давление пара в конденсаторе р₂=
0,004 МПа.

Изобразить
принципиальную схему установки и её
термодинамический цикл на энтропийных
и p,v
диаграммах. Определить параметры
рабочего тела в характерных точках
цикла, термический КПД, удельные расходы
пара, теплоты и топлива, а также мощность
установки, если часовой расход пара
составляет 950 кг/час.

Сделать
вывод об условиях работы последних
ступеней паровой турбины. Задачу решить
с помощью диаграммы h,s
и уточнить по таблицам.

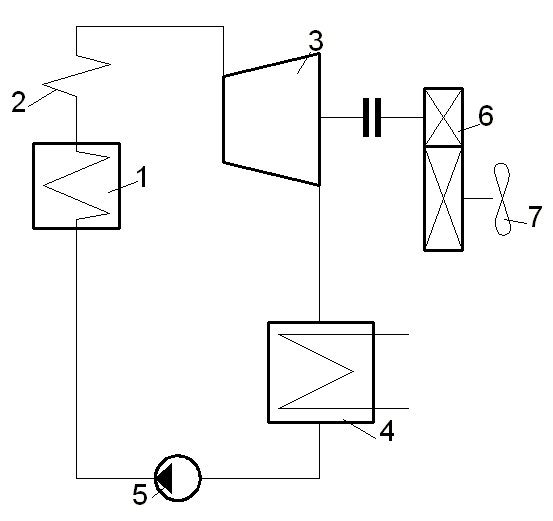
Рис.4.1.
Принципиальная
схема ПТУ, работающей
по циклу Ренкина и её
термодинамический цикл.

На
схеме: 1 –
паровой
котел, 2 – пароперегреватель,
3 – паровая
турбина,
4 – конденсатор, 5 – питательный
насос, 6 – редуктор, 7 – гребной
винт.

Решение
задачи с помощью диаграммы h,s.

Определяем
параметры воды и водяного пара в
характерных точках цикла Ренкина
(1-2-3-4-5-6-1
на рис. 4.1).

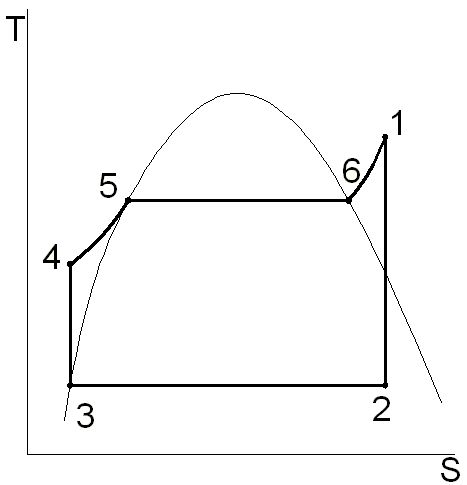
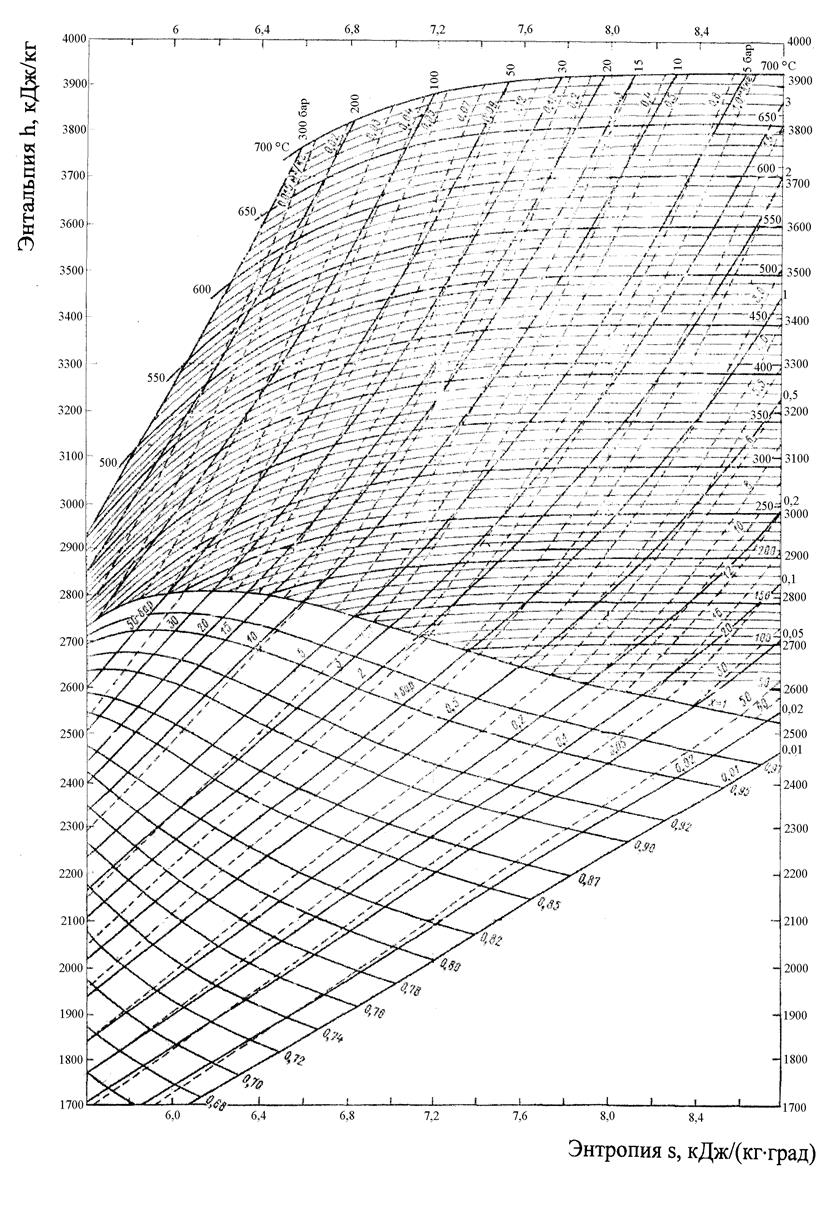
Точка
1
находится в области перегретого пара
на пересечении изобары p₁=
6,0 МПа (черная
линия) и
изотермы t₁= 600С
(красная линия) на диаграмме
h,s
(рис.4.1).
Свойства пара в этом состоянии: удельный
объем v₁=
=0,065 м³/кг;
энтальпия h₁=
3660 кДж/кг; энтропия s₁= 7,18
кДж/(кг·К).

Точка
2.
Из условия
р₂=
0,004 МПа и s₂
= s₁= 7,18
кДж/(кг·К)
устанавливаем,
что точка 2
находится в области влажного пара на
пересечении изобары р₂
= 0,004 МПа и изоэнтропы s₂= 7,18
кДж/(кг·К). Тогда значения удельного
объема v₂
= 29 м³/кг,
энтальпии h₂=
2130 кДж/кг и степени сухости х₂= 0,83.

Точка
3 характеризует
состояние насыщенной жидкости при р₃= р₂= =0,004 МПа.
Энтальпия
в данной точке с помощью диаграммы h,s
рассчитывается по формуле:

При
этом температура насыщения t_s
определяется в точке пересечения изобары
0,004 МПа с правой пограничной кривой (х
=1). Исходящая из этой точки изотерма
(красная линия) и есть искомая t_s.

Точке
4
соответствует состояние жидкости при
давлении р₁
=6,0 МПа. Значение энтальпии h₄
определяем, принимая работу насоса
равной давлению р₁,
выраженному в МПа — l_н
= 6
кДж/кг

h₄=
h₃+|l_н|
= 117+6 = 123 кДж/кг

Точка
5 находится
на пограничной кривой жидкости при
р₁=6,0
МПа. Температура насыщения при указанном
давлении по диаграмме h,
s
равна 275°С, отсюда энтальпия h₅
равна 4,19·275 = 1152,2 кДж/кг.

Точка
6
характеризует состояние насыщенного
пара при р₁=6,0
МПа. Свойства в этом состоянии определяются
по диаграмме h,
s:
t₆= 275°С, v₆
= 0,03 м³/кг,
h₆= 2780 кДж/кг,
s₆
= 5,89 кДж/(кг·К).

Результаты
определения свойств рабочего тела
сводим в таблицу:

Таблица4.1.
Свойства воды и водяного пара в характерных
точках цикла Ренкина, определенные по
диаграмме h,s.

Точка	р, МПа	t, °C	v, м³/кг	h, кДж/кг	S, кДж/(кг·К)	x	Примечание
1	6,0	600	0,065	3660	7,18	—	перегретый пар
2	0,004	28	29	2130	7,18	0,83	влажный пар
3	0,004	28		117		0	насыщенная жидкость
4	6,0			123		—	обычная жидкость
5	6,0	275		1152		0	насыщенная жидкость
6	6,0	275	0,03	2780	5,89	1	насыщенный пар

Отсутствующие
в таблице свойства (пустые клетки) не
могут быть определены с помощью диаграммы
h,s.

Термический
КПД цикла
Ренкина без учёта работы насоса:

КПД
цикла с
учётом работы насоса:

Удельный
расход пара
(на 1 кВт·ч):

Удельный
расход теплоты:

Удельный
расход топлива:

где

— низшая теплотворная способность
топлива (для топлив, используемых в ПТУ,
принимается равной 40000 кДж/кг)

Мощность
установки:

Решение
задачи с помощью таблиц свойств воды и
водяного пара.

Точка
1. Параметры
водяного пара в этой точке определяем
по таблицам [3] (стр. 127) на основании
заданных значений давления и температуры.
При несовпадении заданных значений p
и t
с табличными, применяем интерполяцию
(при необходимости двойную).

Точка
2.
Из условия
s₂= s₁
= 7,1673 кДж/(кг·К) и р₂=0,04
бар определяем степень сухости пара
х₂:

Удельный
объем рассчитываем по аддитивной формуле

либо
по приближенной формуле

В
данном случае точное и приближенное
значения v₂
в пределах пяти значащих цифр совпали.

Энтальпия
также рассчитывается как аддитивная
величина

либо
по соотношению

где
r
= h»
– h’
— теплота парообразования при заданном
давлении.

Точка
3. Свойства
воды в состоянии насыщения определяются
по [3] (табл. II)
при известном давлении р₂
= 0,04 бар.

Точка
4. В этой
точке давление р₄= 60 бар,
энтропия s₄= s₃=
=0,4224 кДж/(кг·К). Тогда коэффициент
интерполяции равен

Определив
k_s,
рассчитываем термодинамические свойства
воды

Точки
5 и 6.
Свойства насыщенных воды и пара определяем
по [3] (табл. ІІ),
зная давление р₁
= 60 бар.

Результаты
определения свойств рабочего тела
сводим в таблицу.

Таблица
4.2. Параметры
воды и водяного пара в характерных
точках цикла Ренкина, определенные по
таблицам:

Точ-ка	р, бар	t,°C	v, м³/кг	h,кДж/кг	s, кДж/(кг·К)	x	Примечание
1	60	600	0,06521	3657,2	7,1673	—	перегретый пар
2	0,04	28,981	29,151	2159,03	7,1673	0,8376	влажный пар
3	0,04	28,981	0,001004	121,41	0,4224	0	насыщенная жидкость
4	60	29,12	0,00100137	127,44	0,4224	—	обычная жидкость
5	60	275,56	0,0013187	1213,9	3,0277	0	насыщенная жидкость
6	60	275,56	0,03241	2783,3	5,8878	1	насыщенный пар

Работа
насоса
рассчитываем по формуле

КПД
установки
с учетом работы насоса

Удельный
расход пара
на 1 кВт·ч:

Удельный
расход теплоты:

Удельный
расход топлива:

Мощность:

Значение
КПД при расчёте по диаграмме на 1,94% выше,
чем при расчете по таблицам. Также
отличаются значения удельного расхода
пара, теплоты, топлива и значение
мощности. Это объясняется меньшей
точностью определения энтальпии по
диаграмме h,
s
по сравнению с таблицами.

Из
расчета
следует,
что
степень
сухости
пара на выходе
из
турбины
равна
84%, то есть
его
влажность
составляет
16%. Из
опыта
эксплуатации
ПТУ известно,
что
влажность
пара не должна
превышать
14% во
избежание
механического
разрушения
лопаток последних
ступеней
турбины
(эрозии).
Для исключения
этого
вводят
промежуточный
перегрев
пара, рассматриваемый
в следующей
задаче .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Просмотров 1.1к. Опубликовано 19.01.2023

Работа паротурбинной установки (ПТУ), как и любого другого теплового двигателя, основана на преобразовании энергии в соответствии с тепловым циклом. По циклу Ренкина работают паросиловые установки (ПСУ). В статье рассмотрена схема паросиловой установки, из каких процессов состоит цикл Ренкина в ts и hs диаграммах и их разновидности.

Схема паросиловой установки, работающей по циклу Ренкина

Простейшая схема паросиловой установки, работающей по циклу Ренкина, изображена на рисунке ниже.

Схема состоит из:

Парового котла (на ТЭС) или парогенератора (на АЭС), предназначенного для подогрева, испарения воды и перегрева пара. Котел состоит из трёх компонентов:

Экономайзер ЭК – для подогрева воды;
Парогенератор ПГ – для испарения воды;
Пароперегреватель ПП – для перегрева пара выше температуры насыщения (кипения).

Важно заметить:

На ТЭС используется пар в перегретом относительно температуры насыщения состоянии.

На АЭС используется насыщенный водяной пар.

Паровая турбина Т – предназначена для получения полезной работы в цикле за счет расширения пара на лопатках.

Паровая турбина ПТ-60-130/13 (внешний вид):
1 – Цилиндр высокого давления (ЦВД); 2 – Цилиндр низкого давления (ЦНД); 3 – механизм управления турбиной; 4 – регулирующие клапаны

Конденсатор К – служит для преобразования отработавшего в турбине пара обратно в жидкое состояние – воду.

Конденсатор паровой турбины

Питательный насос ПН – повышает давление воды, затрачивая работу. Испарение воды с повышенным давлением позволяет получить водяной пар высокой работоспособности.

Питательный насос

Из каких процессов состоит цикл Ренкина

Упрощенная тепловая схема паросиловой установки и цикл Ренкина:
ПГ – парогенератор; ПП – пароперегреватель; Т – турбина; ЭГ – электрогенератор;
К – конденсатор; ПН – питательный насос; ЭК – экономайзер

Цикл Ренкина состоит из следующих процессов:

Адиабатный процесс расширения пара в паровой турбине Т (процесс e-f). Как видно из t-s диаграммы, адиабатный процесс протекает без увеличения энтропии s, это означает, что данный процесс идеальный, без теплообмена с окружающей средой. Рабочее тело в точке f находится в состоянии влажного насыщенного пара, о чем свидетельствует ее расположение ниже кривой насыщения x=1.
Процесс конденсации водяного пара в конденсаторе К (процесс f-а′). Данный процесс представляет собой изотермический процесс отвода теплоты конденсации q₂отработавшего водяного пара в окружающую среду. Количество отведенной теплоты равняется площади фигуры 1a′f2. Заканчивается процесс в точке а′, расположенной на кривой насыщения х=0 (жидкость в состоянии насыщения).
Процесс сжатия (подъема давления) воды в питательном насосе ПН котла. Данный процесс а′-а адиабатный. На подъем давления воды затрачивается работа L_н.
Процесс нагрева питательной воды а-b в экономайзере парогенератора ЭК до состояния насыщения.
Изотермический процесс b-c испарения котловой воды в экранных трубах парогенератора ПГ (котла). В результате данного процесса не происходит изменения температуры рабочего тела, а лишь осуществляется подвод теплоты на преобразование воды в пар. При этом, количество затрачиваемой теплоты будет зависеть от давления в ПГ. Заканчивается процесс в точке с, расположенной на кривой насыщения х=1, где рабочее тело находится в состоянии сухого насыщенного пара.
Процесс перегрева водяного пара c-e относительно температуры насыщения. Данный процесс протекает при постоянном давлении в пароперегревателе ПП парогенератора.

Термический КПД цикла Ренкина

Теплота подводится в течение процессов abce. Количество теплоты, подведённое в цикле:

где h_e,h₀– энтальпия пара в точке e, или энтальпия свежего (острого) пара, кДж/кг;

h_a,h_пв – энтальпия воды в точке а процесса, или энтальпия питательной воды, кДж/кг.

Отвод теплоты осуществляется в процессе f-а′. Количество отводимой теплоты определяется по формуле:

где h_f,h_a_’ – энтальпия пара в точке е, или энтальпия отработавшего в турбине пара, кДж/кг;

h“_к,h”_к – энтальпия воды в точке а, или энтальпия основного конденсата на выходе из конденсатора, кДж/кг.

Полезная теоретическая работа определяется как разность подведенного и отведенного количества теплоты:

При этом:

L_т=h₀-h”_к– работа пара в турбине;

L_пн=h_пв–h’_к – работа на повышение давления воды в питательном насосе.

Энергетическая эффективность цикла оценивается его термическим КПД:

формула расчета термического кпд цикла ренкина

Силовым агрегатом в данной схеме является паровая турбина.

Паровая турбина – это двигатель, в котором происходит преобразование потенциальной энергии пара в механическую работу вращающегося ротора. Это работа по преодолению силы сопротивления приводимой машины, в случае паровых турбин ТЭС и АЭС – электрогенератора.

Чертеж паровой турбины

Цикл Ренкина в ts диаграмме

Наиболее частое представление термодинамических циклов реализовано в ts координатах. Циклы, в этих координатах, удобны для понимания процессов и их анализа. Например, цикл Карно, состоящий из двух адиабат и двух изотерм, выглядит в ts диаграмме в виде прямоугольника.

Цикл Ренкина в ts диаграмме показан на рисунке ниже.

Цикл Ренкина в hs диаграмме

Второй вариант представления термодинамических циклов – изображение в hs координатах.

Цикл Ренкина в hs диаграмме

h – энтальпия, кДж/кг

s – энтропия, кДж/(кг*К)

t – температура, °С

На практике в hs диаграмме изображают не весь цикл Ренкина, а только его одну часть. Наиболее важным и интересным в представлении в hs координатах является процесс расширения пара, протекающий в паровой турбине ТЭС и АЭС.

Процесс расширения пара в hs диаграмме

Процесс расширения пара в hs диаграмме дает полное представление о процессе, его энергетической эффективности и состоянии рабочего тела в любой точке.

Разновидности цикла Ренкина

Выше были рассмотрен классический цикл Ренкина на перегретом водяном паре и входящие в него процессы. Однако, в современных тепловых и атомных электростанциях цикл Ренкина применяется с некоторыми изменениями, такими как:

Промежуточный перегрев
Сверхкритические параметры пара
Регенерация
Комбинация с циклом Брайтона для газотурбинных установок

С промежуточным перегревом пара

Схема паротурбинной установки с промежуточным перегревом пара
1 – питательный насос; 2 – котел; 3 – пароперегреватель; 4 – ЦВД; 5 – промежуточный пароперегреватель; 6 – ЦНД; 7 – конденсатор

Увеличить термический КПД цикла возможно с помощью промежуточного перегрева пара. Перегретый пар после котла поступает в цилиндр высокого давления (ЦВД) паровой турбины. В нем пар расширяется и совершает работу. После ЦВД основная часть пара направляется в промежуточный пароперегреватель парового котла. В промежуточном пароперегревателе водяной пар снова перегревается до высокой температуры. Затем, вторично перегретый пар направляется снова в турбину в цилиндр среднего и низкого давления (ЦСД и ЦНД).

Цикл Ренкина с промежуточным перегревом пара

Кроме повышения КПД цикла, промежуточный перегрев позволяет уменьшить влажность пара, то есть долю капелек воды, в конце процесса расширения на последних ступенях паровой турбины. Это повышает экономичность и надежность электростанции.

На сверхкритических параметрах пара

Следующим способом повышения мощности и КПД паросиловой установки является переход на сверхкритические параметры пара. Давление воды в питательном насосе увеличивают, превышая критическое для воды 22,064 МПа, 221,15 бар, 217,75 атм. Испарение воды при таком давлении протекает без изотермического процесса кипения. Вода превращается в пар минуя процесс кипения в прямоточных котлах сверхкритического давления. Цикл Ренкина на сверхкритических параметрах с промежуточным перегревом пара выглядит следующим образом.

Читайте также: Тепловой насос: виды, схема и принцип работы

С регенерацией

Тепловая схема и процесс расширения пара турбоустановки с регенерацией теплоты:
ПГ – парогенератор; Т – турбина; ЭГ – электрогенератор; К – конденсатор;
ПН – питательный насос

Следующий способ повышения КПД паросиловой установки заключается в применении регенерации – нагрева питательной воды за счет частичного использования тепла пара из турбины. Термический КПД повышается вследствие двух причин:

Увеличивается средняя температура подвода тепла
Уменьшается доля теплоты отводимая в окружающую среду в конденсаторе

Цикл Брайтона-Ренкина

Цикл Ренкина паросиловой установки: состав, диаграмма, термический КПД

К – компрессор; КС – камера сгорания; ГТ – газовая турбина; КУ – котел утилизатор; ПТ – паровая турбина; КН – конденсатор; ЭГ – электрогенератор; Н – насос.

Одним из недостатков классического цикла Ренкина является относительно низкая температура подвода тепла. В современных паросиловых установках она достигает 650°С. Повысить среднюю температуру подвода тепла и термический КПД можно путем дополнения циклом Брайтона для газотурбинных установок. В цикле Брайтона температура подвода тепла достигает 1000-1100°С. В итоге образуется комбинированный цикл Брайтона-Ренкина. Основные процессы:

1-2 – сжатие воздуха в компрессоре;
2-3 – подвод тепла к рабочему телу (сжигание газа в камере сгорания);
3-4 – расширение газов в газовой турбине, совершение работы;
4-5 – охлаждение газов в котле утилизаторе.

Последние научные разработки в области термодинамических циклов посвящены Органическому циклу Ренкина

Источник

From Wikipedia, the free encyclopedia

The Rankine cycle is an idealized thermodynamic cycle describing the process by which certain heat engines, such as steam turbines or reciprocating steam engines, allow mechanical work to be extracted from a fluid as it moves between a heat source and heat sink. The Rankine cycle is named after William John Macquorn Rankine, a Scottish polymath professor at Glasgow University.

Heat energy is supplied to the system via a boiler where the working fluid (typically water) is converted to a high pressure gaseous state (steam) in order to turn a turbine. After passing over the turbine the fluid is allowed to condense back into a liquid state as waste heat energy is rejected before being returned to boiler, completing the cycle. Friction losses throughout the system are often neglected for the purpose of simplifying calculations as such losses are usually much less significant than thermodynamic losses, especially in larger systems.

Description[edit]

The Rankine cycle closely describes the process by which steam engines commonly found in thermal power generation plants harness the thermal energy of a fuel or other heat source to generate electricity. Possible heat sources include combustion of fossil fuels such as coal, natural gas, and oil, use of mined resources for nuclear fission, renewable fuels like biomass and ethanol, or energy capture of natural sources such as concentrated solar power and geothermal energy. Common heat sinks include ambient air above or around a facility and bodies of water such as rivers, ponds, and oceans.

The ability of a Rankine engine to harness energy depends on the relative temperature difference between the heat source and heat sink. The greater the differential, the more mechanical power can be efficiently extracted out of heat energy, as per Carnot’s theorem.

The efficiency of the Rankine cycle is limited by the high heat of vaporization of the working fluid. Unless the pressure and temperature reach super critical levels in the boiler, the temperature range that the cycle can operate over is quite small: Steam turbine entry temperatures are typically around 565 °C and condenser temperatures are around 30 °C.^{[citation needed]} This gives a theoretical maximum Carnot efficiency for the turbine alone of about 63.8% compared with an actual overall thermal efficiency of less than 50% for typical power stations. This low steam turbine entry temperature (compared to a gas turbine) is why the Rankine (steam) cycle is often used as a bottoming cycle to recover otherwise rejected heat in combined-cycle gas turbine power stations.

Rankine engines generally operate in a closed loop where the working fluid is reused. The water vapor with condensed droplets often seen billowing from power stations is created by the cooling systems (not directly from the closed-loop Rankine power cycle). This ‘exhaust’ heat is represented by the «Q_out» flowing out of the lower side of the cycle shown in the T–s diagram below. Cooling towers operate as large heat exchangers by absorbing the latent heat of vaporization of the working fluid and simultaneously evaporating cooling water to the atmosphere.

While many substances can be used as the working fluid, water is usually chosen for its simple chemistry, relative abundance, low cost, and thermodynamic properties. By condensing the working steam vapor to a liquid the pressure at the turbine outlet is lowered and the energy required by the feed pump consumes only 1% to 3% of the turbine output power and these factors contribute to a higher efficiency for the cycle. The benefit of this is offset by the low temperatures of steam admitted to the turbine(s). Gas turbines, for instance, have turbine entry temperatures approaching 1500 °C. However, the thermal efficiency of actual large steam power stations and large modern gas turbine stations are similar.

The four processes in the Rankine cycle[edit]

T–s diagram of a typical Rankine cycle operating between pressures of 0.06 bar and 50 bar. Left from the bell-shaped curve is liquid, right from it is gas, and under it is saturated liquid–vapour equilibrium.

There are four processes in the Rankine cycle. The states are identified by numbers (in brown) in the T–s diagram.

Process 1–2: The working fluid is pumped from low to high pressure. As the fluid is a liquid at this stage, the pump requires little input energy. Process 1-2 is isentropic compression.
Process 2–3: The high-pressure liquid enters a boiler, where it is heated at constant pressure by an external heat source to become a dry saturated vapour. The input energy required can be easily calculated graphically, using an enthalpy–entropy chart (h–s chart, or Mollier diagram), or numerically, using steam tables or software. Process 2-3 is constant pressure heat addition in boiler.
Process 3–4: The dry saturated vapour expands through a turbine, generating power. This decreases the temperature and pressure of the vapour, and some condensation may occur. The output in this process can be easily calculated using the chart or tables noted above. Process 3-4 is isentropic expansion.
Process 4–1: The wet vapour then enters a condenser, where it is condensed at a constant pressure to become a saturated liquid. Process 4-1 is constant pressure heat rejection in condenser.

In an ideal Rankine cycle the pump and turbine would be isentropic, i.e., the pump and turbine would generate no entropy and hence maximize the net work output. Processes 1–2 and 3–4 would be represented by vertical lines on the T–s diagram and more closely resemble that of the Carnot cycle. The Rankine cycle shown here prevents the state of the working fluid from ending up in the superheated vapor region after the expansion in the turbine,
^[1] which reduces the energy removed by the condensers.

The actual vapor power cycle differs from the ideal Rankine cycle because of irreversibilities in the inherent components caused by fluid friction and heat loss to the surroundings; fluid friction causes pressure drops in the boiler, the condenser, and the piping between the components, and as a result the steam leaves the boiler at a lower pressure; heat loss reduces the net work output, thus heat addition to the steam in the boiler is required to maintain the same level of net work output.

Variables[edit]

	Heat flow rate to or from the system (energy per unit time)
	Mass flow rate (mass per unit time)
	Mechanical power consumed by or provided to the system (energy per unit time)
${displaystyle eta _{text{therm}}}$	Thermodynamic efficiency of the process (net power output per heat input, dimensionless)
${displaystyle eta _{text{pump}},eta _{text{turb}}}$	Isentropic efficiency of the compression (feed pump) and expansion (turbine) processes, dimensionless
	The «specific enthalpies» at indicated points on the T–s diagram
$h_{4s}$	The final «specific enthalpy» of the fluid if the turbine were isentropic
	The pressures before and after the compression process

Equations[edit]

In general, the efficiency of a simple rankine cycle can be written as

${displaystyle eta _{text{therm}}={frac {{dot {W}}_{text{thermal}}-{dot {W}}}{{dot {Q}}_{text{in}}}}approx {frac {{dot {W}}_{text{turb}}}{{dot {Q}}_{text{in}}}}.}$

Each of the next four equations^[1] is derived from the energy and mass balance for a control volume. ${displaystyle eta _{text{therm}}}$ defines the thermodynamic efficiency of the cycle as the ratio of net power output to heat input. As the work required by the pump is often around 1% of the turbine work output, it can be simplified.

${displaystyle {frac {{dot {Q}}_{text{in}}}{dot {m}}}=h_{3}-h_{2},}$

${displaystyle {frac {{dot {Q}}_{text{out}}}{dot {m}}}=h_{4}-h_{1},}$

${displaystyle {frac {{dot {W}}_{text{pump}}}{dot {m}}}=h_{2}-h_{1},}$

${displaystyle {frac {{dot {W}}_{text{turbine}}}{dot {m}}}=h_{3}-h_{4}.}$

When dealing with the efficiencies of the turbines and pumps, an adjustment to the work terms must be made:

${displaystyle {frac {{dot {W}}_{text{pump}}}{dot {m}}}=h_{2}-h_{1}approx {frac {v_{1}Delta p}{eta _{text{pump}}}}={frac {v_{1}(p_{2}-p_{1})}{eta _{text{pump}}}},}$

${displaystyle {frac {{dot {W}}_{text{turbine}}}{dot {m}}}=h_{3}-h_{4}approx (h_{3}-h_{4})eta _{text{turbine}}.}$

Real Rankine cycle (non-ideal)[edit]

Rankine cycle with superheat

In a real power-plant cycle (the name «Rankine» cycle is used only for the ideal cycle), the compression by the pump and the expansion in the turbine are not isentropic. In other words, these processes are non-reversible, and entropy is increased during the two processes. This somewhat increases the power required by the pump and decreases the power generated by the turbine.^[1]

In particular, the efficiency of the steam turbine will be limited by water-droplet formation. As the water condenses, water droplets hit the turbine blades at high speed, causing pitting and erosion, gradually decreasing the life of turbine blades and efficiency of the turbine. The easiest way to overcome this problem is by superheating the steam. On the T–s diagram above, state 3 is at a border of the two-phase region of steam and water, so after expansion the steam will be very wet. By superheating, state 3 will move to the right (and up) in the diagram and hence produce a drier steam after expansion.

Variations of the basic Rankine cycle[edit]

The overall thermodynamic efficiency can be increased by raising the average heat input temperature

${displaystyle {bar {T}}_{text{in}}={frac {int _{2}^{3}T,dQ}{Q_{text{in}}}}}$

of that cycle. Increasing the temperature of the steam into the superheat region is a simple way of doing this. There are also variations of the basic Rankine cycle designed to raise the thermal efficiency of the cycle in this way; two of these are described below.

Rankine cycle with reheat[edit]

Rankine cycle with reheat

The purpose of a reheating cycle is to remove the moisture carried by the steam at the final stages of the expansion process. In this variation, two turbines work in series. The first accepts vapor from the boiler at high pressure. After the vapor has passed through the first turbine, it re-enters the boiler and is reheated before passing through a second, lower-pressure, turbine. The reheat temperatures are very close or equal to the inlet temperatures, whereas the optimal reheat pressure needed is only one fourth of the original boiler pressure. Among other advantages, this prevents the vapor from condensing during its expansion and thereby reducing the damage in the turbine blades, and improves the efficiency of the cycle, because more of the heat flow into the cycle occurs at higher temperature. The reheat cycle was first introduced in the 1920s, but was not operational for long due to technical difficulties. In the 1940s, it was reintroduced with the increasing manufacture of high-pressure boilers, and eventually double reheating was introduced in the 1950s. The idea behind double reheating is to increase the average temperature. It was observed that more than two stages of reheating are generally unnecessary, since the next stage increases the cycle efficiency only half as much as the preceding stage. Today, double reheating is commonly used in power plants that operate under supercritical pressure.

Regenerative Rankine cycle[edit]

Regenerative Rankine cycle

The regenerative Rankine cycle is so named because after emerging from the condenser (possibly as a subcooled liquid) the working fluid is heated by steam tapped from the hot portion of the cycle. On the diagram shown, the fluid at 2 is mixed with the fluid at 4 (both at the same pressure) to end up with the saturated liquid at 7. This is called «direct-contact heating». The Regenerative Rankine cycle (with minor variants) is commonly used in real power stations.

Another variation sends bleed steam from between turbine stages to feedwater heaters to preheat the water on its way from the condenser to the boiler. These heaters do not mix the input steam and condensate, function as an ordinary tubular heat exchanger, and are named «closed feedwater heaters».

Regeneration increases the cycle heat input temperature by eliminating the addition of heat from the boiler/fuel source at the relatively low feedwater temperatures that would exist without regenerative feedwater heating. This improves the efficiency of the cycle, as more of the heat flow into the cycle occurs at higher temperature.

Organic Rankine cycle[edit]

The organic Rankine cycle (ORC) uses an organic fluid such as n-pentane^[2] or toluene^[3] in place of water and steam. This allows use of lower-temperature heat sources, such as solar ponds, which typically operate at around 70 –90 °C.^[4] The efficiency of the cycle is much lower as a result of the lower temperature range, but this can be worthwhile because of the lower cost involved in gathering heat at this lower temperature. Alternatively, fluids can be used that have boiling points above water, and this may have thermodynamic benefits (See, for example, mercury vapour turbine). The properties of the actual working fluid have great influence on the quality of steam (vapour) after the expansion step, influencing the design of the whole cycle.

The Rankine cycle does not restrict the working fluid in its definition, so the name «organic cycle» is simply a marketing concept and the cycle should not be regarded as a separate thermodynamic cycle.

Supercritical Rankine cycle[edit]

The Rankine cycle applied using a supercritical fluid^[5] combines the concepts of heat regeneration and supercritical Rankine cycle into a unified process called the regenerative supercritical cycle (RGSC). It is optimised for temperature sources 125–450 °C.

References[edit]

^ Guruge, Amila Ruwan (2021-02-16). «Rankine Cycle». Chemical and Process Engineering. Retrieved 2023-02-15.
^ Canada, Scott; G. Cohen; R. Cable; D. Brosseau; H. Price (2004-10-25). «Parabolic Trough Organic Rankine Cycle Solar Power Plant» (PDF). 2004 DOE Solar Energy Technologies. Denver, Colorado: US Department of Energy NREL. Archived from the original (PDF) on 2009-03-18. Retrieved 2009-03-17.
^ Batton, Bill (2000-06-18). «Organic Rankine Cycle Engines for Solar Power» (PDF). Solar 2000 conference. Barber-Nichols, Inc. Archived from the original (PDF) on 2009-03-18. Retrieved 2009-03-18.
^ Nielsen et al., 2005, Proc. Int. Solar Energy Soc.
^ Moghtaderi, Behdad (2009). «An Overview of GRANEX Technology for Geothermal Power Generation and Waste Heat Recovery». Australian Geothermal Energy Conference 2009. Inc.

^Van Wyllen ‘Fundamentals of thermodynamics’ (ISBN 85-212-0327-6)
^Wong ‘Thermodynamics for Engineers’,2nd Ed.,2012, CRC Press, Taylor & Francis, Boca Raton, London, New York. (ISBN 978-1-4398-4559-2)
Moran & Shapiro ‘Fundamentals of Engineering Thermodynamics’ (ISBN 0-471-27471-2)
Wikibooks Engineering Thermodynamics

Источник

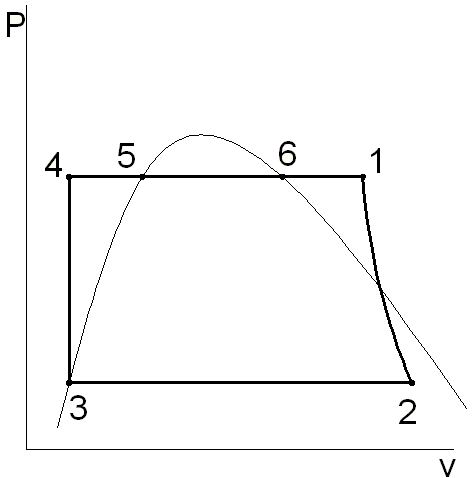
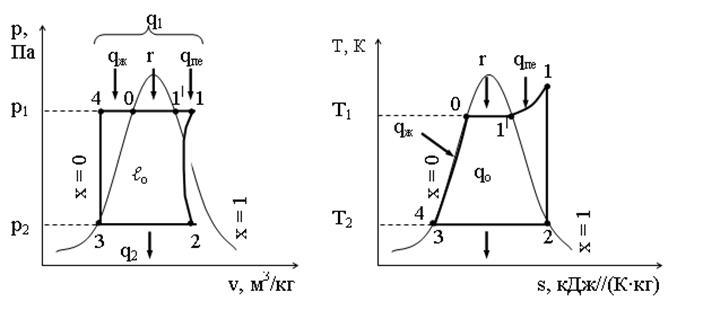
2 цикл Ренкина в pv и Ts координатах

Рисунок 2 – Цикл Ренкина в pv — и Ts-координатах

· т. 4 – состояние воды при выходе из насоса 6 и входе в котел 1 при 0 °С и х = 0; степень сухости пара «х» (паросодержание) – отношение массы сухого насыщенного пара к массе смеси (воды и пара), кг;

· 4-0 – процесс изобарного подвода теплоты qж в котел 1 для нагрева воды от 0 °С до tк °С;

· т. 0 – состояние воды при tк °С;

· 0-1| – процесс изобарного и одновременно изотермического парообразования в котле 1 от х = 0 до х = 1 за счет скрытой удельной теплоты парообразования r – это количество теплоты, необходимое для перевода при р = const 1 кг жидкости (воды), нагретой до tнас в сухой насыщенный пар;

· т. 1| – состояние пара при выходе из котла 1 и входе в пароперегреватель 2;

· 1|-1 – процесс изобарного перегрева пара в пароперегревателе 2 с подводом теплоты qпе;

· т. 1 – состояние пара при выходе из пароперегревателя 2 и входе в паровую турбину 3;

· 1-2 – процесс адиабатного расширения пара в паровой турбине 3 с изменением давления от р1 до р2;

· т. 2 – состояние пара при выходе из паровой турбины 3 и входе в конденсатор 5;

· 2-3 – процесс изобарной конденсации пара в конденсаторе 5 с отводом теплоты q2 и изменением состояния рабочего пара от х = 1 до х = 0;

· т. 3 – состояние конденсата при выходе из конденсатора 5 и входе в насос 6;

· 3-4 – процесс изотермического нагнетания воды в котел 1 насосом 6 с повышением давления от р3 до р4.

3 расчет

3.1 термический КПД цикла Ренкина ηt

термический КПД цикла можно определить, как в любом цикле:

(1)

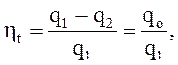
где q1, q2 – подведенная и отведенная удельная теплота в цикле, кДж/кг;

qo – удельная теплота цикла.

q1 = cp(t1 – t4) = i1 – i4; q2 = cp(t2 – t3) = i2 – i3.

Тогда термический КПД ηt цикла можно определить как:

(2)

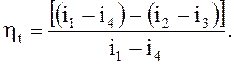
Если не учитывать ничтожного малого повышения температуры при адиабатном сжатии воды в насосе, то i3 = i4, а i3 – удельная энтальпия воды, кДж/кг, = срtводы, где ср – удельная теплота воды при постоянном давлении, кДж/(кг·К), ср = 4,19, тогда (3)

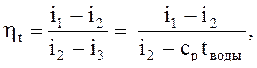
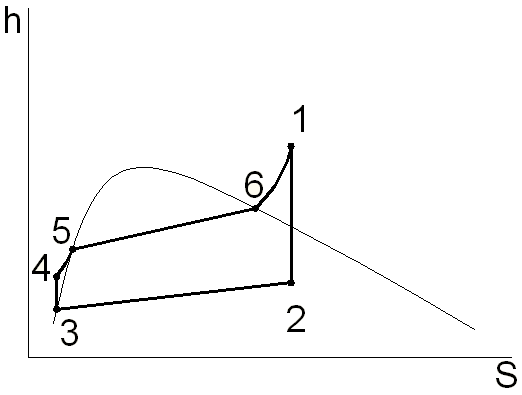
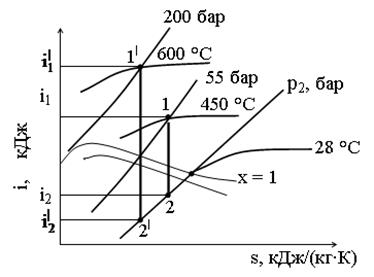
Значения энтальпий i1, i2 и температуру воды tводы (конденсата) находим по диаграмме is(sh), алгоритм нахождения приведен на рисунке 3.

i1 = 3 280 кдж/кг; i2 = 2 290 кДж/кг; t2 = 28 °С;

i2| = 4,19·28 = 117,32 кДж/кг.

i1| = 3 550 кдж/кг; i2| = 2 200 кДж/кг; t2 = 28 °С; i3 = 4,19×28 = 117,32 кДж/кг.

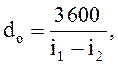
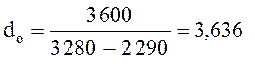
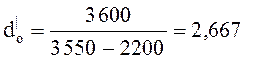
3.2 удельный расход пара dо кг/(кВт-ч), идущего на выработку 1 кВт-ч энергии, (4)

кг/ кВт·ч.

кг/кВт·ч;

3.3 удельный расход пара d0 идущего на выработку единицы выполненной работы, кг /МДж,

(5)

кг/МДж.

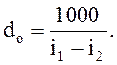
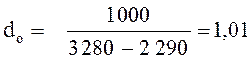
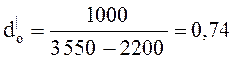
4 выкопировка из s—i (h) диаграммы расчетных процессов расширения пара в паровой турбине

Рисунок 3 – Определение энтальпии пара в процессах цикла Ренкина по диаграмме в is

5 вывод о влиянии повышенных начальных параметров пара при поступлении в турбину

с повышением начальных параметров пара:

1) термический КПД цикла увеличивается;

2) количество пара dо, кг, уменьшается, идущего на выработку 1 кВт-ч энергии или на совершение 1 МДж работы;

3) идеальный цикл Ренкина в паросиловой установке по сравнению с идеальным циклом Карно:

· делает установку компактнее, так как насос по размерам значительно меньше компрессора;

· делает установку экономичнее, так как мощность насоса во много раз меньше мощности компрессора.

Задача № 5

цикл воздушно-компрессорной холодильной установки

Исходные параметры воздуха установки принять по таблице 1.

Таблица 1 – исходные данные для расчета цикла

№ п/п в жур-нале	р1, мПа	р2, мПа	t1, ° C	t3, ° C	Q2, кВт	№ п/п в жур-нале	р1, мПа	р2, мПа	t1, ° C	t3, ° C	Q2, кВт
1	0,1	0,4	– 10	17	100	16	0,1	0,5	– 10	18	160
2	0,1	0,4	– 12	16	110	17	0,1	0,5	– 9	20	150
3	0,1	0,4	– 14	20	120	18	0,1	0,5	– 8	21	140
4	0,1	0,4	– 8	22	130	19	0,1	0,5	– 7	22	130
5	0,1	0,4	– 6	25	140	20	0,1	0,5	– 6	23	120
6	0,1	0,4	– 4	19	150	21	0,1	0,5	– 5	24	110
7	0,1	0,4	– 2	18	160	22	0,1	0,5	– 4	25	100
8	0,1	0,4	– 5	23	170	23	0,1	0,5	– 2	15	90
9	0,1	0,4	– 7	15	180	24	0,1	0,7	– 3	19	100
10	0,1	0,4	– 9	26	190	25	0,1	0,7	– 4	20	100
11	0,1	0,6	– 10	27	200	26	0,1	0,7	– 5	21	110
12	0,1	0,6	– 12	25	180	27	0,1	0,7	– 6	22	120
13	0,1	0,6	– 14	23	160	28	0,1	0,7	– 7	23	130
14	0,1	0,6	– 15	20	150	29	0,1	0,7	– 8	24	140
15	0,1	0,6	– 13	18	140	30	0,1	0,7	– 10	20	150

1. Вычертить принципиальную схему воздушно-компрессорной установки, обозначить позициями ее основные элементы и записать их наименование.

2. рассчитать идеальной цикл воздушно-компрессорной холодильной установки.

2.1. определить неизвестные параметры в узловых точках цикла.

2.2. Определить изменение удельной энтропии ∆s, кдж/(кг·K).

2.3. определить удельную тепловую мощность теплообменника 3 q1, кДж/кг.

2.4. Определить удельную производительность холода холодильной камеры q2, кДж/кг,

2.5. определить расход воздуха М, кг/с.

2.6. определить удельную теоретическую потребляемую мощность (теплоту цикла) qо (кДж/кг) и полную мощность Qо (кВт).

2.7. определить холодильный коэффициент ε.

3. Вычертить цикл установки в pv и Ts-координатах по данным расчета, обозначить узловые точки цикла.

4. ответить на контрольные вопросы:

· что такое холодильный коэффициент?

· за счет чего работают компрессорные холодильные установки?

· чем определяется работа, затраченная на осуществление цикла в данной холодильной установке?

общие теоретические положения

процесс, в течение которого газ, претерпевает ряд изменений своего состояния и вновь возвращается в исходное состояние, называется круговым процессом или циклом.

Холодильные установки предназначены для искусственного охлаждения тел ниже температуры окружающей среды. Рабочее тело в холодильных установках совершает обратный круговой процесс, в котором затрачиваемая внешняя работа расходуется на отъем тепла от охлаждаемого тела. В воздушно-компрессорной холодильной установке рабочим телом является воздух.

Для получения низких температур (производства холода) в данном типе установки используют адиабатное расширение воздуха. Для этого его предварительно сжимают в компрессоре 1, а затем, так как при сжатии температура его повышается, охлаждают до температуры, например, окружающей среды в теплообменнике 2.

Если такой воздух заставить расширятся в расширительном сосуде 3 по адиабате, то он совершит работу за счет своей энергии, при этом его температура понизится и окажется ниже температуры окружающей среды. Охлажденный воздух поступает в холодильную камеру (охлаждаемое помещение) 4, отнимая теплоту от охлаждаемых тел, нагревается и вновь поступает в компрессор 1.

Схема воздушно-компрессорной холодильной установки представлена на рисунке 1.

Установка состоит из следующих элементов:

· компрессора 1, всасывающего воздух и сжимающий его;

· охладителя (теплообменника) 2, в котором охлаждается сжатый воздух водой;

· расширительного цилиндра 3, в котором воздух расширяется, совершая при этом работу и понижая свою температуру;

· холодильной камеры 4, в которой по трубопроводам циркулирует охлажденный воздух, отнимая теплоту от охлаждаемых тел, нагревается и вновь поступает в компрессор 1.

1 – компрессор; 2 – охладитель воздуха (теплообменник);

3 – расширительный цилиндр (детандер);

4 – холодильная камера

Рисунок 1 – Принципиальная схема воздушно-компрессорной

холодильной установки

Рисунок 2 – Теоретический цикл холодильной установки в координатах pv и Ts

На рисунке 2 (теоретический цикл воздушно компрессорной установки в pv и Тs координатах):

· точка 1 – состояние воздуха, поступающего в компрессор;

· линия 1-2 – адиабатный процесс сжатия в компрессоре;

· точка 2 – состояние воздуха, поступающего в охладитель (теплообменник);

· 2 -3 – изобарное охлаждение в теплообменнике;

· точка 3 – состояние воздуха, поступающего в расширительный цилиндр;

· 3 — 4 – адиабатный процесс расширения в расширительном цилиндре;

· точка 4 – состояние воздуха, поступающего в холодильную камеру;

· линия 4-1 –изобарное нагревание воздуха в холодильной камере;

· площадь 1-2-3-6-5- 4-1 – работа, затраченная компрессором на сжатие;

· площадь 3-6-5-4-3 – работа, полученная в расширительном цилиндре;

· площадь 1-2-3-4 – работа цикла.

На диаграмме в координатах Ts:

· площадь под кривой 4-1 – количество теплоты q2, переданной охлаждаемыми телами (пл. 1-4-6-5-1) воздуху в холодильной камере;

· площадь под кривой 3-2 – количество теплоты q1, отданной в охладителе (пл. 2-3-6-5-2) от воздуха воде;

· площадь 1-2- 3-4-1 – удельная теплота цикла qо1.

удельная производительность холода холодильной камеры 4 q2, кДж/кг.

q2 = cp m(T1 – T4), (1)

где T1 – температура воздуха, К, выходящего из холодильной камеры 4 и поступающего в компрессор 1;

T4 – температура воздуха, К, входящего в холодильную камеру 4;

cpm – удельная средняя теплоемкость воздуха при постоянном давлении, Дж/(кг·К).

удельная тепловая мощность теплообменника 2 q1, кДж/кг.

(2)

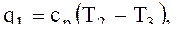
где T2 – температура воздуха, K, входящего в теплообменник 2;

T3 – температура воздуха, K, входящего расширитель 3.

Удельная работа ℓк, Дж/кг, затраченная на привод компрессора 1:

ℓк = cp m(T1 – T2). (3.а)

(3.б)

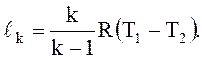
Удельная работа ℓр ц, Дж/кг, полученная в расширительном цилиндре 3:

ℓр. ц = cp m(T3 – T4). (4.а)

(4.б)

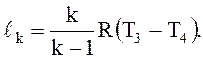
Удельная работа ℓо, Дж/кг, затраченная в цикле:

ℓо = ℓк – ℓр. ц. (5)

Расход холодильного агента (воздуха) М, кг/с,

(6)

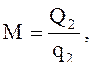
где Q2, q2 – соответственно холодопроизводительность установки, кДж, и удельная холодопроизводительность, кДж/кг.

Холодильный коэффициент:

(7.а)

(7.б)

(7.в)

(7.с)

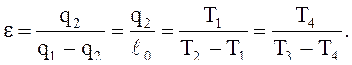
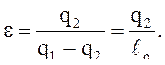
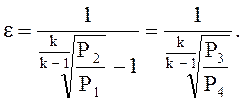
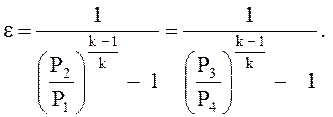
Пример расчета

Дано: р1 = 0,1 мПа; р2 = 0,7 мПа;

t1 = – 10 °C; T1 = 263 K; t3 = 20 ° C;

T3 = 293 K; Q2 (Qх) = 150 кВт.

решение

1 – компрессор; 2 – теплообменник (охладитель);

3 – расширительный цилиндр; 4 – холодильная камера

Рисунок 1 – Принципиальная схема воздушно-компрессорной холодильной установки

2 Расчет идеального цикла

2.1 определение неизвестных параметров в узловых точках цикла

точка 1: р1 = 0,1 МПа; Т1 = 263 K.

удельный объем v1 определим из уравнения состояния:

p1v1 = RT1, (1)

где р1 – давление в начале сжатия, Па; v1 – дельный объем в начале сжатия, м3/кг; R – газовая постоянная воздуха, Дж/(кг·К), R = 287; Т1 – температура в начале сжатия, К.

уравнение (1) выразим относительно удельного объема v1.

.

м3/кг;

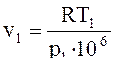
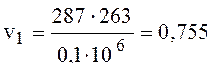
давление: р1 = 0,1 мПа. температура: Т1 = 263 K.

точка 2: р2 = 0,7 мПа; процесс 1-2 – адиабатное сжатие.

Уравнение адиабатного процесса: p1v1к = p2 v2к. (2)

где к – коэффициент адиабаты, к = 1,4.

удельный объем v2, м3/кг, определим из уравнения (2):

температуру Т2, К, определим из формулы (1) относительно точки 2.

точка 3: р3 = р2 = 0,7 мПа, так как процесс 2-3 – изобарное охлаждение в теплообменнике; температура: T3 = 293 K.

удельный объем v3, м3/кг, определим по формуле (1) относительно точки 3.

точка 4: р4 = р1 = 0,1 мПа, так как процесс 4-1 – изобарный нагрев в холодильной камере.

удельный объем v3, м3/кг, определим по формуле (2) относительно точки 4, так как процесс 3-4 – адиабатное расширение в детандере:

.

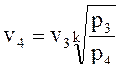
температуру Т4 определим по формуле (1) относительно точки 4:

2.2 Определение изменение удельной энтропии ∆s

Процесс 1-2 – адиабатный, поэтому изменение энтропии ∆s1-2 = 0

Процесс 2-3 – изобарный, поэтому изменение удельной энтропии ∆s, кДж/(кг·К):

∆s2-3 = 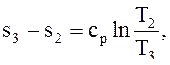(3)

где ср – удельная теплоемкость воздуха при постоянном давлении, кДж/(кг·К), ср = 1,009.

∆s3-2 =

Процесс 3-4 – адиабатный, поэтому изменение удельной энтропии

∆s3-4 = 0.

Процесс 4-1 – изобарный, поэтому изменение удельной энтропии ∆s, кДж/(кг·К), определяем по формуле (3) относительно данного процесса.

∆s4-1 = 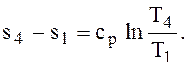(4)

∆s1-4 =

2.3 определение удельной тепловой мощности q1, кДж/кг, теплообменника 2.

(5)

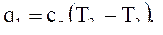
кДж/кг.

2.4 Определение удельной производительности холода холодильной камеры q2, кДж/кг, по формуле (5):

(6)

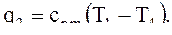
Дж/кг.

2.5 определение расхода воздуха М

(7)

кг/с.

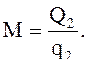
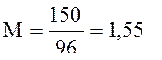
2.6 Определение удельной теплоты qо и теплоты Qо цикла

qo = q2 – q1. (8)

qo = 166,5 – 96 = 70,5 кДж/кг.

. (9)

Qо = 1,55 ×70,5= 109 кВт.

2.7 Определение холодильного коэффициента

(10.а)

(10.б)

(10.в)

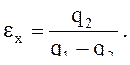
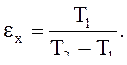
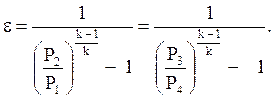
3 цикл установки в координатах pv и Ts

1-2 – адиабатное сжатие в компрессоре; 2-3 – изобарное охлаждение в теплообменнике; 3-4 – адиабатное расширение в детандере;

4-1 – изобарный нагрев в холодильной камере

Рисунок 2 – Цикл холодильной установки в pv и Ts координатах

Задача № 6

рекуперативный теплообменный аппарат типа «Труба в трубе»

Таблица 1 – Исходные данные

Пара-метры

Номер варианта

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

, °С

400

370

450

415

385

460

510

500

480

390

400

370

450

415

385

, °С

165

200

215

250

260

270

280

230

250

225

165

200

215

250

260

, °С

5

5

5

5

5

10

10

10

10

15

15

15

15

15

15

, °С

80

80

80

80

80

140

75

75

75

70

70

65

65

65

65

М1, кг/с

1,5

–

1,8

–

1,5

–

1,8

–

2,0

–

2,0

–

2,4

–

2,4

М2, кг/с

–

4,5

–

4,0

–

3,5

–

3,0

–

2,5

–

2,0

–

1,5

–

α1·10–1

42

42

40

40

38

38

35

35

32

32

30

30

28

28

26

α2·10–2

26

42

28

35

30

30

32

28

35

25

38

20

40

23

27

Распо-ложе-ние труб

Г

Г

В

В

Г

Г

В

В

Г

Г

В

В

Г

Г

В

матер.

С

Л

С

Л

С

Л

С

Л

С

Л

С

Л

С

Л

С

Продолжение таблицы 1

Пара-метры

Номер варианта

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

, °С

400

370

450

415

385

460

510

500

480

390

400

370

450

415

385

, °С

165

200

215

250

260

270

280

230

250

225

165

200

215

250

260

, °С

20

20

20

20

20

25

25

25

25

25

30

30

30

30

30

, °С

60

60

60

60

65

65

65

65

70

70

70

70

75

75

75

М1, кг/с

0,5

–

0,8

–

1,5

–

1,8

–

2,0

–

2,2

–

2,4

–

2,6

М2, кг/с

–

4,5

–

4,0

–

3,5

–

3,0

–

2,5

–

2,0

–

1,5

–

α1·10–1

42

42

40

40

38

38

35

35

32

32

30

30

28

28

26

α2·10–2

26

42

28

35

30

30

32

28

35

25

38

20

40

23

27

Распо-ложе-ние труб

Г

Г

В

В

Г

Г

В

В

Г

Г

В

В

Г

Г

В

матер.

С

Л

С

Л

С

Л

С

Л

С

Л

С

Л

С

Л

С

Греющий теплоноситель – дымовые газы, которые движутся в межтрубном пространстве.

нагреваемый теплоноситель – вода, которая движется по внутренней трубе.

Теплообменник выполнен из металлических труб.

Параметры:

· – начальная температура греющего теплоносителя, ° С;

· конечная температура греющего теплоносителя, ° С;

· – начальная температура нагреваемого теплоносителя, ° С;

· – конечная температура нагреваемого теплоносителя, ° С;

· М1 – расход греющего теплоносителя, кг/с;

· М2 – расход нагреваемого теплоносителя, кг/с;

· α1 – коэффициент теплоотдачи от греющего теплоносителя к поверхности внутренней трубы, Вт/(м2×К);

· α2 – коэффициент теплоотдачи от поверхности внутренней трубы к нагреваемому теплоносителю, Вт/(м2×К);

· d1, d2 – внутренний и наружный диаметр внутренней трубы, м, d1 = 33·10 –3, d2 = 38·10 –3, δ – толщина стенки труб, м, δ = 10 –3(38 – 33)/2 = 2,5·10 – 3 = 0,0025;

· материал труб: сталь – С; латунь – Л;

· расположение труб: горизонтальное – Г; вертикальное – В;

· λ – коэффициент теплопроводности материала стенки труб, Вт/(м×К): сталь – 50; латунь – 100.

Задание

1. определить

(для прямоточной и противоточной схемы движения теплоносителей):

1.1) тепловую мощность Q, Вт, передаваемую от греющего теплоносителя к нагреваемому теплоносителю;

1.2) неизвестный расход М, кг/с, одного из теплоносителей;

1.3) средний температурный напор ∆ tср;

1.4) коэффициент теплоотдачи k, Вт/ (м2×K);

1.5) площадь поверхности нагрева F, м2.

2. Вычертить по результатам расчета графики изменения температуры теплоносителей при прямоточной и противоточной схеме движения теплоносителей и принципиальную схему теплообменника.

3. выводы.

4. ответить на контрольные вопросы:

· какое устройство называется теплообменным аппаратом?

· какие типы теплообменных аппаратов вы знаете?

· схемы движения теплоносителей в теплообменных аппаратах?

· какие уравнения положены в основу теплового расчета теплообменнников?

· какие процессы передачи теплоты происходят в рекуперативном теплообменнике «труба в трубе»?

· в каком случае можно рассчитывать коэффициент теплопередач по формулам полоской пластины?

общие теоретические положения

Устройства, предназначенные для передачи теплоты от одной среды к другой, называют теплообменными аппаратами или теплообменниками.

Среды, участвующие в процессе теплообмена, называют теплоносителями. Теплоносителями могут быть газы, жидкости, пары.

1. По принципу действия и конструктивному исполнению все устройства подразделяются на теплообменники:

· поверхностные;

· контактные (смесительные);

· с внутренним источником теплоты.

Поверхностные теплообменники – устройства, в которых процесс передачи теплоты связан с поверхностью твердого тела, то есть теплообмен от одной среды к другой происходит через разделительную стенку. Они, в свою очередь, разделяются на теплообменники: рекуперативные; регенеративные.

Рекуперативные поверхностные теплообменники – такие устройства, где два теплоносителя с различными температурами текут в пространствах, разделенных твердой стенкой (калориферы, отопительные приборы, конденсаторы, парогенераторы).

Наташа — контент-маркетолог и блогер, но все это не мешает ей оставаться адекватным человеком. Верит во все цвета радуги и не верит в теорию всемирного заговора. Увлекается «нефрохиромантией» и тайно мечтает воссоздать дома Александрийскую библиотеку.

Источник

Физическая структура цикла Ренкина. 1. Насос, 2. Котел, 3. Турбина, 4. Конденсатор

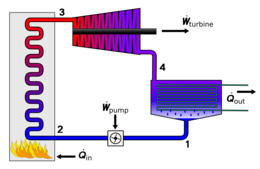
Используемая модель цикла Ренкина для прогнозирования производительности систем паровых турбин. Он также использовался для изучения характеристик поршневых паровых двигателей. Цикл Ренкина представляет собой идеализированный термодинамический цикл теплового двигателя, который преобразует тепло в механическую работу, претерпевая фазовый переход. Это идеализированный цикл, в котором не учитываются потери на трение в каждом из четырех компонентов. Тепло подводится извне к замкнутому контуру, который обычно использует воду в качестве рабочей жидкости. Он назван в честь Уильяма Джона Маккуорна Рэнкина, шотландского эрудита и профессора Университета Глазго.

Содержание

1 Описание
2 Четыре процесса в цикле Ренкина
3 Переменные
4 Уравнения
5 Реальный цикл Ренкина (неидеальный)
6 Варианты основного Цикл Ренкина
- 6.1 Цикл Ренкина с повторным нагревом
- 6.2 Регенеративный цикл Ренкина
7 Органический цикл Ренкина
8 Сверхкритический цикл Ренкина
9 См. Также
10 Ссылки

Описание

Цикл Ренкина подробно описывает процесс, с помощью которого паровые тепловые машины, обычно используемые на тепловых электростанциях, вырабатывают энергию.

Мощность зависит от разницы температур между источником тепла и источником холода. Чем выше разница, тем больше механической энергии может быть эффективно извлечено из тепловой энергии в соответствии с теоремой Карно.

источниками тепла, используемыми на этих электростанциях, обычно ядерным делением или сжигание ископаемого топлива, такого как уголь, природный газ и нефть, или концентрированная солнечная энергия. Чем выше температура, тем лучше.

Эффективность цикла Ренкина ограничена высокой теплотой испарения рабочего тела. Кроме того, если давление и температура в паровом котле не достигают сверхкритических уровней, диапазон температур, в котором может работать цикл, довольно мал: температуры на входе в паровую турбину обычно составляют около 565 ° C, а температуры парового конденсатора около 30 ° С. Это дает теоретический максимум КПД Карно только для паровой турбины около 63,8% по сравнению с фактическим общим тепловым КПД до 42% для современной угольной электростанции. Эта низкая температура на входе в паровую турбину (по сравнению с газовой турбиной ) является причиной того, что цикл Ренкина (паровой) часто используется в качестве нижнего цикла для рекуперации тепла, отбрасываемого иначе в газовой турбине с комбинированным циклом электростанции.

Источником холода (чем холоднее, тем лучше), используемым на этих электростанциях, обычно являются градирни и большой водоем (река или море). Эффективность цикла Ренкина ограничена на холодной стороне более низкой практической температурой рабочего тела.

Рабочая жидкость в цикле Ренкина следует по замкнутому циклу и постоянно используется повторно. Водяной пар со сконденсировавшимися каплями, часто поднимающийся с электростанций, создается системами охлаждения (а не непосредственно из цикла Ренкина с замкнутым контуром). Это «выхлопное» тепло представлено «Q out », истекающим из нижней части цикла, показанного на диаграмме T – s ниже. Градирни работают как большие теплообменники, поглощая скрытую теплоту парообразования рабочей жидкости и одновременно испаряя охлаждающую воду в атмосферу.

В то время как многие вещества могут использоваться в качестве рабочей жидкости в цикле Ренкина, вода обычно является предпочтительной жидкостью из-за ее благоприятных свойств, таких как нетоксичный и инертный химический состав, изобилие и низкая стоимость, а также его термодинамические свойства. За счет конденсации паров рабочего пара в жидкость давление на выходе из турбины снижается, и энергия, необходимая питающему насосу, потребляет только от 1% до 3% выходной мощности турбины, и эти факторы способствуют более высокому КПД цикла. Преимущество этого компенсируется низкими температурами пара, поступающего в турбину (ы). Газовые турбины, например, имеют температуру на входе в турбину, приближающуюся к 1500 ° C. Однако тепловой КПД реальных крупных паровых электростанций и крупных современных газотурбинных станций аналогичен.

Четыре процесса в цикле Ренкина

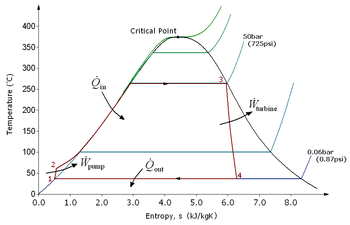
T – s диаграмма типичного цикла Ренкина, работающего между давлениями от 0,06 бар до 50 бар. Слева от колоколообразной кривой находится жидкость, справа — газ, а под ним — равновесие насыщенной жидкости и пара.

В цикле Ренкина есть четыре процесса. Состояния обозначены цифрами (коричневого цвета) на T – s диаграмме.

Процесс 1–2 : рабочая жидкость перекачивается от низкого до высокого давления. Поскольку жидкость на этом этапе является жидкостью, насосу требуется небольшая подводимая энергия.

Другими словами, процесс 1-2 — это [изэнтропическое сжатие]

Процесс 2–3 : жидкость под высоким давлением поступает в бойлер, в котором он нагревается при постоянном давлении внешним источником тепла, превращаясь в сухой насыщенный пар. Требуемая входная энергия может быть легко рассчитана графически, используя диаграмму энтальпия-энтропия (диаграмма h – s, или диаграмма Молье ), или численно, используя таблицы пара.

Другими словами, процесс 2-3 [Подвод тепла при постоянном давлении в котле]

Процесс 3–4 : Сухой насыщенный пар расширяется через турбину, генерируя мощность. Это снижает температуру и давление пара, и может произойти некоторая конденсация. Выход в этом процессе можно легко рассчитать, используя диаграмму или таблицы, указанные выше.

Другими словами, процесс 3-4 — это [Изэнтропическое расширение]

Процесс 4–1 : Затем влажный пар входит в конденсатор, где он конденсируется при постоянном давлении, чтобы стать насыщенной жидкостью.

Другими словами, процесс 4-1 представляет собой [Отвод тепла при постоянном давлении в конденсаторе]

в В идеальном цикле Ренкина насос и турбина должны быть изоэнтропическими, т. е. насос и турбина не генерируют энтропию и, следовательно, максимизируют чистый выход работы. Процессы 1–2 и 3–4 будут представлены вертикальными линиями на диаграмме T – s и более похожи на таковые в цикле Карно. Показанный здесь цикл Ренкина предотвращает попадание рабочего тела в область перегретого пара после расширения в турбине, что снижает энергию, отводимую конденсаторами.

Фактический паросиловой цикл отличается от идеального цикла Ренкина из-за необратимости присущих ему компонентов, вызванных трением жидкости и потерей тепла в окружающую среду; жидкостное трение вызывает падение давления в котле, конденсаторе и трубопроводе между компонентами, и в результате пар выходит из котла под более низким давлением; Потери тепла снижают полезную мощность, таким образом, добавление тепла к пару в котле необходимо для поддержания того же уровня полезной мощности.

Переменные

Q ˙ { displaystyle { dot {Q}}}	Расход тепла в систему или из системы (энергия в единицу времени)
м ˙ { displaystyle { dot {m}}}	Массовый расход (масса в единицу времени)
Вт ˙ { displaystyle { dot {W}}}	Механическая мощность, потребляемая или подается в систему (энергия в единицу времени)
η therm { displaystyle eta _ { text {therm}}} ${ displaystyle eta _ { text {therm}}}$	Термодинамическая эффективность процесса (полезная мощность на единицу подводимого тепла, безразмерная)
η насос, η turb { displaystyle eta _ { text {pump}}, eta _ { text {turb}}} ${ displaystyle eta _ { tex t {насос}}, eta _ { text {turb}}}$	Изэнтропический КПД процессов сжатия (питающий насос) и расширения (турбина), безразмерный
h 1, h 2, h 3, h 4 { displaystyle h_ {1}, h_ {2}, h_ {3}, h_ {4}}	«Удельные энтальпии «в указанных точках на диаграмме T – s
h 4 s { displaystyle h_ {4s}} $h_ {4s}$	Конечная« удельная энтальпия »жидкости, если турбина была изоэнтропический
p 1, p 2 { displaystyle p_ {1}, p_ {2}}	Давления перед до и после процесса сжатия

Уравнения

В общем, эффективность простого цикла Ранкина может быть записана как

η therm = W ˙ термический — W ˙ Q ˙ in ≈ W ˙ turb Q в. { displaystyle eta _ { text {therm}} = { frac {{ dot {W}} _ { text {therm}} — { dot {W}}} {{ dot {Q}} _ { text {in}}}} приблизительно { frac {{ dot {W}} _ { text {turb}}} {{ dot {Q}} _ { text {in}}}}.} ${ displaystyle eta _ { text {therm}} = { frac {{ dot {W}} _ { text {therm} } - { dot {W}}} {{ dot {Q}} _ { text {in}}}} приблизительно { frac {{ dot {W}} _ { text {turb}}} {{ dot {Q}} _ { text {in}}}}.}$

Каждое из следующих четырех уравнений выводится из энергии и баланса массы для контрольного объема. η therm { displaystyle eta _ { text {therm}}} ${ displaystyle eta _ { text {therm}}}$ определяет термодинамическую эффективность цикла как отношение полезной выходной мощности к тепловложению. Поскольку работа, требуемая насосом, часто составляет около 1% от производительности турбины, ее можно упростить.

Q ˙ в м ˙ = час 3 — час 2, { displaystyle { frac {{ dot {Q}} _ { text {in}}} { dot {m}}} = h_ {3 } -h_ {2},} ${ displaystyle { frac {{ dot {Q}} _ { text {in}}} { dot {m}}} = h_ {3} -h_ {2},}$

Q ˙ out m ˙ = h 4 — h 1, { displaystyle { frac {{ dot {Q}} _ { text {out}}} { dot { m}}} = h_ {4} -h_ {1},} ${ displaystyle { frac {{ dot {Q}} _ { text {out}}} { dot {m} }} = h_ {4} -h_ {1},}$

W ˙ насос m ˙ = h 2 — h 1, { displaystyle { frac {{ dot {W}} _ { text { насос}}} { dot {m}}} = h_ {2} -h_ {1},} ${ displaystyle { frac {{ dot {W}} _ { text {pump}}} { dot {m}}} = h_ {2} -h_ {1},}$

W ˙ турбина m ˙ = h 3 — h 4. { displaystyle { frac {{ dot {W}} _ { text {turbine}}} { dot {m}}} = h_ {3} -h_ {4}.} ${ displaystyle { frac {{ dot {W}} _ { text {turbine}}} { dot {m}}} = h_ {3} -h_ {4}. }$

При работе с КПД турбин и насосов необходимо произвести корректировку по условиям работы:

W ˙ насос m ˙ = h 2 — h 1 ≈ v 1 Δ p η насос = v 1 (p 2 — p 1) η насос, { displaystyle { frac {{ dot {W}} _ { text {pump}}} { dot {m}}} = h_ {2} -h_ {1} приблизительно { frac {v_ { 1} Delta p} { eta _ { text {pump}}}} = { frac {v_ {1} (p_ {2} -p_ {1})} { eta _ { text {pump} }}},} ${ displaystyle { frac {{ dot {W}} _ { text {pump}}} { dot {m}}} = h_ {2} -h_ {1} приблизительно { frac {v_ {1} Дельта p} { eta _ { text {pump}}}} = { frac {v_ {1} (p_ {2} -p_ {1})} { eta _ { text {pump}}}},}$

W ˙ турбина m ˙ = h 3 — h 4 ≈ (h 3 — h 4) η турбина. { displaystyle { frac {{ dot {W}} _ { text {turbine}}} { dot {m}}} = h_ {3} -h_ {4} приблизительно (h_ {3} -h_ {4}) eta _ { text {turbine}}.} ${ displaystyle { frac {{ dot {W}} _ { text {turbine}}} { dot {m}}} = h_ {3} -h_ {4} ок (h_ {3} -h_ {4}) eta _ { text {turbine}}.}$

Реальный цикл Ренкина (неидеальный)

Цикл Ренкина с перегревом

В реальном цикле электростанции (название «Ренкин» цикл используется только для идеального цикла), сжатие насосом и расширение в турбине не являются изоэнтропическими. Другими словами, эти процессы необратимы, и энтропия увеличивается во время двух процессов. Это несколько увеличивает мощность, требуемую насосом, и снижает мощность, генерируемую турбиной.

В частности, эффективность паровой турбины будет ограничена образованием капель воды. По мере конденсации воды капли воды ударяются о лопатки турбины с высокой скоростью, вызывая точечную коррозию и эрозию, постепенно сокращая срок службы лопаток турбины и ее эффективность. Самый простой способ решить эту проблему — перегреть пар. На диаграмме T – s выше состояние 3 находится на границе двухфазной области пара и воды, поэтому после расширения пар будет очень влажным. При перегреве состояние 3 переместится вправо (и вверх) на диаграмме и, следовательно, после расширения будет производить более сухой пар.

Варианты основного цикла Ренкина

Общая термодинамическая эффективность может быть увеличена за счет увеличения средней тепла входной температуры

T ¯ in = ∫ 2 3 T d QQ in { displaystyle { bar {T}} _ { text {in}} = { frac { int _ {2} ^ {3} T , dQ} { Q _ { text {in}}}}} ${ displaystyle { bar {T }} _ { text {in}} = { frac { int _ {2} ^ {3} T , dQ} {Q _ { text {in}}}}}$

этого цикла. Повышение температуры пара до зоны перегрева — простой способ сделать это. Существуют также разновидности базового цикла Ренкина, предназначенные для повышения таким образом теплового КПД цикла; два из них описаны ниже.

Цикл Ренкина с повторным нагревом

Целью цикла повторного нагрева является удаление влаги, переносимой паром на конечных стадиях процесса расширения. В этом варианте две турбины работают последовательно. Первый принимает пар от котла под высоким давлением. После того, как пар прошел через первую турбину, он снова поступает в котел и снова нагревается перед прохождением через вторую турбину с более низким давлением. Температуры повторного нагрева очень близки или равны температурам на входе, в то время как оптимальное необходимое давление повторного нагрева составляет лишь одну четвертую от исходного давления в бойлере. Среди других преимуществ это предотвращает конденсацию пара во время его расширения и тем самым снижает повреждение лопаток турбины и повышает эффективность цикла, поскольку больший тепловой поток в цикл происходит при более высокой температуре.. Цикл повторного нагрева был впервые введен в 1920-х годах, но не работал долго из-за технических трудностей. В 1940-х годах он был повторно введен с увеличением производства котлов высокого давления , и, наконец, в 1950-х годах был введен двойной повторный нагрев. Идея двойного подогрева заключается в повышении средней температуры. Было замечено, что более двух стадий повторного нагрева обычно не нужны, поскольку следующая стадия увеличивает эффективность цикла только наполовину, чем предыдущая стадия. Сегодня двойной повторный нагрев обычно используется на электростанциях, работающих при сверхкритическом давлении.

Регенеративный цикл Ренкина

Регенеративный цикл Ренкина назван так потому, что после выхода из конденсатора (возможно, как переохлажденная жидкость ) рабочая жидкость нагревается за счет пар, отбираемый из горячей части цикла. На показанной диаграмме жидкость в точке 2 смешивается с жидкостью в точке 4 (обе при одинаковом давлении), чтобы в итоге получить насыщенную жидкость в точке 7. Это называется «нагрев при прямом контакте». Регенеративный цикл Ренкина (с небольшими вариантами) обычно используется на реальных электростанциях.

Другой вариант отправляет отбираемый пар между ступенями турбины в нагреватели питательной воды для предварительного нагрева воды на пути от конденсатора к котлу. Эти нагреватели не смешивают входящий пар и конденсат, функционируют как обычный трубчатый теплообменник и называются «закрытые нагреватели питательной воды».

Регенерация увеличивает температуру подводимого тепла цикла за счет исключения добавления тепла от котла / источника топлива при относительно низких температурах питательной воды, которые существовали бы без регенеративного нагрева питательной воды. Это повышает эффективность цикла, так как большая часть теплового потока в цикл происходит при более высокой температуре.

Органический цикл Ренкина

Органический цикл Ренкина (ORC) использует органическую жидкость, такую как н-пентан или толуол вместо воды и пар. Это позволяет использовать источники тепла с более низкой температурой, такие как солнечные пруды, которые обычно работают при температуре около 70–90 ° C. КПД цикла намного ниже из-за более низкого диапазона температур, но это может быть целесообразным из-за более низкой стоимости, связанной с сбором тепла при этой более низкой температуре. В качестве альтернативы можно использовать жидкости с точками кипения над водой, и это может иметь термодинамические преимущества (см., Например, турбина на парах ртути ). Свойства фактического рабочего тела имеют большое влияние на качество пара (пара) после стадии расширения, влияя на конструкцию всего цикла.

Цикл Ренкина не ограничивает рабочую жидкость в своем определении, поэтому название «органический цикл» — это просто маркетинговая концепция, и этот цикл не следует рассматривать как отдельный термодинамический цикл.

Сверхкритический цикл Ренкина

Цикл Ренкина, применяемый с использованием сверхкритической жидкости, объединяет концепции регенерации тепла и сверхкритического цикла Ренкина в единый процесс, называемый регенеративным сверхкритическим циклом (RGSC).). Он оптимизирован для источников температуры 125–450 ° C.

См. Также

Потери мощности в режиме когенерации с отбором пара

Ссылки

На Викискладе есть материалы, связанные с циклом Ренкина .

^Канада, Скотт; Г. Коэн; Р. Кейбл; Д. Бросо; Х. Прайс (2004-10-25). «Солнечная электростанция органического цикла Ренкина с параболическим желобом» (PDF). 2004 DOE Solar Energy Technologies. Денвер, Колорадо: Министерство энергетики США NREL. Архивировано из оригинального (PDF) 18 марта 2009 г. Проверено 17 марта 2009 г.
^Баттон, Билл (18 июня 2000 г.). «Двигатели с органическим циклом Ренкина для солнечной энергии» (PDF). Конференция Solar 2000. Barber-Nichols, Inc. Архивировано с оригинального (PDF) 18 марта 2009 г. Проверено 18 марта 2009 г.
^Nielsen et al., 2005, Proc. Int. Solar Energy Soc.
^Могтадери, Бехдад (2009). «Обзор технологии GRANEX для производства геотермальной энергии и утилизации отработанного тепла». Австралийская конференция по геотермальной энергии 2009., Inc.

^Ван Виллен «Основы термодинамики» (ISBN 85-212-0327-6 )
^Вонг «Термодинамика для инженеров», 2-е изд., 2012, CRC Press, Taylor Francis, Boca Raton, London, New York. (ISBN 978-1-4398-4559-2 )
Moran Shapiro «Основы инженерной термодинамики» (ISBN 0-471-27471-2 )
Wikibooks Engineering Thermodynamics

Источник

Пара-метры	Номер варианта
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
, °С	400	370	450	415	385	460	510	500	480	390	400	370	450	415	385
, °С	165	200	215	250	260	270	280	230	250	225	165	200	215	250	260
, °С	5	5	5	5	5	10	10	10	10	15	15	15	15	15	15
, °С	80	80	80	80	80	140	75	75	75	70	70	65	65	65	65
М1, кг/с	1,5	–	1,8	–	1,5	–	1,8	–	2,0	–	2,0	–	2,4	–	2,4
М2, кг/с	–	4,5	–	4,0	–	3,5	–	3,0	–	2,5	–	2,0	–	1,5	–
α1·10–1	42	42	40	40	38	38	35	35	32	32	30	30	28	28	26
α2·10–2	26	42	28	35	30	30	32	28	35	25	38	20	40	23	27
Распо-ложе-ние труб	Г	Г	В	В	Г	Г	В	В	Г	Г	В	В	Г	Г	В
матер.	С	Л	С	Л	С	Л	С	Л	С	Л	С	Л	С	Л	С

4.1. Установка, работающая по циклу Ренкина

Схема паросиловой установки, работающей по циклу Ренкина

Из каких процессов состоит цикл Ренкина

Термический КПД цикла Ренкина

Цикл Ренкина в ts диаграмме

Цикл Ренкина в hs диаграмме

Разновидности цикла Ренкина

С промежуточным перегревом пара

На сверхкритических параметрах пара

С регенерацией

Цикл Брайтона-Ренкина

Description[edit]

The four processes in the Rankine cycle[edit]

Variables[edit]

Equations[edit]

Real Rankine cycle (non-ideal)[edit]

Variations of the basic Rankine cycle[edit]

Rankine cycle with reheat[edit]

Regenerative Rankine cycle[edit]

Organic Rankine cycle[edit]

Supercritical Rankine cycle[edit]

See also[edit]

References[edit]

1 – компрессор; 2 – охладитель воздуха (теплообменник);

Номер варианта

Номер варианта

Содержание

Описание

Четыре процесса в цикле Ренкина

Переменные

Уравнения

Реальный цикл Ренкина (неидеальный)

Варианты основного цикла Ренкина

Цикл Ренкина с повторным нагревом

Регенеративный цикл Ренкина

Органический цикл Ренкина

Сверхкритический цикл Ренкина

См. Также

Ссылки