При
протекании переменного тока по участку
цепи электромагнитное поле совершает
работу, и в цепи выделяется джоулево
тепло. Мгновенная мощность в цепи
переменного тока равна произведению
мгновенных значений тока и напряжения:
P= IU.
Практический интерес представляет
среднее за период переменного тока
значение мощности
P=Pcp=ImUmcosωt·cos(ωt+φ)
(17.36)
Здесь
Im
и Um
– амплитудные значения тока и напряжения
на данном участке цепи, φ – фазовый
сдвиг между током и напряжением. Если
участок цепи содержит только резистор
с сопротивлением R, то фазовый сдвиг
φ = 0:
(17.37)
Для
того, чтобы это выражение по виду
совпадало с формулой для мощности
постоянного тока, вводятся понятия
действующих или эффективных значений
силы тока и напряжения:
и
(17.38)
Средняя
мощность переменного тока на участке
цепи, содержащем резистор, равна
(17.39)
Если
участок цепи содержит только конденсатор
емкости C, то фазовый сдвиг между током
и напряжением.
Поэтому
(17.40)
Аналогично
можно показать, что PL = 0.
Таким
образом, мощность в цепи переменного
тока выделяется только на активном
сопротивлении. Средняя мощность
переменного тока на конденсаторе и
катушке индуктивности равна нулю.
Примеры решения задач
Пример
. Колебательный
контур состоит из воздушного плоского
конденсатора (расстояние между пластинами
d=1мм,
площадь поперечного сечения S=2
см2
каждая)
и соленоида без сердечника (длина ℓ=10см,
площадь поперечного сечения S1=2
см2,
число витков N=100).
Пренебрегая сопротивлением контура,
определите частоту ω0
собственных
колебаний контура.
Дано:
d=1 мм=1∙10-3
м;
S=100 см2=10-2
м2;
ε=1;
ℓ=10см=0,01м;
S1=2
см2=2∙10-4
м2;
N=100; μ=1.
Найти:
ω0.
Решение.
Собственная частота колебательного
контура
,
(1)
где
индуктивность соленоида
(2)
(μ0=4π∙10-7
Гн/м – магнитная постоянная; μ- магнитная
проницаемость среды; ℓ — длина соленоида;
S1—
площадь его поперечного сечения; N
— число витков соленоида) и ёмкость
плоского конденсатора
(3)
(ε0
– 8,85∙10-12
Ф/м – электрическая постоянная; ε-
диэлектрическая проницаемость среды;
d
— расстояние между пластинами конденсатора;
S
— площадь пластин конденсатора).
Подставив
выражения (2) и (3) в формулу (1) и учитывая,
что
(с=3∙108
м/с
– скорость распространения света в
вакууме), найдём искомую частоту
собственных колебаний контура:
.
Ответ:
ω0=2,12∙107
рад/с.
Пример
. Колебательный
контур содержит конденсатор ёмкостью
С=40 нФ и катушку индуктивностью L=1,6
мГн. Определите максимальное напряжение
Um
на обкладках конденсатора, если
максимальная сила тока Im
в колебательном контуре равна 1A.
Сопротивлением контура пренебречь.
Дано:
С=40нФ=40∙10-8
Ф; L=1,6
мГн=1,6∙10-3
Гн; Im=1А;
R=0.
Найти:
Um.
Решение.
Максимальное напряжение на обкладках
конденсатора
,
(1)
где
qm
– амплитуда колебаний заряда на обкладках
конденсатора ёмкостью С.
В
случае свободных незатухающих колебаний
(R=0)
заряд на обкладках конденсатора совершает
гармонические колебания по закону
q=qmcosω0t,
где
собственная частота колебательного
контура
(2)
Сила
тока в колебательном контуре
,
где
максимальная сила тока
Im=ω0qm,
откуда
(3)
[учли
формулу (2)].
Подставив
выражение (3) в Формулу (1), найдём искомое
максимальное напряжение на обкладках
конденсатора
.
Ответ:
Um=200
В.
Пример
. Частота
свободных незатухающих электромагнитных
колебании в контуре, содержащем катушку
индуктивности L=0,5
Гн, составляет 50 Гц. Запишите для данного
контура уравнение изменения заряда на
обкладках конденсатора в зависимости
от времени, если максимальная энергия
магнитного поля Wm
в катушке составляет 4 мкДж.
Дано:
L=0,5
Гн; ν0=50
Гц; Wm
=4 мкДж=4∙10-6
Дж.
Найти:
q(t).
Решение.
В случае свободных незатухающих колебаний
(R≈0)
заряд на обкладках конденсатора совершает
гармонические колебания по закону
q=qmcosω0t,
(1)
где
qm
—
амплитуда колебаний заряда на обкладках
конденсатора с циклической
частотой
ω0=2πν0,
(2)
Максимальная
энергия магнитного поля в катушке
(3)
где
Im
– амплитуда колебаний силы тока. Из
уравнения (3)
.
(4)
Продифференцировав
уравнение (1) по времени, определим силу
тока в колебательном контуре:
,
где
амплитуда силы тока Im=ω0qm.
Тогда
(5)
Подставив
выражение (4) в формулу (5) и учитывая (2),
найдём амплитуду колебаний заряда
Вычисляя,
получаем qm=1,27∙10-5
Кл
Подставив
в уравнение (1) числовые значения qm
и ω0,
искомое уравнение (с числовыми
коэффициентами) изменения заряда на
обкладках конденсатора примет вил:
q=1,27∙10-5cos100πt,
Кл.
Ответ:
q=1,27∙10-5cos100πt,
Кл.
Пример
. Колебательный
контур состоит из конденсатора ёмкостью
С=100 пФ, катушки индуктивности L=0,01
Гн и резистора сопротивлением R=20
Ом. Определите: 1) период затухающих
колебаний; 2) через сколько полных
колебаний амплитуда тока в контуре
уменьшится в е раз..
Дано:
C=100пФ
=1∙10-7
Ф; L=0,01
Гн; R=20
Ом.
Найти:
1)
Т; 2) N.
Решение.
Искомый период электромагнитных
колебаний в контуре
(учли,
что собственная частота контура
и коэффициент затухания
).
Число
полных колебаний, совершаемых за время
уменьшения амплитуды силы
тока
в е раз,
,
(1)
где
время релаксации
.
Подставив
это выражение в формулу (1), найдём искомое
число полных колебаний:
.
Ответ:
1) Т=0,2 мс; 2) N=5.
Пример
. Определите
добротность Q
колебательного контура, если собственная
частота ω0
колебательного контура отличается на
5% от частоты ω свободных затухающих
колебаний.
Дано:
ω0=1,05
ω.
Найти:
Q.
Решение.
В реальном колебательном контуре ( т.е.
обладающем сопротивлением) частота ω
свободных затухающих электромагнитных
колебаний меньше собственной частоты
ω0
колебательного контура (при R≈0):
,
(1)
где
δ– коэффициент затухания.
Добротность
колебательного контура
,
где
логарифмический декремент затухания
Т (Т- период затухающих колебаний ).
Учитывая приведённые формулу, найдём
коэффициент затухания
.
(2)
Подставив
выражение (2) в формулу (1), получаем
или
откуда
искомая добротность
Ответ:
Q=1,56
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Я не претендую на истину в последней инстанции и напишу, как сам думаю. Если я не прав, то умные люди поправят. В цепи переменного тока стоят в данном случае все три типа нагрузок. Индуктивная, емкостная и активная. Активная это резистор 100 Ом. Понятное дело, что он покажет нам активную мощность в этой цепи. Это U/R x U =400 вт. Но это при постоянном токе. Поэтому так считать нельзя! (Активной составляющей катушки пренебрегаем). Нам нужно найти мощность для полной цепи. Для этого нужно найти индуктивное сопротивление.
Х L = 2π fL , а это значит 50 Гц х 2 Гн = 100 Ом. Теперь нам известны все три сопротивления. Найдем общее сопротивление цепи.
Z = V R2+(XL-XC)2 Объясняю формулу: Общее сопротивление будет корень квадратный из суммы квадрата активных сопротивлений (тут оно одно) и квадрата разности реактивных сопротивлений индуктивной и емкостной нагрузки. Получается 112 Ом.
Ток в полной цепи (а значит и мощность), как отношение напряжения к сопротивлениям, множимое на напряжение, можно сразу и не считать Все равно все сократится и останутся Омы. Поэтому косинус ФИ можно подсчитать исходя из отношения сопротивлений в данной цепи.
То есть: Cos фи — Ra/Z = 100/112 = 0,89.
Это и есть ответ данной задачи.
Общий ток в цепи: U/Z = 200/112 = 1.8 А
Теперь по мощностям. Активная (I квадрат R) : I2R = 324 вт.
Теперь реактивную: I2(XL-XC) = 162 ВА.
Общая мощность по Пифагору. Получится 363 ВА
Мощность переменного тока
-
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
-
Мощность тока через резистор
-
Мощность тока через конденсатор
-
Мощность тока через катушку
-
Мощность тока на произвольном участке
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и
— мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени
— настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины
и
можно считать постоянными в течение интервала
.
Пусть за время через наш участок прошёл заряд
(в соответствии с правилом выбора знака для силы тока заряд
считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
(1)
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
к оглавлению ▴
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением
. Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
(2)
График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.
Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается
колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между
и
. Где же именно?
Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2.
Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
(3)
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
(4)
Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением
, то в обоих случаях лампочка будет гореть одинаково ярко.
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
к оглавлению ▴
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на
:
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3.
Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).
Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
к оглавлению ▴
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на
:
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).
Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
к оглавлению ▴
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
(5)
Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:
В результате получим:
(6)
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
(7)
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки
, и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
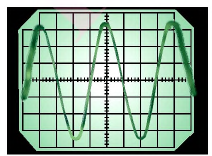
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
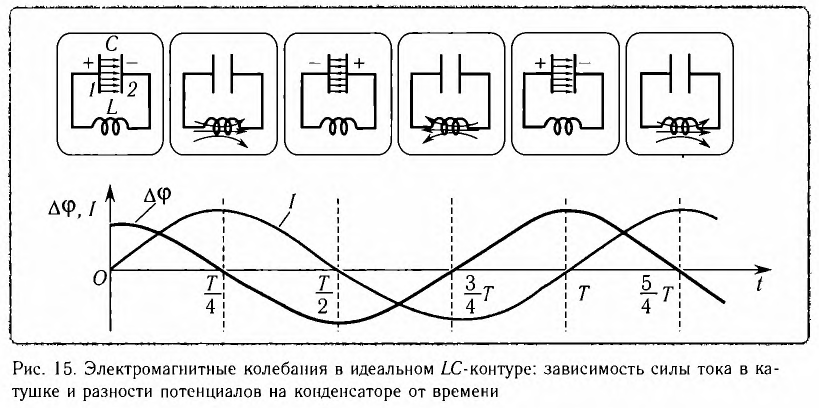
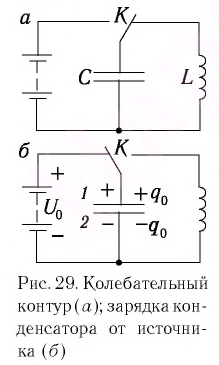
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
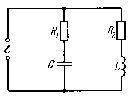
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +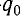

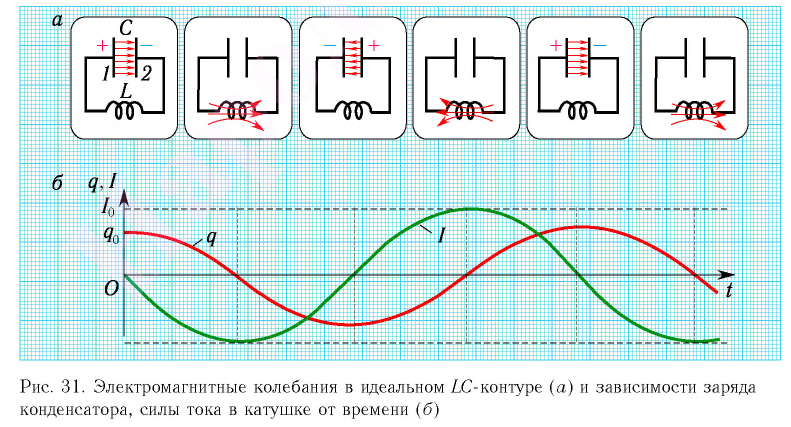
С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
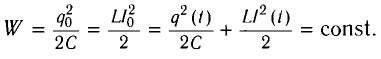
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
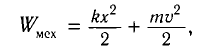
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 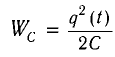
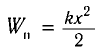
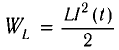
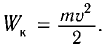
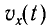
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 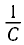
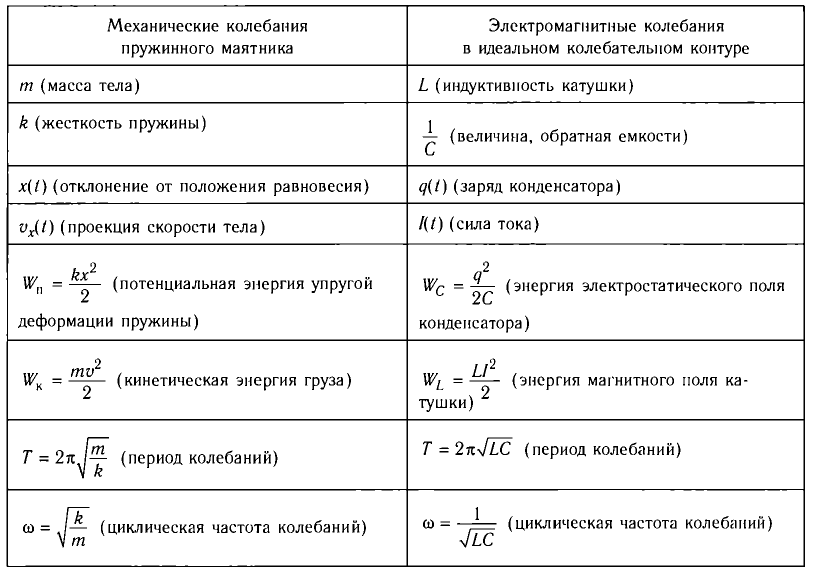
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 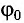
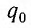
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 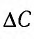
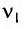
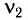
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (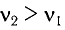
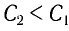
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Откуда находим
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 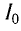
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 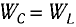
откуда
Ответ: 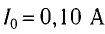
Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 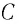
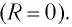
Подключив (при помощи ключа 
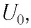
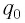
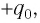
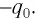
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 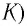
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 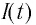
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 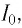
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 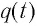
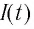
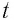
В момент полной разрядки конденсатора 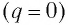
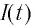
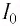
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 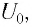
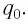
Таким образом, в идеальном 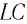
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 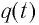
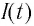
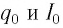
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 
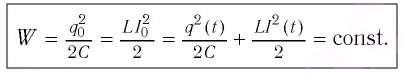
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 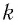
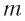
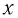
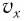
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 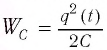
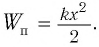
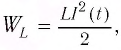
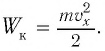
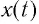
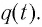
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 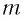
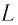
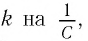
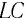
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 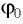
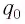
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 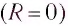
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 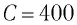
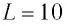
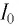
Дано:
Решение
Максимальная энергия электростатического поля конденсатора:
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 
Отсюда
Ответ:
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
|
Закон Ома для полной цепи переменного тока. |
|
|
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае:
|
|
|
|
|
|
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: |
|
|
Сдвиг фаз в цепи переменного тока определяется характером нагрузки:
|
|
|
Мощность в цепи переменного тока. |
|
|
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): |
|
|
или, переходя к действующим значениям, |
|
|
Величина |
коэффициент мощности |
|
Резонанс в электрической цепи. |
|
|
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии |
|
|
Следовательно, |
|
|
Амплитуды колебаний напряжения на индуктивности и емкости будут равны и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
|
Следовательно, |
|
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением |
|
|
При этом если величина то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! |
|
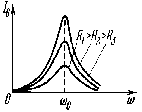
|
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. |
|
|
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа |
|
|
В случае резонанса |
|
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). |








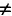
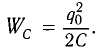
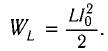
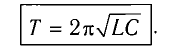
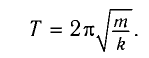
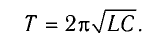
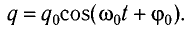
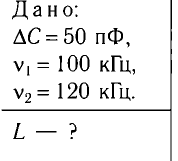
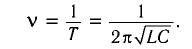
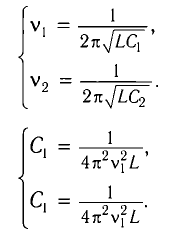
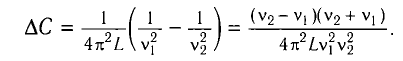
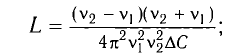
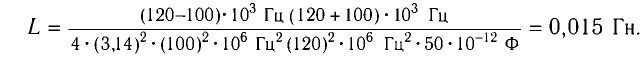
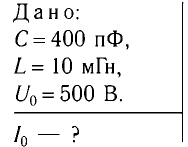
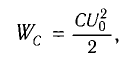
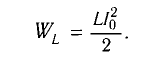
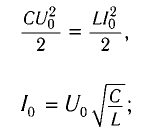
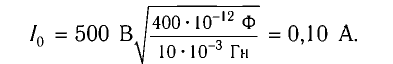
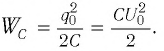
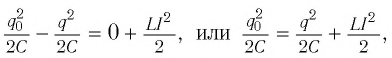
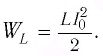
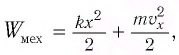
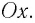
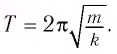
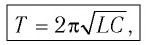
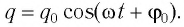
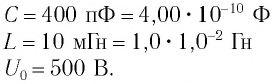

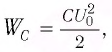
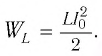
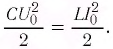
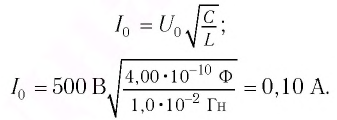
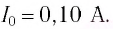
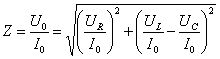 — полное сопротивление переменному току.
— полное сопротивление переменному току.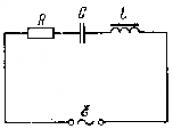
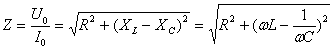 .
.
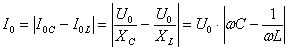 .
.