Как найти мощность в математике

Некоторые сведения о мощности множества приведены в [I].
Здесь мы рассмотрим это понятие более подробно.

Множество А равномощно множеству И, если существует
биекцил f:A→B.

Из того, что существует биекция f:A→B, следует, что
соответствие f^-1 есть биекция В на А (см. 1,4). Поэтому если
А равномощно В, то и В равномощно A, и мы можем говорить,
что множества АиВ равномощны.

Факт равномощности множеств А и В будем записывать
так: А~В.

Из определения равномощности и свойств биекции также
следует, что для любого множества А имеет место А ~ А
(тождественное отображение есть биекция множества А на
себя); а для любых множеств А, В, С из А~В и В~С следует
А~С (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть
отношение эквивалентности*, заданное на „множестве всех
множеств» (на самом деле на множестве всех подмножеств
некоторого универсального множества).

*Зачастую в литературе по теории множеств равномощные множества
и называют „эквивалентными множествами». Однако следует различать
общее понятие отношения эквивалентности и его частный случаи —
эквивалентность, или равномощность, множеств.

Если мы обозначим через |А| класс эквивалентности
множества А по отношению ~, то утверждение о равномощности
множеств Аи В можно записать так: |А| = |В|.

Этот класс эквивалентности |А| называют мощностью
множества А.

Конечные множества А = {а₁,.., а_n} и В = {b₁ ,…, b_n} равномощны тогда и только тогда, когда множества А и В состоят
из одного и того же числа элементов, т.е. n = m. Отсюда, в
частности, следует, что конечное множество не является
номощным никакому своему собственному подмножеству. Это
свойство конечных множеств можно сформулировать так.

Теорема 1.8. Если А — конечное множество и f:A→B
→ А — инъекция, то она является сюръекцией и, следовательно,
биекцией. #

В силу приведенных выше соображений мощностью
конечного множества А = {а₁,.., а_n} можно считать натуральное
число n, так как, задавая такое число, мы задаем и класс всех
(попарно равномощных) множеств вида {а₁,.., а_n}. Обратно,
каждый такой класс однозначно определяет натуральное число
п как число элементов в каждом множестве данного класса.
Естественно считается, что мощность пустого множества
равна нулю.

Перейдем теперь к исследованию мощности бесконечных
множеств. Таковы хорошо известные нам числовые множества
ℕ, ℤ, ℚ, ℝ и ℂ.

Любое множество, равномощное множеству всех
натуральных чисел, называют счетным. Мощность счетного множества
обозначают ℵ₀ (читается „алеф нуль»).

Любую биекцию v: ℕ → М называют нумерацией
счетного множества М; если элемент М есть v(n) для некоторого
n ∈ ℕ, то этот элемент М обозначаем через a_n, называя
туральное число n номером элемента a_n относительно данной
нумерации v.

Таким образом, элементы счетного множества можно
перенумеровать, записав их в виде последовательности а₁,.., а_n, … или {a_n}_n∈ℕ Другими словами, счетное множество есть
область значений некоторой функции натурального аргумента.

Пример 1.21. а. Множество всех нечетных натуральных
чисел счетно. Нумерацию v можно задать так: v(n) = 2n — 1,

б. Множество всех натуральных чисел, делящихся на
заданное число k ≥ 2, счетно. Нумерацию v можно задать так:
v(n) = kn, n∈ℕ. В частности, при k = 2 получаем, что
множество всех четных чисел счетно. Этот и предыдущий
примеры показывают, что бесконечное (счетное) множество может
иметь собственное равномощное ему подмножество.

в. Множество ℤ всех целых чисел счетно. Нумерацию
можно установить так:

Рассмотрим свойства счетных множеств.

Теорема 1.9. Любое бесконечное множество содержит
счетное подмножество.

◀ Пусть М₀ — бесконечное множество. Значит, оно не пусто
и существует элемент а₁ ∈ М₀. Положим М₁ = М₀ {a₁}.
Множество М₁ не пусто, так как в противном случае имело бы
место равенство М₀ = {a_i}, что противоречит предположению
о бесконечности М₀. Выберем элемент а₂ ∈ М₁ и положим
М₂ = М₁ {а₂} = М₀ {a₁, а₂}. Множество М₂ также не пусто,
поскольку иначе мы бы имели М₀ = {a₁, а₂} и множество
было бы конечным.

Методом математической индукции можно показать, что
для любого n ≥ 1 множество М_n = M₀ {a₁,…, a_n}, где а₁ ∈ М₀, …, a_n ∈ М_n-1, не пусто. Тогда существует элемент
a_n+1 ∈ М_n и a_n+1 ∉ M_n+1 = М_n {а_n+1}. Таким образом, все
элементы a_n, n ∈ ℕ, попарно различны и множество {а_n:n ∈ ℕ}
счетно, а его нумерация может быть задана так: v(n) = а_n.

Теорема 1.10. В любом бесконечном множестве можно
выделить два не пересекающихся между собой счетных
подмножества.

◀ Разобьем множество натуральных чисел на два
подмножества: ℕ₁ = {n: n = 2k — 1, k ∈ ℕ} (множество нечетных чисел),
и ℕ₂ = {n: n = 2k, k ∈ ℕ} (множество четных чисел). Оба эти
множества счетны (см. пример 1.21).

Согласно теореме 1.9, бесконечное множество содержит
некоторое счетное подмножество А. Пусть установлена
некоторая его нумерация. Разобьем это подмножество на два
подмножества: всех элементов с четными и всех элементов с
нечетными номерами. По построению эти подмножества не
пересекаются и являются счетными, поскольку счетны множества
четных и нечетных чисел. >

Теорема 1.11. Любое подмножество счетного множества
конечно или счетно.

◀ Пустое подмножество конечно по определению. Пусть М —
счетное множество, а В — его некоторое непустое
подмножество. Поскольку множество М счетно, можно считать, что
задана некоторая его нумерация. Следовательно, каждый
элемент подмножества В имеет свой номер. Запишем номера
элементов множества В в порядке возрастания: i₁, …, i_n, …

Если среди них есть наибольший номер i_p, то подмножество
В конечно. В противном случае получим счетное
подмножество {a_i1, a_i2,…, a_in,…}, нумерация которого установлена так:
v(n) = a_in.

Если множество конечно или счетно, его называют не
более чем счетным. Семейство (А_i)_i∈I множеств называют
не более чем счетным, если множество (индексов) I не более
чем счетно.

Теорема 1.12. Объединение любого не более чем счетного
семейства счетных множеств счетно.

<4 Пусть (А_i)_i∈I — конечное или счетное семейство счетных
множеств. Рассмотрим сначала случай, когда множества А_i
попарно не пересекаются.

В этом случае нумерация объединения конечного семейства
счетных множеств может быть проведена по схеме,
изображенной на рис. 1.14, а нумерация объединения счетного семейства
счетных множеств — по схеме, приведенной на рис. 1.15.

Пусть теперь (А_n)_n∈ℕ — произвольное счетное семейство
счетных множеств, т.е. множества А_i могут пересекаться. В
этом случае, применяя указанные на рис. 1.14 и 1.15 схемы
нумерации к конечному или счетному объединению счетных
множеств, следует пропускать каждый раз элементы, которые
уже получили номера. >

Полезно отметить также и следующий факт.

Теорема 1.13. Объединение конечного и счетного
множеств счетно. #

Теорема 1.14. Пусть М — бесконечное множество, а N —
его не более чем счетное подмножество. Если множество MN
бесконечно, то оно равномощно множеству М.

◀ По теореме 1.10 в множестве MN, поскольку оно
бесконечно, можно выбрать счетное подмножество N’. Ясно, что
N∩N’ = ∅. Множество N∪N’ является счетным как
объединение двух счетных множеств или объединение счетного и
конечного множеств. Поэтому существует биекция f: N∪N’ → N’.
Поскольку (M(N∪N’))∪(N∪N’)=M, M (N∪N’)∪N’ =
= MN, то требуемую биекцию М на МN строим так: на
подмножестве М (N∪N’), общем для М N и М, эта биекция
совпадает с тождественным отображением; на подмножестве
N∪N’ эта биекция есть биекция f. ▶

Следствие 1.1. Если М — бесконечное множество, а N —
не более чем счетное множество, то М ~ М ∪ N.

Существуют бесконечные множества, не являющиеся
счетными. Это вытекает из следующих рассуждений.

Рассмотрим множество всех последовательностей нулей и
единиц, т.е. последовательностей вида {α₁,α₂, …,α_n,…}, где
α_i ∈ {0,1} для каждого i ≥ 1.

Обозначим множество таких „двоичных»
последовательностей через {0,1}^ω.

Теорема 1.15 (теорема Кантора). Множество {0,1}^ω
не есть счетное множество.

◀ Пусть множество {0,1}^ω счетное. Тогда существует биекция
φ: ℕ → {0,1}^ω. Выпишем все последовательности φ(n):

φ(1) = {α₁₁,α₁₂, …,α_1n,…},

φ(1) = {α₁₁,α₁₂, …,α_1n,…},

………………………………………………………

φ(n) = {α_n1,α_n2, …,α_nn,…},

………………………………………………………

Построим последовательность β = {β₁,…, β_n,…}: положим
β_i = 1, если α_ii = 0, и β_i = 0, если α_ii = 1. Ясно, что эта
последовательность не совпадает ни с одной из последовательностей
φ(n), а это противоречит допущению, что любая
последовательность из {0,1}^ω есть φ(k) для некоторого k.

Итак, ℕ не равномощно {0,1}^ω.

В то же время {0,1}^ω содержит подмножество
последовательностей, в каждой из которых только один член отличен
от нуля. Это подмножество равномощно множеству всех
одноэлементных подмножеств ℕ и, следовательно, самому ℕ.
Следовательно, множество {0,1}^ω бесконечно, но не равномощно
счетному множеству и потому не является счетным. ▶

Теорема 1.16. Множество 2^ℕ всех подмножеств множества
натуральных чисел и множество {0,1}^ω равномощны.

◀ Определим отображение φ множества 2^ℕ на множество
{0,1}^ω следующим образом: если X ⊆ ℕ, то φ(Х)_i = 1 при i ∈ X
и φ(Х)_i = 0 при i ∉ X.

Тем самым подмножеству X ставится в соответствие
последовательность φ(Х), i-й член которой равен единице тогда
и только тогда, когда число i есть элемент множества X.
Докажем, что φ — биекция 2^ℕ на {0,1}^ω.

Покажем, что отображение φ — инъекция. Пусть X и Y —
различные подмножества ℕ. Тогда найдется число i ∈ X Y или
число j ∈ YX. В первом случае в последовательности φ(Х) i-й
член будет равен единице, а в последовательности φ(Y) — нулю.
Таким образом, φ(Х) ≠ φ(Y). Во втором случае φ(Y)_j = 1,
φ(Х)_j = 0 и опять φ(Х) ≠ φ(Y). Следовательно, отображение
φ — инъекция.

Покажем, что φ — сюръекция. Возьмем произвольную
последовательность α ∈ {0,1}^ω. Образуем множество Х_α =
= {i: α_i = 1}. Ясно, что φ(Х_α) = α. Таким образом, для
любой последовательности α ∈ {0,1}^ω существует подмножество
Х_α ∈ 2^ℕ, такое, что φ(Х_α) = α. Следовательно, φ —
сюръекция.

Таким образом, мы показали, что φ — биекция, а множества
2^ℕ и {0,1}^ω равномощны. >

Мощность множества 2^ℕ обозначают с и называют
мощностью континуума, а любое множество, эквивалентное
множеству 2^ℕ, называют множеством мощности
континуума или континуальным множеством.

Теорема 1.17. Множество действительных чисел отрезка
[0,1] равномощно множеству всех последовательностей нулей и
единиц {0,1}^ω.

◀ Каждое действительное число из отрезка [0,1] представим в
виде бесконечной дроби в двоичной системе счисления. Число 1
представим в виде периодической дроби, содержащей
бесконечное число единиц — 0,1(1). Конечные рациональные дроби
представим как бесконечные, дополнив справа бесконечным
числом нулей. Таким образом, каждое число из [0,1] представлено
в виде последовательности нулей и единиц. Кроме этого,
выбросим счетное множество всех периодических дробей вида
O,α₀α₁…α_kO(1), поскольку каждая такая дробь представляет
то же самое число, что и дробь O,α₀α₁…α_k1(0), где α_i ∈ {0,1}
для всякого i = 1,k. Легко видеть, что полученное таким
образом множество двоичных дробей равномощно множеству
{0,1}^ω▶

Следствие 1.2. [0,1] ~ 2^ℕ.

◀ Выше была доказана равномощность множеств (0,1)^ω и 2^ℕ.
Тогда имеем [0,1] ~ {0,1}^ω ~ 2^ℕ. ▶

Теорема 1.18. Следующие множества равномощны:

1. множество действительных чисел отрезка [0,1];
2. множество действительных чисел интервала (0,1);
3. множество действительных чисел отрезка [а, b];
4. множество действительных чисел интервала (а, b);
5. множество действительных чисел (числовая ось) ℝ;
6. множество всех подмножеств множества натуральных
   чисел 2^ℕ.

◀ Покажем равномощность множеств [0,1] и (0,1). Из
множества действительных чисел отрезка [0,1] выделим
двухэлементное подмножество {0,1}. Разностью этих множеств будет
множество действительных чисел интервала (0,1), и, согласно
теореме 1.14, [0,1] ~ (0,1).

Отображение у = (b — a)х + а задает биекцию множества
[0,1] на множество [а, b]. Следовательно, эти множества
номощны. Заметим, что аналогично доказывается
равномощность (0,1) и (а, b).

Покажем, что (0,1) ~ ℝ. Биекцию можно установить,
например, с помощью функции у = 1/πarctgx + 1/2.

Поскольку равномощность [0,1] и 2^ℕ ранее доказана, имеем

[0,1] ~ (0,1) ~ [а, b] ~ (а, b) ~ ℝ ~ 2^ℕ. ▶

Замечание 1.7. Заметим, что если в условиях теоремы 1.14
множество М несчетно, а N — его счетное подмножество, то
множество MN бесконечно, ибо иначе получилось бы, что
множество М = (М N) U N счетно как объединение конечного
и счетного множеств.

Таким образом, можно утверждать, что для любого
несчетного множества М и его не более чем счетного подмножества
N имеет место равенство |М N| = |М|. #

До сих пор речь шла о равенстве мощностей. Однако
мощности разных множеств можно в определенном смысле
сравнивать, говоря о большей или меньшей мощности.

Считают, что мощность множества А не превышает
мощность множества В (|А| ≤ |В|), если А равномощно некоторому
подмножеству множества В. Можно показать, что из
соотношений |A| ≤ |В| и |В| ≤ |А| следует, что |A| = |B|.

Мощность множества А считается строго меньшей
мощности множества В (|А| < |В|), если множества А и В
мощны и существует собственное подмножество С множества
В, равномощное множеству А, т.е. (А ≁ В) и (∃С ⊂ В)(А~С).

Можно доказать, что из |А| ≤ |В| и |В| ≤ |С| следует |А| ≤
|С|. Таким образом, на множестве всех мощностей (т.е.
на множестве всех классов эквивалентности по отношению ~)
установлено отношение порядка.

Из определения сразу следует, что мощность любого
конечного множества строго меньше мощности Но, а из
доказательства теоремы 1.15 вытекает, что ℵ₀ < с. Кроме того,
согласно теореме 1.9, мощность счетного множества ℵ₀
является наименьшей на множестве всех бесконечных мощностей (т.е.
мощностей бесконечных множеств). Можно сказать, что
всякое бесконечное множество не менее чем счетно.

Без доказательства приведем две важные теоремы.

Теорема 1.19 (теорема Кантора — Бернштейна).
Для любых двух множеств А и В имеет место в точности одно
из следующих трех условий: либо |А| < |B|, либо |В| < |А|, либо
|B| = |А| #

Таким образом, любые два множества сравнимы по
мощности. Другими словами, „шкала мощностей» линейно
упорядочена.

Теорема 1.20. Для любого множества А верно неравенство
|2^ℕ| > |А|. #

В силу теоремы 1.20 нет наибольшей мощности, так как для
любого множества А существует множество большей
мощности — его булеан. Заметим, что для счетного множества А
теорема 1.20 сводится к теореме Кантора 1.15.

Теорема 1.21 (теорема о квадрате). Для любого
бесконечного множества М его декартов квадрат М × М
мощен самому множеству М.

◀ Доказательство проведем для частных случаев счетного и
континуального множеств.

Сначала обратимся к счетному множеству. Для
доказательства утверждения достаточно показать, что ℕ × ℕ ~ ℕ, т.е.
задать на ℕ × ℕ некоторую нумерацию. Рассмотрим множество
A_i = {(i, j): j ∈ ℕ} упорядоченных пар. Это множество счетно
по построению. Легко видеть, что справедливо равенство

откуда, согласно теореме 1.12, вытекает счетность декартова
квадрата ℕ × ℕ множества ℕ как счетного объединения
счетных множеств.

Перейдем к континуальному множеству. Докажем, что
множество всех упорядоченных пар двоичных последовательностей
эквивалентно множеству всех таких последовательностей, т.е.
2^ℕ × 2^ℕ ~ 2^ℕ.

Паре последовательностей (α, β) поставим в соответствие
последовательность α₀, β₀, α₁, β₁, …, α_n, β_n, … Это
соответствие будет взаимно однозначным, т.е. установлена биекция
между 2^ℕ × 2^ℕ ~ 2^ℕ. ▶

Получается, что — как это ни удивительно — в квадрате
„столько же» точек, сколько и в каждой его стороне. Можно
обобщить это утверждение для произвольной конечной
декартовой степени множества М.

Следствие 1.3. Множество рациональных чисел ℚ счетно.

◀ Каждому рациональному числу, представленному
несократимой дробью a/b, однозначно соответствует упорядоченная пара
(а, b), и, напротив, любая упорядоченная пара (а, b) взаимно
простых целых чисел а и b однозначно определяет
несократимую дробь a/b и значит, рациональное число. Следовательно,
множество ℚ эквивалентно некоторому бесконечному
подмножеству множества ℤ × ℤ. Поскольку множество ℤ × ℤ счетно,
из теоремы 1.11 вытекает, что любое его бесконечное
подмножество счетно. Таким образом, множество ℚ счетно. >

В заключение приведем сводку результатов по мощностям
некоторых конечных множеств.

Теорема 1.22. Если М и N — конечные множества и
|М| = m, a |N| = n, то:

1. мощность множества всех отображений М в N равна n^m;
2. мощность множества всех биекций из N на себя равна P_n=n!;
3. мощность множества всех инъекций из М в N (m ≤ n) равна A^mn =       n!  (n-m)!      ;
4. мощность множества всех подмножеств множества N
   равна 2ⁿ;
5. мощность множества всех k-элементных подмножеств
   множества N равна C^kn =       n!  k!(n-k)!      ;
6. мощность прямого произведения М × N равна mn. #

Напомним [I], что в комбинаторике число Р_n называют
числом перестановок n элементов, число A^mn — числом
размещений без повторений из n элементов по m, число C^kn
(обозначаемое также (^nk )) — числом сочетаний из n элементов по k. Эти
числа называются также биномиальными коэффициентами, поскольку (формула бинома Ньютона).

Мощность множества — это обобщение понятия количества (числа элементов множества), которое имеет смысл для всех множеств, включая бесконечные. Существуют бо́льшие, есть ме́ньшие бесконечные множества, среди них счётное множество является самым маленьким.

Мощность множества, как и другие основные конструкции традиционной теоретико-множественной математики, может достаточно плодотворно рассматриваться и под углом зрения, отличным от широко известной интуиционистской критики в рамках альтернативной теории множеств.

Определение

Пусть даны два множества и Тогда они называются равномощными, если между ними существует биекция . Из свойств биекции следует, что равномощность является отношением эквивалентности. Мощностью или кардинальным числом множества называется соответствующий ему класс эквивалентности. Мощность множества обозначается . Тот факт, что два множества равномощны, записывается:

Связанные определения

Свойства

Упорядочение кардинальных чисел

Будем предполагать, что выполнена аксиома выбора. Будем писать, что если существует инъекция Введённое таким образом бинарное отношение на мощностях множеств не зависит от выбора представителей обоих классов эквивалентности и обладает следующими свойствами:

Таким образом введённое отношение является полным порядком на семействе мощностей. Следуя общей практике, будем также использовать строгое неравенство:

Теорема Кантора

Пусть — произвольное множество, а — его булеан. Тогда

В частности множество вещественных чисел, будучи равномощным множеству подмножеств натуральных чисел, является несчётным.

Континуум-гипотеза

Обобщённая континуум-гипотеза утверждает, что неравенство в теореме Кантора плотное, то есть для любого бесконечного множества не существует множества такого, что

.

Это означает, что мощности множеств могут быть выписаны в виде возрастающей последовательности

где

и в частности

Мощность множества

Множество равномощно множеству , если существует биекция .

Из того, что существует биекция , следует, что соответствие есть биекция на . Поэтому если равномощно , то и равномощно , и мы можем говорить, что множества и равномощны.

Факт равномощности множеств и будем записывать так: .

Из определения равномощности и свойств биекции также следует, что для любого множества имеет место (тождественное отображение есть биекция множества на себя); а для любых множеств из и следует (композиция биекций есть биекция).

Таким образом, отношение равномощности множеств есть отношение эквивалентности, заданное на «множестве всех множеств» (на самом деле на множестве всех подмножеств некоторого универсального множества).

Примечание. Зачастую в литературе по теории множеств равномощные множества и называют «эквивалентными множествами». Однако следует различать общее понятие отношения эквивалентности и его частный случаи — эквивалентность, или равномощность, множеств.

Если мы обозначим через класс эквивалентности множества по отношению , то утверждение о равномощности множеств и можно записать так: .

Этот класс эквивалентности называют мощностью множества .

Конечные множества и равномощны тогда и только тогда, когда множества и состоят из одного и того же числа элементов, т.е. . Отсюда, в частности, следует, что конечное множество не является равномощным никакому своему собственному подмножеству. Это свойство конечных множеств можно сформулировать так.

---

Теорема 1.8. Если — конечное множество и — инъекция, то она является сюръекцией и, следовательно, биекцией.

В силу приведенных выше соображений мощностью конечного множества можно считать натуральное число , так как, задавая такое число, мы задаем и класс всех (попарно равномощных) множеств вида . Обратно, каждый такой класс однозначно определяет натуральное число как число элементов в каждом множестве данного класса. Естественно считается, что мощность пустого множества равна нулю.

Перейдем теперь к исследованию мощности бесконечных множеств. Таковы хорошо известные нам ещё со школы числовые множества и .

Любое множество, равномощное множеству всех натуральных чисел, называют счетным. Мощность счетного множества обозначают (читается «алеф нуль»).

Любую биекцию называют нумерацией счетного множества ; если элемент есть для некоторого , то этот элемент обозначаем через , называя натуральное число номером элемента относительно данной нумерации .

Таким образом, элементы счетного множества можно перенумеровать, записав их в виде последовательности или . Другими словами, счетное множество есть область значений некоторой функции натурального аргумента.

Пример 1.21. а. Множество всех нечетных натуральных чисел счетно. Нумерацию можно задать так:

б. Множество всех натуральных чисел, делящихся на заданное число , счётно. Нумерацию можно задать так: . В частности, при получаем, что множество всех четных чисел счётно. Этот и предыдущий примеры показывают, что бесконечное (счетное) множество может иметь собственное равномощное ему подмножество.

в. Множество всех целых чисел счётно. Нумерацию можно установить так:

---

Свойства счётных множеств

Рассмотрим свойства счетных множеств.

Теорема 1.9. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Пусть — бесконечное множество. Значит, оно не пусто и существует элемент . Положим . Множество не пусто, так как в противном случае имело бы место равенство , что противоречит предположению о бесконечности . Выберем элемент и положим

Множество также не пусто, поскольку иначе мы бы имели и множество было бы конечным.

Методом математической индукции можно показать, что для любого множество , где , не пусто. Тогда существует элемент и . Таким образом, все элементы , попарно различны и множество счетно, а его нумерация может быть задана так: .

---

Теорема 1.10. В любом бесконечном множестве можно выделить два не пересекающихся между собой счетных подмножества.

Доказательство. Разобьем множество натуральных чисел на два подмножества:

(множество нечетных чисел),
(множество четных чисел).

Оба этих множества счетны (см. пример 1.21).

Согласно теореме 1.9, бесконечное множество содержит некоторое счетное подмножество . Пусть установлена некоторая его нумерация. Разобьем это подмножество на два подмножества: всех элементов с четными и всех элементов с нечетными номерами. По построению эти подмножества не пересекаются и являются счетными, поскольку счётны множества четных и нечетных чисел.

---

Теорема 1.11. Любое подмножество счетного множества конечно или счетно.

Доказательство.Пустое подмножество конечно по определению. Пусть — счетное множество, а — его некоторое непустое подмножество. Поскольку множество счетно, можно считать, что задана некоторая его нумерация. Следовательно, каждый элемент подмножества имеет свой номер. Запишем номера элементов множества в порядке возрастания: . Если среди них есть наибольший номер , то подмножество конечно. В противном случае получим счетное подмножество , нумерация которого установлена так: .

Если множество конечно или счетно, его называют не более чем счетным. Семейство множеств называют не более чем счетным, если множество (индексов) не более чем счетно.

Теорема 1.12. Объединение любого не более чем счетного семейства счетных множеств счетно.

Пусть — конечное или счетное семейство счетных множеств. Рассмотрим сначала случай, когда множества попарно не пересекаются.

В этом случае нумерация объединения конечного семейства счетных множеств может быть проведена по схеме, изображенной на рис. 1.14, а нумерация объединения счетного семейства счетных множеств — по схеме, приведенной на рис. 1.15.

Пусть теперь — произвольное счетное семейство счетных множеств, т.е. множества могут пересекаться. В этом случае, применяя указанные на рис. 1.14 и 1.15 схемы нумерации к конечному или счетному объединению счетных множеств, следует пропускать каждый раз элементы, которые уже получили номера.

Полезно отметить также и следующий факт.

Теорема 1.13. Объединение конечного и счетного множеств счетно.

Теорема 1.14. Пусть — бесконечное множество, а — его не более чем счетное подмножество. Если множество бесконечно, то оно равномощно множеству .

По теореме 1.10 в множестве , поскольку оно бесконечно, можно выбрать счетное подмножество . Ясно, что . Множество является счетным как объединение двух счетных множеств или объединение счетного и конечного множеств. Поэтому существует биекция . Поскольку

то требуемую биекцию на строим так: на подмножестве , общем для и , эта биекция совпадает с тождественным отображением; на подмножестве эта биекция есть биекция .

Следствие 1.1. Если — бесконечное множество, а — не более чем счетное множество, то .

Существуют бесконечные множества, не являющиеся счетными. Это вытекает из следующих рассуждений.

Рассмотрим множество всех последовательностей нулей и единиц, т.е. последовательностей вида

, где для каждого .

Обозначим множество таких «двоичных» последовательностей через .

---

Теорема Кантора

Теорема 1.15 (Кантора). Множество не есть счетное множество.

Пусть множество и счетное. Тогда существует биекция . Выпишем все последовательности

Построим последовательность : положим , если , и , если . Ясно, что эта последовательность не совпадает ни с одной из последовательностей , а это противоречит допущению, что любая последовательность из есть для некоторого .

Итак, не равномощно .

В то же время содержит подмножество последовательностей, в каждой из которых только один член отличен от нуля. Это подмножество равномощно множеству всех одноэлементных подмножеств и, следовательно, самому . Следовательно, множество бесконечно, но не равномощно счетному множеству и потому не является счетным.

---

Теорема 1.16. Множество всех подмножеств множества натуральных чисел и множество равномощны.

Определим отображение множества на множество следующим образом: если , то при и при .

Тем самым подмножеству ставится в соответствие последовательность , i-й член которой равен единице тогда и только тогда, когда число есть элемент множества . Докажем, что — биекция на .

Покажем, что отображение — инъекция. Пусть и — различные подмножества . Тогда найдется число или число . В первом случае в последовательности i-й член будет равен единице, а в последовательности — нулю. Таким образом, . Во втором случае и опять . Следовательно, отображение — инъекция.

Покажем, что — сюръекция. Возьмем произвольную последовательность . Образуем множество . Ясно, что . Таким образом, для любой последовательности существует подмножество , такое, что . Следовательно, — сюръекция.

Таким образом, мы показали, что — биекция, а множества и равномощны.

---

Множество мощности континуум (континуальное множество)

Мощность множества обозначают и называют мощностью континуума, а любое множество, эквивалентное множеству , называют множеством мощности континуума или континуальным множеством.

Теорема 1.17. Множество действительных чисел отрезка равномощно множеству всех последовательностей нулей и единиц .

Каждое действительное число из отрезка представим в виде бесконечной дроби в двоичной системе счисления. Число 1 представим в виде периодической дроби, содержащей бесконечное число единиц — . Конечные рациональные дроби представим как бесконечные, дополнив справа бесконечным числом нулей. Таким образом, каждое число из представлено в виде последовательности нулей и единиц. Кроме этого, выбросим счетное множество всех периодических дробей вида , поскольку каждая такая дробь представляет то же самое число, что и дробь , где для всякого . Легко видеть, что полученное таким образом множество двоичных дробей равномощно множеству .

Следствие 1.2. .

Выше была доказана равномощность множеств и . Тогда имеем .

Теорема 1.18. Следующие множества равномощны:

1) множество действительных чисел отрезка ;
2) множество действительных чисел интервала ;
3) множество действительных чисел отрезка ;
4) множество действительных чисел интервала ;
5) множество действительных чисел (числовая ось) ;
6) множество всех подмножеств множества натуральных чисел .

Покажем равномощность множеств и . Из множества действительных чисел отрезка выделим двухэлементное подмножество . Разностью этих множеств будет множество действительных чисел интервала , и, согласно теореме 1.14, .

Отображение задает биекцию множества на множество . Следовательно, эти множества равномощны. Заметим, что аналогично доказывается равномощность и .

Покажем, что . Биекцию можно установить, например, с помощью функции .

Поскольку равномощность и 2W ранее доказана, имеем

Замечание 1.7. Заметим, что если в условиях теоремы 1.14 множество несчетно, а — его счетное подмножество, то множество бесконечно, ибо иначе получилось бы, что множество счетно как объединение конечного и счетного множеств.

Таким образом, можно утверждать, что для любого несчетного множества и его не более чем счетного подмножества имеет место равенство .

---

Сравнение мощностей множеств

До сих пор речь шла о равенстве мощностей. Однако мощности разных множеств можно в определенном смысле сравнивать, говоря о большей или меньшей мощности.

Считают, что мощность множества не превышает мощность множества , если равномощно некоторому подмножеству множества . Можно показать, что из соотношений и следует, что .

Мощность множества считается строго меньшей мощности множества , если множества и неравномощны и существует собственное подмножество множества , равномощное множеству , то есть

и .

Можно доказать, что из и следует .

Таким образом, на множестве всех мощностей (т.е. на множестве всех классов эквивалентности по отношению ) установлено отношение порядка.

Из определения сразу следует, что мощность любого конечного множества строго меньше мощности , а из доказательства теоремы 1.15 вытекает, что . Кроме того, согласно теореме 1.9, мощность счетного множества является наименьшей на множестве всех бесконечных мощностей (т.е. мощностей бесконечных множеств). Можно сказать, что всякое бесконечное множество не менее чем счетно.

Без доказательства приведем две важные теоремы.

---

Теорема Кантора–Бернштейна

Теорема 1.19 (Кантора–Бернштейна). Для любых двух множеств и имеет место в точности одно из следующих трех условий: либо , либо , либо .

Таким образом, любые два множества сравнимы по мощности. Другими словами, «шкала мощностей» линейно упорядочена.

Теорема 1.20. Для любого множества верно неравенство .

В силу теоремы 1.20 нет наибольшей мощности, так как для любого множества существует множество большей мощности — его булеан. Заметим, что для счетного множества теорема 1.20 сводится к теореме Кантора 1.15.

Теорема 1.21 (теорема о квадрате). Для любого бесконечного множества его декартов квадрат равномощен самому множеству .

Доказательство проведем для частных случаев счетного и континуального множеств.

Сначала обратимся к счетному множеству. Для доказательства утверждения достаточно показать, что , т.е. задать на некоторую нумерацию. Рассмотрим множество упорядоченных пар. Это множество счетно по построению. Легко видеть, что справедливо равенство

откуда, согласно теореме 1.12, вытекает счетность декартова квадрата множества как счетного объединения счетных множеств.

Перейдем к континуальному множеству. Докажем, что множество всех упорядоченных пар двоичных последовательностей эквивалентно множеству всех таких последовательностей, т.е. .

Паре последовательностей поставим в соответствие последовательность

Это соответствие будет взаимно однозначным, т.е. установлена биекция между и .

---

Получается, что — как это ни удивительно — в квадрате «столько же» точек, сколько и в каждой его стороне. Можно обобщить это утверждение для произвольной конечной декартовой степени множества .

Следствие 1.3. Множество рациональных чисел счетно.

Каждому рациональному числу, представленному несократимой дробью , однозначно соответствует упорядоченная пара , и, напротив, любая упорядоченная пара взаимно простых целых чисел и однозначно определяет несократимую дробь и, значит, рациональное число. Следовательно, множество эквивалентно некоторому бесконечному подмножеству множества . Поскольку множество счетно, из теоремы 1.11 вытекает, что любое его бесконечное подмножество счетно. Таким образом, множество счетно.

---

В заключение приведем сводку результатов по мощностям некоторых конечных множеств.

Теорема 1.22. Если и — конечные множества и , a , то:

1) мощность множества всех отображений в равна ;
2) мощность множества всех биекций из на себя равна
3) мощность множества всех инъекций из в равна ;
4) мощность множества всех подмножеств множества равна ;
5) мощность множества всех k-элементных подмножеств множества равна ;
6) мощность прямого произведения равна .

Напомним, что в комбинаторике число называют числом перестановок элементов, число — числом размещений без повторений из элементов по , число (обозначаемое также ) — числом сочетаний из элементов по . Эти числа называются также биномиальными коэффициентами, поскольку

(формула бинома Ньютона).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Часто
возникает необходимость сравнивать
множества по числу элементов. В этом
случае возникает понятие мощности
множества.

Определение.
Множества
А и В называются эквивалентными
(обозначается А~В) если существует
биекция f:
АВ
(т.е. между ними можно установить взаимно
однозначное соответствие (в.о.с.)).

Очевидно,
что два конечных множества эквивалентны
тогда и только тогда, когда они имеют
одинаковое число элементов. Если два
множества бесконечны и между ними можно
установить в.о.с., то они обладают также
чем-то общим, что мы будем называть
мощностью. Итак, любые два эквивалентных
множества (конечные или бесконечные)
имеют одинаковую мощность или являются
равномощными. Или более точное определение.

Определение.
Мощностью множества А называется класс
всех множеств, эквивалентных множеству
А (мощность обозначается
).

Имеется
три возможности:

а)
если А — конечное множество, имеет n
элементов, то
=n;

б)
если А — бесконечное множество и
эквивалентно множеству натуральных
чисел N,
то А называют счётным множеством,
записывают
=.
Таким образом, у счётного множества все
элементы можно пронумеровать;

в)
существуют бесконечные множества,
которые нельзя привести во в.о.с. с
множеством натуральных чисел. Например,
установлено, что множество всех
действительных чисел отрезка [0,1] не
является счётным (теорема Кантора).
Принято мощность этого множества
называть континуум (часто обозначается
с), а множества такой мощности
континуальными.

Доказано,
что если А континуальное множество, то
,
т.е. мощность континуума равна мощности
множества всех подмножеств счётного
множества. Вообще, для любого множества
А:
Р(А)=,
гдеР(А)
– булеан.

Примеры
счётных множеств:

а)
множество целых чисел Z,
а также
;

б)
множество рациональных чисел Q;

в)
любое бесконечное подмножество множества
N,
например, {2,4,6,8,…};

г)
(
вообще).

Примеры
континуальных множеств:

а)
множество всех действительных чисел R
или множество точек числовой оси;

б)
множество всех точек плоскости
(пространства)
;

в)
множество всех подмножеств счётного
множества ( т.е. булеан счётного множества).

Как
показано в теории множеств, для множества
любой мощности множество его подмножеств
имеет более высокую мощность. Поэтому
не существует множества максимальной
мощности. На мощность множеств можно
смотреть как на новый объект, называемый
кардинальным числом или кардиналом.
Примерами кардиналов могут быть:

а)
любое натуральное число (как мощность
конечного множества);

б)
и
т.д.

Отметим,
что существование биекции между двумя
множествами позволяет перенести изучение
свойств с одного множества на другое,
что многое упрощает, например, некоторые
свойства конечного множества А,
=n
можно изучать по множеству {0,1,2,3,…n-1}.

2 Элементы математической логики

2.1 Высказывания и логические операции

Логику
чаще всего определяют как анализ методов
рассуждений. Эти методы позволяют
определить истинность или ложность
того или иного рассуждения, причём
логику интересует прежде всего форма,
а не содержание доводов в этом рассуждении.
Если при этом применяют математический
аппарат и изучают математические
рассуждения, то логику называют
математической логикой. Математическая
логика играет большую роль в основах
математики, она – фундамент, на котором
построено здание математики. Логика
применяется в информатике для построения
компьютерных программ и доказательства
их корректности. Понятия, методы и
средства математической логики лежат
в основе современных информационных
технологий.

Определение.
Высказыванием
называется повествовательное предложение,
о котором в данной ситуации можно
говорить, что оно истинно или ложно.

Пример
2.1.1
–
Высказывание:
«дважды два – четыре» — истинно;
высказывание: «тенге – российская
валюта» — ложно.

Определение.
Простое
(элементарное) высказывание рассматривается
как некое неделимое целое. Обозначается
А, В, С,…,Р,…; сложным (составным) называется
высказывание, составленное из простых
с помощью логических связок (операций).

Основными
логическими операциями (связками)
являются:

а)
конъюкция (операция «и», логическое
произведение).

Конъюнкцией
двух высказываний P и Q (обозначается
,
читается “Р и Q”) называется высказывание,
истинное тогда и только тогда, когда
истинны оба высказывания и ложное во
всех остальных случаях;

б)
дизъюнкция (операция «или», логическая
сумма). Дизъюнкцией двух высказываний
P и Q (обозначается
,
читается “Р или Q”) называется
высказывание, ложное, если оба высказывания
ложные и истинное во всех остальных
случаях;

в)
отрицание (инверсия). Отрицанием
высказывания P (обозначается
,
читается “не Р”) называется высказывание,
истинное, когда P ложное и ложное, когда
P истинное;

г)
импликация (логическое следование).
Импликацией
двух
высказываний P и Q (обозначается
,,
читается, “если Р, то Q”, “Р влечёт Q”)
называется высказывание, ложное, когда
Р истинное, а Q ложное и истинное во всех
остальных случаях;

д)
эквиваленция (эквивалентность).
Эквиваленцией двух высказываний

P
и Q (обозначается
,
читается “Р эквиваентно Q”, “Р тогда
и только тогда, когда Q”) называется
высказывание, истинное, когда P и Q — оба
истинны или оба ложны и ложное во всех
остальных случаях.

Формулы
алгебры логики

Рассмотрим
содержание логики высказываний, используя
язык алгебры логики, которая изучает
строение логических высказываний (т.е.
логических формул) и способы установления
их истинности с помощью алгебраических
методов.

Поставим
в соответствие высказыванию P логическую
переменную х,
которая принимает значение 1, если Р
истинно, 0, если Р ложно. Из логических
переменных можно с помощью логических
операций составлять различные конструкции,
которые являются формулами алгебры
логики.

Определение
формулы:

а)
любая логическая переменная является
формулой;

б)
если
иформулы,
то выражения,являются формулами;

в)
никаких других формул, кроме построенных
в а) и б) нет.

Если
формула
построена
из логических переменных, принадлежащих
множеству,
то будем писать.

Действия
логических операций задаются таблицами
истинности, в каждой строке которых
отмечены различные наборы значений
переменных и соответствующее им значение
формулы. Составим таблицы истинности
логических операций в соответствии с
их определением:

Т
а б л и ц а 2.1.1

0	0	0	0	1	1	1
0	1	0	1	1	0
1	0	0	1	0	0	0
1	1	1	1	1	1

Таблицы
истинности придают формулам смысл в
отличие от формальных законов их
построения, данных в определении формулы.

Исходя
из таблиц истинности для логических
операций, можно строить таблицы истинности
для произвольных формул.

Пример
2.1.2
— Для формулы
=таблица
истинности имеет вид:

Т
а б л и ц а 2.1.2

0	0	0	1	1	1	1
0	0	1	1	1	1	1
0	1	0	1	0	1	1
0	1	1	1	0	1	1
1	0	0	0	1	1	1
1	0	1	0	1	1	1
1	1	0	0	0	0	1
1	1	1	0	0	0	0

Введём
новые важные логические операции,
добавляя к пяти основным ещё три операции
(тем самым расширим понятие логической
формулы):

е)
штрих Шеффера
(антиконъюнкция).
Обозначается
.

По
определению
,
или;

ж)
стрелка Пирса
(антидизъюнкция).
Обозначается
.

По
определению
или;

и)
кольцевая сумма (логическое сложение,
сложение по модулю два).

Обозначается
.
Определяетсяили.

Составим
таблицы истинности этих операций, исходя
из определений.

Т
а б л и ц а 2.1.3

0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	0	0	0

При
тождественных преобразованиях, при
составлении формул важно знать приоритеты
операций (какая сильнее, какая слабее),
как раскрывать скобки. Для этих целей
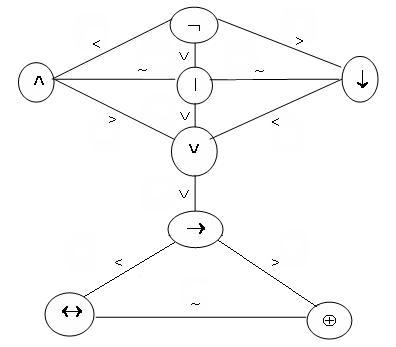
приняты следующие соглашения:

а)
внешние скобки не пишутся, например,
вместо
,
будем писать;

б)
на множестве
вводится
транзитивное отношение

«>»
— быть более сильным и отношение «~» —
быть равносильным, по правилам, указанным
на схеме:

Рисунок
2.1.1

Согласно
этим соглашениям недостающие скобки в
формуле расставляют последовательно,
начиная с наиболее сильных связок и
кончая наиболее слабыми, а для равносильных
связок расстановка скобок выполняется
слева направо.

Пример
2.1.3
–

а)
в формуле
скобки
расставляются так:;

б)
в формуле
скобки
расставляются так:;

в)
в формуле
скобки
опустить нельзя, т.к. в силу наших
соглашений выражениюсоответствует
формула.

Соседние файлы в предмете Математика

• #
• #
• #
• #
• #
• #
• #

Привет, Вы узнаете про мощность множества, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
мощность множества, кардинальное число множества, кардинальное число, кардинал , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..

мощность множества ,

кардинал ьное число мно́жества (лат. cardinalis ← cardo «главное обстоятельство; основа; сердце») — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.

В основе этого понятия лежат естественные представления о сравнении множеств:

1. Любые два множества, между элементами которых может быть установлено взаимно-однозначное соответствие (биекция), содержат одинаковое количество элементов (имеют одинаковую мощность, равномощны).
2. Обратно: равномощные множества должны допускать такое взаимно-однозначное соответствие.
3. Часть множества не превосходит полного множества по мощности (то есть по количеству элементов).

До построения теории мощности множеств множества различались по признакам: пустое/непустое и конечное/бесконечное, также конечные множества различались по количеству элементов. Бесконечные же множества нельзя было сравнить.

Мощность множеств позволяет сравнивать бесконечные множества. Например, счетные множества являются самыми «маленькими» бесконечными множествами.

Мощность множества обозначается через . Иногда встречаются обозначения , и .

блок схема алгоритма определения мощности множества

Кардинальным числом или коротко кардиналом в теории множеств называется объект, который характеризует мощность множества. Кардинальное число какого-либо множества A обозначается как |A|, либо Card A.

Для конечного множества A кардинальное число |A| есть натуральное число, которое означает количество элементов этого множества. Для бесконечных множеств кардинальное число является обобщением понятия числа элементов.

Хотя кардинальные числа бесконечных множеств не имеют отражения в натуральных числах, но их можно сравнивать. Пусть A и B — бесконечные множества, тогда логически возможны следующие четыре случая:

1. Существует взаимно-однозначное соответствие между A и B, т.е. A ~ B и |A|=|B|.
2. Существует взаимно-однозначное соответствие между множеством A и некоторым собственным подмножеством B’ множества B. Тогда говорят, что мощность множества A не больше мощности множества B и записывают |A|≤|B|.
3. Множество A равномощно некоторому подмножеству множества B, и наоборот, множество B равномощно некоторому подмножеству множества A, то есть A~B’ ⊆ B и B~A’ ⊆ A. По теореме Кантора-Бернштейна в этом случае выполняется A ~ B, то есть |A|=|B|.
4. Не существует взаимно-однозначного соответствия между множеством A и любым подмножеством множества B и, также не существует взаимно-однозначного соответствия между множеством B и любым подмножеством множества A. Из этого следует, что мощности множеств A и B несопоставимы между собой.

Однако более глубокие исследования в теории множеств показали, что, опираясь на аксиому выбора, можно доказать невозможность существования четвертого случая.

Таким образом, мощности любых двух множеств A и B всегда сопоставимы между собой. То есть для кардинальных чисел |A| и |B| произвольных множеств A и B выполняется одно из трех соотношений: |A|=|B|, |A|≤|B| или |B|≤|A|. Если |A|≤|B|, но множество A неравномощно множеству B, то тогда |A|<|B|.

Определение

Предполагая аксиому выбора верной, мощность множества формально определяется как наименьшее порядковое число , при котором между и можно установить биективное соответствие. Данное определение также называется распределением кардинальных чисел по фон Нейману.

Если не принимать аксиому выбора, то требуется иной подход. Самое первое определение мощности множества (оно неявно присутствует в работах Кантора и явным образом сформулировано у Фреге, а также в Principia Mathematica) представляет собой класс всех множеств, равномощных . В аксиоматических системах, основанных на теории ZFC, такое определение неприменимо, поскольку при непустом такая совокупность слишком велика, чтобы подходить под определение множества. Точнее, если , то существует инъективное отображение универсального множества в , при котором каждое множество переходит в , откуда, в силу аксиомы ограничения размера следует, что — собственный класс. Данное определение можно использовать в теории типов и «новых основаниях»^[en], а также в связанных с ними аксиоматических системах. В случае ZFC определение можно использовать, если ограничить коллекцию равномощными множествами с наименьшим рангом (этот прием, предложенный Даной Скоттом, работает благодаря тому, что совокупность объектов, обладающих заданным рангом, является множеством).

Формальный порядок среди кардинальных чисел вводится следующим образом: означает, что множество можно инъективно отобразить на . Согласно теореме Кантора — Бернштейна, из пары неравенств и следует, что . Аксиома выбора эквивалентна утверждению о том, что для любых множеств и выполняется, по крайней мере, одно из неравенств или .

Множество называется бесконечным по Дедекинду^[en], если в нем существует такое собственное подмножество , что . В противном случае множество называется конечным по Дедекинду. Конечные кардинальные числа совпадают с обычными натуральными числами — иначе говоря, множество конечно тогда и только тогда, когда при некотором натуральном . Все остальные множества бесконечны. При соблюдении аксиомы выбора можно доказать, что определения по Дедекинду совпадают со стандартными. Кроме того, можно доказать, что мощность множества натуральных чисел (алеф-нуль, или алеф-0 — название образовано от первой буквы еврейского алфавита ) представляет собой наименьшее бесконечно большое кардинальное число, то есть в любом бесконечном множестве есть подмножество мощности . Следующее по порядку кардинальное число обозначается и так далее, число алефов бесконечно. Любому порядковому числу соответствует кардинальное число , причем таким образом можно описать любое бесконечно большое кардинальное число.

Связанные определения

• Для мощностей, как и в случае конечных множеств, имеются понятия: «равенство», «больше», «меньше». То есть для любых множеств и возможно только одно из трех:
  1. , или и равномощны;
  2. , или мощнее , то есть содержит подмножество, равномощное , но и не равномощны;
  3. , или мощнее — в этом случае содержит подмножество, равномощное , но и не равномощны.
• Множества и называются эквивалентными, если существует взаимно однозначное отображение множества на множество .

Примеры

• Множество называется счетным, если оно равномощно множеству всех натуральных чисел . Счетными множествами являются:

• Бесконечные множества, неравномощные множеству , называются несчетными. По теореме Кантора несчетным является множество бесконечных последовательностей, составленных из цифр 0 и 1. Мощность этого множества называется континуум.

• Мощность множества вещественных чисел равна континууму.

Свойства

• Два конечных множества равномощны тогда и только тогда, когда они состоят из одинакового числа элементов. То есть для конечного множества понятие мощности совпадает с привычным понятием количества.
• Для бесконечных множеств мощность множества может совпадать с мощностью своего собственного подмножества, например .
• Более того, множество бесконечно тогда и только тогда, когда оно содержит равномощное собственное (то есть не совпадающее с основным множеством) подмножество.
• Любое бесконечное множество равномощно множеству всех его конечных подмножеств.
• Теорема Кантора Множество всех подмножеств множества A имеет большую мощность, чем A, или .
  • В частности существует множество мощнее любого данного.
• С помощью канторова квадрата можно также доказать следующее полезное утверждение: Декартово произведение бесконечного множества A с самим собой равномощно A.
• Мощность декартова произведения:

  

• Формула включения-исключения для двух и трех множеств:

  

  

• Мощность симметрической разности двух и трех множеств:

  

  

Арифметика кардинальных чисел

Обычные арифметические операции над числами натурального ряда можно обобщить на случай кардинальных чисел. Можно также показать, что в случае конечных кардинальных чисел эти операции совпадают с соответствующим арифметическими действиями над числами. Помимо этого, операции над кардинальными числами сохраняют многие свойства обычных арифметических операций.

Следующее по порядку кардинальное число

При соблюдении аксиомы выбора для каждого кардинального числа можно определить следующее за ним число , причем между и нет других кардинальных чисел. Если конечно, то следующее кардинальное число совпадает с . В случае бесконечных следующее кардинальное число отличается от следующего порядкового числа.

Сложение кардинальных чисел

Если множества и не имеют общих элементов, то сумма мощностей определяется мощностью их объединения. При наличии общих элементов исходные множества можно заменить непересекающимися множествами той же мощности — например, заменить на , а на .

Нейтральность нуля относительно сложения:

Ассоциативность:

Коммутативность:

Монотонность (неубывание) сложения по обоим аргументам:

Сумму двух бесконечных кардинальных чисел можно легко вычислить при соблюдении аксиомы выбора. Если одно из чисел или бесконечно, то

Вычитание

При соблюдении аксиомы выбора для любого бесконечного кардинального числа и произвольного кардинального числа существование , при котором , эквивалентно неравенству . Такое единственно (и совпадает с ) тогда и только тогда, когда .

Умножение кардинальных чисел

Произведение двух кардинальных чисел выражается через декартово произведение множеств:

Свойства нуля:

Нейтральность единицы относительно умножения:

Ассоциативность:

Коммутативность:

Монотонность (неубывание) умножения по обоим аргументам:

Дистрибутивность умножения относительно сложения:

По аналогии со сложением, произведение двух бесконечных кардинальных чисел можно легко вычислить при соблюдении аксиомы выбора. Если числа и отличны от нуля и хотя бы одно из них бесконечно, то

Деление

При соблюдении аксиомы выбора для любой пары кардинальных чисел и , где бесконечно, а не равно нулю, существование , при котором , эквивалентно неравенству . Такое единственно (и совпадает с ) тогда и только тогда, когда .

Возведение кардинальных чисел в степень

Возведение в степень определяется следующим образом:

,

где обозначает множество всех функций из в .

(в частности, ), см. Пустая функция

Монотонность:

Заметим, что представляет собой мощность булеана и, следовательно, для любого множества (см. Диагональный метод Кантора). Отсюда следует, что среди кардинальных чисел нет наибольшего (поскольку для любого кардинального числа можно указать большее число ). В действительности класс всех кардинальных чисел является собственным (хотя в некоторых аксиоматизациях теории множество этого доказать нельзя — к таковым, например, относится система «Новых оснований»^[en]).

Все последующие утверждения, приведенные в этом разделе, опираются на аксиому выбора.

Если и — конечные числа, большие 1, а — бесконечное кардинальное число, то Если кардинальное число бесконечно, а конечно и отлично от нуля, то .

Если и , причем хотя бы одно из них бесконечно, то

.

Используя теорему Кенига, можно доказать, что для любого бесконечного кардинального числа выполняются неравенства:

,

где обозначает конфинальность .

Извлечение корней

При условии соблюдения аксиомы выбора для любого бесконечного кардинала и конечного кардинала существует кардинальное число , при котором , причем .

Логарифмы

При соблюдении аксиомы выбора кардинальное число , удовлетворяющее условию , при заданном бесконечном и конечном , существует не всегда. Если же такое существует, то оно бесконечно и меньше , причем любое конечное кардинальное число также будет удовлетворять равенству .

Логарифмом бесконечного кардинального числа называется наименьшее кардинальное число , удовлетворяющее условию . Несмотря на то, что логарифмы бесконечно больших кардинальных чисел лишены некоторых свойств, характерных для логарифмов положительных вещественных чисел, они оказываются полезными в некоторых областях математики — в частности, при изучении кардинальных инвариантов топологических пространств.

Континуум-гипотеза

Согласно утверждению континуум-гипотезы, между и не существует других кардинальных чисел. Кардинальное число также обозначается и представляет собой мощность континуума (то есть множества вещественных чисел). В данном случае . Обобщенная континуум-гипотеза отрицает существование кардинальных чисел, заключенных строго между и , для любого бесконечного множества . Континуум-гипотеза является независимой от стандартной аксиоматизации теории множеств, то есть системы аксиом Цермело-Френкеля в сочетании с аксиомой выбора (см. Теория множеств Цермело-Френкеля).

Вау!! 😲 Ты еще не читал? Это зря!

• Порядковое число

• ТРАНСФИНИТНОЕ ЧИСЛО

В общем, мой друг ты одолел чтение этой статьи об мощность множества. Работы в переди у тебя будет много. Смело пишикоментарии, развивайся и счастье окажется в ваших руках.
Надеюсь, что теперь ты понял что такое мощность множества, кардинальное число множества, кардинальное число, кардинал
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.