Как найти mrs для функций

$MRS$ (предельная норма замещения) – это мера, которая позволяет оценить максимальный объем продукции, от которой покупатель в состоянии отказаться ради приобретения других товаров.

Понятие предельной нормы замещения

Повышение полезности от покупки одних товаров должно уравновесить уменьшение потребления других. В конечном счете данные замещения обеспечивают одинаковую полезность на одинаковые денежные затраты личного бюджета потребителей. Повышая полезность своих расходов, рациональные покупатели стремятся уравновесить и взаимно замещаемые товары, и цены данных товаров. Именно цены позволяют достичь равновесия в пропорциях взаимного замещения продукции. Предельная норма замены (замещения) одной продукции другой должна равняться соотношению цен взаимозаменяемых товаров. К примеру, если представить, что $X$ и $Y$ – это товары, замещаемые потребителем с целью максимизации полезности своих денежных затрат на их покупку, то он будет руководствоваться нормой замещения для данных товаров, которая выражается следующим равенством:

$MRS х,у = MUx / MUy = Px / Py$.

Для рационального потребителя максимизация полезности достигается при распределении его бюджета таким образом, что предельная полезность денежной единицы затрат будет одинаковой для каждого приобретаемого товара. Если же полезность от расхода дополнительных единиц денежных затрат на товар $X$ будет выше, чем от единицы денежных затрат на товар $Y$ то покупатель будет стараться максимизировать общую полезность путем приращения покупок товаров $X$, и наоборот.

Со временем предельная полезность приобретаемых товаров снизится, а потребитель уменьшит приращение затрат денежных средств на его покупку, перераспределяя их на иные товары, имеющие для покупателя предельную полезность несколько выше.

Распределяя постоянно денежные затраты из фиксированного бюджета, потребители обеспечивают равновесие и доступное им максимальное благосостояние в том случае, когда предельная полезность каждых дополнительных денежных единиц затрат одинакова для всех приобретаемых товаров.

Очевидно, что нарушается принцип равной предельной полезности затрат денежных средств, когда предельная полезность товаров $X$ и $Y$ вдвое или втрое выше их стоимости.

Особенности предельной нормы замещения

Как правило все стандартные кривые безразличия характеризуются не только отрицательным наклоном, но и вогнуты к началу координат. Степень вогнутости прямо зависит от степени замещения одних товаров другими.

Предельная норма замены товаром $Q_1$ товара $Q_2$ показывает то число товара $Q_2$, которым покупатель готов пожертвовать для покупки дополнительной единицы $Q_1$, с неизменным уровнем общего удовлетворения

$MRS = ∆ Q_2 / ∆ Q_1$

Данное соотношение будет всегда отрицательным из-за убывающего характера кривой безразличия. Для удобства иногда в правой части ставится минус, что делает значение $MRS$ положительным. Если описать зависимость количества $Q_1, Q_2$ и уровня полезности $U$ в виде функции $Q_2 = f(Q_1)$, то предельная норма замены будет равняться производной функции полезности: $MRS = f(Q_1)$.

Анализируя предельную норму замены необходимо учитывать некоторые особенности:

• Максимизация полезности продукции для покупателя при распределении его бюджета достигается в том случае, когда идентична предельная полезность какого-либо объекта затрат;
• Если уровень полезности дополнительного товара выше, то покупатель имеет право свести к минимуму полезность путем приращения покупок интересующих товаров;
• Предельную полезность на приобретаемые товары можно снизить при условии, что потребитель уменьшит приращение своих финансовых расходов на покупку товаров, распределяя при этом свои средства на приобретение другой продукции с большей полезностью;
• Постоянное перераспределение финансовых расходов из личного бюджета позволяет потребителям обеспечивать максимальное равновесие и благосостояние в то время, когда идентична наибольшая полезность для дополнительных товаров;
• Будет нарушен принцип предельной полезности тогда, когда полезность одних товаров в несколько раз выше их цены. В такой ситуации предпочтение будет отдано объектам с большей полезностью. Уменьшая объемы закупок товаров с меньшей полезностью, потребитель будет оптимизировать свои расходы и приближать их к условной равновесной точке.

Свойства $MRS$

При движении по кривой безразличия степень замещения товара $Q_2$ товаров $Q_1$ не будет оставаться постоянной (Рисунок 1).

При перемещении по кривой предельная норма замены будет уменьшаться, поскольку оставшиеся единицы товара $Q_2$ будут приобретать в глазах покупателя большую ценность, а дополнительные товары $Q_1$ будут приносить все меньшее дополнительное удовлетворение.

Перечислим важнейшие свойства $MRS$:

1. Предельная норма замены товара $Q_2$ товаром $Q_1$ равняется отношению их предельной полезности, т.е. $MU_1$ к $MU_2$. — $∆ Q_2 / ∆ Q_1 = MU_1 / MU_2$. Отрицательный знак означает, что чем больше товаров $Q_1$, то тем меньше должно быть товаров $Q_2$ в потребительском наборе, для того, чтобы совокупная полезность оставалась неизменной.
2. Если две любые точки на кривой безразличия сливаются воедино, то $MRS$ будет равняться тангенсу угла наклона прямой к кривой безразличия;
3. Предельная норма замены обладает значением только лишь при движении по кривой, но не имеет значения при перемещении между рассматриваемыми кривыми;
4. Не является универсальным принцип убывания $MRS$, он выполняется только при кривых безразличия, имеющих стандартный вид.

From Wikipedia, the free encyclopedia

In economics, the marginal rate of substitution (MRS) is the rate at which a consumer can give up some amount of one good in exchange for another good while maintaining the same level of utility. At equilibrium consumption levels (assuming no externalities), marginal rates of substitution are identical. The marginal rate of substitution is one of the three factors from marginal productivity, the others being marginal rates of transformation and marginal productivity of a factor.^[1]

As the slope of indifference curve[edit]

Under the standard assumption of neoclassical economics that goods and services are continuously divisible, the marginal rates of substitution will be the same regardless of the direction of exchange, and will correspond to the slope of an indifference curve (more precisely, to the slope multiplied by −1) passing through the consumption bundle in question, at that point: mathematically, it is the implicit derivative. MRS of X for Y is the amount of Y which a consumer can exchange for one unit of X locally. The MRS is different at each point along the indifference curve thus it is important to keep locus in the definition. Further on this assumption, or otherwise on the assumption that utility is quantified, the marginal rate of substitution of good or service X for good or service Y (MRS_xy) is also equivalent to the marginal utility of X over the marginal utility of Y. Formally,

It is important to note that when comparing bundles of goods X and Y that give a constant utility (points along an indifference curve), the marginal utility of X is measured in terms of units of Y that is being given up.

For example, if the MRS_xy = 2, the consumer will give up 2 units of Y to obtain 1 additional unit of X.

As one moves down a (standardly convex) indifference curve, the marginal rate of substitution decreases (as measured by the absolute value of the slope of the indifference curve, which decreases). This is known as the law of diminishing marginal rate of substitution.

Since the indifference curve is convex with respect to the origin and we have defined the MRS as the negative slope of the indifference curve,

Simple mathematical analysis[edit]

Assume the consumer utility function is defined by , where U is consumer utility, x and y are goods. Then the marginal rate of substitution can be computed via partial differentiation, as follows.

Also, note that:

where is the marginal utility with respect to good x and is the marginal utility with respect to good y.

By taking the total differential of the utility function equation, we obtain the following results:

, or substituting from above,

, or, without loss of generality, the total derivative of the utility function with respect to good x,

, that is,

.

Through any point on the indifference curve, dU/dx = 0, because U = c, where c is a constant. It follows from the above equation that:

, or rearranging

The marginal rate of substitution is defined as the absolute value of the slope of the indifference curve at whichever commodity bundle quantities are of interest. That turns out to equal the ratio of the marginal utilities:

.

When consumers maximize utility with respect to a budget constraint, the indifference curve is tangent to the budget line, therefore, with m representing slope:

Therefore, when the consumer is choosing his utility maximized market basket on his budget line,

This important result tells us that utility is maximized when the consumer’s budget is allocated so that the marginal utility per unit of money spent is equal for each good. If this equality did not hold, the consumer could increase his/her utility by cutting spending on the good with lower marginal utility per unit of money and increase spending on the other good. To decrease the marginal rate of substitution, the consumer must buy more of the good for which he/she wishes the marginal utility to fall for (due to the law of diminishing marginal utility).

Diminishing Marginal rate of Substitution[edit]

An important principle of economic theory is that marginal rate of substitution of X for Y diminishes as more and more of good X is substituted for good Y. In other words, as the consumer has more and more of good X, he is prepared to forego less and less of good Y.

It means that as the consumer’s stock of X increases and his stock of Y decreases, he is willing to forego less and less of Y for a given increment in X. In other words, the marginal rate of substitution of X for Y falls as the consumer has more of X and less of Y. That the marginal rate of substitution of X for Y diminishes can also be known from drawing tangents at different points on an indifference curve.

Using MRS to determine Convexity[edit]

When analyzing the utility function of consumer’s in terms of determining if they are convex or not. For the horizon of two goods we can apply a quick derivative test (take the derivative of MRS) to determine if our consumer’s preferences are convex. If the derivative of MRS is negative the utility curve would be concave down meaning that it has a maximum and then decreases on either side of the maximum. This utility curve may have an appearance similar to that of a lower case n. If the derivative of MRS is equal to 0 the utility curve would be linear, the slope would stay constant throughout the utility curve. If the derivative of MRS is positive the utility curve would be convex up meaning that it has a minimum and then increases on either side of the minimum. This utility curve may have an appearance similar to that of a u. These statements are shown mathematically below.

For more than two variables, the use of the Hessian matrix is required.

See also[edit]

• Marginal concepts
• Marginal rate of technical substitution (the same concept on production side)
• Indifference curves
• Consumer theory
• Convex preferences
• Implicit differentiation
• Labour economics

References[edit]

Adam Hayes. (2021, March 31). Inside the marginal rate of substitution. Investopedia.
Jerelin, R. (2017, May 30). Diminishing marginal rate of substitution | Indifference curve | Economics. Economics Discussion

• Krugman, Paul; Wells, Robin (2008). Microeconomics (2nd ed.). Palgrave. ISBN 978-0-7167-7159-3.
• Pindyck, Robert S.; Rubinfeld, Daniel L. (2005). Microeconomics (6th ed.). Pearson Prentice Hall. ISBN 0-13-008461-1.
• Dorfman, R. (2008). «Marginal Productivity Theory». In Palgrave Macmillan (ed.). The New Palgrave Dictionary of Economics. London: Palgrave Macmillan. pp. 1–5. doi:10.1057/978-1-349-95121-5_988-2. ISBN 978-1-349-95121-5 – via SpringerLink.

Мы
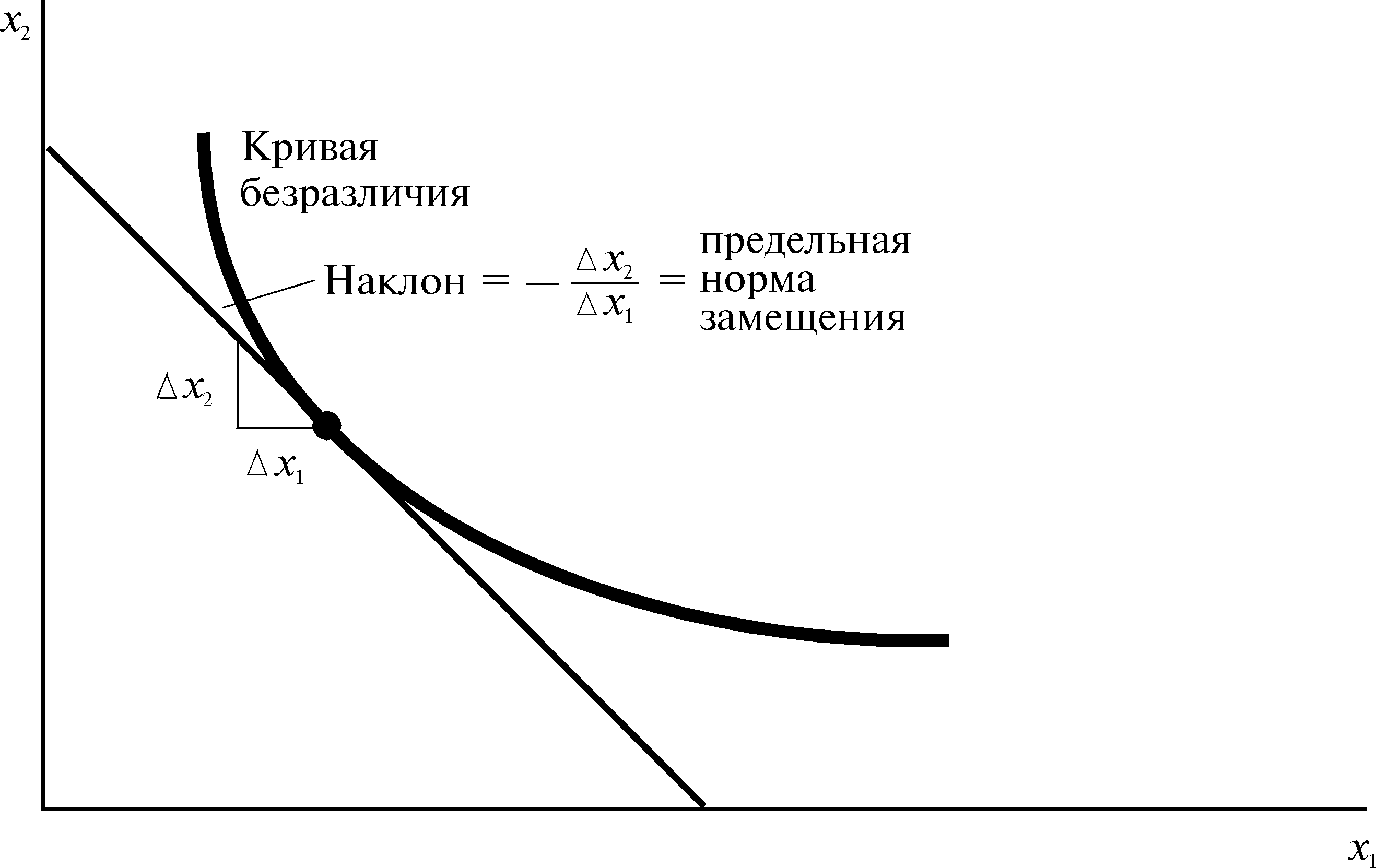
часто будем пользоваться наклоном
кривой безразличия в конкретной точке.
Эта идея столь полезна, что даже получила
название: наклон кривой безразличия
известен как предельная
норма замещения
(MRS).
Данное название проистекает из того
факта, что MRS измеряет пропорцию, в
которой потребитель готов заместить
один товар другим.

Предположим,
что мы отбираем у потребителя немножко
товара 1, x₁.
Затем мы добавляем ему x₂
— количество, как раз достаточное для
того, чтобы вернуть его на его кривую
безразличия, так что после этой замены
x₁
на x₂
благосостояние потребителя не изменится.
Мы рассматриваем отношение x₂/x₁
как
пропорцию,
в которой потребитель готов заместить
товар 1 товаром 2.

Будем
теперь считать x₁
очень малым изменением — предельным
изменением. Тогда пропорция x₂/x₁
измеряет предельную
норму замещения товара 1 товаром 2. По
мере того как x₁
уменьшается, x₂/x₁,
как это видно из рис.3.11, приближается к
наклону кривой безразличия.

Записывая
отношение x₂/x₁,
всегда будем считать и числитель, и
знаменатель малыми числами, описывающими
предельные
изменения по сравнению с исходным
потребительским набором. Поэтому
отношение, определяющее MRS, всегда будет
описывать наклон кривой безразличия —
пропорцию, в которой потребитель готов
заместить чуть большим потреблением
товара 2 чуть меньшее потребление товара
1. (Обратим внимание читателя на то, что
в параграфе 3.7 автор отходит от этого
“нестандартного” определения предельной
нормы замещения, пользуясь в дальнейшем
традиционным ее определением, построенным
на замещении товара 2 товаром 1, а не
наоборот. Как мы увидим в параграфе 3.8,
такой возврат автора к традиционному
определению предельной нормы замещения
имеет важное значение для понимания
поведения MRS — прим.
науч. ред.)

Слегка
смущающим моментом в отношении MRS
является то, что, как правило, это число
отрицательное.
Мы уже видели, что монотонные предпочтения
подразумевают отрицательность наклона
кривых безразличия. Поскольку MRS есть
численная мера наклона кривой безразличия,
она, естественно, будет отрицательным
числом.

Предельная
норма замещения количественно
характеризует интересный аспект
поведения потребителя. Допустим, что
предпочтения потребителя стандартны,
т. е. монотонны и выпуклы, и что в
настоящий момент он потребляет некий
набор (x₁,
x₂).
Предложим ему сделку: он может обменять
товар 1 на товар 2 или товар 2 на товар 1
в любых количествах по «норме обмена»,
равной E.

Иными
словами, если потребитель откажется от
x₁
единиц товара 1, он может получить взамен
Ex₁
единиц товара 2. Или наоборот, если он
откажется от x₂
единиц товара 2, то может получить x₂/E
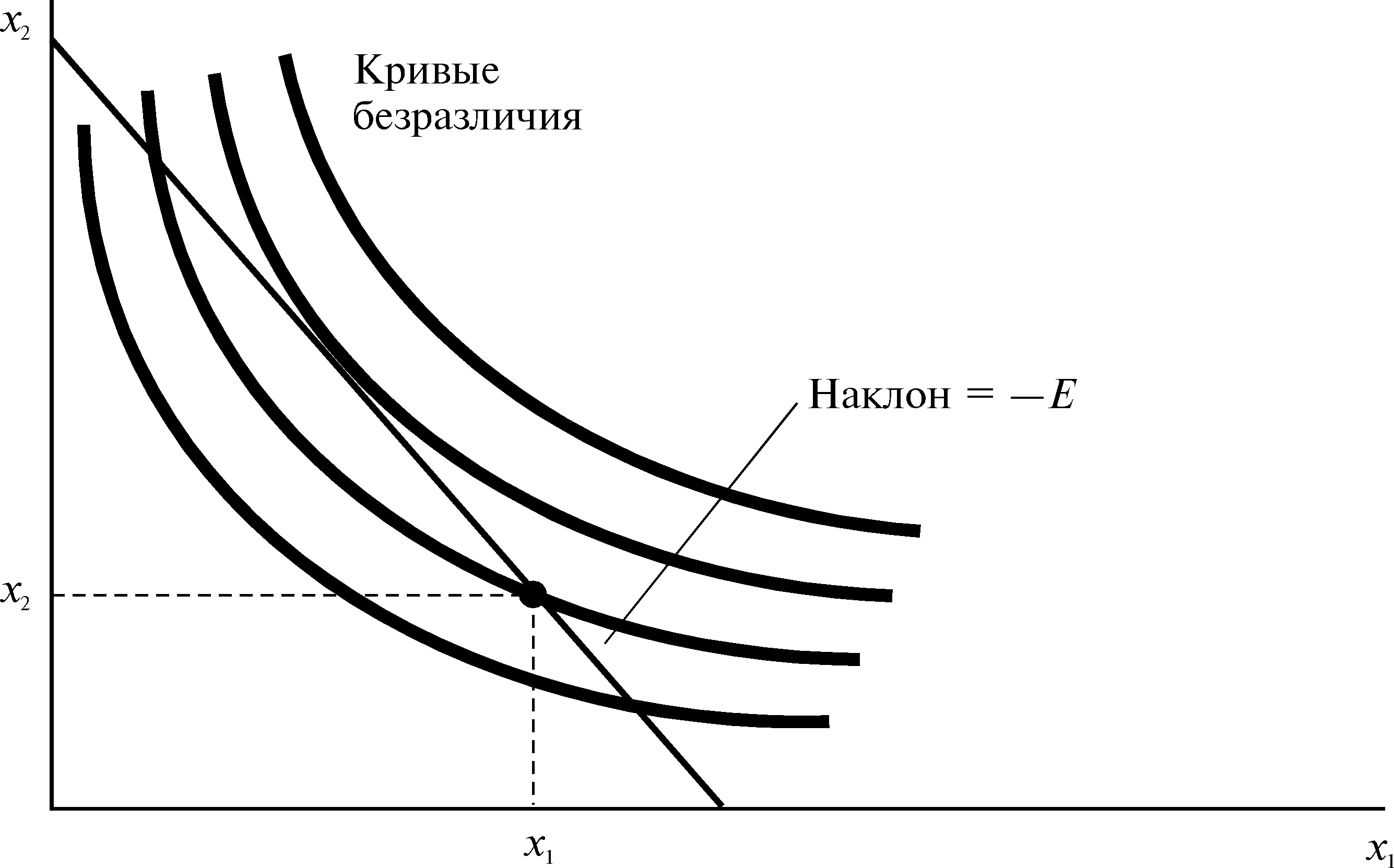
единиц товара 1. На языке геометрии это
означает, что мы предоставляем потребителю
возможность, как показано на рис.3.12,
двигаться в любую точку вдоль линии с
наклоном –E,
проходящей через (x₁,
x₂).
Движение влево вверх от точки (x₁,
x₂)
предполагает обмен товара 1 на товар 2,
а движение вправо вниз — обмен товара
2 на товар 1. При движении и в том, и в
другом направлениях норма обмена
составляет E.
Поскольку обмен всегда предполагает
отказ от одного товара в обмен на другой,
норма
обмена E
соответствует наклону
–E.

Теперь
зададим вопрос: какой должна быть норма
обмена, чтобы потребитель захотел
остаться в точке (x₁,
x₂)?
Для ответа на этот вопрос мы просто
отметим, что при пересечении
линией обмена кривой безразличия на
этой линии всегда будут иметься какие-то
точки, предпочитаемые точке (x₁,
x₂),
а именно те, которые лежат над кривой
безразличия. Следовательно, если мы не
хотим двигаться из точки (x₁,
x₂),
то линия обмена должна являться
касательной к кривой безразличия. Иными
словами, наклон линии обмена –E,
должен быть наклоном кривой безразличия
в точке (x₁,
x₂).
При любой другой норме обмена линия
обмена пересекала бы кривую безразличия
и тем самым позволяла бы потребителю
двигаться в более предпочитаемую точку.

Таким
образом, наклон кривой безразличия —
предельная норма замещения — показывает
норму обмена, при которой потребитель
колеблется, производить обмен или нет.
При любой норме обмена, отличной от MRS,
у потребителя возникло бы желание
обменять один товар на другой. Если же
норма обмена равна MRS, потребитель хочет
остаться в данной точке.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #

  05.03.2016568.83 Кб40G3.doc

• #
• #

  05.03.2016717.82 Кб11G5.doc

• #

  05.03.2016680.96 Кб23G6.doc

• #
• #