Как найти мультипликативную инверсию числа

Инверсии

Когда мы работаем в модульной арифметике, нам часто нужно найти операцию, которая позволяет вычислить величину, обратную заданному числу. Мы обычно ищем аддитивную инверсию (оператор, обратный сложению) или мультипликативную инверсию (оператор, обратный умножению).

Аддитивная инверсия

В Z_n два числа a и b аддитивно инверсны друг другу, если b = n – a. Например,

В Z_n аддитивная инверсия числу a может быть вычислена как b = n – a. Например, аддитивная инверсия 4 в Z₁₀ равна 10 – 4 = 6.

В модульной арифметике каждое целое число имеет аддитивную инверсию. Сумма целого числа и его аддитивной инверсии сравнима с 0 по модулю n .

Обратите внимание, что в модульной арифметике каждое число имеет аддитивную инверсию, и эта инверсия уникальна; каждое число имеет одну и только одну аддитивную инверсию. Однако инверсия числа может быть непосредственно тем же самым числом.

Пример 2.21

Найдите все взаимно обратные пары по сложению в Z₁₀.

Решение

Даны шесть пар аддитивных инверсий — (0, 0), (1, 9), (2, , (3, 7), (4, 6) и (5, 5). В этом списке 0 — инверсия самому себе; так же и 5. Обратите внимание: аддитивные инверсии обратны друг другу; если 4 — аддитивная инверсия 6, тогда 6 — также аддитивная инверсия числу 4.

Мультипликативная инверсия

В Z_n два числа a и b мультипликативно инверсны друг другу, если

Например, если модуль равен 10, то мультипликативная инверсия 3 есть 7. Другими словами, мы имеем .

В модульной арифметике целое число может или не может иметь мультипликативную инверсию. Целое число и его мультипликативная инверсия сравнимы с 1 по модулю n .

Может быть доказано, что a имеет мультипликативную инверсию в Z_n, если только НОД(n, a) = 1. В этом случае говорят, что a и n взаимно простые.

Пример 2.22

Найти мультипликативную инверсию 8 в Z₁₀.

Решение

Мультипликативная инверсия не существует, потому что 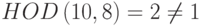. Другими словами, мы не можем найти число между 0 и 9, такое, что при умножении на 8 результат сравним с 1 по mod 10.

Пример 2.23

Найти все мультипликативные инверсии в Z₁₀.

Решение

Есть только три пары, удовлетворяющие условиям существования мультипликативной инверсии: (1, 1), (3, 7) и (9, 9). Числа 0, 2, 4, 5, 6 и 8 не имеют мультипликативной инверсии.

Мы можем проверить, что

(1 x 1) mod 10 = 1       (3 x 7) mod 10 = 1        (9 x 9) mod 10 = 1

Пример 2.24

Найти все мультипликативные обратные пары в Z₁₁.

Решение

Мы имеем следующие пары: (1, 1), (2, 6), (3, 4), (5, 9), (7, и (10, 10). При переходе от Z₁₀ к Z₁₁ число пар увеличивается. При Z₁₁ НОД (11, a) = 1 (взаимно простые) для всех значений a, кроме 0. Это означает, что все целые числа от 1 до 10 имеют мультипликативные инверсии.

Целое число a в Z_n имеет мультипликативную инверсию тогда и только тогда, если НОД (n, a) = 1(mod n)

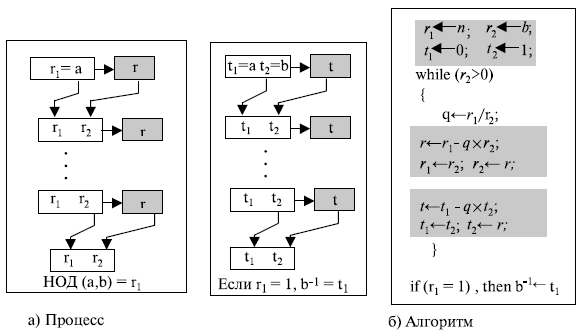
Расширенный алгоритм Евклида, который мы обсуждали ранее в этой лекции, может найти мультипликативную инверсию b в Z_n, когда даны n и b и инверсия существует. Для этого нам надо заменить первое целое число a на n (модуль). Далее мы можем утверждать, что алгоритм может найти s и t, такие, что 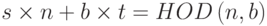. Однако если мультипликативная инверсия b существует, НОД (n, b) должен быть 1. Так что уравнение будет иметь вид

(s x n) + (b x t) = 1

Теперь мы применяем операции по модулю к обеим сторонам уравнения. Другими словами, мы отображаем каждую сторону к Z_n. Тогда мы будем иметь

(s x n + b x t) mod n =1 mod n
[(s x n) mod n] + [(b x t) mod n] = 1 mod n
0 + [(b x t) mod n ] = 1
(b x t) mod n =1  ->  Это означает, что t – это мультипликативная инверсия  b в Zn

Обратите внимание, что на третьей строке — 0, потому что, если мы делим , частное — s, а остаток — 0.

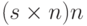
Расширенный алгоритм Евклида находит мультипликативные инверсии b в Z_n , когда даны n и b и НОД (n, b) = 1 .
Мультипликативная инверсия b — это значение t , отображенное в Z_n .

Рисунок 2.15 показывает, как мы находим мультипликативную инверсию числа, используя расширенный алгоритм Евклида.

Пример 2.25

Найти мультипликативную инверсию 11 в Z₂₆.

Решение

Мы используем таблицу, аналогичную одной из тех, которые мы уже применяли прежде при данных r₁ = 26 и r₂ = 11. Нас интересует только значение t.

НОД (26, 11) = 1, что означает, что мультипликативная инверсия 11 существует. Расширенный алгоритм Евклида дает t₁ = (–7).

Мультипликативная инверсия равна (–7) mod 26 = 19. Другими словами, 11 и 19 — мультипликативная инверсия в Z₂₆. Мы можем видеть, что .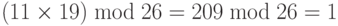

Пример 2.26

Найти мультипликативную инверсию 23 в Z₁₀₀.

Решение

Мы используем таблицу, подобную той, которую применяли до этого при r₁ = 100 и r₂ = 23. Нас интересует только значение t.

НОД (100, 23) = 1, что означает, что инверсия 23 существует. Расширенный Евклидов алгоритм дает t₁ =-13. Инверсия — (–13) mod 100 = 87. Другими словами, 13 и 87 — мультипликативные инверсии в Z₁₀₀. Мы можем видеть, что .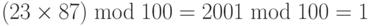

Пример 2.27

Найти мультипликативную инверсию 12 в Z₂₆.

Решение

Мы используем таблицу, подобную той, которую мы применяли раньше при r₁ = 26 и r₂ = 12.

, что означает отсутвствие для числа 12 мультипликативной инверсии в Z₂₆

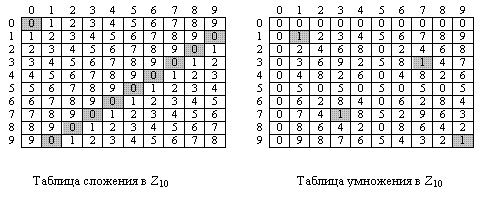
Сложение и умножение таблиц

Рисунок 2.16 показывает две таблицы для сложения и умножения. При сложении таблиц каждое целое число имеет аддитивную инверсию. Обратные пары могут быть найдены, если результат их сложения — ноль. Мы имеем (0, 0), (1, 9), (2, , (3, 7), (4, 6) и (5, 5). При умножении таблиц мы получаем только три мультипликативных пары (1, 1), (3, 7) и (9, 9). Пары могут быть найдены, когда результат умножения равен 1. Обе таблицы симметричны по диагонали, от левой вершины к нижней вершине справа. При этом можно обнаружить свойства коммутативности для сложения и умножения ( a+b = b+a и ). Таблица сложения также показывает, что каждый ряд или колонка может поменяться с другим рядом или колонкой. Для таблицы умножения это неверно.

Различные множества для сложения и умножения

В криптографии мы часто работаем с инверсиями. Если отправитель посылает целое число (например, ключ для шифрования слова), приемник применяет инверсию этого целого числа (например, ключ декодирования). Если это действие (алгоритм шифрования/декодирования) является сложением, множество Z_n может быть использовано как множество возможных ключей, потому что каждое целое число в этом множестве имеет аддитивную инверсию. С другой стороны, если действие (алгоритм шифрования/декодирования) — умножение, Z_n не может быть множеством возможных ключей, потому что только некоторые члены этого множества имеют мультипликативную инверсию. Нам нужно другое множество, которое является подмножеством Z_n и включает в себя только целые числа, и при этом в Z_n они имеют уникальную мультипликативную инверсию. Это множество обозначается Z_n*. Рисунок 2.17 показывает некоторые
случаи двух множеств. Обратите внимание, что множество Z_n*
может быть получено из таблицы умножения типа показанной на рис. 2.16.

Каждый член Z_n имеет аддитивную инверсию, но только некоторые члены имеют мультипликативную инверсию. Каждый член Z_n* имеет мультипликативную инверсию, но только некоторые члены множества имеют аддитивную инверсию.

Мы должны использовать Z_n , когда необходимы аддитивные инверсии; мы должны использовать Z_n* , когда необходимы мультипликативные инверсии.

Еще два множества

Криптография часто использует еще два множества: Z_p, и Z_p*. Модули в этих двух множествах — простые числа. Простые числа будут обсуждаться в следующих лекциях; пока можно сказать, что простое число имеет только два делителя: целое число 1 и само себя.

Множество Z_p — то же самое, что и Z_n, за исключением того, что n — простое число. Z_p содержит все целые числа от 0 до p – 1. Каждый элемент в Z_p имеет аддитивную инверсию; каждый элемент кроме 0 имеет мультипликативную инверсию.

Множество Z_p* — то же самое, что Z_n*, за исключением того, что Z_p* содержит все целые числа от 1 до p – 1. Каждый элемент в Z_p имеет аддитивную и мультипликативную инверсии. Z_p* очень хороший кандидат, когда мы нуждаемся во множестве, которое поддерживает аддитивную и мультипликативную инверсии.

Ниже показаны два множества, когда p = 13.

Z13 = {0,1,2,3,4,5,6,7,8,9,10,11,12}, 
Z13* = {1,2,3,4,5,6,7,8,9,10,11,12},

In mathematics, particularly in the area of arithmetic, a modular multiplicative inverse of an integer a is an integer x such that the product ax is congruent to 1 with respect to the modulus m.^[1] In the standard notation of modular arithmetic this congruence is written as

which is the shorthand way of writing the statement that m divides (evenly) the quantity ax − 1, or, put another way, the remainder after dividing ax by the integer m is 1. If a does have an inverse modulo m, then there are an infinite number of solutions of this congruence, which form a congruence class with respect to this modulus. Furthermore, any integer that is congruent to a (i.e., in a‘s congruence class) has any element of x‘s congruence class as a modular multiplicative inverse. Using the notation of to indicate the congruence class containing w, this can be expressed by saying that the modulo multiplicative inverse of the congruence class is the congruence class such that:

where the symbol denotes the multiplication of equivalence classes modulo m.^[2]
Written in this way, the analogy with the usual concept of a multiplicative inverse in the set of rational or real numbers is clearly represented, replacing the numbers by congruence classes and altering the binary operation appropriately.

As with the analogous operation on the real numbers, a fundamental use of this operation is in solving, when possible, linear congruences of the form

Finding modular multiplicative inverses also has practical applications in the field of cryptography, i.e. public-key cryptography and the RSA algorithm.^[3][4][5] A benefit for the computer implementation of these applications is that there exists a very fast algorithm (the extended Euclidean algorithm) that can be used for the calculation of modular multiplicative inverses.

Modular arithmetic[edit]

For a given positive integer m, two integers, a and b, are said to be congruent modulo m if m divides their difference. This binary relation is denoted by,

This is an equivalence relation on the set of integers, ℤ, and the equivalence classes are called congruence classes modulo m or residue classes modulo m. Let denote the congruence class containing the integer a,^[6] then

A linear congruence is a modular congruence of the form

Unlike linear equations over the reals, linear congruences may have zero, one or several solutions. If x is a solution of a linear congruence then every element in is also a solution, so, when speaking of the number of solutions of a linear congruence we are referring to the number of different congruence classes that contain solutions.

If d is the greatest common divisor of a and m then the linear congruence ax ≡ b (mod m) has solutions if and only if d divides b. If d divides b, then there are exactly d solutions.^[7]

A modular multiplicative inverse of an integer a with respect to the modulus m is a solution of the linear congruence

The previous result says that a solution exists if and only if gcd(a, m) = 1, that is, a and m must be relatively prime (i.e. coprime). Furthermore, when this condition holds, there is exactly one solution, i.e., when it exists, a modular multiplicative inverse is unique:^[8] If b and b’ are both modular multiplicative inverses of a respect to the modulus m, then

therefore

If a ≡ 0 (mod m), then gcd(a, m) = a, and a won’t even have a modular multiplicative inverse. Therefore, b ≡ b’ (mod m).

When ax ≡ 1 (mod m) has a solution it is often denoted in this way −

but this can be considered an abuse of notation since it could be misinterpreted as the reciprocal of (which, contrary to the modular multiplicative inverse, is not an integer except when a is 1 or -1). The notation would be proper if a is interpreted as a token standing for the congruence class , as the multiplicative inverse of a congruence class is a congruence class with the multiplication defined in the next section.

Integers modulo m[edit]

The congruence relation, modulo m, partitions the set of integers into m congruence classes. Operations of addition and multiplication can be defined on these m objects in the following way: To either add or multiply two congruence classes, first pick a representative (in any way) from each class, then perform the usual operation for integers on the two representatives and finally take the congruence class that the result of the integer operation lies in as the result of the operation on the congruence classes. In symbols, with and representing the operations on congruence classes, these definitions are

and

These operations are well-defined, meaning that the end result does not depend on the choices of representatives that were made to obtain the result.

The m congruence classes with these two defined operations form a ring, called the ring of integers modulo m. There are several notations used for these algebraic objects, most often or , but several elementary texts and application areas use a simplified notation when confusion with other algebraic objects is unlikely.

The congruence classes of the integers modulo m were traditionally known as residue classes modulo m, reflecting the fact that all the elements of a congruence class have the same remainder (i.e., «residue») upon being divided by m. Any set of m integers selected so that each comes from a different congruence class modulo m is called a complete system of residues modulo m.^[9] The division algorithm shows that the set of integers, {0, 1, 2, …, m − 1} form a complete system of residues modulo m, known as the least residue system modulo m. In working with arithmetic problems it is sometimes more convenient to work with a complete system of residues and use the language of congruences while at other times the point of view of the congruence classes of the ring is more useful.^[10]

Multiplicative group of integers modulo m[edit]

Not every element of a complete residue system modulo m has a modular multiplicative inverse, for instance, zero never does. After removing the elements of a complete residue system that are not relatively prime to m, what is left is called a reduced residue system, all of whose elements have modular multiplicative inverses. The number of elements in a reduced residue system is , where is the Euler totient function, i.e., the number of positive integers less than m that are relatively prime to m.

In a general ring with unity not every element has a multiplicative inverse and those that do are called units. As the product of two units is a unit, the units of a ring form a group, the group of units of the ring and often denoted by R^× if R is the name of the ring. The group of units of the ring of integers modulo m is called the multiplicative group of integers modulo m, and it is isomorphic to a reduced residue system. In particular, it has order (size), .

In the case that m is a prime, say p, then and all the non-zero elements of have multiplicative inverses, thus is a finite field. In this case, the multiplicative group of integers modulo p form a cyclic group of order p − 1.

Example[edit]

For any integer , it’s always the case that is the modular multiplicative inverse of with respect to the modulus , since . Examples are , , and so on.

The following example uses the modulus 10: Two integers are congruent mod 10 if and only if their difference is divisible by 10, for instance

since 10 divides 32 − 2 = 30, and

since 10 divides 111 − 1 = 110.

Some of the ten congruence classes with respect to this modulus are:

and

The linear congruence 4x ≡ 5 (mod 10) has no solutions since the integers that are congruent to 5 (i.e., those in ) are all odd while 4x is always even. However, the linear congruence 4x ≡ 6 (mod 10) has two solutions, namely, x = 4 and x = 9. The gcd(4, 10) = 2 and 2 does not divide 5, but does divide 6.

Since gcd(3, 10) = 1, the linear congruence 3x ≡ 1 (mod 10) will have solutions, that is, modular multiplicative inverses of 3 modulo 10 will exist. In fact, 7 satisfies this congruence (i.e., 21 − 1 = 20). However, other integers also satisfy the congruence, for instance 17 and −3 (i.e., 3(17) − 1 = 50 and 3(−3) − 1 = −10). In particular, every integer in will satisfy the congruence since these integers have the form 7 + 10r for some integer r and

is divisible by 10. This congruence has only this one congruence class of solutions. The solution in this case could have been obtained by checking all possible cases, but systematic algorithms would be needed for larger moduli and these will be given in the next section.

The product of congruence classes and can be obtained by selecting an element of , say 25, and an element of , say −2, and observing that their product (25)(−2) = −50 is in the congruence class . Thus, . Addition is defined in a similar way. The ten congruence classes together with these operations of addition and multiplication of congruence classes form the ring of integers modulo 10, i.e., .

A complete residue system modulo 10 can be the set {10, −9, 2, 13, 24, −15, 26, 37, 8, 9} where each integer is in a different congruence class modulo 10. The unique least residue system modulo 10 is {0, 1, 2, …, 9}. A reduced residue system modulo 10 could be {1, 3, 7, 9}. The product of any two congruence classes represented by these numbers is again one of these four congruence classes. This implies that these four congruence classes form a group, in this case the cyclic group of order four, having either 3 or 7 as a (multiplicative) generator. The represented congruence classes form the group of units of the ring . These congruence classes are precisely the ones which have modular multiplicative inverses.

Computation[edit]

Extended Euclidean algorithm[edit]

A modular multiplicative inverse of a modulo m can be found by using the extended Euclidean algorithm.

The Euclidean algorithm determines the greatest common divisor (gcd) of two integers, say a and m. If a has a multiplicative inverse modulo m, this gcd must be 1. The last of several equations produced by the algorithm may be solved for this gcd. Then, using a method called «back substitution», an expression connecting the original parameters and this gcd can be obtained. In other words, integers x and y can be found to satisfy Bézout’s identity,

Rewritten, this is

that is,

so, a modular multiplicative inverse of a has been calculated. A more efficient version of the algorithm is the extended Euclidean algorithm, which, by using auxiliary equations, reduces two passes through the algorithm (back substitution can be thought of as passing through the algorithm in reverse) to just one.

In big O notation, this algorithm runs in time O(log²(m)), assuming |a| < m, and is considered to be very fast and generally more efficient than its alternative, exponentiation.

Using Euler’s theorem[edit]

As an alternative to the extended Euclidean algorithm, Euler’s theorem may be used to compute modular inverses.^[11]

According to Euler’s theorem, if a is coprime to m, that is, gcd(a, m) = 1, then

where is Euler’s totient function. This follows from the fact that a belongs to the multiplicative group ^× if and only if a is coprime to m. Therefore, a modular multiplicative inverse can be found directly:

In the special case where m is a prime, and a modular inverse is given by

This method is generally slower than the extended Euclidean algorithm, but is sometimes used when an implementation for modular exponentiation is already available. Some disadvantages of this method include:

One notable advantage of this technique is that there are no conditional branches which depend on the value of a, and thus the value of a, which may be an important secret in public-key cryptography, can be protected from side-channel attacks. For this reason, the standard implementation of Curve25519 uses this technique to compute an inverse.

Multiple inverses[edit]

It is possible to compute the inverse of multiple numbers a_i, modulo a common m, with a single invocation of the Euclidean algorithm and three multiplications per additional input.^[12] The basic idea is to form the product of all the a_i, invert that, then multiply by a_j for all j ≠ i to leave only the desired a⁻¹
_i.

More specifically, the algorithm is (all arithmetic performed modulo m):

1. Compute the prefix products for all i ≤ n.
2. Compute b⁻¹
   _n using any available algorithm.
3. For i from n down to 2, compute
   • a⁻¹
     _i = b⁻¹
     _ib_i−1 and
   • b⁻¹
     _i−1 = b⁻¹
     _ia_i.
4. Finally, a⁻¹
   ₁ = b⁻¹
   ₁.

It is possible to perform the multiplications in a tree structure rather than linearly to exploit parallel computing.

Applications[edit]

Finding a modular multiplicative inverse has many applications in algorithms that rely on the theory of modular arithmetic. For instance, in cryptography the use of modular arithmetic permits some operations to be carried out more quickly and with fewer storage requirements, while other operations become more difficult.^[13] Both of these features can be used to advantage. In particular, in the RSA algorithm, encrypting and decrypting a message is done using a pair of numbers that are multiplicative inverses with respect to a carefully selected modulus. One of these numbers is made public and can be used in a rapid encryption procedure, while the other, used in the decryption procedure, is kept hidden. Determining the hidden number from the public number is considered to be computationally infeasible and this is what makes the system work to ensure privacy.^[14]

As another example in a different context, consider the exact division problem in computer science where you have a list of odd word-sized numbers each divisible by k and you wish to divide them all by k. One solution is as follows:

1. Use the extended Euclidean algorithm to compute k⁻¹, the modular multiplicative inverse of k mod 2^w, where w is the number of bits in a word. This inverse will exist since the numbers are odd and the modulus has no odd factors.
2. For each number in the list, multiply it by k⁻¹ and take the least significant word of the result.

On many machines, particularly those without hardware support for division, division is a slower operation than multiplication, so this approach can yield a considerable speedup. The first step is relatively slow but only needs to be done once.

Modular multiplicative inverses are used to obtain a solution of a system of linear congruences that is guaranteed by the Chinese Remainder Theorem.

For example, the system

X ≡ 4 (mod 5)

X ≡ 4 (mod 7)

X ≡ 6 (mod 11)

has common solutions since 5,7 and 11 are pairwise coprime. A solution is given by

X = t₁ (7 × 11) × 4 + t₂ (5 × 11) × 4 + t₃ (5 × 7) × 6

where

t₁ = 3 is the modular multiplicative inverse of 7 × 11 (mod 5),

t₂ = 6 is the modular multiplicative inverse of 5 × 11 (mod 7) and

t₃ = 6 is the modular multiplicative inverse of 5 × 7 (mod 11).

Thus,

X = 3 × (7 × 11) × 4 + 6 × (5 × 11) × 4 + 6 × (5 × 7) × 6 = 3504

and in its unique reduced form

X ≡ 3504 ≡ 39 (mod 385)

since 385 is the LCM of 5,7 and 11.

Also, the modular multiplicative inverse figures prominently in the definition of the Kloosterman sum.

See also[edit]

• Inversive congruential generator – a pseudo-random number generator that uses modular multiplicative inverses
• Rational reconstruction (mathematics)

Notes[edit]

References[edit]

• Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (2nd ed.), Springer-Verlag, ISBN 0-387-97329-X
• Rosen, Kenneth H. (1993), Elementary Number Theory and its Applications (3rd ed.), Addison-Wesley, ISBN 978-0-201-57889-8
• Schumacher, Carol (1996). Chapter Zero: Fundamental Notions of Abstract Mathematics. Addison-Wesley. ISBN 0-201-82653-4.
• Trappe, Wade; Washington, Lawrence C. (2006), Introduction to Cryptography with Coding Theory (2nd ed.), Prentice-Hall, ISBN 978-0-13-186239-5

External links[edit]

• Weisstein, Eric W. «Modular Inverse». MathWorld.
• Guevara Vasquez, Fernando provides a solved example of solving the modulo multiplicative inverse using Euclid’s Algorithm

Содержание

• Примеры мультипликативного обратного
• Пример 1
• Пример 2
• Пример 3
• Пример 4
• Обучение
• Упражнение 1
• Упражнение 2.
• Упражнение 3.
• использованная литература

Это понимается Обратный мультипликативный числа, другое число, умноженное на первое, дает в результате нейтральный элемент произведения, то есть единицу. Если у вас есть реальный номер к то его мультипликативный обратный обозначается через к^-1, и это правда, что:

а а^-1 = а^-1 а = 1

Обычно число к принадлежит набору действительных чисел.

Рис. 1. Y — мультипликативная инверсия X, а X — мультипликативная инверсия Y.

Если, например, взять а = 2, то его мультипликативный обратный равен 2^-1 = ½ поскольку подтверждается следующее:

2 ⋅ 2^-1 = 2^-1⋅ 2 = 1

2⋅ ½  = ½ ⋅ 2 = 1

К Обратный мультипликативный числа также называют взаимный, поскольку мультипликативная обратная величина получается заменой числителя и знаменателя, например, мультипликативная обратная величина 3/4 равна 4/3.

Как правило, можно сказать, что для рационального числа (п / д) его мультипликативная обратная (p / q)^-1 Это взаимно (q / p) как можно проверить ниже:

(p / q) ⋅ (p / q)^-1 = (p / q) ⋅ (q / p) = (p⋅ q) / (q⋅ p) = (p⋅ q) / (p⋅ q) = 1

Мультипликативное обратное не существует в числовом наборе целых чиселНапример, если взять целое число 2, его мультипликативная обратная величина в соответствии с тем, что было показано выше, будет ½, но ½ не является целым числом.

Также не существует мультипликативного обратного нулевого элемента умножения. Другими словами, число ноль (0), являющееся нулевым элементом операции умножения, не имеет обратного мультипликативного числа, поскольку нет числа, умноженного на единицу нуля.

Мультипликативный обратный существует в рациональных числах, в действительных числах и в комплексных числах.

Примеры мультипликативного обратного

Пример 1

Найдите мультипликативное значение, обратное 3/2, и убедитесь, что оно удовлетворяет свойству мультипликативных целых чисел.

Согласно приведенному выше правилу числитель и знаменатель меняются местами, так что мультипликативная обратная величина (3/2) равна (2/3). Для проверки умножение двух чисел проводится:

(3/2) ⋅ (2/3) = (3 ⋅ 2) / (2 ⋅ 3) = 6/6 = 1.

Чтобы умножить два дробных числа, просто умножьте числитель первого числа на числитель второго, чтобы получить числитель результата.

Чтобы получить знаменатель произведения дробных чисел, действуйте аналогичным образом, то есть знаменатели перемножаются, и результат является знаменателем произведения. В нашем примере проверено, что числитель произведения числа и его обратной величины равен 6, а знаменатель равен 6, а дробь 6/6 равна 1.

Пример 2

Мультипликативное обратное значение -5 не следует путать с его симметричным (+5), которое иногда называют арифметическим обратным. Мультипликативный обратный будет получен следующим образом:

(-5) ⋅ X = 1

Где X — мультипликативная обратная величина, которую нужно получить. Одна из возможных процедур — найти неизвестное X. Поскольку (-5) умножает неизвестное X в левом члене, тогда происходит деление правого члена:

Х = 1 / (-5)

Поскольку известно, что + между — это -, то, наконец, получается X:

X = — ⅕.

В заключение — ⅕ — мультипликативная величина, обратная -5.

Пример 3

Получите мультипликативное значение, обратное -√2. Предположим, что мультипликативная обратная величина — это X, тогда -√2, умноженное на X, должно быть единицей, условие, которое мы налагаем ниже:

-√2 ⋅ X = 1

Затем оба члена делятся на -√2, чтобы получить:

(-√2 ⋅ X) / (-√2) = 1 / (-√2)

В первом члене -√2 упрощается, оставляя:

Х = 1 / (-√2)

Это выражение можно рационализировать, то есть исключить корень знаменателя, умножив в числителе на (-√2) и в знаменателе на ту же величину, чтобы результат не изменился:

X = (-√2) / [(-√2) (- √2)] = — (√2 / 2)

В заключение — (√2 / 2) является мультипликативным обратным (-√2).

Пример 4

Предположим любое число x, получите его обратное мультипликативное число и изобразите его графически.

В данном случае это функция f (x) = x, получение мультипликативного обратного преобразования означает нахождение такой функции g (x), которая умножается на первое число единицы. Функция g является обратной функцией f, и ее ни в коем случае не следует путать с ее обратной функцией.

Другими словами, мультипликативный обратный x — это y такой, что верно следующее:

х ⋅ у = 1

откуда расчистка и у вас есть:

у = 1 / х.

Вышеупомянутое интерпретируется таким образом, что при заданном значении x предыдущая формула дает нам его мультипликативную обратную величину.

Его можно представить в графическом виде, как показано на следующем рисунке:

Рис. 2. Мультипликативная величина, обратная x, равна y = 1 / x.

Обучение

Упражнение 1

Дано x = 2 — √2, получим его мультипликативную обратную y.

Решение:

Чтобы y был мультипликативным обратным x, должно выполняться следующее равенство:

х ⋅ у = 1

Замените x его значением:

(2 — √2) ⋅ y = 1

Затем он очищается и:

у = 1 / (2 — √2)

Чтобы рационализировать результат, умножьте числитель и знаменатель на их сопряженный бином:

у = (2 + √2) / ((2 + √2) (2 — √2))

В знаменателе определяется замечательное произведение, называемое произведением суммы и разницы, то есть разностью квадратов. Таким образом исчезает корень в знаменателе.

у = (2 + √2) / (2 ^ 2 — (√2) ^ 2)

Решение полномочий:

у = (2 + √2) / (4-2)

Упрощение:

у = (2 + √2) / 2

Упражнение 2.

Получите мультипликативную обратную величину (1 / a + 1 / b), где a и b — ненулевые действительные числа.

Решение:

Мы называем Y мультипликативной обратной величиной (1 / a + 1 / b), поэтому должно выполняться следующее уравнение:

И ⋅ (1 / a + 1 / b) = 1

Переменная Y очищается:

Y = 1 / (1 / a + 1 / b)

Знаменатель решается:

Y = 1 / ((b + a) / a b)

Как известно из правил алгебры, знаменатель знаменателя переходит в числитель:

Y = (а б) / (б + а)

Приказано окончательно получить:

(a b) / (a ​​+ b), который является мультипликативным обратным к (1 / a + 1 / b).

Упражнение 3.

Получите мультипликативную обратную величину (a — b) / (a ​​^ 2 — b ^ 2).

Решение:

Помните, что мультипликативная обратная величина также называется обратной, потому что она получается в точности заменой числителя и знаменателя.

Тогда мультипликативная величина, обратная (a — b) / (a ​​^ 2 — b ^ 2), будет:

(а ^ 2 — Ь ^ 2) / (а — Ь)

Но это выражение можно упростить, если мы признаем, согласно правилам алгебры, что числитель — это разность квадратов, которую можно разложить на множители как произведение суммы на разность:

((a + b) (a — b)) / (a ​​- b)

Поскольку в числителе и знаменателе есть общий множитель (a — b), мы переходим к упрощению и в итоге получаем:

(a + b), который является мультипликативным обратным к (a — b) / (a ​​^ 2 — b ^ 2).

использованная литература

1. Фуэнтес, А. (2016). ОСНОВНАЯ МАТЕМАТИКА. Введение в исчисление. Lulu.com.
2. Гаро, М. (2014). Математика: квадратные уравнения: как решить квадратное уравнение. Марилу Гаро.
3. Хаусслер, Э. Ф., и Пол, Р. С. (2003). Математика для управления и экономики. Pearson Education.
4. Хименес, Дж., Рофригес, М., и Эстрада, Р. (2005). Математика 1 сен. Порог.
5. Прециадо, К. Т. (2005). Курс математики 3-й. Редакция Progreso.
6. Рок, Н. М. (2006). Алгебра I — это просто! Так просто. Team Rock Press.
7. Салливан, Дж. (2006). Алгебра и тригонометрия. Pearson Education.

«Взаимное (математика)» перенаправляется сюда. Не следует путать с возвратно- поступательным движением (геометрией). Обратная функция: y = 1 / x. Для каждого x, кроме 0, y представляет его мультипликативную инверсию. Граф образует прямоугольную гиперболу.

В математике, А мультипликативный обратная или обратная для числа х, обозначим через 1 / х или х ^-1, представляет собой число, которое, когда умножается на х дает мультипликативный идентичность, 1. мультипликативный обратный из фракции A / B является б / а. Для мультипликативного обратного действительного числа разделите 1 на число. Например, обратная величина 5 равна одной пятой (1/5 или 0,2), а обратная величина 0,25 — 1, деленная на 0,25 или 4. Обратная функция, функция f ( x), которая отображает x в 1 / x, является одним из простейших примеров функции, которая является своей собственной обратной ( инволюцией ).

Умножение на число аналогично делению на обратное, и наоборот. Например, умножение на 4/5 (или 0,8) даст тот же результат, что и деление на 5/4 (или 1,25). Следовательно, умножение на число с последующим умножением на обратное дает исходное число (поскольку произведение числа на обратное равно 1).

Термин « взаимное» широко использовался, по крайней мере, еще в третьем издании Британской энциклопедии (1797 г.) для описания двух чисел, произведение которых равно 1; геометрические величины в обратной пропорции описаны как reciprocall в 1570 переводе Евклид «ы элементов.

Во фразе « мультипликативный обратный» квалификатор « мультипликативный» часто опускается, а затем неявно понимается (в отличие от аддитивного обратного ). Мультипликативные инверсии могут быть определены во многих математических областях, а также в числах. В этих случаях может случиться так, что ab ≠ ba ; тогда «инверсия» обычно подразумевает, что элемент является и левым, и правым инверсией.

Обозначение f ⁻¹ иногда также используется для обратной функции функции f, которая в общем случае не равна мультипликативной обратной функции. Например, мультипликативный обратный синус 1 / (sin x) = (sin x) ⁻¹ является косекансом x, а не обратным синусом x, обозначенным sin ⁻¹ x или arcsin x. Только для линейных карт они сильно связаны (см. Ниже). Различия терминологии « реципрокный» и « обратный» недостаточны, чтобы провести это различие, поскольку многие авторы предпочитают противоположное соглашение об именах, вероятно, по историческим причинам (например, во французском языке обратная функция предпочтительно называется реципрокной биекцией ).

СОДЕРЖАНИЕ

• 1 Примеры и контрпримеры
• 2 Комплексные числа
• 3 Исчисление
• 4 алгоритма
• 5 Обратные иррациональные числа
• 6 Дополнительные замечания
• 7 приложений
• 8 См. Также
• 9 Примечания
• 10 Ссылки

Примеры и контрпримеры

В действительных числах ноль не имеет обратного значения, потому что никакое действительное число, умноженное на 0, не дает 1 (произведение любого числа с нулем равно нулю). За исключением нуля, обратные значения каждого действительного числа являются действительными, обратные значения каждого рационального числа являются рациональными, а обратные значения каждого комплексного числа являются комплексными. Свойство, что каждый элемент, отличный от нуля, имеет мультипликативную инверсию, является частью определения поля, все эти примеры являются его примерами. С другой стороны, никакое целое число, кроме 1 и -1, не имеет обратного целого числа, и поэтому целые числа не являются полем.

В модульной арифметике, то модульное мультипликативное обратное из также определяются: это число х такие, что ах = 1 ( по модулю п). Этот мультипликативный обратный существует тогда и только тогда, когда и п являются взаимно простыми. Например, 3 по модулю 11 равно 4, потому что 4 ⋅ 3 ≡ 1 (mod 11). Для его вычисления можно использовать расширенный алгоритм Евклида.

В sedenions являются алгебра, в которой каждый ненулевой элемент имеет мультипликативный обратный, но, тем не менее, который имеет делителей нуля, то есть ненулевые элементы х, у такие, что х  = 0.

Квадратная матрица имеет обратную, если и только если ее определитель имеет обратный в коэффициенте кольца. Линейная карта, которая имеет матрицу A ^-1 относительно некоторой базы, тогда является обратной функцией карты, имеющей A в качестве матрицы в той же базе. Таким образом, два различных понятия обратной функции сильно связаны в этом случае, в то время как в общем случае их следует тщательно различать (как отмечалось выше).

Эти тригонометрические функции связаны взаимной идентичности: котангенс является обратной касательной; секущая обратна косинусу; косеканс обратен синусу.

Кольцо, в котором каждый ненулевой элемент имеет мультипликативный обратный, называется телом ; аналогично алгебра, в которой это верно, является алгеброй с делением.

Сложные числа

Как упоминалось выше, величина, обратная каждому ненулевому комплексному числу z = a + bi, является комплексным. Это может быть найдено путем умножения как верхнюю и нижнюю часть 1 / г его комплексно сопряженное и используя свойство, что, то абсолютное значение из г в квадрат, который является действительным числом ² + Ь ²: z ¯ знак равно а — б я { displaystyle { bar {z}} = а-би} z z ¯ знак равно ‖ z ‖ 2 { displaystyle z { bar {z}} = | z | ^ {2}}

1 z знак равно z ¯ z z ¯ знак равно z ¯ ‖ z ‖ 2 знак равно а — б я а 2 + б 2 знак равно а а 2 + б 2 — б а 2 + б 2 я . { displaystyle { frac {1} {z}} = { frac { bar {z}} {z { bar {z}}}} = { frac { bar {z}} { | z | ^ {2}}} = { frac {a-bi} {a ^ {2} + b ^ {2}}} = { frac {a} {a ^ {2} + b ^ {2} }} — { frac {b} {a ^ {2} + b ^ {2}}} i.}

Интуиция такова, что

z ¯ ‖ z ‖ { displaystyle { frac { bar {z}} { | z |}}}

дает нам комплексное сопряжение с величиной, уменьшенной до значения, поэтому повторное деление на гарантирует, что величина теперь также равна обратной величине исходной величины, следовательно: 1 { displaystyle 1} ‖ z ‖ { Displaystyle | г |}

1 z знак равно z ¯ ‖ z ‖ 2 { displaystyle { frac {1} {z}} = { frac { bar {z}} { | z | ^ {2}}}}

В частности, если || z || = 1 ( z имеет единицу величины), тогда. Следовательно, мнимые единицы, ± i, имеют аддитивное обратное значение, равное мультипликативному обратному, и являются единственными комплексными числами с этим свойством. Например, аддитивные и мультипликативные обратные значения i равны — ( i) = — i и 1 / i = — i, соответственно. 1 / z знак равно z ¯ { displaystyle 1 / z = { bar {z}}}

Для комплексного числа в полярной форме z = r (cos φ + i  sin φ) обратная величина просто принимает обратную величину и отрицательное значение угла:

1 z знак равно 1 р ( потому что ⁡ ( — φ ) + я грех ⁡ ( — φ ) ) . { displaystyle { frac {1} {z}} = { frac {1} {r}} left ( cos (- varphi) + i sin (- varphi) right).}

Геометрическая интуиция для интеграла от 1 / x. Три интеграла от 1 до 2, от 2 до 4 и от 4 до 8 равны. Каждая область — это предыдущая, разделенная пополам по вертикали и удвоенная по горизонтали. Расширяя это, интеграл от 1 до 2 ^k равен k, умноженному на интеграл от 1 до 2, так же, как ln 2 ^k = k ln 2.

Исчисление

В реальном исчислении, то производная от 1 / х = х ^-1 задается правилом питания с силой -1:

d d Икс Икс — 1 знак равно ( — 1 ) Икс ( — 1 ) — 1 знак равно — Икс — 2 знак равно — 1 Икс 2 . { displaystyle { frac {d} {dx}} x ^ {- 1} = (- 1) x ^ {(- 1) -1} = — x ^ {- 2} = — { frac {1} {x ^ {2}}}.}

Правило степени для интегралов ( квадратурная формула Кавальери ) не может использоваться для вычисления интеграла от 1 / x, потому что это приведет к делению на 0:

∫ d Икс Икс знак равно Икс 0 0 + C { displaystyle int { frac {dx} {x}} = { frac {x ^ {0}} {0}} + C}

Вместо этого интеграл определяется как:

∫ 1 а d Икс Икс знак равно пер ⁡ а , { displaystyle int _ {1} ^ {a} { frac {dx} {x}} = ln a,}

∫ d Икс Икс знак равно пер ⁡ Икс + C . { displaystyle int { frac {dx} {x}} = ln x + C.}

где ln — натуральный логарифм. Чтобы показать это, обратите внимание, что, если и, у нас есть:

d d Икс е Икс знак равно е Икс { textstyle { frac {d} {dx}} e ^ {x} = e ^ {x}}

у знак равно е Икс { Displaystyle у = е ^ {х}}

Икс знак равно пер ⁡ у { Displaystyle х = пер у}

d у d Икс знак равно у ⇒ d у у знак равно d Икс ⇒ ∫ d у у знак равно ∫ d Икс ⇒ ∫ d у у знак равно Икс + C знак равно пер ⁡ у + C . { displaystyle { frac {dy} {dx}} = y quad Rightarrow quad { frac {dy} {y}} = dx quad Rightarrow quad int { frac {dy} {y} } = int dx quad Rightarrow quad int { frac {dy} {y}} = x + C = ln y + C.}

Алгоритмы

Обратную величину можно вычислить вручную с использованием длинного деления.

Вычисление обратной величины важно во многих алгоритмах деления, поскольку частное a / b можно вычислить, сначала вычислив 1 / b, а затем умножив его на a. Отметив, что имеет ноль при x = 1 / b, метод Ньютона может найти этот ноль, начиная с предположения и повторяя, используя правило: ж ( Икс ) знак равно 1 / Икс — б { Displaystyle f (x) = 1 / xb} Икс 0 { displaystyle x_ {0}}

Икс п + 1 знак равно Икс п — ж ( Икс п ) ж ′ ( Икс п ) знак равно Икс п — 1 / Икс п — б — 1 / Икс п 2 знак равно 2 Икс п — б Икс п 2 знак равно Икс п ( 2 — б Икс п ) . { displaystyle x_ {n + 1} = x_ {n} — { frac {f (x_ {n})} {f ‘(x_ {n})}} = x_ {n} — { frac {1 / x_ {n} -b} {- 1 / x_ {n} ^ {2}}} = 2x_ {n} -bx_ {n} ^ {2} = x_ {n} (2-bx_ {n}).}

Это продолжается до тех пор, пока не будет достигнута желаемая точность. Например, предположим, что мы хотим вычислить 1/17 ≈ 0,0588 с точностью до 3 знаков. Принимая x 0 = 0,1, получается следующая последовательность:

х 1 = 0,1 (2-17 × 0,1) = 0,03

х 2 = 0,03 (2-17 × 0,03) = 0,0447

х 3 = 0,0447 (2-17 × 0,0447) ≈ 0,0554

х 4 = 0,0554 (2-17 × 0,0554) ≈ 0,0586

х 5 = 0,0586 (2-17 × 0,0586) ≈ 0,0588

Типичное начальное предположение можно найти, округлив b до ближайшей степени 2, а затем используя битовые сдвиги, чтобы вычислить обратную величину.

В конструктивной математике для того, чтобы действительное число x было обратным, недостаточно, чтобы x ≠ 0. Вместо этого должно быть задано рациональное число r такое, что 0 lt;  r  lt;| х |. С точки зрения алгоритма аппроксимации , описанного выше, это необходимо для доказательства того, что изменение y в конечном итоге станет сколь угодно малым.

График f ( x) = x ^x, показывающий минимум в (1 / e, e ^{−1 / e}).

Эту итерацию можно также обобщить на более широкий вид инверсий; например, обратная матрица.

Обратные иррациональные числа

Каждое действительное или комплексное число, за исключением нуля, имеет обратную величину, а обратные величины некоторых иррациональных чисел могут иметь важные особые свойства. Примеры включают обратную величину e (≈ 0,367879) и обратную величину золотого сечения (≈ 0,618034). Первое обратное число является особенным, потому что никакое другое положительное число не может дать меньшее число, если поставить его во власть самого себя; является глобальным минимумом в. Второе число является единственным положительным числом, которое равно ее обратным плюс один:. Его добавка обратный является единственным отрицательным числом, которое равно его взаимного минус один:. ж ( 1 / е ) { displaystyle f (1 / e)} ж ( Икс ) знак равно Икс Икс { Displaystyle е (х) = х ^ {х}} φ знак равно 1 / φ + 1 { Displaystyle varphi = 1 / varphi +1} — φ знак равно — 1 / φ — 1 { displaystyle — varphi = -1 / varphi -1}

Функция дает бесконечное количество иррациональных чисел, которые отличаются друг от друга на целое число. Например, это иррациональное. Его обратная величина — ровно меньше. Такие иррациональные числа обладают очевидным свойством: они имеют ту же дробную часть, что и их обратная величина, поскольку эти числа отличаются на целое число. ж ( п ) знак равно п + ( п 2 + 1 ) , п ∈ N , п gt; 0 { textstyle f (n) = n + { sqrt {(n ^ {2} +1)}}, n in mathbb {N}, ngt; 0} ж ( 2 ) { displaystyle f (2)} 2 + 5 { displaystyle 2 + { sqrt {5}}} 1 / ( 2 + 5 ) { displaystyle 1 / (2 + { sqrt {5}})} — 2 + 5 { displaystyle -2 + { sqrt {5}}} 4 { displaystyle 4}

Дальнейшие замечания

Если умножение является ассоциативным, элемент x с мультипликативным обратным элементом не может быть делителем нуля ( x является делителем нуля, если некоторый ненулевой y, xy = 0). Чтобы убедиться в этом, достаточно умножить уравнение xy = 0 на обратное к x (слева), а затем упростить, используя ассоциативность. В отсутствие ассоциативности sedenions представляют собой контрпример.

Обратное неверно: элемент, который не является делителем нуля, не обязательно имеет мультипликативный обратный. В Z все целые числа, кроме -1, 0, 1, являются примерами; они не являются делителями нуля и они не обратимы в Z. Однако, если кольцо или алгебра конечны, то все элементы a, не являющиеся делителями нуля, имеют обратный (левый и правый). Для сначала заметьте, что отображение f ( x) = ax должно быть инъективным : f ( x) = f ( y) влечет x = y:

а Икс знак равно а у ⇒ а Икс — а у знак равно 0 ⇒ а ( Икс — у ) знак равно 0 ⇒ Икс — у знак равно 0 ⇒ Икс знак равно у . { Displaystyle { begin {align} ax amp; = ay amp; quad Rightarrow amp; quad ax-ay = 0 \ amp;amp; quad Rightarrow amp; quad a (xy) = 0 \ amp;amp; quad Rightarrow amp; quad xy = 0 \ amp;amp; quad Rightarrow amp; quad x = y. end {align}}}

Разные элементы отображаются в разные элементы, поэтому изображение состоит из одного и того же конечного числа элементов, а карта обязательно сюръективна. В частности, ƒ (а именно умножение на a) должно отображать некоторый элемент x в 1, ax = 1, так что x является обратным для a.

Приложения

Расширение обратного 1 / q по любому основанию также может действовать как источник псевдослучайных чисел, если q является «подходящим» безопасным простым числом, простым числом формы 2 p  + 1, где p также является простым числом. Последовательность псевдослучайных чисел длины q  — 1 будет произведена расширением.

Смотрите также

• Отдел (математика)
• Экспоненциальный спад
• Дробь (математика)
• Группа (математика)
• Гипербола
• Список сумм обратных величин
• Повторяющаяся десятичная дробь
• Шестисферные координаты
• Дроби единицы — обратные числа целых чисел

Примечания

1. ^ «В равных параллелепипедах основания равны своей высоте». ДОО «Взаимный» §3а. Переводсэра Генри Биллингсли Elements XI, 34.
2. ^ Энтони, доктор «Доказательство того, что INT (1 / x) dx = lnx». Спросите доктора Математики. Дрексельский университет. Проверено 22 марта 2013 года.
3. ^ Митчелл, Дуглас В., «Нелинейный генератор случайных чисел с известной большой длиной цикла», Cryptologia 17, январь 1993 г., 55–62.

использованная литература

• Максимально периодические взаимные числа, Бюллетень Мэтьюза Р.Дж. Института математики и его приложений, том 28, стр. 147–148, 1992 г.