Задача: посчитать N-е число последовательности, в которой каждый элемент равен сумме двух предыдущих. Такая последовательность называется последовательностью Фибоначчи: 1, 1, 2, 3, 5, 8…
Очень часто на разнообразных олимпиадах попадаются задачи вроде этой, которые, как думается на первый взгляд, можно решить с помощью простого перебора. Но если мы подсчитаем количество возможных вариантов, то сразу убедимся в неэффективности такого подхода: например, простая рекурсивная функция, приведенная ниже, будет потреблять существенные ресурсы уже на 30-ом числе Фибоначчи, тогда как на олимпиадах время решения часто ограничено 1-5 секундами.
int fibo(int n)
{
if (n == 1 || n == 2) {
return 1;
} else {
return fibo(n - 1) + fibo(n - 2);
}
}Давайте подумаем, почему так происходит. Например, для вычисления fibo(30) мы сначала вычисляем fibo(29) и fibo(28). Но при этом наша программа «забывает», что fibo(28) мы уже вычисляли при поиске fibo(29).
Основная ошибка такого подхода «в лоб» в том, что одинаковые значения аргументов функции исчисляются многократно — а ведь это достаточно ресурсоемкие операции. Избавиться от повторяющихся вычислений нам поможет метод динамического программирования — это прием, при использовании которого задача разбивается на общие и повторяющиеся подзадачи, каждая из которых решается только 1 раз — это значительно повышает эффективность программы. Этот метод подробно описан в нашей статье, там же есть и примеры решения других задач.
Самый просто вариант улучшения нашей функции — запоминать, какие значения мы уже вычисляли. Для этого нужно ввести дополнительный массив, который будет служить как бы «кэшем» для наших вычислений: перед вычислением нового значения мы будем проверять, не вычисляли ли его раньше. Если вычисляли, то будем брать из массива готовое значение, а если не вычисляли — придётся считать его на основе предыдущих и запоминать на будущее:
int cache[100];
int fibo(int n)
{
if (cache[n] == 0) {
if (n == 1 || n == 2) {
cache[n] = 1;
} else {
cache[n] = fibo(n - 1) + fibo(n - 2);
}
}
return cache[n];
}Так как в данной задаче для вычисления N-ого значения нам гарантированно понадобится (N-1)-е, то не составит труда переписать формулу в итерационный вид — просто будем заполнять наш массив подряд до тех пор, пока не дойдём до нужной ячейки:
cache[0] = 1;
cache[1] = 1;
for (int i = 2; i <= n; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
cout << cache[n-1];Теперь мы можем заметить, что когда мы вычисляем значение F(N), то значение F(N-3) нам уже гарантированно никогда не понадобится. То есть нам достаточно хранить в памяти лишь два значения — F(N-1) и F(N-2). Причём, как только мы вычислили F(N), хранение F(N-2) теряет всякий смысл. Попробуем записать эти размышления в виде кода:
//Два предыдущих значения:
int cache1 = 1;
int cache2 = 1;
//Новое значение
int cache3;
for (int i = 2; i <= n; i++) {
cache3 = cache1 + cache2; //Вычисляем новое значение
//Абстрактный cache4 будет равен cache3+cache2
//Значит cache1 нам уже не нужен?..
//Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации.
//cache5 = cache4 - cache3 => через итерацию потеряет актуальность cache2, т.е. он и должен стать cache1
//Иными словами, cache1 -- f(n-2), cache2 -- f(n-1), cache3 -- f(n).
//Пусть N=n+1 (номер, который мы вычисляем на следующей итерации). Тогда n-2=N-3, n-1=N-2, n=N-1.
//В соответствии с новыми реалиями мы и переписываем значения наших переменных:
cache1 = cache2;
cache2 = cache3;
}
cout << cache3;Бывалому программисту понятно, что код выше, в общем-то ерунда, так как cache3 никогда не используется (он сразу записывается в cache2), и всю итерацию можно переписать, используя всего одно выражение:
cache[0] = 1;
cache[1] = 1;
for (int i = 2; i <= n; i++) {
cache[i%2] = cache[0] + cache[1];
//При i=2 устареет 0-й элемент
//При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый
//При i=4 последним элементом мы обновляли cache[1], значит ненужное старьё сейчас в cache[0]
//Интуитивно понятно, что так будет продолжаться и дальше
}
cout << cache[n%2];Для тех, кто не может понять, как работает магия с остатком от деления, или просто хочет увидеть более неочевидную формулу, существует ещё одно решение:
int x = 1;
int y = 1;
for (int i = 2; i < n; i++) {
y = x + y;
x = y - x;
}
cout << "Число Фибоначчи: " << y;Попробуйте проследить за выполнением этой программы: вы убедитесь в правильности алгоритма.
P.S. Вообще, существует единая формула для вычисления любого числа Фибоначчи, которая не требует никаких итераций или рекурсии:
const double SQRT5 = sqrt(5);
const double PHI = (SQRT5 + 1) / 2;
int fibo(int n){
return int(pow(PHI, n) / SQRT5 + 0.5);
}Но, как можете догадаться, подвох в том, что цена вычисления степеней нецелых чисел довольно велика, как и их погрешность.
Загрузить PDF
Загрузить PDF
Последовательность Фибоначчи – это ряд чисел, в котором каждое последующее число равно сумме двух предыдущих чисел. Числовые последовательности часто встречаются в природе и искусстве в виде спиралей и «золотого сечения». Самый простой способ вычислить последовательность Фибоначчи – это создать таблицу, но такой метод не применим к большим последовательностям. Например, если нужно определить 100-й член последовательности, лучше воспользоваться формулой Бине.
-
1
Нарисуйте таблицу с двумя столбцами. Количество строк таблицы зависит от количества чисел последовательности Фибоначчи, которые нужно найти.
- Например, если нужно найти пятое число последовательности, нарисуйте таблицу с пятью строками.
- Используя таблицу, нельзя найти некоторое случайное число без вычисления всех предыдущих чисел. Например, если нужно найти 100-е число последовательности, нужно вычислить все числа: от первого до 99-ого. Поэтому таблица применима только для нахождения первых чисел последовательности.
-
2
В левом столбце напишите порядковые номера членов последовательности. То есть напишите цифры по порядку, начиная с единицы.
- Такие цифры определяют порядковые номера членов (чисел) последовательности Фибоначчи.
- Например, если нужно найти пятое число последовательности, в левой колонке напишите следующие цифры: 1, 2, 3, 4, 5. То есть нужно найти с первого по пятое число последовательности.
-
3
В первой строке правой колонки напишите 1. Это первое число (член) последовательности Фибоначчи.
- Имейте в виду, что последовательность Фибоначчи всегда начинается с 1. Если последовательность начинается с другого числа, вы неправильно вычислили все числа вплоть до первого.
-
4
К первому члену (1) прибавьте 0. Получится второе число последовательности.
- Запомните: чтобы найти любое число последовательности Фибоначчи, просто сложите два предыдущих числа.
- Чтобы создать последовательность, не забудьте о 0, который стоит перед 1 (первым членом), поэтому 1 + 0 = 1.
-
5
Сложите первый (1) и второй (1) члены. Получится третье число последовательности.
- 1 + 1 = 2. Третий член равен 2.
-
6
Сложите второй (1) и третий (2) члены, чтобы получить четвертое число последовательности.
- 1 + 2 = 3. Четвертый член равен 3.
-
7
Сложите третий (2) и четвертый (3) члены. Получится пятое число последовательности.
- 2 + 3 = 5. Пятый член равен 5.
-
8
Сложите два предыдущих числа, чтобы найти любое число последовательности Фибоначчи. Этот метод основан на формуле:
.[1]
Эта формула не является замкнутой, поэтому при помощи этой формулы нельзя найти любой член последовательности без вычисления всех предыдущих чисел.Реклама
-
1
-
2
В формулу подставьте порядковый номер числа (вместо
).
– это порядковый номер любого искомого члена последовательности.
-
3
В формулу подставьте золотое сечение. Золотое сечение приблизительно равно 1,618034; подставьте в формулу это число.[5]
-
4
Вычислите выражение в скобках. Не забывайте про правильный порядок выполнения математических операций, в котором выражение в скобках вычисляется в первую очередь:
.
-
5
Возведите числа в степени. Возведите в соответствующие степени два числа, которые находятся в числителе.
-
6
Вычтите два числа. Перед тем как приступить к делению, вычтите числа, которые находятся в числителе.
-
7
Полученный результат разделите на квадратный корень из 5. Квадратный корень из 5 приблизительно равен 2,236067.
- В нашем примере:
.
- В нашем примере:
-
8
Полученный результат округлите до ближайшего целого числа. Последний результат будет десятичной дробью, которая близка к целому числу. Такое целое число представляет собой число последовательности Фибоначчи.
- Если в вычислениях использовать неокругленные числа, вы получите целое число. Работать с округленными числами намного легче, но в этом случае вы получите десятичную дробь.[6]
- В нашем примере вы получили десятичную дробь 5,000002. Округлите ее до ближайшего целого числа и получите пятое число последовательности Фибоначчи, которое равно 5.
Реклама
- Если в вычислениях использовать неокругленные числа, вы получите целое число. Работать с округленными числами намного легче, но в этом случае вы получите десятичную дробь.[6]
Об этой статье
Эту страницу просматривали 27 790 раз.
Была ли эта статья полезной?
Fibonacci sequence is one of the most known formulas in number theory. In the Fibonacci sequence, each number in the series is calculated by adding the two numbers before it. Generally, the first two terms of the Fibonacci series are 0 and 1. Fibonacci sequence was known in India hundreds of years before Leonardo Pisano Bigollo know about it. November 23rd is celebrated as Fibonacci Day, as it has the digits “1, 1, 2, 3” which is part of the sequence.
The Fibonacci sequence is as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946,….
Fibonacci’s sequence is useful for its operations in advanced mathematics and statistics, computer science, economics, and nature.
Fibonacci Series
Formula of Fibonacci Number
Fn = Fn-1 + Fn-2
- Fn is term number “n”
- Fn−1 is the previous term (n−1)
- Fn−2 is the term before that (n−2)
Calculation of Fibonacci numbers
To calculate the 5th Fibonacci number, add the 4th and 3rd Fibonacci numbers.
Golden Ratio
On choosing any two consecutive (one after the other) Fibonacci numbers, their ratio is near to 1.618034 and it is called Golden Ratio. It is denoted by “φ”. The golden ratio is generally can be seen in nature, and when applied in a design, it fosters natural-seeming works that are pleasing to the eye. There are numerous operations of the golden ratio in the field of architecture. For illustration, the Great Pyramid of Egypt and the Great Mosque of Kairouan is many of the architectural miracles in which the notion of the golden ratio has been applied.
For example:
| X | Y | Y/X |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6666 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 13 | 21 | 1.6154 |
| 21 | 34 | 1.6190 |
| 34 | 55 | 1.6176 |
| 55 | 89 | 1.6181 |
| 89 | 144 | 1.6179 |
Note: Golden Ratio can be calculated from Any Fibonacci sequence, it does not necessarily have to start with 2 and 3.
Calculation of Fibonacci number using Golden Ratio
Any Fibonacci number can be calculated by using this formula,
xn = (φn − (1−φ)n)/√5
xn denotes Fibonacci number to be calculated
φ is Golden ratio that is 1.618034
For example: If you want to calculate the 7th term:
x7 = ((1.618034)7-(1-1.618034)7)/√5
x7 = 13.0000007
x7 = 13(rounded off)
The next Fibonacci number can also be calculated using Golden Ratio. Multiplying a Fibonacci number with a golden ratio will give the next Fibonacci number of the sequence. But that only works for numbers greater than 1.
Example: 13*1.618034 = 21.034442 = 21(rounded off)
Some Problems based on Golden Ratio
Question 1: Calculate the 9th Fibonacci number if given golden ratio is 1.618034.
Solution:
We can calculate the 9th Fibonacci number by using the formula:
xn = (φn − (1−φ)n)/√5
x9 = ((1.618034)9-(1-1.618034)9)/√5
x9 = (76.0131604-(-0.0131556197))/√5 = 34.0000021
x9 = 34
Question 2: Find the next Fibonacci number of answers calculated in the above question.
Solution:
Next Fibonacci number of 34 can be easily found by multiplying it by the Golden ratio that is 1.618034.
x10 = 34×1.61803 = 55.01302
x10 = 55(rounded off)
Some Problems based on Fibonacci Numbers
Question 1: If the 5th and 6th terms of a Fibonacci sequence are 3 and 5 respectively, find the 7th term of the sequence.
Solution:
With the use of the Fibonacci Sequence formula, we can easily calculate the 7th term of the Fibonacci sequence which is the sum of the 5th and 6th terms.
seventh term = 5th term + 6th term
= 3+5
= 8
The 7th term of the Fibonacci sequence is 8.
Question 2: The first 4 numbers in the Fibonacci sequence are given as 1,1,2,3.
(a) What is the eighth term of the Fibonacci sequence?
(b) What is the eleventh term of the Fibonacci sequence?
Solution:
By the use of the Fibonacci number formula, we can calculate the rest of the Fibonacci numbers like 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
(a) Therefore, the 8th term will be 21.
(b) 11th term will be 89.
Question 3: Find the next 3 terms for each of the following Fibonacci-style sequences.
(a) x, 4x, 5x, 9x,…
(b) 3a, 3a+b, 6a+b, 9a+2b….
Solution:
With the use of the Fibonacci Sequence formula, we can easily calculate the rest of the terms
(a) Fifth term = 5x+9x = 14x,
Sixth term = 9x+14x = 23x,
Seventh term = 14x+23x = 37x
(b) Fifth term = 6a+b+9a+2b = 15a+3b,
Sixth term = 9a+2b+15a+3b = 24a+5b,
Seventh term = 15a+3b+24a+5b = 39a+8b
Question 4: John wants to generate a Fibonacci series with the first term as 3 and the second term as 4.
(a) Find the 3rd and 4th terms.
(b) He thinks that the sum of the first ten terms is equal to eleven times the seventh term of his sequence. Check if he is correct.
Solution:
Using the 3 and 4 as first and second terms, we can calculate the rest of the terms by simply adding the last two terms.
(a) First term = 3,
Second term = 4,
Third Term = 3+4=7,
Forth term = 4+7 = 11
(b) On calculating the first ten terms of the series: 3,4,7,11,18,29,47,76,123,199.
Sum of first ten terms = 3+4+7+11+18+29+47+76+123+199 = 517
7th term = 47
Eleven times the 7th term = 11*47 = 517
As we can see that the sum of the first ten terms is equal to eleven times the seventh term of his sequence. Therefore, John was correct.
Question 5: What is the first three-digit square number that appears on the list of Fibonacci numbers, if the first 4 terms are 0,1,1,2.
Solution:
With the use of the Fibonacci Sequence formula, we can easily calculate the rest of the terms:
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,…
As we can see the first three-digit number which is a square that appears on the list of Fibonacci numbers is 144(square of 12).
Время на прочтение
5 мин
Количество просмотров 306K
Введение
Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.
Код предназначен для Python 3, хотя должен идти и на Python 2.
Для начала – напомню определение:
Fn= Fn-1+ Fn-2
и F1= F2=1.
Замкнутая формула
Пропустим детали, но желающие могут ознакомиться с выводом формулы. Идея в том, чтобы предположить, что есть некий x, для которого Fn = xn, а затем найти x.
что означает
сокращаем xn-2
Решаем квадратное уравнение:
Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:
что и используем для вычисления Fn.
from __future__ import division
import math
def fib(n):
SQRT5 = math.sqrt(5)
PHI = (SQRT5 + 1) / 2
return int(PHI ** n / SQRT5 + 0.5)
Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления Fn красиво с математической точки зрения, но уродливо — с компьютерной.
Рекурсия
Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:
fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1
Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека
Запоминание
У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.
Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.
M = {0: 0, 1: 1}
def fib(n):
if n in M:
return M[n]
M[n] = fib(n - 1) + fib(n - 2)
return M[n]
(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)
Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии
Динамическое программирование
После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.
Это решение часто приводится в качестве примера динамического программирования.
def fib(n):
a = 0
b = 1
for __ in range(n):
a, b = b, a + b
return a
Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.
Матричная алгебра
И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что
А обобщение этого говорит о том, что
Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.
Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что
где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.
def pow(x, n, I, mult):
"""
Возвращает x в степени n. Предполагает, что I – это единичная матрица, которая
перемножается с mult, а n – положительное целое
"""
if n == 0:
return I
elif n == 1:
return x
else:
y = pow(x, n // 2, I, mult)
y = mult(y, y)
if n % 2:
y = mult(x, y)
return y
def identity_matrix(n):
"""Возвращает единичную матрицу n на n"""
r = list(range(n))
return [[1 if i == j else 0 for i in r] for j in r]
def matrix_multiply(A, B):
BT = list(zip(*B))
return [[sum(a * b
for a, b in zip(row_a, col_b))
for col_b in BT]
for row_a in A]
def fib(n):
F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply)
return F[0][1]
Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи
Сравнение быстродействия
Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.
n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.
Теоретические замечания
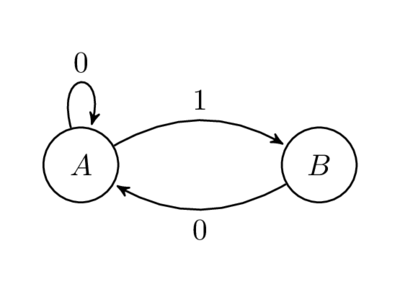
Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:
Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности Fn. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в Аn — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).
Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием «подсдвиги конечного типа», представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» {11}. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.
|
0 / 0 / 0 Регистрация: 25.10.2020 Сообщений: 5 |
|
|
1 |
|
|
25.10.2020, 18:07. Показов 12285. Ответов 4
Для n-го члена в последовательности Фибоначчи существует явная формула
0 |
|
48 / 43 / 10 Регистрация: 20.10.2020 Сообщений: 99 |
|
|
25.10.2020, 18:13 |
2 |
|
«Явная формула» предполагает округление. О каких 1e-3 идёт речь? Или речь об оригинальной формуле Бине?
0 |
|
0 / 0 / 0 Регистрация: 25.10.2020 Сообщений: 5 |
|
|
25.10.2020, 18:19 [ТС] |
3 |
|
не совсем понял, вот скрин задания Миниатюры
0 |
|
Gdez 7258 / 4047 / 1780 Регистрация: 27.03.2020 Сообщений: 6,875 |
||||
|
25.10.2020, 19:12 |
4 |
|||
|
Решениеstewie1342,
2 |
|
vpArth 48 / 43 / 10 Регистрация: 20.10.2020 Сообщений: 99 |
||||
|
25.10.2020, 19:22 |
5 |
|||
|
Решение
2 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
25.10.2020, 19:22 |
|
5 |























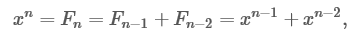

 Сообщение было отмечено stewie1342 как решение
Сообщение было отмечено stewie1342 как решение