Чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец.
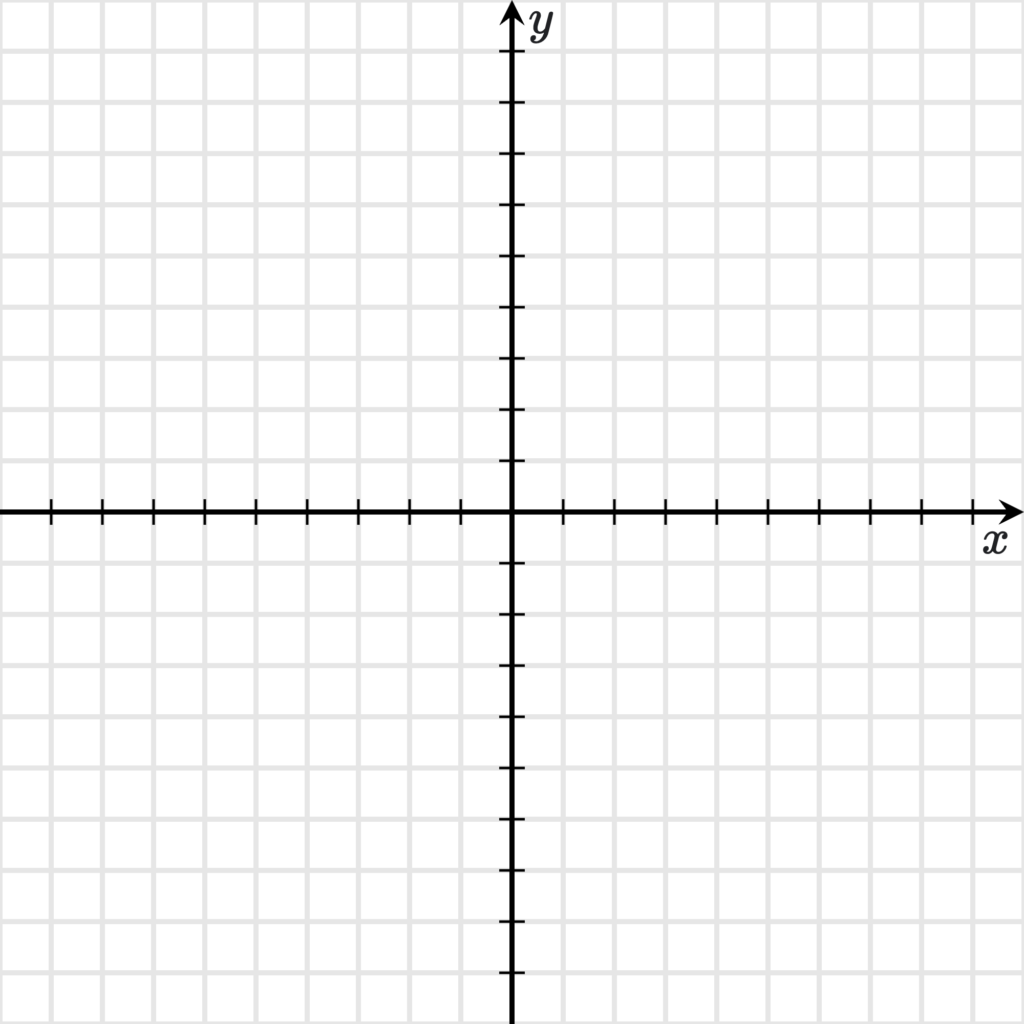
В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).
Абсцисса, ордината, начало координат и единичный отрезок
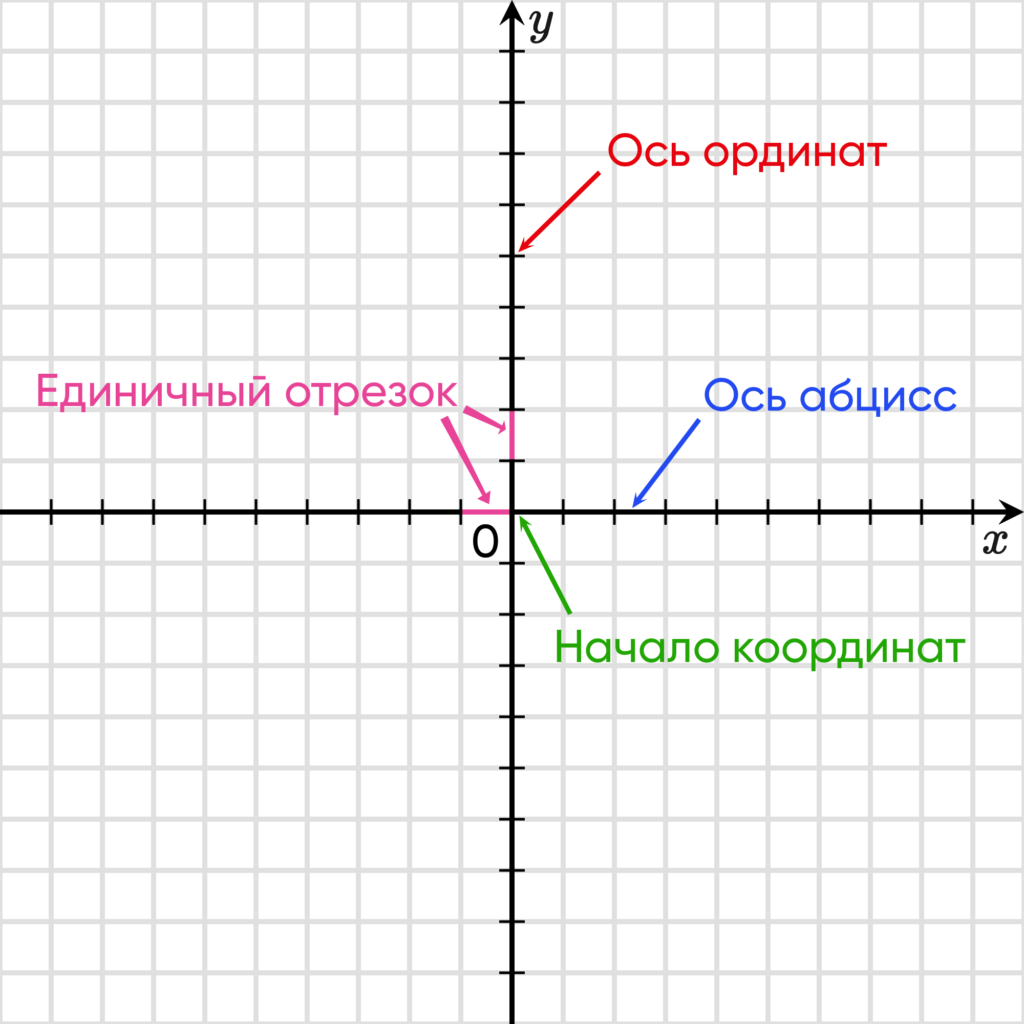
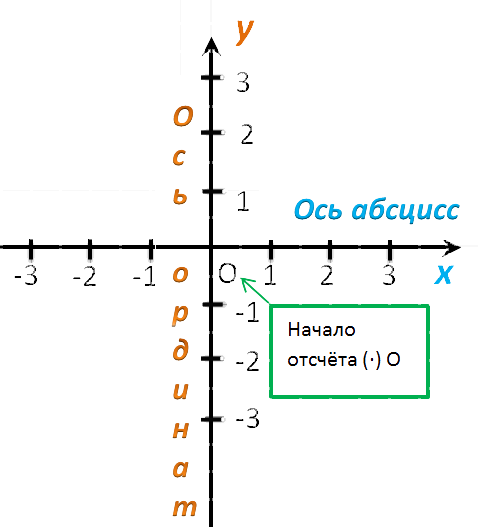
Эти оси имеют общепринятые наименования. А именно, горизонтальную ось именуют осью абсцисс и на письме обозначают $Оx$
Вертикальную ось называют осью ординат и на письме обозначают $Оy$
Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.
Место пересечения осей координат является началом отсчета. Обычно эту точку обозначают буквой $О$ и называют началом координат. Ее называют еще иногда нулевой точкой.
На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.
Положительное и отрицательное направление
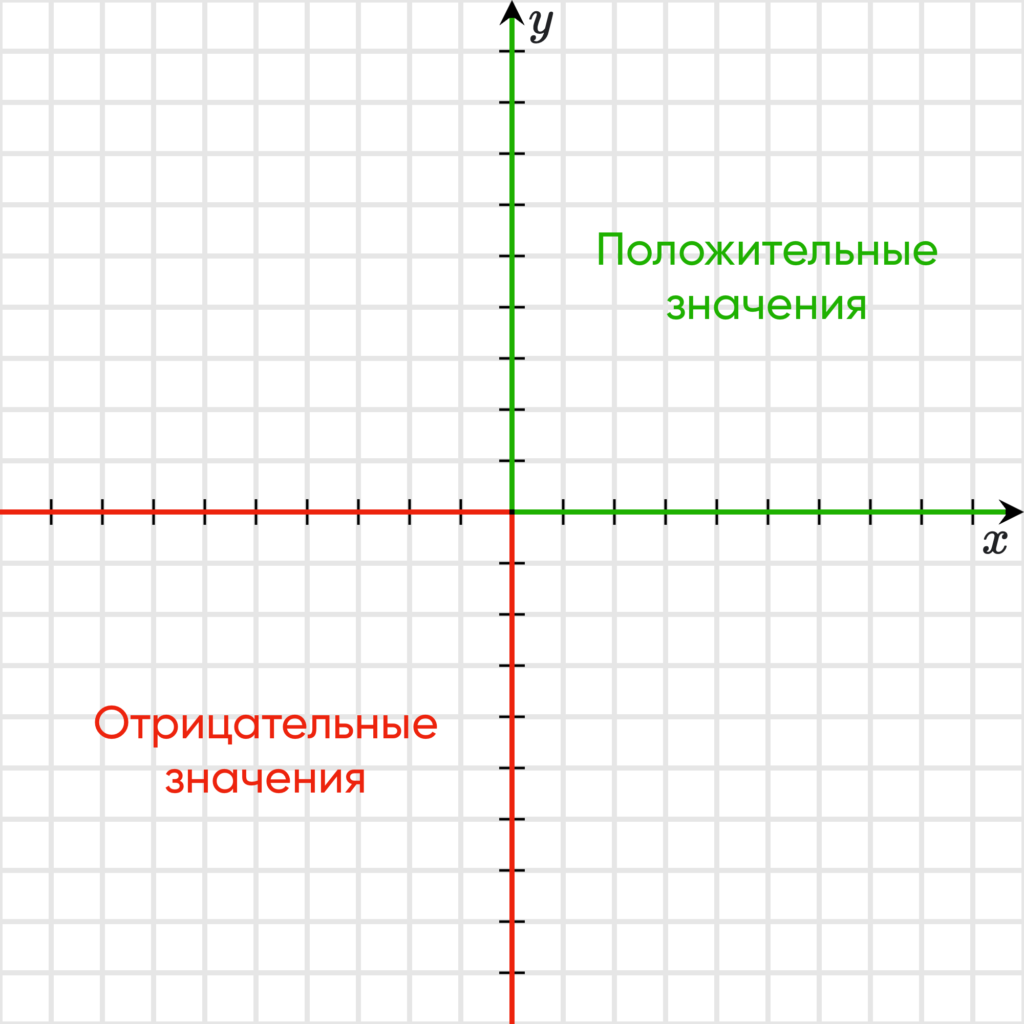
У осей стрелкой задается положительное направление:
- так обычно у оси $Оx$ положительным считается направление вправо;
- у оси $Оy$ положительным считается направление снизу вверх.
В таком случае часть прямой $Оx$ левее точки $О$ будет принимать отрицательные значения. Аналогично часть прямой $Оy$ ниже точки отсчета $О$ будет также принимать отрицательные значения.
Таким образом, все вместе:
- начало координат $О$
- пересекающиеся под прямым углом оси $Оx$ и $Оy$ с заданными направлениями
- заданный единичный отрезок
образуют в математике прямоугольную систему координат, плоскость называют координатной.
Или другими словами:
Прямоугольная система координат – это две взаимно перпендикулярные координатные оси с заданными направлениями, единицей длины и точкой отсчета в месте их пересечения.
На письме система координат обозначается $Оxy$
Четверти
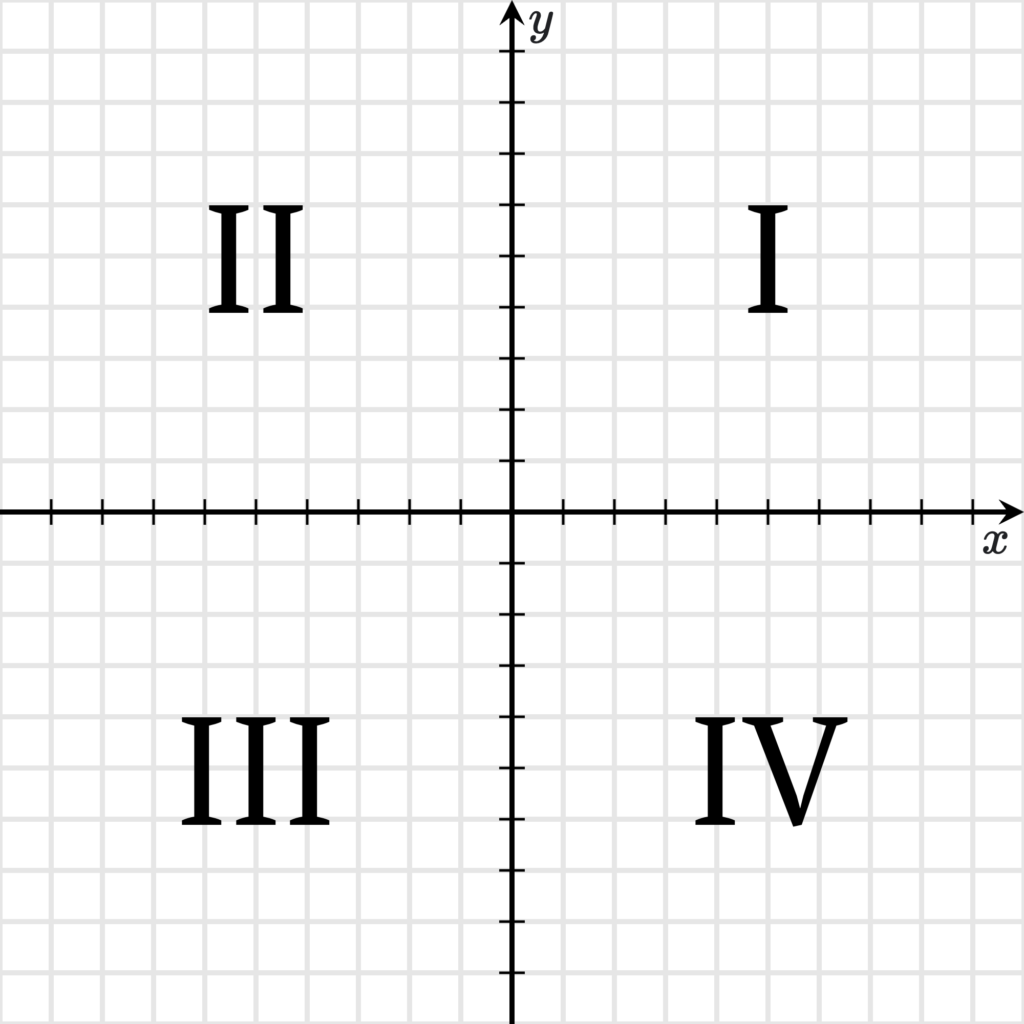
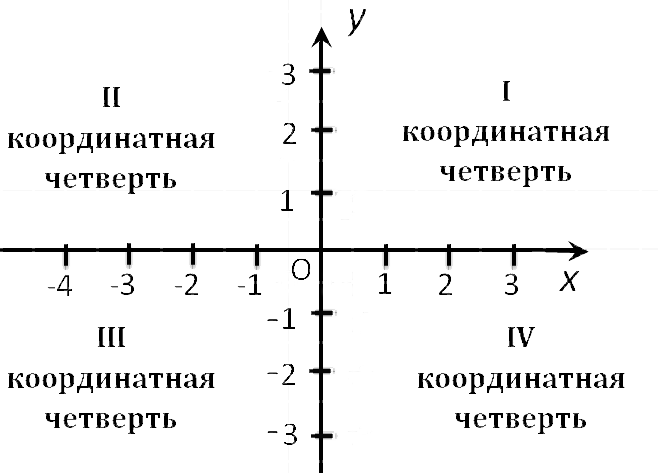
Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.
В квадранте I значения $x$ и $y$ будут положительными. Отсюда следует, что если координаты объекта $x$ и $y$ – числа положительные, то он находится в I квадранте.
В квадранте II значение $y$ будет положительными, а $x$ отрицательным.
В квадранте III обе координаты $x$ и $y$ будут иметь отрицательные значения.
В последнем IV квадранте значение $x$ будет положительным, а $y$ отрицательным.
Немного из истории
В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».
Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара.
Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».
From Wikipedia, the free encyclopedia
Illustration of a Cartesian coordinate plane, showing the absolute values (unsigned dotted line lengths) of the coordinates of the points (2, 3), (0, 0), (–3, 1), and (–1.5, –2.5). The first value in each of these signed ordered pairs is the abscissa of the corresponding point, and the second value is its ordinate.
In common usage, the abscissa refers to the (x) coordinate and the ordinate refers to the (y) coordinate of a standard two-dimensional graph.
The distance of a point from the y-axis, scaled with the x-axis, is called the abscissa or x coordinate of the point. The distance of a point from the x-axis scaled with the y-axis is called the ordinate or y coordinate of the point.
For example, if (x, y) is an ordered pair in the Cartesian plane, then the first coordinate in the plane (x) is called the abscissa and the second coordinate (y) is the ordinate.
In mathematics, the abscissa (; plural abscissae or abscissas) and the ordinate are respectively the first and second coordinate of a point in a Cartesian coordinate system:
- abscissa
-axis (horizontal) coordinate
- ordinate
-axis (vertical) coordinate
Usually these are the horizontal and vertical coordinates of a point in plane, the rectangular coordinate system. An ordered pair consists of two terms—the abscissa (horizontal, usually x) and the ordinate (vertical, usually y)—which define the location of a point in two-dimensional rectangular space:
The abscissa of a point is the signed measure of its projection on the primary axis, whose absolute value is the distance between the projection and the origin of the axis, and whose sign is given by the location on the projection relative to the origin (before: negative; after: positive).
The ordinate of a point is the signed measure of its projection on the secondary axis, whose absolute value is the distance between the projection and the origin of the axis, and whose sign is given by the location on the projection relative to the origin (before: negative; after: positive).
Etymology[edit]
Though the word «abscissa» (from Latin linea abscissa ‘a line cut off’) has been used at least since De Practica Geometrie published in 1220 by Fibonacci (Leonardo of Pisa), its use in its modern sense may be due to Venetian mathematician Stefano degli Angeli in his work Miscellaneum Hyperbolicum, et Parabolicum of 1659.[1]
In his 1892 work Vorlesungen über die Geschichte der Mathematik («Lectures on history of mathematics«), volume 2, German historian of mathematics Moritz Cantor writes:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Abscisse in lateinischen Originalschriften. Vielleicht kommt das Wort in Uebersetzungen der Apollonischen Kegelschnitte vor, wo Buch I Satz 20 von ἀποτεμνομέναις die Rede ist, wofür es kaum ein entsprechenderes lateinisches Wort als abscissa geben möchte.[2]
At the same time it was presumably by [Stefano degli Angeli] that a word was introduced into the mathematical vocabulary for which especially in analytic geometry the future proved to have much in store. […] We know of no earlier use of the word abscissa in Latin original texts. Maybe the word appears in translations of the Apollonian conics, where [in] Book I, Chapter 20 there is mention of ἀποτεμνομέναις, for which there would hardly be a more appropriate Latin word than abscissa.
The use of the word “ordinate” is related to the Latin phrase “linea ordinata appliicata”, or “line applied parallel”.
In parametric equations[edit]
In a somewhat obsolete variant usage, the abscissa of a point may also refer to any number that describes the point’s location along some path, e.g. the parameter of a parametric equation.[3] Used in this way, the abscissa can be thought of as a coordinate-geometry analog to the independent variable in a mathematical model or experiment (with any ordinates filling a role analogous to dependent variables).
See also[edit]
- Dependent and independent variables
- Function (mathematics)
- Relation (mathematics)
- Line chart
References[edit]
- ^ Dyer, Jason (March 8, 2009). «On the Word «Abscissa»«. numberwarrior.wordpress.com. The number Warrior. Retrieved September 10, 2015.
- ^ Cantor, Moritz (1900). Vorlesungen über Geschichte der Mathematik (in German). Vol. 2 (2nd ed.). Leipzig: B.G. Teubner. p. 898. Retrieved 10 September 2015.
- ^ Hedegaard, Rasmus; Weisstein, Eric W. «Abscissa». MathWorld. Retrieved 14 July 2013.
External links[edit]
The dictionary definition of abscissa and ordinate at Wiktionary
В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты».
В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.
Координаты могут обозначаться самыми разными наборами цифр или букв.
Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого
она города и кто ёё владелец.
Важно!
Координаты — это набор данных, по которому определяется положение того или иного объекта.
Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте,
запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.
Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или
других символов, мы задаём координаты объекта.
Декартова система координат
Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.
Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.
- На плоскости такими ориентирами будут служить две числовые оси. На чертеже обычно первую ось рисуют горизонтально, её
называют осью АБСЦИСС и обозначают буквой «X», записывают ось
«Ox». Положительное направление на оси абсцисс выбирают
слева направо и
показывают стрелкой. - Вторую ось проводят вертикально, её называют
осью ОРДИНАТ и обозначают буквой «Y», записывают ось
«Oy».
Положительное направление на оси ординат выбирают
снизу вверх и
показывают стрелкой.
Оси взаимно перпендикулярны (т.е. угол между ними равен 90°) и
пересекаются в точке, которую обозначают «O».
Точка «O» является началом отсчёта для каждой из осей.
Запомните!
Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является
началом отсчёта для каждой из них.
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс «Ox» — горизонтальная ось.
Ось ординат «Oy» — вертикальная ось.
Координатная плоскость — плоскость, в которой построена система координат.
Обозначается плоскость как «x0y».
Обращаем ваше внимание на выбор длины единичных отрезков по осям.
Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева
от оси «Oy». Цифры
на оси «Ox», как правило, пишут внизу под осью.
Обычно единичный отрезок на оси «0y» равен единичному
отрезку на оси «0x». Но бывают случаи,
когда они не равны друг другу.
Оси координат делят плоскость на 4 угла, которые называют координатными четвертями. Четверть, образованная положительными
полуосями (правый верхний угол), считают первой I.
Отсчитываем четверти (или координатные углы) против часовой стрелки.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
28 сентября 2016 в 11:11
Вероника Диянова
Профиль
Благодарили: 0
Сообщений: 1
Вероника Диянова
Профиль
Благодарили: 0
Сообщений: 1
На оси абсцисс найти точку, расстояние которой от прямой 8х+15у+10=0 равно 1. Сделать чертеж
0
Спасибо
Ответить
28 сентября 2016 в 15:07
Ответ для Вероника Диянова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Графиком функции является прямая. Задайте два значения x, получите y и проведите линию через 2 точки, думаю это не самая сложная задача. Далее либо по графику, либо аналитически решаем задачу. Аналитически: если надо найти точку удалённую от оси абсцис на 1, значит нужно подставить вместо y = 1.
8x + 15 · 1 + 10 = 0.
8x = ?25
x = ? = ? 3 = ? 3,125
Если построите график, то увидите, что это так.
Ответ: (1; ? 3,125)
0
Спасибо
Ответить
1 октября 2016 в 22:35
Ответ для Вероника Диянова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
(7/8; 0); (?27/8; 0).
? = = 1. => |8a + 10| = 17.
0
Спасибо
Ответить
6 сентября 2016 в 15:15
Николай Шамов
Профиль
Благодарили: 0
Сообщений: 1
Николай Шамов
Профиль
Благодарили: 0
Сообщений: 1
Вообщем, прошу помочь, проблема касется изображения на координатной оси объединение и пересечения.Т.е. допустим, задание «Изобразите на координатной оси числовые промежутики A и B, найдите их объединение и пересечение, если: A=[-3;4],B=[0;7). Я понимаю, что Объединение [-3;7)
Пересечение [0;4]
но не понимаю, как это изобразить это на координатной оси, прошу помощи
0
Спасибо
Ответить
19 сентября 2016 в 14:31
Ответ для Николай Шамов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Проще всего изобразить это цветными карандашами или ручками. Нарисовать на одной оси оба промежутка и выделив разными цветами объединение и пересечение.
0
Спасибо
Ответить
Для обозначения числами точного положения точки на плоскости
проведём две перпендикулярные координатные прямые (x) и (y),
которые пересекаются в начале отсчёта — точке (O).
Так мы задали на плоскости прямоугольную систему координат,
а плоскость стала координатной плоскостью.
Начало координат — точка (O) (точка пересечения прямых (x) и (y)),
оси координат — координатные прямые (x) и (y),
координатные углы — прямые углы, образованные при пересечении осей координат.
Координатные углы нумеруют против часовой стрелки:
Отметим в прямоугольной системе координат точку (M).
Проведём через точку (M) прямую, параллельную оси (y).
Прямая пересечёт ось (x) в некоторой точке, координата которой равна (-2).
Эту координату называют абсциссой точки (M).
Далее проведём через точку (M) прямую, параллельную оси (x). Прямая пересечёт ось (y) в некоторой точке, координата которой равна (3).
Эту координату называют ординатой точки (M).
Коротко пишем так: (M(x; y)).
Эту пару чисел называют координатами точки (M).
Абсциссу записываем на первое место, ординату — на второе место.
Имеем (M(-2; 3)).
Число (-2) называют абсциссой точки (M), а число (3) — ординатой точки (M).
Горизонтальную координатную прямую (x) называют осью абсцисс, или осью (x), а
вертикальную координатную прямую (y) — осью ординат, или осью (y).
Координатные углы ещё называют координатными четвертями. Рассмотрим координаты точки (M(x; y)) в разных четвертях и на осях:
в (1) четверти: (x>0; y>0);
во (2) четверти: (x<0; y>0);
в (3) четверти: (x<0; y<0);
в (4) четверти: (x>0; y<0);
на оси (x): координата (y=0), то есть (M(x; 0));
на оси (y): координата (x=0), то есть (M(0; y)).
Каждой точке на координатной плоскости соответствует пара чисел: её абсцисса и ордината — и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Для построения этой точки, требуется найти точку пересечения прямых (x=a) и (y=b).
Это будет точка (M(a; b)).
Содержание:
- § 1 Система координат: определение и способ построения
- § 2 Координатная ось и координатная плоскость
- § 3 Построение точки на плоскости
§ 1 Система координат: определение и способ построения
В этом уроке познакомимся с понятиями «система координат», «координатная плоскость», «оси координат», научимся строить точки на плоскости по координатам.
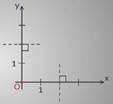
Возьмем координатную прямую х с началом координат точкой О, положительным направлением и единичным отрезком.
Через начало координат точку О координатной прямой х проведем еще одну координатную прямую y, перпендикулярную х, положительное направление зададим вверх, единичный отрезок такой же. Таким образом, мы построили систему координат.
Дадим определение:
Две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом координат каждой из них, образуют систему координат.
§ 2 Координатная ось и координатная плоскость
Прямые, которые образуют систему координат, называют координатными осями, каждая из которых имеет свое название: координатная прямая х – ось абсцисс, координатная прямая y – ось ординат.
Плоскость, на которой выбрана система координат, называется координатной плоскостью.
Описанная система координат называется прямоугольной. Часто ее называют декартовой системой координат в честь французского философа и математика Рене Декарта.
Каждая точка координатной плоскости имеет две координаты, которые можно определить, опустив из точки перпендикуляры на оси координат. Координаты точки на плоскости – это пара чисел, из которых первое число – абсцисса, второе число – ордината. Абсциссу показывает перпендикуляр к оси х, ординату – перпендикуляр к оси y.
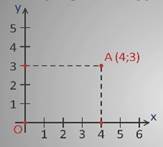
Отметим на координатной плоскости точку А, проведем из неё перпендикуляры к осям системы координат.
По перпендикуляру к оси абсцисс (ось х) определяем абсциссу точки А, она равна 4, ординату точки А – по перпендикуляру к оси ординат (ось у) – это 3. Координаты нашей точки 4 и 3. А (4;3). Таким образом, координаты можно найти для любой точки координатной плоскости.
§ 3 Построение точки на плоскости
А как построить точку на плоскости с заданными координатами, т.е. по координатам точки плоскости определить её положение? В данном случае действия выполняем в обратном порядке. На координатных осях находим точки соответствующие заданным координатам, через которые проводим прямые, перпендикулярные осям х и y. Точка пересечения перпендикуляров и будет искомой, т.е. точкой с заданными координатами.
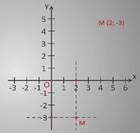
Выполним задание: построить на координатной плоскости точку М (2;-3).
Для этого на оси абсцисс находим точку с координатой 2, проводим через данную точку прямую перпендикулярную оси х. На оси ординат найдем точку с координатой -3, через нее проведем прямую перпендикулярную оси y. Точка пересечения перпендикулярных прямых и будет заданной точкой М.
А теперь рассмотрим несколько частных случаев.
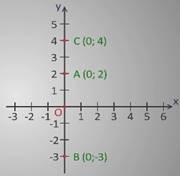
Отметим на координатной плоскости точки А (0; 2), В (0; -3), С (0; 4).
Абсциссы данных точек равны 0. На рисунке видно, что все точки находятся на оси ординат.
Следовательно, точки, абсциссы которых равны нулю, лежат на оси ординат.
Поменяем координаты данных точек местами.
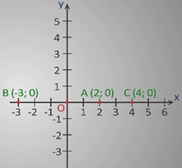
Получится А (2;0), В (-3;0) С (4; 0). В этом случае все ординаты равны 0 и точки находятся на оси абсцисс.
Значит, точки, ординаты которых равны нулю, лежат на оси абсцисс.
Разберем еще два случая.
На координатной плоскости отметим точки М (3; 2), N (3; -1), Р (3; -4).
Легко заметить, что все абсциссы точек одинаковые. Если эти точки соединить, получится прямая, параллельная оси ординат и перпендикулярная оси абсцисс.
Напрашивается вывод: точки, имеющие одну и ту же абсциссу, лежат на одной прямой, которая параллельна оси ординат и перпендикулярна оси абсцисс.
Если поменять координаты точек М, N, Р местами, то получится М (2; 3), N (-1; 3), Р (-4; 3). Одинаковыми станут ординаты точек. В данном случае, если эти точки соединить, получится прямая параллельная оси абсцисс и перпендикулярная оси ординат.
Таким образом, точки, имеющие одну и ту же ординату, лежат на одной прямой параллельной оси абсцисс и перпендикулярной оси ординат.
В этом уроке Вы познакомились с понятиями «система координат», «координатная плоскость», «оси координат — ось абсцисс и ось ординат». Узнали, как найти координаты точки на координатной плоскости и научились строить точки на плоскости по ее координатам.
Список использованной литературы:
- Математика. 6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//автор-составитель Л.А. Топилина. – Мнемозина, 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И.Зубарева, А.Г.Мордкович.- М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для общеобразовательных учреждений/Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др./по редакцией Г.В. Дорофеева, И.Ф. Шарыгина; Рос.акад.наук, Рос.акад.образования. — М.: «Просвещение», 2010
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru