Как найти на окружности удаленные точки

Найдите множество точек, удаленных от окружности x ^ 2 + y ^ 2 = 16 на расстояние , равное 3?

Геометрия | 10 — 11 классы

Найдите множество точек, удаленных от окружности x ^ 2 + y ^ 2 = 16 на расстояние , равное 3.

Т к центр этой окружности находится в точке (0 ; 0) и радиус равен 4, тоточки, удаленные от окружности x ^ 2 + y ^ 2 = 16 на расстояние , равное 3, лежат на окружностях с этим же центром и радиусом R = 4 + 3 = 7 и R = 4 — 3 = 1, т ена окружностяхx ^ 2 + y ^ 2 = 49 и x ^ 2 + y ^ 2 = 1

Рисунок простой, сделай сама.

Наибольшее и наименьшее расстояния от данной точки, расположенной внутри окружности, до точек окружности равны соответственно 20 см и 4 см?

Наибольшее и наименьшее расстояния от данной точки, расположенной внутри окружности, до точек окружности равны соответственно 20 см и 4 см.

Найдите радиус данной окружности.

Найдите геометрические места точек, удаленных на 0, 5 от окружности х² + у² — х + у — 0, 5 = 0?

Найдите геометрические места точек, удаленных на 0, 5 от окружности х² + у² — х + у — 0, 5 = 0.

К окружности радиуса 36 проведена касательная из точки, удаленной от центра на расстояние, равное 85?

К окружности радиуса 36 проведена касательная из точки, удаленной от центра на расстояние, равное 85.

Найдите длину касательной.

Даны неразвернутый угол АВС и отрезок PQ?

Даны неразвернутый угол АВС и отрезок PQ.

Что представляет собой множество всех точек, лежащих внутри данного угла и удаленных от прямой ВС на расстояние PQ.

Точка М лежит на отрезке АВ?

Точка М лежит на отрезке АВ.

На окружности с диаметром АВ взята точка С, удаленная от точек А, М и В на расстояния 20, 14 и 15 соответственно.

Найдите площадь треугольника ВМС.

Расстояние от центра окружности до прямой равно радиусу окружности?

Расстояние от центра окружности до прямой равно радиусу окружности.

Сколько окружность и прямая имеют общих точек?

Дана окружность с центром в точке О радиуса 3 см?

Дана окружность с центром в точке О радиуса 3 см.

Построить прямые, удаленные от центра окружности на расстоянии 2 см, 3 см, 5 см.

Сколько точек пересечения у окружности с этими прямыми?

Как доказать, что хорды, удаленные от центра окружности на равные расстояния, равны?

Как доказать, что хорды, удаленные от центра окружности на равные расстояния, равны?

Расстояние d от центра окружности до прямой меньше радиуса R этой окружности?

Расстояние d от центра окружности до прямой меньше радиуса R этой окружности.

Найдите наибольшее расстояние от точек данной окружности до прямой.

Расстояние между точками A и B равно 2?

Расстояние между точками A и B равно 2.

Найдите множество всех точек M , для которых AM ^ 2 + BM ^ 2 = 20.

На этой странице находится вопрос Найдите множество точек, удаленных от окружности x ^ 2 + y ^ 2 = 16 на расстояние , равное 3?. Здесь же – ответы на него, и похожие вопросы в категории Геометрия, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

Имеем трапецию АВСД. Из вершин В и С опустим перпендикуляры ВЕ и СК на АД. Из равных треугольников АВе или СКД находим высоту трапеции по Пифагору : ВЕ = √(СД² — ((АД — ВС) / 2)²) = √(5² — 3²) = √(25 — 9) = √16 = 4. Средняя линия равна (10 + 4) / ..

1) треугольник NOM — р / б Угол ONM = углу OMN = (180° — 64°) : 2 = 58° Угол NMP = 90° Угол OMP = 90° — 58° = 32°.

A = 3 см b = 16 см c = 12 см V — ? V = abc = 3 * 16 * 12 = 576 (см³) Ответ : 576 см³.

Формула объёма для куба с ребром «a» : V = a * a * a = a ^ 3.

У куба шесть равных граней. 1) Полная поверхность куба по формуле Sполн = 6 * S = 6 * a² — ответ 2) Объем куба по формуле V = a³ — ответ.

Т. к а║b значит накрест лежащие углы равны х = 70°.

Ахахахахах, угол АСВ уже найдет, я нашла остальные углы, . Выбирай какой надо, посмотри сам там он уже задан и равен 65 градусов, если что — то измениться , то напиши я решу.

Рассмотрим ∆АВМ и ∆DCM BM = CM, AM = CD(по условию), АВ = CD(противоположные стороны параллелограмма) ∆ABM = ∆DCM(по 3 признаку) значит угл. В = угл. С тк АВ / / CD, то углы В и С односторонние, а значит B + C = 180° тогда С = В = 180 : 2 = 90° A =..

FN, NM, EN, FM, EF. — вроде бы так.

Треугольник — часть плоскости, ограниченная трем точками, не лежащими на одной прямой. У него есть 3 вершины и 3 стороны.

Самостоятельная работа 7. Вариант 1. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите найти множество точек

Найдите множество точек, удаленных от окружности х 2 + у 2 = 16 на расстояние, равное 3.

Радиус окружности равен 4, это 2 окружности с тем же центром и равными 7 и 1. Ответ х 2 + у 2 = 49 и х 2 + у 2 = 1.

Привет. Запуталась при решении, нужна помощь знатоков.

Три прямые, проходящие через одну точку и не лежащие в одной ( Подробнее. )

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.

9.
Определите ряд, в котором в обоих словах пропущена одна и та же буква. Выпишите
эти слова, вставив пропущенную букву. ( Подробнее. )

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь ( Подробнее. )

Лекция 5. Метод геометрических множеств

Геометрическим множеством (ГМ) называется множество геометрических элементов (ГЭ), обладающих каким-либо общим геометрическим свойством.

5.1. Геометрические множества

Геометрические множества некоторых геометрических элементов

ГМ точек	ГМ прямых	ГМ плоскостей
1. Удаленных от заданной точки О на расстояние l
Сфера радиусом l с центром в точке О.	Совокупность прямых, касательных к сфере радиусом l с центром в точке О.	Совокупность плоскостей, касательных к сфере радиусом l с центром в точке О.
2. Удаленных от данной прямой m на расстояние l
Цилиндрическая поверхность радиусом l и осью m.	Совокупность прямых, касательных к поверхности цилиндра радиусом l и осью m, а также все образующие этой цилиндрической поверхности.	Совокупность плоскостей, касательных к поверхности цилиндра радиусом l и осью m.
3. Удаленных от данной плоскости σ на расстояние l
Две плоскости τ 1 и τ 2 //σ, расположенные по разные стороны от неё на расстоянии l
4. Равноудаленных от точек А и В
Все точки плоскости σ⊥АВ, проходящей через середину отрезка АВ.	Совокупность прямых, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.	Совокупность плоскостей, касательных к поверхностям сфер равного диаметра с центрами в точке А и В.
5. Равноудаленных от двух параллельных прямых
Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему.	Совокупность прямых, лежащих в плоскости, проходящей через сере-дину отрезка (расстояния между данными прямыми) и перпендикулярной ему.	Плоскость, проходящая через середину отрезка (расстояния между данными прямыми) и перпендикулярная ему, а также две плоскости, касательные к двум цилиндрическим поверхностям с осями – данными прямыми и равного диаметра.

5.2. Алгоритм решения задач методом геометрических множеств

1. 1. Условие задачи разбиваем на ряд простейших условий, каждому из которых должно отвечать определенное свойство искомого элемента (или элементов).

1. 1. Для каждого простейшего условия определяем удовлетворяющее ему геометрическое множество элементов.

1. 1. Находим общее решение задачи как некое геометрическое множество элементов, удовлетворяющих одновременно всем простейшим условиям. Оно представляет собой пересечение выбранных элементарных геометрических множеств.

1. Проводим анализ возможных решений, цель которого выявить когда, сколько и каких решений может быть в данной задаче в зависимости от взаимного положения заданных геометрических элементов, а, следовательно, связанных с ним геометрических множеств.

Упражнение

1. На заданной прямой m построить точку, удаленную от точки О на расстояние l (Рисунок 5.1).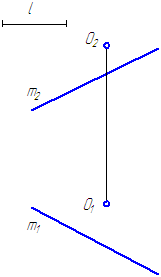

Рисунок 5.1
I. Геометрическое решение в пространстве

1. Искомые точки должны принадлежать прямой m, следовательно, решение по первому условию – любая точка на прямой.
2. Множество точек, удаленных от точки О на расстояние l образуют в пространстве сферу, с центром в точке О и радиусом равным l.
3. Общее решение задачи – точки, одновременно принадлежащие прямой m и сфере, то есть точки пересечения прямой m со сферой.

II. Графическое решение задачи (Рисунок 5.2).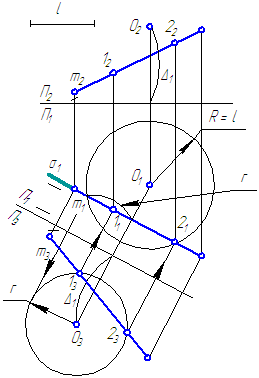

Рисунок 5.2
III. Анализ возможных решений (Рисунок 5.3).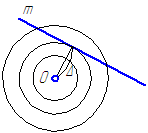

Рисунок 5.3

Обозначим Δ – расстояние от точки О до прямой m:

• l > Δ – прямая пересечет сферу в двух точках;
• l = Δ – m – касательная к сфере → одна точка;
• l Краткая запись построения

1. 1. Строим проекцию сферы с центром в точке О и радиусом l.

1. 1. Через прямую m проводим секущую плоскость, например, σ⊥π₁. Плоскость σ пересекает сферу, в сечении – окружность.
   2. Вводим ДПП π₃⊥π₁ и π₃//σ.

1. Строим на π₃ проекции прямой m и окружности сечения, определяем точки пересечения прямой с окружностью, которые являются искомыми.

Упражнение

2. В плоскости σ=ΔАВС через точку А провести прямую AD, удаленную от точки О на расстояние l (О∈σ) (Рисунок 5.4). Геометрическое решение в пространстве

1. Прямая AD, удаленная от точки О на расстояние l, является касательной к сфере радиусом R_сф = l с центром в точке О.
2. Прямая AD∈σ.

Плоскость σ пересекает сферу по окружности.
Искомая прямая AD – касательная к окружности сечения плоскости σ и сферы.
II. Графическое решение задачи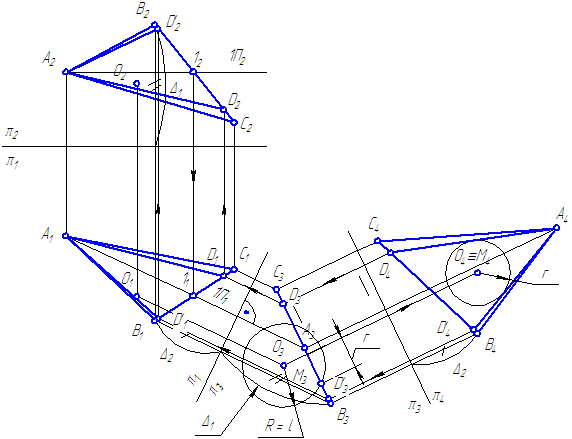

Рисунок 5.4
III. Анализ возможных решений
Обозначим Δ – расстояние от точки О до плоскости σ:

• l > Δ – плоскость пересечет сферу по окружности, → две прямые, проходящие через точку А и касательные к окружности сечения (если точка А вне окружности); если точка А на окружности сечения – одна прямая;если точка А внутри окружности сечения – решения нет;
• l = Δ – плоскость касается сферы → одна прямая, проходящая через точку А и точку касания; если точка А совпала с точкой касания → бесконечное множество прямых принадлежащих плоскости σ;
• l Краткая запись построения
  Находим истинную величину треугольника АВС, например, с помощью введения ДПП:

1. π₃⊥π₁ и π₃⊥σ.
2. π₄⊥π₃ и π₄//σ.
3. Строим окружность сечения σ со сферой. Строим касательные к этой окружности, проходящие через точку А.

5.3. Задачи для самостоятельной работы

1. Задана плоскость α=∆АВС и прямая m – общего положения. Определить угол между прямой m и плоскостью α. 2. Задана плоскость α=∆АВС и точка D вне плоскости. Повернуть точку D так, чтобы она совпала с плоскостью α. Ось вращения i⊥π₁.

Пусть дан отрезок А1В1,

точка А и окружность .

Найти точку В на окружности , удалённую от т. А на расстояние ,равное А1В1.

Для решения этого простого задания по геометрии , нужно просто внимательно прочесть условие и понять — что нужно сделать. Так как «пляшем » от т.А , то замеряем раствором циркуля отрезок А1В1 , переносим ножку циркуля в т.А и делаем засечку на окружности , и получим точку В , и АВ = А1В1 ,так как размах циркуля не менялся.

К сожалению и такое задачи ставят в тупик 6-классников.

Радиус окружности равен половине диаметра. Раствором циркуля, равным 7:2=3,5 см начертите окружность. Отметьте на ней т.А в любом месте. Расстояние между двумя точками равно длине отрезка, который их соединяет. 

По линейке разведите ножки циркуля на 4 см и этим раствором от т.А отметьте на окружности по обе стороны точки В и С . 

АВ=АС=4 см

What about this?

1. Calculate A-B.
   We now have a vector pointing from the center of the circle towards A (if B is the origin, skip this and just consider point A a vector).
2. Normalize.
   Now we have a well defined length (the length is 1)
3. If the circle is not of unit radius, multiply by radius. If it is unit radius, skip this.
   Now we have the correct length.
4. Invert sign (can be done in one step with 3., just multiply with the negative radius)
   Now our vector points in the correct direction.
5. Add B (if B is the origin, skip this).
   Now our vector is offset correctly so its endpoint is the point we want.

(Alternatively, you could calculate B-A to save the negation, but then you have to do one more operation to offset the origin correctly.)

By the way, it works the same in 3D, except the circle would be a sphere, and the vectors would have 3 components (or 4, if you use homogenous coords, in this case remember — for correctness — setting w to 0 when «turning points into vectors» and to 1 at the end when making a point from the vector).

EDIT:
(in reply of pseudocode)
Assuming you have a vec2 class which is a struct of two float numbers with operators for vector subtraction and scalar multiplicaion (pretty trivial, around a dozen lines of code) and a function normalize which needs to be no more than a shorthand for multiplying with inv_sqrt(x*x+y*y), the pseudocode (my pseudocode here is something like a C++/GLSL mix) could look something like this:

vec2 most_distant_on_circle(vec2 const& B, float r, vec2 const& A)
{
    vec2 P(A - B);
    normalize(P);
    return -r * P + B;
}

Most math libraries that you’d use should have all of these functions and types built-in. HLSL and GLSL have them as first type primitives and intrinsic functions. Some GPUs even have a dedicated normalize instruction.

Категория: ГДЗ Математика учебник 6 класс Мерзляк, Полонский, Якир